Motor Proteins and Molecular Motors: How to Operate Machines at Nanoscale

Abstract

Several classes of biological molecules that transform chemical energy into mechanical work are known as motor proteins or molecular motors. These nanometer-sized machines operate in noisy stochastic isothermal environment, strongly supporting fundamental cellular processes such as transfer of genetic information, transport, organization and functioning. In last two decades motor proteins have become a subject of intense research efforts that were aimed to uncover fundamental principles and mechanisms of molecular motors dynamics. In this review, we critically discuss a recent progress in experimental and theoretical studies on motor proteins. Our focus is on analyzing fundamental concepts and ideas that have been utilized for explaining non-equilibrium nature and mechanisms of molecular motors.

1. Introduction

Biological cells are very complex dynamic and heterogeneous systems that operate under non-equilibrium conditions, supporting a large number of biochemical and biophysical processes that include gene replication, transcription, translation, cellular transport, cell motility and cell division [1–4]. An important role in sustaining cellular functions is played by several classes of active enzymatic molecules generally called motor proteins or molecular motors [1–10, 16, 17]. Despite significant research efforts in recent years, fundamental mechanisms of their functioning remain not fully understood [5,8–10].

There are many different types of molecular motors that are expressed in living cells [1, 2, 5, 7]. First motor proteins, myosins, which are important for muscle contraction, were discovered in 1940s [1,2,5,11]. Another class of motor proteins, dyneins, that are responsible for propelling sperm, bacteria and other cells, were first reported in 1963 [12]. Surprisingly, the most experimentally studied kinesin motor proteins, which support cellular transport processes, were first purified and analyzed only in 1985 [13–15]. A different type of rotating molecular motors, ATP synthase proteins, have been fully analyzed in early 1990s [18]. Since then many classes of molecular motors have been discovered and classified, and new motor protein systems are constantly added [10]. However, it is widely believed that all these nanoscale machines convert chemical energy into mechanical work probably using similar principles, although it is still not clear if there is one mechanism or several different, and in most cases the microscopic details of underlying processes are still not clear [8, 9]. Motor proteins typically consume a chemical energy, which can be transformed into mechanical work, by accelerating various biochemical reactions such as the hydrolysis of ATP (adenosine triphosphate) or related compounds, and polymerization processes in DNA, RNA and other protein molecules. During these catalytic processes, a fraction of the released chemical energy is somehow channeled by molecular motors into the mechanical motion. Understanding the microscopic details of these processes is one of the most important fundamental scientific problem.

Analyzing dynamics of motor proteins, one can clearly view them as tiny engines that consume fuel (energy of biochemical reactions) to produce a mechanical work useful for their biological functions [4,5]. However, their working conditions are very different from the environment of macroscopic engines: motor proteins operate in stochastic non-equilibrium isothermal systems that are also crowded by a large number of other chemically active biological molecules. At the same time, these molecular motors display a very efficient and robust performance, and any major malfunction in them will most probably lead to a cell death. Significant advances in experimental studies of motor proteins dynamics and their functions have been achieved [19–69]. Application of advanced spectroscopic and microscopic methods allowed researchers to visualize and manipulate motor proteins with a single-molecule precision and high temporal resolutions, providing an important information on how molecular motors operate. This success led to a development of multiple theoretical approaches that discussed different aspects of motor proteins dynamics [8,10,70–114].

In this review I present a brief progress report based on some recent experimental and theoretical investigations that provide important information on fundamental mechanism governing dynamic behavior and functioning of motor proteins. It should be noted that there are several excellent reviews on molecular motors that appeared in recent years [7–10,16,17]. However, most of them discuss only biological or experimental aspects of motor proteins motility, while my intention is to concentrate more on main theoretical concepts and ideas in the field. As a result, I will not be able to cover all subjects related to molecular motors, but rather the goal of this review is to present an emerging unified theoretical picture of motor proteins dynamics consistent with basic laws of Chemistry and Physics. Artificial molecular motors have also been developed in recent years as a way of mimicking and copying the useful properties of highly efficient, versatile and robust biological motor proteins [115–119]. There is a lot of promise in the application of these synthetic molecular motors for fundamental scientific and technological purposes. However, they are still not well investigated and even much less is understood about mechanisms that control them. In this review I will discuss only the advances and developments in experimental and theoretical studies of biological motor proteins. Furthermore, this report on molecular motors represents obviously a subjective theoretician's view of the field which might not always agree with other existing ideas surrounding motor proteins dynamics.

2. Classifications of Motor Proteins

Motor proteins usually become active enzymes after binding to some static or dynamic cellular structures such as cytoskeleton protein filaments, cellular membranes, nucleic acids or other protein complexes. This observation allows us to divide motors in several groups:

1. Cytoskeleton filaments motor proteins, such as dyneins, kinesins and myosins, start to work by associating to and moving along the cytoskeleton filaments (actin filaments and microtubules). These motor proteins utilize the energy of hydrolysis of ATP (adenosine triphosphate) or related compounds, and they are the main players in cellular transport processes. Cytoskeleton-bound motor proteins are the most studied systems from dynamic and structural point of view, and our current understanding of mechanisms of energy transduction in molecular motors comes mainly from experiments on kinesin and myosin motor proteins [5,8–10,17].

2. Nucleic acids motor proteins, such as polymerases, topoisomerases, gyrases, helicases and many others, usually function by associating with DNA and RNA molecules, and the source of chemical energy for these motors is the polymerization reactions of nucleic acids, synthesis of proteins and/or ATP hydrolysis. These motor proteins are important for maintenance and processing of genetic information, as well as for the synthesis of all protein molecules in cells [10, 40, 120, 121]. These enzymes are currently in the center of intense experimental investigations, however the available information on how they work is still quite limited, especially in comparison with cytoskeleton motor proteins, most probably due to a very high complexity of biological systems.

3. Rotary motor proteins, such as bacterial flagella (essential for bacterial migration) and F₀F₁-ATP synthase (which is used to synthesize ATP molecules, the main source of energy in biological systems, in mitochondria), are usually bound to cellular membranes. They are involved in circular motions in the membrane or outside of the cell, although, to be more exact, only parts of the molecule outside of the membrane usually move. Some of rotary motors utilize the electrochemical energy of various ion gradients that exist across cellular membranes. These molecular motors are very important for cell motility and chemotaxis ( i.e., for the cellular motion in the direction of available nutrients) [27, 49, 50, 122, 123], but mechanisms of these rotary motor proteins are understood much less in comparison with linear motor proteins.

Most of experimental and theoretical studies concentrate on molecular motors that transform a chemical energy into linear motion. These proteins typically translocate along the protein filaments and/or nucleic acids in effectively 1D fashion which helps to quantify their dynamic properties [5,8,10]. The properties of rotary molecules motors, which are generally more complex systems, are not so well quantified. However, one could argue that mechanisms of energy conversion in rotary motor proteins probably are similar to linear motor proteins [8]. Thus, theoretical ideas developed for linear motor proteins can be easily extended to rotary molecular motors, although one still has to be careful in application of these methods [8]. For this reason, in this review we concentrate on molecular motors involved in the linear translocation.

Linear molecular motors could also be divided in two groups depending on how many enzymatic cycles can be performed for each encounter with the cytoskeleton filament or nucleic acid. There are several classes of motor proteins that are strong enough to function as single independent species, similarly to train locomotives or heavy tracks on highways. They translocate along cytoskeleton filaments or nucleic acids in preferred directions by repeatedly hydrolyzing ATP molecules or polymerizing DNA, RNA or other protein molecules and taking hundreds of discrete steps before finally dissociating. These motor proteins are called processive molecular motors. The most known examples include kinesin and dynein motor proteins that move in opposite directions along the microtubule filaments. Similarly, myosins V and VI motor proteins translocate in opposite directions along the actin filaments. RNA and DNA polymerases move with a high fidelity long distances along the DNA molecules. It is important to note here that protein filaments, as well as nucleic acids, can be viewed as polar tracks for motor proteins, effectively breaking the symmetry and specifying the preferred direction of the motors motion. This directionality of molecular motors is critically important for their biological functions. In simple terms, different cellular vesicles and organelles must be transported fast in all directions in the cell and the versatile motor proteins are able to do it.

There are other motor proteins, most notably the muscle myosins [5], that function in cells only via working together in large groups. However, details of cooperative mechanisms of these non-processive molecular motors currently are much less understood. Such non-processive motors typically make only one or few steps before detaching from their tracks. It is widely believed that the specific processivity of motor proteins is closely related to their structure [10,17,124,125]. Non-processive molecular motors are often monomers, while processive motors mostly exist in multi-domain dimeric or oligomeric forms [3,5]. It is frequently argued that these structural properties of processive motors explain why these motor proteins could stay attached to the filamentous track for long times while performing their functions. For active oligomeric motor proteins the probability that all motor heads (where enzymatic reactions are taking place) dissociate from the track simultaneously is much lower than the probability for a monomer molecular motor to detach. In nucleic motor proteins the increased processivity is frequently due to non-motor domains of the molecules that remain attached to the nucleic acid track in the “clamp-like” fashion, keeping the catalytic domains of the motor close to the nucleic acid for significant amount of time.

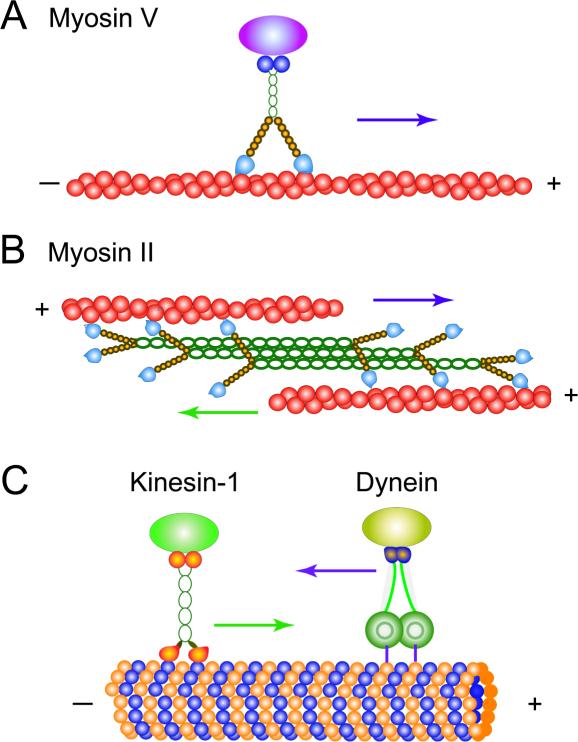
All motor proteins have a multi-domain structure to support their successful functioning in the complex cellular environment - see Fig. 1. The regions of the molecule where biochemical reactions are catalyzed are known as motor domains. There are also domains that responsible for binding to cellular cargoes, as well as the regions that provide necessary mechanical flexibility and chemical stability. It is interesting to note that for some motor proteins various domains might strongly interact with each other, modifying their individual enzymatic activities. For example, experiments indicate that for some kinesins and myosins partial unfolding of cargo-binding domain might completely inhibit the catalytic activities of the motor head domains [126–128]. In other words, these nanoscale trucks move only when there is an available load, and there is little futile consumption of the fuel from the cellular point of view. Full structural information is naturally very important for understanding microscopic details of motor proteins functioning.

Figure 1.

Schematic view of most important linearly translocating motor proteins. A) Dimeric Myosin V motor proteins step unidirectionally along actin cytoskeleton filaments. B) A group of monomeric myosin-II motor proteins combined in the filament can move together along several actin filaments. C) Conventional kinesin motor proteins translocate along the microtubules in the positive direction, while the dynein motors step along the microtubules in the opposite direction.

3. Experimental Investigations

Motor proteins have been investigated by a variety of experimental methods that provide a complimentary information on their mechanisms. Bulk biochemical experiments have measured rates of chemical reactions associated with motor proteins activity [28, 32, 129–132]. The application of well-established chemical-kinetic methods that include stopped flow, isotope exchange, fluorescent labeling and temperature quenching, has shown that motor proteins catalytic activities involve a complex network of biochemical states and conformations [129,131], although for many myosins and kinesins motor proteins one or few dominating biochemical pathways related to ATP hydrolysis have been identified [28,32,64,129,130]. But the problem with bulk chemical experiments is that average properties of large number of molecular motors (both active and inactive) are measured, complicating the determination of mechanisms of motility at the single-molecule level. Structural information has been obtained by utilizing x-ray crystallography and cryomicroscopy methods [5, 26, 133, 134]. These experiments provide images of various biochemical states of single molecular motors with atomic-scale resolutions. However, it is not clear how realistically these measurements describe motor proteins activity since in many cases experimental conditions differ significantly from the cellular conditions. In addition, these experiments probe only static properties, while the many intriguing questions are related to dynamics of motor proteins.

3.1. Single-Molecule Experimental Methods

The largest fraction of information concerning microscopic mechanisms of motor proteins came from single-molecule experimental techniques that have been developed in the last 20 years [5, 8, 9, 135]. These methods, including optical-trap and magnetic tweezers spectroscopy, Förster resonance energy transfer (FRET), single-molecule AFM (atomic force microscopy), fluorescent labeling and super-resolution spectroscopy, have allowed to observe and to modify the activity of individual motor protein molecules with unprecedented spatial and temporal resolution [19, 20, 22, 24–27, 29–31, 33–53, 55–66], providing powerful tools for investigating dynamics of molecular motors. The latest advances in single-molecule experimental methods and their applications have been described in detail in several recent reviews [9, 135–137], so here I will present only a brief discussion of several techniques especially important for studying molecular motors.

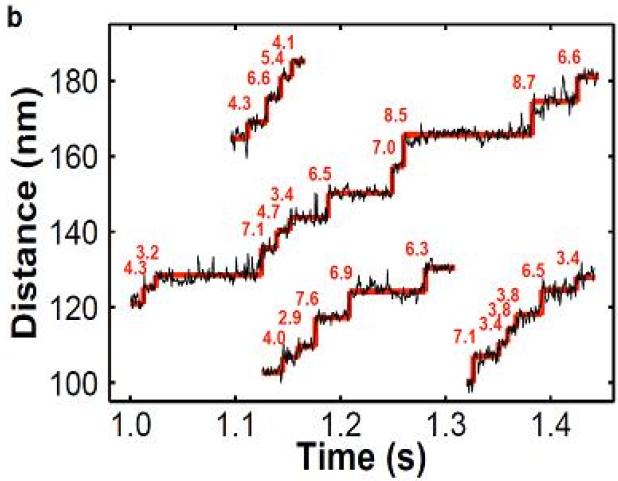
Optical-trap spectroscopy is one of the most powerful single-molecule experimental methods that have been widely applied for studying dynamic properties of different classes of molecular motors [24,25,30,33–38,42,44,48,52,57,60,63,64,66]. This approach uses a laser beam to monitor the displacements of a bead to which a single motor protein molecule is chemically attached [5,22,25,30,85,136,137]. The bead experiences a trapping force that pushes it closer to the focus region of the non-uniform laser field, while the connected motor protein drags the bead in the direction of its motion along the cellular track [5]. The effective potential of interactions created by optical tweezers setup is very close to a harmonic potential and it can be calibrated with a high precision. The bead motion can be visualized and monitored with a high precision, allowing to quantify dynamic properties of motor proteins. This experimental method measures nanometer displacements and piconewton forces, which is very appropriate for studying mechanochemical couplings in motor protein systems [9]. The example of typical particle trajectories observed in optical-trap spectroscopic measurements is presented in Fig. 2. The original setups have been also modified to include force clamps via the feedback control and to add vectorial forces (parallel to the filament tracks) that allowed to measure long runs of molecular motors at constant external forces [136,137]. It has been argued that the spatial resolution of improved optical-trap systems could reach ~1 nm, while conformational transitions lasting not less than ~100 μs could also be successfully resolved [9,137]. Another advantage of the optical tweezers is the ability to be coupled with other methods such as fluorescent labeling approaches [9]. Thus, optical trapping is one of the most successful single-molecule methods in uncovering dynamic properties of motor proteins in in vitro systems. However, the method is very difficult to apply for studying dynamic processes in live cells due to heterogeneous cellular environment and complex geometry of the experimental setup [9].

Figure 2.

Typical particle trajectories obtained in optical-trap spectrometry experiments. In this case, dynamics of two-kinesins assemblies at low ATP concentration to visualize discrete steps is measured. Note that observed steps sizes in many cases is a fraction of the single kinesin step size d = 8.2 nm, as expected since only one motor molecule can step at the given time. A courtesy of M.R. Diehl.

A closely related to optical-trap spectrometry is method known as magnetic tweezers. It utilizes the magnetic field for manipulating single molecules [40,45,137,138]. In these experiments the motor protein molecule is simultaneously chemically bound to the surface and to the magnetic bead. Tracking the vertical position of the bead as well as the lateral (parallel to the surface) fluctuations allows to calibrate the force acting on the bead via the equipartition theorem. One of the biggest advantages of magnetic tweezers is the ability to apply relatively large torques (up to ~1000 pN nm^–1) [137, 138]. It makes this method especially powerful for investigating nucleic acids motor proteins, such as topoisomerases, helicases, polymerases, gyrases and others, for which rotational degrees of freedom are critically important for the proper functioning [40, 45, 137–139]. These DNA and RNA bound molecular motors must unzip, untangle, or remove topological defects during their motion, and it cannot be accomplished without the rotation. The method has been successfully used to analyze many nucleic acids motor proteins [40,139]. However, the magnetic tweezers method has a low temporal resolution limiting its application to slow dynamic processes associated with molecular motors [137].

Light microscopy plays a very important role in clarifying structural and dynamic properties of motor proteins [9, 136, 137]. In typical experiments fluorescent dyes are directly attached to enzyme molecules, which allows to localize and track single molecular motors in a microscope with a high precision. However, there is a fundamental barrier in spatial resolution due to diffraction that limits the size of the object that can be observed by the wavelength of the light used to interrogate the system [140–142]. For microscopy methods currently utilized it means that the objects smaller than ~100 nm cannot be clearly observed, which is far larger than the sizes of most motor proteins [140–142]. This problem stimulated significant efforts to push the resolution below the diffraction limit that resulted in development of several successful experimental methods, generally known as a super-resolution spectroscopy [140–142].

There are 3 main super-resolution techniques that currently are used to a large degree in studies of biological systems: structured illumination microscopy (SIM), stimulated emission depletion (STED) and single-molecule localization and composition methods as realized in photoactivated localization microscopy (PALM) and in stochastic optical reconstruction microscopy (STORM) [140–142]. In SIM experiments a biological sample is projected with a fine pattern of stripes that are varied in space and time. After processing all images and analyzing the signal variations, a high-resolution view of the studied object can be obtained. However, the resolution improvement is limited and the best method of SIM can only visualize objects larger than ~50 nm, while the temporal resolution is getting low. Another popular super-resolution method, STED, utilizes a second doughnut-shaped laser beam that stimulates the deactivation of the excited fluorophores back into the ground state, except for the central hole area [140–142]. Thus STED effectively switches off fluorophores at the periphery of the studied object, significantly increasing the spatial resolution (up to 10-20 nm). The disadvantage of this method is a limited choice of appropriate fluorophores groups and difficulty in developing multi-color experiments that use fluorophores with different wavelengths. A different approach is exploited in super-resolution PALM/STORM methods where the idea that the increasing number of photons emitted from the source allows to localize the center of mass of the image with a high precision is applied [140–142]. In these experiments fluorophores are randomly switched on and off, and analysis of images collected at different times leads to improved spatial resolutions (~20-30 nm) in many biological systems. Again, the drawback of these methods is a special choice of the fluorophores groups and low temporal resolution. Methods related to PALM/STORM approach have been successfully applied for tracking different motor proteins in vivo and in vitro [9,39,46,143–145].

Various single-molecule methods have reliably measured many structural, biochemical and dynamic properties of molecular motors. It has been shown for conventional kinesins that these processive motor proteins move along a single protofilament in the plus direction of the microtubule with speeds up to 1 μm/s and making at average around a hundred steps (each of the size d = 8.2 nm) before detaching into the solution [20, 22, 23, 25, 30]. It is also known that chemical cycle of these motor proteins are tightly coupled to the mechanical motion (1 ATP molecule is consumed to make 1 forward step), and to stop these motors one has to exert the force of the order 7-8 pN, which is known as a stall force [23, 25, 30]. Cytoplasmic dynein motor proteins move along microtubules in the opposite direction with the same step sizes and probably exerting smaller forces, although these observations are still controversial [52, 53, 146]. Another well-studied class of processive motor proteins, myosins V, hop along actin cytoskeleton filaments with d = 36 nm steps and stall forces of up to 2-3 pN. Single-molecule particle-tracking methods clearly prove that kinesins, myosins and dyneins utilize a hand-over-hand mechanism in their motion by alternating leading and trailing positions of their motor heads [38, 39, 46, 147]. Single-molecule experiments explicitly determined the responses of various motor proteins to external forces via measuring the force-velocity curves [9, 25, 30, 42, 54, 146]. These experiments also measured the fluctuations of each motor protein during their motion along linear tracks via a so-called randomness parameter [8, 30, 148]. One of the most important fundamental observations obtained via single-molecule experimental methods is the fact that all associated chemical and mechanical transitions in motor proteins are fully reversible [9,48,67].

4. Theoretical Studies

4.1. General Remarks

Experimental studies provided a significant amount of quantitative information that stimulated strong theoretical discussions on mechanisms of motor proteins functioning [5,8,10,70,72,87,88,95,103,110,148]. The main goal of theoretical models for molecular motors is to explain coupling between biochemical transitions and mechanical motions in order to understand the energy conversion at the microscopic level. It is known that all chemical processes can proceed in both directions, i.e., they are reversible, although available experimental data might not provide a direct evidence for this reversibility. At given experimental conditions backward transitions could be very slow and not observable during the limited time of the experimental measurement. However, for molecular motors the reversibility of involved chemical reactions cannot be neglected since it might lead to unphysical conclusions and wrong assumptions about the mechanisms [8, 48, 75, 92]. From the chemical point of view, motor proteins are catalytic molecules that, by definition, accelerate both forward and backward chemical reactions. This observation suggests that molecular motors which help to hydrolyze ATP when moving forward at one set of conditions could also accelerate the synthesis of ATP at another conditions. This conclusion has been experimentally shown for F₀F₁ ATP synthase rotary motors [45, 50] and for some other kinesin motor proteins [152,153]. It will be impossible to explain fully mechanisms of molecular motors without properly taking into account the reversibility of associated biochemical processes. From theoretical point of view, it is also important to note that although ATP hydrolysis is a complex biochemical process that involves multiple reaction steps, often a single transition can limit progression through the enzymatic cycle.

A large number of processive motor proteins, which are most studied experimentally, typically function in cells by moving in a linear fashion along the cytoskeleton proteins such as actin filaments and microtubules [1, 3, 5]. Because of the polymeric structure of these filaments the dynamics of molecular motors can be viewed as effectively one-dimensional periodic biased motion [8, 10, 81]. All existing theoretical approaches adopt this view, although the implementation of this picture is rather different. In the so-called continuum ratchet models [8, 10, 72, 87, 88, 95] the motion of motor proteins along some continuum potentials is assumed. A different approach argues that the motion of motor proteins can be described by a network of discrete stochastic transitions between specific biochemical states with variable spatial positions [8].

It is important to note that to develop a successful theoretical framework for describing motor proteins one has to follow several rules. Theoretical models should take into account the symmetries of the system such as periodic structure, polarity and chirality of molecular motors tracks. They also cannot violate basic laws of Physics and Chemistry. A successful theoretical method should also provide a reasonable quantitative description of available experimental observations that can shed the light on microscopic mechanisms of underlying processes, as well as predictions that can be tested in future experiments. These arguments present a set of criteria that should be used in evaluating the applicability of different theoretical approaches for analyzing motor proteins dynamics. Unfortunately, many proposed theoretical models do not satisfy these conditions and their results cannot be fully trusted [8].

4.2. Continuum Ratchet Potentials Methods

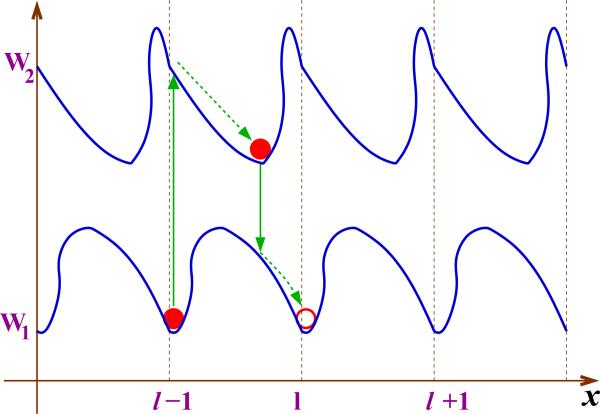
In this continuum method a molecular motor is viewed as a particle that moves along several spatially parallel, periodic but generally asymmetric free-energy potentials as shown in Fig. 3 [8,10,71–73,81,87,88,95]. Different potential surfaces are the result of interactions of motor proteins with the filaments, fuel molecules (ATP) and hydrolysis products in different biochemical states, and the molecular motor can stochastically switch between these states due to the released chemical energy. At each free-energy potential surface the molecule mainly diffuses in the direction of the local minimum. The sustained unidirectional motion of the particle requires a constant supply of the chemical energy that underlies the non-equilibrium nature of molecular motors dynamics. No net motion can be observed at equilibrium conditions. One can introduce a function P_i(x, t) that defines the probability density for the motor protein to be found at location x at time t at the potential surface W_i(x): see Fig. 3. The temporal evolution of the system can be described by a set of Fokker-Planck equations with source terms [10,72,88,95],

$$\frac{\partial P_i(x,t)}{\partial t}+\frac{\partial J_i}{\partial x}=\sum _j{u}_{ji}{P}_j(x,t)-\sum _j{u}_{ij}{P}_i(x,t),$$ (1)

where u_ij are transition rates between states i and j. The particle current has contributions from diffusion, from the interaction potential and from the action of possible external fields [72],

$$J_i={\mu }_i\left[-k_{B}T\frac{\partial P_i(x,t)}{\partial x}-P_i(x,t)\frac{\partial W_i\left(x\right)}{\partial x}-P_i(x,t)\frac{\partial W_{ext}\left(x\right)}{\partial x}\right],$$ (2)

with μ_i describing a mobility of the molecular motor in the state i. These equations in principle can be solved if potential functions are known. Several simple cases have been analyzed [72].

Figure 3.

A schematic representation of the motion of molecular motors in continuum thermal ratchet models. The simplest situation with two periodic asymmetric potentials is shown. Solid vertical lines correspond to stochastic transitions driven by chemical reactions, e.g., ATP hydrolysis. Dashed arrow lines describe the diffusional motion along each potential surface.

These chemically-driven ratchets models [72,88] are also known as Markov-Fokker-Planck models [95]. They provide a simple and consistent description of the motor protein's dynamics and mechanochemical coupling with relatively small number of parameters. Continuum models are well suited for mathematical treatments using established analytical and numerical tools. The ratchets models are also a starting point of fundamental studies on the nature of non-equilibrium phenomena in molecular motors [154, 155]. However, there are several properties of these continuum models that complicate their application for modeling molecular motors dynamics. With the exception of a few oversimplified and unrealistic potential surfaces, general analytical results cannot be obtained. For most situations numerical calculations should be performed, but they are typically also quite demanding. Furthermore, it is almost impossible to derive the realistic potentials from the available structural information on motor proteins, and approximations must be employed in the computation of dynamic properties of molecular motors. In addition, ratchet models are not very flexible in analyzing systems with complex biochemical networks. As a result, it is hard to estimate the reliability and applicability of ratchet models for uncovering mechanisms of real motor proteins. This analysis suggests also that continuum models can be reasonable utilized now only for description of some qualitative features of molecular motors dynamics as well as for discussing general fundamental features of non-equilibrium systems [8, 154]. Despite this relatively unoptimistic conclusion, it can be argued that the increased amount and quality of structural information and improving the computational power of full atomistic simulations should make this continuum approach much more valuable and attractive for motor proteins in the future.

4.3. Discrete-State Stochastic Models

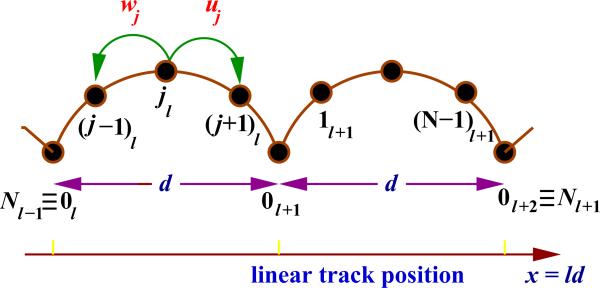
The catalytic activities of motor proteins involve a variety of biochemical reactions. Stimulated by importance of these chemical processes in relation to dynamics of molecular motors a different theoretical approach, based on discrete-state stochastic models of traditional chemical kinetics, has been developed [8,10,77–80]. It argues that the motion of molecular motors can be described as a network of chemical transitions between discrete biochemical states with variable spatial positions. In the simplest linear sequential model, as shown in Fig. 4, it is assumed that during the enzymatic cycle the motor protein moves from the binding site l on the filament to the identical binding site l+1 via a sequence of N intermediate biochemical states that might have different spatial locations. Two identical binding sites are separated by a distance d which corresponds to the step size of the molecular motor. It is known that for kinesin and dynein motor proteins translocating along microtubules in opposite directions d is equal to 8.2 nm, while for myosins V that proceed along actin filaments the step is larger, d ≈ 36 nm. The motor protein in the mechanochemical state j_l (j = 0, 1, · · · , N –1) can step forward to the state (j + 1)_l with a rate u_j, or it might move backward to the state (j – 1)_l with a rate w_j. Discrete states j_l describe different stages of ATP hydrolysis catalyzed by the action of the motor protein molecules. For example, one might assume that 0_l corresponds to the state when the motor protein is strongly bound to the molecular track, awaiting the arrival of the ATP molecule. In these discrete-state models reverse transitions are explicitly taken into account, in agreement with fundamental concepts of Physics and Chemistry, and supporting the experimental observations on backward steps [8,48,64,67,68,148].

Figure 4.

A schematic view of a linear sequential discrete-state stochastic model for analyzing dynamics of single molecular motors. Transition rates u_j and w_j describe forward and backward rates for the motor protein to step out of the site j. The distance between neighboring binding sites is d.

In discrete-state stochastic models dynamics of molecular motors can be described by analyzing a function P_j(l, t) which is a probability to find the molecule in the state j_l at time t. Its temporal evolution is governed by Master equations [8],

$$\frac{d{P}_j(l,t)}{dt}=u_{j-1}{P}_{j-1}(l,t)+w_{j+1}{P}_{j+1}(l,t)-(u_j+w_j)P_j(l,t).$$ (3)

These expressions can be easily understood since they are kinetic equations for motor proteins related biochemical transitions, and they reflect the conservation of the probability to find the motor protein molecule in the given state. It can be shown also that the same equations also describe a motion of a single random walker on a periodic (with a period of size N) one-dimensional infinite lattice [8]. Then this mapping allows one to utilize the mathematical formalism, developed by Derrida in 1983 [149], to obtain exact and explicit expressions for all dynamic properties, such as the mean asymptotic large-time velocity

$$V=V\left(\{u_j,w_j\}\right)=\underset{t\to \infty }{\lim }\frac{d\langle x\left(t\right)\rangle }{dt},$$ (4)

and the mean dispersion (or effective diffusion constant)

$$D=D\left(\{u_j,w_j\}\right)=\frac{1}{2}\underset{t\to \infty }{\lim }\frac{d}{dt}[\langle x^2\left(t\right)\rangle -{\langle x\left(t\right)\rangle }^2].$$ (5)

Here x(t) defines a position of the molecular motor on linear track at time t. These expressions directly connect transition rates u_j and w_j, that can be obtained independently from bulk chemical kinetic experiments, with dynamic properties (V and D) of motor proteins measured in single-molecule experiments. This is a significant advantage in comparison with the continuum ratchet approach since the input parameters in discrete-state models are independently measured experimental quantities [8]. For the simplest model with N = 2 states this theoretical approach gives the following expressions for the mean velocity and dispersion [8,86]:

$$V=d\frac{u_0{u}_1-w_0{w}_1}{u_0+u_1+w_0+w_1},D=\frac{d^2}{2}\frac{(u_0{u}_1+w_0{w}_1)-2{(V∕d)}^2}{u_0+u_1+w_0+w_1}.$$ (6)

The big advantage of the discrete stochastic method is the ability to obtain analytical expressions for any dynamic property of motor proteins systems. The molecular motor catalyzes hydrolysis of ATP or related compounds and it utilizes part of the released chemical energy to exert a force in the direction of its motion. This driving force can be explicitly estimated as outlined in the discrete-state stochastic approach [75,76]. It was shown that for the simplest sequential model (see Fig. 4) the exerting force is equal to

$$F_S=\frac{k_{B}T}{d}\ln \prod _{j=0}^{N-1}\frac{u_j}{w_j}.$$ (7)

This simple result can be easily understood by using standard thermodynamic arguments. One can define a function $K={\prod }_{j=0}^{N-1}\left(\frac{u_j}{w_j}\right)$ and it can be shown that it corresponds to an effective equilibrium constant for the process of moving the motor protein molecule from the binding site l to the binding site l + 1. Then, the expression ΔG₀ = –k_BT ln K gives the free energy released in the system when the protein molecule moves between two neighboring binding sites. This difference is a result of hydrolyzing 1 ATP molecule after making one forward step via N intermediate transitions. All this free energy might be converted into mechanical work to move the motor protein by the step size d, thus exerting the force equal to F_S = ΔG₀/d. This is a stall force since it is equal to the external force needed to stop the molecular motor. For linear sequential models (see Fig. 4) the stalling condition corresponds to equilibrium, while for more complex biochemical networks this might not be the case. It should be noted that neglecting any of the backward transitions, i.e., assuming that even one specific rate w_j = 0, leads to the unphysical prediction of the diverging stall force and the infinite free-energy change. This argument clearly shows that theoretical models that assume irreversible transitions cannot be reliably utilized for understanding fundamental mechanisms of motor proteins [8].

Molecular motors in cellular environment are subjected to many external forces and fields. Single-molecule experiments are able to impose a measured force F directly to single motor protein molecules [5, 148, 150, 151]. In discrete-state stochastic models the effect of external forces can be easily incorporated by introducing load distribution factors, ${\theta }_j^{\pm }$ [8,75,76]. These parameters quantitatively describe how the work performed by external forces is distributed between various biochemical transitions. It also provides a measure of the change in the free-energy landscape of the system under the influence of the external field. Assuming that the external force acts parallel to the filament, a single molecular motor produces a work F d during one enzymatic cycle. It can be shown using reaction-rate theories [8] that transition rates are modified under the effect of external forces in the following way,

$$u_j\left(F\right)=u_j\left(0\right)\exp (-{\theta }_j^{+}Fd∕k_{B}T),w_j\left(F\right)=w_j\left(0\right)\exp ({\theta }_j^{-}Fd∕k_{B}T),$$ (8)

with the additional requirement that

$$\sum _{j=0}^{N-1}({\theta }_j^{+}+{\theta }_j^{-})=1.$$ (9)

It also should be mentioned that the products ${\theta }_j^{\pm }d$ correspond to projections of free-energy landscape extrema along the reaction coordinate, defining the substeps for the motion of molecular motors [8]. This is a valuable theoretical prediction of discrete-state approach since the substeps for dynamical motion of various motor proteins have been observed in single-molecule experiments [42, 54, 156]. It is important to note that this method of taking into account the effect of external forces on transition rates is not exact. It implicitly assumes that the position and energy of the transition-state complex for each chemical transition do not change with the external force, making the parameters ${\theta }_j^{\pm }$ independent of F. One could argue that this approximation should work well for large energy barriers between individual states which is a reasonable description for most motor proteins. However, there are theoretical arguments that point out to the danger of using such over-simplified pictures for some chemical processes in biopolymers [159]. It will be important to investigate this issue in more detail in the future.

As illustrated in Fig. 2, the single-molecule experiments provide a comprehensive information on residence times of molecular motors in different spatial positions associated with some specific biochemical states. These quantities are also known as dwell times, and they are frequently measured with a high precision [29, 34, 48]. From theoretical point of view, they are related to a concept of first-passage processes which is a well developed and widely utilized theoretical method in Chemistry, Physics and Biology [160, 161]. It has been argued that full distributions of dwell times (or first-passage times) might help to identify the details of microscopic mechanisms of motor proteins [8,89,90], however in experiments this approach is rarely used. To illustrate the method, let us consider a linear sequential model [see Fig. 4)] and introduce a function F_j,N(t) which is defined as a probability for the molecular motor to reach the state N for the first time at time t if it started at the site j at t = 0 [160,161]. This probability function can be found by analyzing a set of backward Master equations that control its temporal evolution,

$$\frac{d{F}_{j,N}\left(t\right)}{dt}=u_j{F}_{j+1,N}\left(t\right)+w_j{F}_{j-1,N}\left(t\right)-(u_j+w_j)F_{j,N}\left(t\right).$$ (10)

Note that these expressions are different from the normal Master equations (as in Eq. 3) since they discuss the arrival probability densities [160,161]. Solving these equations allows to determine all dynamic properties of molecular motors. Theoretical analysis of mean first-passage times and its application for motor proteins have been performed for various systems [8,10,89,90,162]. One of the most surprising results is a prediction that full-cycle dwell times before the forward and backward steps, τ₊ and τ_– correspondingly, are the same for motor proteins in linear sequential models, although the probabilities of forward and backward steps are very different [90]. One would naively think (and many researchers still do!) that these times are different. This relation is a consequence of a fundamental law, known as a principle of microscopic reversibility, that applies for all chemical processes. For N = 2 models it was shown that

$${\tau }_{+}={\tau }_{-}=\frac{(u_0+u_1+w_0+w_1)}{(u_0{w}_0+u_1{w}_1)}.$$ (11)

It is important to note that these theoretical predictions have been confirmed in several experiments on motor proteins [34,48]. In addition, extending the theory of first-passage processes for specific motor protein systems it has been argued that more detailed analysis of statistics of events is a powerful but still not frequently applied tool for uncovering mechanisms of molecular motors [8,162].

The analogy of molecular motors with nanoscale machines have stimulated theoretical investigations on the efficiency of these engines that underlined the fundamental difference with the macroscopic systems [163–166]. Since molecular motors operate at isothermal conditions the classical approach to evaluate the efficiency that utilize Carnot cycle cannot be applied. The motor proteins operate at non-equilibrium, and only for some systems the equilibrium might be reached at the stalling conditions when the molecular motor velocity is zero. In this case, the efficiency is close to the thermodynamic limit 1, but the power output is vanishing since the motor does not move. To better quantify the performance of these nanoscale machines, many researchers have investigated the efficiency at the maximum power [163–166]. It has been shown that for weak external forces, when the linear response can be utilized, the efficiency is close to 1/2, while for more realistic external potentials it can vary between 0 and 1. One interesting observation of these studies is the effect of asymmetry of the underlying free-energy potential surface on the molecular motor efficiency. It has been shown that for the systems with the transition state closer to the reactant the efficiency is higher in comparison with the case when the transition state resembles more the product state. Based on experimental observations, it has been argued that single motor proteins operate with a maximal possible efficiency [163–166].

A major advantage of discrete-state stochastic models is their flexibility in handling more complex biochemical networks with a topology that deviates from simple chains [8]. Biochemical experiments on many molecular motors suggest that they do not follow a single linear sequence of states that connects the neighboring binding sites. In many case, the more realistic picture of underlying biochemical networks for motor proteins includes multiple parallel pathways, loops, branched states that do not lead to directed motion, and effectively irreversible detachments. Theoretical approach that generalizes the original Derrida's method allows to compute explicitly dynamic properties of motor proteins with complex networks of biochemical transitions [8, 85, 100, 111–114]. In addition, discrete-state stochastic models have been successfully used to describe interactions between domains of motor proteins and its effect on the overall mechanisms of motility [8, 91]. Furthermore, the original models have been extended to describe explicitly the motion in two-dimensional and three-dimensional free-energy landscapes [8, 92, 93]. Discrete-state stochastic models can account for all available experimental observations and they provide a flexible and convenient theoretical framework for understanding mechanism of motor proteins.

4.4. Mechanochemical and Structural Models

Although discrete-state stochastic models can provide a satisfactory description of dynamic properties of motor proteins, the weakest point of this approach is a limited connection to molecular structures. In other words, given a free-energy landscape the motion of molecular motors can be well predicted, while the microscopic origins of this specific potential surface, which is the result of complex intra-molecular and inter-molecular interactions of motor proteins with other molecules, are not accessible in this method. It is important to incorporate structural information into a theoretical framework for analyzing molecular motors and for understanding fundamental principles of energy conversion.

The necessity to account for structural properties of motor proteins have been realized in several recent theoretical developments [96–98, 107–110, 157, 158]. Lan and Sun proposed a mechanochemical approach that calculates explicitly the free-energy landscape for motor protein's motion [110]. It has two contributions: the chemical energy, which can be obtained from kinetic measurements, and the mechanical part, which is estimated from known structural information on motor proteins using simple mechanical models. This approach has been successfully applied for analyzing dynamic behavior of myosins V and VI, showing how different domains in these motor proteins interact to transmit forces and to synchronize their motion [96, 97, 110]. Similar method was also productive in analyzing and explaining complex features of dynein motor proteins [158]. A related structure-based model based on coarse-grained molecular simulations and theoretical ideas from protein folding has also been utilized for investigating dynamics of kinesins motor proteins [107–109]. Although these structure-related theoretical methods are promising in uncovering fundamental principles of energy conversion of molecular motors, currently there are several problems that limit their applicability. It includes the use of the oversimplified models from polymer physics, the assumption of mechanical (but not chemical) equilibrium, the use of coarse-grained potentials that are not well justified and tested for motor protein systems. It is expected that this theoretical approach will be significantly improved with future experimental advances in determining structures of molecular motors and with increasing power of modern computer simulations. It is also important to couple these structural methods with more phenomenological discrete-state stochastic models in order to develop a comprehensive multi-scale theoretical analysis of motor proteins.

5. Collective Dynamics of Motor Proteins

One of the main biological functions of motor proteins is to support cellular processes by transporting vesicles and organelles along cytoskeleton filaments [1, 2, 4]. Recent in vivo experiments indicate that during the cellular transport motor proteins always operate in groups [167–170]. This is a surprising observation since several in vitro studies have shown that some motor proteins are strong enough to function efficiently as single particles [5, 48, 148]. It suggests that the combined action of motor proteins is important for overcoming many challenges during the transportation in the crowded and dynamic cellular environment. It is often assumed that grouping motor proteins should lead to higher force productions, longer travel distances and larger speeds, and the efficiency of single motors interacting with other molecular motors is higher [166]. However, mechanisms of cooperative dynamics of molecular motors are still not well understood, and the impact of the collective motor behaviors on cellular processes remains unclear [103,171–173].

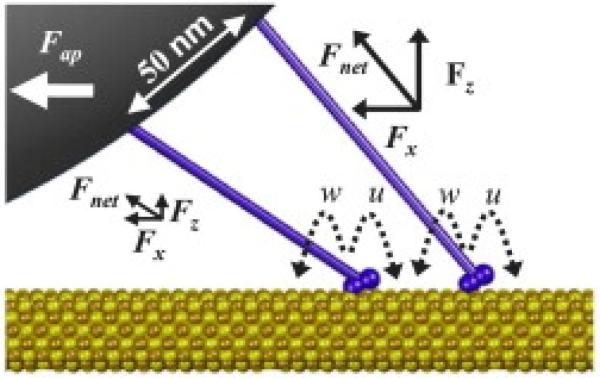
One of the most serious problems for in vivo experimental studies of multi-motor dynamics is the fact that frequently it is very difficult to determine and to control the number and structures of motors on transported cellular cargoes [103,171]. This observation stimulated a development of several experimental methods that utilized synthetic approaches (via protein or DNA scaffolding) to prepare multi-motor complexes of known composition [60,174–179], as shown schematically in Fig (5). These experimental studies on engineered multi-motor complexes have revealed surprising differences in collective behavior of various classes of biological molecular motors. Using optical-trap spectrometry it was found that motor complexes consisting of two kinesins molecule cooperate negatively, i.e., these two motor proteins do not work together and most of the time the cellular cargo is transported primarily by a single molecular motor [60,176]. These weak collective responses of kinesins contrast with experimental results on other motor proteins, such as NCD [174] and myosins V [178], where molecular motors cooperate much more productively, sharing the load and increasing the travel distances and speeds.

Figure 5.

A simplified view of the system of two kinesins motor proteins that transport the cargo along the microtubule filament track. Adopted from Ref. [103].

To explain the complex behavior of molecular motor complexes several theoretical ideas have been proposed [101–103,172,173,180,181]. Klumpp and Lipowsky introduced a theoretical approach which postulates that a cellular cargo is driven by a system of non-interacting motor proteins that independently bind to their cytoskeleton track or dissociate from it [101]. It can be viewed as an extension of discrete-state stochastic models [8] that have been successfully applied for analysis of single motor proteins. This theoretical model predicted increased run lengths of motor complexes as well as a linear dependence of the stall forces on the number of motor proteins. It turns out to be a convenient theoretical picture for analyzing collective dynamics of molecular motors [179,180]. However experimental results on two kinesins motor protein complexes do not agree with these theoretical predictions [60]. In addition, several weak points of this approach have been criticized [103, 171], namely: unrealistic linear force-velocity for single motors, assumed equal sharing of external loads and thermodynamically inconsistent description of binding/unbinding events.

More advanced but related theoretical method that takes into account interactions of motor proteins with cargoes and with cytoskeleton tracks has been proposed recently [103, 171]. This approach enumerates most relevant discrete states of the system depending on the chemical conformation of each motor (bound/unbound) and on the distance between bound motors, and it calculates then energies for each state using single-molecule mechanical data and chemical kinetic measurements. The transition rates between different states of the system are estimated using the calculated energy differences between the states and detailed balance arguments, which connect the ratio of forward and backward transition rates to the free-energy difference associated with this transition [103]. The advantages of this method are the consistent thermodynamic description of all chemical transitions and the use of single-molecule chemical and mechanical data as the input parameters for calculating dynamic properties of multi-motor complexes [103].

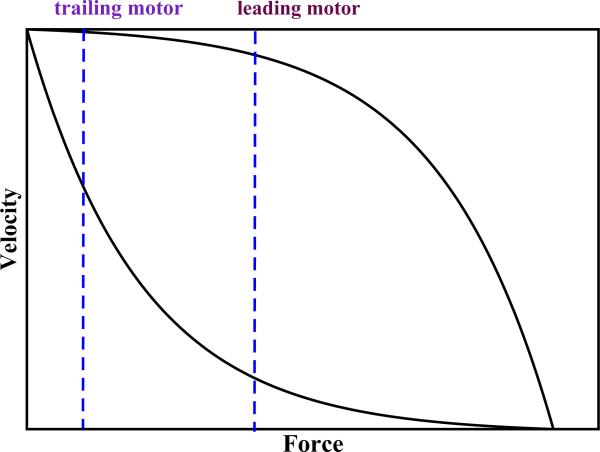
This approach has been tested by analyzing in vitro experiments on engineered twokinesins complexes [60]. In agreement with experiments, it was found that interactions between kinesins reduce the probability for two molecular motors to share the load and to drive the cargo together. The model predicts that geometric and kinetic constraints largely limit how effectively a group of kinesin molecules can cooperate as a team [103]. These theoretical ideas have been generalized to other motor proteins and it has been argued that fast and efficient motor proteins, like kinesins, will unlikely collaborate transporting cellular cargoes. At the same time, less-efficient molecular motors whose velocities decrease more rapidly with increasing the load are more capable of cooperating productively. To understand this qualitatively let us consider typical force-velocity curves for single motor proteins as shown in Fig. 6. In the group of motor proteins that move the cargo the leading molecule experiences the largest share of the load. For strong and efficient motors (upper curve in Fig. 6) the leading and the trailing molecules move with similar velocities for most loads below the stall force, and the trailing particle has a lower probability to catch the leader and there is a higher probability for leading motor to unbind, leading to lower cooperativity in the motor protein complex as observed for kinesins. For weak and less-efficient motors (the lower curve in Fig. 6) the trailing particle moves significantly faster and it has a higher probability to catch the forward molecular motor before the unbinding, increasing the probability of load-sharing configurations and thus leading to a more cooperative behavior. In addition, the relative strength of motor protein interactions with the filament track has also a strong effect on cooperativity. Weak interactions will probably do not support the cooperative motion, while the stronger interacting molecular motors have a higher probability to share the load and to be more cooperative. Based on these arguments, it has been suggested that more cooperative behavior most probably will be observed for dyneins and myosins V. This analysis also leads to a very important prediction, which is still experimentally not tested, that dyneins and myosins V, but not kinesins, serve as strong regulators of cellular transport processes [103].

Figure 6.

Typical force-velocity curves for single motor proteins. The upper curve corresponds to strong and efficient molecular motors, while the lower curve is for weaker and less efficient motors. Vertical dashed lines correspond to forces felt by leading and trailing molecules in two-motor assemblies - see the text for more details.

This theoretical method has been recently extended to account for chemical interactions between bound motor proteins, and it was argued that this effect is important for understanding dynamics in the high-loads regime of multiple-motor complexes [172]. In addition, this approach has been also utilized to quantify the collaborative behavior in multiple kinesins transport by varying structural and chemical properties [173]. It was shown that the cooperation in kinesins is much more sensitive to changes in chemical but not mechanical interactions. It seems that this discrete-state stochastic approach currently is probably the most efficient theoretical framework for understanding complex interactions in dynamics of multiple molecular motors.

6. Perspective: Future Directions

In recent years the field of molecular motors have seen huge developments and strong advances in both experimental and theoretical investigations. It is now possible to visualize and to modify dynamics of single motor proteins with unprecedented spatial and temporal resolutions, while structural studies provided the detailed information on molecular conformations during the biochemical processes associated with the molecular motors motion. These striking experimental observations have stimulated strong discussions on functioning and mechanisms of motor proteins that led to a development of several theoretical methods that were able to successfully explain a large fraction of experimental results. Although many properties of molecular motors are still not fully determined, one could clearly say that dynamic behavior of single motor proteins in in vitro conditions currently is much better understood. However, the situation is very different for understanding dynamics of multiple motor proteins. Despite some recent progress, the cooperative dynamics of molecular motors remain not fully specified from both experimental and theoretical point of views. To understand the complex dynamics of motor protein assemblies one has to take into account many factors including various chemical and mechanical interactions, the responses to external fields, and relaxation dynamics to the stationary states. It will be important in the future to develop a unified comprehensive theoretical framework that will take into account all these effects.

Another important and very difficult task for the field is to develop quantitative experimental and theoretical methods to understand motor protein dynamics in real cellular conditions. The successful methods must account for complex interactions with other motor proteins and with cytoskeleton filaments as well as with many other active biological molecules that are present in the cells. It is also important to understand how the cellular signaling system controls the dynamics of molecular motors at strongly non-equilibrium conditions. It is clear that the future progress in understanding complex phenomena associated with motor proteins strongly depends on combined experimental and theoretical efforts.