Abstract
Although there are many studies that focus on understanding the consequence of pumping mode (continuous vs. pulsatile) associated with ventricular assist devices (VADs) on pediatric vascular pulsatility, the impact on local hemodynamics has been largely ignored. Hence, we compare not only the hemodynamic parameters indicative of pulsatility but also the local flow fields in the aorta and the great vessels originating from the aortic arch. A physiologic graft anastomotic model is constructed based on a pediatric, patient specific, aorta with a graft attached on the ascending aorta. The flow is simulated using a previously validated second-order accurate Navier–Stokes flow solver based upon a finite volume approach. The major findings are: (1) pulsatile support provides a greater degree of vascular pulsatility when compared to continuous support, which, however, is still 20% less than pulsatility in the healthy aorta; (2) pulsatile support increases the flow in the great vessels, while continuous support decreases it; (3) complete VAD support results in turbulence in the aorta, with maximum principal Reynolds stresses for pulsatile support and continuous support of 7081 and 249 dyn/cm2, respectively; (4) complete pulsatile support results in a significant increase in predicted hemolysis in the aorta; and (5) pulsatile support causes both higher time-averaged wall shear stresses (WSS) and oscillatory shear indices (OSI) in the aorta than does continuous support. These findings will help to identify the risk of graft failure for pediatric patients with pulsatile and continuous VADs.
Keywords: Anastomosis, Reynolds stress, Hemolysis, Wall shear stress, Oscillatory shear index
PURPOSE
Congenital heart disease (CHD) is the leading cause of infant death from birth defects in the United States.36 Over 35,000 babies are born with heart defects annually in the United States, with a quarter of these patients requiring invasive treatment.1,2 Transplantation, an excellent option for these patients, is limited by an inadequate number of donor organs.4 There are no mechanical circulatory support devices (MCSDs) approved in the United States for pediatric patients. For this reason, the National Institutes of Health (NIH) initiated The National Heart, Lung and Blood Institute (NHLBI) Pediatric Circulatory Support Program in 2004.2 Five contracts were awarded with the task of creating MCSDs for children ranging from 2 to 25 kg. Three of the five MCSDs are designed to deliver continuous blood flow.2 The fourth, the Penn State pediatric ventricular assist device (PVAD), is a pulsatile, seamless blood sac design based on the successful, pneumatic Pierce-Donachy/Thoratec adult device.3 The last pump is a pediatric cardiopulmonary assist system (pCAS), which in addition to continuous flow can deliver pulsatile flow.2
The use of pulsatile and continuous pediatric pumps has raised questions about the potential complications of non-pulsatile flow during acute and chronic support. Some problems with continuous pumps have been reported for adult patients undergoing cardiopulmonary bypass.16,26,32,34,35,37 One of the most severe is a significant systemic and pulmonary vasoconstriction, which increases ventricular work and reduces perfusion of the peripheral organs, leading to a potential reduction in end-organ function. Recognizing the favorable characteristics of pulsatile over continuous flow for adult patients, researchers have also investigated the effect of pulsatility for pediatric patients. Taylor et al.33 demonstrated that the pulsatility of cerebral flow helped to regulate the blood flow to the brain for infants during extracorporeal membrane oxygenation (ECMO). Undar et al.39 studied the flow in a neonatal piglet and found that pulsatile perfusion improved cerebral, renal and myocardial blood flow after cardiopulmonary bypass (CPB). Pantalos et al.29 performed an acute animal study in piglets of left ventricular dysfunction with the pCAS to study differences between pulsatile and continuous flows. They found that pulsatile flow produced three times greater pulsatility than continuous flow in cases of less than total left ventricular bypass by the pCAS. The impact of pulsatile vs. continuous flows on the local hemodynamics near the graft sites has received less attention. Previous hemodynamic studies on the aortic graft flow focused on either continuous24,25,42 or pulsatile flow.30,41 The objective of this study is to compare the effects of pulsatile and continuous flows on the hemodynamics in a pediatric ascending aortic graft model based on patient specific, pediatric aorta morphology. A second-order accurate Navier–Stokes solver is used to simulate the flow based on a finite volume method (FVM).28 An implicit large eddy simulation (ILES)5,10,13,14 is used to resolve the turbulence. The flow splitting among the three great vessels on the aortic arch, the brachiocephalic (innominate) artery, the left common carotid artery, and the left subclavian artery, is modeled using resistance boundary conditions.7,40 Hemolysis indices are predicted and compared using a linear advection-reaction transport equation.
METHODS
Geometrical Model
A physiologically correct aortic model is important for the study of an aortic graft flow. To generate the aortic geometry used in the present study, a series of slices of a pediatric aorta (8 years old) is acquired in vivo using magnetic resonance imaging (MRI) to reconstruct a pediatric patient specific aorta morphology (NIH-Georgia Tech Fontan Anatomy Database ID: CHOP007). The model then is scaled down to a pediatric aorta of a 1 year old with an aortic inlet diameter of 11.6 mm (Fig. 1a). The primary dimensions of the model are found to be in good agreement with morphological measurements reported by Machii and Becker.23 The three great vessels on the aortic arch are extended to roughly ten times their diameters, so that the effect of each branch exit velocity boundary condition on the branch inflow is negligible (Fig. 1b). A PVAD outflow graft with an internal diameter of 6 mm is attached to the ascending aorta, as show in Fig. 1b. The outflow graft is designed for pediatric patients from 0 to 12 months, weighing 2–8 kg.3 The nomenclature of the end-to-side anastomosis used in this study is presented in Fig. 1c.
FIGURE 1.
(a) Pediatric patient specific aortic model; (b) whole view of the end-to-side anastomotic model; (c) enlarged distal view of the graft junction indicated by the black square in (b).
Mathematical Model
Blood flow is modeled using the time-dependent Navier–Stokes equations, which can be written as
| (1) |
| (2) |
where p, u⃑, ρ, and μ represent pressure, velocity, blood density, and blood dynamic viscosity, respectively. The flow with the graft bypass is more complicated than the natural aortic flow, as it often exhibits transitional turbulence near peak systole22,41 under pulsatile flow conditions. Turbulence was also observed by Yang et al.42 under continuous flows, albeit of lower intensity. Therefore, it is important to model the transitionally turbulent nature of the bypass flow. In this study, an ILES method, based upon a FVM, is used to resolve the large scales of the flow, while the effect of the sub-grid scale (SGS) motion is incorporated through the discretization errors of a second-order total variation diminishing (TVD) scheme.9 Yang et al.42 have demonstrated the capability of this method of resolving turbulent eddies without significant numerical dissipation by studying a fully developed turbulent channel flow.
To model blood damage in the flow, an additional linear advection-reaction transport equation of hemolysis fraction H is introduced as6,11,21
| (3) |
where the reaction coefficient R is a function of the stress which red blood cells are exposed to, and is defined as6,12,43
| (4) |
where α, β, and γ are constants, defined as
| (5) |
and τv and τt are the von Mises equivalent viscous and Reynolds stress scalars,6 respectively. The step function δ is used to account for the hemolytic threshold for Reynolds stresses,21 defined as
| (6) |
where the threshold limit τs is taken as 4000 dyn/cm2.31
If the hemolysis fraction at the inlets is assumed to be zero, the average hemolysis fraction H̄ for pulsatile flows can be calculated as
| (7) |
where T is the period of flow cycle, and n⃑ is unit normal vector on the outlet surfaces (S). For steady flows, Eq. (7) can be simplified to
| (8) |
The modified index of hemolysis (MIH) of the flow can be calculated as6
| (9) |
Hemodynamic Parameters
To make meaningful comparisons between the continuous and pulsatile modes of the PVAD, the surplus hemodynamic energy (SHE, ergs/cm3) is used to characterize the pulsatile hemodynamic performance of the flow, and is defined as
| (10) |
where energy equivalent pressure (EEP, mmHg) and time-averaged pressure (TAP, mmHg) are defined as
| (11) |
| (12) |
where q is the flow rate. SHE, which represents the extra energy generated by flow pulsations, has been used extensively in the literature.29,37,38
Time-averaged wall shear stress (WSS) and oscillatory shear index (OSI), two important hemodynamic parameters for vascular remodeling,22 are defined as
| (13) |
and
| (14) |
where WSS is defined as
| (15) |
where the superscript tr represents the transpose of a matrix, and n⃑ is unit normal vector on the wall. OSI represents the temporal oscillation of the WSS vector.
Boundary Conditions
Five different flow conditions are studied in this work (Table 1). Case 1 represents a natural aortic flow condition with a cardiac output (CO) of 1.0 L/min and a heart rate of 120 beat per minute (BPM). It serves as a reference flow without PVAD support. Cases 2 and 3 are intermediate VAD support conditions with 50% of CO going through the PVAD. Case 2 represents pulsatile support, while case 3 represents continuous support. Cases 4 and 5 represent 100% PVAD support in pulsatile and continuous modes, respectively. For simplicity, only synchronized flow is studied in the present study. The beat rates of the left heart and PVAD are taken to be 120 BPM for all pulsatile inflow boundary conditions in cases 2–5.
TABLE 1.
Summary of flow conditions.
| Case | Percentage support (%) |
PVAD mode |
Beat rate of PVAD |
Heart beat rate (bpm) |
Total flow (L/min) |
Maximum Reynolds number at aortic inlet |
Maximum Reynolds number at outflow graft |
Womersley Number based on the aortic inlet |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | N/A | N/A | 120 | 1.0 | 2400 | 0 | 11 |
| 2 | 50 | Pulsatile | 120 bpm | 120 | 1.0 | 1200 | 2134 | 11 |
| 3 | Continuous | N/A | 120 | 1.0 | 600 | 506 | 11 | |
| 4 | 100 | Pulsatile | 120 bpm | 0 | 1.0 | 0 | 4269 | 11 |
| 5 | Continuous | N/A | 0 | 1.0 | 0 | 1011 | 0 |
The flow waveforms at the inlets of the aorta and outflow graft for cases 1, 2, and 4 are scaled from an in vivo animal study by Pantolos et al.29 For case 3 (50% continuous support), a scaled waveform based on the measurement by Pantolos et al. is applied to the aortic inlet with a steady plug inflow applied at the cannula inlet. For case 5 (100% continuous support), a steady plug inflow profile is applied at the cannula inlet while zero velocity is applied at the aortic inlet. A zero normal gradient is applied at each branch exit as a velocity boundary condition, with an outflow resistance boundary condition applied for pressure defined as
| (16) |
where p is the pressure, Q is the flow rate, R is the resistance constant, and p0 is the pressure at the aortic outlet. In this study, p0 is taken as 60 mmHg to maintain a physiological pressure level in the system.20 The resistance of each outlet is calculated such that the flow splits among the great vessels, the brachiocephalic artery, the left common carotid artery, and the left subclavian artery, are 21.41, 10.58, and 14.76%, respectively, in the healthy aortic model. The flow splits are taken proportional to the cross-sectional area of each vessel and the total flow splitting in the major branch vessels is 46.75%, which is within the range reported by Fogel et al.8 We assume that the resistance of each vessel maintains its value throughout PVAD support. The aorta and outflow graft are assumed to be rigid and a no-slip boundary condition is applied at the walls. The boundary conditions for the hemolysis fraction H are zero at the inlets and walls, with zero normal gradients at the outlets for all five cases.
Grid Generation
A systematic grid study was performed by Yang et al.41 on the same pediatric aorta model used in the present study. Three different high-quality unstructured grids (coarse grid = ~180,000 cells; medium grid = ~580,000 cells; fine grid = ~1,600,000 cells) were used in their study. No significant difference was found among the three grids for volumetric flow rate and pressure at each branch exit. The three-component wall shear stress (WSS), however, was very sensitive to grid density. The time-averaged relative error of WSS through the flow cycle between the medium and fine grids was less than 5% in five of the six locations, with the maximum error of 25% at the inner wall of the aortic arch. Due to limited computational resources, we use the same medium grid in the present study. The grid is generated using GAMBIT 2.3.16 (Fluent Inc., Lebanon, NH, USA). A set of fine grids is used near the walls with a height of the near-wall spacing of 0.05 mm. A hybrid of tetrahedral, hexahedral, and prism grids is used in the interior volumes of the geometries with a nearly isotropic size of 0.5 mm.
Flow Solver and Numerical Algorithms
The Navier–Stokes and hemolysis transport equations are discretized into algebraic ones using a FVM28 and solved separately. The momentum and continuity equations are solved first. The hemolysis transport equation is solved based on the resolved flow field. A second-order accurate, backward scheme is used to discretize the time derivative terms for both the Navier–Stokes and hemolysis transport equations. The convective termsofthe momentum and hemolysis transport equations are discretized using a previously validated second-order TVD scheme42 and a first-order upwind scheme, respectively. Only the first-order scheme is used for the hemolysis equation due to the numerical instability of higher-order schemes. The linear solvers are a generalized geometric/algebraic multi-grid (GAMG) solver for the pressure and preconditioned bi-conjugate gradient (PBICG) solvers for the velocity and hemolysis fraction H. A pressure-implicit with splitting of operators (PISO) scheme19 is used for the pressure–velocity coupling. The flow solver has been validated by Yang et al.41 by studying a fully developed laminar pulsatile straight pipe flow with a high-frequency flow instability. Good agreement was found between the numerical and the analytical results.
Fluid Properties and Computational Parameters
Blood is assumed to be an incompressible Newtonian fluid with a density, ρ, of 1.057 × 10−3 kg/m3 and a dynamic viscosity, μ, of 3.7 × 10−3 kg/ms. The time steps are chosen for each case such that the Courant number through the flow cycle is less than 1. The residuals of all the variables are converged to 10−6 at all time steps. Simulations are run in parallel with sixteen processors using a PC cluster on the Penn State High Performance Computing Group, with the high-speed Silverstorm Infiniband network. Three cycles are required to achieve convergence of the flow field for cases 1 (healthy aortic flow), 2 (50% pulsatile support), and 3 (50% continuous support), which is based on the maximum time averaged relative error of WSS of the fifth cycle to the fourth cycle being less than 1%. This indicates that the flows for cases 1, 2, and 3 are laminar. Large variance in WSS (over 100% at peak systole from cycle to cycle for case 4) is found for cases 4 and 5, suggesting that transitional turbulence occurs. For case 4 (100% pulsatile support), the simulation first runs three cycles to eliminate the initial effect, and then the flow data are sampled for ten flow cycles to collect turbulent statistics (due to limited computational resources). The computation takes roughly a day per flow cycle. For case 5 (100% continuous support), the flow data are sampled at every time step for roughly five flow-through times to collect flow statistics after the flow is statistically stable. The flow-through time, 0.2 s, is the time taken by a fluid particle to traverse from the aortic inlet along the aortic arch to the aortic outlet with mean graft inlet velocity. The flow results presented from here on for cases 4 and 5 are averaged for ten flow cycles and five flow-through times, respectively. The hemolysis fractions H for cases 1, 2, and 3 are calculated based on the flow fields of the fourth flow cycle, while H for cases 4 and 5 are calculated based on the mean flow fields.
RESULTS
Pulsatile Hemodynamic Performance
Figures 2a and 2b give the volumetric flow rate and pressure waveforms at the boundaries for all five cases. A slight retrograde flow is found at early diastole in the great vessels for the healthy aortic flow (case 1), which is reduced with the PVAD support (cases 2–5), as shown in Fig. 2a. The large pressure pulse found at early diastole at the aortic inlet for case 1, as shown in Fig. 2b, is a result of the lack of systematic compliance.
FIGURE 2.
(a) Flow waveforms at the boundaries for all five cases; (b) pressure waveforms at the boundaries for all five cases.
The calculated values of EEP, TAP, and SHE, as shown in Table 2, are functions of flow condition. For the healthy pediatric aorta (case 1), 104, 103, 93, and 20% of the inlet SHE are delivered to the brachiocephalic artery, left common carotid artery, left subclavian artery, and aortic outlet, respectively. In comparison, vascular pulsatility is dampened during the left ventricular assistance (50% support and 100% support), as suggested by the SHE values in Table 2.
TABLE 2.
Comparison of pulsatile hemodynamic performance parameters between the pulsatile and continuous PVAD support.
| Case | Aorta inlet |
Outflow graft |
Brachiocephalic artery |
Left common carotid artery |
Left subclavian artery |
Aortic outlet |
|---|---|---|---|---|---|---|
| EEP (mmHg) | ||||||
| 1 | 84.23 | N/A | 83.85 | 83.71 | 81.44 | 65.22 |
| 2 | 81.40 | 83.12 | 80.07 | 78.93 | 77.35 | 64.43 |
| 3 | 72.26 | 65.71 | 68.79 | 68.62 | 67.99 | 62.51 |
| 4 | N/A | 90.79 | 81.53 | 80.38 | 77.63 | 64.07 |
| 5 | N/A | 66.40 | 64.58 | 64.37 | 64.24 | 61.82 |
| TAP (mmHg) | ||||||
| 1 | 66.17 | N/A | 65.07 | 65.01 | 64.65 | 61.68 |
| 2 | 66.08 | 67.26 | 65.31 | 64.89 | 64.46 | 61.66 |
| 3 | 65.05 | 64.71 | 64.53 | 64.38 | 64.16 | 61.84 |
| 4 | 65.71 | 69.16 | 65.89 | 65.64 | 64.89 | 61.47 |
| 5 | 64.58 | 66.40 | 64.58 | 64.37 | 64.24 | 61.82 |
| SHE (ergs/cm3) | ||||||
| 1 | 2.41 × 104 | N/A | 2.50 × 104 | 2.49 × 104 | 2.24 × 104 | 4.72 × 103 |
| 2 | 2.04 × 104 | 2.11 × 104 | 1.97 × 104 | 1.87 × 104 | 1.72 × 104 | 3.69 × 103 |
| 3 | 9.61 × 103 | 0 | 5.68 × 103 | 5.65 × 103 | 5.10 × 103 | 8.96 × 102 |
| 4 | N/A | 2.88 × 104 | 2.08 × 104 | 1.96 × 104 | 1.70 × 104 | 3.47 × 103 |
| 5 | N/A | 0 | 0.07 | 0.25 | 0.22 | 0.01 |
A comparison of pulsatility between the PVAD operating in the continuous and pulsatile modes, as indicated by percentage change in SHE from case 1 for the great vessels and the aortic outlet, is given in Fig. 3. Striking differences are found in pulsatility between the pumping modes. In the pulsatile mode, roughly 20% reduction in pulsatility is found at each outlet for both the 50 and 100% support. In the continuous mode, however, a roughly 80% reduction in pulsatility is found at each outlet for the 50% support, while for the 100% support no pulsatility is found in the flow, as expected.
FIGURE 3.
Comparison of percentage change in surplus hemodynamic energy (SHE) from the healthy aortic flow (case 1) for 50 and 100% support in the pulsatile mode (PM) and continuous mode (CM).
Flow Splitting
The effect of the PVAD support on flow splitting in the great vessels is summarized in Table 3. It is found that the pulsatile PVAD support (cases 2 and 4) increases the flow in the great vessels when compared to the unassisted condition (case 1), while the continuous support (cases 3 and 5) decreases the flow. Specifically, as the percentage of the PVAD support in the pulsatile mode increases, the flow in the great vessels increases significantly, with a maximum increase of 12.77% from the healthy aorta flow for 100% support (case 4). In contrast, the increase of the PVAD support has only slight impact on the flow splitting when the PVAD operates in the continuous mode. The 50% (case 3) and 100% support (case 5) in the continuous mode give a total flow reduction in the three branch vessels of 11.11 and 9.8%, respectively.
TABLE 3.
Flow splitting in the three great vessels originating from the aortic arch.
| Case | Brachiocephalic artery (%) |
Left common carotid artery (%) |
Left subclavian artery (%) |
Total flow percentage in three great vessels (%) |
Total flow percentage change in three great vessels from case 1 (%) |
|---|---|---|---|---|---|
| 1 | 21.41 | 10.58 | 14.76 | 46.75 | 0 |
| 2 | 22.48 | 10.33 | 14.14 | 46.95 | 0.43 |
| 3 | 19.13 | 9.25 | 13.20 | 41.58 | −11.11 |
| 4 | 25.02 | 12.09 | 15.61 | 52.72 | 12.77 |
| 5 | 19.42 | 9.26 | 13.49 | 42.17 | −9.80 |
The flow percentage shown above is defined as the cycle-averaged flow rate at each great vessel divided by the CO (1 L/min).
Velocity Contours
Figure 4 demonstrates the velocity contours at peak systole for cases 1–4 and the mean velocity contour for case 5 (100% continuous support). Note that the velocity contour for case 4 (100% pulsatile support) is ten-cycle average. The velocity contours are presented in three different orientations for multiple locations, as shown in Fig. 5. For the healthy aortic flow (case 1), the flow is skewed first toward the inner wall at the aortic arch entrance and then toward the outer wall as the flow moves downstream. Interestingly, the flow reaches its maximum velocity in the descending aorta, as a result of the aortic tapering, as shown in Fig. 4a. The flow is highly altered during the PVAD support. The 50% PVAD support in the pulsatile mode (case 2) leads to a jet into the aorta, with a maximum velocity of 2.13 m/s, as shown in Fig. 4b. The flow for the 50% support in the continuous mode (case 3) is relatively uniform in the aorta, with a maximum velocity of 1.05 m/s occurring in the descending aorta at peak systole, as indicated in Fig. 4c. The 100% support causes a high-velocity jet to impinge on the aortic floor (posterior wall) for both the pulsatile (case 4) and continuous modes (case 5), as shown in Figs. 4d and 4e. The jet is then diverted for the most part into the brachiocephalic artery. The maximum velocities for the pulsatile and continuous support are 3.6 and 0.95 m/s, respectively. A large flow separation is found downstream of the graft toe for cases 4 and 5, as indicated in Figs. 4d and 4e.
FIGURE 4.
Velocity magnitude contour (unit: m/s): (a) case 1, (b) case 2, (c) case 3, (d) case 4, (e) case 5. Notice the contour scales are different.
FIGURE 5.
Planes used in this study for velocity contours.
Principal Reynolds Stress
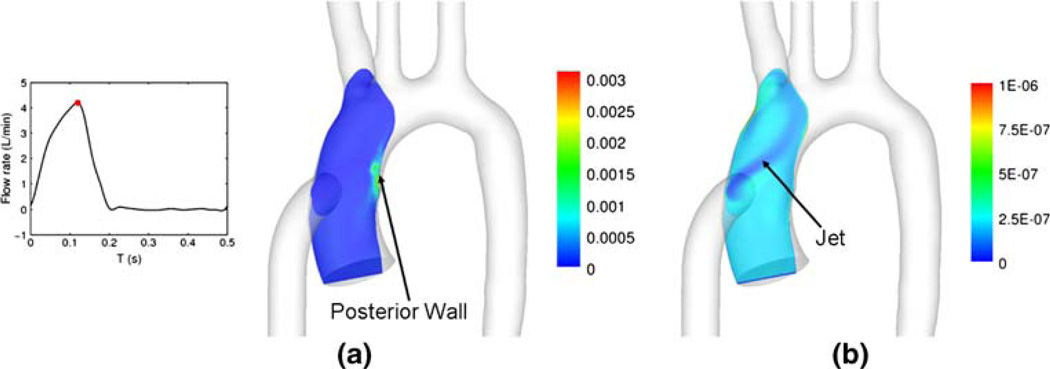
To compare the turbulence level between the pulsatile mode (case 4) and continuous mode (case 5) during the 100% PVAD support, the principal values of normal Reynolds stresses are acquired as the eigenvalues of Reynolds stress tensor.15,17 Reynolds stresses vary for different coordinate systems as they are not invariant to coordinate transformations. Hence, the principal Reynolds stresses are used in this study because they represent the maximum Reynolds stresses, and therefore are potentially the most destructive. The principal normal Reynolds stresses for case 4, calculated at peak systole, are based on ten flow cycles, while the stresses for case 5 are based on five flow-through times. The peak Reynolds number based on the graft diameter for the pulsatile mode (case 4) is 4269, while the Reynolds number for the continuous mode (case 5) is 1011. Figure 6 shows the maximum principal normal Reynolds stress fields for cases 4 and 5 in the plane shown in Fig. 5c. The high-velocity jets from the cannula causes high Reynolds stresses exclusively near the jet impingement on the posterior wall, for both cases. The Reynolds stresses for case 4 are much higher than for case 5 due to its higher Reynolds number. The maximum principal normal Reynolds stresses for cases 4 and 5 are 7081 dyn/cm2 (95% confidence interval of ±4566 dyn/cm2, sample size n = 10) and 249 (95% confidence interval of 2 dyn/cm2, sample size n = 100,000), respectively. The large confidence interval for case 4 is a result of its relative small sample size.
FIGURE 6.
Magnitude contour of maximum principal normal Reynolds stress (unit: dyn/cm2) for 100% PVAD support: (a) case 4 (pulsatile mode) at peak systole, (b) case 5 (continuous mode).
Hemolysis
Table 4 presents the MIH for all five cases. The MIH for the healthy aortic flow (case 1) is 17.75. The PVAD support in the pulsatile mode causes an increase of hemolysis, with MIH values of 1.18 and 22.4 times of the physiological value (MIH for case 1) for the 50 and 100% support, respectively. The continuous support, however, causes less hemolysis, with a decrease of MIH by 72 and 61% for the 50 and 100% support, respectively. This is due to lower velocities and corresponding shears for the continuous support when compared to that for the healthy aortic flow, as shown in Fig. 4. Figures 7a and 7b show the distribution of hemolysis fraction H at peak systole for the 100% support in the pulsatile (case 4) and continuous (case 5) modes, respectively, along a plane shown in Fig. 5c. For case 4, high H is found exclusively on the aortic floor near the jet impingement region, coinciding with the high Reynolds stress region shown in Fig. 6a. The H distribution for case 5, however, is much lower when compared to that for case 4, as indicated in Fig. 6b. High H for case 5 is found closely associated with the high shear layers, whereas low H is found in the core of the jet.
TABLE 4.
Comparison of MIH for all five cases.
| Case | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| MIH | 17.75 | 20.91 | 4.91 | 397.57 | 6.91 |
| MIH ratio | 1 | 1.18 | 0.28 | 22.40 | 0.39 |
FIGURE 7.
Hemolysis fractions H contour for 100% PVAD support: (a) case 4 (pulsatile mode) at peak systole, (b) case 5 (continuous mode).
WSS Distribution
Figure 8 shows the distribution of time-averaged WSS for all five cases. High WSS occurs along the outer wall of the aortic arch between the branch entrances and the distal wall of the branch vessels (cases 1–5), on the suture line (cases 2–5), and on the aortic floor across from the suture line (cases 4 and 5). The 50% support in the pulsatile mode (case 2) causes an increase of WSS at the aortic wall downstream of the graft site but a decrease upstream when compared to the healthy aortic flow (case 1). The continuous 50% support (case 3), however, leads to an overall decrease of WSS in the aorta, as a result of the lower velocities, as shown in Fig. 4. The maximum time-averaged WSS occurs on the suture line with values of 420 and 258 dyn/cm2 for cases 2 and 3, respectively. The 100% support (cases 4 and 5) causes a higher WSS distribution in the aorta when compared to the 50% support except in the aortic entrance upstream of the graft site. A large increase of WSS is found on the aortic floor across from the suture line. Two stagnation points, identified by combining lowest WSS and highest pressure, are found on the aortic floor for both cases 4 (pulsatile) and 5 (continuous) (Fig. 9). The maximum WSS regions are located on the suture line with values of 575 and 371 dyn/cm2 for cases 4 and 5, respectively.
FIGURE 8.
Time-averaged WSS magnitude (unit: dyn/cm2) contour: (a) anterior view, (b) posterior view.
FIGURE 9.
Posterior view of pressure contour (unit: mmHg) for 100% bypass: (a) case 4 (pulsatile mode) at peak systole, (b) case 5 (continuous mode).
Figure 10 compares the OSI distribution for all five cases. High OSI, indicating flow separation and retrograde flow in these regions, are located on the proximal walls of the branch vessels near the entrances (cases 1–4), the aortic floor across the suture line (cases 2 and 3), the anterior wall downstream of the graft toe (cases 2–5), the ascending aortic wall upstream of the graft site (cases 4 and 5), the stagnation points (cases 4 and 5), and the graft hood and inner wall of the graft close to the suture line (cases 2 and 4). The maximum OSI (0.47) for the healthy aortic flow (case 1) occurs on the proximal wall of the brachiocephalic artery, as shown in Fig. 10. The OSI distribution during the 50% pulsatile support (case 2) is similar to that during the 50% continuous support (case 3) except in two major locations. First, for case 2, relatively high OSI is also found on the graft hood (0.19) and on the inner wall of the graft close to the suture line (0.49). The OSI in the graft for case 3 is nearly zero, which suggests that the flow in the graft is steady through the flow cycle. Second, the OSI in the descending aorta for case 2 is much higher than that for case 3, as shown in Fig. 10. During the 100% support, high OSI distributions are found on the ascending aorta upstream of the graft junction for both the pulsatile (case 4) and continuous support (case 5). Low OSI is found on the aorta floor opposite the suture line for cases 4 and 5, except the flow stagnation points. In contrast to case 4, only one of the two stagnation points shows relatively high OSI for case 5. Striking differences in the OSI distribution are found between cases 4 and 5 on the aortic wall downstream of the graft, the proximal walls of the branch vessels, and the graft wall. As in the 50% continuous support (case 3), the OSI in the graft for the 100% continuous support (case 5) is close to zero. The maximum OSIs occur on the anterior wall downstream of the graft toe (0.47) and the inner aortic wall upstream of the graft junction (0.44) for cases 4 and 5, respectively. Note that the time-averaged WSS and OSI for case 4 are integrated based on the ten flow cycles averaged WSS, and the time-averaged WSS and OSI for case 5 are integrated over the same period T (0.5 s) as for cases 1–4.
FIGURE 10.
OSI contour: (a) anterior view, (b) posterior view.
DISCUSSION
Pulsatility
SHE at the aortic inlet for the healthy aortic model (case 1) is 2.41 × 104 ergs/cm3, which is close to the data ((1.6020 ± 0.5639) × 104 ergs/cm3) reported by Pantalos et al.29 in their in vivo infant animal study. It is interesting that SHE values in the brachiocephalic artery (104%) and the left common carotid artery (103%) are slightly higher than SHE at the aortic inlet for case 1. This is mainly due to the rigid walls. Greater pulsatility is found at the outlets of the brachiocephalic artery, the left common carotid artery, the left subclavian artery, and the aorta when the PVAD operates in the pulsatile mode than when it is used in the continuous mode, although both cause significant reduction in pulsatility when compared to the healthy aortic flow. During intermediate support (50%), the pulsatile mode gives over three times greater pulsatility at each outlet than does the continuous mode. This is very close to the data reported by Travis et al.37 and Pantolos et al. in their adult clinical patients (five times) and an infant animal model (three times), respectively. Our SHE data (nearly zero) for maximum VAD support (100%) in the continuous mode, however, is significantly less than the experimental data (1842 ± 1243 ergs/cm3) by Pantolos et al., simply because in their in vivo animal experiment, the aortic valve was not completely closed and the natural heart could contribute some pulsatility to the systemic circulation during continuous support. It is interesting that an increase of PVAD support in the pulsatile mode has no significant impact on pulsatility in the great vessels.
Flow Splitting
Flow splitting in the great vessels increases during the pulsatile PVAD support and decreases during the continuous support when compared to the healthy aortic flow. This is a result of higher pressures at the branch outlets for the pulsatile support and lower pressures for the continuous support, as indicated by TAP values in Table 2. The total flow split to the branch vessels increases with the increasing level of pulsatile PVAD support, as a result of the increase of TAP at each outlet, as shown in Table 2. The maximum difference in the total splitting between the pulsatile and continuous support is 10.55% of CO, which occurs during 100% support. It should be noted that our flow splitting results only provide insight into the initial responses of the aorta caused by PVAD support. Significant change in vascular structure to maintain homeostasis may take place with time.
Flow Field
The flow field in the aorta varies widely with the increasing PVAD assistance in both the pulsatile and continuous modes. Significant differences are found between the pulsatile and continuous modes for 50% assistance. The 50% pulsatile support causes a high-velocity jet into the aorta while the flow for the 50% continuous support is relatively uniform due to the reduced constant graft inflow. In contrast, the flow fields for the 100% pulsatile (at peak systole) and continuous support look similar in shape but are significantly different in velocity magnitude. The maximum velocities for the pulsatile and continuous supports are 3.6 and 0.95 m/s, respectively. Turbulence is observed exclusively near the posterior wall of the aorta for the 100% assistance, as a result of the jet and its wall impingement. The maximum principal normal Reynolds stress for the pulsatile support at peak systole is nearly thirty times greater than that for the continuous support. We remind the readers that the Reynolds stress results for case 4 are based on only ten flow cycles, so that the confidence band is very large.
Hemolysis
The hemolysis levels between the pulsatile and continuous support were compared in the aorta. The MIH value for the healthy aortic flow is 17.75, which is roughly 23% of the MIH value reported by Pekkan et al.30 for their neonatal aortic model. Pekkan et al. calculated the blood damage index by integrating the Giersiepen–Wurzinger correlation12 along the particle path lines based on the flow field at peak systole. This approach requires calculation of streamline and residence time, and assumes that blood damage is time-independent. The MIH data by Pekkan et al., therefore, represents the blood damage at peak systole. The methodology adopted in this study, in comparison, is a volume integration of blood damage over the computational domain, and can be used to calculate time-dependent blood damage under pulsatile flows. Our MIH data, as shown in Eqs. (7)–(9), represents a cycle average. This explains why our calculated MIH value is much lower, as the hemolysis is dependent on shear stresses and maximum shear stresses occur at peak systole.
The hemolysis level increases during the pulsatile support whereas it decreases during the continuous support when compared to the healthy aortic flow. This can be explained by the higher velocity (higher shear stress) for the pulsatile support and the lower velocity (lower shear stress) for the continuous support at peak systole when compared to that for the healthy aortic flow, as shown in Fig. 4, as the most hemolysis occurs during peak systole. The highest hemolysis level occurs during the 100% pulsatile support, with the MIH value of 397.57. This is higher than the MIH (299) reported by Pekkan et al. for their cardiopul-monary bypass model at peak systole, partly because the contribution of Reynolds stresses was ignored in their calculation.
One advantage of the present methodology over the streamline approach is its capability of identifying local time-dependent hemolysis sites. As shown in Fig. 7a, for the 100% pulsatile support, the most blood damage occurs near the jet impingement, where the most turbulence occurs. We remind the reader that the reaction coefficient R in Eq. (4) is derived based on the Giersiepen-Wurzinger correlation,6 which is only valid for laminar flows. A simple integration of the Reynolds stresses using the empirical formula could significantly overestimate the blood damage index.43 Therefore, a step function is introduced in this study to account for the threshold limit for hemolysis in turbulent flow.
WSS and OSI
The time-averaged WSS is found to increase with the increasing PVAD support, except in the ascending aorta upstream of the graft site. For the same percentage of PVAD support, the pulsatile mode leads to higher WSS and OSI distributions than does the continuous mode, due to the higher velocity and pulsatility for the pulsatile mode. Two stagnation points are found on the aortic floor during the 100% assistance in both the pulsatile and continuous modes, which is common in arterial bypass flows.18,22,27 For the pulsatile support, two stagnation points oscillate through the cycle, as indicated by their high OSI values (Fig. 10). For the continuous support, however, the stagnation point close the outer aortic wall is nearly stationary throughout the cycle, as indicated by its low OSI value (Fig. 10).
This work compares hemodynamics in the aorta during pulsatile and continuous PVAD support and discusses the possible clinical implications in the consequence of continuous vs. pulsatile flow choice. These efforts could provide significant improvement for patients with PVAD implants by optimizing the PVAD implant technique and cannula design. The development of the reliable CFD model, as demonstrated in this work, could significantly reduce the number of parametric studies and therefore, provide a quick tool in evaluating different anastomotic techniques and cannula designs.
CONCLUSION
We find that the continuous PVAD support largely reduces the pulsatility in the great vessels originating from the aortic arch and also in the descending aorta. In the case of the intermediate PVAD support, the pulsatile pump yields more than three times greater pulsatility in the branch vessels than does the continuous support. The pulsatile PVAD support increases the flow percentage in the great vessels, with a maximum total increase of 12.77% from the healthy aorta for the 100% PVAD support. In comparison, the continuous support decreases the flow rate in the great vessels by 11.11 and 9.8% for the 50% support and 100% support, respectively. The flow in the aorta is highly disturbed with the graft inflow, depending on the mode of PVAD operation. Transitional turbulence is observed during the 100% PVAD support in both the pulsatile and continuous modes due to the jet and its impingement on the aortic posterior wall. The correspondingly maximum principal normal Reynolds stresses are 7081 and 249 dyn/cm2, respectively. The pulsatile support increases hemolysis level in the aorta while the continuous support decreases it. The 100% pulsatile support causes a significant increase of hemolysis in the aorta than does the healthy aortic flow. Finally, the pulsatile mode gives higher time-averaged WSS and OSI distribution when compared to the continuous mode during both the intermediate and complete PVAD support. Overall, the pulsatile support provides better pulsatility, while the continuous support causes less blood damage.
ACKNOWLEDGMENTS
This work was supported by NIH NHLBI HV 48191. The authors would like to thank Jason Holmes and Jeff Nucciarone of the High Performance Computing Group at the Pennsylvania State University for their technical support with PC clusters. The authors would also like to thank Dr. Ajit Yoganathan and Mr. Chris Haggerty from the Department of Biomedical Engineering at the Georgia Institute of Technology for providing the pediatric aortic model.
REFERENCES
- 1.Moller JH, editor. Surgery of Congenital Heart Disease: Pediatric Cardiac Care Consortium 1984–1995. vol. 6. Armonk, NY: Futura Publishing Company; 1998. Prevalence and incidence of cardiac malformations; p. 20. [Google Scholar]
- 2.Baldwin JT, Borovetz HS, Duncan BW, Gartner MJ, Jarvik RK, Weiss WJ, Hoke TR. The National Heart, Lung, and Blood Institute pediatric circulatory support program. Circulation. 2006;113:147–155. doi: 10.1161/CIRCULATIONAHA.105.571422. [DOI] [PubMed] [Google Scholar]
- 3.Connell JM, Khalapyan T, Myers JL, Rosenberg G, Weiss WJ. Anatomic fit assessment for the Penn state pediatric ventricular assist device. ASAIO J. 2007;53:687–691. doi: 10.1097/MAT.0b013e318155741d. [DOI] [PubMed] [Google Scholar]
- 4.Dellgren G, Coles JG. Pediatric heart transplantation: improving results in high-risk patients. Semin. Thorac. Cardiovasc. Surg. Pediatr. Card. Surg. Annu. 2001;4:103–114. [PubMed] [Google Scholar]
- 5.Driscoll RJ, Kennedy LA. A model for the turbulent energy spectrum. Phys. Fluids. 1983;26:1228–1233. [Google Scholar]
- 6.Farinas MI, Garon A, Lacasse D, N’dri D. Asymptotically consistent numerical approximation of hemolysis. J. Biomech. Eng. 2006;128:688–696. doi: 10.1115/1.2241663. [DOI] [PubMed] [Google Scholar]
- 7.Figueroa CA, Vignon-Clementel IE, Jansen KE, Hughes TJR, Taylor CA. A coupled momentum method for modeling blood flow in three-dimensional deformable arteries. Comput. Methods Appl. Mech. Eng. 2006;195:5685–5706. [Google Scholar]
- 8.Fogel MA, Weinberg PM, Rychik J, Hubbard A, Jacobs M, Spray TL, Haselgrove J. Caval contribution to flow in the branch pulmonary arteries of Fontan patients with a novel application of magnetic resonance presaturation pulse. Circulation. 1999;99:1215–1221. doi: 10.1161/01.cir.99.9.1215. [DOI] [PubMed] [Google Scholar]
- 9.Fureby C, Grinstein FF. Large eddy simulation of high-Reynolds-number free and wall-bounded flows. J. Comp. Phys. 2002;181:68–97. [Google Scholar]
- 10.Fureby C, Tabor G, Weller HG, Gosman AD. A comparative study of subgrid scale models in homogeneous isotropic turbulence. Phys. Fluids. 1997;9:1416–1429. [Google Scholar]
- 11.Garon A, Farinas MI. Fast three-dimensional numerical hemolysis approximation. Artif. Organs. 2004;28:1016–1025. doi: 10.1111/j.1525-1594.2004.00026.x. [DOI] [PubMed] [Google Scholar]
- 12.Giersiepen M, Wurzinger LJ, Opitz R, Reul H. Estimation of shear stress-related blood damage in heart valve prostheses—in vitro comparison of 25 aortic valves. Int. J. Artif. Organs. 1990;13:300–306. [PubMed] [Google Scholar]
- 13.Grinstein FF, Fureby C. On flux-limiting-based implicit large eddy simulation. J. Fluid Eng. 2007;129:1483–1492. [Google Scholar]
- 14.Grinstein FF, Fureby C, DeVore CR. On MILES based on flux-limiting algorithm. Int. J. Numer. Methods Fluids. 2005;47:1043–1051. [Google Scholar]
- 15.Healy TM, Ellis JT, Fontaine AA, Jarrett CA, Yoganathan AP. An automated method for analysis and visualization of laser Doppler velocimetry data. Ann. Biomed. Eng. 1997;25:335–343. doi: 10.1007/BF02648047. [DOI] [PubMed] [Google Scholar]
- 16.Heiss KF, Clark RH, Cornish JD, Stovroff M, Ricketts R, Kesser K, Stonecash M. Preferential use of venovenous extracorporeal membrane oxygenation for congenital diaphragmatic hernia. J. Pediatr. Surg. 1995;30:416–419. doi: 10.1016/0022-3468(95)90045-4. [DOI] [PubMed] [Google Scholar]
- 17.Higdon A, Ohlsen E, Stiles WB. Mechanics of Material. New York: John Wiley & Sons; 1988. [Google Scholar]
- 18.Huo Y, Guo X, Kassab GS. The flow field along the entire length of mouse aorta and primary branches. Ann. Biomed. Eng. 2008;36:685–699. doi: 10.1007/s10439-008-9473-4. [DOI] [PubMed] [Google Scholar]
- 19.Issa RI. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1985;62:40–65. [Google Scholar]
- 20.Kent AL, Kecskes Z, Shadbolt B, Falk MC. Blood pressure in the first year of life in healthy infants born at term. Pediatr. Nephrol. 2007;22:1743–1749. doi: 10.1007/s00467-007-0561-8. [DOI] [PubMed] [Google Scholar]
- 21.Lacasse D, Garon A, Pelletier D. Development of an adaptive discontinuous-Galerkin finite element method for advection–reaction equations. Comput. Methods Appl. Mech. Eng. 2007;196:2071–2083. [Google Scholar]
- 22.Loth F, Fischer PF, Bassiouny HS. Blood flow in end-to-side anastomosis. Annu. Rev. Fluid Mech. 2008;40:367–393. [Google Scholar]
- 23.Machii M, Becker AE. Morphologic features of the normal aortic arch in neonates, infants, and children pertinent to growth. Ann. Thorac. Surg. 1997;64:511–515. doi: 10.1016/S0003-4975(97)00445-1. [DOI] [PubMed] [Google Scholar]
- 24.May-Newman K, Hillen B, Dembitsky W. Effect of left ventricular assist device outflow conduit anastomosis location on flow patterns in the native aorta. ASAIO J. 2006;52:132–139. doi: 10.1097/01.mat.0000201961.97981.e9. [DOI] [PubMed] [Google Scholar]
- 25.Minakawa M, Fukuda I, Yamazaki J, Fukui K, Yanaoka H, Inamura T. Effect of cannula shape on aortic wall and flow turbulence: hydrodynamic study during extracorporeal circulation in mock thoracic aorta. Artif. Organs. 2007;31:880–886. doi: 10.1111/j.1525-1594.2007.00481.x. [DOI] [PubMed] [Google Scholar]
- 26.Nose Y. Nonpulsatile mode of blood flow required for cardiopulmonary bypass and total body perfusion. Artif. Organs. 1993;17:92–102. [PubMed] [Google Scholar]
- 27.Ojha M. Spatial and temporal variations of wall shear stress within an end-to-side arterial anastomosis model. J. Biomech. 1993;26:1377–1388. doi: 10.1016/0021-9290(93)90089-w. [DOI] [PubMed] [Google Scholar]
- 28.OpenFOAM 1.5 User Guide. UK: OpenCFD Ltd; [Google Scholar]
- 29.Pantalos GM, Giridharan G, Colyer J, Mitchell M, Speakman J, Lucci C, Johnson G, Gartner M, Koenig SC. Effect of continuous and pulsatile flow left ventricular assist on pulsatility in a pediatric animal model of left ventricular dysfunction: pilot observations. ASAIO J. 2007;53:385–391. doi: 10.1097/MAT.0b013e318050d210. [DOI] [PubMed] [Google Scholar]
- 30.Pekkan K, Dur O, Sundareswaran K, Kanter K, Fogel M, Yoganathan A, Undar A. Neonatal aortic arch hemodynamics and perfusion during cardiopulmonary bypass. J. Biomech. Eng. 2008;130:061012. doi: 10.1115/1.2978988. [DOI] [PubMed] [Google Scholar]
- 31.Sallam AM, Hwang NH. Human red blood cell hemolysis in a turbulent shear flow: contribution of Reynolds shear stresses. Biorheology. 1984;21:783–797. doi: 10.3233/bir-1984-21605. [DOI] [PubMed] [Google Scholar]
- 32.Taylor KM, Bain WH, Maxted KJ, Hutton MM, McNab WY, Caves PK. Comparative studies of pulsatile and non-pulsatile flow during cardiopulmonary bypass I. Pulsatile system employed and its hematologic effects. J. Thorac. Cardiovasc. Surg. 1978;75:569–573. [PubMed] [Google Scholar]
- 33.Taylor GA, Martin GR, Short BL. Cardiac determinants of cerebral blood flow during extracorporeal membrane oxygenation. Invest. Radiol. 1989;24:511–516. doi: 10.1097/00004424-198907000-00001. [DOI] [PubMed] [Google Scholar]
- 34.Taylor KM, Wright GS, Bain WH, Caves PK, Beastall GS. Comparative studies of pulsatile and nonpulsatile flow during cardiopulmonary bypass III. Response of anterior pituitary gland to thyrotropin-releasing hormone. J. Thorac. Cardiovasc. Surg. 1978;75:579–584. [PubMed] [Google Scholar]
- 35.Taylor KM, Wright GS, Reid JM, Bain WH, Caves PK, Walker MS, Grant JK. Comparative studies of pulsatile and nonpulsatile flow during cardiopulmonary bypass II. The effects on adrenal secretion of cortisol. J. Thorac. Cardiovasc. Surg. 1978;75:574–578. [PubMed] [Google Scholar]
- 36.Thom T, Haase N, Rosamond W, Howard VJ, Rumsfeld J, Manolio T, Zheng ZJ, Flegal K, O’Donnell C, Kittner S, Lloyd-Jones D, Goff DC, Jr, Hong Y, Adams R, Friday G, Furie K, Gorelick P, Kissela B, Marler J, Meigs J, Roger V, Sidney S, Sorlie P, Steinberger J, Wasserthiel-Smoller S, Wilson M, Wolf P. and American Heart Association Committee and Stroke Statistics Subcommittee. Heart disease and stroke statistics–2006 update: a report from the American Heart Association Statistics Committee and Stroke Statistics Subcommittee. Circulation. 2006;113:e85–e151. doi: 10.1161/CIRCULATIONAHA.105.171600. [DOI] [PubMed] [Google Scholar]
- 37.Travis AR, Giridharan GA, Pantalos GM, Dowling RD, Prabhu SD, Slaughter MS, Sobieski M, Undar A, Farrar DJ, Koenig SC. Vascular pulsatility in patients with a pulsatile- or continuous-flow ventricular assist device. J. Thorac. Cardiovasc. Surg. 2007;133:517–524. doi: 10.1016/j.jtcvs.2006.09.057. [DOI] [PubMed] [Google Scholar]
- 38.Undar A, Masai T, Frazier OH, Fraser CD., Jr. Pulsatile and nonpulsatile flows can be quantified in terms of energy equivalent pressure during cardiopulmonary bypass for direct comparisons. ASAIO J. 1999;45:610–614. doi: 10.1097/00002480-199911000-00017. [DOI] [PubMed] [Google Scholar]
- 39.Undar A, Masai T, Yang SQ, Goddard-Finegold J, Frazier OH, Fraser CD., Jr. Effects of perfusion mode on regional and global organ blood flow in a neonatal piglet model. Ann. Thorac. Surg. 1999;68:1336–1342. doi: 10.1016/s0003-4975(99)00913-3. [DOI] [PubMed] [Google Scholar]
- 40.Vignon-Clementel IE, Figueroa CA, Jansen KE, Taylor CA. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Comput. Methods Appl. Mech. Eng. 2006;195:3776–3796. [Google Scholar]
- 41.Yang N, Deutsch S, Paterson EG, Manning KB. Hemodynamics of a end-to-side anastomotic graft for a pulsatile pediatric ventricular assist device. J. Biomech. Eng. doi: 10.1115/1.4000872. in press. [DOI] [PubMed] [Google Scholar]
- 42.Yang N, Deutsch S, Paterson EG, Manning KB. Numerical study of blood flow at the end-to-side anastomosis of a left ventricular assist device for adult patient. J. Biomech. Eng. doi: 10.1115/1.3212114. in press. [DOI] [PubMed] [Google Scholar]
- 43.Yano T, Sekine K, Mitoh A, Mitamura Y, Okamoto E, Kim DW, Nishimura I, Murabayashi S, Yozu R. An estimation method of hemolysis within an axial flow blood pump by computational fluid dynamics analysis. Artif. Organs. 2003;27:920–925. doi: 10.1046/j.1525-1594.2003.00034.x. [DOI] [PubMed] [Google Scholar]