Network Based Prediction Model for Genomics Data Analysis

Abstract

Biological networks, such as genetic regulatory networks and protein interaction networks, provide important information for studying gene/protein activities. In this paper, we propose a new method, NetBoosting, for incorporating a priori biological network information in analyzing high dimensional genomics data. Specially, we are interested in constructing prediction models for disease phenotypes of interest based on genomics data, and at the same time identifying disease susceptible genes. We employ the gradient descent boosting procedure to build an additive tree model and propose a new algorithm to utilize the network structure in fitting small tree weak learners. We illustrate by simulation studies and a real data example that, by making use of the network information, NetBoosting outperforms a few existing methods in terms of accuracy of prediction and variable selection.

1 Introduction

Molecular diagnostics refers to the diagnostic practice whereby clinicians make diagnoses based on the measurements of biological molecules. In the past decade, this field has attracted a large amount of attention due to recent advances in high throughput microarray technology. Many gene expression signatures have been identified, some even validated for potential clinical implications. One successful example is the 70-gene expression signature that has been shown to accurately predict the prognosis of patients with node-negative breast cancer [20, 19, 4, 3]. In these and similar studies, once gene expression microarray data and clinical phenotypes were collected for each patient, an analytical goal is to build an efficient prediction model for the clinical phenotypes based on the gene expression data. Specifically, suppose there are n patients in the study. Denote the clinical phenotypes of the n patients as Y_n×1, a vector of length n. Let p be the total number of genes on the array. Denote the expression data of the n patients as X_n×p, a matrix of n rows and p columns with row indicating subject and column indicating gene. The goal is to predict Y with some function of X denoted as f(X).

On a separate topic, biological functions involve molecular interactions following all kinds of mechanisms, such as metabolic/signaling pathways, regulatory networks and protein complexes. These interactions play essential roles in shaping the cell phenotypes. Large amounts of biological information on these interaction networks have accumulated in the literature. Intuitively, efficient use of this information will help to better characterize the important molecular changes in disease samples, and thus increase our understanding of the biological systems. Our objective in this paper is to introduce a new method for integrating the expression array data with the a priori biological knowledge on genes/proteins interaction network when constructing a prediction model for disease phenotypes. Specifically, represent the biological interaction network among genes/proteins with a graph G(V, E) such that each node (i ∈ V) in the graph represents one gene/protein, and an edge ((i, j) ∈ E) connects nodes i and j if the corresponding two genes/proteins interact with each other. We aim to fit a prediction model: Y ~ f(X, G).

A natural assumption about interaction network G and disease phenotype Y is that: the genes connected in the network shall influence Y in a coherent way. This can be interpreted in two aspects: (i) gene pairs connected in the network tend to be in or out of the prediction model simultaneously; (ii) gene pairs connected in the network may have strong interaction effects for predicting the outcomes. We refer to this assumption as the network-knowledge assumption hereafter.

Some pioneer work has been done to address the first aspect of the network-knowledge assumption under the framework of linear regression. [16] proposed to use spectral decompositions of gene expression profiles with respect to the eigenfunctions of the graph as predictors for disease phenotype in a ridge regression model. The final coefficient for each gene is “smooth along the network” in the sense that genes connected in the network tend to have similar coefficients. In another work, [13] introduced a regularized linear regression model with network-constrained penalties, which not only encourages the smoothness of the coefficients along the network but also controls the sparsity of the final model. Both papers successfully demonstrate the benefit of incorporating the a priori network information in the regression models. Nevertheless, forcing coefficients to be smooth along the network might not be a robust strategy when dealing with complicated biological systems. Suppose gene A is a significant predictor for the phenotype. While it is highly likely that other genes interacting with A shall serve as significant predictors as well, the directions and magnitudes of the influences of those genes on the phenotype are not necessarily the same as that of A. In a follow-up paper, [14] extended their network-constrained regularization regression model to allow for the possibility of different signs of the regression coefficients for neighboring variables. More recently, [15] proposed to enforce the network constraints on variable selection instead of on coefficient estimation. They adopted the Bayesian variable selection framework and utilized an Ising prior on the model space to encourage the smoothness of variable selection along the network, which appears to be a more appropriate assumption for handling the complicated biological system compared to the assumption of smooth coefficients.

While linear regression is an effective tool for solving prediction problems, it is limited in terms of modeling the higher level interactions among covariates — the second aspect of the network-knowledge assumption mentioned above. As mentioned earlier, interactions among genes play significant roles in shaping the phenotypes of cells. Thus, the efficiency of the methods is compromised if these interactions are ignored. To bridge this gap, in this paper, we propose a new algorithm NetBoosting that accounts for both aspects of the network-knowledge assumption. The algorithm builds additive tree models to predict the outcome Y. Trees are well-known powerful tools for modeling the complicated interactions among covariates. In NetBoosting, we propose a new way to build trees that makes direct usage of the topology of the biological network. Specifically, we limit the search space of interaction effects to the gene pairs closely linked in the biological network. The structures of the resulting trees then resemble the topologies of neighborhoods in the network. And thus, the final tree model not only nicely incorporates the interactions among genes closely linked in the network, but also encourages the smoothness of variable selection along the network. Since individual tree models usually have limited prediction power, we further adopt boosting techniques, which has been demonstrated to enhance the prediction power [5, 6, 8, 7]. The performances of the proposed methods are illustrated through simulation studies and one breast cancer expression data, in which we investigate changes in the accuracy of prediction and variable selection when usage of the network information varies.

The rest of paper is organized as follows. In Section 2, we present in details the NetBoosting algorithm. In Section 3, we illustrate the performance of the proposed methods to a series of simulation examples. In Section 4, we apply the method to a breast cancer expression data set. We conclude the paper with a brief summary in Section 5.

2 Method

Before introducing the NetBoosting algorithm, we will first review the gradient descent boosting procedure.

2.1 Review of gradient descent boosting

Boosting is a method for iteratively building an additive model F(x) = Σ_j α_jh_j(x) to minimize the empirical loss function $\mathcal{L}\{Y,F(X)\}=n^{-1}{\sum }_{i=1}^{n}L\{y^i,F(x^i)\}$. Here h_j ∈ and is a large family of candidate predictors or “weak learners”; yⁱ and xⁱ denote the outcome and predictors of the i^th subject. In [8], the authors raised a statistical perspective that connects the boosting methods with forward stagewise (FS) modeling (see Algorithm 1). When y belongs to {−1, 1}, the loss function L(y, F) = exp(−yF) and ε = 1, the above FS algorithm is exactly the popular Adaboost [6]. In addition, the shrinkage parameter ε in the algorithm provides a regularization mechanism for boosting. It has been shown that, for least square loss function L(y, F) = (y − F)², if we consider linear regression and set the candidate predictor family = {X_i}, then the solution path of FS is strikingly similar to the solution path of lasso for small ε values [9, 2]. This suggests that, besides the superior prediction power, boosting is also capable to do variable selection and coefficient shrinkage, which makes it particularly appealing for high dimensional problems.

Algorithm 1.

Forward stagewise

Initialize F0(X) = 0. For m = 1 to M: For b(·, γ) ∈ , compute $$({\beta }_m,{\gamma }_m)=arg\underset{\beta ,\gamma }{min}\mathcal{L}\{Y,F_{m-1}(X)+\beta b(X,\gamma )\}.$$ Set Fm(X) = Fm−1(X) + εβmb(X; γm), where ε is a small number for shrinkage.

When the loss function L and/or the function family are complicated, the optimization step in 2(a) of the FS algorithm could be very challenging. Thus, [7] further proposed the gradient descent boosting method, which solves 2(a) approximately using the steepest-descent approach (see Algorithm 2). Based on the framework of gradient descent boosting, in the following section, we introduce the new NetBoosting algorithm which incorporates the a priori network information into the prediction model.

Algorithm 2.

Gradient descent boosting

Initialize F0(X) = 0. For m = 1 to M, let Fm(X) = Fm−1(X) + ερmgm(X), where $$g_m(X)=-{\left[\frac{\partial \mathcal{L}\{Y,F(X)\}}{\partial F(X)}\right]}_{F(X)=F_{m-1}(X)};$$ (1) and ρm is given by the line search ρm = arg minρ {y, Fm−1(X) + ρgm(X)}.

2.2 Tree model

We first introduce a new way for building a single tree model. Recall the two aspects of the network-knowledge assumption: (i) gene pairs connected in the network tend to be in or out of the prediction model simultaneously; (ii) gene pairs connected in the network may have strong interaction effects for predicting the outcomes. While the ultra large number of possible two-way or higher order interactions pose great difficulties for modeling interaction effects in prediction models, the availability of a priori network information enables us to constrain the search space of interactions to a much smaller subset.

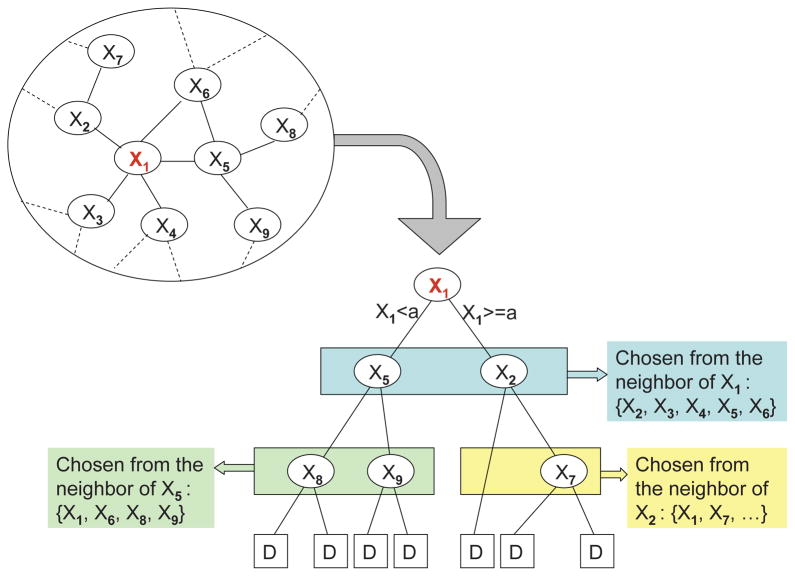
Specifically, we propose to grow trees along the network topology. The idea is to constrain the splitting variables of the child nodes in the tree to be the network neighbors of the splitting variables of the parent nodes in the tree. We use a simple example shown in Figure 1 to illustrate this idea. Note that neighborhood considered here and subsequently in the text is of degree one, unless specified otherwise. Suppose we are interested in building a tree with X₁ as the root node, whose neighborhood in the network is plotted in the top-left circle in Figure 1. After we split the observations into two parts based on X₁ < a and X₁ ≥ a, we shall only consider the network neighbors of X₁ ({X₂, X₃, X₄, X₅, X₆}) as candidate splitting variables for the second level nodes in the tree. Similarly, suppose the optimal splitting for the left (right) branch is based on X₅ (X₂), then the candidate splitting variables for the corresponding third level nodes are the one degree network neighbors of X₅ (X₂). In this way, the splitting variables of each tree belong to a connected neighborhood in the network, and thus the variable selection of the final model tends to be smooth along the network. Moreover, the proposed strategy can also be viewed as a regularization on the model space: only interactions among closely linked variables in the network are considered in the tree model. Since when analyzing genomic data, the parameter dimension (p) is usually much larger than the sample size (n), proper regularization on model space is rather important, which shall help to enhance the efficiency and robustness of the resulting model.

Figure 1.

An example for illustrating the idea of growing weaker learner trees along the network in NetBoosting.

Note that for each singleton in the network (i.e. variable with empty neighborhood), we allow for construction of weak learner tree just based on the variable itself. In other words, only main effect for a singleton variable is modeled. Here our goal is to achieve better risk prediction by incorporating auxiliary information about interactions among candidate genes determined by their relationships in the network, which is used to restrict the search space when considering interactions among genes. Thus, with a priori knowledge that certain genes have no connection with others in the candidate set, it seems reasonable to model their main effects only in the boosting steps.

2.3 NetBoosting

Using trees described above as weak learners in gradient descent boosting, we propose the NetBoosting (NetB) algorithm, as outlined in the table of Algorithm 3.

In NetB, instead of estimating the optimal step length by doing a linear search, we choose to move a fixed length ν along the selected tree direction. By setting ν to be a small value, regularization is imposed on the boosting process, which helps to maintain the robustness of the numerical optimization process and also facilitates the variable selection. Moreover, the total number of boosting steps (M) is a tuning parameter in the NetB algorithm, which can be selected by examining the prediction errors estimated from a separate testing dataset or through cross validation.

The proposed method relates closely to two existing methods: the gradient boosting tree (GBT) algorithm [7] and the nonparametric pathway based regression (NPR) method [21]. GBT is an immediate extension of the gradient descent boosting method (Algorithm 2), which utilizes small regression tree models to approximate the gradient descent direction g_m(X) in each boosting iteration. While GBT takes into no consideration of the information on the relationships among predictors, NPR is designed to take advantage of the known biological pathway information of genes when building the boosting tree models. Particularly, in NPR, each weak learner tree only involves genes coming from the same biological pathway. This constraint was motivated from the same assumption as we used to develop NetB, that interactions among functionally related genes could contribute significantly to predict the disease outcomes. However, merely utilizing the pathway information while ignoring the interaction patterns among genes within pathways makes the method less ideal, as biological “pathways” typically have very complex interaction patterns and such patterns usually play significant roles in shaping the cell phenotypes. Thus, by further taking into consideration the topology of the interaction patterns among pathway components, NetB could be more efficient than NPR, as will be demonstrated later in numerical studies.

Algorithm 3.

NetBoosting

Initialize F0(X) = 0. For m = 1 to M (boosting steps), Calculate the gradients w.r.t Fm−1(X) over observed samples $${\stackrel{\sim }{y}}^i=-{\left[\frac{\partial L\{y^i,F(x^i)\}}{\partial F(x^i)}\right]}_{F(x^i)=F_{m-1}(x^i)},i=1,\dots ,n.$$ Fit regression trees to the gradient vector {ỹi}. For each j = 1, ···, p, Begin with Xj and grow a tree hj(X) along the network topology. Specifically, splitting variable for a child node is selected from the network neighborhood of the splitting variable for its parent node (when this neighborhood is not empty) or otherwise is chosen as the same splitting variable for the parent node. Pick the best tree among ${\{h_j(X)\}}_{j=1}^p$ to be Tm(X). For a given learning rate ν, update Fm(X) = Fm−1(X) + νTm(X).

We also want to point out that, when fitting regression trees in each iteration, NetB first build p trees with each variable serving as the root node variable once, and then select the best among the p trees. Such a strategy could achieve better performance than first selecting the root node variable based only on its marginal performance as commonly done in practice, due to the fact that an important predictor having a significant interaction effect may not have a strong marginal effect. This extra “optimization” is computationally feasible here because we have imposed regularizations on the search space according to a priori information on the network structure. Specifically, the computational cost of one boosting step in NetB is about O(pL^K), where L is the maximum neighborhood size in the network, and K is the total number of splitting nodes allowed in each weak learner tree. On the other hand, the computational cost of one boosting step in GBT is about O(p^K). So, for large p and small L (sparse network), the computational cost for NetB is at a much smaller scale than that for GBT. In addition, the computational cost for one boosting step in NPR is about O(MH^K), where M is the total number of pathways and H is the size of the largest pathway. Usually H shall be larger than L, and thus the computational cost of NetB should be at least comparable to if not smaller than that of NPR.

2.4 NetBoosting for directed network

In some biological networks, the interaction relationships among genes have intrinsic directions. For example, in a genetic regulatory network, upstream genes in a pathway regulate the downstream genes in the same pathway; and in a cancer oncogenic-pathway network, tumor initiation mutations that cause genome instability proceed other disease mutations resulting from genome instability. The directions of interactions in these network may also contribute helpful information towards building a good prediction model by further restricting the search space. In this section, we discuss a modified NetBoosting algorithm that handles directed graph.

We take the the cancer oncogenic-pathway networks as a motivating example. A cancer oncogenic-pathway network consists of a series of genetic (or proteomic) events whose accumulation gradually turns a normal cell into a tumor cell. It often starts with one or multiple driver mutations and “progress” as each new mutation leads to a slightly increased disease risk. To make use of such knowledge about disease developing mechanism when building the prediction model, an intuitive idea is to force the “flow” of the weak learner trees in the boosting process to assemble the “flow” of the directed graph. Specifically, we propose to select the splitting variable of a child node in a weak learner tree among the descendent neighbors of the splitting variable for its parent node in the directed graph. When an edge is bi-directed, the two vertices at the opposite ends of the edge are deemed as neighbors of each other, such that if the variable for one vertex is used to split a parent node in the tree construction, the variable for the other vertex will be considered as one candidate for splitting the corresponding children nodes. Employing this new way of building h_j(X) in step 2.2 (a) of Algorithm 3, we get a modified NetBoosting algorithm, which is referred to as NetBD hereafter.

2.5 Variable importance score

To facilitate the interpretation of the final model, we adopt the variable importance scores proposed by [1] and [7] to evaluate the contribution of each variable in the final model. For a single tree model, the importance of one predictor can be measured by the overall “improvement” achieved when this predictor is selected as a splitting variable in the tree [1]. Specifically, the importance score of the j^th variable is defined as $I_j^2(T)={\sum }_{t=1}^K{\widehat{i}}_t^{2}I\{v(t)=j\}$, where K is the number of internal nodes, v(t) is the splitting variable for the t^th internal node and ${\widehat{i}}_t^2$ is the reduction in sum of squared error as a result of the split at this particular node. For an additive model with M trees, we summarize the importance of the j^th variable as the average of its importance over all M trees, i.e., $I_j^2={\sum }_{m=1}^M{I}_j^2(T_m)/M$ [7]. We further scale the importance scores to make ${max}_j{I}_j^2=1$. These scores provide useful information for the purpose of variable selection.

3 Simulation

In this section, we conduct simulation studies to assess the impact of exploiting a priori network information on prediction model building. We will focus on binary outcomes (Y ∈ {1, −1}), and use binomial loss function:

$$L\{Y,F(X)\}=\sum _{i=1}^{n}L\{Y_i,F(X_i)\}=\sum _{i=1}^{n}log[1+exp\{-2Y_{i}F(X_i)\}]$$

We compare the performance of NetB and NetBD with two existing methods: the Gradient Boosting Tree (GBT) algorithm [7] and the nonparametric pathway based regression (NPR)[21]. For the latter we construct regression trees based on either known biological pathways or pathways derived from the interaction network as will be shown next (see section 2.3 for more details about GBT and NPR).

3.1 Data generation

We consider examples for both undirected and directed networks.

Simulation I and II — Undirected network

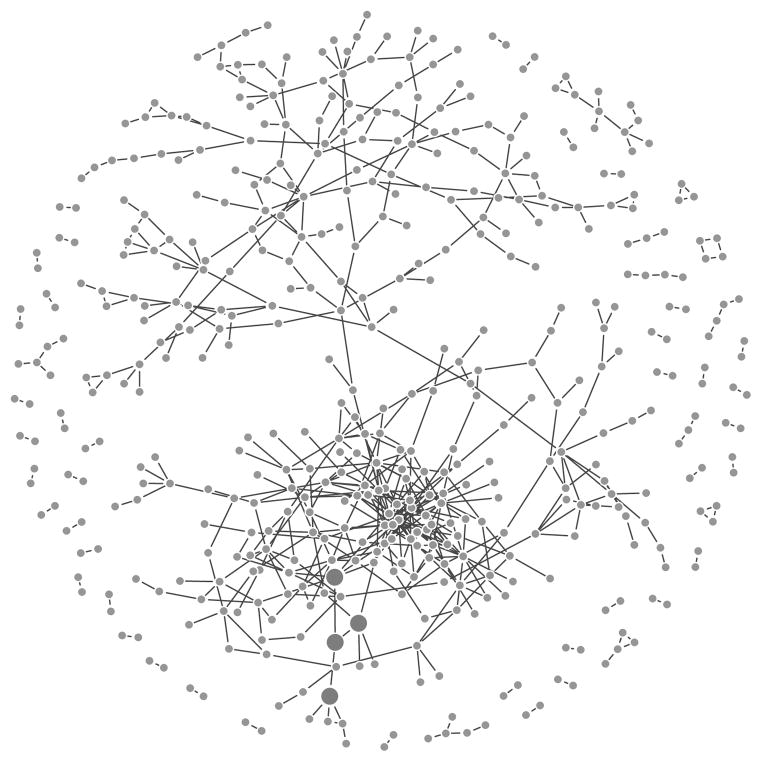
The first two simulations are for undirected networks in which an empirical gene interaction network is derived from a breast cancer expression array dataset. Specifically, the array data and clinical information for 244 breast cancer patients are obtained from the public website of the Netherland Cancer Institute. Among the 24136 genes/clones in the array data set, we select 794 genes/clones whose expression levels are significantly associated with the patient survival outcomes based on univariate Cox regression (false discovery rate ≤ 0.01). We then estimate the concentration matrix Σ⁻¹ = [(σ^ij)] of these 794 genes using the space algorithm [12]. Under the gaussian assumption, σ^ij ≠ 0 implies that the i^th and j^th variables are conditional dependent. In our case, this suggests that the activities of the i^th and j^th genes relate to each other. The resulting concentration network is illustrated in Figure 2: each vertex represents one gene, and an edge connecting two vertices if the corresponding σ̂^ij ≠ 0. We then generate X based on the estimated concentration matrix Σ̂⁻¹. Specifically, set p = 794 and for i = 1, ···, n, we generate $X^i={(X_1^i,\dots ,X_p^i)}^T$ independently and identically from N(0, Σ̂).

Figure 2.

Undirected network structure of the genes in the simulation settings (I) and (II) (only those with at least one neighbors are shown). The large dots indicate the genes involved in the risk models: genes from X₁ ∪ A₁. Please see the text for details of the risk models.

We consider two different risk models varying in degrees of complexities. In each model, a gene X₁ and its neighborhood in the concentration network, denoted as A₁ = {X₂, X₃, X₄}, contribute to the disease risk.

I) Polynomial model

$$\frac{1}{2}\text{logit}\{P(Y=1\mid X)\}=0.6X_1+0.6X_2+X_1{X}_2-X_1{X}_3.$$

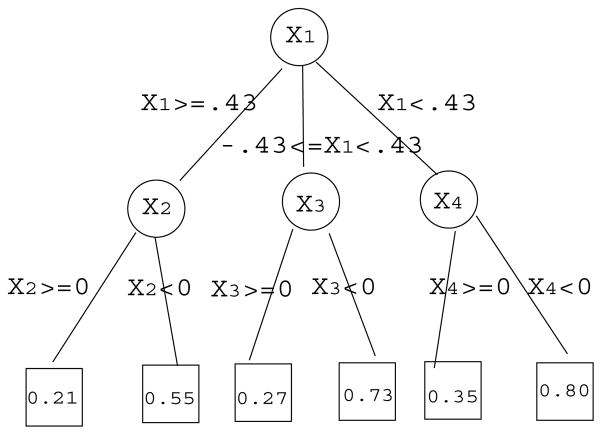
II) Ternary tree model

X₁ is the top node and X₂, X₃, X₄ are the lower level nodes. The structure of the ternary tree is also displayed in Figure 3.

Figure 3.

The disease risk model for the ternary tree model in simulation setting (II).

$$\begin{array}{l}\frac{1}{2}\text{logit}\{P(Y=1\mid X)\}=-2.8+1.5I(X_1\ge 0.43)I(X_2\ge 0)+3I(X_1\ge 0.43)I(X_2<0)\\ +1.8I(-0.43\le X_1<0.43)I(X_3\ge 0)+3.8I(-0.43\le X_1<0.43)I(X_3<0)\\ +2.2I(X_1<-0.43)I(X_4\ge 0)+4.2I(X_1<-0.43)I(X_4<0).\end{array}$$

In simulations I and II, comparisons are made between NetB, NPR, and GBT. Here NPR is an extended version of what was proposed in [21] in the sense that it utilizes “pathways” derived from the interaction network. Specifically, neighborhood of each non-singleton node in the network or the singleton itself is considered as one input pathway, which leads to 794 pathways in total.

Simulation III — Directed network

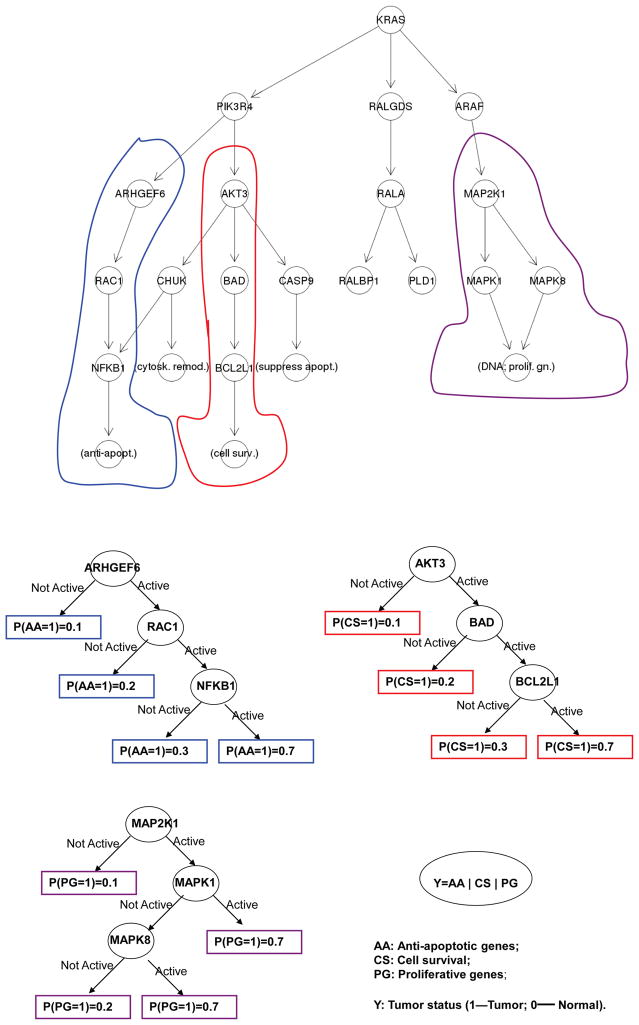
For the third simulation, we use part of the initiation pathway of pancreatic cancer from the KEGG database (upper panel of Figure 4) as the known directed network. 18 genes are involved in this pathway including anti-apoptotic genes, cytoskeleton remodeling genes, cell survival genes, DNA proliferative genes, and genes suppressing apoptosis. The disease model used in our simulation is illustrated in the bottom panels of Figure 4. Specifically, we assume three different subsets of genes (overall 9 of them in this pathway) controlling anti-apoptosis, cell survival, and DNA proliferation respectively contribute to pancreatic cancer risk. And in each subset, genes interact with each other on disease risk through a tree structure along the directed regulatory pathway.

Figure 4.

Pancreatic cancer initiation pathway for simulation setting (III). 15 Top panel: the regulatory pathway, genes circled contributed to pancreatic cancer risk; Bottom four panels: the pancreatic cancer risk model based on the three subset of genes. Here, “Active” (“Not Active”) means the expression level of the splitting gene is greater (less) than 0.

We then utilize sample covariance matrix of the 18 genes derived from the normalized expression array data of 22 pancreatic cell lines (downloaded from http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE21654) to generate data matrix. Denote the sample covariance matrix of the 18 genes as S. We make a block matrix of dimension 18 × 30 = 540 with each diagonal block being S. In the end, we simulate each observation vector of length 540 from a multivariate normal distribution with variance equal to this big block matrix, and use the 9 selected genes in the first block to generate Y according to the disease model in Figure 4.

In simulation III, comparisons are made between NetB, NetBD, NPR, and GBT. Here for NetBD the neighborhood of a node comprises its children in the directed pathway, while for NetB the neighborhood of a node comprises both its parents and children in the directed pathway. For NPR, each block of 18 genes is considered a pathway with 30 pathways in total.

Simulation IV — Effect of mis-specifications of the network structure

In this simulation, we are interested in evaluating the robustness of the proposed NetBoosting procedure to mis-specifications of the network structure. Specifically, we consider the directed network example in Simulation III, and study the impact of perturbing the underlying network on the performance of NetBD. For A% = 20%, 40%, and 60% respectively, we perform three types of perturbations:

1. False positives: we randomly add A% * 540 noise directed edges to the network, where 540 is the total number of true edges in the network;

2. False negatives: we randomly remove A% true edges from the network;

3. Reverse directions: we randomly reverse the direction of A% edges in the network.

The perturbed network structures are then fed to NetBD to build the prediction models.

In all four simulation settings, we generate 100 independent training sets of size 244 and one test set of size 100,000. For each training data, we apply all methods and record the corresponding classification errors on the testing dataset at each boosting iteration for up to 500 iterations; the total iteration number for boosting is the only tuning parameter, selected to minimize the testing error. All other parameters are fixed to be the same for fair comparison. Specifically, the neighborhood is of degree one; the maximum depth of weak learner trees is set to be 2 (4 leaves at most); and the learning rate ν is set to be 0.05.

3.2 Result

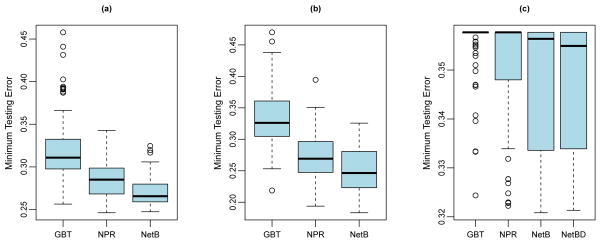
Figure 5 shows the optimal testing error rates across boosting iterations each method can achieve for the 100 training data sets, under correctly specified network structure (simulations I–III). For all risk models considered, exploiting network structure in boosting (NetB, NetBD, or (extended) NPR) leads to reduced testing errors compared to GBT. In the scenario of undirected network (the polynomial and ternary tree models) (Figures 5(a),(b)), the NetB procedure achieves the best precision. In the scenario of directed network, both NetB and NetBD perform better compared to NPR and GBT, with the performance of NetBD slightly better than NetB.

Figure 5.

Distribution of minimum testing error achieved using GBT, (extended) NPR, NetB, and NetBD (if applicable) for each simulation setting: (a) polynomial model, (b) ternary tree model, and (c) directed network model.

Compared to GBT, the reduction in median testing error is 8.3% for extended NPR and 14.6% for NetB for the polynomial model; 17.5% for extended NPR and 24.4% for NetB for the ternary tree model. For both models, all the boosting procedures are in general effective in terms of leading to smaller testing error compared to simply classifying a subject as diseased with a probability equal to the disease prevalence in the population. In contrast, for the more complicated directed regulatory pathway model, it is more challenging to build a prediction model out of the high-dimensional gene set. The proportion of effective boosting procedures are 19% for GBT, 40% for NPR, 54% for NetB, and 59% for NetBD. Compared to GBT, the reduction in median testing error is 0% for NPR, 0.4% for NetB, and 0.8% for NetBD.

We then compare the various boosting procedures with respect to their capacities for variable selection. Specifically, for each training set, we consider the models achieving the optimal testing errors and calculate the corresponding variable importance scores for all selected genes. We then derive the receiver operating characteristic (ROC) curves based on these scores to characterize models’ variable selection power. Figure 6 displays the ROC curves for the three different settings. Here specificity given a threshold c is defined as the average probability that an irrelevant gene has an importance score smaller than or equal to c, and the sensitivity given c is defined as the average probability that a relevant gene has an importance score larger than c. For both polynomial and ternary tree models (Figures 6(a)(b)), NetB and extended NPR show superior variable selection performance compared to GBT, with the performance of NetB slightly better. For the directed network, NetBD has the best variable selection performance and GBT the worst. The comparison between NetB and NPR depends on the threshold for importance score: NetB performs better when more stringent thresholds are chosen.

Figure 6.

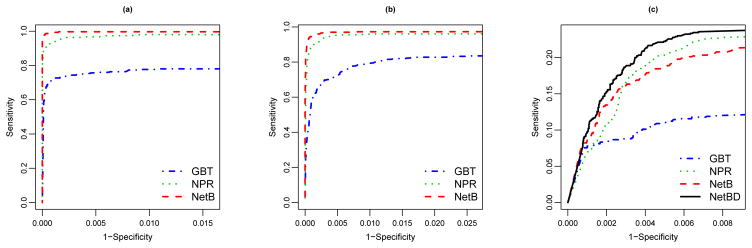
ROC curves for GBT, (extended) NPR, NetB and NetBD (when applicable) when risk model is polynomial (a), ternary tree (b), and directed network (c). Sensitivity is the average probability that a relevant gene is identified, and specificity is the average probability that an irrelevant gene is excluded.

Table 1 presents results comparing performance of different boosting procedures with respect to the capacities to select all relevant genes and to exclude all irrelevant genes. Define zero false negative(zero-FN) as the case that all relevant genes are selected; and zero false positive(zero-FP) as the case that none of the irrelevant genes are selected, with a threshold of zero for importance score. For the polynomial and ternary tree models, NetB and extended NPR both have above 90% probability of identifying all relevant genes (zero-FN), whereas the probability is only 34% in GBT; NetB also has the highest probability of excluding all irrelevant genes (zero-FP). For the more complicated directed network model, it is unlikely for any procedure to select all relevant genes altogether. Instead, we examined the probability that at least one of the three subsets of relevant genes are selected altogether. NetBD performs best, followed by NetB, NPR, and then GBT. The same order is observed in terms of the probability of excluding all irrelevant genes in this setting.

Table 1.

Percentage of zero false negative (zero-FN) and zero false positive (zero-FP) in the simulation results. Here zero-FN refers to cases where any gene related to disease risk has positive importance score; and zero-FP refers to cases where any gene unrelated to disease risk has zero importance score.

	GBT	NPR	NetB	NetBD
	Polynomial
% with zero-FN	34	94	99
% with zero-FP	6	16	31
% with zero-FN and zero-FP	6	16	31
	Ternary tree
% with zero-FN	50	84	89
% with zero-FP	2	15	20
% with zero-FN and zero-FP	0	10	15
	Directed Network
% with zero-FN	0	0	0	0
% with zero-FP	0	17	18	28
% with zero-FN in any subseta	1	10	24	29
% with zero-FN in any subseta and zero-FP	0	0	3	10

^aa relaxed criteria is used where a zero-FN is defined if any of the three subsets related to disease risk are fully selected.

In the end, to evaluate the robustness of the proposed NetBoosting procedure to mis-specifications of the network structure, we calculate the ratio of optimal testing error achieved by NetBD using the perturbed networks v.s. using the true network (simulation IV). The results for 100 training sets are summarized in Figure 7. All the density curves of optimal testing error ratios have means anchoring at 1.0; and the relative increases in optimal testing error due to using perturbed network are below 5% (i.e. ratio < 1.05) in 98% of training sets for all three types of perturbations. These results suggest the performance of NetBD is rather robust to the level of perturbations considered here. Among the three types of perturbations, false positive edges have the least impact on testing errors in terms of the spread of the testing error ratios, while edges with reverse directions have the largest impact on testing errors.

Figure 7.

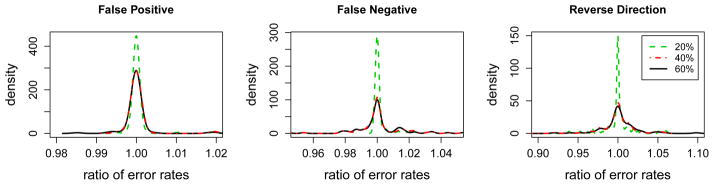
The distributions (density curves) of the ratios between optimal test error rates based on the perturbed networks v.s. the error rates based on the true network applying NetBD to 100 independent training data sets (simulation IV). The left, middle and right panels correspond to three different types of perturbations of the network structure. The different curves in each panel represent different degrees of perturbations (as illustrated in the legend).

4 Real Application

We apply our proposed methods to the breast cancer expression data described in Section 3. Using survival at year 5 as the binary disease outcome, our analysis set includes 234 subjects uncensored before year 5. We focus on the top 1000 genes which are most significantly associated with the survival outcome according to their marginal p-values in the Cox regression models. This first step screening helps to reduce the dimensionality of the original dataset. In general, constructing a prediction model in a super high-dimensional space with sparse signals could result in severe overfitting in the sense that the model’s performance when applied to a testing data is much inferior to its performance in the training data. The first step selection based on marginal analysis is important to subsequent model-building by filtering out substantial “noise” in the dataset.

We obtain information of 215 directed regulatory pathways from the KEGG database. Overall, 191 out of the 1,000 genes in the expression dataset appear in one of the 152 different KEGG pathways; 99 of the 152 pathways contain more than one of the 1000 genes, with the number of genes within each pathway ranges from 2 to 57. The union of these pathways gives a directed network, in which there are 96 edges in total, and 49 nodes have non-empty descendent neighborhoods. In addition, the skeleton of this directed network naturally serves as an undirected network, in which 74 genes have non-empty neighborhoods.

Based on trees of depth 2, we compare performances of NetB, NetBD, to that of GBT, and NPR. Here GBT serves as a reference method that does not use the a priori pathway information. NPR makes use of the pathway information but do not explicitly exploit the network topology when constructing the weak leaner trees. In addition, in NPR, only genes appearing in the same pathways can be used together to build a tree; whereas in NetBD and NetB, genes not in the same pathway can appear together in a tree as long as they share a common parent in NetBD, or is directly connected to a common gene in NetB.

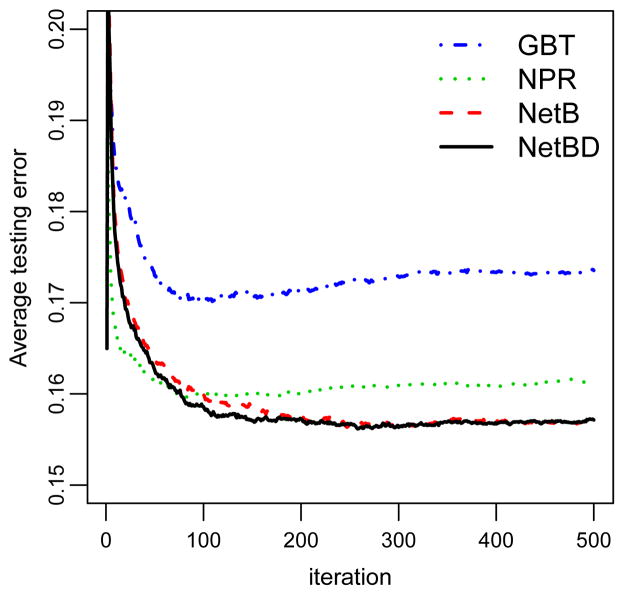
We employ 2,000 random cross-validations to assess the performances of these methods. In each cross-validation, the data is randomly split into two parts: about 9/10 observations as the training set and the rest 1/10 observations as the testing set. Figure 8 displays the average cross-validation testing errors versus boosting iterations for each algorithm. The three network-related procedures — NetBD, NetB, and NPR — outperform the GBT procedure with NetBD and NetB performing best and having pretty similar cross-validation errors.

Figure 8.

Average cross-validation error versus iteration for GBT, NPR, NetB, and NetBD in the breast cancer data set.

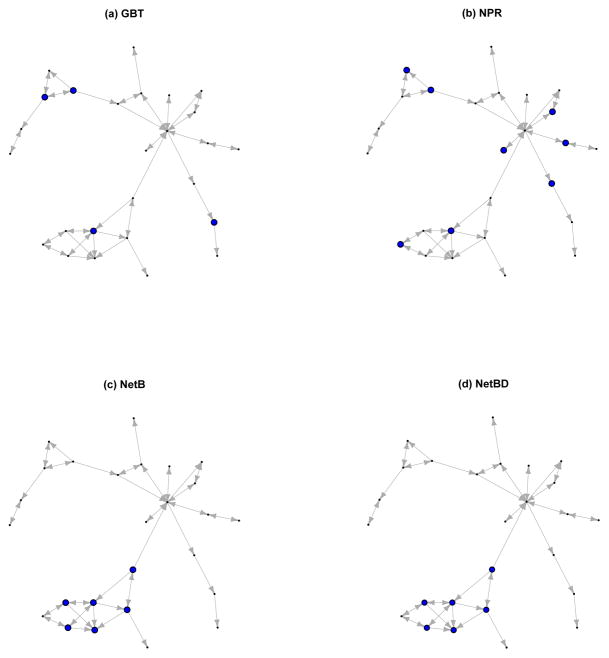
Based on the iteration where the minimum average testing error is achieved (258, 247, 88, and 98 for NetBD, NetB, NPR, and GBT respectively), we investigate genes selected by the four boosting procedures. The number of genes selected by NetBD, NetB, and NPR are 52, 51, and 54 respectively; and a much larger number 77 is selected by GBT. The directed network based on NetBD consists of 14 connected neighborhoods with the number of components ranging from 2 to 26. Figure 9 highlights the selected genes on the largest connected neighborhood, which includes 26 genes spanning 32 of the KEGG pathways involved in processes such as steroid biosynthesis, lysine degradataion, and arginine and proline metabolism. All three network-related boosting procedures tend to select more genes in this connected neighborhood, with genes selected by NetB and NetBD more densely connected compared to genes selected by NPR.

Figure 9.

Genes identified by (a)GBT, (b)NPR, (c)NetB, and (d)NetBD procedures. The large dots in the plots indicate genes with important score greater than zero.

An interesting gene — PCNA (proliferating cell nuclear antigen) — ranks 1^st by variable importance scores in both NetBD and NetB. PCNA is a BRCA1-associated component required for efficient sister chromatid cohesion and has been shown to be associated with survival in early breast cancer [17]. For comparison, PCNA ranks 3^rd in NPR and 42^nd by GBT, suggesting the impact of extracting potentially useful pathway or network information prior to gene identification.

5 Discussion

In this paper, we introduce new methods — NetB and NetBD — for incorporating a priori information about biological network when building prediction models. NetB is designed to handle undirected graphs, while NetBD is for directed graphs. Both methods build additive tree models utilizing the gradient boosting procedure. The weak learners in each boosting iteration are small trees whose topologies mimic the topologies of neighborhoods in the network. Such tree models help to characterize the interaction effects of functionally related genes in the final prediction model, under the assumption that functionally related genes are closely connected in the network. Furthermore, focusing on a small neighborhood in the network when building a tree helps to reduce the search space while maintain the quality of model fitting.

The proposed methods relate closely to the nonparametric pathway based regression (NPR)[21], which constructs regression trees based on known biological pathways. The key difference between NetB (NetBD) and NPR is the former takes into consideration the interaction patterns among genes within the same pathway during the tree construction. In the simulation studies, we compare the performance of NetB (NetBD) with that of NPR and GBT. The results suggest that proper usage of a priori network information in NetB (NetBD) leads to better accuracy in both prediction and variable selection. When various methods are applied to a breast cancer dataset, NetB and NetBD achieve slightly better cross-validation error rates. In addition, genes selected by NetB and NetBD are more densely connected in the network, and thus the results are more interpretable in terms of biological insights.

Based on our simulation settings, we find the proposed procedure is relatively robust to a few different perturbations on the network structure. There are possible ways to further enhance the robustness of the proposed methods. For example, we can include variables selected in the earlier boosting steps in the search space for weak learner tree in the later boosting steps, which allows the interactions among genes from different part of the network. Moreover, when network structure is based on the estimated concentration matrix from an existing data, an ensemble idea can be entertained by re-sampling the data to acknowledge the variability in the network structure. Those are the topics for future research.

In all of the numeric examples studied in the paper, a tree-depth of 2 is pre-determined for building weak learners in all the methods. For boosting methods applied to the high dimensional problem with sparse signals, it is beneficial to keep weak learners simple to minimize the over-fitting issue. Thus we choose to use a simple tree function in each boosting iteration that accounts for two-way interactions only. In our software package, however, we provide the options for users to specify other depth values when exploration of multi-way interactions are of interest. Another parameter that has been fixed in the model-building is the neighborhood degree which is chosen to be one. In practice, we believe the degree of the neighborhood should be pre-determined based on our faith about the quality of the network structure and the dimension of the search space. In general, we recommend using small neighborhoods when dealing with high-dimensional data, in order to constrain the search space and alleviate the overfitting issue. In the breast cancer example, we have further explored this issue by increasing the neighborhood degree, and found that using neighborhood of degree two in NetB and NetBD methods leads to larger cross-validation error compared to neighborhood of degree one (details omitted).

The proposed algorithms are implemented with efficient computer programs. It took about 5 seconds to process a data set with 244 samples and 500 genes using an Intel Xeon X5670 3.33GHz processor. The R package NetBoosting is available from the authors upon request. It will also be made available through CRAN shortly.