When, why, and how does like like like?

Abstract

In the Derjaguin-Landau-Verwey-Overbeek (DLVO) framework of the past 60 years, colloidal interaction between similarly charged particles has been claimed to be simply repulsive, and an attraction such as the van der Waals interaction is attached to the Coulombic repulsion. Statistical-thermodynamic considerations show that the electrostatic Helmholtz free energy ΔF^el is generally not equal to the electrostatic Gibbs free energy ΔG^el for simple ionic solutions, and the difference ΔG^el–ΔF^el (corresponding to the electrostatic osmotic pressure p^el) becomes larger with increasing charge number. Thus, it is expected that ΔG^el–ΔF^el be large for highly charged macroions. In the DLVO framework, however, ΔG^el = ΔF^el was postulated. Sogami showed that a mean field approach reproduced repulsion at the level of ΔF^el but resulted in (repulsion and) attraction at the level of ΔG^el. Overbeek’s critique of Sogami theory is shown to be in error. If this criticism were correct, then not only the Sogami theory but also the Debye-Hückel theory would be wrong. The attraction is thus confirmed to exist not only for multi-valent but also mono-valent counterions.

Introduction

In a series of previous publications,¹⁾ we have experimentally demonstrated that the distribution of ionic solute species in condensed systems such as solutions or colloidal dispersions is not homogeneous in contrast to frequent presumptions explicitly or implicitly invoked in theoretical considerations. In other words, the solute distribution can be non-space-filling. Such an inhomogeneous distribution was taken by us to be due to an electrostatic (counterion-mediated) attractive interaction between similarly charged ions. However, the findings and interpretation were not readily and widely accepted, even more so in colloid science. In the present article, it is intended to survey why and how such a situation has arisen.

Condensed systems require repulsion and attraction

In principle, condensed systems cannot exist in a finite volume if attraction and repulsion are not working in them. If the attraction did not exist, the system would occupy an infinitely large volume, whereas it would collapse if only attraction were in action without repulsion. Thus, we can’t have one without the other. It seems that this was taken into account in early considerations of interparticle interactions in colloidal dispersions. Actually, in the Derjaguin-Landau-Verwey-Overbeek (DLVO)²⁾ framework, the electric interparticle interaction was demonstrated to be repulsive, and a van der Waals (attractive) interaction was combined with it in an ad hoc manner. As is widely known, the latter contribution was formulated with a so-called Hamaker constant H, which characterizes the van der Waals attraction between colloidal particles. Initially various theoretical justifications were advanced on its physical meaning but, later on, H came to be often treated as an adjustable parameter. Thus, various experimental observations were seemingly accounted for by the DLVO framework. On the other hand, there have recently been reported phenomena in which the long-range interaction was overwhelmingly important, so that the short-range van der Waals interaction could be ignored. It has frequently been claimed that the colloidal interaction is purely repulsive and that attraction need not be considered. Though we find this interpretation generally invalid, it shows how mistakenly the DLVO framework has been employed.

Electrostatic attraction in macroionic systems

It is readily accepted that there should exist electrostatic repulsion between similarly charged macroions. In other words, the electrostatic repulsion described by the DLVO framework is understandable, at least qualitatively. Another important facet of macroionic systems is that the attraction experimentally observed is also of an electrostatic origin. This was concluded from the observed influences of added salt and dielectric constant of solvent ɛ on the intermacroion spacing. Generally, the spacing was observed to become smaller with increasing salt concentration. A typical example is given in Table 1, in which the interparticle spacing 2D_exp observed by microscopic measurements is shown together with the average spacing 2D₀ obtained from the particle concentration.³⁾ Clearly, the spacing decreases with increasing salt concentration up to 6.84 × 10⁻⁵ M, above which the colloid crystal melts to liquid state. Since the measurements are done at a fixed volume fraction ϕ of 0.0020, the 2D₀ is kept constant, so that the ratio 2D_exp/2D₀ decreases to 0.60 For homogeneous systems, 2D_exp/2D₀ must be unity, so that the present colloidal dispersion is seen to be highly inhomogeneous.

Table 1.

Salt concentration dependence of the interparticle spacing

[NaCl]/M	2Dexp/nm	2Dexp/2D0
0	1,270	0.94
1.71 × 10−5	1,130	0.84
6.84 × 10−5	800	0.60
1.37 × 10−4	Not measurable due to melting of colloid crystal

Polymer latex particle-H₂O (particle radius a = 227 nm, analytical charge density σ_a = 4.4 μCcm⁻²), volume fraction. ϕ : 0.0020

It is reminded here that the attraction has been observed for mono-valent counterions, protons.

With respect to the salt concentration dependence, it should be mentioned that the traditional way of understanding in colloid field in terms of the combined contribution of the electrostatic repulsion and the van der Waals attraction is not satisfactory. According to this understanding, the secondary potential minimum created by these two forces shifts toward shorter distances with increasing salt concentration, which agrees with experimental findings. On the other hand, the depth of the potential minimum becomes larger and larger with increasing salt concentration, implying that colloidal crystals become more and more stabilized. This is in clear contradiction with experiments, since colloidal crystals can exist only at low salt concentrations and cannot exist under high salt conditions.

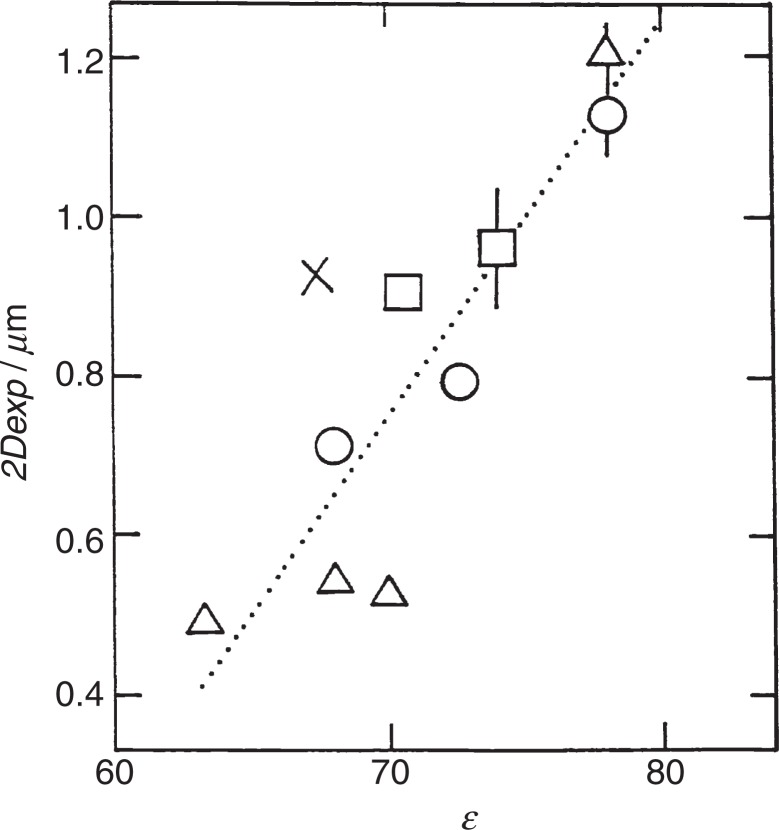
The influence of ɛ is shown in Fig. 1.³⁾ The ɛ of solvent is diminished from 80 to 60 by mixing organic solvent with light water. Clearly, with decreasing ɛ the 2D_exp decreases from 1,200 to 500 nm. An independent conductance measurement showed that the charge number of latex particles was not sensitive toward varying ɛ in the range between 60 and 80.⁴⁾ Thus, we take this result as implying that, as ɛ decreases, the interparticle interaction is intensified, the interaction is attractive, and the attraction is electrostatic. If the interaction is electrostatistically repulsive as the DLVO theory claims, the spacing could not decrease but stay unchanged with varying ɛ because the repulsion also must be enhanced due to the inverse proportionality to ɛ.

Fig. 1.

Dependence of the interparticle spacing on the dielectric constant. Sample: latex particle (a = 185 nm, σ_a = 7.2μCcm⁻²), ϕ = 0.013, Binary solvents (light water)-ethyl-eneglycol (○), water-methanol (×), water-DMF (▵), water-DMSO (□). The dotted line is an eye-guide. Taken from Ref. 3 with the permission of the American Chemical Society.

The Helmholtz free energy is not necessarily equal to the Gibbs free energy in ionic systems

In order to know the characteristic feature of the interaction forces in colloidal systems, it is therefore important to dwell carefully on how the repulsion was obtained in the DLVO framework, which has been the bottom line in most of theoretical considerations of colloidal phenomena. For this purpose, we go back to fundamental statistical thermodynamics. Since a detailed discussion has been presented in recent monographs,^5)–7) we briefly review here the essential features of the problem. According to a cautious analysis of the Debye-Hückel (D-H) theory of strong electrolyte solutions⁸⁾ by Fowler and Guggenheim⁹⁾ and McQuarrie,¹⁰⁾ the electrostatic Helmholtz free energy ΔF^el in the limit of κa → 0 is given by

$$\frac{\beta \mathrm{\Delta }{F}^{\mathit{el}}}{V}=-\frac{{\kappa }^3}{12\pi },$$ [1]

where β is 1/kT (thermal energy), V the solution volume and

$${\kappa }^2=\frac{4\pi \beta }{\varepsilon V}\sum _s{q_s}^2{c}_s$$ [2]

where q_s and c_s are the charge and number of species s. The electrostatic chemical potential of the ith ionic species μ_i^el is given by

$${\mu }_i^{\mathit{el}}={\left(\frac{\partial \mathrm{\Delta }{F}^{\mathit{el}}}{\partial N_i}\right)}_{T,V},$$ [3]

where N_i is the number of the species i. Since the electrostatic Gibbs free energy ΔG^el is given by

$$\mathrm{\Delta }{G}^{\mathit{el}}=\sum _i{N}_i{\mu }_i^{\mathit{el}}$$

we have

$$\frac{\beta \mathrm{\Delta }{G}^{\mathit{el}}}{V}=-\frac{{\kappa }^3}{8\pi }$$ [4]

Clearly, ΔG^el ≠ ΔF^el. The thermodynamics requires that

$$\frac{\beta \mathrm{\Delta }{G}^{\mathit{el}}}{V}=\frac{\beta \mathrm{\Delta }{F}^{\mathit{el}}}{V}+\beta p^{\mathit{el}}$$ [5]

where p^el is the electrostatic osmotic pressure. From Eqs. [1], [4], and [5], it follows that

$$\beta p^{\mathit{el}}=-\frac{{\kappa }^3}{24\pi }.$$ [6]

This consideration shows that ΔG^el cannot generally be equal to ΔF^el even at the level of the D-H theory, or for simple ionic dilute solutions. It is noteworthy that the magnitude of the difference (p^el) becomes larger with increasing κ³, which in turn increases with increasing charge number. This suggests, at least qualitatively, that the difference might be much larger for highly charged systems, including macroions and colloidal particles, having much higher charges than simple ions.

The thermodynamics tells us that the natural function for the determination of equilibrium is the Gibbs free energy, because experiments are performed at constant pressure and temperature. In the DLVO framework, however, the difference was ignored, and ΔG^el was assumed to be equal to ΔF^el. Although we believe that whether this assumption is permissible or not should be argued in comparison with experimental observation, to our knowledge, such a comparison has not been undertaken, and the equality relation has been taken for granted in the colloid field.

It is noted that Overbeek unduly justified the equality relation ΔF^el = ΔG^el on the basis that the solvent is not compressible during the charging-up process. Certainly the volume change in this process is small, which was taken to manifest a constant volume process. This interpretation has been widely accepted in the colloid field but it is misleading for the following reason. As shown by McQuarrie, generally speaking, ΔF^el is not equal to ΔG^el in ionic solutions as a result of interionic interaction, not because of the incompressibility of the solvent.

If ΔF^el = ΔG^el were valid, p^el = 0, and the solution must be ideal. This is not the case even at very low ionic concentrations. Since the osmotic pressure p is given by

$$\beta p=\sum c_s+\beta p^{\mathit{el}}$$ [7]

the osmotic coefficient g is

$$g=\frac{\beta p}{\sum c_s}$$ [8]

In the D-H theory, we have

$$g=1-\frac{{\kappa }^3}{24\pi \sum c_s}$$ [9]

which agrees with experimental findings, as widely recognized, pointing out the failure of the ΔF^el = ΔG^el assumption.

As was pointed out by Sogami¹¹⁾ in a mean field approach, the electrostatic interparticle interaction is purely repulsive at the level of ΔF^el whereas a long-range attractive component appears at the level of ΔG^el. Thus, as far as ΔF^el is assumed to be equal to ΔG^el, in other words, in the DLVO framework, the interaction between similarly charged particles is repulsive, as often claimed.

However, the assumption is questionable in light of Eqs. [1] and [4]. In other words, the contribution of the osmotic pressure, which is determined predominantly by counterions, particularly for high charge particles, was not properly treated in the DLVO theory. The imperfection should become more serious for colloidal particles, particularly of high charge numbers. In other words, the DLVO theory would satisfactorily describe colloidal interactions only in dispersions of low charge particles. As a matter of fact, experimental observations, which were claimed to be accountable in terms of repulsion (DLVO be havior), have been reported for dispersions of low charge particles. For high charge particle systems, however, observation showed that the repulsion was not adequate and attraction had to be invoked (Table 9.1 of Refs. 5 and 6).

It is to be again recalled that the long-held view that interaction between similarly charged particles is repulsive, is not axiomatically correct. It happened to originate from the assumption ΔG^el = ΔF^el and the related model adopted by the DLVO theory.

Repulsion and attraction in Sogami potential

In order to obtain a generally valid picture of colloidal interactions, therefore, it is necessary to discuss the problem in terms of not only ΔF^el but also ΔG^el. Sogami developed a mean-field theory for spherical macroions along these lines.¹¹⁾ Since this theory has often been discussed in detail,^5),6) we show only the results here. The pair (adiabatic) potentials U^E(r), U^F(r) and U^G(r) refer to the total electrostatic energy of the system E, the Helmholtz free energy F and the Gibbs free energy G, respectively. They are derived in terms of the net charge number Z as follows:

$$U^E=\frac{Z^2{e}^2}{\varepsilon }\left[\frac{\kappa a\hspace{0.17em}\text{coth}(\mathit{ka})}{r}-\frac{1}{2}\kappa \right]\hspace{0.17em}\text{exp}\hspace{0.17em}(-\kappa a)$$ [10]

$$U^F=\frac{Z^2{e}^2}{\varepsilon }\hspace{0.17em}\frac{1}{r}\hspace{0.17em}\text{exp}\hspace{0.17em}(-\kappa r)$$ [11]

$$U^G=\frac{Z^2{e}^2}{\varepsilon }\left[\frac{1+ka\hspace{0.17em}\text{coth}(ka)}{r}-\frac{1}{2}\kappa \right]\hspace{0.17em}\text{exp}\hspace{0.17em}(-kr)$$ [12]

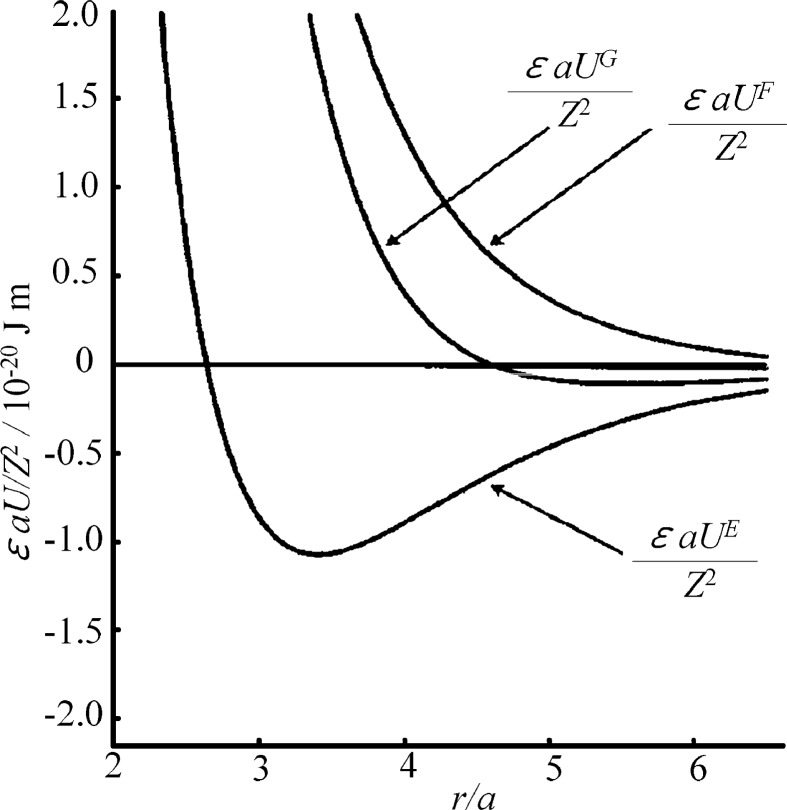
where e is the electron charge, a the particle radius, and r the interparticle distance. To help understanding, the potentials are shown in Fig. 2. U^E is seen to be composed of a shielded repulsion between particles and exponentially varying strong attraction and is approximately equal to the potential derived by Levine and Dube.¹²⁾ However, an important thermodynamic factor, i.e., the entropic contribution, is not included in this potential, which is an error, as pointed out by Overbeek (Appendix of Ref. 2). By contrast, U^F is purely repulsive at all distances. This implies that the entropic factor, which was obtained by considering the (Helmholtz) free energy, overshadows the attraction associated with the electrostatic energy consideration. Overbeek regarded the use of the electrostatic (field) energy instead of the free energy as fallacious.

Fig. 2.

Comparison of the pair potentials for particles as a function of r for κa = 1. Taken from Ref. 11 with the permission of the American Institute of Physics.

It is worth mentioning that U^F given by Eq. [11] reduces to the purely repulsive, well-known DLVO potential. However, U^G (Eq. [12]) shows a short-range repulsion and a long-range attraction. As stated above, the basic assumption of the DLVO framework was to equate the Helmholtz and Gibbs free energies. As far as we stay in the DLVO framework, the frequent statement that the interparticle interaction is repulsive is not avoidable. However it is not realistic. The existence of the attraction experimentally confirmed in colloidal dispersions (Chapters 4 and 5 of Refs. 5 and 6) and macroionic solutions (Chapter 3 of Refs. 5 and 6) therefore cannot even qualitatively be reproduced by U^F (and hence the DLVO potential), but is consistent with U^G.

We explicitly consider that colloidal crystals are formed when the second particle is captured by the potential minimum. Its position, r_min, of U^G is given by, for any value of κa

$$r_{\text{min}}=\frac{\kappa a\hspace{0.17em}\text{coth}(\kappa a)+1+\sqrt{[\kappa a\hspace{0.17em}\text{coth}(\kappa a)+1]\hspace{0.17em}[\kappa a\hspace{0.17em}\text{coth}(\kappa a)+3]}}{\kappa }$$ [13]

which reduces to, for κa ≪ 1

$$r_{\text{min}}\cong \frac{1+\sqrt{3}}{\kappa }$$ [14]

Equation [14] shows that the interparticle spacing becomes smaller with increasing κ, and hence increasing concentration of added salt. It should be noted that the potential minimum (U^G(r_min)) becomes first deeper with increasing κa and thereafter shallower. At large κa values, the minimum disappears. From this salt concentration dependence of U^G(r_min) it is concluded that the interparticle spacing becomes smaller with increasing salt concentration and the colloidal crystals melt at high salt concentration. This is exactly what was described in Table 1. (See also Refs. 5 and 6). Such an observed trend cannot be accounted for in terms of the DLVO framework, which shows that the spacing simply decreases and the potential is increasingly lowered (that is, systems are more and more stabilized) with increasing salt concentration.

Criticism of the Sogami potential by Overbeek is in error

In the previous section, the Sogami potential was shown to excel over the DLVO framework in that the attraction can be derived, not in an ad hoc manner, but directly from the Poisson-Boltzmann equation. Since the former most explicitly challenged the long-held view, various criticisms were presented, which have been refuted in detail in recent monographs.^5)–7) Because it is contextually relevant to the ongoing discussion, in the present paper we confine ourselves to the most outstanding criticism by Overbeek,¹³⁾ who stated that “the Sogami theory leading to an attraction between particles with charges of the same sign contains errors and, when the errors are corrected, the attraction disappears.” However, this is totally untrue. Careful examination of Overbeek’s paper reveals an elementary error in his mathematical derivation, as discussed already (Chapters 2 and 6 in Refs. 5 and 6). In short, the partial differentiation of the Helmholtz free energy with respect to N was carried out erroneously after the system volume V was replaced by V = Nv₀ (N: number of solvent molecules, v₀: volume of solvent molecule). In other words, ΔF^el(V, T, N_i) was misinterpreted to be ΔF^el(Nv₀, T, N_i) and was differentiated with respect to N. This replacement prior to the differentiation happened to cause “exact” cancellation of the contributions of the solvent and solutes due to the fact that κ² is a homogeneous function of order 1 with respect to N_i and of order −1 with respect to N. Thus, Overbeek’s criticism of the Sogami theory is in error.

The consideration in the preceding sections suggests that, if Overbeek’s argument were correct, not only the Sogami theory but also the D-H theory would be wrong. Once again it is to be noted that the long-range electrostatic attraction between similarly charged macroions or particles originates directly from the mean-field approach at the level of the Gibbs free energy, and is due to counterions surrounding the high charge macroions. Therefore, we called it a counterion-mediated attraction.

The Coulomb law says that cation (anion) repels cation (anion) while cation attracts anion. This is axiomatically correct. However, in ionic systems, cations cannot be independent from anions because of electric neutrality. Therefore, when we discuss the interaction between two similarly charged ions, it cannot simply be a Coulombic repulsion in the narrow sense of the word. The nearby counterions must play a role that cannot be ignored in influencing the pure repulsion. Debye and Hückel described such a situation as follows.⁸⁾ “Considering any one ion, we shall find on an average more dissimilar than similar ions in its surroundings, an immediate consequence of the electrostatic forces effective between the ions.” It is to be emphasized that the attraction between dissimilar ions always overweighs the repulsion between similar ions, because the distance between ions appears in the denominator of the interionic interaction energy. Because of its fundamental character in ionic systems, such a situation is also expected to occur for highly charged macroions and colloidal particles. In these systems much larger number of counterions than in simple ion solutions are generated, resulting in stronger macroion-counterion attraction, even though the macroion-macroion repulsion is also intensified.

It is to be emphasized that the attraction in question has been observed with protons as counter-ions and the statistical-mechanical consideration above is valid for not only mono-valent, but also multi-valent counterions. The frequent claim,¹⁴⁾ that the like-like-like attraction is not possible for mono-valent counterions, is not correct.

Overlooking the basic error in Overbeek’s critique, some researchers^15),16) explicitly stated that the Sogami potential has been proved to be erroneous, and that its errors were exposed by Overbeek. These authors did not cautiously examine the relevant articles, intentionally or not.

Concluding remarks

In the present article, we have demonstrated how the widely accepted repulsion-only assumption was derived. The very often advanced claim that macroions having the same sign of charges must repel each other, resulted from the rather artificial premise of the equality of ΔF^el and ΔG^el. The fundamental analysis of the Debye-Hückel theory clarifies that ΔF^el ≠ ΔG^el even for simple ionic systems and the difference between the two (p^el) becomes larger with increasing charge number. It is recalled that the inequality relation originates from interionic interactions, irrespectively of the solvent incompressibility. Thus, the equality relation is inferred to be less satisfactory for colloidal systems than in simple ionic solutions. As a matter of fact, Sogami took a broader view and found pure repulsion between macroions at the level of ΔF^el but attraction and repulsion at the level of ΔG^el. This is a counterion-mediated attraction and is the “immediate consequence of the electrostatic interactions”. Overbeek’s criticism of Sogami theory is shown to be wrong owing to an improper mathematical treatment.

Profile

Norio Ise was born in 1928. After finishing the doctoral thesis on physico-chemical properties of polyelectrolyte solutions in Kyoto University, he joined Professor Manfred Eigen’s group in Max-Planck-Institut für Physikalische Chemie, Göttingen, in 1959. During his stay, he was exposed to intensive discussion of various basic facets of ionic solutions, which later on developed to the bottom line of the present article. Upon returning to Kyoto University, he initiated structural study of ionic polymer solutions by using X-ray scattering and came to a conclusion that macroions formed more or less ordered spatial arrangement, though in solutions. To make it double sure, systematic investigation was concurrently carried out on aqueous dispersions of ionic colloidal particles, which can be seen under microscope, by the Grant-in-Aids for Specially Promoted Research in 1981 and 1988. All these studies demonstrated that macroscopically homogeneous ionic solutions or dispersions are not microscopically homogeneous, indicating the presence of electrostatic attraction between similarly charged ionic species. This shows that the traditional view in condensed matter physics is not necessarily correct. With Professor Ikuo Sogami, Kyoto Sangyo University, he authored a monograph, “Polymer Physics: Structure Formation in Macroionic Systems”, Asakura-Shoten, Tokyo, 2004 (in Japanese) and its English version “Structure Formation in Solution: Ionic Polymers and Colloidal Particles”, Springer, Heidelberg, 2005. Its Chinese version by Sharon Chen was published in 2007 by Shanxi Science and Technology Press, Sian, PRC. He was awarded the Chemical Society of Japan Award in 1987 and the Japan Academy Prize in 1998.