Effect of Sodium Ions on RNA Duplex Stability

Abstract

The standard sodium concentration for RNA optical melting experiments is 1.021 M. Algorithms that predict T_m, ΔG°₃₇, and secondary structure from sequence generally rely on parameters derived from optical melting experiments performed in 1.021 M sodium. Physiological monovalent cation concentrations are much lower than 1.021 M. In fact, many molecular biology techniques require buffers containing monovalent cation concentrations other than 1.021 M. Predictions based on the 1.021 M Na⁺ parameters may not be accurate when the monovalent cation concentration is not 1.021 M. Here, we report thermodynamic data from optical melting experiments for a set of 18 RNA duplexes, each melted in a wide range of sodium ion concentrations (71, 121, 221, and 621 mM). Using this data and previously published data for the same sequences melted in 1.021 M Na⁺, we report T_m and ΔG°₃₇ correction factors to scale the standard 1.021 M Na⁺ RNA parameters to other sodium ion concentrations. The recommended T_m correction factor (eq 21) predicts the melting temperature within 0.7 °C, and the recommended ΔG°₃₇ correction factor (eq 26) predicts the free energy within 0.14 kcal/mol. These correction factors can be incorporated into prediction algorithms that predict RNA secondary structure from sequence and provide T_m and ΔG°₃₇ values for RNA duplexes.

INTRODUCTION

RNA is one of the most important biomolecules in all forms of life. RNA, however, needs to fold into appropriate secondary and three-dimensional structures (3D) so that it can function properly (1, 2). Therefore, knowing the secondary and 3D structures of RNA will help scientists better understand its function and mechanism of action (3, 4). However, the number of solved RNA 3D structures is significantly smaller than the soaring number of available RNA sequences (5). Hence, structure prediction may be the most efficient way to elucidate RNA tertiary structure.

Predicting RNA secondary structure can be an intermediate step in predicting RNA 3D structure (6). The nearest-neighbor model (7, 8), which is based on sets of adjacent base pairs, is currently the most widely used algorithm for predicting RNA secondary structure from sequence. The nearest-neighbor model can be used to predict the stability of simple Watson-Crick duplexes and duplexes containing more complicated secondary structure motifs such as bulges, internal loops, and hairpins. The parameters used in the nearest-neighbor model were derived from a large series of optical melting experiments for RNA duplexes in salt buffers normally containing 1 M NaCl, 20 mM sodium cacodylate, and 0.5 mM Na₂EDTA, which results in a total Na⁺ concentration of 1.021 M (9).

Cations are crucial for RNA folding and function. The polyanionic backbone of RNA requires cations (specific or non-specific binding) to neutralize the negative charge (10). Theoretical studies on the relationship between cations and nucleic acids were pioneered by Manning who proposed the counterion condensation theory (11). Recently, the Poisson-Boltzmann equation (12), Monte Carlo simulations (13), and the tightly bound ion (TBI) theory (14) have also been used to describe the distribution of cations around RNA. A NaCl concentration of 1 M (along with 20 mM sodium cacodylate and 0.5 mM Na₂EDTA) was initially chosen by the pioneers of RNA optical melting studies (15) to stabilize short RNA oligonucleotides. Therefore, 1.021 M Na⁺ has become the standard sodium concentration for RNA optical melting experiments, which secondary structure prediction algorithms are based on.

Extracellular and intracellular monovalent cation concentrations, however, are much lower than 1.021 M. In addition, buffer conditions of numerous molecular biology techniques require cation concentrations other than 1.021 M. For instance, PCR experiments usually use buffer conditions containing between 20–100 mM monovalent cations (16). The success of these molecular biology techniques, including antisense RNA and RNAi, are largely dependent on the specific and accurate hybridization between RNA strands (17). Therefore, it would be beneficial to be able to accurately predict the thermodynamics of RNA, especially the melting temperature (T_m) and free energy change (ΔG°₃₇). Many scientists who perform these techniques predict T_m and ΔG°₃₇ of duplexes utilizing the nearest-neighbor model. The major limitation of using the nearest-neighbor model to calculate T_m and ΔG°₃₇ is that the parameters in the nearest-neighbor model were derived from RNA duplexes in 1.021 M Na⁺, which may not be consistent with the thermodynamics in other salt conditions. This difference could lead to unanticipated results or even complete failure of the experiments.

There have been extensive experimental studies on the relationship between sodium ion concentrations and DNA thermodynamics (18–24). Recently, a systematic study on the sodium ion dependence of DNA duplex stability was completed by Owczarzy et al. (17), and correction factors were proposed to adjust the DNA thermodynamic parameters at 1.021 M Na⁺ to parameters corresponding to other monovalent cation concentrations. Moreover, Nakano et al. (25) also proposed correction factors for nucleic acids. However, the data in this study were mainly from DNA duplexes, with a few RNA/DNA hybrids and RNA duplexes, so the correction factors may not be accurate for RNA duplexes. Also, the correction factors proposed by Nakano et al. (25) were limited to 100 mM Na⁺. Despite these efforts on nucleic acids, systematic studies on the relationship between sodium ion concentrations and RNA duplex stability have not been completed.

Here, we report thermodynamic data from optical melting experiments for a set of 18 RNA duplexes, each melted in a wide range of sodium ion concentrations (71, 121, 221, and 621 mM). Using the DNA results of Owczarzy et al. (17) as a guide, we report T_m and ΔG°₃₇ correction factors to scale the standard 1.021 M Na⁺ RNA parameters to other sodium ion concentrations. These correction factors can be incorporated into prediction algorithms that predict RNA secondary structure from sequence and provide T_m and ΔG°₃₇ values for RNA duplexes.

MATERIALS AND METHODS

Oligonucleotide Selection, Synthesis, and Purification

RNA duplexes were selected from the sequences that were used by Xia et al. (9) to derive the RNA nearest-neighbor parameters in 1.021 M Na⁺. The oligomers were ordered from Integrated DNA Technologies, Inc. (Coralville, IA). Purification of oligonucleotides was performed using standard procedures described previously (26–28).

Optical Melting Experiments

All of the strands used here were self-complementary; therefore, mixing of strands was not necessary. After purification, the RNA oligonucleotides were lyophilized and redissolved in melting buffer containing 20 mM sodium cacodylate, 0.5 mM Na₂EDTA, and 50, 100, 200, or 600 mM NaCl, adjusted to pH 7.0. The resulting total sodium ion concentrations were 71, 121, 221, and 621 mM, respectively. Each duplex was melted at least nine times, using a different concentration each time, to ensure that the total oligonucleotide concentration range was at least 50-fold. Using a heating rate of 1 °C/min on a Beckman-Coulter DU800 spectrophotometer, absorbance versus temperature melting curves were obtained between 0 and 90 °C. For sequences containing at least 50% G-C base pairs, absorbances were measured at 280 nm, while the absorbance of A-U rich oligonucleotides was measured at 260 nm (15). Meltwin (29) was used to determine the thermodynamic parameters of each duplex. Thermodynamic parameters, which were used in developing correction factors, were derived from the 1/T_m vs ln C_T plots, and melting temperatures were calculated at 10⁻⁴ M strand concentration.

Predicting T_m

The accuracy of 10 previously published DNA T_m correction factors was evaluated with the RNA data collected here. Using the experimental 1.021 M Na⁺ T_m as the starting point, the DNA correction factors were applied to predict T_m values at 71, 121, 221, and 621 mM Na⁺, which correspond to the RNA data reported here. The accuracy of the 10 models was tested using |ΔT_m|_ave:

$${\left|\mathrm{\Delta }{T}_m\right|}_{\mathit{\text{ave}}}=\frac{\sum _{j=1}^{j=n}|T_m(j,\mathit{\text{prediction}})-T_m(j,\text{exp}eriment)|}{N}$$ 1

For each correction factor, a total of 72 (18 duplexes studied at four different Na⁺ concentrations) melting temperatures were predicted and used to calculate |ΔT_m|_ave.

Although some of the previously published DNA correction factors worked well for the RNA data reported here, the coefficients for some of the previously published DNA correction factors were updated for the RNA data reported here by using the LINEST function of Microsoft Excel. These RNA correction factors were then tested in a similar manner using |ΔT_m|_ave.

Predicting ΔG°₃₇

Although there are 10 previously published DNA T_m correction factors, there is only one previously published DNA ΔG°₃₇ correction factor (24). The accuracy of this DNA ΔG°₃₇ correction factor was evaluated with the RNA data collected here in a similar manner using |ΔΔG°₃₇|_ave.

$${\left|\mathrm{\Delta }\mathrm{\Delta }{G°}_{37}\right|}_{\mathit{\text{ave}}}=\frac{\sum _{j=1}^{j=n}|\mathrm{\Delta }\mathrm{\Delta }{G°}_{37}(j,\mathit{\text{prediction}})-\mathrm{\Delta }\mathrm{\Delta }{G°}_{37}(j,\text{exp}eriment)|}{N}$$ 2

The coefficient in this previous correction factor was also updated for the RNA data reported here by using the LINEST function of Microsoft Excel. The updated version was then tested using |ΔΔG°₃₇|_ave.

In addition to updating the previous DNA correction factor, several new ΔG°₃₇ correction factors were tested. The first set of new ΔG°₃₇ correction factors were derived from the T_m correction factors. Combining the Gibbs free energy equation and the van’t Hoff equation (9) yields the following equation:

$$T_m^{-1}=\frac{\mathrm{\Delta }H°-\mathrm{\Delta }{G}_{37}^{°}}{310.15\mathrm{\Delta }H°}+\frac{R\text{ln}{C}_t}{\mathrm{\Delta }H°}$$ 3

For every T_m correction factor derived, it can be inserted into this equation to yield a ΔG°₃₇ correction factor. For example, if the T_m correction factor was:

$$T_m^{-1}(2)=T_m^{-1}(1)+10$$ 4

Substituting this correction factor (eq. 4) into eq. 3 would yield:

$$\frac{\mathrm{\Delta }H°-\mathrm{\Delta }{G}_{37}^{°}(2)}{310.15\mathrm{\Delta }H°}+\frac{R\text{ln}{C}_t}{\mathrm{\Delta }H°}=\frac{\mathrm{\Delta }H°-\mathrm{\Delta }{G}_{37}^{°}(1)}{310.15\mathrm{\Delta }H°}+\frac{R\text{ln}{C}_t}{\mathrm{\Delta }H°}+10$$ 5

Simplifying this equation results in the corresponding ΔG°₃₇ correction factor:

$$\mathrm{\Delta }{G}_{37}^{°}(2)=\mathrm{\Delta }{G}_{37}^{°}(1)-3101.5\mathrm{\Delta }H°$$ 6

The accuracy of correction factors derived from this method was evaluated by using |ΔΔG°₃₇|_ave. It is important to note that ΔG°₃₇ correction factors derived in this way rely on three assumptions (16): (i) RNA duplexes melted in a two-state process, (ii) counterion effects were mainly entropic (24, 30, 31), and (iii) the ΔC_p of melting reactions was zero, which means enthalpies and entropies are temperature independent. All of these assumptions were valid for the oligonucleotides studied here (16).

A second set of correction factors was derived based on linear or quadratic relationships between ΔG°₃₇ or 1/ΔG°₃₇ and ln [Na⁺]. These resulting ΔG°₃₇ correction factors were similar to the previously published DNA T_m correction factors. The RNA ΔG°₃₇ data reported here and the LINEST function of Microsoft Excel were used to derive the coefficients for these ΔG°₃₇ correction factors. The accuracy of these ΔG°₃₇ correction factors was also evaluated using |ΔΔG°₃₇|_ave.

RESULTS

RNA Thermodynamic Parameters

Eighteen duplexes in five different sodium ion concentrations were melted. Experimental ΔG°₃₇, ΔH°, ΔS°, and T_m values are available in Table S1. All the oligonucleotides melted in a two-state model. The experimental T_m and ΔG°₃₇ values for all of the duplexes and all Na⁺ concentrations are summarized in Tables 1 and 2, respectively. On average, the T_m of duplexes in 71, 121, 221, and 621 mM Na⁺ were 9.1, 6.4, 3.9, and 1.0 °C lower, respectively, than the same duplex in 1.021 M Na⁺. Similarly, duplexes melted in 71, 121, 221, and 621 mM Na⁺ were on average 1.62, 1.15, 0.69, and 0.16 kcal/mol less stable, respectively, than the same duplex in 1.021 M Na⁺.

Table 1.

Experimental Melting Temperatures of RNA Duplexes in Various Sodium Ion Concentrations^a

		Tmb (°C)
RNA sequence (5' to 3')d	fGCe	71 mM	121 mM	221 mM	621 mM	1.021 Mc
CGCGCG	1.00	51.3	53.7	55.2	57.8	57.8
CGGCCG	1.00	55.2	57.4	59.9	61.9	63.2
GCCGGC	1.00	60.1	62.6	65.0	67.6	67.4
GCGCGC	1.00	55.3	57.8	59.9	62.3	62.5
ACCGGU	0.67	43.7	47.2	50.1	52.0	53.9
AGCGCU	0.67	41.3	45.7	47.9	51.4	52.0
CACGUG	0.67	33.6	36.2	38.5	41.0	42.8
CAGCUG	0.67	35.3	37.2	39.7	42.1	43.1
CCAUGG	0.67	35.7	37.0	40.4	43.5	46.4
CCUAGG	0.67	39.7	42.4	44.7	47.4	50.0
CUGCAG	0.67	37.1	39.9	41.9	44.8	45.3
GACGUC	0.67	38.5	41.2	43.1	46.0	46.2
GAGCUC	0.67	40.2	42.7	45.0	47.7	48.7
GCAUGC	0.67	37.8	40.2	42.6	45.8	45.7
AACUAGUU	0.25	34.0	37.0	40.0	43.8	45.7
ACUAUAGU	0.25	32.9	36.2	38.8	42.7	44.0
ACUUAAGU	0.25	29.8	32.4	35.8	39.3	40.3
AGAUAUCU	0.25	31.0	33.9	37.7	41.7	41.4

^aT_m values are from the 1/T_m vs ln C_T plots.

^bCalculated for 0.1 mM oligomer concentration.

^cAll 1.021 M data, except for GCCGGC and GCGCGC, are from Xia et al. (9).

^dAll oligomers are self-complementary and are forming duplexes in solution.

^ff_GC is the fraction of G-C base pairs.

Table 2.

Experimental ΔG°₃₇ Values for RNA Duplexes in Various Sodium Ion Concentrations^a

		ΔG°37 (kcal/mol)
RNA sequence (5' to 3')c	fGCd	71 mM	121 mM	221 mM	621 mM	1.021 Mb
CGCGCG	1.00	−8.12	−8.52	−8.87	−9.23	−9.12
CGGCCG	1.00	−8.76	−9.09	−9.40	−9.70	−9.90
GCCGGC	1.00	−10.23	−10.73	−10.90	−11.41	−11.69
GCGCGC	1.00	−8.85	−9.32	−9.83	−10.29	−10.56
ACCGGU	0.67	−6.85	−7.25	−7.67	−8.07	−8.51
AGCGCU	0.67	−6.32	−6.91	−7.38	−7.82	−7.99
CACGUG	0.67	−5.10	−5.54	−5.94	−6.45	−6.59
CAGCUG	0.67	−5.37	−5.72	−6.18	−6.60	−6.68
CCAUGG	0.67	−5.44	−5.68	−6.34	−7.02	−7.30
CCUAGG	0.67	−6.22	−6.76	−7.18	−7.68	−7.80
CUGCAG	0.67	−5.69	−6.20	−6.53	−7.03	−7.11
GACGUC	0.67	−5.96	−6.44	−6.77	−7.26	−7.35
GAGCUC	0.67	−6.24	−6.70	−7.13	−7.59	−7.98
GCAUGC	0.67	−5.81	−6.26	−6.69	−7.31	−7.38
AACUAGUU	0.25	−5.09	−5.68	−6.24	−6.92	−7.16
ACUAUAGU	0.25	−4.86	−5.53	−6.04	−6.87	−6.98
ACUUAAGU	0.25	−4.37	−4.76	−5.46	−6.11	−6.16
AGAUAUCU	0.25	−4.45	−5.05	−5.82	−6.59	−6.58

^aΔG°₃₇ values are from the 1/T_m vs ln C_T plots.

^bAll 1.021 M data, except for GCCGGC and GCGCGC, are from Xia et al. (9).

^cAll oligomers are self-complementary and are forming duplexes in solution.

^df_GC is the fraction of G-C base pairs.

T_m Correction Factors

RNA duplexes in buffers containing 71–621 mM Na⁺ melt at lower temperatures than the same duplex in 1.021 M Na⁺. Therefore, T_m correction factors are needed for accurate predictions. Several previously published DNA T_m correction factors are shown in Table 3. The SantaLucia (24) and Owczarzy (17) DNA correction factors work particularly well for the RNA data reported here, with |ΔT_m|_ave < 2.5 °C. Because these worked so well, an attempt was made to further improve these correction factors by deriving updated coefficients based on the RNA data reported here. These newly derived correction factors are shown in Table 4. With the updated coefficients, the accuracy of these models improves, resulting in |ΔT_m|_ave ≤ 1.0 °C. Due to its accuracy (|ΔT_m|_ave = 0.7 °C) and consistency with the ΔG°₃₇ correction factor (discussed below), we recommend eq 21 (Table 4) as the T_m correction factor to be used for Na⁺ concentrations lower than 1.021 M.

Table 3.

Previously Published DNA Correction Factors

Eq no.	Name	ref	Equation	Accuracyc
DNA Tm Correction Factors
7	Schildkraut-Lifson Tm equation	13	$T_m(2)=T_m(1)+16.6\text{log}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	7.2 °C
8	Wetmur Tm equation	14	$T_m(2)=T_m(1)+16.6\text{log}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2(1+0.7{\left[{\mathit{\text{Na}}}^{+}\right]}_1)}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1(1+0.7{\left[{\mathit{\text{Na}}}^{+}\right]}_2)}$	4.5 °C
9	Frank-Kamenetskii Tm equation	15	$T_m(2)=T_m(1)+(7.95-3.057fGC)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	5.1 °C
10	Marmur-Schildkraut-Doty Tm equation	16, 17	$T_m(2)=T_m(1)+(8.75-2.83fGC)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	6.7 °C
11	Tm and 12.5log[Na+] equation	18	$T_m(2)=T_m(1)+12.5\text{log}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	4.2 °C
12	SantaLucia Tm equationa, b	19	$\frac{1}{T_m(2)}=\frac{1}{T_m(1)}+\frac{0.368N}{\mathrm{\Delta }H°}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	1.4 °C
13	Owczarzy Tm linear equation	12	$T_m(2)=T_m(1)+(-3.22fGC+6.39)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	2.3 °C
14	Owczarzy 1/Tm linear equationb	12	$\frac{1}{T_m(2)}=\frac{1}{T_m(1)}+(3.85fGC-6.18)\times {10}^{-5}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	1.5 °C
15	Owczarzy Tm quadratic equation	12	$T_m(2)=T_m(1)+(-4.62fGC+4.52)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}-0.985({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$	1.5 °C
16	Owczarzy 1/Tm quadratic equationb	12	$\frac{1}{T_m(2)}=\frac{1}{T_m(1)}+(4.29fGC-3.95)\times {10}^{-5}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}+9.40\times {10}^{-6}({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$	1.1 °C
DNA ΔG°37 Correction Factor
17	SantaLucia ΔG°37 equationa	19	$\mathrm{\Delta }{G°}_{37}(2)=\mathrm{\Delta }{G°}_{37}(1)-0.114\times N\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	0.21 kcal/mol

^aN is the total number of phosphates in the duplex divided by 2.

^bIn this equation, T_m should be in units of K.

^cAs described in Materials and Methods, |ΔT_m|_ave is used to evaluate the accuracy of previously published DNA T_m correction factors in predicting RNA T_m values, and |ΔΔG°₃₇|_ave is used to evaluate the accuracy of the previously published DNA ΔG°₃₇ correction factor in predicting RNA ΔG°₃₇ values.

Table 4.

Newly Derived RNA Correction Factors

Eq no.	Name	Equation	Accuracyc
RNA Tm Correction Factors
18	Modified SantaLucia Tm equationa, b	$\frac{1}{T_m(2)}=\frac{1}{T_m(1)}+\frac{0.3153N}{\mathrm{\Delta }H°}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	1.0 °C
19	Modified Owczarzy Tm linear equation	$T_m(2)=T_m(1)+(-1.842fGC+4.314)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	0.9 °C
20	Modified Owczarzy 1/Tm linear equationb	$\frac{1}{T_m(2)}=\frac{1}{T_m(1)}+(2.297fGC-4.575)\times {10}^{-5}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	0.9 °C
21	Modified Owczarzy Tm quadratic equation	$T_m(2)=T_m(1)+(-1.842fGC+2.675)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}-0.7348({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$	0.7 °C
22	Modified Owczarzy 1/Tm quadratic equationb	$\frac{1}{T_m(2)}=\frac{1}{T_m(1)}+(2.297fGC-2.886)\times {10}^{-5}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}+7.575\times {10}^{-6}({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$	0.7 °C
RNA ΔG°37 Correction Factors
23	ΔG°37 derived equation	$\mathrm{\Delta }{G°}_{37}(2)=\mathrm{\Delta }{G°}_{37}(1)-310.15\times \mathrm{\Delta }H°\times [(2.297fGC-2.886)\times {10}^{-5}\times \text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}+7.575\times {10}^{-6}\times ({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)]$	0.14 kcal/mol
24	ΔG°37 linear equation	$\mathrm{\Delta }{G°}_{37}(2)=\mathrm{\Delta }{G°}_{37}(1)+(0.324fGC-0.765)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	0.17 kcal/mol
25	1/ΔG°37 linear equation	$\frac{1}{\mathrm{\Delta }{G°}_{37}(2)}=\frac{1}{\mathrm{\Delta }{G°}_{37}(1)}+(-0.0213fGC+0.0261)\times {10}^{-5}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	0.19 kcal/mol
26	ΔG°37 quadratic equation	$\mathrm{\Delta }{G°}_{37}(2)=\mathrm{\Delta }{G°}_{37}(1)+(0.324fGC-0.468)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}+0.133({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$	0.14 kcal/mol
27	1/ΔG°37 quadratic equation	$\frac{1}{\mathrm{\Delta }{G°}_{37}(2)}=\frac{1}{\mathrm{\Delta }{G°}_{37}(1)}+(-0.0213fGC+0.016)\times {10}^{-5}\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}-0.0045({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$	0.17 kcal/mol
28	Modified SantaLucia ΔG°37 equationa	$\mathrm{\Delta }{G°}_{37}(2)=\mathrm{\Delta }{G°}_{37}(1)-0.1016\times N\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}$	0.18 kcal/mol

^aN is the total number of phosphates in the duplex divided by 2.

^bIn this equation, T_m should be in units of K.

^cAs mentioned in Materials and Methods, |ΔT_m|_ave is used here for evaluating the accuracy of the RNA T_m correction factors, and |ΔΔG°₃₇|_ave is used here for evaluating the accuracy of the RNA ΔG°₃₇ correction factors.

ΔG°₃₇ Correction Factors

One previously published DNA ΔG°₃₇ correction factor is shown in Table 3. This SantaLucia correction factor (24) works particularly well for the RNA data reported here, with a |ΔΔG°₃₇|_ave value of 0.21 kcal/mol. Because it worked so well, an attempt was made to further improve this correction factor by deriving updated coefficients based on the RNA data reported here. This newly derived correction factor is shown in Table 4. With the updated coefficients, the accuracy of this model improves slightly, resulting in a |ΔΔG°₃₇|_ave value of 0.18 kcal/mol. Because this was the only DNA ΔG°₃₇ correction factor available in the literature, several additional ΔG°₃₇ correction factors were derived and tested. These ΔG°₃₇ correction factors are shown in Table 4. Due to its accuracy (|ΔΔG°₃₇|_ave = 0.14 kcal/mol) and relative simplicity, we recommend eq 26 (Table 4) as the ΔG°₃₇ correction factor to be used for Na⁺ concentrations lower than 1.021 M.

DISCUSSION

Dependence of RNA Duplex Thermal Stability on Sodium Ion Concentrations

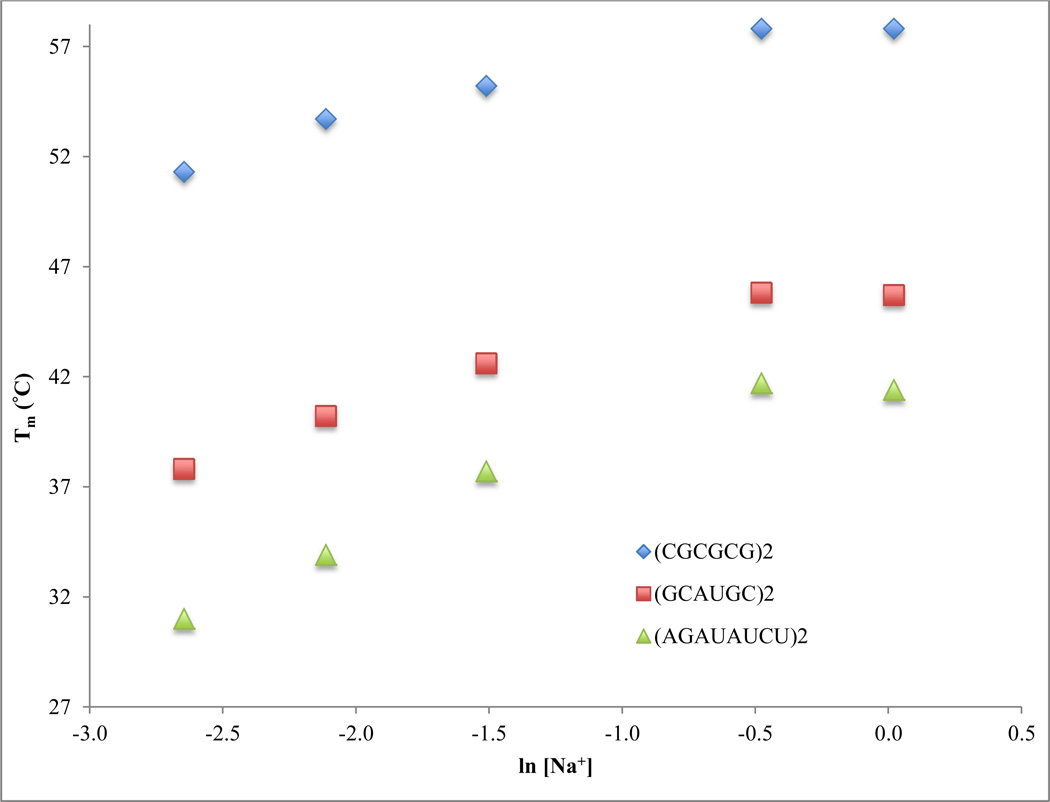
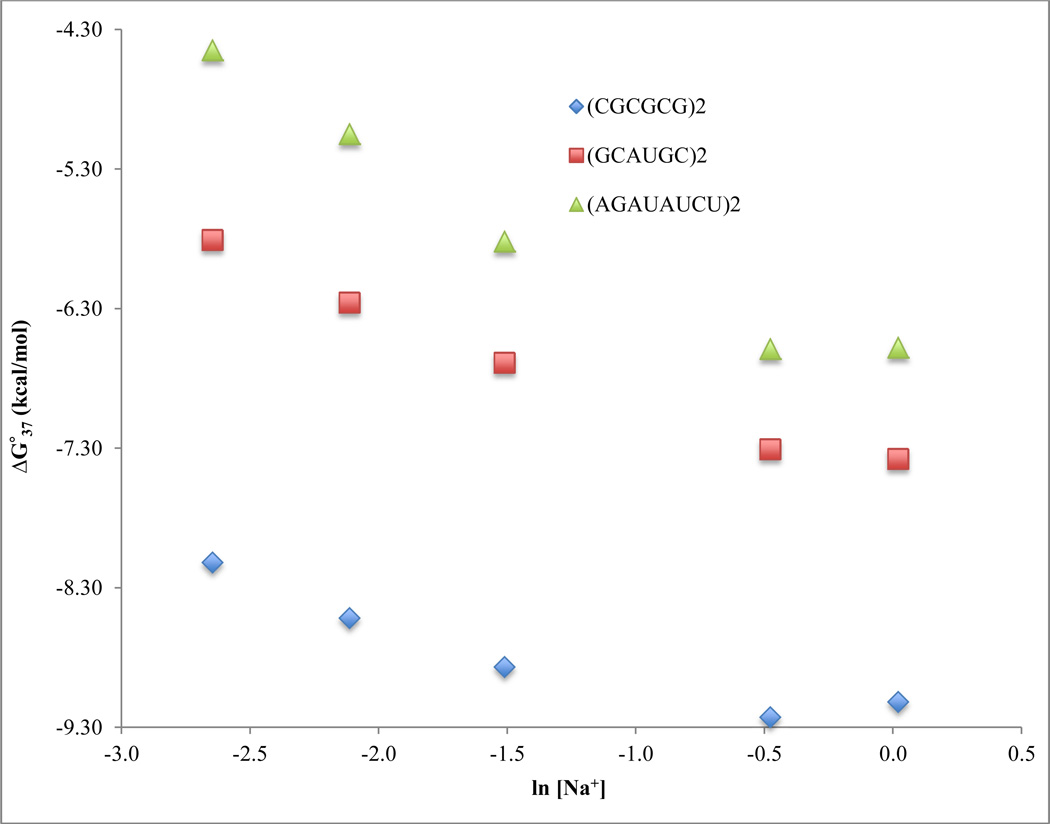
As expected, when [Na⁺] is increased from 71 mM to 621 mM, RNA T_m values increase (Table 1). Previous data and theories have suggested that RNA duplexes will become saturated with Na⁺ at high [Na⁺] (11, 14, 17, 32). As anticipated, increasing [Na⁺] from 621 mM to 1.021 M results in very little (increase or decrease) or no effect on the RNA T_m values. Figure 1 shows the relationship between T_m and ln [Na⁺] for representative RNA oligonucleotides, and it confirms that these RNA duplexes become saturated with Na⁺ at high sodium ion concentrations. Similar observations are found with the relationship between ΔG°₃₇ and sodium ion concentrations, as shown in Table 2 and Figure 2. As expected, when [Na⁺] is increased from 71 mM to 621 mM, RNA ΔG°₃₇ values become more negative. Increasing [Na⁺] from 621 mM to 1.021 M results in very little (increase or decrease) or no effect on the RNA ΔG°₃₇ values. Figure 2 shows the relationship between ΔG°₃₇ and ln [Na⁺] for representative RNA oligonucleotides. Similar to what was observed for T_m in Figure 1, saturation of RNA with sodium ions is also observed here at high sodium ion concentrations. In general, RNA duplexes become more thermally stable as sodium ion concentrations increase until reaching a certain saturation point.

Figure 1.

Relationship between melting temperatures and ln [Na⁺] for representative RNA oligomers of different G-C base pair contents: 100% GC, 5’-(CGCGCG)₂-3’; 66.7% GC, 5’-(GCAUGC)₂-3’; and 25% GC, 5’-(AGAUAUCU)₂-3’.

Figure 2.

Relationship between ΔG°₃₇ and ln [Na⁺] for representative RNA oligomers of different G-C base pair contents: 100% GC, 5’-(CGCGCG)₂-3’; 66.7% GC, 5’-(GCAUGC)₂-3’; and 25% GC, 5’-(AGAUAUCU)₂-3’.

Theoretical Discussion

Classical counterion condensation theory proposes the effect of sodium ion concentration on melting temperature by the following equation (17, 33, 34):

$$\frac{d{T}_m}{d\text{ln}\left[{\mathit{\text{Na}}}^{+}\right]}=\frac{-\alpha R{T}_m^2}{\mathrm{\Delta }H°}·\mathrm{\Delta }n$$ 29

or its equivalent form:

$$\frac{d\left(\frac{1}{T_m}\right)}{d\text{ln}\left[{\mathit{\text{Na}}}^{+}\right]}=\frac{\alpha R}{\mathrm{\Delta }H°}·\mathrm{\Delta }n$$ 30

Here, α is the correction term for the Na⁺ activity coefficient (17, 25, 33), ΔH° is the enthalpy change, R is the ideal gas constant, and Δn is the net sodium ion uptake from single strands to duplex (17). Duplex RNA has a higher charge density than single strands because duplex is more compact than single strands, and this compaction contributes to the uptake of Na⁺ during duplex formation (11). The two equations above are the theoretical foundation for deriving the correction factors using the relationship between T_m or 1/T_m and ln [Na⁺] (17).

T_m Correction Factors

Previously published DNA T_m correction factors (Table 3) are mostly based on the functions between melting temperatures (or their reciprocal values) and the common (or natural) logarithm of the sodium ion concentration. The accuracy of 10 previously published correction factors is tested by |ΔT_m|_ave (Table 3), which range from 1.1 to 7.2 °C. Under close scrutiny, these correction factors can be sorted into three groups.

The first group consists of three correction factors (Equations 7, 8, and 11) that use only the relationship between T_m (or 1/T_m) and ln [Na⁺] (or log [Na⁺]). Equations 7 and 11 are among the most simple correction factors. Although equation 8 is somewhat more complicated, it does not employ any other additional parameters. |ΔT_m|_ave values for equations in this group, Eq. 7, 8, and 11, are 7.2, 4.5, and 4.2 °C, respectively. It appears as if this type of equation is too simple to accurately describe the relationship between sodium ion concentrations and melting temperatures. As a result, this type of T_m correction factor was not pursued further.

The second group is a modification on the first group and only consists of one correction factor. This correction factor, equation 12, introduces two additional parameters into the equation, N and ΔH°, in order to improve the accuracy. Here, N is half of the total number of phosphates in the duplex, and it is a way to reflect the effect of oligomer length in the correction factor. ΔH° is the enthalpy change, which could be either an experimental or predicted value, and is based on the assumption that counterion effects are mainly entropic (24, 30, 31). The |ΔT_m|_ave value for this equation is 1.4 °C. Due to its accuracy, the coefficients were revised based on the RNA data reported here, resulting in equation 18, with a |ΔT_m|_ave value of 1.0 °C (Table 4).

The third group introduces a special parameter into the equations, the fraction of G-C base pairs (f_GC). Equations 9, 10, 13, and 14 are linear functions in this group, and equations 15 and 16 are quadratic functions in this group. The linear functions in this group, eq 9, 10, 13, and 14 predict RNA T_m values with |ΔT_m|_ave values of 5.1, 6.7, 2.3, and 1.5 °C, respectively. The quadratic functions in this group, eq 15 and 16, predict RNA T_m values with |ΔT_m|_ave values of are 1.5 and 1.1 °C, respectively. These accurate RNA T_m predictions are not too surprising since these functions which account for f_GC were previously found to be among the most accurate for predicting DNA T_m values (17). Due to their accuracy, the coefficients for the linear and quadratic functions in this group were revised based on the RNA data reported here, resulting in equations 19–22, with |ΔT_m|_ave values of 0.9, 0.9, 0.7, and 0.7 °C, respectively (Table 4). It is important to note that eq 9 and 10 are same linear function as eq 13, except for different coefficients. Therefore, when eq 9, 10, and 13 are revised based on the RNA data reported here, they converge to eq 19.

A previous DNA study (17) took this third type of correction factor even further by expanding it into a more complex form that accounts for sequence dependence by including nearest neighbor parameters. Because there are 12 unique nearest-neighbor doublets including ends (35), the expanded version of this correction factor that accounts for nearest neighbors resulted in an increase of fitted parameters from 2 in the linear form of the f_GC equation to 12 in the linear form of the nearest neighbor equation and from 3 in the quadratic form of the f_GC equation to 24 in the quadratic form of the nearest neighbor equation. Surprisingly, the results in the DNA study show very little improvement on T_m prediction. Given its complex form and little improvement on accuracy, the nearest-neighbor version was not investigated here.

In general, equations 21 and 22 have the best accuracy for predicting RNA T_m. They are in quadratic form and could be developed into more complicated forms, such as a cubic or quartic function between T_m (or 1/T_m) and ln [Na⁺]. However, since |ΔT_m|_ave values are already relatively low, and T_m measurement errors needs to be considered at very low |ΔT_m|_ave values, we think it is accurate and convenient to utilize equations 21 and 22 for predictions. Due to the fact that equation 21 (Table 4) is consistent with the ΔG°₃₇ correction factor (discussed below), we recommend it as the T_m correction factors for RNA in [Na⁺] other than 1.021 M.

Here, we illustrate an example calculation using T_m correction factor equation 21. We have chosen an independent oligonucleotide, one that was not used in the derivation of the T_m correction factors proposed here. The example oligonucleotide is 5’-CCAUAUGG-3’/3’GGUAUACC5’. Serra et al. (10) measured the T_m of this oligonucleotide in 0.111 M Na⁺, and we will use the correction factor to predict this experimental T_m. Because the experimental T_m in 1.021 M Na⁺ is not available, we will use the predicted T_m in 1.021 Na⁺ based on the standard nearest neighbor parameters (9), 51.7 °C. We apply the correction to predict the T_m at 0.111 M Na⁺. The correction calculation is shown below:

$$T_m(0.111M)=T_m(1.021M)+(-1.842fGC+2.675)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}-0.7348({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$$ 31

$$T_m(0.111M)=51.7+(-1.842\times 0.5+2.675)\text{ln}\frac{0.111}{1.021}-0.7348({\text{ln}}^{2}0.111-{\text{ln}}^{2}1.021)$$ 32

$$T_m(0.111M)=44.3°C$$ 33

The T_m reported in the literature (10) for this oligonucleotide in 0.111 M Na⁺ is 45.7°C, resulting in a difference of only 1.4 °C between the experimental and the predicted temperatures.

ΔG°₃₇ Correction Factors

The only DNA ΔG°₃₇ correction factor available in the literature is equation 17 (Table 3). Similar to some of the T_m correction factors, it includes N to account for oligomer length. The |ΔΔG°₃₇|_ave of this correction factor is 0.21 kcal/mol. Due to its accuracy, the coefficients were revised based on the RNA data reported here, resulting in equation 28, with a |ΔΔG°₃₇|_ave value of 0.18 kcal/mol (Table 4).

Because there was only one DNA ΔG°₃₇ correction available in the literature, several new ΔG°₃₇ correction factors were derived and tested. Equation 23 (Table 4) was derived from a T_m correction factor described above, Equation 22. Equation 22 was chosen because it is one of the most accurate T_m correction factors, and its form is compatible with insertion into equation 3. The |ΔΔG°₃₇|_ave of equation 23 is 0.14 kcal/mol.

Other new ΔG°₃₇ correction factors were derived by simply using the relationship between ΔG°₃₇ (or 1/ΔG°₃₇) and ln [Na⁺]. These ΔG°₃₇ correction factors (Equations 24–27 in Table 4) have similar formats as some of the T_m correction factors (equations 19–22 in Table 4). The |ΔΔG°₃₇|_ave values for Equations 24–27 are 0.17, 0.19, 0.14, and 0.17 kcal/mol, respectively.

The two ΔG°₃₇ correction factors having the best accuracy for the RNA data reported here are equations 23 and 26, both resulting in |ΔΔG°₃₇|_ave values of 0.14 kcal/mol. Because both result in the same |ΔΔG°₃₇|_ave but equation 23 requires an extra parameter (ΔH°), we recommend equation 26 as the ΔG°₃₇ correction factors for RNA in [Na⁺] other than 1.021 M.

Here, we show an example calculation using ΔG°₃₇ correction factor equation 26. We have chosen an independent oligonucleotide, one that was not used in the derivation of the ΔG°₃₇ correction factors proposed here. The example oligonucleotide is 5’-AAGUGAUC-3’/3’-UUCACUAG5’. Nakano et al. (25) measured the ΔG°₃₇ of this oligonucleotide in 0.122 M Na⁺, and we will use the correction factor to predict this experimental ΔG°₃₇. Because the experimental ΔG°₃₇ in 1.021 M Na⁺ is not available, we will use the predicted ΔG°₃₇ in 1.021 M Na⁺ based on the standard nearest neighbor parameters (9), −8.62 kcal/mol. We apply the correction to predict the ΔG°₃₇ at 0.122 mM Na⁺. The calculation is shown below:

$$\mathrm{\Delta }{G°}_{37}(0.122M)=\mathrm{\Delta }{G°}_{37}(1.021M)+(0.324fGC-0.468)\text{ln}\frac{{\left[{\mathit{\text{Na}}}^{+}\right]}_2}{{\left[{\mathit{\text{Na}}}^{+}\right]}_1}+0.133({\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_2-{\text{ln}}^2{\left[{\mathit{\text{Na}}}^{+}\right]}_1)$$ 34

$$\mathrm{\Delta }{G°}_{37}(0.122M)=-8.62+(0.324\times 0.375-0.468)\text{ln}\frac{0.122}{1.021}+0.133({\text{ln}}^{2}0.122-{\text{ln}}^{2}1.021)$$ 35

$$\mathrm{\Delta }{G°}_{37}(0.122M)=-7.30\mathit{\text{kcal}}/\mathit{\text{mol}}$$ 36

The ΔG°₃₇ reported in the literature (25) for this oligonucleotide in 0.122 M Na⁺ is −7.26 kcal/mol, resulting in a difference of only −0.04 kcal/mol between the experimental and the predicted free energies.

Effect of [Na⁺] on ΔH° and ΔS°

In the sodium ion concentration range studied here, ΔH° is assumed to be independent of [Na⁺] (17, 24, 30). Figure S1 in Supporting Information shows the relationship between ΔH° and ln [Na⁺] for representative oligomers. Considering the proximity of ΔH° values in five different sodium ion concentrations and the errors of ΔH° in Table S1 and Figure S1, the assumption that ΔH° is independent of [Na⁺] appears valid. Thus, a correction factor for ΔH° was not derived.

ΔG°₃₇ and T_m are typically more accurate than either ΔH° and ΔS° because of enthalpy-entropy compensation (9). This is confirmed by both Figure S2, which illustrates the relationship between ΔS° and ln [Na⁺] for representative oligomers, and the ΔS° data in Table S1. Thus, a correction factor for ΔS° was not derived.

Oligomer Length and Sequence

Previous studies propose different ways to account for the effect of oligomer length and sequence on the stability of DNA in various sodium ion concentrations. SantaLucia et al. incorporate N into their correction factors for T_m, ΔG°₃₇, and ΔS° (24). Using N is a way to account for the effect of oligomer length in the correction factor. However, Owczarzy et al. only incorporate f_GC into their quadratic correction factor (17). f_GC is not a length parameter but rather a sequence dependent parameter, and the authors state that this correction factor can be used for duplexes ranging from 6 to at least 60 base pairs in length (17). Although the correction factor incorporating f_GC works best for the short RNA duplexes studied here, further studies with longer duplexes are needed to test the accuracy of this correction factor on longer duplexes.

Range of Sodium Ion Concentrations Appropriate for Correction Factors

The correction factors derived here were a result of data from RNA melting studies with sodium ion concentrations ranging from 71 mM to 1.021 M. Therefore, it is appropriate to use these corrections factors with sodium ion concentrations within this range. Very few experiments are performed in buffers containing more than 1.021 M Na⁺, and further studies would need to be done to test the accuracy of the correction factors at these high sodium concentrations. For concentrations below 71 mM Na⁺, a linear relationship between T_m and [Na⁺] is predicted by counterion condensation theory (17, 33, 36). However, the results of a DNA study show that the quadratic form of f_GC can be used to predict T_m for [Na⁺] lower than 71 mM (17). Therefore, future work needs to be done to investigate RNA behavior in very low sodium ion concentrations.

Comparison of Correction Factors to a Generalized Tightly Bound Ion Model

Tan and Chen (2007) previously developed a generalized tightly bound ion (TBI) model to correct RNA ΔG°₃₇ and T_m values at 1 M NaCl to other Na⁺ concentrations (32). In that study, the authors compared their model to a limited dataset of experimental data. With the data reported here, a much larger experimental dataset is available to compare to their generalized TBI model. When comparing the experimental data reported here to the generalized TBI model, the average difference for T_m is only 0.97 °C, and the average difference for ΔG°₃₇ is only 0.16 kcal/mol. Although these differences are slightly larger than the differences resulting from the correction factors derived here, their generalized TBI model works quite well.

CONCLUSIONS

In summary, the effect of sodium ion concentration on RNA duplex thermal stability was systematically studied. The accuracy of previously published DNA T_m correction factors and newly derived T_m correction factors was evaluated using the RNA data obtained here. The newly derived correction factors have higher accuracy than previous correction factors, and equation 21 has the best prediction accuracy, which is 0.7 °C for the RNA data reported here. Similarly, the accuracy of a previously published DNA ΔG°₃₇ correction factor and newly derived ΔG°₃₇ correction factors was evaluated using the RNA data obtained here. Equation 26 resulted in an average prediction error of 0.14 kcal/mol for the RNA data reported here and is in a similar form as the recommended T_m correction factor, Equation 21. The RNA T_m (Equation 21) and ΔG°₃₇ (Equation 26) correction factors proposed here can be incorporated into RNA secondary structure prediction software to accurately predict T_m and ΔG°₃₇ in Na⁺ buffers between 71 mM and 1.021 M.