Analyses of mineral specific surface area and hydroxyl substitution for intact bone

Abstract

Bone minerals possess two primary hydrogen sources: hydroxide ions in the nanocrystalline core and structural water in the amorphous surface layer. In order to accurately measure their concentrations using hydrogen to phosphorus cross polarization NMR spectroscopy, it is necessary to analyze the dependence of signal intensities on serial contact times, namely, cross polarization kinetics. A reliable protocol is developed to iteratively decompose the severely overlapped spectra and to analyze the cross-polarization kinetics, leading to measurement of hydroxyl and structural water concentrations. Structural water concentration is used to estimate mineral specific surface area and nanocrystal thickness for intact bone.

Introduction

Nuclear Magnetic Resonance (NMR) spectroscopy has been successfully exploited to characterize many biological hard tissues, such as bone, dentin, and enamel [1-4]. Bone consists of approximately 65% mineral, 25% organic matrix, and 10% water by weight [5]. Electron microscopy studies have revealed that chemically isolated bone minerals have globular morphologies of sizes from 70 to 90 nm, which are aggregates of smaller particles with sizes around 20 nm [6]. The in situ mineral nanocrystals are generally considered platelets of 20-50 nm length, 10-30 nm width, and 4-10 nm thickness, with organic matter filling space between platelets [7-9]. Bone mineral is analogous to hydroxyapatite (HA), Ca₁₀(PO₄)₆(OH)₂, which has unit cell dimensions a=b=9.424, c=6.879 Å, and angles α=β=90°, γ=120° [10]. However, bone mineral has extensive ion-substitutions at the Ca²⁺, PO₄³⁻, and OH⁻ sites [1,8]. The quality of bone reflects deviations from the ideal hydroxyapatite composition and crystal structure that occur via formation of ionic vacancies and substitutions. For example, the number of phosphate-carbonate exchanges increases with age [11-13]. The crystal size is believed to strongly influence the response of the bone to load [14]. Fragile bones from old or osteoporotic animals exhibit relatively large and uniform crystal sizes, while the stronger young bones tend to have a mixture of newly formed small crystals and matured larger crystals [14].

The biological apatite nanocrystal consists of a nanocrystalline apatite core enclosed by a 1-2 nm amorphous layer of calcium phosphate that has been postulated to be a precursor of hydroxyapatite formation [4,5,7,8,16,17]. Minerals octacalcium phosphate (Ca₈(HPO₄)₂(PO4)₄·5H₂O) and brushite (CaHPO₄·2H₂O) have been considered possible compositions of the amorphous layer [15,16]. However, no mineral phases other than apatite have been directly detected in bone samples [17-19]. In agreement with this, ¹H-³¹P 2D NMR spectra of biological apatites [4,20,21] do not show any cross peak (at 14 ppm and −0.2 ppm for ¹H and ³¹P, respectively) corresponding to the HPO₄²⁻ group in octacalcium phosphate [15]. Using ¹H-³¹P 2D NMR spectra, Mathew and coworkers have unambiguously established that in biomimetic amorphous calcium phosphates the PO₄³⁻ groups are only close to water molecules but not hydroxides or acidic protons [22]. This is consistent with the amorphous calcium phosphates being built by aggregated Posner’s clusters, Ca₉(PO₄)₆, with water molecules occupying their interstices [22]. The Posner’s cluster, which has its structure extracted from the unit cell of hydroxyapatite, seems to be an attractive model for the amorphous phase [22,23]. The Posner’s cluster is roughly spherical with diameter 9.5 Å, matching the length of a and b in hydroxyapatite unit cells. According to this model, transformation from the amorphous to apatite phase occurs by dissociating the clusters from their aggregated form, rather than completely dissolving into ions [24].

Existence of structural water in the biological minerals has been evasive. In ¹H-³¹P 2D NMR spectra, a strong water to phosphorus cross polarization (CP) [25] peak has been observed [21]. However, the lack of spinning sidebands indicates that these water molecules are mobile. Instead of structural water, the peak was attributed to surface adsorbed water molecules, which were considered immobile enough to establish CP but subject to exchange among multiple adsorption sites [21]. The existence of structural water was proven unequivocally just recently by Yoder and coworkers using thermal analysis of water loss [26]. In the same work, deuterium NMR resonance for structural water gave a narrow peak, rather than a broad pattern as expected for immobile species. The observed narrow peak was explained by dynamics similar to tetrahedral jumps of water molecules in an ice lattice without translational motion. The same dynamics can readily explain why water protons do not display spinning sidebands. Our data (vide infra) on crystalline hydroxyapatite further demonstrated that adsorbed water molecules cannot establish CP with phosphorus. Therefore, water molecules detected via CP are structural water inside the amorphous surface layer, not adsorbed water.

Proton species can be quantitatively measured using a one-pulse ¹H NMR experiment for synthetic apatites or deproteinated bone minerals, with water resonating at ca. 5 ppm and hydroxide ions at ca. 0 ppm [27]. In bone, however, proton signals from the collagen matrix overwhelm mineral signals [21]. To solely select proton sources in the mineral, ¹H-³¹P CP has been employed [5,28]. CP relies on heteronuclear dipolar coupling to transfer polarization, usually, from proton to other nuclei. The signal sensitivity depends on local proton density and the dipolar coupling strength [25]. The effective coupling strength can be affected by the distance between the coupled nuclei, dynamics, and the rate of magic-angle spinning (MAS) [29]. Therefore, a single CP spectrum is not quantitative due to non-uniform sensitivity enhancements across various resonance moieties, in addition to those factors influencing the coupling strength. To quantitatively retrieve compositional and structural information, the dependence of CP signal intensity on the contact time, namely CP kinetics, has to be analyzed with the assistance of theoretical models [30].

The ¹H-³¹P CP spectra of bone mineral show a single peak consisting of a narrow component (ca. 2 ppm full width at half height) from sites near the internal hydroxide ions and a broad component (ca. 5 ppm width) from structural water molecules, while their centers are nearly identical at ca. 3.3 ppm [31]. One could construct a kinetics curve by integrating the whole peak or taking the peak height, followed by fitting the curve with a pair of kinetics models [5]. The potential problem with this approach is that the kinetics curve can very likely be fit with many combinations of a relatively large number of parameters (at least 6), and the fitting program may become trapped in a local minimum. Another approach reported in the literature is to first decompose each spectrum by Gaussian lineshapes, followed by fitting two kinetics curves separately [31]. However, lineshapes of individual components, especially the broad component from the amorphous surface, may not be faithfully represented by Gaussians. Here we report a strategy to better extract the lineshapes and the individual kinetics curves using an iterative algorithm.

Very importantly, the mineral surface mediates interactions between the mineral and the organic matrix, including collagens and other proteins that regulate the homeostasis of calcium phosphate [35,36]. Kolodziejski and coworkers have estimated specific surface area (SSA) of biominerals by using the linewidth difference between cross-polarization (CP) and direct-polarization phosphorus NMR spectra [32]. As the NMR linewidths are determined by short-range interactions, the NMR method measures SSA for the thin platelet nanocrystal, which should be much larger than SSA measured on bigger isolated globular mineral particles using other analytical methods including gas adsorption [33]. Here we report an alternative method for assessing SSA of intact bone by measuring the concentration of structural water.

1. Experimental

Material Preparation

Synthetic hydroxyapatite (Sigma-Aldrich, St. Louis, MO; catalogue number 574791, ≥99.995% trace metals basis) was ground to powder using pestle and mortar. Chicken bones were obtained from a local supermarket. Two chickens were used for investigating potential influence by animal age and weight: a Tyson 5 lb roaster and a Prospect Farms 1 lb Cornish game hen. Cortical bone samples of a non-weight bearing radius and a weight bearing tibia from each chicken were cleaned with water and chiseled to fit into the 5 mm NMR rotor. Mouse cortical bone specimens were collected from male C57BL/6 mice (Charles River Laboratories International, Inc., Wilmington, MA, USA) maintained on a semi-purified diet (AIN93M) and housed in an environmentally controlled animal research facility [34]. The mice were anesthetized with a ketamine/xylazine cocktail (70 and 30 mg/kg body weight, respectively) exsanguinated via the carotid artery at ages 7 and 29 weeks. The tibiae were harvested and the bone marrow flushed with saline. The cortical diaphysis of each bone was extracted, soft tissue wiped and washed away. All procedures strictly adhered to the guidelines set forth by the Oklahoma State University Animal Care and Use Committee.

Nuclear Magnetic Resonance

Intact, rather than pulverized, mouse cortical bones were used in NMR experiments. The bones were first weighed for mass (ca. 10 mg for mouse samples and 40-120 mg for chicken samples), volume, and density using Archimedes’ Principle, and then were packed into 5 mm rotors. To balance the rotor for MAS and to keep the bone hydrated, 0.2% saline solution was added to fill empty space within the rotor. NMR experiments were performed on a Chemagnetics CMX-II 300 MHz spectrometer with a double resonance MAS probe operating at 300.998 MHz for ¹H and 121.847 MHz for ³¹P. Experiments were performed with room-temperature air gently blowing on the rotor, which was spinning at 5 kHz. For cross polarization ³¹P 1D or ¹H-³¹P 2D experiments, 5.4 μs proton 90° pulse width, about 50 kHz locking field on each channel during CP with a linear ramp of ±2 kHz applied on the ³¹P channel, 2.5 s recycle time was used for bone and 100 s for synthetic hydroxyapatite. Very long recycle time was necessary for this hydroxyapatite sample, opposite to what has been reported in literature that crystalline hydroxyapatite has faster spin-lattice relaxation than bone and tooth [22,35]. The slow relaxation observed here is most likely a result of the high purity and lack of crystal defects in the material used. Two-pulse phase modulated (TPPM) decoupling [36] of ca. 50 kHz were applied in the direct dimension for all types of experiments. NMR data were processed using NMRPipe [37]. Each spectrum was first divided by the sample mass and the number of scans used during data acquisition and analyzed using Matlab R2012a (The MathWorks, Natick, MA).

2. Results and discussion

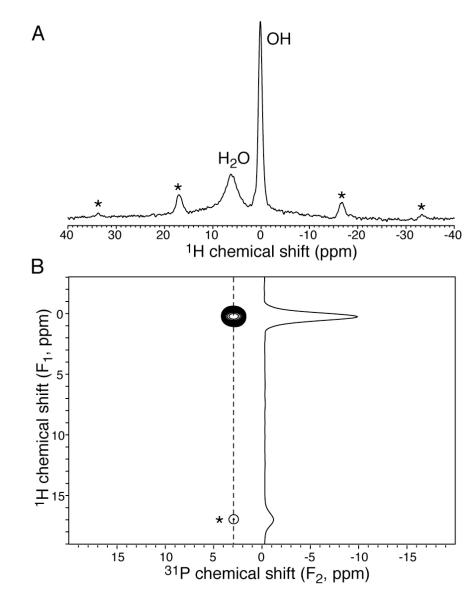
The direct-polarization proton spectrum of crystalline hydroxyapatite excited all proton sites, which included hydroxide and adsorbed water signals (Fig. 1A). However, in the 2D ¹H-³¹P cross-polarization spectrum (Fig. 1B), the water resonance is missing. This indicates that the adsorbed water is too mobile to establish CP with phosphorus.

Figure 1.

NMR spectra showing that adsorbed water on crystalline hydroxyapatite does not generate a cross-polarization signal. (A) One-pulse direct-polarization spectrum detected both hydroxides and water signals. (B) Two-dimensional ¹H-³¹P cross-polarization spectrum (2 ms contact time) detected only hydroxides. Spinning sidebands of hydroxides are marked by asterisks.

For bone samples, cross-polarization from ¹H to ³¹P gives a single, unresolved peak in the phosphorus dimension that can be fit with two components (Fig. 2). As the CP contact time increases, the peak progressively narrows. This change in lineshape reveals the different proton species [38]. Fig. 2A shows the broad lineshape at a short contact time (0.5 ms), which comes primarily from phosphate groups near the surface water protons. The narrow lineshape in Fig. 2B at a longer contact time (22 ms) is dominated by phosphate groups near hydroxide ions. Middle-range contact times produce a convolution of spectra from both species. The spectrum at each contact time has a specific ratio of both components, and will be decomposed to determine this ratio using an iterative spectral deconvolution and kinetics analysis procedure.

Figure 2.

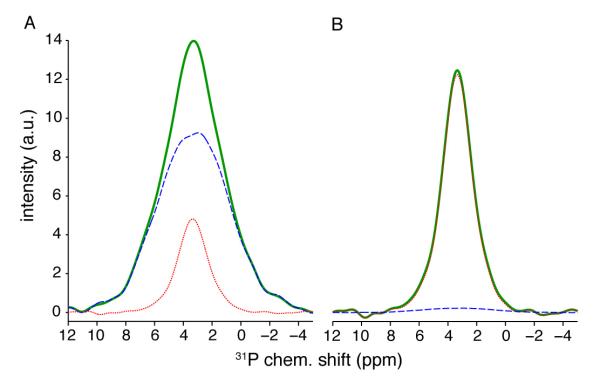
Extraction of lineshapes for the broad (A) and narrow (B) components. In (A), the initial trial lineshape (thick solid, online green) started from a CP spectrum with 0.5 ms contact time for Tyson chicken tibia. The final lineshape (dashed, online blue) was obtained using the iterative process as described in the following text. The difference spectrum (thin dotted, online red) has identical shape to the final lineshape for narrow component (red thin dotted line in B). In (B), the trial started from a CP spectrum with 22 ms contact time. The difference spectrum (dashed, online blue) between the trial (thick solid, online green) and final (thin dotted, red online) has identical shape to the final lineshape of the broad component (blue dashed line in A).

For the bone samples, we found that it is not necessary to use a non-classical CP model to fit the kinetics curves [5,30,31], presumably due to a much lower concentration of hydroxides in the bone than hydroxyapatite [21]. The amplitude I of each component independently follows the classical CP kinetics model:

$$I\left({\tau }_{\mathit{CP}}\right)=I_0\left[\exp \right(-{\tau }_{\mathit{CP}}∕T_{1\rho })-\exp (-{\tau }_{\mathit{CP}}∕T_{\mathit{CP}}\left)\right]∕(1-T_{\mathit{CP}}∕T_{1\rho }),$$ (1)

where τ_CP is the CP contact time, I₀ the signal amplitude, T_CP the CP time constant between proton and phosphorus nuclei, and T_1ρ the spin-lattice relaxation time of proton in the rotating frame [20,30]. The CP time constant governs the growth of the CP kinetics curve while the spin-lattice relaxation determines the decay [39]. Assuming A is the fast decaying, broad component and B the slow decaying, narrow component, with $T_{\mathit{CP}}^A<T_{\mathit{CP}}^B$ and $T_{1\rho }^A<T_{1\rho }^B$, the algorithm for the iterative spectral deconvolution and CP kinetics analysis is described as follows.

1. Select a CP spectrum acquired with a short contact time (e.g., ${\tau }_{\mathit{CP}}^A<T_{\mathit{CP}}^B∕3$) to be the trial broad lineshape S_A. Select another spectrum with a long contact time (e.g., ${\tau }_{\mathit{CP}}^B>3T_{1\rho }^A$) for the trial narrow lineshape S_B.

2. Normalize S_A and S_B so that s_A and s_B have unit peak area.

3. Deconvolute each CP spectrum according to S(τ_CP) = c_A (τ_CP)s_A + c_B (τ_CP)s_B.

4. Fit the two kinetics curves, i.e., series of c_A and c_B values with different contact times, using a selected CP kinetics model, such as the classical model in Eq. 1. It is of course allowed to use different kinetics models for the two curves. This results in two sets of kinetics parameters $I_0^A,T_{\mathit{CP}}^A,T_{1\rho }^A$ and $I_0^B,T_{\mathit{CP}}^B,T_{1\rho }^B$.

5. Subtract the predicted narrow component contribution from the trial broad lineshape, ${\mathrm{S}}_{\mathrm{A}}={\mathrm{S}}_{\mathrm{A}}-I({\tau }_{\mathit{CP}}^A;I_0^B,T_{\mathit{CP}}^B,T_{1\rho }^B){\mathrm{s}}_B$. Subtract the predicted broad component contribution from the trial narrow lineshape, ${\mathrm{S}}_{\mathrm{B}}={\mathrm{S}}_{\mathrm{B}}-I({\tau }_{\mathit{CP}}^B;I_0^A,T_{\mathit{CP}}^A,T_{1\rho }^A){\mathrm{s}}_A$.

6. Repeat from Step 2 until all kinetics parameters converge. In most cases, 50 iterations should be sufficient.

The final lineshapes for components A and B are shown in Fig. 2. The integrated intensity of the final lineshape of A (B) is 81% (96%) of the initial trial spectrum. Deconvolution of spectra of four contact times (1, 4, 10, 18 ms) using the two final lineshapes are shown in Fig. 3. In Fig. 4, the final CP kinetics curves for the Tyson tibia constructed with the iterative process are fit by Eq. 1, yielding parameters listed in Tables 1 and 2. In agreement with previous studies, water in the amorphous surface (component A) has much shorter T_CP and T_1ρ values (0.54 and 5 ms) than the hydroxide ions in the crystalline core (component B, 2.1 and 33.8 ms). The spectrum of 22 ms contact time satisfies ${\tau }_{\mathit{CP}}^B>3T_{1\rho }^A$, having a diminishing amount of A, and was thus a very good trial B lineshape. On the other hand, the ratio of A to B intensities in a spectrum with very short contact times is roughly $T_{\mathit{CP}}^B∕T_{\mathit{CP}}^A$, since the square bracket in Eq. 1 can be approximated by ^{1− exp(−τ_CP/T_CP) ≈ τ_CP/T_CP}. Therefore, it is impossible to find a contact time such that the spectrum dominantly consists of lineshape A. Therefore, B contribution has to be subtracted to obtain lineshape A in the iterative procedure.

Figure 3.

Deconvolution of CP spectra using lineshapes of broad and narrow components extracted by the iterative deconvolution and CP kinetics analysis procedure. The CP spectra, which are represented by thick lines (green online), were obtained for Tyson chicken tibia with contact times 1, 4, 10, and 18 ms for (A), (B), (C), and (D), respectively. The fit spectra are shown in black thin lines, the broad components in dashed lines (blue online), and the narrow components in thin dotted lines (red online).

Figure 4.

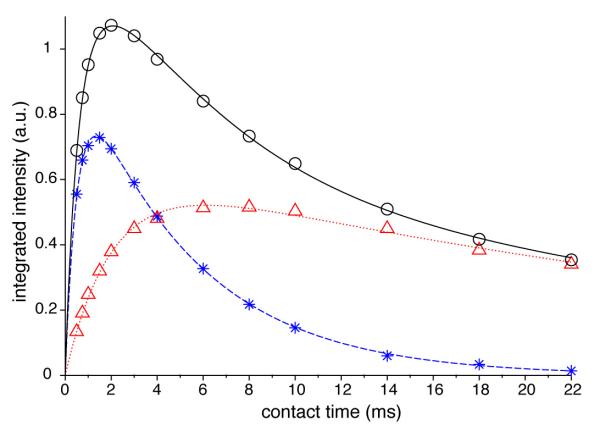
CP kinetics of tibia sample from Tyson chicken. Dependences of signal intensity on contact time for the broad A-component (star, online blue) and the narrow B-component (triangle, online red) are fit with the classical model using parameters listed in Table 1. The intensities for the whole peak (circle) are fit by the sum of the fitting curves for the individual components.

Table 1.

Classical CP kinetics model parameters for the component B with hydroxide ions as signal source.

Sample	ρ (g/cm3)	finorg (wt%)a	I0 (a.u.)	TCP (ms)	T1rho (ms)	rOH (%)b	nc	COH (mmol/g)d	COHfull (mmol/g)e	fOH (%)f
HA			3.00 (0.05)	1.73 (0.08)	600 (200)			1.99
TysTib	1.84 (0.01)	60.3 (0.3)	0.62 (0.01)	2.05 (0.08)	34 (2)	20.7 (0.7)	0.84 (0.07)	0.63 (0.05)	1.39 (0.06)	45 (6)
TysRad	1.85 (0.02)	60.6 (0.6)	0.79 (0.01)	1.96 (0.06)	35 (2)	26.3 (0.8)	0.88 (0.07)	0.81 (0.06)	1.25 (0.08)	65 (9)
ProTib	1.73 (0.01)	55.6 (0.2)	0.56 (0.01)	1.69 (0.07)	32 (2)	18.8 (0.6)	1.02 (0.09)	0.68 (0.06)	1.32 (0.06)	51 (7)
ProRad	1.84 (0.01)	60.3 (0.5)	0.714 (0.009)	2.75 (0.06)	36 (1)	23.8 (0.7)	0.63 (0.04)	0.62 (0.04)	1.33 (0.07)	47 (6)
ms29wkTib	2.03 (0.05)	67 (2)	0.86 (0.02)	2.3 (0.1)	27 (2)	29 (1)	0.75 (0.07)	0.74 (0.08)	1.42 (0.08)	52 (9)
ms7wkTib	1.88 (0.05)	62 (2)	0.98 (0.02)	2.33 (0.09)	32 (2)	33 (1)	0.74 (0.06)	0.9 (0.1)	1.39 (0.09)	65 (12)

^aSee Eq. 4.

^bRelative hydroxide content – hydroxide amount in unit mass of bone with respect to unit mass of hydroxyapatite.

^cSee Eq. 3. For unit cells contain hydroxide ions, on average there are 2n OH⁻ ions per cell.

^dConcentration of hydroxide per unit mass of inorganic matter, see Eq. 5b.

^eSee Eq. 8. The concentration of hydroxide ions with regard to mineral content assuming full occupancy of 2 OH⁻ per unit cell in the crystalline phase. It is proportional to the content of crystalline phase.

^fSee Eq. 9. It is the abundance of hydroxide ions with respect to the content of crystalline phase.

Table 2.

Classical CP kinetics model parameters for the component A with structural water as signal source.

Sample	I0 (a.u.)	TCP (ms)	T1rho (ms)	n b	CH2O (mmol/g)c	CPC (mmol/g)d	SSA (m2/g)e
HA
TysTib	0.998 (0.007)	0.536 (0.009)	5.04 (0.06)	3.2 (0.2)	0.98 (0.04)	0.31 (0.03)	144 (15)
TysRad	1.19 (0.01)	0.58 (0.02)	5.6 (0.1)	3.0 (0.2)	1.13 (0.05)	0.38 (0.04)	177 (20)
ProTib	1.08 (0.01)	0.50 (0.01)	5.2 (0.1)	3.5 (0.2)	1.21 (0.05)	0.34 (0.03)	162 (15)
ProRad	1.05 (0.01)	0.60 (0.01)	5.2 (0.1)	2.9 (0.2)	0.98 (0.04)	0.34 (0.04)	160 (17)
ms29wkTib	1.15 (0.01)	0.45 (0.01)	4.42 (0.09)	3.8 (0.3)	1.11 (0.08)	0.29 (0.04)	137 (20)
ms7wkTib	1.08 (0.02)	0.48 (0.02)	5.9 (0.2)	3.6 (0.3)	1.10 (0.08)	0.30 (0.05)	143 (23)

^aSee Eq. 4.

^bSee Eq. 3.

^cConcentration of water molecules (not protons) per unit mass of inorganic matter, see Eq. 5a.

^dConcentration of Posner’s clusters (not protons) per unit mass of inorganic matter, see Eq. 7.

^eSee Eq. 6a.

Spectra and kinetics curves of all bone samples were well fit (Fig. S1 and Fig. S2 in Supplementary Data) with parameters listed in Tables 1 and 2. Parameters for the hydroxyapatite are also listed in the Table 1, with the kinetics data in Fig. S3. Its intensity (I₀ = 3.00 a.u.) provides a reference of proton quantification for other samples. Compared to large deviation from stoichiometry known for OH⁻ [21], phosphorus loss is less significant; for example, the variation of the Ca/P ratio in bone after birth is below 5% [40,41]. Therefore, the CP signal intensities are mainly determined by the amount of protons. The T_CP value of hydroxyapatite (1.73 ms) agrees with literature [22]. A large range of T_CP values are observed for the B component of bone samples, corresponding to CP between the hydroxide proton to phosphorus in the nanocrystalline interior (Table 1). The value 1.7 ms for the Prospect chicken tibia sample is nearly identical to hydroxyapatite within experimental error, implying that these phosphorus sites exist in domains having full hydroxide occupancy in the unit cells. Longer T_CP values for other samples indicate lower than stoichiometry hydroxide occupancy. In hydroxyapatite, a phosphorus atom neighbors two O-H groups linearly aligned on the unit cell c-edge [10,42]. Contributions to the CP rate constant, namely the inverse of T_CP, from neighboring protons are additive according to the following equation [22,43],

$$\frac{1}{T_{\mathit{CP}}}\propto \sum _i{b}_{\mathit{Si}}^2$$ (2)

Parameter b_Si represents the dipolar coupling strength, which is inversely proportional to the cubic of distance between the phosphorus (S) and a proton identified by index i. Due to the fast decrease of b_Si with distance, only the closest protons may be considered. The rate constants of the amorphous component A for bone samples are ca. 3 to 4 times larger than hydroxyapatite. This is slightly higher than the 2-fold increase for biomimetically grown amorphous calcium phosphates observed by Mathew and coworkers, who interpreted the result by assigning two water molecules to each Posner’s cluster [22]. It is convenient to define

$$n=\frac{T_{\mathit{CP}}^{\mathit{HA}}}{T_{\mathit{CP}}},$$ (3)

which according to the additive property means 2n OH⁻ per apatite unit cell (for component B) or n water molecules per Posner’s cluster (for component A). From the n values in Table 1, the average occupancy ranges from 1.2 to 2 hydroxide ions per unit cell. This average does not account for proton-deficient domains with all hydroxide sites replaced by F⁻, CO₃²⁻, etc [4]. Since the CP time constants are measured over the whole sample, which may have variation of proton occupancy locally, the averaged n value determined in Eq. 3 need not to be integer.

The signal amplitude, I₀, is proportional to the square root of the number of protons in each environment for adiabatic CP, rather than proportional to the proton number directly [25]. Adiabatic passage CP under MAS is often implemented by ramping the locking field of one rf channel in a tangent shape [44]. According to our experiences [45,46], a linear ramp reaches similar efficiency as the tangent shape. It is interesting to assess water and hydroxide amounts with regard to bone mineral in addition to the total bone mass. Bone density has been found to have a well-defined relationship with compositions (inorganic, organic, and water) since these components have distinctive densities. The inorganic content f_inorg (wt %) and density ρ (g/cm³) data presented by Robinson et al. [47] can be fit by

$$f_{\mathit{inorg}}=-199.14+302.77\rho -120.85{\rho }^2+17.89{\rho }^3.$$ (4)

The inorganic content includes ash and the so-called CO₂ space that accounts for materials (crystallization water, potassium, sodium, chloride, and soluble organic matter) lost during ashing at 600 °C [47]. The concentrations (mmol/g) of water molecules and hydroxide ions per unit mass of bone minerals can be calculated, respectively, as

$$C_{H_{2}O}=\frac{\sqrt{n}(I_0^A∕2)C_{\mathit{OH}}^{\mathit{HA}}}{I_0^{\mathit{HA}}{f}_{\mathit{inorg}}},$$ (5a)

$$C_{\mathit{OH}}=\frac{\sqrt{n}{I}_0^B{C}_{\mathit{OH}}^{\mathit{HA}}}{I_0^{\mathit{HA}}{f}_{\mathit{inorg}}},$$ (5b)

where $I_0^{\mathit{HA}}$ is the intensity fitting parameter and $C_{\mathit{OH}}^{\mathit{HA}}=1.99$ mmol/g the stoichiometric hydroxide concentration for hydroxyapatite. One study reported that a hydroxyapatite sample contained 93% of the stoichiometric hydroxide content [21]. However, evidences based on extremely long relaxation times (Experimental section) support that the reference sample used in this study has high purity and no correction for hydroxide deficiency was made. In these equations, a representative apatite unit cell with an average of 2n OH⁻ or Posner’s cluster with n H₂O is used in the spirit of mean-field theories [48]. The relative hydroxide content (r_OH, Table 1) in unit mass of bone (including both organic and inorganic contents) with respect to unit mass of hydroxyapatite is determined by the ratio of I₀ for B component of bone samples and I₀ for the reference hydroxyapatite sample. These ratios are between 19-33%, agreeing with 21% reported by Ackerman and coworkers [21].

The concentration of structural water molecules (C_H2O) ranges from 0.98 to 1.2 μmol/mg for these bone samples. This concentration can be used to extract SSA of bone mineral platelets. The crystalline core of the mineral platelets is modeled by stacking apatite unit cells with axis c along the length of the platelet and axis a along the thickness (Fig. S4). Meanwhile, the amorphous surface is modeled by either one or two layers of Posner’s clusters, and each cluster associates n water molecules. Over 8,000 model mineral platelets were simulated (Matlab script in Table S1). The relations between SSA and water concentration were found to be

$$\mathit{SSA}=470.7C_{\mathit{PC}},$$ (6a)

$$\mathit{SSA}=138.2C_{\mathit{PC}}-32.8$$ (6b)

for single-layer and double-layer models, respectively. The concentration of Posner’s cluster can be determined from experimentally measured concentration of structural water

$$C_{\mathit{PC}}=C_{H_{2}O}∕n.$$ (7)

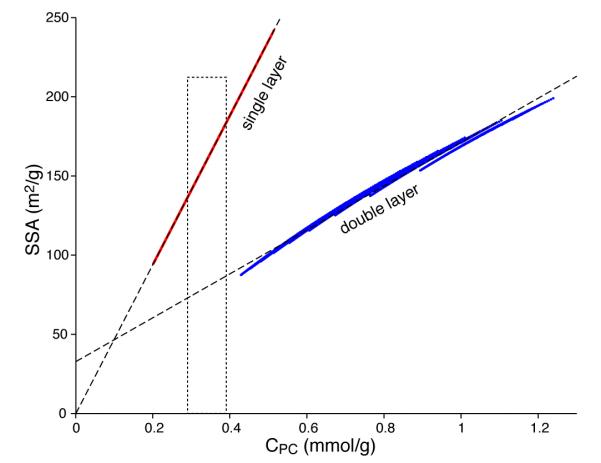
SSA values for the bone samples (Table 2) range from 130 to 180 m²/g, within the 100-200 m²/g range reported in literature [23]. Fig. 5 clearly shows that the concentrations of Posner’s clusters produced by the double-layer assumption are all higher than the observed values. Therefore, the single layer model is more consistent with NMR data. Thickness of platelet models is plotted against Posner cluster concentration in Fig. S5, showing that it is possible to make a very crude estimation of platelet thickness from structural water measurements.

Figure 5.

Relationship between the specific surface area of model apatite platelets and concentration of Posner’s clusters, which can be determined from experimentally measured concentration of structural water using Eq. 7. More than 8,000 platelet models of length between 20 to 50 nm, width 10 to 30 nm, and thickness 4 to 11 nm were investigated, each of which is represented by a dot (not resolved). The concentration of Posner’s clusters is determined assuming that either one layer (online in red) or two layers (online in blue) of clusters make up the amorphous platelet surface. The dashed straight lines represent data fitting by Eqs. 6a,b. The dotted rectangle indicates the range of concentration determined using NMR for bone samples used in this study.

In addition to the concentration of hydroxide ions with respect to the whole mineral content (Eq. 5b), it is also interesting to find abundance of hydroxide ions with respect to the content of the crystalline apatite phase. The concentration of hydroxide ions with regard to mineral content assuming full occupancy of 2 OH⁻ per unit cell in the crystalline phase, $C_{\mathit{OH}}^{\mathit{full}}$ (mmol/g), is proportional to the content of crystalline phase. Its relation with the concentration of Posner’s clusters is plotted in Fig. S6, which is fit with

$$C_{\mathit{OH}}^{\mathit{full}}=1.99-1.96C_{\mathit{PC}}.$$ (8)

This makes the abundance of hydroxide ions in the crystalline phase

$$f_{\mathit{OH}}=C_{\mathit{OH}}∕C_{\mathit{OH}}^{\mathit{full}}.$$ (9)

The range of abundance is 45 to 65% for the bone samples investigated (Table 1). On the other hand, the n values, which reflect the occupancy of the hydroxide sites for unit cells having at least one OH⁻, range from 0.6 to 1 (Eq. 3 and Table 1). The fact that overall abundance f_OH is lower than local occupancy n supports the existence of domains without hydroxide ions inside the crystalline core [4].

When modeling the crystalline core, the apatite unit cell c axis was chosen to be in the mineral platelet plane. This choice was based on the fact that sizes determined by the breadth of the [002] reflection in X-ray diffraction spectra are often significantly above 10 nm [41], the upper limit for thickness of mineral platelets [8]. The SSA values directly calculated from these model platelets of typical sizes are all bigger than 94 m²/g, which was reported for dentin, dental cementum, and cortical bone based on linewidth difference between cross-polarization and direct-polarization phosphorus NMR spectra [32]. The SSA calculated from the models is mainly determined by the dimensions of the platelets, not by details of the model such as the use of Posner’s cluster for the amorphous phase. Therefore, SSA determined with the linewidth method might have a systematic deviation.

The two Tyson chicken samples exhibit large variation in SSA (144 and 177 m²/g). The two Prospect chicken samples have nearly the same SSA (162 and 160 m²/g), but they have large variation in the number of water molecules per Posner’s cluster (3.5 and 2.9). Many factors could contribute to these differences: species, age, gender, weight, and rearing conditions. The 29 wk mouse bone (estimated to be comparable to a 22 yr human) shows larger density and more inorganic content than the 7 wk mouse (estimated to be comparable to a 5 yr human), this trend is consistent with bone maturation [41]. Their SSA values (137 and 143 m²/g for the 29 and 7 wk bones, respectively) display a small difference that is consistent with crystal size increasing with age [14]. Also the younger mouse bone has significantly higher hydroxide content than the mature bone, attesting that ion substitutions occur progressively with age [40].

In contrast to the iterative procedure reported above, Fig. S7 shows two methods of analyzing CP kinetics curve without spectral deconvolution. The curve can be nicely fit with a pair of CP kinetics models, but the parameters are different from each other and the iterative procedure. This demonstrates that there are many ways to fit the kinetics curve with six (3 for each model) or more parameters, and that the fitting program may be trapped in local minimum. Fig. S8 shows decomposition by two Gaussian lineshapes before kinetics analysis. The results are not reliable since Gaussians cannot faithfully represent the lineshapes.

3. Conclusions

Protons found in bone mineral can be reliably quantified by analyzing cross-polarization kinetics. ¹H-³¹P CP requires less experimental time than inverse ³¹P-¹H methods [31]. While a single ¹H-³¹P cross-polarization spectrum produces a single peak, it can be deconvoluted to reveal the distinct proton environments. Iterative spectral deconvolution and kinetics curve analysis gives reliable parametric and structural information. Concentration of structural water determined from CP kinetics has been used to calculate SSA of bone minerals, which were modeled by an apatite core covered by an amorphous surface layer of Posner’s clusters. Concentration of hydroxide ions displays dependence on animal species and ages. The CP time constant reveals organization of domains rich or deficient of hydroxide ions. This iterative deconvolution and kinetics analysis technique is also applicable to other biominerals such as dentin and cementum.

Highlights.

• Bone mineral specific surface area and thickness without deproteination.

• Concentration of hydroxyl groups in the crystalline apatite phase.

• Concentration of structural water in the amorphous phase.

• New algorithm for NMR spectral decomposition and cross-polarization kinetics.