Specimen-specific predictions of contact stress under physiological loading in the human hip: validation and sensitivity studies

Abstract

Hip osteoarthritis may be initiated and advanced by abnormal cartilage contact mechanics, and finite element (FE) modeling provides an approach with the potential to allow the study of this process. Previous FE models of the human hip have been limited by single specimen validation and the use of quasi-linear or linear elastic constitutive models of articular cartilage. The effects of the latter assumptions on model predictions are unknown, partially because data for the instantaneous behavior of healthy human hip cartilage are unavailable. The aims of this study were to develop and validate a series of specimen-specific FE models, to characterize the regional instantaneous response of healthy human hip cartilage in compression, and to assess the effects of material nonlinearity, inhomogeneity and specimen-specific material coefficients on FE predictions of cartilage contact stress and contact area. Five cadaveric specimens underwent experimental loading, cartilage material characterization and specimen-specific FE modeling. Cartilage in the FE models was represented by average neo-Hookean, average Veronda Westmann and specimen- and region-specific Veronda Westmann hyperelastic constitutive models. Experimental measurements and FE predictions compared well for all three cartilage representations, which was reflected in average RMS errors in contact stress of less than 25%. The instantaneous material behavior of healthy human hip cartilage varied spatially, with stiffer acetabular cartilage than femoral cartilage and stiffer cartilage in lateral regions than in medial regions. The Veronda Westmann constitutive model with average material coefficients accurately predicted peak contact stress, average contact stress, contact area and contact patterns. The use of subject- and region-specific material coefficients did not increase the accuracy of FE model predictions. The neo-Hookean constitutive model underpredicted peak contact stress in areas of high stress. The results of this study support the use of average cartilage material coefficients in predictions of cartilage contact stress and contact area in the normal hip. The regional characterization of cartilage material behavior provides the necessary inputs for future computational studies, to investigate other mechanical parameters that may be correlated with OA and cartilage damage in the human hip. In the future, the results of this study can be applied to subject-specific models to better understand how abnormal hip contact stress and contact area contribute to OA.

1 Introduction

One in four people develop hip osteoarthritis (OA) during their lifetimes (Murphy et al. 2010). Abnormal cartilage contact mechanics may predict the onset and progression of OA (Carter et al. 2004; Guilak et al. 2004; Wilson et al. 2005). Altered mechanics may initiate OA through damage to the physical integrity of cartilage or by initiating changes in cartilage metabolism. For example, altered pressures change the metabolism of cartilage explants (Guilak et al. 2004; Guilak and Hung 2005). Additionally, high stresses cause cartilage fissuring during impact loading in vitro (Atkinson and Haut 1995; Haut et al. 1995; Li et al. 1995; Newberry et al. 1998; Silyn-Roberts and Broom 1990).

Cartilage contact stresses cannot be measured directly in vivo, so finite element (FE) methods have been applied to predict hip cartilage stresses in the hip in vivo. Previous FE models of the human hip have provided insight into the mechanics of normal and pathologic hips, using both subject-specific and idealized geometries (Anderson et al. 2008a; Anderson et al. 2010; Brown and DiGioia 1984; Chegini et al. 2009; Harris et al. 2012; Henak et al. 2011; Rapperport et al. 1985; Russell et al. 2006). Models have demonstrated inter-subject variability in the normal population (Harris et al. 2012), the influence of subject-specific geometry (Anderson et al. 2010) and altered mechanics in hips with bony pathology compared to normal hips (Chegini et al. 2009; Henak et al. 2011; Russell et al. 2006). Model validation was not performed in some of these studies. In other studies, model validation included only a single specimen. All of these previous studies have assumed spatially homogeneous, quasi-linear or linear elastic cartilage constitutive behavior.

Confidence in FE predictions and the effects of modeling assumptions on those predictions can be evaluated via direct validation and parametric analysis, respectively. Direct validation is the process of comparing experimental results and computational predictions using identical (or nearly identical) boundary conditions, loading conditions and geometry (Anderson et al. 2007a; Henninger et al. 2010; ASME Committee (PT60) on Verification and Validation in Computational Solid Mechanics 2006). Parametric analysis is the systematic evaluation of the effects of modeling assumptions on model predictions. One specimen-specific FE model of the human hip was validated (Anderson et al. 2008a); however, a series of hip models has not been validated. Validation using a series of specimens provides two advantages over validation using a single specimen. First, validation on a series of specimens demonstrates the predictive capabilities of the FE models across specimen-specific geometries and elucidates the expected inter-specimen variability. Second, statistical methods can determine the effect of model parameters when multiple specimens are modeled.

While it is known that cartilage material behavior includes material nonlinearity and spatial inhomogeneity, the effects of cartilage constitutive model on FE predictions of cartilage contact stress and contact area in the human hip are unknown. Cartilage material behavior is time- and rate-dependent, but nearly incompressible elastic material behavior is an appropriate simplification under fast loading rates such as those experienced during physiological loading, including walking (Ateshian et al. 2007; Wong et al. 2000). Although advanced constitutive models have not been employed to represent articular cartilage in the human hip, FE predictions in the human knee suggest that some of the more advanced aspects of cartilage constitutive behavior are unnecessarily complicated for predictions of contact mechanics (Gu and Li 2011; Mononen et al. 2012). Even with these simplifications, previous FE models of the human hip have used cartilage behavior with coefficients from other joints or other animals because data regarding the instantaneous response of healthy human hip cartilage were not available (here, “instantaneous” is used to indicate loading that occurs over a period ≤0.5 s) (Anderson et al. 2008a; Anderson et al. 2010; Chegini et al. 2009; Harris et al. 2012; Henak et al. 2011). Biphasic and linear elastic analyses of hip cartilage suggest that behavior from other joints and other animals does not match the behavior of human hip cartilage (Athanasiou et al. 1995; Shepherd and Seedhom 1999; Treppo et al. 2000; Taylor et al. 2012). Therefore, regional instantaneous material behavior of healthy human hip cartilage must first be characterized to investigate whether features of the assumed cartilage constitutive model affect FE predictions of hip contact stress and contact area. The required complexity and specificity of cartilage constitutive model can then be determined by comparing results obtained with constitutive models that describe different levels of material nonlinearity and spatial inhomogeneity.

Therefore, there were three objectives to this study (1) to develop and validate a series of specimen-specific FE models by directly comparing FE predictions of contact stress and contact area to experimental measurements; (2) to characterize the regional instantaneous response of healthy human hip cartilage in compression using quasi-linear and nonlinear constitutive models and (3) to assess the effects of material nonlinearity, inhomogeneity and specimen-specific material coefficients on FE predictions of cartilage contact stress and contact area. These objectives were carried out with a focus on predictions of contact stress and contact area, which were measured experimentally on a subject-specific basis. These parameters are often used in the interpretation of mechanical loading relevant to the development of OA (Creamer and Hochberg 1997; Henak et al. 2013; Russell et al. 2006; Segal et al. 2009, 2012).

2 Methods

Contact stress and contact area were investigated in five normal male cadaveric hips using a combined experimental and computational protocol (40 ± 14 years old, weight 62.8 ± 13.8 kg, height 176.5 ± 8.9 cm) (Anderson et al. 2008a). All specimens were screened for hip pathology with an anteroposterior radiograph and known medical history. Cartilage was macroscopically examined during dissection. No osteoarthritic changes or degenerative lesions were found.

2.1 Experimental methods

All soft tissue except cartilage was dissected from each specimen. Registration blocks were attached to the hemipelvis and the femur (Anderson et al. 2008a; Fischer et al. 2001). Volumetric CT scans were obtained of the fully dissected, disarticulated specimens (Siemens Somatom Emotion, 512 × 512 pixel acquisition matrix, 276–420 mm FOV, 0.7 mm slice thickness). Scanner settings were based on our previous study, which demonstrated less than 10% error in cartilage thickness using CT (Anderson et al. 2008b). Anatomical coordinate systems were established using bony landmarks and were digitized relative to the registration blocks with a Microscribe G2X or MLX digitizer (accuracy ≤0.23mm, CNC Services, Inc., Amherst, VA, USA) (Bergmann et al. 2001; Anderson et al. 2008a). The femur and pelvis were cemented into custom test fixtures that provided rotation about the internal/external, flexion/extension and abduction/adduction axes as well as translation to align the joint (Fig. 1). Testing was completed using an MTS 858 with a 4 kN load cell (MTS Systems Corporation, Eden Prairie, MN, USA). The entire loading system allowed for the femur to impart a non-vertical joint reaction force onto the acetabulum, as experienced in vivo (Anderson et al. 2008a; Bergmann et al. 2001).

Fig. 1.

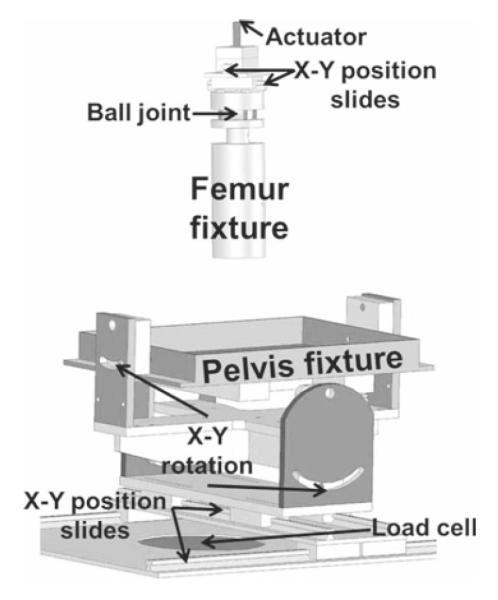
Fixture used to experimentally load specimens. The pelvis and femur were placed into anatomical positions and aligned prior to loading. Both the pelvis and the femur fixtures were able to translate and rotate to achieve the correct anatomical position

Four physiological loading scenarios were tested based on instrumented implant and gait data: heel strike during walking, mid-stance during walking, heel strike during stair descent and heel strike during stair ascent (Bergmann et al. 2001). Each position was achieved using an iterative process until all three kinematic angles were within ±3° of the target positions.

Low-range pressure-sensitive film cut into rosette patterns was used to measure contact stress and contact area (Fuji Prescale®, Sensor Products, Inc., NJ, USA) (Anderson et al. 2008a). Pressure-sensitive film measures the pressure or the stress normal to the film. Thus, the pressure measured by the film can best be interpreted as the contact stress on the articular surface of the femur. Rosettes were placed between two polyethylene sheets and secured over the femoral head prior to each trial. Three trials were captured for each loading scenario, and one trial from each loading scenario was selected for further analysis. The resultant loads for the selected trials were 1560 ± 335, 1520 ± 327, 1723 ± 326 and 1464 ± 284 N for heel strike during walking, mid-stance during walking, heel strike during stair descent and heel strike during stair ascent, respectively. Following each trial, the positions of the registration blocks and the pressure-sensitive film rosettes were digitized.

To determine the correlation between pixel intensity and applied pressure, sections of unused pressure-sensitive film were compressed between two flat platens layered with cellophane to a range of loads. All pressure-sensitive film was scanned and converted to gray-scale digital images for processing.

2.2 Cartilage material testing methods

Unconfined compression testing was used to characterize the depth-averaged constitutive behavior of healthy human hip cartilage under fast loading rates, such as those applicable to the loading scenarios used during whole joint testing. On the day of soft tissue dissection, cartilage samples were harvested from nine regions on the femoral head and six regions on the acetabulum of the non-tested joint of each specimen (Fig. 2) (Athanasiou et al. 1994). One to two samples were obtained from each region. The number of samples was limited by the size and curvature of each anatomical region. A coring tool and scalpel excised each sample, which included the full cartilage thickness as well as some underlying subchondral bone. Samples were stored at −72 °C until testing.

Fig. 2.

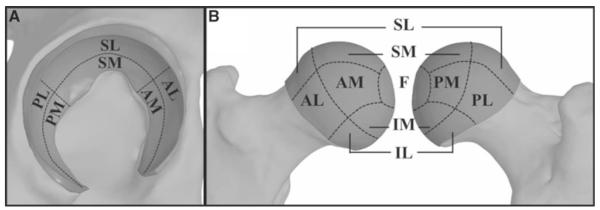
Anatomical regions defined for cartilage material characterization. a acetabular cartilage. b femoral cartilage. S superior, P posterior, A anterior, I inferior, M medial, L lateral, F foveal

Each sample was sectioned serially using a microtome to remove subchondral bone and to create a deep surface parallel to the articular surface. Samples were then resized to 3.4-mm diameter cylinders and split in half along the long axis of the cylinder, resulting in two to four samples from each region. Sample height was measured three times using a resistance micrometer, and measurements were averaged.

Samples underwent unconfined compression testing between two glass slides. The custom test system consisted of a servo-controlled mechanical stage (Model MRV22, Tol-O-Matic, Hamel, MN, USA), LVDT (Model ATA 2001, Schaevitz, Hampton, VA, USA) and 10 lb load cell (LSB200, Futek Advanced Sensor Technology, Inc., Irvine, CA, USA). A tare load of 58.9 ± 5.0 kPa was applied and held for 30 min, resulting in a stretch of 0.85 ± 0.08 (Huang et al. 2003; Krishnan et al. 2003; Park et al. 2004; Soltz and Ateshian 2000). The height of the sample following tare loading was determined from the position of the test system and was subsequently used as the reference height for loading.

After 30 min of tare loading, samples were compressed to a stretch ratio of 0.85 relative to the reference height over 1 s (15%/s). The loading rate was the approximate loading rate of walking (Bergmann et al. 2001), as well as a rate at which cartilage material behavior can be approximated as nearly incompressible (Ateshian et al. 2007). Cartilage testing was displacement driven, while load was measured. All testing was completed in a PBS bath at room temperature (Park et al. 2004; Soltz and Ateshian 2000).

Material coefficients for two hyperelastic constitutive models were fitted to the experimental data. The neo-Hookean constitutive model represents a quasi-linear relationship between stress and stretch. This model was selected because it is the simplest hyperelastic model, and therefore, serves as a baseline. Further, previous hip FE models assumed neo-Hookean or linear elastic cartilage constitutive behavior, and therefore, this material model allows direct comparison with previous FE results (Anderson et al. 2008a; Anderson et al. 2010; Brown and DiGioia 1984; Chegini et al. 2009; Harris et al. 2012; Henak et al. 2011; Rapperport et al. 1985; Russell et al. 2006). In the Veronda Westmann model, stress is exponentially dependent on stretch (Veronda and Westmann 1970). This constitutive model was chosen to capture the material nonlinearity present in cartilage constitutive behavior, in contrast to the quasi-linear neo-Hookean model.

For both constitutive models, a least squares fit minimized the difference between experimental and predicted stress–stretch curves to determine material coefficients (SigmaPlot 11.0, Systat Software Inc., San Jose, CA, USA). Uncoupled neo-Hookean strain energy was in the form (Maas et al. 2011):

$$W=\frac{1}{2}\mu \left({\tilde{I}}_1-3\right)+\frac{1}{2}K{\left(\ln J\right)}^2.$$ (1)

Here, μ is the shear modulus under infinitesimal strain, ${\tilde{I}}_1$ is the first deviatoric invariant, K is the bulk modulus and J is the determinant of the deformation gradient. For an incompressible material subjected to unconfined compression by a stretch ratio γ₃, the neo-Hookean Cauchy stress σ₃₃ is:

$${\sigma }_{33}=\frac{1}{2}\mu \left({\lambda }_3^2-\frac{1}{{\lambda }_3}\right).$$ (2)

Thus, μ was the coefficient that was determined by curve fitting in the neo-Hookean constitutive model. Veronda Westmann strain energy was in the form (Maas et al. 2011; Veronda and Westmann 1970):

$$\begin{array}{cc}\hfill W=C& {}_1\left(\exp \left[C_2\right({\tilde{I}}_1-3\left)\right]-1\right)-\frac{C_1{C}_2}{2}({\tilde{I}}_2-3)\hfill \\ \hfill & +\frac{1}{2}K{\left(\ln J\right)}^2.\hfill \end{array}$$ (3)

Here, ${\tilde{I}}_2$ is the second deviatoric invariant. For an incompressible material subjected to unconfined compression by a stretch ratio γ₃, the Veronda Westmann Cauchy stress σ₃₃ is:

$$\begin{array}{cc}\hfill {\sigma }_{33}=C_1{C}_2& [\left(2{\lambda }_3^2-\frac{2}{{\lambda }_3}\right)\exp \left[C_2\left({\lambda }_3^2+\frac{2}{{\lambda }_3}-3\right)\right]\phantom{]}\hfill \\ \hfill & \phantom{[}-{\lambda }_3+\frac{1}{{\lambda }_3^2}].\hfill \end{array}$$ (4)

The product C₁C₂ was defined as the Veronda Westmann modulus in the reference configuration and denoted E₀ for statistical comparisons between regions. The coefficients C₁ and C₂ were both determined by curve fitting the Veronda Westmann constitutive model to the data. For both constitutive models, the uniqueness of the best-fit material coefficients was verified by perturbing initial guesses.

The stretch ratio, γ₃, was derived from the applied crosshead displacement and the known sample height. Cauchy stress was derived from the measured load, initial cross-sectional area and stretch ratio, assuming material incompressibility (Quapp and Weiss 1998).

2.3 Computational methods

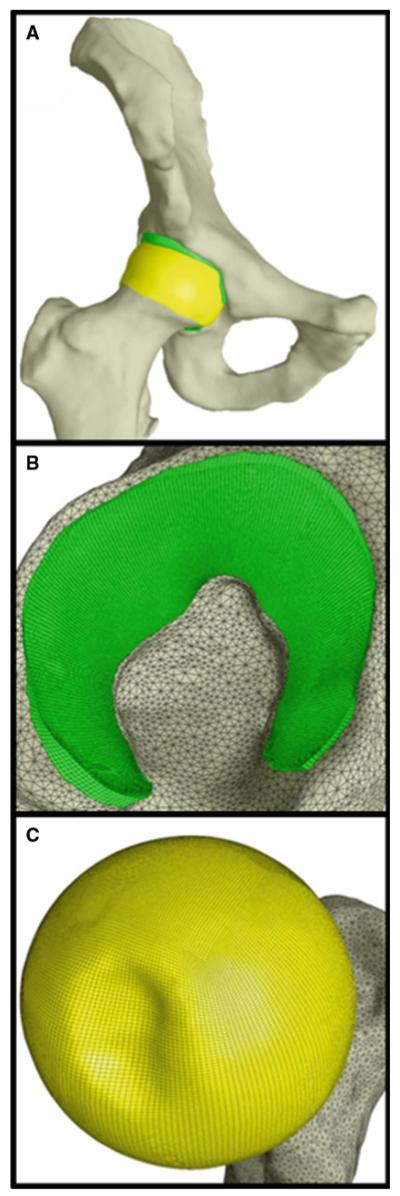
CT data were segmented using a combination of automated thresholding based on image intensity and manual segmentation methods in the Amira software (5.3, Visage Imaging, San Diego, CA, USA) (Anderson et al. 2008a, 2005). Polygonal surfaces of the bone and cartilage were generated from the segmented data (Anderson et al. 2008a; Harris et al. 2012; Henak et al. 2011). Cartilage surfaces were imported into TrueGrid (XYZ Scientific, Livermore, CA, USA) to generate hexahedral FE meshes (Fig. 3). Cortical bone surfaces were discretized into triangular shell elements with position-dependent thickness (Anderson et al. 2005). Cortical bone was represented as isotropic linear elastic (E = 17 GPa, ν = 0.29) (Dalstra and Huiskes 1995). Representation of the cortical bone was based on a previous validation study evaluating the effects of FE representation of bone on bone strain (Anderson et al. 2005). Mortar tied contact attached cartilage to bone, while mortar sliding contact governed the interaction between cartilage layers (Puso 2004; Puso and Laursen 2004). All analyses were completed in NIKE3D (Puso et al. 2007).

Fig. 3.

Representative FE model. Cortical bones are shown in white, femoral cartilage is shown in yellow and acetabular cartilage is shown in green. a whole joint. b acetabular cartilage. c femoral cartilage

Finite element models were generated with three different cartilage representations to determine the effects of cartilage material nonlinearity, inhomogeneity and specimen specificity on FE predictions. The most specific cartilage representation used a Veronda Westmann constitutive model with specimen-specific regional material coefficients. To generate these models, a continuous heterogeneous distribution of the material coefficients was required. This was obtained using Laplace interpolation over the FE mesh, with the material coefficients for each region serving as Dirichlet boundary conditions at the center of the region (Press et al. 2007; Chapra and Canale 2002). Since the steady-state heat transfer equation is an example of Laplace’s equation, the interpolation was performed using the heat transfer module in FEBio (Maas et al. 2012b; Chapra and Canale 2002). The resulting continuous distribution was discretized into 25 specimen-specific sets of material coefficients on the femur and 25 specimen-specific sets of material coefficients on the acetabulum (this is referred to as “VW specific”). A second set of Veronda Westmann material coefficients was averaged across all specimens and regions (this is referred to as “VW average”). Similarly, neo-Hookean material coefficients were averaged across all specimens and regions (this is referred to as “nH average”). Bulk moduli were selected to enforce material near incompressibility. The Veronda Westmann constitutive equation was implemented in NIKE3D, and the implementation was verified by comparing the results of single element analyses with analytical solutions.

Boundary and loading conditions for the FE simulations were matched to experimental trials using the digitized data. Positions of the registration blocks segmented from CT data were aligned to their digitized experimental positions for each trial. Each model was run to the corresponding experimental load. For model validation, cartilage contact stress and cartilage contact area were obtained on the articular surface of the femoral cartilage. To compare the three methods for modeling cartilage, contact stress and contact area were obtained on the acetabular cartilage. All FE post-processing was completed using PostView (Maas et al. 2012a).

A mesh convergence study determined the appropriate number of elements through the cartilage thickness to achieve converged contact stress and contact area predictions. Cartilage meshes with three, four, five and six elements through the thickness were generated for one specimen and analyzed with VW average cartilage. Overall mesh density was adjusted to maintain element aspect ratios and element Jacobians. Meshes were considered converged when the average change in contact stress and contact area across all four loading scenarios between subsequent meshes was less than 5%. Based on the results of the mesh convergence study, all further analyses were completed with five elements through the cartilage thickness.

2.4 Data and statistical analysis

To validate the FE models, nodal contact stress results reported on the femoral head of the FE models were compared to experimental results from the matched trial. Intraclass correlation coefficients compared agreement between experimental and FE results for each of the four loading scenarios. A Bland–Altman analysis with an adjustment for clustered data compared the differences and tolerance intervals between experimental and FE results over all loading scenarios (Allen et al. 2010; Bland and Altman 1999; McCarthy and Thompson 2007). Finally, a pixel-wise calculation of RMS error between FE and experimental contact stress was completed in a custom program that we developed for a previous study (Anderson et al. 2008a) (Fig. 4).

Fig. 4.

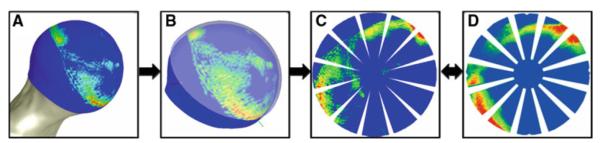
Process for comparing experimental and FE results pixel-wise. a FE results were extracted from the articular surface of the femoral head. b FE results were projected to a sphere, and the experimental position of the pressure-sensitive film is overlaid. c The spherical projection was mapped to a planar rosette, creating a simulated rosette with the same dimensions as the experimental rosette. d The experimental rosette was used as the reference standard for pixel-wise comparison against the simulated rosette

To investigate the influence of cartilage representation on FE predictions, FE nodal contact stress results from the three cartilage representations were compared in six regions of the acetabular cartilage (Fig. 2). Contact stress and contact area were sampled on the articular surface of the acetabular cartilage. A pairwise comparison of results from each cartilage representation was completed using random effects linear regression, accounting for the non-independence of data clustered within each specimen and loading scenario. Finner’s procedure corrected the resulting p values for multiple comparisons (Finner 1993).

Regional differences in FE results and cartilage material coefficients clustered within each specimen were also evaluated using random effects linear regression. FE results were compared pairwise between all six acetabular regions, as well as between lateral and medial regions. Material coefficients from six acetabular regions and nine femoral regions were pooled, and the following comparisons were performed: all femoral regions versus all acetabular regions, all medial regions versus all lateral regions, medial regions versus lateral femoral regions and medial regions versus lateral acetabular regions. Additionally, all six acetabular regions and all nine femoral regions were compared pairwise. Finner’s procedure corrected the resulting p values for multiplicity (Finner 1993). Significance for all tests was set at p ≤ 0.05.

3 Results

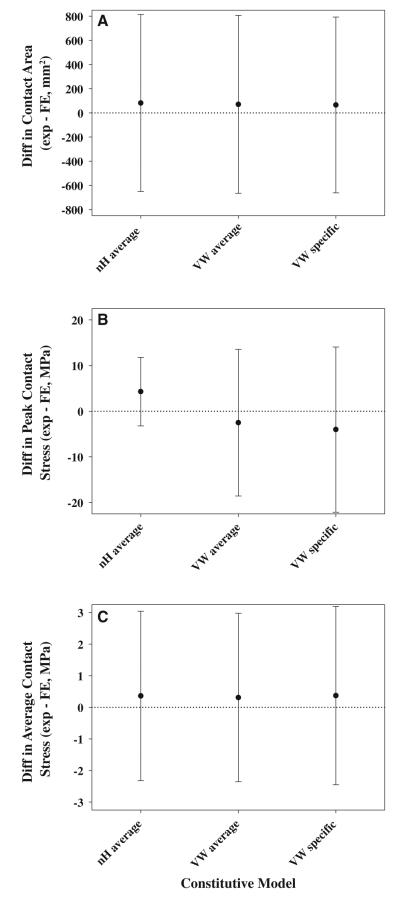
Experimental and computational results compared well for most specimens and loading scenarios (Fig. 5 and Online Resource Figure S1). Inter-specimen variability within each loading scenario was larger than inter-scenario variability within each specimen (Fig. 5 and Online Resource Figure S1). Distinct contact patterns for each specimen were multicentric, banded or combinations of the two. Qualitative differences between the three cartilage representations were nearly indistinguishable, which was reflected in minimal effects on RMS error in contact stress, minimal effects on contact stress differences and minimal effects on contact area differences (Fig. 6 and Online Resource Figure S1). RMS error in contact stress was 23.8 ± 4.8, 23.9 ± 4.8 and 23.3 ± 4.8 % in the nH average, VW average and VW specific models, respectively. Experimental contact area was larger than FE predicted contact area with all cartilage representations (Fig. 6a). Experimental peak contact stress was larger than FE predicted peak contact stress in the nH average models. Conversely, experimental peak contact stress was smaller than FE predicted peak contact stress in the VW average and VW specific models (Fig. 6b). Experimental average contact stress was larger than FE predicted average contact stress with all cartilage representations (Fig. 6c).

Fig. 5.

Comparisons between experimental and FE contact pressure for heel strike during stair descent in VW average models. Results compared well across specimen-specific geometry

Fig. 6.

Comparisons of experimental and FE results show that validation metrics were insensitive to constitutive model. a Bland–Altman analysis of contact area. b Bland–Altman analysis of peak contact stress. c Bland–Altman analysis of average contact stress. Differences were calculated by subtracting the FE predicted value from the experimentally measured value. Differences greater than zero indicate larger experimental results than FE predictions. Error bars tolerance intervals corrected by the design effect

Cartilage material coefficients exhibited significant regional variation within the hip joint (Table 1 and Online Resource Table SI). When the data were pooled, both μ and E₀ were larger in the acetabular cartilage than in the femoral cartilage, and larger in the lateral cartilage than in the medial cartilage. In the acetabulum, both μ and E₀ were larger in the AL region than in all other regions except the PL region. Both μ and E₀ in the acetabulum were also larger in the PL region than in the PM and SM regions. In the SL region, μ was larger than in the SM region of the acetabulum. In the femur, E₀ was larger in the IL region than in the IM, PL, SM and AL regions. E₀ was also larger in the AM region than in the IM region in the femur. In the SM region, μ was smaller than in the SL, PM, PL and AL regions. In the PL region, μ was larger than in the AM region. In the SL region, μ was larger than in the IM region in the femur. Although many of the regional differences were consistent for both constitutive models, the quasi-linear behavior exhibited in the neo-Hookean constitutive model overpredicted stress at stretch values near unity and underpredicted stress at smaller stretch values (Fig. 7).

Table 1.

Constitutive model coefficients determined from curve fitting experimental Cauchy stress versus stretch data

Side	Region	neo-Hookean μ (MPa)	Veranda Westmann C1 (MPa)	Veronda Westmann C2 (no units)
Femur	AL	5.72 ± 2.74	0.30 ± 0.17	6.70 ± 1.51
	AM	4.06 ± 0.98	0.31 ± 0.27	5.87 ± 1.86
	SL	5.50 ± 1.52	0.34 ± 0.17	6.45 ± 2.13
	SM	3.46 ± 2.04	0.19 ± 0.18	8.40 ± 3.05
	PL	6.22 ± 2.32	0.38 ± 0.30	6.93 ± 2.33
	PM	4.74 ± 1.38	0.29 ± 0.08	6.98 ± 1.13
	IL	6.34 ± 0.74	0.48 ± 0.21	5.26 ± 0.94
	IM	3.92 ± 0.62	0.23 ± 0.18	7.23 ± 2.23
	F	4.98 ± 2.16	0.29 ± 0.17	6.34 ± 1.89
	Lateral	5.88 ± 2.10	0.36 ± 0.21	6.36 ± 1.42
	Medial	4.08 ± 1.52	0.26 ± 0.18	7.10 ± 2.68
	Whole	4.88 ± 2.02	0.30 ± 0.21	6.71 ± 2.27
Acetabulum	AL	9.34 ± 3.20	0.72 ± 0.37	5.31 ± 1.09
	AM	4.82 ± 1.12	0.22 ± 0.12	7.42 ± 1.51
	SL	6.54 ± 2.62	0.29 ± 0.16	7.31 ± 0.59
	SM	4.68 ± 0.58	0.26 ± 0.08	7.21 ± 0.94
	PL	7.96 ± 1.80	0.45 ± 0.10	6.13 ± 0.34
	PM	5.74 ± 1.78	0.31 ± 0.19	6.60 ± 1.09
	Lateral	7.74 ± 2.28	0.47 ± 0.27	6.33 ± 1.29
	Medial	5.04 ± 1.60	0.26 ± 0.15	7.20 ± 1.43
	Whole	6.44 ± 2.58	0.37 ± 0.25	6.69 ± 1.42
Both	Lateral	6.50 ± 2.54	0.40 ± 0.26	6.22 ± 1.48
	Medial	4.40 ± 1.56	0.28 ± 0.20	6.86 ± 2.44
	Whole	5.32 ± 2.32	0.34 ± 0.24	6.55 ± 2.07

Mean ± SD. Anatomical regions are shown in Fig. 2. The pooled lateral, medial and whole regional coefficients were obtained by averaging across all samples

Fig. 7.

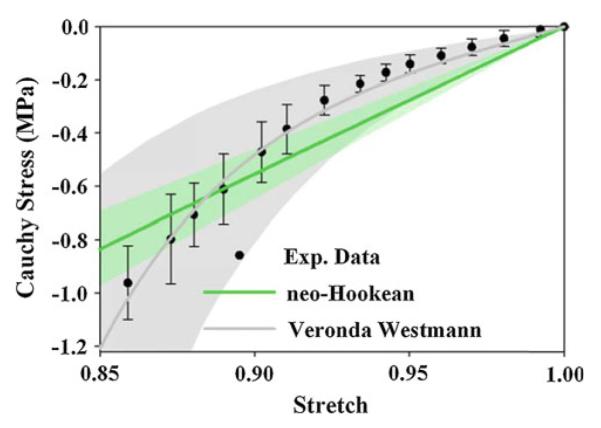
Experimental Cauchy stress versus stretch curve for one specimen in the femoral SM region. Error bars standard deviation. Solid lines for each fit represent the response with average coefficients, shaded areas SD. The neo-Hookean constitutive model overpredicted stress magnitudes at stretch values near unity and underpredicted stress magnitudes at smaller stress values. The Veronda Westmann constitutive model captured cartilage material nonlinearity

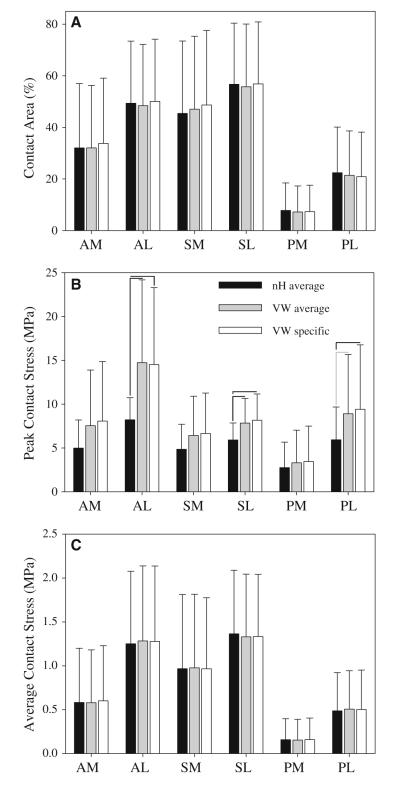
When comparing model predictions within each region between FE models, nH average models predicted lower peak contact stress than both VW average and VW specific models in some regions (Fig. 8b). However, there were no significant differences in average contact stress or in contact area between the three cartilage representations (Figs. 8a, c). There were no significant differences in FE results between VW average and VW specific models (Fig. 8).

Fig. 8.

Contact area and contact stress for all constitutive models, by anatomical region. a Contact area. b Peak contact stress. c Average contact stress. Error bars SD. Black lines significant differences (p ≤ 0.05) and gray lines nearly significant differences (0.05 < p ≤ 0.1). The only significant differences were in peak contact stress in the lateral regions

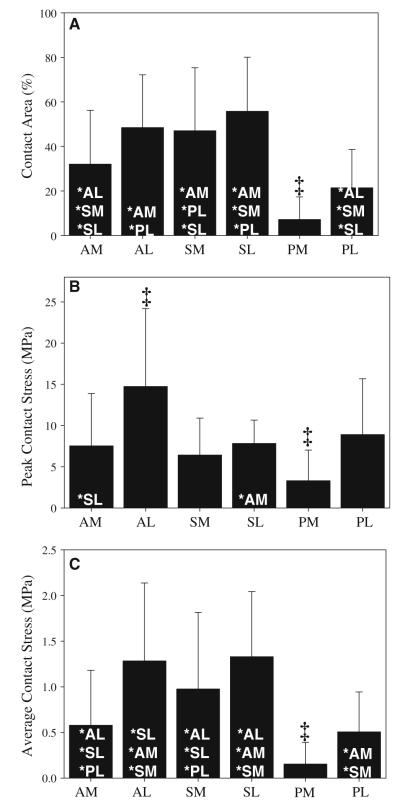
Peak contact stress, average contact stress and contact area varied by region, with higher values in several of the lateral regions (Fig. 9). For all three cartilage representations, peak contact stress, average contact stress and contact area were smaller in the medial cartilage than in the lateral cartilage. For the VW average models, peak contact stress, average contact stress and contact area were smaller in the PM region than in all other regions. Peak contact stress was larger in the AL region than in all other regions. Contact area in the SL region was larger than in all medial and both posterior regions. Contact area in the AL region was larger than in both posterior regions and the AM region. Contact area in the SM region was larger than in the AM region and both posterior regions. Average contact stress in the AL and SL regions was larger than in all medial regions. Although significant results varied slightly between the VW average models and the other two cartilage representations, the trends were similar.

Fig. 9.

Contact area and contact stress VW average models. a Contact area. b Peak contact stress. c Average contact stress. Error bars SD. ^‡Indicates p ≤ 0.05 against all other regions. *Indicates p ≤ 0.05 against listed region. Results were generally larger in the lateral regions and were smaller in the PM region

4 Discussion

Qualitative and quantitative comparisons between FE and experimental results indicate that the quality of validation for contact stress is relatively insensitive to the choice of cartilage constitutive model. Further, the lack of difference in model predictions between analyses with specimen-specific material coefficients and analyses with averaged material coefficients suggests that predictions of hip contact stress and contact area are insensitive to regional variations in material coefficients in hips with healthy articular cartilage (Fig. 8). These results are consistent with previous analyses in the hip, wherein contact stress patterns resulted primarily from model geometry (Anderson et al. 2010; Harris et al. 2012), and in the knee, which reported that contact stress predictions were insensitive to variations in cartilage anisotropy (Mononen et al. 2012). The influence of model geometry also reiterates previous findings of inter-subject variability in contact stress patterns in a population of normal hips (Harris et al. 2012). The relative insensitivity of contact pattern to cartilage representation and the relative importance of model geometry can be explained by the fact that contact stress as measured by pressure-sensitive film is primarily a measure of the interstitial fluid pressure on the surface when the cartilage is loaded quickly (Ateshian et al. 1994).

This is the first study to characterize the instantaneous regional material behavior of healthy human hip cartilage. These data demonstrate distinct regional differences, including the finding that lateral cartilage is stiffer than medial cartilage. Previous studies have suggested that regional variations in cartilage properties result from adaptation to loading, with stiffer properties in areas of frequent loadbearing (Seedhom et al. 1979; Shepherd and Seedhom 1999; Swann and Seedhom 1993; Yao and Seedhom 1993; Athanasiou et al. 1991). Indeed, in the present study, the stiffer lateral regions of the acetabulum experienced larger peak contact stress, average contact stress and contact area than medial regions. Since walking accounts for most of the time when cartilage undergoes fast loading (Vissers et al. 2011), these data suggest that the instantaneous material properties of healthy human hip cartilage may result from adaptation to the loading distribution.

The regional variations in instantaneous material behavior in this study are different than previously reported variations in the biphasic material behavior of cartilage. Athanasiou et al. 1994 demonstrated that the linear biphasic aggregate moduli were larger in the medial acetabulum and femur than in the lateral acetabulum and femur, but there were no differences in aggregate modulus between the pooled femoral cartilage and the pooled acetabular cartilage. In contrast, we found that lateral cartilage was stiffer than medial cartilage under fast loading rates, and pooled acetabular cartilage was stiffer than pooled femoral cartilage. Our findings do not necessarily contradict the results reported by Athanasiou et al.; the aggregate modulus is a measure of equilibrium behavior of the solid matrix, while μ and E₀ are measures of solid–fluid interactions. Further, the linear biphasic representation is valid for small strains, while the hyperelastic representations used in the present study are valid for arbitrarily large deformations. Therefore, these coefficients reflect different mechanisms and provide unique information regarding the ways in which cartilage responds to load.

The neo-Hookean constitutive model overpredicted the experimental stress–strain curve at small strain magnitudes and underpredicted stress at large strain magnitudes, which affected the FE predictions of contact stress. At large strain magnitudes, FE models with nH average cartilage underpredicted peak contact stress in comparison with both FE models with VW cartilage and experimental results (Figs. 6b and 8b). However, when the results were evaluated over the entire range of strains, average contact stress, contact area and qualitative contact patterns were indistinguishable between cartilage representations (Figs. 5, 8a, c). Therefore, a simple neo-Hookean constitutive model is sufficient to provide predictions of average contact stress on the articular surface and contact area that in reasonable agreement with experimental measurements. This is consistent with the findings reported in previous FE studies, as well as the ability of discrete element analysis to accurately predict contact mechanics in the human hip (Anderson et al. 2008a, 2007b; Donahue et al. 2002; Abraham et al. 2013).

The experimental and computational results of this study for contact stress and contact patterns compare well with previous studies. In vitro peak contact stresses measured using piezoelectric pressure sensors, pressure-sensitive film and transducers range between ~5 and ~10MPa (Adams and Swanson 1985; Afoke et al. 1987; Anderson et al. 2008a; Brown and Shaw 1983; von Eisenhart et al. 1999; von Eisenhart-Rothe et al. 1997). An instrumented prosthesis measured peak pressures of up to ~10MPa in vivo during activities of daily living (Hodge et al. 1989). In the present study, pressure-sensitive film measured peak contact stress at 13.8±2.8 MPa and FE models with VW average cartilage predicted peak contact stress at 16.4 ± 7.8 MPa. While the peak contact stresses in the present study are somewhat larger than previously published values, some of the previous studies were limited by upper thresholds on the pressure-sensing devices or by the use of spherical implants, which results in lower predictions of contact stress (Anderson et al. 2010). Qualitatively, the non-uniform and specimen-specific contact patterns in the present study are consistent with previous observations in experimental studies of hip contact (Adams and Swanson 1985; Afoke et al. 1987; Anderson et al. 2008a; Brown and Shaw 1983; Rushfeldt et al. 1981; von Eisenhart et al. 1999; von Eisenhart-Rothe et al. 1997; Bay et al. 1997).

There were several limitations in this study. The primary dependent variables in this study, contact stress and contact area, were chosen because they can be measured experimentally, allowing direct validation against experimental measurements in the cadaveric hips, and because they have been suggested as important variables in the pathogenesis of OA (Russell et al. 2006; Henak et al. 2013; Creamer and Hochberg 1997; Segal et al. 2009, 2012). However, these variables only reflect the state of stress on the articular surface. Other variables, such as maximum shear stress and the first principal (most tensile) strain, or variables at other locations such as at the osteochondral interface, are likely to be even more important for predicting cartilage damage and delamination (Brand 2005; Henak et al. 2013; Mononen et al. 2012). While average contact stress and contact area were more sensitive to geometry than to cartilage constitutive model in the present study, the selected constitutive model may be more important in the evaluation of other variables. For example, a previous FE model of the knee demonstrated that a constitutive model which took into account spatial variance in the split line directions did not affect contact stress predictions but did affect other variables, including first principal strain (Mononen et al. 2012). A detailed investigation of the sensitivity of model predictions to other variables such as first principal strain and maximum shear stress will require further analysis of the strain and stress fields through the thickness, necessitating more refined experimental measurements, constitutive representations and new mesh convergence studies.

Although the cartilage constitutive behavior in these models captured material nonlinearity and spatial inhomogeneity, the constitutive models included several simplifying assumptions. Cartilage behavior was assumed to be nearly incompressible and hyperelastic. While this assumption is justified by both theoretical analysis and experimental data for the loading rates and activities that were considered in this study (Ateshian et al. 2007; Wong et al. 2000), it may have a minor effect on model results and will limit the interpretation of the results of this study to activities that occur at relatively high loading rates. The inclusion of cartilage tension–compression nonlinearity, wherein the modulus in tension is one to two orders of magnitude stiffer than that in compression, could also affect the FE model predictions (Huang et al. 2005). Other characteristics of cartilage material behavior, such as depth-dependent variation in properties and material anisotropy, are considered to be higher-order effects when compared to material nonlinearity and tension–compression nonlinearity and would therefore be expected to have less pronounced effects on model predictions (Henak et al. 2013; Buckley et al. 2008; Chen et al. 2001; Maroudas et al. 1980; Mow and Guo 2002; Schinagl et al. 1997; Setton et al. 1993). In addition to the limitations of the selected constitutive models, it is possible that freezing the cartilage samples prior to testing affected the material properties. While freezing was necessary due to the lengthy experimental protocol, literature suggests that this procedure has either no effect on cartilage stiffness or decreases cartilage stiffness up to 31% (Changoor et al. 2010; Kennedy et al. 2007; Szarko et al. 2010; Willett et al. 2005). In either case, since all samples were frozen, there was no bias in the comparisons between groups.

Finally, there are limitations associated with the use of pressure-sensitive film for model validation. We used pressure-sensitive film because of its high spatial resolution (5 – 15 μm) (Fuji Prescale® Brochure, Sensor Products, Inc., NJ, USA) and broad use in studies of joint contact mechanics (Brown et al. 2004). A previous study demonstrated that the peak contact stress measured by pressure-sensitive film may differ from that in a native joint by 10–26% for a plane–strain analysis of a surrogate contact mechanics problem (R₁ = 20 mm, R₂ 30 mm or larger, cartilage thickness = 0.6 mm) (Wu et =al. 1998). Because hip cartilage is thicker and the hip joint is more congruent than in the model problem described above, we constructed and analyzed similar FE models using dimensions from spherical fits to the articular surfaces of one of our specimens (R₁ = 25 mm, R₂ = 27 mm, cartilage thickness = 2.0 mm). These models predicted differences in peak contact stress of less than 1% between the models with and without film. Independent of errors induced by the presence of film between the articular layers, pressure-sensitive film has an error of 10–15% when measuring contact stress (Hale and Brown 1992). This error may contribute to the large tolerance intervals in the Bland–Altman analysis (Fig. 6).

In summary, this study provides a validated modeling protocol for a series of cadaveric specimens, and the results support the use of average cartilage material coefficients for predictions of specimen-specific contact stress and contact area in hips with normal articular cartilage. This protocol can be used in vivo to understand how abnormal hip contact stress and contact area lead to OA. The Veronda Westmann constitutive model with average material coefficients accurately predicted peak contact stress, average contact stress, contact area and contact patterns. The use of subject- and region-specific material coefficients did not increase the accuracy of FE model predictions with the Veronda Westmann constitutive model. The neo-Hookean constitutive model accurately predicted average contact stress, contact area and contact patterns, but underpredicted peak contact stress in areas of high stress. Therefore, the Veronda Westmann constitutive model with average material coefficients is preferred for future predictions of hip contact mechanics. The use of average material coefficients simplifies subject-specific modeling in vivo because subject-specific material coefficients are difficult to obtain. This protocol can be used for hips with healthy articular cartilage, but should be applied with caution to joints with degenerated cartilage. The equilibrium tensile modulus of osteoarthritic cartilage can be up to 15 times smaller than that of healthy cartilage (Akizuki et al. 1986), which is much larger than the largest inter-region differences in the present study (up to four times in E₀). Additionally, the structural changes associated with OA cause decreased stiffness and increased permeability in human hip cartilage with increased matrix disruption (Makela et al. 2012). Finally, this is the first report of the regional instantaneous material behavior of healthy cartilage in the hip, providing the necessary inputs for future computational studies investigating mechanical parameters other than contact stress and area in the human hip.