The role of partial knowledge in statistical word learning

Abstract

A critical question about the nature of human learning is whether it is an all-or-none or a gradual, accumulative process. Associative and statistical theories of word learning rely critically on the later assumption: that the process of learning a word's meaning unfolds over time. That is, learning the correct referent for a word involves the accumulation of partial knowledge across multiple instances. Some theories also make an even stronger claim: Partial knowledge of one word–object mapping can speed up the acquisition of other word–object mappings. We present three experiments that test and verify these claims by exposing learners to two consecutive blocks of cross-situational learning, in which half of the words and objects in the second block were those that participants failed to learn in Block 1. In line with an accumulative account, Re-exposure to these mis-mapped items accelerated the acquisition of both previously experienced mappings and wholly new word–object mappings. But how does partial knowledge of some words speed the acquisition of others? We consider two hypotheses. First, partial knowledge of a word could reduce the amount of information required for it to reach threshold, and the supra-threshold mapping could subsequently aid in the acquisition of new mappings. Alternatively, partial knowledge of a word's meaning could be useful for disambiguating the meanings of other words even before the threshold of learning is reached. We construct and compare computational models embodying each of these hypotheses and show that the latter provides a better explanation of the empirical data.

Since its empirical beginnings, the study of human memory has been a study of graded, rather than binary, phenomena. Ebbinghaus's (1913) early work on savings in memory showed that information remains in the system, and influences future learning, even when it can no longer be recalled. Subsequent studies have provided a wealth of further evidence for both the positive (Bentin, Moscovitch, & Heth, 1992; Nelson, 1978; Nissen & Bullemer, 1987; Wixted & Carpenter, 2007) and negative (Anderson, 1995; Bouton, 1993; Shiffrin & Schneider, 1977) effects on learning of information that is not directly accessible. In a similar vein, theories of associative learning in both humans (Gluck & Bower, 1988; Kruschke, 2001; Shiffrin & Schneider, 1977) and animals (Le Pelley, 2004; Mackintosh, 1975; Rescorla & Wagner, 1972) have taken as their central thesis that learning is a gradual, accumulative process and that the accumulation of past learning changes future learning.

But Gallistel, Fairhurst, and Balsam (2004) have recently questioned this idea of incremental learning, arguing that the learning curves found in classic associative learning experiments may have been an artifact of group averaging. Instead, they suggest that individual learners' behavior may be better explained by all-or-none step functions. This type of learning appears to be particularly likely in the face of surprising or highly consequential outcomes, as in the case of “flashbulb memories” (Brown & Kulik, 1977) or taste aversion (Garcia, Kimeldorf, & Koelling, 1955). Distinguishing these two fundamentally different characterizations of the learning process is at the heart of understanding the way that humans learn about their world. Here, we consider this question in the context of word–referent learning in language acquisition.

Partial knowledge in word learning

Many discussions of children's early word learning suggest a form of one-shot, all-or-none learning called fast-mapping (Carey & Bartlett, 1978; Heibeck & Markman, 1987; Houston-Price, Plunkett, & Harris, 2005; Markson & Bloom, 1997; Woodward, Markman, & Fitzsimmons, 1994). In one variant of these studies, the experimenter presents one novel and one known object to the child and then provides a novel spoken label (e.g., “blicket”). Children consistently map the novel label to the novel object and, given this single trial, consistently treat that name as referring to that object. This suggests one-shot learning (Markson & Bloom, 1997; Woodward, Markman, & Fitzsimmons, 1994). But the everyday visual world is much more complex than laboratory experiments, with potentially many more referents. Consequently, determining which words in an utterance refer to which objects is nontrivial. How do children resolve this ambiguity? One possibility is that they avoid the problem altogether, ignoring any utterances or scenes that are too complex, learning only from less ambiguous naming instances. For example, children could wait until some cue—whether social (Baldwin, Markman, Bill, Desjardins, & Irwin, 1996; Brooks & Meltzoff, 2005; Kuhl, 2004) or linguistic (Bloom & Markson, 1998; Gleitman, 1990)—made an instance more favorable to fast-mapping. By this view of learning, either a single naming event gives all of the information necessary for mapping a word to an object, or it is thrown away.

But there are reasons to doubt the interpretation of fast-mapping as all-or-none learning even in simplified learning situations. First, although some experimental studies support a within-experiment fast-mapping phenomenon, retention across even short time spans turns out to be quite fragile. Horst and Samuelson (2008) showed that children could succeed in the fast-mapping task—demonstrating one-shot learning of a word's referent—but fail to retain this mapping after a 5-min delay. Indeed, in the paper in which the term fast-mapping was coined, Carey and Bartlett (1978) considered the initial learning to be partial and incomplete and to be only the beginning of an accumulative learning process (Swingley, 2010). Second, a large literature of indirect evidence suggests that adults and children aggregate information about words and their meanings over many encounters, amassing statistical evidence about the latent structure underlying not just pairs of words and referents, but the whole system of words (Bowers, Davis, & Hanley 2005; Gershkoff-Stowe, 2002; Landauer & Dumais, 1997; Ratcliffe & McKoon, 1978; Seidenberg, 1997; L. B. Smith, Jones, Landau, Gershkoff-Stowe, & Samuelson, 2002; Xu & Tenenbaum, 2007; Yoshida & Smith, 2003; Yu, 2008; Yu & Smith, 2007). If information is accumulated, the highly ambiguous learning instances that do not support fast-mapping may still be of use. Statistical learners would seem to benefit from not throwing data away, even if the data are incomplete or ambiguous (Recchia & Jones, 2009).

This idea—that words can be learned by combining information across situations (Gleitman, 1990; Pinker, 1994; Yu & Smith, 2007)—is central to all associative (e.g., McMurray, Horst, & Samuelson, 2012; Plunkett, 1997; Rogers & McClelland, 2004; L. B. Smith et al., 2002;) and statistical (e.g., Frank, Goodman, & Tenenbaum, 2009; Siskind, 1996; Yu, 2008) models of language acquisition. Words should not go from unlearned to learned in one fell swoop, but should pass through a state of partial knowledge. Indeed, the existence of such partial states is both critical for these models and the source of some of their most interesting predictions. For instance, children's word learning is known to accelerate prodigiously during their second year of life. Previous theories have taken this to be evidence of a change in learning mechanism. In a computational model, McMurray (2007) showed that no change in mechanism is necessary to explain a “vocabulary explosion” as long as words vary in difficulty and are learned through the accumulation of partial knowledge.

However, although contemporary statistical learning models are built on the assumption of partial knowledge, a plausible alternative method might be to aggregate information across only learned words and referents, with no partial knowledge entering into the statistical calculations. While work in categorization suggests that partial knowledge should play a key role in such learning (Billman & Knutson, 1996; Kellog, 1980; Rosch & Mervis, 1975; Trabasso & Bower, 1966), there is significant controversy on this question in the contemporary word-learning literature.

Cross-situational word learning

Although cross-situational word learning accounts appeared in the literature earlier (Gleitman, 1990; Pinker, 1994; Siskind, 1996), Akhtar and Montague (1999) reported the first empirical demonstration that children could learn words by intersecting evidence across multiple individually ambiguous situations. They showed that 2-, 3-, and 4-year-olds could determine whether a novel adjective referred to shape or texture by observing a series of back-to-back labeling events (e.g., “this is a modi one”) in which multiple objects were similar on one of these dimensions and different on the other. However, the recent explosion of interest in cross-situational word learning and, consequently, partial knowledge was kindled by a set of papers from Yu and Smith (2007; Smith & Yu, 2008). In their cross-situational word-learning paradigm, learners are exposed to series of trials in which they hear a number of words and see an equal number of objects. On each trial, the mapping between words and objects is ambiguous; words co-occur with many potential referents. However, because words co-occur much more often with their correct referents than with other objects, learners can discover the correct word–object mappings by tracking co-occurrence information across trials. These papers extended Akhtar and Montague's (1999) results in several directions. First, they showed that learning was robust to significantly greater ambiguity on individual learning trials. Second, they showed that significantly more time could pass between learning trials. Third, they showed that multiple words could be learned at once from the same set of ambiguous naming events. Fourth, they showed that at least rudimentary cross-situational learning abilities were present in 12- and 14-month-old infants. All of these extensions increased the plausibility of cross-situational word learning as an important process in early language learning.

Subsequent papers have explored the relationship between cross-situational word learning and other language-learning mechanisms (Suanda & Namy, 2012; Yoshida, Rhemtulla, & Vouloumanos, 2012; Yurovsky, Yu, & Smith, in press), the possibility of learning other classes of words through cross-situational statistics (Scott & Fischer, 2012), and the impact of natural language statistics on cross-situational word learning (Monaghan & Mattock, 2012; Vogt, 2012; Yurovsky, Yu, & Smith, 2012). However, the most contentious questions have concerned the representational basis and mechanistic underpinnings of cross-situational learning (Kachergis, Yu, & Shiffrin, 2012; Medina, Snedeker, Trueswell, & Gleitman, 2011; K. Smith, Smith, & Blythe, 2009, 2011; Trueswell, Medina, Hafri, & Gleitman, 2013; Vouloumanos, 2008; Yu & Smith, 2011, 2012; Yu, Zhong, & Fricker, 2012; Yurovsky, Smith, & Yu, in press). One of the central issues in this debate, and the focus of this article, is the role of partial knowledge in word learning.

In particular, Yu and Smith's (2007; L. B. Smith & Yu, 2008) original papers explicitly propose that learners accumulate an approximation to the co-occurrence structure in their input by remembering the words and objects that co-occur on each trial. Consequently, this hypothesis predicts that learners' representations at any point in time contain not just a set of word–object mappings (highest co-occurrence word–object pairs), but also some partial knowledge of how often other objects have occurred with each word. This prediction was confirmed by Vouloumanos (2008), at least for low-ambiguity learning trials. In these experiments, learners saw a single object on each trial, but a number of different words co-occurred with each object across trials, each with a different frequency (1×, 2×, 6×, 8×, or 10×). After training, adults showed fine-grained sensitivity to this statistical structure, discriminating between each of these frequencies of co-occurrence.

K. Smith et al. (2011) asked about the fidelity of learners' approximations to word–object co-occurrence distributions over the course of learning as they programmatically varied the ambiguity of individual learning trials. They asked learners to indicate which object they believed to be the most likely referent for each word on each of its 12 occurrences. These guesses were then used to determine which of four learning models best accounted for participants' behavior: (1) perfect memory for all co-occurrences, (2) noisy approximate memory for all co-occurrences, (3) memory for only a single co-occurring object, or (4) random selection. K. Smith et al. (2011) found that as ambiguity increased, participants were less likely to have perfect memory for cooccurrence frequencies but that they nonetheless accumulated an approximate co-occurrence distribution rather than a single guess. Their data thus support accumulative accounts of word learning and, by extension, an important role for partial knowledge.

However, it is possible that even the highest levels of ambiguity in K. Smith et al. (2011) underestimate the levels of ambiguity relevant for real-world word learning. Medina et al. (2011) recorded natural parent-child interactions, extracted the ambiguous object-labeling events, and presented these to adult learners in a cross-situational version of the human simulation paradigm (Gillette, Gleitman, Gleitman, & Lederer, 1999). In their analyses of learning trajectories, Medina et al. found no evidence that learners were accumulatively tracking co-occurrence distributions. They concluded that their data were more consistent with learners storing and tracking only a single guess for the referent of each word. Thus, they argued that in the ambiguous environments that characterize the natural world, word learning is a step function and there is no partial knowledge.

In response, Yurovsky Smith, and Yu (in press) argued that Medina et al. (2011) mischaracterized the ambiguity of natural labeling events. These authors replicated Medina et al.'s experiments, recording parent–child interaction not only from a third-person perspective, but also from a camera placed on each child's forehead. They then analyzed the learning trajectories observed for cross-situational learners from each perspective. Yurovsky, Smith, and Yu found that participants who observed ambiguous naming events from a “child's-eye” view did accumulate co-occurrence distribution information, showing indirect evidence of partial knowledge even in learning from natural naming events.

Finally, the most recent data on partial knowledge come from Trueswell et al. (2013), who applied the analysis used by Medina et al. (2011) to learning trajectories observed in a task very much like that used by K. Smith et al. (2011). Adult learners saw a series of trials in which they heard a novel label and were asked to guess which of the objects they saw on the screen was its most likely referent. In contrast to K. Smith et al. (2011), however, Trueswell et al. found no evidence of accumulative learning, even at very low levels of ambiguity. Unfortunately, this discrepancy is difficult to interpret for several reasons. First, Trueswell et al. asked participants to learn novel names for familiar objects (e.g., cats, doors) rather than novel names for novel objects. Second, in Trueswell et al., words referred to categories of objects, the exemplars of which were different on each occurrence. This is a departure from the cross-situational learning paradigms used in previous work (e.g., Kachergis et al., 2012; K. Smith et al., 2011; Yoshida et al., 2012; Yu & Smith, 2007; Yurovsky, Yu, & Smith, in press). Third, participants' final word–object mapping accuracies were significantly lower in Trueswell et al. than in previous cross-situational learning experiments. Altogether, it is thus difficult to know whether the absence of evidence for partial knowledge in these data should count as evidence of absence.

In order to move toward a resolution to these discrepancies, we address the question of partial knowledge in statistical word learning through a combination of experiments and computational models. These experiments provide a more direct, and perhaps more sensitive, measure of partial knowledge than those used in previous work, and the models provide insight into the role of this partial knowledge in bootstrapping subsequent learning.

Measuring partial knowledge

In the experiments to follow, the role of partial knowledge in word learning was examined directly in adult learners engaged in the cross-situational word-learning task (Yu & Smith, 2007). In the task, learners are exposed to a series of trials in which they are asked to learn the correct words for a set of novel objects. To simulate ambiguous word-learning environments, each individual training trial contains multiple words and multiple candidate referents. At the end of training, learners select a referent for each word and typically demonstrate knowledge of a statistically significant proportion of the mappings. In contrast to previous studies, however, we focus not on the correctly selected referents, but, instead on the words for which participants give incorrect answers. If the accumulative theories of word learning are correct, some proportion of these words are neither learned nor unlearned but, rather, exist in an in-between state of partial knowledge. The crucial manipulation in the present experiments was to expose participants to a second block of learning in which half of the stimuli were drawn from this set of incorrectly associated words and objects. If word learning is all-or-none, participants should not benefit from seeing these items again. In fact, learning might be impaired by the formation of incorrect all-or-none hypotheses about these word–object mappings in Block 1 (Yurovsky, Yu, & Smith, in press). In contrast, if word learning proceeds by the accumulation of partial, incomplete, and ambiguous knowledge, learning should be significantly improved by earlier experience with these mappings, even if that experience did not yield measurable knowledge of the correct word–referent mappings.

In addition to testing for partial knowledge in this new, potentially more sensitive paradigm, we also address a further question about the role of partial knowledge. One way in which partial knowledge could benefit later learning is through item-by-item savings (McMurray, 2007). That is, partial knowledge of one word–referent pair could mean faster learning of that one pair from future experiences. Alternatively, partial knowledge could be an effective bootstrapping mechanism not just for one partially learned word, but for the whole set of to-be-learned words: partial knowledge of one word–object mapping could facilitate the learning of other words and objects with which it appears (Fazly, Alishahi, & Stevenson, 2010; Regier, 2005; Siskind, 1996; Yu, 2008). That is, partial knowledge could accelerate learning the latent structure of the whole system of words and referents. To study these issues, we developed two computational models, each embodying one of these hypotheses and asked which provided a better account of the empirical data. We focused particularly on the role of learning-by-exclusion mechanisms (e.g., Markman, 1990) in driving system-wide acceleration. We begin by presenting the empirical work.

Experiment 1

To determine the role of partial knowledge in statistical word learning, we followed Yu and Smith's (2007) cross-situational word-learning paradigm. In this task, participants are exposed to a series of individually ambiguous learning trials, each of which contains multiple co-occurring words and potential referents. While each trial is individually ambiguous, words always co-occur with their correct referent. Thus, participants who correctly track co-occurrence frequencies between words and objects across trials can learn the correct pairings. In Experiment 1, adult participants were exposed to two consecutive blocks of cross-situational word learning. At the end of training in Block 1, participants selected the referent that they believed was correct for each word. Each participant then engaged in a second block of cross-situational word learning, but the stimuli to which they were exposed varied by condition.

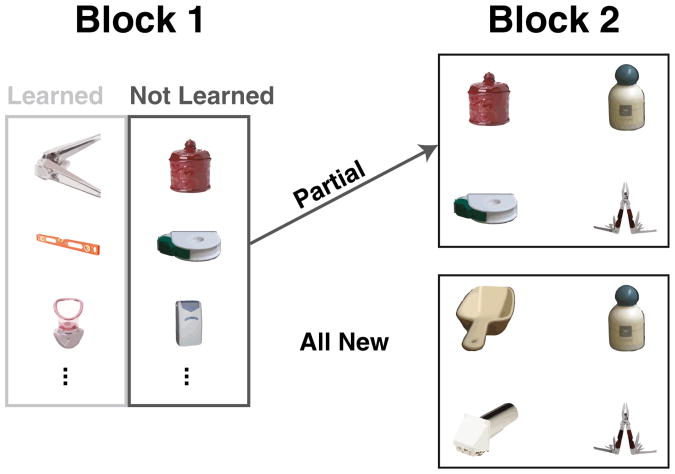
In the All New condition, each of the 18 words and objects seen in the second block of learning was completely novel. In contrast, in the Partial condition, half of the words and objects seen in the second block were drawn from the words and objects that participants had incorrectly mapped in the previous block. If word learning is all-or-none, participants' incorrect selections in Block 1 should be the result of either an incorrect hypothesis or random guessing. Consequently, one would expect participants in the Partial condition to perform no better than participants in the All New condition in Block 2. In contrast, if participants encoded some of the distributional information in Block 1 even for those words that they mapped incorrectly, one would expect learning in the Partial condition to be significantly better than that in the All New condition.

The training trials in Block 2 were designed to be identical across the two conditions except for the substitution of nine incorrectly mapped words and objects for new words and objects in the Partial condition. This allowed us to test one further hypothesis. If participants had encoded partial knowledge of the incorrectly mapped words, it could be useful in one of two ways. First, partial knowledge of the distributional information encoded for a particular word in Block 1 could be useful for learning that same word in Block 2; learning an individual word might be accumulative (McMurray, 2007). But, that knowledge could be useful in a further way. Not only could partial knowledge of a word speed learning of that same word, it also could aid in the acquisition of novel word–object mappings through reduction of ambiguity in training (Siskind, 1996; Yurovsky, Yu, & Smith, in press). We thus ask not only whether learning is improved in the Partial condition relative to the All New condition, but also whether it improved for both the nine repeated pairs and the nine all new pairs.

Method

Participants

Eighty undergraduate students at Indiana University received class credit in exchange for volunteering. Forty of these students participated in the Partial condition, and 40 participated in the All New condition. Because the Partial condition required at least nine items to be mis-mapped in Block 1, not all of these participants could be included in the final sample. To ensure a fair comparison across conditions, a similar inclusion criterion was applied to participants in both conditions. The final sample included 18 participants in the Partial condition and 20 in the All New condition. The criterion for inclusion is described fully in the Stimuli and Design section below.

Stimuli and design

Participants were exposed to a series of trials consisting of multiple referents and multiple words. Referents were represented by pictures of unusual objects that were easy to distinguish from each other but difficult to name. Words were one- and two-syllable pseudowords constructed to be phonotactically probable in English and synthesized using the AT&T Natural Voices® system. All words and objects have been used in previous cross-situational learning experiments (Kachergis et al., 2012; Yu & Smith, 2007; Yurovsky, Yu, & Smith, in press). Forty-two unique words and objects were used in total—24 in Block 1 and 18 in Block 2.

Training trials for Block 1 presented two pictures—one on each side of the screen—and played two labels, following Yu and Smith's (2007) 2×2 condition. Training trials for Block 2 presented four objects—one in each corner of the screen—and played four labels, following Yu and Smith's (2007) 4×4 condition. The 2×2 condition was used in Block 1 because it minimized variance in accuracies and, thus, minimized the number of participants excluded from the final sample (see the inclusion criterion explanation below).

Trials in both conditions were designed such that each was individually ambiguous: word order did not correlate with referents' on-screen positions. However, words always co-occurred with their correct referents. In Block 1, each of the 24 words appeared 5 times with its correct referent and 2 or fewer times with each of the other 23 referents. In Block 2, each of the 18 words appeared 4 times with its correct referent and 2 or fewer times with each of the other 17 referents. Thus, participants could, in principle, determine correct word–object mappings by tracking co-occurrence information across trials. In total, training in Block 1 consisted of sixty 2 word × 2 object training trials, and training in Block 2 consisted of eighteen 4 word × 4 object training trials. Word–object pairings and trial orders were selected randomly for each participant and were yoked across conditions.

After each block of training, participants were tested for their knowledge of word–object mappings. Each test trial presented all of the referents seen in that block of training and played one label word. Because all referents were present on each test trial, participants could not learn word-object mappings from co-occurrence at test. Participants received one test trial for each word in the training set. The order in which words were tested and the screen positions of referent objects on each test trial were random across participants.

The critical manipulation in this experiment was the connection between Blocks 1 and 2. In the Partial condition, 9 of the words for which each participant selected an incorrect referent at test in Block 1 were heard again by that participant in Block 2. The correct referents for these repeated words were also carried over into Block 2, and the mapping between them remained the same. This allowed us to test the hypothesis that participants had acquired partial knowledge of these mappings despite their incorrect answers in Block 1. Each of the 18 individual training trials in Block 2 contained 2 repeated words and objects carried over from Block 1 and 2 novel words and objects. In the All New condition, no words or objects were carried over into Block 2, and thus each participant in this condition was exposed to 18 novel words and objects in Block 2. Critically, half of the items on each training trial in Block 2 were identical—and novel—for participants in both conditions. The other half were repeated items for participants in the Partial condition but novel for participants in the All New condition. Figure 1 shows a schematic of this design. In the results, these items will be referred to as repeated versus new mappings. To recapitulate, a comparison of repeated items between conditions refers to a comparison between items that were repeated for participants in the Partial condition but novel for participants in the All New condition. A comparison of new items refers to a comparison between items that were new, and identical, for participants in both conditions.

Fig. 1.

A schematic of the design of Experiment 1's Partial and All New conditions. In the Partial condition, nine items that participants incorrectly mapped at test in Block 1 were subsequently repeated in the stimuli in Block 2. In the All New condition, all 18 words and objects in Block 2 were new

Since nine of the items in Block 2 of the Partial condition were those that participants had mapped incorrectly in Block 1, each participant in the final sample was required to mis-map at least nine words in Block 1. However, learning ability varies across participants; some learn all of the mappings in a cross-situational learning task. Thus, all participants who learned more than 15 of the word–object mappings in Block 1 were excluded from the final sample. Since cutting off only the right tail of the distribution of learners would produce a biased estimate of learning abilities, we also excluded participants who learned fewer than 9 of the word–object mappings in Block 1. To ensure accurate comparison between the All New and Partial conditions, this sampling was performed on participants in both conditions. Thus, the final sample in each condition consisted only of participants who learned between 9 and 15 of the 24 word– object mappings in Block 1. Pilot studies showed that learning scores vary less across participants in a 2 word × 2 object design than in a 4 × 4 design, and thus each trial of Block 1 contained two words and two objects. This increased the proportion of participants included in the final sample.

Procedure

Participants were told that they would be seeing a series of slides consisting of multiple words and multiple objects and that they would be subsequently tested on their knowledge of which word referred to which object. At the beginning of the test portion, they were told that they should click on the on-screen object that they believed was the correct referent for each word they heard. At the end of Block 1, participants were asked to step out of the testing booth for a moment while the experimenter set up the second block of training. After the participant had left the booth, the experimenter ran a Python script that determined which words and objects the participant had mis-mapped and set up the second block appropriately. The participants were then invited back into the booth and completed the training and testing portions of Block 2. If participants had learned too many or too few items in Block 1, they were run in a dummy Block 2.

Results

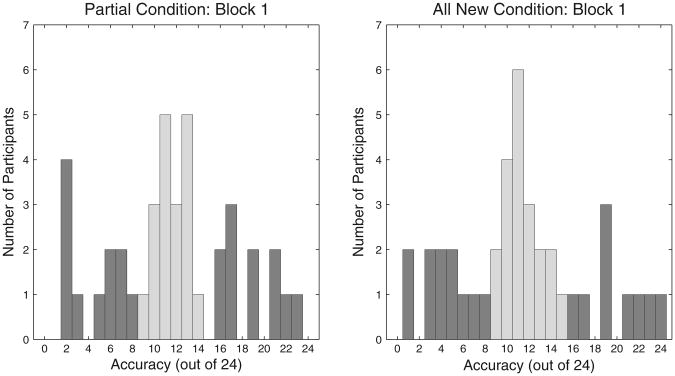
Since only a subset of the participants was included in the final sample, we first demonstrate that the full samples were similar across conditions. Figure 2 shows histograms of participants' accuracies in Block 1, with lighter bars indicating participants who were included in the final sample. All of the following analyses were performed on this final sample of participants.

Fig. 2.

Accuracy histograms for all participants in Block 1 of both the Partial (left) and All New (right) conditions. The lighter bars indicate the participants who were in the analyzed subset

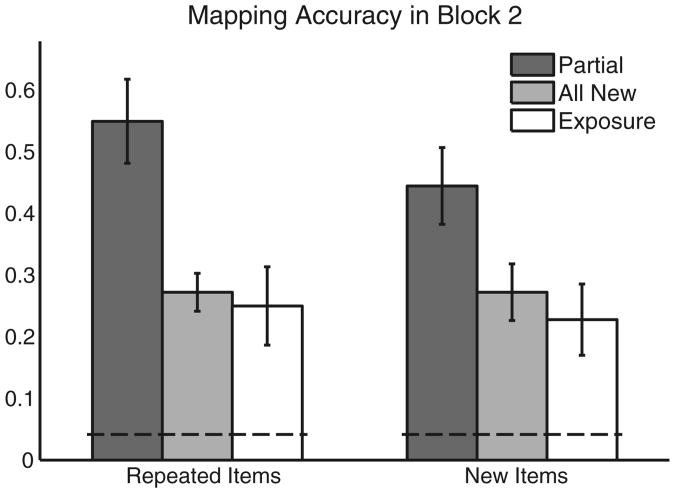
Participants in both conditions experienced identical training trials in Block 1. An independent samples t-test analysis showed that accuracy on this block did not differ significantly between conditions, t(36) = 0.32, n.s., licensing comparison of Block 2 learning scores between conditions. Participants' test accuracies in Block 2 were submitted to a 2 (condition) × 2 (word type) mixed design ANOVA. For participants in the Partial condition, word type was coded as either new or repeated (previously encountered in Block 1). All words and objects were novel for participants in the All New condition. However, since training trials in the Partial condition each contained two repeated and two new words, the items in those same slots were coded as repeated and new for participants in the All New condition (see Fig. 1). The new items were identical for participants in both conditions. The ANOVA showed a significant main effect of condition, F(1, 36) = 13.92, p < .001,η² = .20, but no effect of word type F(1, 36) = 1.46, n.s., and no interaction between word type and condition, F(1, 36) = 1.46, n.s. Thus, participants in the Partial condition outperformed participants in the All New condition not only for the subset of repeated words that they had experienced, but also for the words that were novel to participants in both conditions.¹ Figure 3 below shows mapping accuracies for participants for both word types in both conditions.

Fig. 3.

Mapping accuracy for Block 2 in the Partial and All New conditions (Experiment 1), as well as the Exposure condition (Experiment 2). Error bars represent ± SE. Participants in the Partial condition outperformed those in the All New and Exposure conditions both for the items they had mis-mapped in Block 1 (repeated) and for items novel to all participants (new). Thus, partial knowledge of word–object mappings from Block 1 facilitated not only the acquisition of those mappings, but also the acquisition of new word–object mappings

Discussion

Experiment 1 was designed to answer two questions: (1) do statistical word learners store and accumulate partial knowledge across learning situations, and (2) if so, does partial knowledge of one word lead to accelerated acquisition of other co-occurring words? To answer these questions, participants in the Partial condition were re-exposed to words and objects that they had previously mis-mapped. Because participants in the Partial condition significantly outperformed participants in the All New condition in Block 2, we can conclude that they must have stored some partial information about words and objects they mis-mapped in Block 1. Furthermore, this increased performance was seen not only for repeated words encountered previously in Block 1, but also for novel words. Thus, in answer to the second question, statistical learners can recruit partial knowledge of some word–object mappings to learn other word–object mappings at a faster rate (Siskind, 1996). We investigate the potential mechanistic underpinnings of this bootstrapping in the Computational Model section below.

But perhaps this conclusion is premature. The results of Experiment 1 are certainly consistent with the claim that participants acquire and use partial knowledge of word–object mappings, but there is an alternative explanation. Each trial of Block 2 for participants in the Partial condition consisted of two repeated pairings and two new pairings. If participants had encoded no mapping information for the repeated items but only had previously seen and heard these items, they could have outperformed participants in the All New condition by treating the 4 word × 4 object trials as two 2 word × 2 object training trials. That is, they could have partitioned the words and objects into two sets: familiar and new. They could then have mapped familiar words only onto familiar objects and new words only onto new objects. Experiment 2 was designed to rule out this partitioning explanation.

Experiment 2

In Experiment 1, participants in the Partial condition could have entered Block 2 with two potentially beneficial sources of information: knowledge of which words and objects were in Block 1, and knowledge of the mapping structure between these words and objects. In order to claim that partial knowledge of word–object mappings drives the learning benefit for these participants, we must determine that mere exposure does not produce an equal benefit. Thus, Block 1 of Experiment 2 was designed to give learners identical exposure to the individual words and objects but to none of the mapping structure.

Method

Participants

Twenty undergraduates at Indiana University received class credit for volunteering. None had previously participated in Experiment 1 or any other cross-situational learning experiments.

Stimuli and design

The individual words and objects and the manner of presentation were identical to those of Experiment 1. However, word–object co-occurrence distributions for Block 1 were different in one important way. Twelve of the words maintained identical distributions to those in the previous experiment: co-occurring 5 times with their correct referent and less frequently with each of the 23 incorrect referents. The other 12 words had nearly flat co-occurrence distributions, appearing at most once with each of the 24 objects in the set. Nine of these 12 flat-distribution words were then carried over into Block 2. In this way, participants received five exposures to each word and object, just as in Experiment 1, but received uninformative distributional information. In Block 2, these words and objects had informative distributional structures identical to the corresponding words and objects in the Partial condition of Experiment 1: each repeated word mapped onto its correct repeated referent 4 times. Importantly, the correct referent for these words in Block 2 was never the one that the participant had selected by chance at test in block 1. This ensures that any potential learning at test would operate the same way as in the Partial condition of Experiment 1. That is, participants who noticed a familiar item in Block 2 could potentially have inferred that their previous guess was incorrect. Because the referent participants chose for the flat-distribution words in Block 1 was never made the correct referent in Block 2, the utility of this pragmatic inference would have been the same across experiments.

In the analyses that follow, the 12 flat-distribution items in Block 1 are labeled uninformative, and the 12 learnable items are labeled informative. In Block 2, the repeated items were those that had flat distributions in Block 1.

Procedure

Participants were given the same instructions as before. At the end of Block 1, they were again instructed to step out of the booth for a moment while the experimenter set up Block 2. The Participants then completed training and testing for the second block as before.

Results and discussion

Participants in Experiment 2 were exposed to 24 words and objects. However, in contrast to the previous experiments, statistical information specified correct referents for only 12 of the words. Of these 12 items, participants learned an average of 5.05 (SD = 2.48). This proportion, along with the proportions from the Partial and All New conditions of Experiment 1, were submitted to a one-way ANOVA for accuracy in Block 1. Condition was not found to be a significant factor, F(2, 55) = 1.24, n.s. Since Block 1 accuracy was comparable across conditions, we analyzed accuracy in Block 2. Figure 3 shows accuracy for Block 2 of the Partial and All New conditions, as well as the new Exposure condition.

In order to determine whether mere exposure to words and objects in Block 1 produces comparable learning benefits to partial word–object mapping knowledge, accuracy for Block 2 was compared across all three experimental conditions—the Partial and All New data from Experiment 1 and the Exposure data from Experiment 2. Proportion correct was submitted to a 3 × 2 mixed ANOVA with a between-subjects factor of condition (Partial, All New, Exposure) and a within-subjects factor of word type (repeated, new). Results again showed a significant main effect of condition, F(2, 55) = 8.31, p < .001, η² = .18, but not of word type, F(2, 55) = 1.67, n.s., and no interaction between the two, F(2, 55) = 0.92, n.s. Bonferonni-corrected t-tests showed that the Exposure condition was not significantly different from the All New condition, t(38) = 0.59, n.s., but was significantly different from the Partial condition, t(36) = 3.73, p < .01, η² = .28.

Thus, unlike participants who entered Block 2 with partial mapping knowledge, those who were merely pre-exposed to the words and objects did not show accelerated learning. This rules out the old/new partitioning hypothesis as a possible explanation for the difference between the Partial and All New conditions. It also rules out the possibility that the benefit observed in the Partial condition was due entirely to participants inferring that the answers they gave at test in Block 1 were incorrect. However, participants in the Exposure condition did show slightly lower accuracy in Block 1. If these participants noticed that a subset of the words were unlearnable in the first block, they may have lost motivation to learn in Block 2. That is, participants may have benefitted from prior exposure but suffered from learned helplessness (Maier & Seligman, 1976). Experiment 3 was designed to rule out this explanation.

Experiment 3

In Block 1 of Experiment 2, half of the word–object mappings were essentially unlearnable. This could have reduced motivation to learn in the subsequent block and, thus, counteracted the benefit of exposure to these repeated words and objects. If such an effect occurred, however, it was not localized to the repeated words: Participants learned both repeated and new words equally well in Block 2. Consequently, if the information structure of Block 1 led to learned helplessness, it should have done so even if all of the items in Block 2 were novel. This suggests a natural control condition.

Participants in Experiment 3 were again first exposed to a block of training in which half of the items were unlearnable; Block 1 was identical to Block 1 of the Exposure condition (Experiment 2). Then participants were exposed to a second block of training containing 18 new words and objects. Thus, Block 2 was identical to the All New (Experiment 1) condition. If Block 1 of the Exposure condition induced learned helplessness, we should see similar helplessness in Experiment 3. Consequently, if Block 1 induces learned helplessness, learning in Block 2 of Experiment 3 should be less effective than in Block 2 of the All New condition.

Method

Participants

Twenty undergraduate students at Indiana University received class credit in exchange for volunteering. None had previously participated in Experiment 1 or 2 or any other cross-situational learning experiments.

Stimuli, design, and procedure

The Learned Helplessness (LH) Control condition of Experiment 3 was exactly Block 1 of the Exposure condition (Experiment 2) followed by Block 2 of the All New (Experiment 1) condition. Participants received the same instructions as in Experiments 1 and 2.

Results

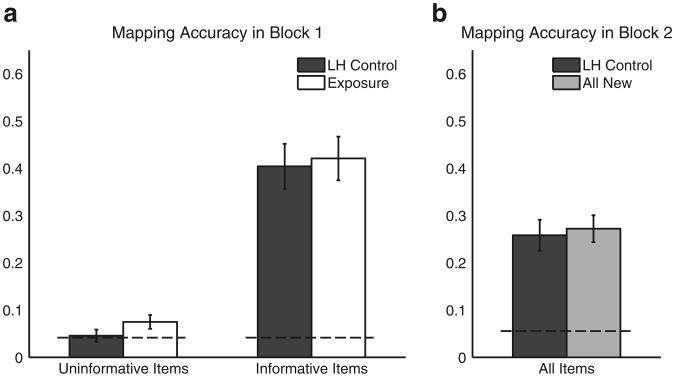
As in Experiment 2, only 12 of the 24 items in Block 1 had correct referents. Of these 12, participants in Experiment 3 learned an average of 4.85 (SD = 2.56). A t-test showed that this number was not significantly different from the number learned by participants in the Exposure condition, t(19) = 0.26, n.s. This indicates that the sample of participants in the LH Control condition was not significantly different from the sample in the Exposure condition.

But did the information structure of Block 1 produce learned helplessness? If it did, learning in Block 2 of the LH Control condition should have been reduced relative to learning in Block 2 of the All New condition. A t-test showed that this was not the case: learning rates in Block 2 did not differ significantly across these conditions, t(19) = 0.32, n.s. Figure 4 shows learning scores in Blocks 1 and 2 and the relevant data for comparison from Experiments 1 and 2. Thus, if uninformative mappings for some items in Block 1 did decrease motivation to learn in Block 2, they did not do so to an extent sufficient to explain the difference between the Partial and Exposure conditions.

Fig. 4.

Mapping accuracy for Blocks 1 and 2 in the Learned Helplessness (LH) Control condition, as compared with the relevant conditions from Experiments 1 and 2. Error bars represent ± SE. a In Block 1, participants in the LH Control condition learned as many of the learnable mappings as did participants in the Exposure condition. b In Block 2, participants in the LH Control condition learned just as many mappings as those in the All New condition, suggesting that statistical structure in which half of the distributions are flat does not induce learned helplessness

Discussion

In Experiment 1, we demonstrated that even when participants do not show knowledge of the correct referent for a word, they may nonetheless have encoded some information about it. This information increases the probability of learning that word's correct referent from subsequent exposure. What is the nature of this information?

In Experiments 2 and 3, we ruled out the possibility that the information is simple familiarity. Participants who received equal exposure to the words and objects, but not their mapping structure, did not show accelerated learning. Thus, since the benefit depends on experience with the mapping structure, the useful information must be partial knowledge of the correct referents of these words. We have thus provided direct empirical evidence for the accumulation of partial information in word learning (cf. Medina et al., 2011; Trueswell et al., 2013).

But more than this, the partial knowledge of some word– object mappings facilitated the acquisition of other, wholly novel word–object mappings. This outcome indicates that cross-situational word learning cannot be a process of merely tallying co-occurrences (cf. K. Smith et al., 2011; Yu & Smith, 2012); word–object mappings cannot be learned by independent accumulators (cf. McMurray, 2007). Instead, it must involve a kind of leveraged learning (Mitchell & McMurray, 2009), in which information about the words and objects encountered in a single instance interacts and competes (Yurovsky, Yu, & Smith, in press). But by what mechanism does this interaction occur? To determine how partial knowledge of words and referents facilitates learning new co-occurring words and referents, we implemented two computational models designed to test competing hypotheses.

Computational models

How do cross-situational learners make use of partial knowledge of word–referent mappings? The experiments above demonstrate a learning benefit not only for words and objects for which partial knowledge exists, but also for wholly new words and objects. In some way, then, partial knowledge accelerates learning the whole system of word–referent mappings. One obvious candidate mechanism would be some kind of mutual exclusivity (Golinkoff, Hirsh-Pasek, Bailey, & Wenger, 1992; Markman & Wachtel, 1988; Merriman & Bowman, 1989) or highlighting (Kruschke, 2003). That is, learners who had mapped a word to one object could have ruled out that object as a candidate referent for other words. But one can imagine two kinds of mechanisms by which this could happen.

First, partial knowledge of a word–object mapping could reduce the time (and information) required to successfully learn that mapping through exposure to statistics. Then, once that specific mapping is learned, the correct referent of this word could be ruled out as a possible referent of other words. We call this model the Full Knowledge Mutual Exclusivity model, because the amount of knowledge required to correctly learn a word–referent mapping is the same as the amount required to rule its elements out as candidates for other mappings. This is a model in which the learning of individual word–referent mappings is incremental, but only once a mapping is learned (all-or-none) can it benefit the learning of other words and referents.

Alternatively, as was suggested by Siskind (1996), the competition that gives rise to mutual exclusivity may operate on partial knowledge (Yurovsky, Yu, & Smith, in press). That is, partial knowledge of a word–object mapping may not only decrease the amount of information required to learn that word, but may also limit that object from being the referent of other words. On this account, mutual exclusivity operates at a lower threshold of knowledge than does the ability to map a word to a referent at test, and thus partial knowledge of a word–referent pairing is actively involved in learning even before it is fully known. We will refer to this as the Partial Knowledge Mutual Exclusivity model.

Both of these accounts can, in principle, predict leveraged learning of new words in the Partial condition as compared with the All New condition. However, they disagree about the detailed mechanistic process through which this learning benefit occurs (Suanda & Namy, 2012; Yu & Smith, 2012). In the Full Knowledge ME account, participants enter Block 2 with partial knowledge of the repeated word–referent mappings. Over the course of several trials, they learn about word–object mappings, independently, for both repeated and new items. Then, at some point, the repeated mappings become fully learned, and their component words and objects can be ruled out as contenders for mapping to new words and objects. Because, at the beginning of Block 2, the repeated items are already partially known, the number of trials to reach full knowledge of these mappings is lower than the number required for new words and objects. Consequently, learning by exclusion would happen faster in the Partial than in the All New condition, and thus the number of both repeated and new items known at the end of Block 2 should be higher in the Partial than in the All New condition. The Partial Knowledge ME account provides a different explanation for the observed data. On this account, from the first trial of Block 2, participants already know enough about the repeated words to begin leveraging them to learn by exclusion. Consequently, participants in the Partial condition will be learning faster than participants in the All New condition throughout the entirety of Block 2 and, thus, will know more of both the repeated and new mappings by the end.

While these models make the same qualitative predictions, they can be discriminated quantitatively. In particular, they make different predictions about the rate at which learning will happen in Block 2 of the Partial condition, relative to the rate at which learning occurs in Block 1 and Block 2 of each of the learning conditions. Formalizing these models allows us to leverage all of the data from each of the conditions to constrain the predictions of both the Full Knowledge ME and the Partial Knowledge ME models. In the section that follows, we formalize both of these models, as well as a Baseline model without mutual exclusivity. We show that the Partial Knowledge ME model provides the best account for the experimental data.

Model framework

In formalizing the models, we make the following explicit assumptions. First, on the basis of the data in the three experiments, we assume that learners are tracking and accumulating statistical information across learning trials. We formalize this representation as a type of associative matrix in which the value in each cell represents the strength of association between a word and a corresponding object (see also Fazly et al., 2010; Frank, Goodman, & Tenenbaum, 2009; Yu, 2008). In particular, A(w, o) maintains the strength of association between word w and object o.

Second, we assume that a learner does not have direct access to the cells in this matrix. Rather, the learning system uses a function, S(w, o), that evaluates the strength of evidence for mapping w to object o. Intuitively, two factors should contribute to the strength of evidence for such a mapping: (1) the strength of association between the word and object [A(w, o)] and (2) the strengths of association between the word and other candidate referent objects [A(w, o′)].

Third, when presented with a word at test, learners must select one of the objects as its correct referent. We propose that they do so according to a simple rule: If the evidence for mapping a word to one of the referents is above a threshold, the learner selects that referent [S(w, o) > K]. If it is not, the learner selects randomly among the objects.

Finally, we must specify how the associative matrix A grows over the course of training. We assume that on a given learning trial, for each word, the learner has a certain amount of attention and doles it out among the set of available objects (see also Kachergis et al., 2012; Kruschke, 2003; Mackintosh, 1975; L. B. Smith, 2000). The manner in which this attention is distributed is the only difference among the proposed models. In the Baseline model, attention is distributed randomly across all possible objects. The other two models modify this distribution of attention as a function of the word–object mapping information already acquired by the learner. In the Full Knowledge ME model, upon hearing a word w, if one of the objects present (e.g., o) has already been learned as a referent for that word [S(w, o) > K], all attention for the word is allocated to that object. If no object is already known to be the correct referent, attention for the word is doled out randomly among all objects that are not known to be referents of any other words [S(w′, o′)> K]. Thus, the model implements a form of mutual exclusivity in which once a word–referent mapping is known, that referent is not mapped to other words. The Partial Knowledge ME model operates identically, except that the threshold for mutual exclusivity is lower. That is, the strength of evidence for a word–referent mapping does not need to have crossed the high threshold (K) to induce the use of mutual exclusivity. Rather, it must only cross a lower threshold (PK). Thus, the Partial Knowledge ME model captures the idea that there may be interactions among partially learned mappings even at low levels of partial knowledge that are not evident in explicit tests of word–referent knowledge.

The learning model thus steps through training, trial by trial, just as do human learners. On each trial, updates are made to stored associations between the words and objects present on each trial as a function of prior knowledge. Then the model is tested via alternative forced choice, as were human learners. The two block designs used in our experimental studies were simulated by first training the model on the training input from Block 1 and then testing the model for each of these words. After that, training trials for Block 2 were constructed on the basis of the model's responses to these Block 1 test trials, just as they were for human participants. Finally, the model was exposed to a second block of training and tested again on the words from Block 2. Bayesian model comparison was used to determine which model provided the best fit to the observed empirical data. In the next section, we provide a formal specification of the models.

Critically, two assumptions—indirect access to cooccurrence information and thresholds of knowledge—facilitate discrimination of the two different ways in which partial knowledge can accelerate the learning of novel words. Thus, we developed the Full Knowledge ME model to formalize an indirect role for sub-threshold knowledge. The Partial Knowledge ME model was intended to be a direct contrast to this model and a strong test for the direct role of sub-threshold knowledge. As such, we see the two-threshold model as the appropriate stand-in for fully probabilistic models (e.g., Fazly et al., 2010; Frank, Goodman, & Tenenbaum, 2009; McMurray et al., 2012; Yu, 2008) and see these models as falling into the same class as the Partial Knowledge ME model; partial knowledge plays a direct role. In brief, the present two models were developed to discriminate between two kinds of mechanisms rather than their details. We also note that there are many other ways of formalizing associative learning, some of which are significantly more flexible and more powerful (e.g., Kehoe, 1988; Kohonen, 1984; Kruschke, 2008). Because these models are also in the same general class as the Partial Knowledge ME model, we use the simpler formulation for clarity and as a more rigorous and fair test of our particular hypothesis.

Formal model

Each model learner begins training with a matrix in which each cell A(w, o) corresponds to the strength of association between word w and object o. All entries were initialized to zero before the first training trial was encountered. In order to determine whether the model has learned to map a word onto an object, the associative matrix is passed through a function S(w, o) that determines the strength of the evidence for mapping word w to object o. S(w, o) compares the value in the associative matrix between w and o with the values for other candidate objects o′. Formally, S(w, o) returns the average ratio between A(w, o) and each other nonzero A(w, o′) divided by the number of nonzero A(w, o′):

$$\begin{array}{c}{O}^{+}:=\{o\prime :A(w,o\prime )>0\}\\ S(w,o)=\frac{\left({\sum }_{o\prime \in O^{+}}\frac{A(w,o)}{A(w,o\prime )}\right)}{{\left|O^{+}\right|}^2}\end{array}.$$ (1)

That is, S(w, o) provides a measure of how much more evidence one has for mapping w to o than to each other viable candidate o′. Note that, if we did not divide again by the number of nonzero candidates, adding a new low-probability candidate would raise the average ratio and, thus, increase the evidence. This function assumes that at some (perhaps implicit) level, humans are sensitive to the entire distributional structure of a word, and not just the most commonly co-occurring object. Evidence from other statistical learning paradigms (e.g., Perruchet & Pacton, 2006; Vouloumanos, 2008) suggests that this is a reasonable assumption. This is certainly not the only possible function S(w, o), but it is the one that provides the best fit to the empirical data. For a discussion of other alternatives (e.g., negentropy; Schrödinger, 1944), see the Appendix.

To connect this function to the learner's behavior at test, we propose that the learner knows the referent for a word—and selects it at test—when the value of the function S rises above a threshold K. Below this threshold, the learner does not yet know the correct mapping for a word and will choose randomly among all available objects at test.

Formally, then, when a learner is tested with word w and a set of candidate objects O,

$$P\left(o\right|w)=\{\begin{array}{cc}1& S(w,o)\ge K\\ 0& \mathit{\text{otherwise}}\end{array}$$ (2)

Finally, the association matrix A grows as the learner engages in cross-situational learning. The nature of this growth is the feature on which the three models differ. In each, the learner doles out a fixed quantity of associative strength for each word on each learning trial. In the Baseline model, this associative strength is distributed randomly among all candidate objects in the trial. Formally, random distribution among the referents is implemented by selecting a random value I(w, o) for each word–referent mapping (w, o) and normalizing for each word. Thus, if trial t contains the words W_t and objects O_t,

$$\begin{array}{c}\forall w\in W_t,\forall o\in O_{t}I(w,o)\sim \text{Uniform}(0,1)\\ A_t(w,o)=A_{t-1}(w,o)+\frac{I(w,o)}{{\sum }_{o\prime \in O_t}I(w,o\prime )}\end{array}$$ (3)

In the other models, this distribution of attention is moderated by the learner's knowledge (see also Kachergis et al., 2012). If the mapping strength between a word w and any of the objects has passed threshold, that object receives all of the word's association for the trial. Furthermore, if the strength between any other word w′ and any of the objects has reached threshold, those objects receive none of w's association on this trial. The two models differ in the threshold of knowledge necessary for both of these effects. In the Full Knowledge ME model, the threshold for mutual exclusivity is the same as that for knowing the word: K. In contrast, in the Partial Knowledge ME model, the threshold is a different, lower value PK. We describe this rule below for the Partial Knowledge ME model:

$$\begin{array}{c}{O}_u:=\{\forall o\in O_t:\forall w\in W_t,S(w,o)<\mathit{\text{PK}}\}\}\\ A_t(w,o)=A_{t-1}(w,o)+\{\begin{array}{cc}1& S(w,o)\ge \mathit{\text{PK}}\\ \frac{I(w,o)}{{\sum }_{o\prime \in O_u}I(w,o\prime )}& \mathit{\text{otherwise}}\end{array}\end{array}$$ (4)

We address two concerns before presenting the results. First, we present here a set of process models but wish to establish an in-principle distinction between two-threshold and one-threshold models. An alternative would be to begin with a Bayesian ideal observer model. However, since normative models of cross-situational learning routinely outperform participants by a large margin (e.g., Frank, Goodman, & Tenenbaum, 2009) and do not address trial-by-trial learning, we believe the present process-oriented approach to be a more direct and more transparent way to compare these two different mechanisms for using partial knowledge. Nonetheless, the conclusions are certainly contingent on the assumptions we have made in formalizing our models.

Second, all of these models use an associative representation—essentially, a matrix with words along the rows and objects along the columns. Each cell represents the strength of the association between the corresponding word and object. Use of this matrix need not be taken as a commitment to an associative account of word learning. Rather, such a matrix is a useful representational tool, commonly employed across both associative (Fazly et al., 2010; Yu, 2008) and Bayesian hypothesis-testing (Frank, Goodman, & Tenenbaum, 2009) models of word learning. For present purposes, the representation is a mathematical tool rather than a theoretical commitment. We return to this point in more detail in the General Discussion section.

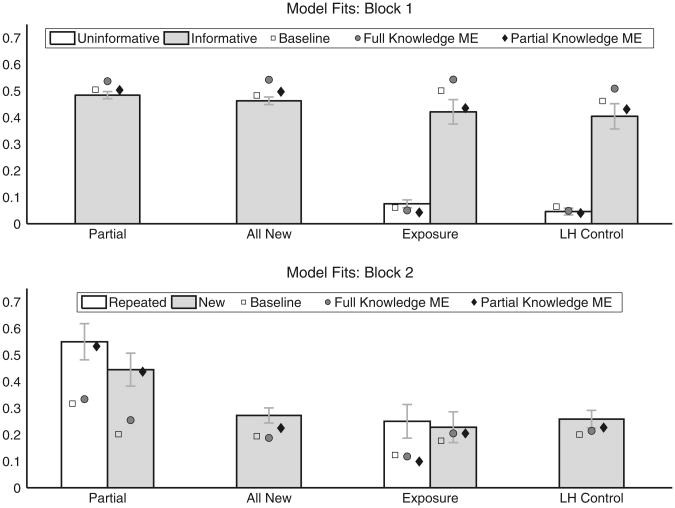
Model results

Optimal parameters for each model were found by grid search on the parameter space from 0 to 20 in steps of .1, under the constraint that, for the Partial Knowledge ME model, the partial knowledge threshold (PK) was lower than the full knowledge threshold (K). At each parameter setting, 1,000 simulated participants were averaged together to produce model predictions and to compute the sum of squared errors (SSE) between the model predictions and the data. Optimal parameters were chosen to minimize the SSE across all blocks in all conditions. The resulting SSEs were used to approximate the Bayesian information criterion (BIC) for each model under the assumption of Gaussian errors (Schwarz, 1978). This criterion trades off fit to the data with model parsimony, penalizing models both for misprediction and for number of parameters. Since the Partial Knowledge ME model has an additional parameter, it must provide a better fit to the data. The BIC allows one to determine whether the improvement in fit merits the additional complexity of the second parameter. Table 1 lists optimal parameter values, SSEs, and BIC values for each of the three models.

Table 1. Parameters and fits for computational models.

Model	Parameters	SSE	BIC
Baseline	K = 1.4	.152	−49.92
Full Knowledge ME	K = 2.6	.149	−50.2
Partial Knowledge ME	K = 13.5, PK = 1.0	.032	−66.2

Note. SSE, sum of squared error; BIC, Bayesian information criterion; ME, mutual exclusivity

In BIC comparisons, the model with the lower value is preferred. Furthermore, the size of the difference indicates the strength of evidence in favor of the better fitting model. Although this difference can be interpreted directly as a continuous measure, it is useful, as in null-hypothesis testing, to have a set of discrete values to act as heuristics for interpretation. Kass and Raftery (1995) provide the most commonly used standard. On their scale, a difference in BICs of 0–2 is “not worth more than a bare mention,” a difference of 2–6 is positive evidence, a difference of 6–10 is strong evidence, and a difference of more than 10 is very strong evidence. We use this scale in interpreting the comparison between the Baseline, Full Knowledge ME, and Partial Knowledge ME models.

Table 1 shows that the Full Knowledge ME model fit the data slightly better than the baseline model but that the difference in BICs was small, “not worth more than a bare mention” (Kass & Raftery, 1995). However, the Partial Knowledge ME model fit the data much better than did both of the other models. Even after controlling for its greater complexity, the difference in fits provides very strong evidence that it is a better account for the data than either the Baseline or the Full Knowledge ME model (Kass & Raftery, 1995).

Thus, the Full Knowledge ME model does not provide a good account of the way in which partial knowledge is used in cross-situational learning. At the setting of its parameters that provides the best fit to the data, it does not perform much better than the Baseline model—a model in which partial knowledge does not spread through the system at all. The Partial Knowledge ME, in contrast, provides a convincing fit to the data, as can be seen in Fig. 5. Thus, in order for partial knowledge of one word–object mapping to speed the acquisition of other mappings, it must play a direct role prior to explicit knowledge of the mapping. Even when an object has not yet been fully mapped to a word, its partial mapping to one word will limit its mapping to another word. In other words, partial knowledge plays a role in disambiguation and in finding the latent structure of word–referent pairings in a system of words and referents (Siskind, 1996; Yurovsky, Yu, & Smith, in press).

Fig. 5.

Mapping accuracy for all blocks of all conditions and the corresponding fits produced by the optimal parameterization of the Baseline, Full Knowledge ME, and Partial Knowledge ME models. Error bars represent ± SE. Markers indicate each model's performance

Model discussion

The models developed and compared in this section were designed to discriminate between two broad ways in which partial knowledge of some words could speed up the acquisition of others. The Full Knowledge ME model embodied an indirect route: partial knowledge of a given word might reduce time to acquire a high-fidelity mapping for that word, and this strong mapping could subsequently help the acquisition of new mappings through mutual exclusivity. Alternatively, mutual exclusivity could operate on partial knowledge, with an object only weakly associated with a word already being less likely to be mapped to a different word (Partial Knowledge ME). The model comparison showed a direct role for partial knowledge to be much more likely than an indirect role.

Of course, the Partial Knowledge ME model formalized only one way of performing mutual exclusivity through partial knowledge. This particular way makes a distinction between two thresholds: threshold to give a correct response at test and threshold to direct attention for exclusion. This distinction parallels work on low- and high-threshold theories of detection in visual search (e.g., Palmer, Verghese, & Pavel, 2000). Alternatively, the whole system could be probabilistic, with exclusion not operating on a binary threshold but being directly proportional to the strength of a given word–object mapping (e.g., Fazly et al., 2010; McMurray et al., 2012; Yu, 2008). Additionally, the mechanisms underlying mutual exclusivity are also in debate, ranging from attentional explanations (e.g., Merriman & Bowman, 1989), to constraint-based explanations (e.g., Markman, 1990), to social and pragmatic explanations (e.g., Diesendruck & Markson, 2001). We have formalized these models in attentional language, but other implementations of the mechanistic basis of competition are possible (see also McMurray et al., 2012). The critical point that the models make is that partial knowledge is used directly. Even when words are not well known, they already directly impact the learning of other co-occurring words and objects.

General discussion

Two critical assumptions of statistical and distributional approaches to language acquisition are that information is accumulated over time (Gillette et al., 1999; McMurray, 2007; Plunkett, 1997; Saffran, 2003) and that learning is principally about building not only individual mappings, but also coherent systems of mappings (Frank, Goodman, & Tenenbaum, 2009; Landauer & Dumais, 1997; Yu, 2008). However, the literature contains no direct empirical evidence about how such accumulation works or how human language learners bring about these system effects. Here, we presented evidence on one key issue: the role of partial knowledge in statistical learning. Using the cross-situational word-learning paradigm (Yu & Smith, 2007), the experiments in this article provide clear evidence of an important role for partial knowledge in accelerating learning. When words and objects that participants failed to learn in one block of cross-situational learning were re-encountered in a second block, word–object mapping accuracy improved dramatically. Thus, while learners had not encoded enough about word–object distributions to select correct mappings at the initial test, they had nonetheless encoded some partial knowledge of these distributions, and this partial knowledge sped up their word learning in Block 2. What's more, word-object mapping accuracy in Block 2 was improved not only for these previously seen items, but for wholly novel words and objects as well. Thus, partial knowledge of one mapping not only sped up acquisition of that mapping, but also eased the acquisition of novel mappings through mutual exclusivity (Golinkoff et al., 1992; Markman & Wachtel, 1988). Two follow-up experiments ruled out an alternative explanation of these results as arising from pure familiarity with items from block 1.

This key finding—that partial knowledge of a subset of the items in Block 2 sped up the acquisition of correct mappings for new items—was consistent with two mechanistic explanations. First, it was possible that partial knowledge played an indirect role. Partial knowledge of a word–object mapping could have shortened the time to acquisition of complete knowledge of that mapping, and mutual exclusivity could have supported learning of new mappings only once this complete knowledge was acquired. Alternatively partial knowledge could have played a direct role, with only partial knowledge of a word–object mapping being necessary for the word and object to be ruled out as candidates for other mappings (Siskind, 1996; Yu, 2008; Yurovsky Yu, & Smith in press). We formalized these two explanations as computational models and showed that the second—mutual exclusivity from partial knowledge—provided a significantly better quantitative fit to the empirical data. Taken together, the empirical results and the model comparison provide evidence for a word-learning process that is not only accumulative, but also self-bootstrapping (L. B. Smith, 2000). Because language is learned as a system and not a series of individual components, gaining even partial knowledge of one part can yield a benefit for learning another (L. B. Smith & Yu, 2008).

Bootstrapping from partial knowledge

It may at first seem strange that the word-learning system could know enough about a word–object mapping to limit consideration of its components as candidates for other mappings but, at the same time, not know enough about them to reliably link them at test. However, this kind of learning mechanism is in line with the extant evidence about both adults' and infants' language-processing systems. One of the most robust findings in the memory literature is semantic priming (McRae & Boisvert, 1998; Neely 1977). In semantic priming tasks, two words are presented to the participant in rapid succession. The first word, the prime, is present for only a short duration—on the order of 150 ms. The target word is then presented, and the participant makes a lexical decision judgment (for instance). Although the prime is not present long enough to be identified at above-chance levels, it nevertheless improves performance on identification of the target word. Thus, although the prime is activated to only a low threshold, it still impacts the processing of a target word. Mani and Plunkett (2010) have extended this finding, in a modified paradigm, to 18-month-old infants.

Such processing is also consonant with properties of the neural system. Although it is common to abstract neural processing to a series of discrete firings, or action potentials, and then to model the rate of such firing, neural processing is known to be significantly more complex. For example, membrane potentials below threshold can modulate the release of neurotransmitters—in effect, producing analog rather than digital changes (Alle & Geiger, 2006; Marder, 2006). The interaction of sub-threshold activations is also a cornerstone of neurally inspired dynamic field theory models (e.g., Erlhagen & Schoner, 2002; Thelen, Schöner, Scheier, & Smith, 2001). In these models, representations consist of patterns of activation across a field of neuron-like units. Critically, items represented in similar parts of the neural field can interact, such that if both are active at sub-threshold levels, their overlap can push one over threshold. Spencer and colleagues have used these representations to explain aspects of spatial (Schutte, Spencer, & Schöner, 2003) and visual (Johnson, Spencer, & Schöner, 2008) cognition, as well as their interaction (Simmering & Spencer, 2008).

This article extends these ideas beyond processing and memory and into language acquisition (although see Samuelson, Schutte, & Horst, 2009). We show that even sub-threshold knowledge of a word's referent can change the acquisition of new words. Although McMurray (2007) showed that acceleration in rate of vocabulary acquisition should be predicted even if words are learned independently, the quantitative pattern may require a mechanism in which partial knowledge of words interacts. Taking this proposal seriously suggests that, in fact, learning the whole system of language may be easier than learning the independent parts. Recently, computational studies have shown this indeed to be the case. For instance, Frank, Goodman, and Tenenbaum (2009) showed that learning the meanings of words is more successful if learners perform joint inference over both meaning and intention, rather than just meaning alone. Feldman, Griffiths, and Morgan (2009) modeled phonetic category learning and showed the task to be easier if learners simultaneously try to learn words and phonetic categories. Johnson, Frank, Demuth, and Jones (2010) similarly showed that joint inference of words and syllables produces better speech segmentation than does inference over syllables alone. Hidaka and Smith (2010) showed that learning the features relevant for multiple natural language categories allows rapid acquisition of new categories and may help to explain fast-mapping. Because language contains structure at multiple levels and regularities are related across levels, learning something about one level is informative about aspects at other levels. This idea is also key to both semantic (Pinker, 1994) and syntactic (Gleitman, 1990) bootstrapping.

Children are inundated with language. The average American child can expect to hear between 10 and 33 million words in the first 3 years of life (Hart & Risley, 1995). This is a tremendous amount of input, and most of it is likely to occur in noisy, ambiguous learning environments. Finding the latent structure in such data may depend on using less than clear-cut information and on representations that are not strong enough to show up as explicit knowledge. If language learning is really about recovering structure from noisy statistics (Kemp, Perfors, & Tenenbaum, 2007), even the noisiest data may have an important role to play (Kalish, Rogers, Lang, & Zhu, 2011; Recchia & Jones, 2009).

Partial knowledge and accumulative learning

While language acquisition is a problem of discovering of latent structure, it is only one example of a general class of such problems (Kemp & Tenenbaum, 2008). In any domain that contains structure, a learning system will benefit prodigiously from exploiting such structure. The present experiments demonstrate that human learners can exploit a set of partially learned word–object mappings to learn other word– object mappings, but similar effects are seen across a variety of domains.

In memory, items related by semantic similarity (McRae & Boisvert, 1998), temporal contiguity (Clayton & Habibi, 1991), and typical location (Estes, Verges, & Barsalou, 2008) facilitate each others' processing. Also, when an item cannot be recalled, people can often nonetheless retrieve partial information about that item (Brown & Kulik, 1977; Durso & Shore, 1991; Hicks & Marsh, 2002; Koriat, 1993). Furthermore, when the partially retrieved item is followed by a related item, complete retrieval is facilitated (Meyer & Bock, 1992). All of this suggests that memory storage is highly interconnected and operates in a graded manner.

In categorization, the relationship among features plays a significant role in the resulting knowledge acquisition. For instance, irrelevant features encountered during learning in a categorization task can alter subsequent generalization gradients (Little & Lewandowsky, 2009). This suggests that even when information does not directly impact learning of the experienced correlations, it can nonetheless play a role in organizing future learning. Consistent with this idea, a number of experimenters have demonstrated significant effects of prior learning on future category learning. For instance, Heit (1994) showed that prior knowledge of exemplars from a category in one condition affects the acquisition of information about that category in a new condition. Billman and Knutson (1996) showed that categories are easier to learn when the relational structure of their features follows two principles: value systematicity and value contrast. High value systematicity occurs when features that predict other features are likely to predict still other features. That is, features that have been predictive in the past are given high weight when new categories are learned. High value contrast occurs when, if one value that a feature can take is predictive, so are the other values. In both of these cases, acquiring partial information about the feature structure of categories bootstraps the acquisition of further information about related categories. Further studies have confirmed these findings, showing that correlations are easier to learn if they are embedded in a rich system of correlations than if they are experienced in isolation (Kersten & Billman, 1997; Yoshida & Smith, 2005).

The experiments in this article add two novel contributions to this discussion. First, they provide direct evidence of states of partial information on the trajectory between no knowledge and complete knowledge (see also Bion, Borovsky, & Fernald, 2013). Second, and most importantly, they provide evidence for a driving role of partial knowledge in a system still in the process of learning. In the memory literature, information that has previously been well learned is known to be interconnected with other previously well-learned information. Similarly, in the categorization literature, well-learned prior knowledge (e.g., Heit, 1994) is known to affect the acquisition of future knowledge, as is the static relational structure of the knowledge to be acquired. The empirical and computational evidence presented in this article shows that even if information was never well learned, it can still play an important role in organizing future learning.

None of this is intended to deny that significant learning can happen in a single trial (Brown & Kulik, 1977; Gallistel et al., 2004; Markson & Bloom, 1997). Rather, the central claim is that significant partial knowledge from related learning, accumulated over a series of past experiences, plays a critical role in creating one-shot learning opportunities in noisy learning environments. Once a learner has accumulated information about the structure of the information to be learned (Kemp et al., 2007; L. B. Smith et al., 2002), the acquisition of new knowledge can be quite rapid. It is the high degree of interactivity in the human word-learning system, and in the learning system in general, that may help to explain its remarkable success even when embedded in the complex environment of the natural world.

Scaling up: word learning in the world

Although we can ask many questions about word learning via laboratory experiments, the laboratory is not the world. With any such endeavor, there is always a translational question: Will this behavior scale? Previous demonstrations suggest that it may. For instance, laboratory experiments investigating the operations of memory processes typically ask participants to remember just a few or a few dozen objects. However, Brady, Konkle, Alvarez, and Oliva (2008) showed that humans can rapidly learn to remember thousands of objects. Similarly, short learning experiences in the laboratory can have striking consequences for real-world learning. L. B. Smith et al. (2002) showed that 17-month-old infants who were taught to categorize objects by shape in the lab subsequently showed a prodigious acceleration in vocabulary development, learning many more words than infants who did not receive such training.

In the present study, the input for word learning was simplified in a number of ways. Words were presented in isolation rather than in sentential contexts, words referred to individual objects rather than types, and potential referents were clearly individuated and available on-screen. Clearly, this is a different problem from that faced in “the wild” (Medina et al., 2011; Quine, 1960). Nonetheless, the core hypothesis in this article—that words are learned through accumulation of partial knowledge, and that partial knowledge of some words can accelerate the acquisition of other words—is likely to scale. This is because while the real world is more complex than the lab, it is not uniformly and arbitrarily complex. In some cases, this additional variability can be good for learning (Apfelbaum & McMurray 2011; Hills, Maouene, Riordan, & Smith, 2010; Perry, Samuelson, Malloy, & Schiffer, 2010; Rost & McMurray, 2010).

For instance, while words are often embedded in sentential contexts, a significant proportion of speech to infants consists of isolated words (Brent & Siskind, 2001), and these isolated words measurably improve statistical speech segmentation in 8- to 10-month-old infants (Lew-Williams, Pelucchi, & Saffran, 2011). Furthermore, even when important words are not produced in isolation, they are placed in sentence-final position and preceded by determiners, making them more salient and easing their segmentation (Aslin, Woodward, LaMendola, & Bever, 1996). Recent work shows that this structure also facilitates cross-situational word learning (Monaghan & Mattock, 2012; Yurovsky et al., 2012).

Similarly, although objects that receive a given label are not identical, they typically vary along predictable dimensions (Hidaka & Smith, 2010). Thus, even though L. B. Smith et al. (2002) exposed children to mappings in which shape was identical across instances, the acceleration in these children's real-world word learning was for categories whose exemplars were not identical in shape. Furthermore, increasing the dissimilarity of the laboratory training objects on other dimensions actually improves real-world word learning (Perry et al., 2010).

Understanding how learning words across ambiguous situations scales, thus, is surely more than a matter of presenting learners with more and more words and objects per trial (cf K. Smith et al., 2011). Making progress will involve documenting the statistical properties of auditory and visual input to children and understanding how these interact with statistical word learning (Blythe, Smith, & Smith, 2010; Vogt, 2012). It will also require caution: assumptions may creep in that re-introduce arbitrary, rather than natural, complexity. For example, although Medina et al. (2011) showed that cross-situational word learning fails to cope with the ambiguity of natural naming events, Yurovsky, Yu, and Smith (in press) showed that this conclusion resulted from an incorrect assumption. When identical natural naming events were observed from a child's first-person perspective, cross-situational learning succeeded. Thus, experiments designed to isolate a particular learning problem may sometimes remove exactly the information that real children use in real learning (see, e.g., Bergelson & Swingley, 2012; Frank, Slemmer, Marcus, & Johnson, 2009; Shukla, White, & Aslin, 2011; Thiessen & Saffran, 2009).

By extension, we argue that even partial knowledge of sounds, words, objects, and mappings may be critical for bootstrapping language acquisition. For instance, Bortfeld, Morgan, Golinkoff, and Rathbun (2005) showed that 6-month-old infants could use words with which they were familiar but for which they had, at best, partial knowledge of meaning as a wedge into speech segmentation. In the other direction, Hochmann, Endress, and Mehler (2010) pre-exposed 17-month-old infants to natural French speech and subsequently presented these infants with a word–object mapping task in which words from the speech stream served as labels. Infants associated objects more strongly with the nouns in this language than the determiners. Why? The hypothesis is that even though these infants had not yet learned much about syntax, they had already learned that very high frequency words do not have referents. Thus, although our findings are in a setting very different from that in which children and adults learn language, they may be at the core of understanding these mechanisms.

Finally, the move to understand word learning at scale will require a serious investigation of the role of time in encoding, remembering, and forgetting the meanings of words (Kachergis et al., 2012; McMurray et al., 2012; Medina et al., 2011; Spencer, Perone, Smith, & Samuelson, 2011; Vlach, Sandhofer, & Kornell, 2008).For instance, although children sometimes fast-map words to objects after a single exposure, memory for these mappings can be quite short-lived (Bion et al., 2013; Horst & Samuelson, 2008; Munro, Baker, McGreggor, Docking, & Arciuli, 2012). Similarly, inferences that learners make about the objects to which a word refers can be different when these objects are presented sequentially versus simultaneously (Spencer et al., 2011). Thus, although one of the recent debates in the word-learning literature has been whether the extant data is best explained by hypothesis testing or associative learning (e.g., Colunga & Smith, 2005; Kemp et al., 2007; Medina et al., 2011; Sloutsky, 2009; Waxman & Gelman, 2009; Yu & Smith, 2007), we join Yu and Smith (2012) in advocating that it has not been productive. As models in both classes become more complex, the differences between them become semantic rather than material. Since hypothesized hypothesis-testers are allowed to entertain multiple, probabilistic hypotheses (Frank, Goodman, & Tenenbaum, 2009; Xu & Tenenbaum, 2007) and associative models incorporate competition, nonmonotonic learning rules, and complex measures of association and uncertainty (Kachergis et al., 2012; McMurray et al., 2012; Regier, 2005; Yu, 2008; Yu & Smith, 2011; Yurovsky, Yu, & Smith, in press), these classes of models become difficult (or impossible) to discriminate (see also Shi, Griffiths, Feldman, & Sanborn, 2010; Townsend, 1990; Townsend & Wenger, 2004). A more productive modeling endeavor might be to work on understanding how statistical word learning unfolds across multiple scales—from how information is selected in a single trial (Fitneva & Christiansen, 2011; L. B. Smith & Yu, 2013; Yu & Smith, 2011; Yu et al., 2012), to how information is accumulated across multiple trials (as in this article) (K. Smith et al., 2011; Trueswell et al., 2013; Yurovsky, Yu, & Smith, in press), how information is stored and forgotten across days (Medina et al., 2011; Vlach & Sandhoffer, in press), and how learning trajectories for large-scale lexicons ultimately unfold across months and years (Frank, Tenenbaum, & Gibson, 2013). It may be that once models of both classes have grappled with constraints from all of these levels, we will be able to tell them apart. Or it may be that we decide they are truly indistinguishable. In either case, we will have made progress in understanding how statistical word learning might scale. The experiments and models in this article provide one such set of constraints.

Conclusion

Learning a language requires learning a massive set of word–object mappings. While some words could be learned pedagogically, perhaps even from a single instance, this may leave many words unlearned. Statistical and associative approaches suggest that children and adults may solve this problem by tracking word–object co-occurrences across time, gradually learning the meanings of many words over repeated exposures. The present article provides support for these kinds of theories, demonstrating empirical evidence of partial knowledge in ambiguous word-learning situations: words that are not yet learned to criterion, but for which learners have nonetheless acquired some knowledge. Furthermore, the experiments and models in this article show that partial knowledge plays a direct role in bootstrapping future learning, accelerating the acquisition of novel words and objects. This article thus makes three main contributions. First, it provides direct evidence of sub-threshold knowledge in statistical word learning, an assumption made by many theories, but not demonstrated directly (Medina et al., 2011; K. Smith et al., 2009). Second, it shows that this partial knowledge plays an interactive, system-level role: partial knowledge of some words accelerates the acquisition of other, co-occurring words. Third, the modeling results indicate that partial knowledge plays this role quite early, with very little exposure needed to potential mappings before they begin to bias the learning system. In addition, this article also explores several possible representations of this partial knowledge (see the Appendix). Together, these new results point to a framework that clarifies the origins of such bootstrapping and the relationship between partial knowledge and vocabulary development.

Appendix.

In developing any computational model, one must make a decision about how to move from the conceptual model to its implementation. In these models, we made just such a decision about how the strength of evidence for a word-object mapping [S(w, o)] is derived from the cells in the associative matrix (A). There were, however, a number of alternative possibilities that we also considered but rejected due to poorer fits to the empirical data. Here, we present those alternatives and their goodness of fit for the Baseline, Full Knowledge ME, and Partial Knowledge ME models.

The most straightforward metric is to use pure frequency; once the cell in the associative matrix [A(w, o)] crosses a threshold, the word is known. This takes into account what is known about the co-occurrence of word w and object o but ignores information about w's co-occurrence with other objects. One way of using the distributional information is to measure the proportion of associative strength for w and all objects accounted for by a particular object o—that is, to normalize each cell by the sum of its row (Luce, 1959).

Third, because psychological distance is known to be an exponential function of true distance (Shepard, 1987), it is reasonable to take an exponential transform of the proportion of association computed in the previous metric. Exponentiated proportion is different from proportion in two basic ways. First, the same amount of difference between two proportions is treated as more significant in higher parts of the space (e.g., .9 vs. 8) than in lower parts of the space (e.g., .4 vs. .3). Second, it assigns nonzero weight to zero-strength associations. This encodes the idea that since there are more candidate referents, there is less certainty in any individual referent.

Finally, a natural candidate for the strength function is the reciprocal of the entropy (Shannon, 1948) of the proportion space, or negentropy (Schrödinger, 1944). Entropy is a measure of the uncertainty of a distribution; in this case, setting a threshold on negentropy requires there be a lower bound on uncertainty before a mapping is known. Table 2 below presents BIC values for these metrics, as well as for the metric used in body of the article: Average ratio. Since average ratio significantly outperforms several other plausible candidate metrics, it was used in the models presented in the main text.

Table 2. Model BICs for alternative strength metrics.

Metric	Baseline	Full Knowledge ME	Partial Knowledge ME
Frequency	−38.24	−38.07	−35.43
Proportion	−34.44	−34.9	−38.53
Exp. proportion	−34.49	−34.7	−39.03
Negentropy	−34.49	−34.04	−38.67
Average ratio	−49.92	−50.2	−66.2

Note. BIC, Bayesian information criterion; ME, mutual exclusivity; Exp., exponentiated