Non-ignorable loss to follow-up: correcting mortality estimates based on additional outcome ascertainment

Abstract

Loss to follow-up (LTFU) is a common problem in many epidemiological studies. In antiretroviral treatment (ART) programmes for patients with HIV mortality estimates can be biased if the LTFU mechanism is non-ignorable, i.e. mortality differs between lost and retained patients. In this setting, routine procedures for handling missing data may lead to biased estimates. To appropriately deal with non-ignorable LTFU, explicit modeling of the missing data mechanism is needed. This can be based on additional outcome ascertainment for a sample of patients LTFU, for example through linkage to national registries or through survey-based methods. In this paper, we demonstrate how this additional information can be used to construct estimators based on inverse probability weights (IPW) or multiple imputation. We use simulations to contrast the performance of the proposed estimators with methods widely used in HIV cohort research for dealing with missing data. The practical implications of our approach are illustrated using South African ART data which are partially linkable to South African national vital registration data. Our results demonstrate that while IPWs and proper imputation procedures can be easily constructed from additional outcome ascertainment to obtain valid overall estimates, neglecting non-ignorable LTFU can result in substantial bias. We believe the proposed estimators are readily applicable to a growing number of studies where LTFU is appreciable but additional outcome data are available through linkage or surveys of patients LTFU.

1. Introduction

In biomedical research missing data are a common problem. A broad range of methods, including multiple imputation and weighted estimating equations, can be employed when the missingness mechanism is ignorable, i.e. if the probability that a response is missing at any occasion depends only on observed data [1, 2, 3].

However, many studies deal with missing data where the probability of missingness depends on the missing data itself. In observational cohort studies missingness of the outcomes may be related to the unobserved outcomes while additional ignorable missing covariate data are relevant to the analyses [4, 5]. For instance, in survival analyses of patients treated with antiretroviral therapy (ART) for human immunodeficiency virus (HIV), in resource-limited settings loss to follow-up (LTFU) is often high. Lost patients are typically more likely to have died than those retained, indicating non-ignorable loss to follow-up [6]. In addition both baseline and time-varying covariates measuring disease severity may be partly missing. Despite this, in most studies, LTFU is either ignored through non-informative censoring or methods such as complete case analysis or multiple imputation are used [7, 8, 9].

Valid inference under non-ignorable missingness requires specification of a model for the missing-data mechanism. The use of joint models for the response vector and the missingness-mechanism are well-established and provide unbiased estimation under certain assumptions. Both selection- and pattern-mixture models belong to this class of models and are based on the factorization of the joint distribution. They have proved to be useful, particularly for sensitivity analysis, in a variety of situations (see [4, 10, 11, 12, 13, 14 ] among others). However, these methods often rely on strong modeling assumptions, may face identifiability problems, and need intensive development in cases of additional missing covariate data [4, 15].

When additional information about missing values can be obtained, this information could be included in the analysis [16, 4 ]. Linkage of patients to national databases as well as the systematic tracking of samples of patients LTFU are emerging as viable approaches to outcome ascertainment [17, 6, 18 ]. Nevertheless, there is currently no clear guidance on the appropriate method for including a subsample of ascertained outcomes when confronted with non-ignorable missingness. However, in some applied epidemiological work [18, 19 ] a valuable pragmatic approach has been applied to correct estimates when outcomes from a sample of those lost can be ascertained. In this approach a subsample of lost patients are tracked and simple mortality estimates are corrected by upweighting the tracked patients arithmetically to represent all patients lost. Unfortunately, the subsample may differ in important ways from those who are lost but cannot be tracked - for example it may be difficult to track patients in remote areas yet these patients may have been sicker when lost. This highlights the need to appropriately incorporate the updated data into mortality estimates and estimates of the corresponding risk factors.

We present a general framework for constructing inverse probability weights (IPW) that yield consistent estimates in the presence of non-ignorable losses and additional outcome ascertainment. We model, among those LTFU, the probability of a patient’s outcome being ascertained, and explore different approaches to ensuring correct model specification, e.g. via logistic regression, generalized additive models, and Bayesian model averaging. In building this model, the weights, which are based on the inverse of the estimated predicted probabilities of ascertainment, make the ascertained subjects representative of all lost subjects. Our framework demonstrates that patients who are not lost can easily be incorporated into the analysis with constant weights of 1.

When confronted with ART data, many important analytic issues arise including how to construct appropriate weights, how much ascertainment is needed to reliably correct estimates, and how to deal with additional (ignorable) covariate data. Given these issues, it is essential to know how well IPW-based estimators perform compared to alternative approaches. Our framework, analyses and simulations are specifically geared towards these questions with the aim of clearly understanding the consequences of implementing the proposed IPW estimators in survival analyses of ART data and related research. Our comparisons of the various methods for dealing with missing data under different levels of ascertainment may be instructive for applying these methods in practice.

Furthermore, we discuss if and in what cases multiple imputation can be used in conjunction with the ascertained data as an alternative to the aforementioned IPW approach. Along these lines, it is of interest to explore appropriate imputation models and relate these to our statistical framework.

We specifically aim 1) to describe the consequences of neglecting nonignorable loss to follow-up and explore the extent to which methods most commonly employed in HIV cohort research might be biased, 2) to quantify the benefits of incorporating additional outcome ascertainment, and 3) to examine how this additional data can best be incorporated and how the proposed estimators perform in real settings.

The paper proceeds with a detailed outline of our illustrative example in Section 2. Our statistical framework is explained in detail in Section 3, highlighting different approaches to estimating appropriate inverse probability weights, how to deal with missing covariate data, and how to use multiple imputation after utilizing outcome ascertainment. Section 4 explores the performance of the proposed estimators through comparison to alternative approaches via Monte Carlo simulations. Analyses based on the illustrative example demonstrate the practical implications of our approach in Section 5. The relevance of the framework to studies in different settings and with different outcomes are discussed in Section 6, followed by the conclusion (Section 7).

2. Antiretroviral treatment in Southern Africa, IeDEA-SA

The motivation for our statistical framework arises from attempts to accurately describe mortality and associations with mortality in patients being treated for HIV in Southern Africa, where the introduction of ART has led to substantial reductions in mortality and morbidity. However, in many resource-limited settings, including many countries in sub-Saharan Africa, outcomes are unknown for a substantial proportion of patients who are recorded as being LTFU. Reasons include deaths that were unrecorded, clerical errors in which attendance was not recorded, and patient factors such as fear of disclosure, relocation, concerns about treatment, transport challenges, and poor health [20]. Due to unrecorded deaths being an important reason for patients being defined as LTFU, and high mortality in those who do leave care, mortality is usually substantially higher in those defined as LTFU than those remaining in care, resulting in LTFU being non-ignorable when describing mortality.

The International epidemiologic Databases to Evaluate AIDS (IeDEA) was established with the aim of creating regional data centers for collecting HIV treatment data to address high priority research questions. Currently 126 facilities in 18 cohorts contribute data to the Southern African network (IeDEA-SA). Existing data suggest that LTFU varies in the region between settings and duration on ART from 15% to 55% [21]. Recent linkages of patients LTFU in South African cohorts to national death registration data confirm that patients who were LTFU were more likely to have died than those who remained in care [6, 22 ]. In our example in Section 5 we use IeDEA-SA data from three South African cohorts including 30901 patients receiving ART in which data on lost patients were linked to the national death registry for those patients in whom a civil ID number was available to enable the linkage. Table 1 shows that a substantial proportion of patients meet the LTFU definition (21.7%) with higher mortality among linkable patients LTFU than among patients who are in care.

Table 1.

Summary of the data used for the example in Section 5

	Adults	LTFU	Linked	Non-LTFU died	linkable LTFU died
Cohort A	13016	3634 (27.9%)	11345 (87.2%)	3.0%	25.5%
Cohort B	7214	689 (9.6%)	3649 (50.6%)	8.3%	31.4%
Cohort C	10671	2376 (22.3%)	6657 (62.4%)	6.4%	33.1%
Total	30901	6699 (21.7%)	21651 (70.1%)	5.6%	27.8%

3. Statistical Framework

In the following we consider survival data where the time T until a single event of interest occurs is defined to be the outcome. Not all of the n subjects may experience an event during the period they are followed and may thus be right-censored. Let T_i and C_i denote the survival and censoring times of subject i, i = 1, …, n, let Z_i = min(T_i, C_i) be the observed survival time, and y_i = (Z_i, d_i) is the observed outcome tuple where d_i = I(T_i < C_i) relates to the respective outcome status for subject i. Further let x_i = (x_i1, …, x_ip) be the covariate vector associated with the outcome of individual i. The covariate vectors are collected in the matrix X = (x₁′, …, x_n′)′. Thus, all measurements are contained in the n × (p + 2) datamatrix 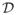= {y, X}.

It is common that in research studies some of these data will be missing: Individuals may not provide all the information that is required, measurements may not be taken on a regular basis, or study participants may simply be lost to follow-up. Here, the data consists of both observed and missing values, = { 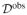, 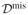}, and valid statistical inference depends on the missingness mechanism. Consider the n × (p + 2) missing-indicator matrix with R_il denoting whether the observation of the i^th individual for the l^th variable is observed (R_il = 0) or not (R_il = 1). In the context of survival analysis missingness of the outcome may refer to drop-out or loss to follow-up which means that sequences of measurements on some subjects terminate prematurely and hence follow-up data is missing, and therefore the correct time to event or time to censoring is missing. We thus define R_il = 1 for the outcome if a subject is lost to follow-up since we cannot observe y_i, i.e. Z_i = min(T_i, C_i) and d_i = I(T_i < C_i). If the probability of missingness depends only on observed quantities and thus Pr( | 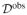, , 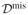ψ) = Pr( | 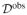, ψ), where ψ refers to the parameterization of the missingness process, the data are said to be ‘missing at random’ [23]. Here, the missingness mechanism is ignorable and various methods exist that yield valid statistical inference when used correctly (see also [1], [2], and [24] among others for an overview, and [3] for an interesting review of software implementations of these methods).

We consider the scenario in which data are missing not at random (MNAR) and thus the missingness mechanism is non-ignorable. In this case the probability of missingness may also depend on unobserved quantities, i.e. the missing data itself: Pr( | 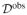, , 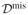ψ) = Pr( | 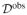, , ψ). For the survival outcome, if the drop out process depends on unobserved measurements (i.e. the unobserved time to event) and subjects are censored at the time of their last measurement, one would often also speak of informative censoring instead of MNAR [25]. Valid inference is difficult to obtain without either making assumptions about the missingness process or including additional information. In either case, it is essential to model the joint probability of the data and the missingness indicator, that is Pr( , ). Now consider, without loss of generality, that the survival outcome is missing and covariates are fully observed; the pattern-mixture factorization of the joint distribution of y and , that also forms the basis of the aforementioned pattern mixture models [10, 11], is then given by

$$Pr\{\mathbf{y},\mathcal{R}\mid \mathbf{X},\theta ,\psi \}=Pr\{\mathbf{y}\mid \mathcal{R},\mathbf{X},\theta \}·Pr\{\mathcal{R}\mid \mathbf{X},\psi \}$$ (1)

whereby θ refers to the parameterization of the analysis model.

Suppose we ascertain values for a subset ${\mathbf{y}}_{\text{mis}}^{+}\subset {\mathbf{y}}_{\text{mis}},{\mathbf{y}}_{\text{mis}}={\mathbf{y}}_{\text{mis}}^{+}\cup {\mathbf{y}}_{\text{mis}}^{-}$: this corresponds to ascertaining a subset of both the outcome status $d_{\text{mis}}^{+}$ as well as the observed survival time $Z_{\text{mis}}^{+}$, e.g. the vital status of a patient at an analysis endpoint as well as his/her follow-up time until the event or censoring occurred. Now, we assume the ascertainment process to be ignorable, i.e. the probability that patient information can be obtained depends only on observed quantities such as distance from the health care facility or severity of illness and define

$${\delta }_i=\{\begin{array}{ll}1,\hfill & \text{for}\text{a}\text{complete}\text{or}\text{ascertained}{i}^{th}\text{observation}{y}_i\hfill \\ 0,\hfill & \text{for}\text{an}\text{incomplete}{i}^{th}\text{observation}{y}_i\hfill \end{array},i=1,\dots ,N,$$

which is an indicator of whether an observation belongs to ( ${\mathbf{y}}_{\text{mis}}^{+}\cup {\mathbf{y}}_{\text{obs}}$) or ${\mathbf{y}}_{\text{mis}}^{-}$. Now, the joint distribution of y and , as factorized in (1), may be extended to

$$Pr\{\mathbf{y},\mathcal{R},\Delta \mid \mathbf{X},\theta ,\psi ,\varphi \}=Pr\{\mathbf{y}\mid \mathcal{R},\delta ,\mathbf{X},\theta \}Pr\{\delta \mid \mathcal{R},\mathbf{X},\varphi \}Pr\{\mathcal{R}\mid \mathbf{X},\psi \}.$$ (2)

where ϕ relates to the parameterization of the ascertainment process. However, to model the association between different covariates and the outcome, we would typically be interested in the conditional distribution of y given X if there were no missing values, i.e. there is no informative censoring. Thus we are interested in this distribution if all subjects’ values were ascertained, which in our framework corresponds to setting δ_j = 1 for all observations. This is a counterfactual question which can be answered using techniques from causal inference such as Pearl’s intervention calculus [26].

In causal inference one is interested in the causal effect of an intervention on a particular outcome. It is however not possible for the same subjects to be both exposed and not exposed to an intervention of interest. We therefore aim to estimate the distribution of an outcome A if all subjects had received intervention B = b₁ compared to if everyone had received intervention B = b₂. To estimate and evaluate these potential (counterfactual, hypothetical) outcomes, it is necessary to understand the underlying data-generating mechanism in terms of the causal relationship of variables, especially for observational data. Our assumption about these causal relationships can be specified in a directed acyclic graph (DAG) where each variable is represented by a node and any potential causal mechanism between two variables by an arrow which identifies cause and effect (Figure 1a); no arrows between two variables imply that they are not causally related. The DAG induces the conditional (in)dependence structure of the variables: (i) the joint distribution can be represented by the product of each variable given its parents (who point with an arrow towards the respective variable and are thus defined to have an influence on this variable – in Figure 1a, C is a parent of B and A, B is a parent of A); and therefore (ii) the conditional (in)dependence structure of variables is implicitly defined [26, pp.16–18]; moreover, (iii) confounding variables can easily be identified as confounding relates to common causes of a variable (in Figure 1a, C is a common cause of A and B and thus a confounder).

Figure 1.

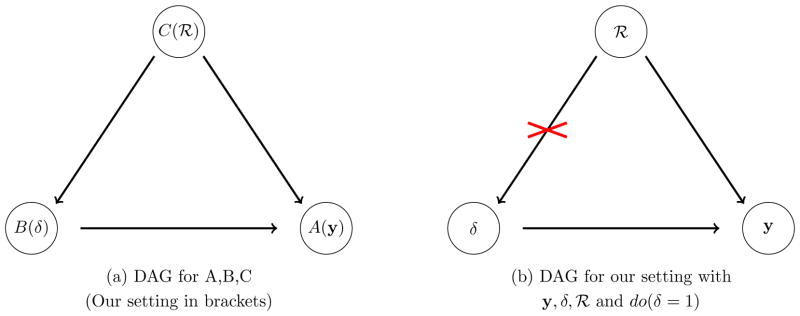
Directed Acyclic Graphs (DAGs): Pearls do-calculus and its application for our framework.

Several techniques have been developed to estimate a causal quantity given pre-specified knowledge about the data-generating process [27, 28, 29 ]. Many of them can be related to Judea Pearl’s structural causal model framework [26]. In this framework, the ‘what if’ question is translated into an intervention on the DAG (such as removing the arrow from C to B in Figure 1a). This intervention modifies the conditional independence structure by removing the corresponding factor in the factorisation of the joint distribution. Thus, the counterfactual distribution of A (when we ‘do(B = b)’) can be written as

$$Pr(A\mid do(B=b))-\sum _{c\in C}Pr(A\mid C,B=b)Pr(C=c)$$ (3)

under the assumptions that B is conditionally independent of A|C and thus there are no unmeasured confounding variables and Pr(A|C = c) > 0 if Pr(C = c) ≠ 0, see also [26, p.79 ff.] and [27]; This means that the counterfactual distribution of A, given that every subject had received B = b, can be obtained from the observed data (where not everyone has B = b) by stratifying by C. More generally, measuring those ‘back door’ variables Z that point towards the intervention B and block the ‘back door path’ from A to B (via Z) is sufficient to identify the causal effect of B on A from the observed data. The latter graphical condition also verifies the conditional independence of B and A|Z [26] and is often called ‘general back door adjustment’ – echoing that adjusting for the confounding variables Z is sufficient to estimate Pr(A |do(B = b)), and in our example Z = C, see also Figure 1a. Note that the graphical representation of our knowledge in a DAG is enough therefore to verify the conditional independence assumption and apply the do-calculus, where utilizing the do-calculus via (3) requires only deleting the arrows pointing towards the intervention, which corresponds here to deleting the arrow from C to B.

If we now interpret δ as being an intervention, then Pr{y |do(δ = 1), X, θ} is our counterfactual distribution of interest, which relates to the conditional distribution of y given X where there is no missing data. Figure 1a (brackets) represents the DAG for our framework: The outcome distribution depends on whether a subject is lost to follow-up (missing) or not ( ) and whether an observation remains unascertained or not (δ); moreover, the probability of ascertainment is different for subjects lost when compared to those observed, represented by the arrow from to δ. Interestingly, this DAG induces a conditional independence structure which specifies the decomposition of the joint distribution Pr(y, , δ) as described before in (2) (though (2) itself does not guarantee any conditional independence). Moreover, y and δ are conditionally independent given in our DAG which relates to the fact that given a subject is LTFU (or not LTFU) the distribution of the outcome (i.e. the survival time) is determined independently of δ (but conditional on X). Thus we can now apply (3) to our framework and get

$$\begin{array}{l}Pr\{\mathbf{y}\mid do(\delta =1),\mathbf{X},\theta \}=\sum _{r\in \mathcal{R}}Pr\{\mathbf{y}\mid \mathcal{R},\delta =1,\mathbf{X},\theta \}Pr\{\mathcal{R}\mid \mathbf{X},\psi \}\\ =\sum _{r\in \mathcal{R}}\frac{Pr\{\mathbf{y},\mathcal{R},\delta =1\mid \mathbf{X},\theta ,\psi \}}{Pr\{\delta =1\mid \mathcal{R},\mathbf{X},\varphi \}},\end{array}$$ (4)

which is also illustrated in Figure 1b where deleting the arrow from to δ applies the do-calculus. As a result, Pr{y |do(δ = 1), X, θ} can be estimated by means of the observed and ascertained observations and weighted MLE, the weights being estimated via the inverse probabilities p⁻¹ = Pr{δ = 1 | , X, ϕ}⁻¹. Since every subject that was originally not LTFU has a known outcome we get

$$w_j=\{\begin{array}{ll}1,\hfill & \text{if}{R}_j=0\hfill \\ {\delta }_j{\{Pr({\delta }_j=1\mid {\mathbf{x}}_j,\varphi )\}}^{-1},\hfill & \text{if}{R}_j=1\hfill \end{array}.$$ (5)

where R_j = 1 if the j^th observation belongs to a lost subject and R_j = 0 otherwise. Therefore by using the weights above and MLE we get consistent estimates in the non-ignorable loss to follow-up setting after ascertainment [30, 31 ]. For applied data analyses, this results in simply fitting the weighted model of interest, e.g. any regression model with observations weighted by (5). These weights have certain characteristics for the three groups of interest:

1. subjects never lost (R_j = 0, δ_j = 1) receive weights w_j = 1,

2. subjects lost but ascertained (R_j = 1, δ_j = 1) obtain weights w_j > 1, estimated via $p_j^{-1}=Pr{({\delta }_j=1\mid {\mathbf{x}}_j,\varphi )}^{-1}$,

   subjects lost and unascertained (R_j = 1, δ_j = 0) are excluded from the analysis by means of weights w_j = 0.

3.1. Modeling of IP Weights

As we have seen previously, we must model the probability of having a complete observation after incorporating additional information given the subset of observations obtained from patients LTFU. A common choice is a logistic regression model,

$$p_j=Pr({\delta }_j=1\mid {\mathbf{x}}_j,R_j=1,\varphi )=F({\mu }_j),$$ (6)

where δ is the binary outcome, ${\mu }_j={\varphi }_0+{\mathbf{x}}_j^{\prime }{\mathit{\varphi }}_1$, ϕ = {ϕ₀, ϕ₁}, j = 1, …, N, F (.) = 1={1 + exp(−.)}, ϕ₀ is the intercept coefficient, and ϕ₁ is a vector of coefficients corresponding to the covariate vector x_j. If no covariates are considered then we have constant weights reflecting approaches that have previously been applied in epidemiologic research (see also Section 6).

Note that IPWs only yield consistent estimates if the model on which the weights are based (weight model) is specified correctly and provides a good tradeoff between bias and variance [2]. To build a good model, various different modeling strategies can be considered: For example, it is often argued, see e.g. [32], that inverse probability models should be highly flexible and generalized additive models [33] provide a more flexible alternative to simple logistic regression models. Presuming the factors potentially associated with missingness have been carefully selected based a priori on the putative mechanism, the application of additional model selection approaches to reduce variance while retaining important associations can also be considered.

In order to account for the uncertainty in the model selection process, model averaging is an alternative to model selection: Under model averaging, one chooses a set of logistic-type regression models consisting of different subsets of potential covariates (from a master set selected a priori as described above) and calculates a weighted average of the corresponding estimates – whereby ‘better’ models receive a higher weight. By averaging over many different models, this approach incorporates variable selection uncertainty in conclusions about parameters and predictions and provides robust and stable estimates (see, e.g., [34], [35] and [36]). From the Bayesian perspective the quality of a (logistic) model M_κ ∈ = {M₁, …, M_K} may be judged upon the estimated posterior probability that a model is correct, that is

$$Pr(M_{\kappa }\mid \mathbf{y})\propto Pr(M_{\kappa }){\int }_{{\mathrm{\Phi }}_{\kappa }}Pr(\mathbf{y}\mid M_{\kappa },{\varphi }_{\kappa })·Pr({\varphi }_{\kappa }\mid M_{\kappa })d{\varphi }_{\kappa },$$

where Pr(M_κ) is the a-priori probability for the model M_κ to be correct, Pr(ϕ_κ|M_κ) reflects the prior of ϕ for model M_κ, ϕ_κ ∈ Φ _κ, Φ κ ⊂ 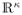, and Pr(y|M_κ, ϕ_κ) represents the corresponding likelihood. Since, for large N, Pr(M_κ|y) can be approximated via the Bayes-Criterion of Schwarz (BCS, BIC, [37], [38]), it is often suggested that

$$\widehat{\overline{\varphi }}=\sum _{\kappa =1}^K{s}_{\kappa }^{\mathit{BCS}}{\widehat{\varphi }}_{\kappa },\text{with}{s}_{\kappa }^{\mathit{BCS}}=\frac{exp(-\frac{1}{2}{\mathit{BCS}}_{\kappa })}{{\sum }_{\kappa =1}^{K}exp(-\frac{1}{2}{\mathit{BCS}}_{\kappa })}$$ (7)

is used as the Bayesian Model Averaging estimator. The BCS corresponds to −2 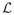(ϕ̂) + ln N · P, where 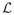(·) is the log-likelihood function and P corresponds to the number of parameters. In Section 4 we rely on (7) to estimate the weights (5) and use the R-implementation based on the package BMA [39] which uses an algorithm based on Occam’s Window [36] to find a set of good models .

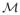3.2. Additional MAR (covariate) data

If additional covariate data are missing, and the corresponding missingness mechanism is assumed to be ignorable, then one may use multiple imputation (MI) in conjunction with the framework developed above. Here, one would first create M imputed sets of data. For each set of data the predicted probabilities $p_j^{(m)}$ in line with (6) are calculated and used to fit the analysis model Pr(y|X^(m), w^(m), θ). The final estimates are then obtained by applying standard MI combining rules [24] to the M estimates of θ, that is θ̂₁, …, θ̂_M. The average probabilities ${\overline{p}}_{j,M}=M^{-1}{\sum }_{m=1}^M{p}_j^{(m)}$ may be used to summarize the feature of the weights ${\overline{w}}_M={\overline{p}}_M^{-1}$ as also suggested by White et al. [40] in a different context. The covariates for the corresponding logistic-type regression models may either be fixed based on prior (epidemiological) knowledge or model selection/averaging may be applied to each imputed dataset [41, 42].

To obtain M proper multiple imputations for this procedure one needs to randomly draw from the predictive posteriori distribution of the missing data given the observed data or an approximation thereof. These draws can (i) either be generated by specifying a multivariate distribution of the data 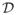(joint modeling) and simulate the predictive posteriori distribution with a suitable algorithm (ii) or by specifying individual conditional distributions for each variable X_j given the other variables (fully conditional modeling) and iteratively drawing and updating imputed values from these distributions which will then (ideally) converge to draws of the theoretical joint distribution [43]. In our simulations and analyses we use the EMB algorithm from the R-package Amelia II which uses the first approach and assumes a multivariate normal distribution for the data, 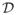~ N(μ, Σ). Skewed variables can be transformed by logarithmic and square root transformations and categorical variables are represented by binary dummy variables which often can be considered to be appropriate even under the assumption of a normal distribution [44]. Then M bootstrap samples are drawn and the EM algorithm [45] is performed on each of the bootstrap samples to obtain estimates of the posteriori modi ${\mu }_{(m)}^{\ast }$ and ${\mathrm{\sum }}_{(m)}^{\ast }$, m = 1, …, M. Based on the multivariate normal assumption and the estimated posteriori modi, imputations can be generated by means of predictions from a linear regression in the original data [46]. Each bootstrap sample offers then the possibility to create a single imputed set of data.

Another option which is commonly employed in applied work to deal with missingness, is to categorize the data, where missing data are treated as one category. However, as Vach [47, p. 21–22, 92] notes, this approach can introduce substantial bias, even though this is difficult to establish. There may even be situations where categories for missing data can produce valid results. An example of this would be when the missing data have a meaning and represent a specific category of the data, for example when the absence of a laboratory value might be related to quality of clerical procedures and hence the availability of linkage variables.

3.3. Using multiple imputation instead of IPW

In our current discussions we have taken the perspective that it is valuable to include ascertained data by means of inverse probability weighting. However, solutions other than IPW to incorporate the data of the ascertainment process are possible. One referee suggested that given the partially ascertained data and the consequential knowledge about the difference between subjects lost (R_j = 1) and subjects never lost (R_j = 0), it is possible to view the leftover missing data of subjects lost and unascertained as being ignorable since the missingness now only depends on observed quantities, namely the covariates and . Hence, it is possible to impute missing outcomes, i.e. time to event or censoring, when including all this knowledge in the imputation model. For instance, consider the imputation procedure of Amelia II as described in Section 3.2 above: Using the data of the updated outcome, covariates, and the indicator of missingness ( ), 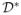= {y, X, }, a multivariate normal distribution is imposed on 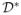, and proper multiple imputations are generated by means of the EMB algorithm. Note that with the imputation model we now explicitly approximate the joint distribution of the data and the missingness mechanism which is equivalent to Pr{y, , X}, the left hand side of (1) unconditional of X.

It is however important to stress that using an incomplete imputation model, i.e. a model that does not incorporate , may still yield biased estimates. Furthermore, applying multiple imputation to the unascertained data will also lead to bias as the missingness process is non-ignorable under this circumstance.

4. Simulation Study

4.1. Outline

We set the sample size as n = 1000 and create p = 5 covariates in a survival study with life-, censoring and loss to follow-up times (T, C, L). The observations for the (baseline) covariates are generated by the following distributions: X₁ ~ N(1, 1), X₂ ~ log N(1, 0.5), X₃ ~ Weibull(1.75, 1.9), X₄ ~ Bin(1, 0.3) and X₅~ Gamma(0.25, 2). To model the dependency between the covariates we use a Clayton Copula [48] with a copula parameter of 1 which indicates medium correlation among the covariates which are ‘quasi-standardized’ in the sense that the variance of each continuous variable is ≈ 1. The lifetimes are realized via draws from T ~ Exp(exp(μ₁)) with μ₁ = Xβ₁ with corresponding ‘true’ coefficients (including intercept) β₁ = (0.5, 0.2, 0.1, 0, 0.5, 0)′. The censoring times are C ~ Exp(12.5) and the LTFU times L ~ Exp(μ₂), μ₂ = 2.5 + 12.5 · I(C > T), indicating non-ignorable drop out with higher event-rates (≙death) for patients lost to follow-up. The LTFU times also depend on covariates, since T depends on μ₁. The observed times are min(T, C, L) and events are observed only if min(T, C, L) = T.

Thus in this experiment we consider a set of data (n = 1000) with medium correlation between the covariates where three out of the 5 co-variables (X₁, X₂, X₄) influence the lifetime of an individual to a different degree and loss to follow-up is non-ignorable.

We now assume that for patients LTFU, some can be tracked/linked and hence their status can be ascertained providing either the correct time to death or time to censoring. The probability of ascertainment depends on X₂ and X₄ and is defined as π_X2,X4 (Asc) = A + ({exp(η)=[1 + exp(η)]} − 0.5) whereby $\eta =X_2/3.5-\overline{X_2/3.5}+X_4/3.5-\overline{X_4/3.5},\overline{X./3.5}$ is $n^{-1}{\sum }_{i=1}^n(X_{·i}/3.5)$ and A represents the average ascertainment we would like to have.

We compare estimated survival based on Kaplan-Meier curves and parameter estimates in a Cox model for seven different strategies: 1) non-informative censoring (NIC), i.e subjects LTFU are treated as censored 2) complete cases (CC), i.e. discarding observations for patients LTFU, 3) multiple imputation (MI) of survival times and event status by using Amelia II [49] (with all measured variables included in the imputation model), 4) multiple imputation after including the ascertained data (& adding and δ to the imputation model), and including ascertained values with IPW where the upweighting is based on 5) constant weights relating to (6) with no covariates (IPW (asc.,cw)), 6) logistic regression weights including all covariates (IPW (asc.,lw)) and 7) Bayesian model averaging weights (IPW (asc.,maw)) respectively.

For those observations that are lost to follow-up, levels of outcome ascertainment correspond to A = 10%, 20%, …, 90% respectively. All results are based on 1000 simulation runs.

4.2. Results

On average 21% of observations are LTFU. Of those not LTFU 14% experience an event (e.g. death) compared to 48% in the LTFU population.

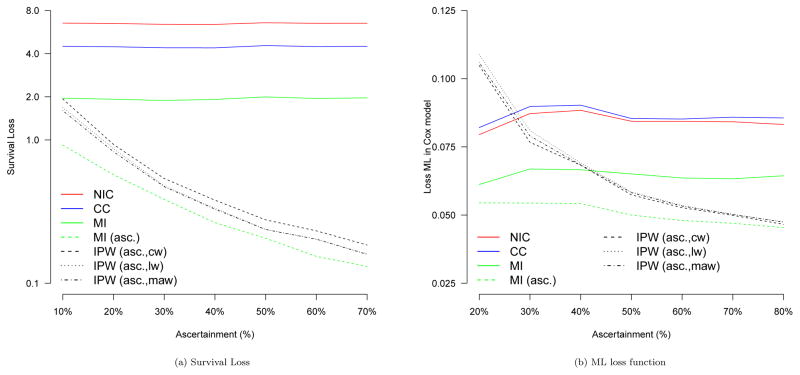
To compare the different approaches we first calculate the average squared survival loss between the true median survival time T₅₀ and the predicted survival T̂_50,s of the Kaplan-Meier curve corresponding to strategy s, that is ${\text{SL}}_s={\mathcal{R}}^{-1}{\sum }_{r=1}^R{(T_{50,r}-{\widehat{T}}_{50,r,s})}^2$. The results are presented in Figure 2a and indicate that the Kaplan-Meier estimates are, as expected, worst for the strategy of non-informative censoring, followed by using only complete cases and multiple imputation before including ascertained data. All strategies that up-weight ascertained observations yield improvement when compared to the aforementioned three approaches. There are gains when using regression-based weights compared to simple constant weights. For low ascertainment there are also modest gains in using model averaging compared to simple logistic regression. Overall, the best results are obtained when using multiple imputation after including ascertainment data.

Figure 2.

Simulation results for 7 different strategies: Non-informative censoring (NIC), complete case analysis (CC), multiple imputation before ascertainment (MI), multiple imputation after ascertainment (MI (asc.)), IPW estimates after ascertainment with constant weights (IPW (asc,cw)), logistic regression based weights (IPW (asc,lw), and Bayesian model averaging weights (IPW (asc,maw)). Levels of ascertainment relate to the percentage of missing outcome information that was ascertained.

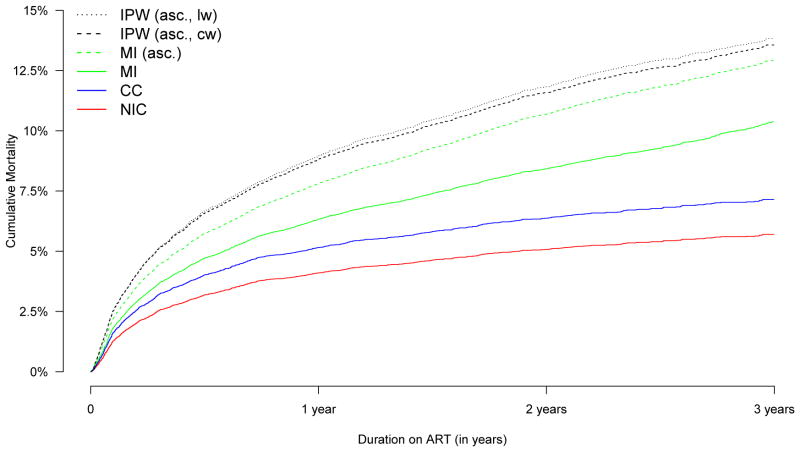
We now compare the regression coefficients in a Cox model including all five covariates. For this purpose we define the loss function for strategy s as ${\text{ML}}_s={\mathcal{R}}^{-1}{\sum }_{r=1}^R{\sum }_{j=1}^5{({\widehat{\beta }}_{j,r,s}-{\beta }_{j,r,\text{true}})}^2$ which one may interpret as a MSE-summary of all regression coefficients. The results are summarized in Figure 2b.

As expected, the higher the outcome ascertainment, the better the Cox regression estimates of the methods that incorporate ascertainment data. For example, in the current simulation setting 30% ascertainment is needed for the IPW estimators to outperform complete cases and non-informative censoring approaches and more than 40% to clearly outperform multiple imputation with respect to the loss function ML. Low levels of ascertainment provide rather poor IPW-based performance as only a small subsample of outcome-covariate combinations is used for the upweighting process. However, in a real data analysis these numbers might be different, and a smaller percentage of ascertained outcome information might guarantee good regression results if the ascertained subjects adequately reflect the associational relationship one is modeling, see also Section 5 for more insights. It is important to highlight that the best performance was obtained using the multiple imputation procedure which takes the ascertained data into account. Remarkably, even for low ascertainment very good results are obtained.

With respect to the IPW estimators, we note that more detailed analyses we have conducted show that higher ascertainment provides typically more stable and less variable weights and model averaging weights have the highest precision and lowest variability. We did not observe any gains when using generalized additive models for the weight model in the current simulation setting.

4.3. Missing covariate data

We now set values of X₁ and X₄ to be missing. Since the probability of missingness is defined to depend on X₂ and X₃, respectively,

$${\pi }_{X_1}(X_2)=1-\frac{1}{(1+(0.02·(X_2^3))},{\pi }_{X_4}(X_3)=1-\frac{1}{1+exp(1-2·(X_3))}$$

these covariate values are missing at random (MAR). We compare the performance of noninformative censoring (with multiple imputation for X₁ and X₄), complete case analysis (with respect to both X and y), multiple imputation for both the covariates and the outcome, multiple imputation after including ascertainment data, and inverse probability weighting based on logistic regression (IPW (asc.,lw)) and BMA weights (IPW (asc.,maw)). To estimate the weights both multiple imputation (MI) and the strategy of including a ‘missing category’ (MC) are used, see also Section 3.2. The quality of the estimated survival (SL, see above), the quality of Cox regression estimates (ML, see above) and the estimated MSE of the weights are summarized in Table 2 for both 20% and 50% of ascertainment.

Table 2.

Performance of different strategies when dealing with additional missing covariate data: Non-informative censoring (NIC), complete case analysis (CC), multiple imputation before ascertainment (MI), multiple imputation after ascertainment (MI (asc.)), IPW estimates after ascertainment with logistic regression based weights (IPW (asc.,lw)), and Bayesian model averaging weights (IPW (asc.,maw)). Missing covariate data was either multiple imputed (MI) or treated as a separate category (MC) when estimating the weights. Levels of ascertainment relate to the percentage of missing outcome information that was ascertained.

Asc.		IPW (asc.) (lw,MI)	IPW (asc.) (lw,MC)	IPW (asc.) (maw,MI)	IPW (asc.) (maw,MC)	NIC	CC	MI	MI (asc.)
20%	SL	0.8580	0.9230	0.8150	0.8590	6.4900	4.4660	1.9240	0.5720
	ML	0.1100	0.1155	0.1067	0.1052	0.0821	0.2069	0.0612	0.0545
	MSEw	0.7000	0.9200	0.6500	0.8900
50%	SL	0.2370	0.2460	0.2350	0.2390	6.5720	4.5540	1.9960	0.2060
	ML	0.0649	0.0655	0.0641	0.0641	0.0844	0.1994	0.0742	0.0570
	MSEw	0.1600	0.2300	0.1500	0.2100

The missing covariate data introduce additional bias for the complete case analysis, using multiple imputation to estimate the weights typically outperforms the strategy of using a missing category, and model averaging can improve the quality of logistic regression weights in the context of additional missing co-variate data.

5. Application to IeDEA-SA ART data

We now analyze South African ART data as introduced in Section 2. The data consist of 30,901 HIV-infected patients from three cohorts of patients receiving antiretroviral treatment. The outcomes we consider are the time to death and the hazard of death respectively. Possible covariates that influence the hazard of death are gender, age, year of treatment initiation, cohort, baseline weight, and CD4 count (in cells/μL, with categories of 0–25,25–50,50–100,100–200,200+). CD4 count is time-varying and one typically either uses baseline values to predict mortality or all time-varying information if available and relevant. In our main example we focus on the baseline information, but also briefly discuss the implications when including longitudinal CD4 count information. As indicated in Table 1, 21.7% of patients were LTFU and the loss mechanism is expected to be non-ignorable. After linkage to national South African vital registration data the vital status of more than two thirds of lost patients is known. In addition, 13.8% of baseline CD4 values, and 16.1% of baseline weight values are missing.

In line with our simulation study we compare the aforementioned seven different strategies for dealing with patients lost to follow-up. To estimate both the Cox models and the weights for strategy 6) & 7) all covariates are considered and multiple imputation by means of Amelia II (as described in Section 3.2) is applied to missing baseline covariate values of both weight and CD4. The imputation models included both the outcome (follow-up time, death) and all measured covariates as well as and δ if applicable.

Figure 3 shows the Kaplan-Meier curves for the first six approaches. Estimating the IP weights based on model averaging (strategy 7) yields very similar results to estimating the weights based on a simple logistic regression model and hence this curve is not plotted. Mortality estimates are highest for the IPW approaches based on a logistic regression model and Bayesian model averaging (13.8% after 3 years on ART respectively), and lowest for non-informative censoring (5.7%). The second-highest mortality estimate was obtained using the IP approach with constant weights (13.6%), followed by multiple imputation after including ascertainment data (12.9%), multiple imputation before including ascertainment data (10.1%), and complete case analysis (7.1%).

Figure 3.

Kaplan-Meier curves for different strategies: Non-informative censoring (NIC), complete case analysis (CC), multiple imputation before ascertainment (MI), multiple imputation after ascertainment (MI (asc.)), IPW estimates after ascertainment with constant weights (IPW (asc.,cw)), logistic regression based weights (IPW (asc.,lw))

Table 3 presents the results of the Cox regression analysis. Estimates for the effect of age, gender, and weight are generally very similar and there are subtle differences in the estimates for the effect of CD4. While both complete cases and non-informative censoring produce a negative association with year, multiple imputation and all ascertainment methods do not. With regards to the effect of the individual cohorts, estimates differ substantially since the probability of being ascertained varied strongly by cohort (see also Table 1). Complete cases and non-informative censoring based estimates lead to conclusions that the hazard of death is highest in cohort B, followed by cohorts C and A. Using multiple imputation before including ascertainment data the same conclusions would be made but estimates about the differences of the cohorts are much smaller.

Table 3.

Cox Regression estimates after imputation for the seven main strategies: Non-informative censoring (NIC), complete cases (CC), multiple imputation before ascertainment (MI), multiple imputation after ascertainment (MI (asc.)), IPW estimates after ascertainment with constant weights (IPW (asc.,cw)), logistic regression based weights (IPW (asc.,lw)), and model averaging weights (IPW (asc.,maw)). Two further analyses: IPW estimates after ascertainment with logistic regression weights for the longitudinal data (Longit./IPW (asc.,lw)), and the extended dataset (> 3 cohorts/IPW (asc.,lw)).

	CC	NIC	MI	MI (asc.)	IPW (asc.,cw)	IPW (asc.,lw)	IPW (asc.,maw)	Longit./IPW (asc.,lw)	> 3 cohorts/IPW (asc.,lw)
age	1.02 (1.01, 1.03)	1.02 (1.02, 1.03)	1.01 (1.01, 1.02)	1.02 (1.01, 1.02)	1.02 (1.02, 1.02)	1.02 (1.02, 1.02)	1.02 (1.02, 1.02)	1.02 (1.02,1.02)	1.02 (1.02, 1.02)
gender	0.80 (0.71, 0.91)	0.81 (0.73, 0.91)	0.79 (0.69, 0.91)	0.80 (0.74, 0.87)	0.80 (0.75, 0.86)	0.79 (0.73, 0.85)	0.80 (0.74, 0.86)	0.78 (0.72,0.84)	0.76 (0.72, 0.81)
year	0.83 (0.79, 0.87)	0.86 (0.83, 0.90)	0.98 (0.94, 1.03)	1.01 (0.98, 1.05)	1.00 (0.97, 1.03)	1.01 (0.98, 1.04)	1.01 (0.98, 1.05)	1.00 (0.97,1.04)	0.99 (0.97, 1.02)
CD4 (25–50)	0.71 (0.60, 0.83)	0.68 (0.57, 0.81)	0.70 (0.59, 0.83)	0.72 (0.63, 0.82)	0.74 (0.66, 0.83)	0.75 (0.67, 0.84)	0.75 (0.67, 0.84)	0.74 (0.66,0.83)	0.74 (0.68, 0.81)
CD4 (50–100)	0.48 (0.40, 0.56)	0.45 (0.38, 0.52)	0.52 (0.43, 0.63)	0.53 (0.47, 0.60)	0.53 (0.48, 0.58)	0.52 (0.47, 0.58)	0.53 (0.48, 0.59)	0.52 (0.47,0.58)	0.54 (0.49, 0.60)
CD4 (100–200)	0.30 (0.26, 0.36)	0.29 (0.24, 0.33)	0.40 (0.35, 0.44)	0.37 (0.33, 0.42)	0.36 (0.33, 0.40)	0.37 (0.34, 0.41)	0.37 (0.34, 0.41)	0.35 (0.32,0.39)	0.37 (0.34, 0.41)
CD4 (200+)	0.29 (0.22, 0.38)	0.26 (0.20, 0.35)	0.36 (0.29, 0.45)	0.30 (0.25, 0.36)	0.29 (0.24, 0.34)	0.29 (0.25, 0.35)	0.29 (0.24, 0.34)	0.29 (0.25,0.34)	0.30 (0.27, 0.35)
weight	0.96 (0.96, 0.97)	0.96 (0.96, 0.97)	0.97 (0.97, 0.98)	0.97 (0.97, 0.97)	0.97 (0.97, 0.97)	0.97 (0.97, 0.97)	0.97 (0.97, 0.97)	0.97 (0.97,0.97)	0.97 (0.96, 0.97)
cohort B	2.04 (1.68, 2.48)	2.62 (2.21, 3.10)	1.68 (1.44, 1.97)	1.09 (0.96, 1.22)	0.92 (0.82, 1.03)	1.16 (1.04, 1.29)	1.15 (1.03, 1.29)	1.14 (1.02,1.27)	1.04 (0.94, 1.15)
cohort C	1.50 (1.26, 1.79)	1.66 (1.43, 1.94)	1.53 (1.36, 1.72)	0.98 (0.89, 1.08)	0.87 (0.80, 0.95)	1.12 (1.03, 1.22)	1.12 (1.03, 1.22)	1.02 (0.94,1.12)	1.07 (0.99, 1.16)

Using ascertained values with constant IPWs alters the conclusions: The highest effect is found in cohort A. On the contrary, logistic regression-based weights indicate slightly higher mortality for cohorts B and C. Results using inverse probability weights based on Bayesian model averaging produce similar results whereas after using multiple imputation and incorporating linkage data there was no association of the cohorts with mortality at all.

We now discuss two further analyses: First, we repeat the analysis using data from 48,124 patients where only 30,901 patients belong to linkable cohorts and the remainder do not. The probability of being ascertained depends here both on whether or not a patient belongs to a linkable cohort (LC) and if s/he has a civil ID allowing linkage with the death registry (ID). Hence, P(δ_j = 1|R_j = 1, x_j, ϕ) = Pr(ID ∩ LC) = Pr(ID|LC) Pr(LC). By fitting two logistic models, i.e. via strategy 6, we construct inverse probability weights to generate a final Cox regression estimate for all available cohorts, despite the fact that we do not have linkage information for all of them. We assume that the non-linkable cohorts are similar to the linkable cohorts. The results are presented in Table 3 (column ‘> 3 cohorts/IPW (asc.,lw)’).

Second, we calculated an IPW based estimator based on the longitudinal data of the 30901 patients, taking time-varying CD4 data into account. To deal with missing covariate data within the longitudinal follow-up (a patient was expected to have CD4 measurements at least every 6 months) we used multiple imputation by means of the Amelia II R-package to create 5 imputed datasets. This imputation model included again both the outcome and all measured covariates as well as a non-linear time trend. In addition, the imputation algorithm of Amelia II allowed us to account explicitly for the longitudinal structure of the data, see also [46] for more details. The estimation of the weights is based on strategy 6 (IPW (asc.,lw)) and the corresponding logistic model included all available covariates as well as baseline, current and 6 month lagged CD4 information. Results are presented in Table 3. As expected, the estimates are very similar to the results where weights were based just on data available at study entry and duration of follow-up (Table 3, IPW (asc.,lw)) since the cohorts are the main drivers of the probability of being ascertained whereas CD4 data plays a rather minor role.

Furthermore, it is worthwhile to note that all IP weights of the analysis were stable, with reasonable maximal values and variability (logistic regression weights: 2.81 (max.)/0.44 (s.e.); BMA weights: 2.33/0.44; longitudinal data & logistic regression weights: 4.60/0.30; data for 8 cohorts & logistic regression weights: 4.03/0.56).

6. Further Aspects

6.1. Active Tracing of patients

So far we have focused our discussions on cases where patient information is ascertained by large national registries. However, in many studies there are either no resources to facilitate linking to large registries or no national databases with meaningful vital status or other outcome data. Another popular approach in these cases is to ascertain vital information by means of tracing a subsample of lost patients. Approaches that have been applied in a few of these studies upweight patients arithmetically in the context of obtaining simple mortality estimates [18]. This would be a special case of our framework as, referring to θ as a Kaplan-Meier estimate using (6), ϕ₁ = ∅ and ϕ₀ = 1. Typically a random subsample S of lost patients is first selected for tracing and then a tracker ascertains the status of patients for a subsample of the subsample S (FT ≙ Found by Tracker). Hence, the probability of a patient’s status to be ascertained is P(δ_j = 1|R_j = 1, x_j, ϕ) = Pr(FT ∩ S) = Pr(FT |S) Pr(S). This refers to a two-stage weighting procedure where both the probability of being in a subsample and the probability of being found by the tracker have to be modeled and combined appropriately, e.g. by means of the methods proposed in Section 3. Again, geographical information (e.g. by ‘remote-area indicators’) as well as health status are potential predictors for ascertainment in such situations and should be included in the weight models rather than applying simple upweighting. The two-stage approach has the advantage of explicitly considering the potential selection biases at both sample selection and response.

6.2. Possible other outcomes and information about them

In large-scale projects linkage is becoming more and more common. Not only do vital registration systems enable researchers to ascertain patient information, but both national laboratory services and tuberculosis- and cancer registries do as well [50]. In resource-limited settings LTFU is often non-ignorable for these outcomes: Very sick TB or cancer patients may fail to continue care and hence overall morbidity estimates are likely biased. Co-infections likely increase the complexity. The proposed IPW framework may be helpful in correcting estimates in corresponding studies, however it is important to use an appropriate model to describe the ascertainment process. For instance in South Africa patients with a civil identification number (ID) can be linked to national registries, but undocumented persons and refugees living in informal settlements have no ID. These patients may fear presenting to health care providers and become even sicker. Hence, the probability of ascertainment likely depends both on geographic information (e.g. health care facility information) and health related outcomes, and hence covariate information is needed to construct meaningful inverse probability weights. Augmenting our mechanistic understanding of the ascertainment process and associated model specification, generalized additive models, model selection and model averaging are possible approaches that may assist in the construction of appropriate and stable weights.

7. Conclusions

The proposed framework enables researchers to construct inverse probability and multiple imputation based estimators in situations where the missingness mechanism is non-ignorable and a subsample of missing values can be ascertained. We have demonstrated their practical implementation in HIV cohort and related research. Comparisons to other widely used methods for dealing with missing outcome data demonstrate that neglecting non-ignorable loss to follow-up can lead to substantial bias and it is almost inevitable that the collection of additional outcome information is advisable where this is posible. The suggested estimators yield improved overall mortality estimates in our simulations. An important consideration in applying the IPW approach is building a well thought out and robust model to estimate the IP weights.

To our knowledge, this is the first thorough statistical discussion on this topic. A particular strength of our analysis is the inclusion of both simulated and highly relevant real world application examples. Our comparison to alternative approaches gives applied researchers a clear understanding of the potential biases that could result from the correction method chosen, and provides guidance on circumstances under which the proposed estimators may improve the quality of their estimates.

Among the limitations, as with all Monte Carlo experiments, the results we have reported are limited to specific settings and models, and care must be exercised in attempting to generalize our conclusions to cases other than those investigated here. Further, as with all inverse probability based methods, instability of weights can lead to poor estimates in some situations. To address this we explored our approach under different levels of additional outcome ascertainment among patients LTFU. This confirms the need for a reasonably sized subsample of lost patients for linkage or tracing together with correct specification and modeling of the ascertainment mechanism and related weights. Furthermore, we have demonstrated that using multiple imputation after incorporating linkage or tracing data, in conjunction with a well-specified imputation model, is an appealing option to successfully incorporate linkage data in our setting. This approach seems to be more robust than IPW when dealing with low levels of ascertainment.

In conclusion, our example, analyses and discussion demonstrate the need to carefully account for non-ignorable loss to follow-up, especially in the applied context of antiretroviral treatment cohort studies. We proposed a practical framework to address this challenge when a subsample of missing outcome data can be ascertained.