Abstract
Membrane current through voltage-sensitive calcium ion channels at the postsynaptic density of a dendritic spine is investigated. To simulate the ion channels that carry such current and the resulting temporal and spatial distribution of concentration, current, and voltage within the dendritic spine, the immersed boundary method with electrodiffusion is applied. In this simulation method a spatially continuous chemical potential barrier is used to simulate the influence of the membrane on each species of ion. The amplitudes of these barriers can be regulated to simulate channel gating. Here we introduce this methodology in a one-dimensional setting. First, we study the current-voltage relationship obtained with fixed chemical potential barriers. Next, we simulate stochastic ion-channel gating in a calcium channel with multiple subunits, and observe the diffusive wave of calcium entry within the dendritic spine that follows channel opening. This work lays the foundation for future three-dimensional studies of electrodiffusion and advection electrodiffusion in dendritic spines.
Keywords: current-voltage relationship, continuous-time Markov process, the immersed boundary method, electrodiffusion
1. Introduction
Dendritic spines are small protrusions in the dendritic trees of neurons. Many synapses are made onto dendritic spines (Shepherd, 1996), which function as diffusively isolated chemical compartments. Calcium dynamics within dendritic spines are important in learning and memory (Harris and Kater, 1993;Brunig et al., 2004; Sheng and Kim, 2002; Yasuda et al., 2003; Bloodgood and Sabatini, 2007a). The influx of calcium occurs through voltage-sensitive calcium ion channels as well as through NMDA and AMPA receptors (Sabatini and Svoboda, 2000; Bloodgood and Sabatini, 2007b). It is the voltage-sensitive calcium ion channel that is the focus of the present work. These channels are few in number (about 5-20 per spine). Thus, the stochastic opening or closing of any one of these channels is a significant event. Spatial localization of the calcium signal near an open channel is also important. These features of Ca2+ channels are not restricted to dendritic spines, but occur elsewhere, e.g., in the neuronal presynaptic terminal, and in the cardiac diadic cleft (Langer, 1996). Thus, the modeling methodology introduced here may have broad applicability.
Ionic species of importance within dendritic spines include Na+, K+, Cl−, and Ca2+ (Kandel et al., 2000). These four ions will be called “bio-ions” (Eisenberg, 2012, 2013). Each ionic species is transported across the membrane by a specific type of ion channel in a selective way (Hille, 2001). In the present work, ion selectivity is a consequence of an assumed chemical potential barrier across the membrane for each of the different ionic species that may be present. Electroneutrality is explicitly enforced only at the initial time; at later times we observe local electroneutrality as a consequence of the electrodiffusion equations, except in the space charge layers that arise adjacent to membranes (Lee, 2007; Lee et al., 2010).
The modeling described in this paper proceeds in two stages. First, we study the current-voltage relationship of a membrane permeable to Ca2+ in a one-dimenstional setting by applying electric fields to a system comprised of a pair of membranes. We consider the four ionic species mentioned above together with background charge. The initial concentrations are chosen to satisfy electroneutrality, with each species having an (intracellular) concentration between the two membranes different from its (extracellular) concentration in the regions outside of the two membranes. The chemical potential barriers are chosen so that the membranes are permeable to Ca2+ but effectively impermeable to Na+, K+, and Cl−.
The next model employs the same one-dimensional setting as before, with a pair of membranes. This time, however, only one of the two membranes contains a Ca2+ channel, which is voltage-sensitive and stochastic. The opening and closing of the channel are modeled by lowering and raising the height of the chemical potential barrier according to a continuous-time Markov process. The channel has four independent subunits, and three states of inactivation, two of which are related to fast and slow voltage sensitive inactivation, and the other with the inactivation from the intracellular local calcium concentration (Findlay, 2003; Imredy and Yue, 1994; Stotz and Zamponi, 2001; Yue et al., 1990). The channel is open only when all four subunits are in the open state. The transitions between the open and closed states of the subunits are governed by voltage sensitive rate constants, and the transitions to and from inactivated states are governed either by voltage or by calcium concentration (Bondarenko et al., 2004). This model was developed for the L-type calcium channel of the cardiac myocyte; our use of it here is for illustrative purposes only. When detailed kinetic information becomes available for postsynaptic voltage-sensitive calcium channels, it will be a simple matter to substitute those kinetics for the ones used here.
This kind of stochastic ion channel gating modeling has been done previously (Faber et al., 2007; Tanskanen et al., 2005; Geneser et al., 2007). Here, however, we study such stochastic ion channel gating in the context of electrodiffusion. This allows us to study the spatial consequences of stochastic channel gating.
The computer simulation methodology of this paper is based on the immersed boundary method with advection-electrodiffusion (Lee, 2007; Lee et al., 2010); but here the membrane is fixed in place and fluid flows are not considered. The focus is on the temporal and spatial consequences of stochastic ion channel gating, which was not included in our previous papers. However, a significant feature in our approach is that the proposed method can seamlessly extend to the mechanisms of membrane movement such as osmotic volume swelling, cell contraction, and migration.
The paper is organized in the following way; in Section 2, the mathematical formulation of electrodiffusion of ion species, ion-channel gating as a continuous-time Markov process, and the resulting regulation of the chemical potential barriers that model ion-channel selectivity are described. In Section 3, the two stages of modeling (one-dimensional study of the current-voltage relationship of the model calcium ion channel, one-dimensional study of stochastic calcium ion-channel gating) are carried out, and the results are presented. In the appendix, a numerical algorithm for the continuous-time Markov process that governs channel gating is briefly described.
2. Mathermatical Formulation
In this section we consider a fixed one-dimensional computational domain with dissolved ions. Immersed within the domain is a pair of membranes, which are fixed in place. The membranes may be permeable or impermeable to each ion species, the permeability being controlled in a graded manner by its chemical potential barrier. We use the following notation:
Di: diffusion coefficient of the ith ion species
q: the elementary electrical charge (charge on a proton)
qzi: charge of the ith species
KB: Boltzmann constant
T: absolute temperature (degrees in Kelvin)
ε: dielectric constant
ψi(x, t): chemical potential of the ith ion species
Ψw(x): chemical potential kernel with the influence range 4w
Ai(t): contribution of membrane to chemical potential of ith ion species
ci(x, t): concentration of the ith ion species
Fi(x, t): flux per unit area of the ith ion species
φ(x, t): electrical potential
E(x, t): externally applied electrical field
ρ0(x): background electrical charge density
2.1. The chemical potential
The chemical potential is expressed in the following way:
| (1) |
The left and right membranes are placed at positions Xa and Xb. The chemical potential amplitude in each membrane is denoted by and , respectively. The chemical kernel Ψw defines how the contribution Ai(t) is to be spread out in space in the neighborhood of the membrane.
In general, any bell-shaped function with compact support could be used for the chemical potential kernel. Here, we make use of the smoothed Dirac delta function of the immersed boundary method (Peskin, 2002), which is defined as follows:
| (2) |
| (3) |
where w is a scaling factor such that Ψw has a support of width 4w.
2.2. The electrostatic potential: the Poisson equation
The electrical potential is a solution of the Poisson equation:
| (4) |
where ρ0 represents the background electrical charge density. The background charges reside on large molecules such as proteins or nucleic acids, and the net background charge is typically negative. The background charge density is assumed constant intracellularly and constant extracellularly, but these two constants are different. This equation is to be solved on a periodic domain. Because of this it is necessary for the existence of a solution that the integral of the right-hand side over the domain is zero, i.e., that the system as a whole is electrically neutral (even though electroneutrality can be violated locally.) In practice, electroneurality is also satisfied locally to a good approximation except in the space charge layer near the membrane (Lee, 2007). Eq.(4) defines φ uniquely up to an additive constant. The choice of this constant has no significance since only potential difference has physical effects.
For output purposes we define transmembrane voltages Va and Vb, as follows:
| (5) |
| (6) |
where
| (7) |
| (8) |
Here, Δxa is the distance between Xa,L and Xa,R. In the same way, Δxb is the distance between Xb,L and Xb,R. The computational electrode positions of Xa,L, Xa,R, Xb,L, and Xb,R are chosen in a symmetric way with respect to the center line of the dendritic spine. They are outside the domains of the space charge layers and the support of the chemical potential, but close to the membranes. Their sign conventions are chosen so that they measure intracellular potential with respect to extracellular potential, where the space between the two membranes represents the intracellular space, and the rest of the domain represents the extracellular space.
2.3. The electrodiffusion equations
The electrodiffusion equations are formulated in the following way:
| (9) |
| (10) |
and the ionic currents from the electrodiffusion are the following:
| (11) |
Eq.(9) is the conservation law (continuity equation) for the ith species of ion. In this equation ci is the concentration and Fi is the flux per unit area of this ion species. Eq.(10) gives the flux per unit area as a sum of three terms: diffusion, drift caused by chemical potential, and drift caused by the electrical potential and by the externally applied electric field. In Eq.(11), Ii represents the current density (current per unit area) of ith ionic species.
2.4. Continuous-time Markov process for stochastic ion channel gating
For the individual ion channel gating, a continuous-time Markov process is applied (Peskin, 2000). The ion channel is assumed to have 4 independent subunits; each of them has an open and a closed state.
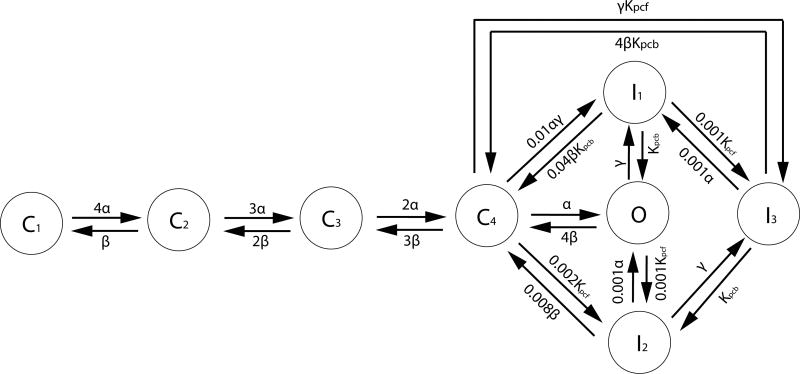
The channel as a whole is open only when all 4 subunits are in the open state, and when the channel is not inactivated. The diagram for the Markov process is presented in Fig.(2). In the discrete states labeled Ci, i — 1 represents the number of subunits in the open state. The state with all 4 subunits open, however, is given the special symbol O. The ion channel is open when all those subunits are open, i.e. when the channel is in the state O.
Figure 2.
Markov chain of calcium ion channel: The calcium ion channel has 4 subunits. In the state Ci, i – 1 subunits are open. In the states Ij, the channel is inactivated and closed. The ion channel is open only in state O. The rate constants for the opening and closing of each subunit are denoted by α and β. Courtesy of Rasmusson et al.(Bondarenko et al., 2004)
The transition between closed and open states of each subunit is expressed as follows:
| (12) |
where CS and OS represent closed and open states of a subunit. The rate constants α and β are functions of membrane voltage Vm. We describe the states of subunits and the ion channel as a whole by the following random variables:
| (13) |
| (14) |
where χs indicates the open/closed state of sth subunit, and S the state of ion channel. When we express the transition probability between open and closed state of each subunit based on Eq.(12),
| (15) |
| (16) |
| (17) |
| (18) |
where α0 = 0.4 ms−1 and β0 = 0.05 ms−1, and where Vm is in mV. Eq.(15) gives the probability that the sth subunit will make a transition from its closed state at time t to its open state at time t+dt in the infinitesimal time interval dt. Similarly, Eq.(16) gives the probability that the sth subunit will make a transition from its open state at time t to its closed state at time t + dt in the infinitesimal time interval dt.
In the reactions involving the inactivated states (See Fig.(2)), the [Ca2+] dependence and membrane voltage dependence of the reaction rates are given by
| (19) |
| (20) |
that are dependent on intracellular calcium concentration [Ca2+]i or membrane voltage Vm, and is 13.0 ms−1. The maximum rate constant, Kpc,max is 0.23324 ms−1, and the half-saturation constant, Kpc,half is 20.0μM for Ca2+ induced inactivation. In the transitions from I1 → O and I1 → C4 in Fig.(2), Kpcb is the voltage-insensitive rate constant for recovery from inactivation, 0.0005 ms−1. The numerical algorithm for the ion channel gating is described in the Appendix.
2.5. Connection between the channel model and the electrodiffusion model
In one of the two studies reported here (see Results), we put a channel of the type described above in the left membrane (denoted by the subscript “a”) of the two-membrane one-dimensional electrodiffusion simulation. Such a channel feels a membrane potential Vm that is equal to Va, as defined by Eq.(5), and its intracellular calcium concentration [Ca2+]i is the calcium concentration of the electrodiffusion simulation evaluated at Xa,R (see Eq.(7)), that is, on the right (intracellular) side of the left membrane. The output of the channel model is its state, S, and this controls the amplitude of the chemical potential barrier in the following simple way:
| (21) |
where is high enough that the membrane is essentially impermeable to calcium, and is low enough that significant calcium flux can occur.
3. Results and Discussion
Two different studies are reported here. Both are one-dimensional and are conducted on a periodic domain of length 4 microns, discretized by 512 equally spaced grid points. The model dendritic spine is centered within the domain and is bounded by two membranes which are 1.88 microns apart. We call these the “left” and “right” membranes of the model dendritic spine. The space between the membranes is intracellular, and the rest of the domain is extracellular.
In the first study, we investigate the current-voltage of Ca2+ with fixed chemical potential barriers. In this study, the two membranes are identical, and the chemical potential barriers for all ions other than Ca2+ are set high enough that essentially all of the transmembrane current is carried by Ca2+.
In the second study, we put a Ca2+ channel of the type described in Sec 2.4 in the left membrane only, and we set the chemical potential barriers to Cl− at a low enough level that both membranes have significant Cl− permeability. The remaining chemical potential barriers are set high enough that both membranes are effectively impermeable to Na+ and K+ ions, and the right membrane is effectively impermeable to Ca2+ ions (as is the left membrane when the Ca2+ channel in the left membrane is closed). We do, however, transiently lower the chemical potential barrier to Na+ in both membranes in order to produce a voltage change that may (or may not, since the channel is stochastic) initiate Ca2+ channel opening.
3.1. Current-voltage relationship of Ca2+ with fixed chemical potential barriers
We consider four bio-ions, each with a different concentration between the two membranes from its concentration in the regions outside the two membranes. The initial concentrations are shown in Table 1. Note that there is fixed negative background charge in each compartment. The symbol X− in the table denotes these background charges. Electrodiffusion is applied to all four ionic species, in the presence of the background charges.
Table 1.
Initial concentrations in all simulations. X− denotes fixed background charge and the concentrations stated for X− refer to the concentration of background charges, not the concentration of the molecules that carry the background charges.
| Ion species | exterior concentration | interior concentration |
|---|---|---|
|
| ||
| Ca2+ | 2.0mM | 0.0002 mM |
| Cl− | 150mM | 13mM |
| Na+ | 150mM | 15mM |
| K+ | 5mM | 100mM |
| X− | 9mM | 102.0004 mM |
In order to study Ca2+-selective ion channels, we assign a low chemical potential barrier (0.15 KBT) to Ca2+ and a high chemical potential barrier (52.5 KBT) to each of the other ions, in both membranes. In real life, the height, and perhaps also the shape, of each chemical potential barrier might well depend on the concentrations of the different ions in the intracellular and extracellular domains, but we do not consider such complications here. We allow the height of a chemical potential barrier to change to simulate gating, but we assume that the chemical potential profile of the channel in any given state of its gating variables is fixed.
An electric field is applied to drive a current through the system. Note that the two membranes are identical and that the steady-state currents through both of them are necessarily the same. One of their currents, however, flows from the extracellular to the intracellular space and the other from intracellular to extracellular. Therefore, in any one simulation, we get two data points on the current-voltage relation of the membrane, one corresponding to the current I, and the other to -I. In this way, we can determine the entire current-voltage relationship merely by considering applied electric fields of one sign.
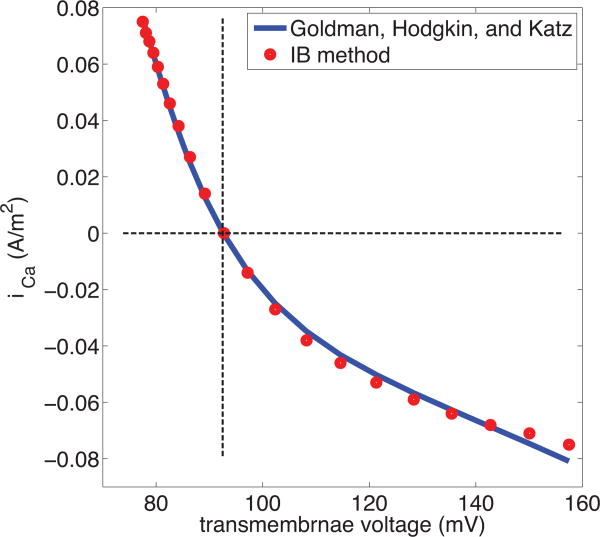
The nonlinear relation between membrane voltage and current obtained from our simulation is shown in Fig.(3), where it is compared to the result predicted by the Goldman-Hodgkin-Katz (GHK) formula:
Figure 3. Current-voltage relationship of Ca2+with fixed chemical potentials.
The configuration of the simulation is described in the text. It involves two identical membranes, with an intracellular space between them, and an extracellular space external to them both. A uniform electric field drives current through the system. Since the two membranes face in opposite directions, the steady-state current has the same magnitude but opposite sign as measured through each of the membranes, thus providing two data points (red circles) on the current-voltage relationship. Transmembrane current is here considered positive when it flows from the extracellular to the intracellular space, and transmembrane voltage is measured as the voltage on the intracellular side of the membrane minus the voltage on the extracellular side. The blue curve is the prediction of the Goldman-Hodgkin-Katz formula. The horizontal line indicates zero current, and the vertical line indicates the transmembrane voltage (Nernst potential) at which zero current is expected to occur.
| (22) |
In this formula, the ionic current I is expressed as a function of the concentration of the permeant ion outside of the membrane cout, its concentration inside of the membrane cin, and the membrane voltage Vm.
In applying the GHK formula to our data we evalulate all three variables (Vm, cout, cin) for each applied electric field at the positions of the electrodes, which are placed close to the membrane but outside the space charge layers, as discussed above. The constant α, which merely scales the current is chosen to get a best fit to the slope of the current-voltage relationship (i.e. to the conduntance of the channel) at I=0.
The special case of zero current, which is obtained in our setup by setting the applied electric field E=0, is of particular interest, since the membrane voltage in this case is predicted by thermodynamics to be given the Nernst equation:
| (23) |
The Nernst equation Eq.(23) is easily derived from the GHK formula Eq.(22) by setting I=0, but it is important to remark that the Nernst equation actually holds under much more general condition than the GHK equation, since it is thermodynamically derived and does not depend on any specific mechanism of ion transport. Note in Fig.(3) that our computational results are in quantitative agreement with both the Nernst equation and the GHK equation. Note that we are here simulating only the current-voltage relationship of an open channel, in the absence of gating. Even with that restriction, we do not expect that the GHK theory will be applicable to all channels. In particular, we do not expect it to apply to situations in which there are binding sites within the channel that can become saturated by the permeant ions. Nevertheless, it is of interest to know that our model does reproduce the textbook nonlinear current-voltage relationship of the simplest kind of ion channel, including the concentration dependence of that current-voltage relationship.
3.2. Stochastic ion channel gating
Here we consider the same configuration of two membranes separating an intracellular space from an extracellular space as before, and also the same four ion species. In this case, however, the membranes are almost impermeable (in their resting states) to Ca2+, Na+, and K+, with a chemical potential barrier height of 40KBT, and the membranes are somewhat permeable to Cl−, with a chemical potential barrier height of 8.0KBT.
In the left membrane only, we incorporate a calcium channel, the dynamics of which is described in Section 2.4. When the channel is open, the chemical potential barrier height for Ca2+ is lowered to 16KBT.
Two different timestep durations are used in this simulation: Δt = 3 ns for the electrodiffusion process and Δt = 15μs for the Markov chain simulation of the calcium channel. Thus, each random update of the channel state is followed by 5000 time steps of electrodiffusion with the channel state held constant while the spatial profiles of the ionic concentration and of the electrical potential evolve.
We manipulate the membrane potential to induce calcium channel opening by temporarily lowering the chemical potential barrier for Na+ on both membranes to 0.8KBT. This is done during the time interval from t=0.75 ms to t=3.75 ms.
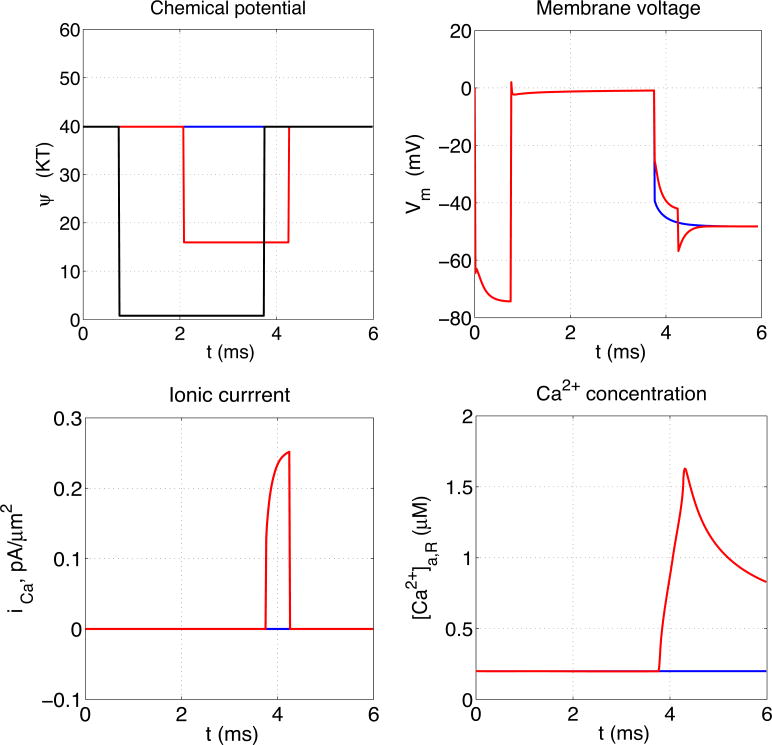
As a result of this increase in Na+ permeability, both membranes depolarize; their transmembrane potentials change from about -70 mV to nearly 0 mV. This depolarization lasts as long as the increase in Na+ permeability, i.e. for about 3 ms. During this time, the calcium channel, which is located in the left membrane, may or may not open. An example of each possibility is shown in Figure 4. In the case that the calcium channel does open, the temporal progression of calcium wave is shown in Figure 5.
Figure 4.
Stochastic calcium channel gating. Upper left panel shows chemical potential barriers for Na+ (black) and Ca2+ (blue if channel did not open, red if it did) as functions of time. The Na+ channel barrier height as a function of time is prescribed, and is the same in both cases, but the Ca2+ channel opening and closing follows the stochastic process described in the text. The remaining panels show the resulting transmembrane potentials (upper right), transmembrane Ca2+ currents, and Ca2+ concentrations measured at the site Xa,R, which is near the membrane containing the calcium channel and on its intracellular side, all as functions of time, with the same color code as in the upper left panel. Note in particular that the onset of significant transmembrane Ca2+ current (red curve in the lower left panel) is delayed following channel opening (downward step of red curve in upper left panel) until the membrane repolarizes (downward movement of red curve in upper right panel) because of closure of the Na+ channels (upward step of the black curve in the upper left panel).
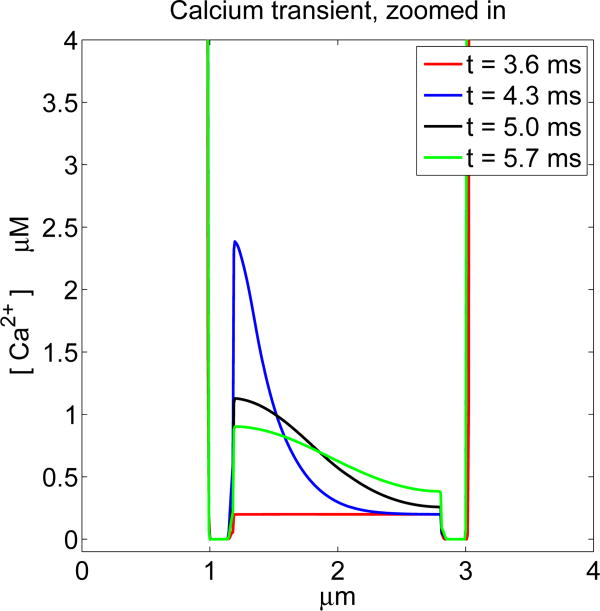
Figure 5.
Ca2+ concentration at selected times for a case in which the Ca2+ channel opens. The times shown are t = 3.6, 4.3, 5.0, 5.7 ms. The calcium channel opens at t = 2.07 ms and closes at t = 4.26 ms, but significant Ca2+ current does not begin to flow until the membrane repolarizes at t = 3.75 ms. Note the wave of intracellular Ca2+ concentration that progresses from left to right. The extracellular Ca2+ concentration is much too large to be seen on the scale of this plot.
In the case in which the channel does open, note in particular the delay between channel opening and the onset of significant Ca2+ current. Even though the channel is open, significant Ca2+ current does not flow through it until the transmembrane voltage has returned to near resting levels after the Na+ permeability is turned off. This is because a negative intracellular potential is much more favorable to the inflow of Ca2+ ions than the depolarized near-zero potential that caused the channel to open. This same phenomenon occurs naturally in the presynaptic terminal of neurons, where it has the result that Ca2+ inflow, and hence the release of neurotransmitter, occurs on the downstroke of the action potential, hence the synaptic delay (Sabatini and Regehr, 1996).
4. Conclusions
In three-dimensional simulations, boundary conditions on immersed interfaces of arbitrary (and especially time-dependent) geometry are complicated to impose. The task is simplified if the boundary conditions can be incorporated into the equations that hold away from the boundaries, so that a uniform system of equations is solved everywhere. This is the philosophy of the immersed boundary method (Peskin, 2002), which we apply here to electrodiffusion. In the present context, we replace interface conditions by spatially continuous chemical potential barriers that have the same physical effect.
In the present paper, we try out this methodology in a one-dimensional setting. The goal is to see whether we can construct chemical potential barriers that simulate membrane physiology. This is accomplished in two examples, one involving fixed chemical potential barriers, and another involving chemical potential barriers with heights that change in a stochastic manner. In the first case, we find that we can reproduce the Goldman-Hodgkin-Katz (GHK) current-voltage relationship, and in the second we find qualitatively reasonable behavior for a voltage-sensitive calcium channel.
Although the motivation for this work comes from the dendritic spine, there are several steps of future work needed before we can claim applicability to dendritic spine physiology. One of these is to step up from one dimension to three, and to simulate the actual morphology of dendritic spines. Another is to model the several different types of channels that actually occur in dendritic spine membranes, including Na+ and K+ channels, and neurotransmitter-gated calcium channels in addition to the voltage-gated calcium channel considered here. For channels whose instantaneous current-voltage relationships are not of the GHK type, it will be necessary to consider other chemical potential profiles besides the simple bell-shaped one that is used in the paper, or perhaps to allow for reversible ionic binding sites within the model channel. Finally, it will be important to model the shape changes of dendritic spines that are a consequence of the calcium inflow. Fortunately, the immersed boundary approach makes it possible to do this in a seamless way. Thus, the present paper should be regarded as a small but important preliminary step towards the realistic modeling of the electromechanical activity of dendritic spines, or indeed of other similarly small electrophysiological systems in which space charge layers need to be resolved, ion concentration changes are important, and electrodiffusion plays an important role.
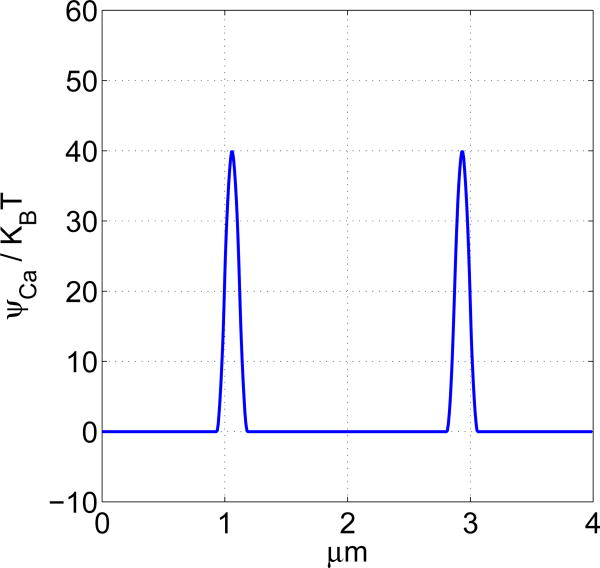
Figure 1. Chemcal potential distribution as a function of position.
The support of the chemical potential kernel is 0.0625μm. In this example, the height of each of the two chemical potential barriers is 40KBT. These heights can be stochastically regulated to simulate gating.
Acknowledgments
EAS and CSP were supported in part by the Systems Biology Center New York (NIH grant P50GM071558).
Appendix
The numerical algorithm for the continuous-time Markov process in the ion channel gating is based on the following transition probability.
| (24) |
where S(t) is the ion channel state at time t. The rate constant ri,j is the probability per unit time of the transition from state Si to Sj. In principle, Eq.(24) applies only to infinitesimal dt, that is, one should divide by dt and then let dt → 0 to get a mathematically correct statement. In practice, one gets an accurate result if dt is small enough that ri,jdt « 1 for all (i,j).
| {S = 1,2, …, Nstates} |
| {rates(j,k) = rate constant for j → k, rates(j,j) = 0} |
| for clock=1:clockmax do |
| t = clock * dt |
| rates = updaterates(S, rates) |
| {updaterates(S, rates) updates row S of the matrix rates, since that is the only row that will be used in the current time step} |
| ratesum = sum(rates(S, :)) |
| if rand < ratesum * dt then |
| cp = cumsum(rates(S,:) / ratesum) |
| {cumulative summation of the rates in the state S and its normalization} |
| r = rand {random number between 0 and 1 with uniform distribution} |
| forS = 1:Nstates do |
| if r < cp(S) then |
| break |
| end if |
| end for |
| end if |
| end for |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Shepherd GM. The Dendritic Spine: A Multifunctional Integrative Unit. J Neurophysiol. 1996;75:2197–2210. doi: 10.1152/jn.1996.75.6.2197. [DOI] [PubMed] [Google Scholar]
- Harris KM, Kater SB. Dendritic Spines: Cellular Specializations Imparting Both Stability and Flexibility to Synaptic Function. Annu Rev Neurosci. 1993;17:341–371. doi: 10.1146/annurev.ne.17.030194.002013. [DOI] [PubMed] [Google Scholar]
- Brunig I, Kaech S, Brinkhaus H, Oertner TG, Matus A. Influx of Extracellular Calcium Regulates Actindependent Morphological Plasticity in Dendritic Spines. Neuropharmacology. 2004;47:669–676. doi: 10.1016/j.neuropharm.2004.07.038. [DOI] [PubMed] [Google Scholar]
- Sheng M, Kim M. Postsynaptic Signaling and Plasticity Mechanisms. Science. 2002;298:776–780. doi: 10.1126/science.1075333. [DOI] [PubMed] [Google Scholar]
- Yasuda R, Sabatini BL, Svoboda K. Plasticity of Calcium Channels in Dendritic Spines. Nat Neurosci. 2003;6:948–955. doi: 10.1038/nn1112. [DOI] [PubMed] [Google Scholar]
- Sabatini BL, Svoboda K. Analysis of Calcium Channels in Single Spines Using Optical Fluctuation Analysis. Nature. 2000;408:589–593. doi: 10.1038/35046076. [DOI] [PubMed] [Google Scholar]
- Bloodgood BL, Sabatini BL. Ca2+Signalling in Dendritic Spines. Curr Opin Neurobiol. 2007b;17:345–351. doi: 10.1016/j.conb.2007.04.003. [DOI] [PubMed] [Google Scholar]
- Bloodgood BL, Sabatini BL. Nonlinear Regulation of Unitary Synpatic Signals by CaV2.3 Voltage-Sensitive Calcium Channels Located in Dendritic Spines. Neuron. 2007a;53:249–260. doi: 10.1016/j.neuron.2006.12.017. [DOI] [PubMed] [Google Scholar]
- Peskin CS. Lecture Note, Courant Institute of Mathematical Sciences. New York University; 2000. Mathematical Aspects of Neurophysiology. [Google Scholar]
- Peskin CS. The Immersed Boundary Method. Act Num. 2002;11:479–517. [Google Scholar]
- Lee P. Ph D thesis, Courant Institute of Mathematical Sciences. New York University; 2007. The Immersed Boundary Method with Advection-Electrodiffusion. [Google Scholar]
- Lee P, Griffith BE, Peskin CS. The Immersed Boundary Method for Advection-Electrodiffusion with Implicit Timestepping and Local Mesh Refinement. J Comp Phys. 2010;229:5208–5227. doi: 10.1016/j.jcp.2010.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandel ER, Schwartz JH, Jessel TM. Principles of Neural Science. 4 McGraw-Hill Medical; 2000. [Google Scholar]
- Hille B. Ion Channels of Excitable Membranes. 3 Sinauer Associates; 2001. [Google Scholar]
- Faber GM, Silva J, Livshitz L, Rudy Y. Kinetic Properties of Cardiac L-type Ca2+ Channel and Its Role in Myocyte Electrophysiology: a Theoretical Investigation. Biophys J. 2007;92:1522–1543. doi: 10.1529/biophysj.106.088807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanskanen AJ, Greenstein JL, O'Rourke B, Winslow RL. The Role of Stochastic and Modal Gating of Cardiac L-Type Ca2+ Channels on Early After-Depolarizations. Biophys J. 2005;88:85–95. doi: 10.1529/biophysj.104.051508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geneser SE, Kirby RM, Xiu D, Sachse FB. Stochastic Markovian Modeling of Electrophysiology of Ion Channels: Reconstruction of Standard Deviations in Macroscopic Current. J Theor Biol. 2007;245:627–637. doi: 10.1016/j.jtbi.2006.10.016. [DOI] [PubMed] [Google Scholar]
- Bondarenko VE, Szigeti GP, Bett GCL, Kim SJ, Rasmusson RL. Computer Model of Action Potential of Mouse Ventricular Myocytes. Am J Physiol Heart Circ Physiol. 2004;287:H1378–H1403. doi: 10.1152/ajpheart.00185.2003. [DOI] [PubMed] [Google Scholar]
- Findlay I. Physiological Modulation of Inactivation in L-type Ca2+ Channels: One Switch. J Physiol. 2003;554:275–283. doi: 10.1113/jphysiol.2003.047902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imredy JP, Yue DT. Mechanism of Ca2+-Sensitive Inactivation of L-type Ca2+ Channels. Neuron. 1994;12:1301–1318. doi: 10.1016/0896-6273(94)90446-4. [DOI] [PubMed] [Google Scholar]
- Stotz SC, Zamponi GW. Structural Determinants of Fast Inactivation of High Voltage-Activated Ca2+Channels. Trends Neurosci. 2001;24:176–181. doi: 10.1016/s0166-2236(00)01738-0. [DOI] [PubMed] [Google Scholar]
- Yue DT, Backx PH, Imredy JP. Calcium-Sensitive Inactivation in the Gating of Single Calcium Channels. Science. 1990;250:1735–1738. doi: 10.1126/science.2176745. [DOI] [PubMed] [Google Scholar]
- Sabatini BL, Regehr WG. Timing of Neurotransmission at Fast Synapses in the Mammalian Brain. Nature. 1996;384:170–172. doi: 10.1038/384170a0. [DOI] [PubMed] [Google Scholar]
- Eisenberg B. A Leading Role for Mathematics in the Study of Ionic Solutions. SIAM News. 2012;45:11–12. [Google Scholar]
- Eisenberg B. Ionic Interactions in Biological and Chemical Systems: a Variational Approach. Trans Faraday Soc. 2013;160:279–296. doi: 10.1039/c2fd20066j. [DOI] [PubMed] [Google Scholar]
- Langer GA, Peskoff A. Calcium Concentration and Movement in the Diadic Cleft Space of the Cardiac Ventricular Cell. Biophys J. 1996;70:1169–1182. doi: 10.1016/S0006-3495(96)79677-7. [DOI] [PMC free article] [PubMed] [Google Scholar]