Genomic prediction in CIMMYT maize and wheat breeding programs

Abstract

Genomic selection (GS) has been implemented in animal and plant species, and is regarded as a useful tool for accelerating genetic gains. Varying levels of genomic prediction accuracy have been obtained in plants, depending on the prediction problem assessed and on several other factors, such as trait heritability, the relationship between the individuals to be predicted and those used to train the models for prediction, number of markers, sample size and genotype × environment interaction (GE). The main objective of this article is to describe the results of genomic prediction in International Maize and Wheat Improvement Center's (CIMMYT's) maize and wheat breeding programs, from the initial assessment of the predictive ability of different models using pedigree and marker information to the present, when methods for implementing GS in practical global maize and wheat breeding programs are being studied and investigated. Results show that pedigree (population structure) accounts for a sizeable proportion of the prediction accuracy when a global population is the prediction problem to be assessed. However, when the prediction uses unrelated populations to train the prediction equations, prediction accuracy becomes negligible. When genomic prediction includes modeling GE, an increase in prediction accuracy can be achieved by borrowing information from correlated environments. Several questions on how to incorporate GS into CIMMYT's maize and wheat programs remain unanswered and subject to further investigation, for example, prediction within and between related bi-parental crosses. Further research on the quantification of breeding value components for GS in plant breeding populations is required.

Introduction

In plants, quantitative trait locus (QTL) mapping was initiated more than 20 years ago (Bernardo, 2008) and has been used very successfully in the genetic analysis of several non-complex traits and, in particular, of abiotic and biotic stress tolerance traits where much of the genetic variance is conditioned by one or a few loci. This has led to the wide-scale deployment in farmers' fields of alleles that confer resistance to submergence and salinity in rice and fungal leaf diseases in wheat and maize, and to identifying and mobilizing alleles with large effects. However, exploiting QTL for more complex traits to predict candidates for selection in practical breeding programs has had limited impact because, among other factors, of the small genetic variance accounted for by QTL owing to the model being used, and because many detected QTLs are specific to a particular genetic background.

With high-density single-nucleotide polymorphism (SNP) markers, it is possible to use multi-locus linkage disequilibrium (LD) between QTLs and markers across the whole genome to predict genetic values that can be used in predictive genomic selection (GS) methodologies. As first proposed by Meuwissen et al. (2001), breeding values can be predicted as the sum of all marker effects by regressing phenotypic values on all available markers. In animals, the first to implement GS was the US dairy industry (vanRaden, 2007; VanRaden et al., 2008); later Hayes et al. (2009) and Goddard and Hayes (2009) successfully implemented GS in other animal species. Daetwyler et al. (2008) showed how to use genomic prediction for analyzing the genetic risk of human diseases, and Bernardo and Yu (2007), Lorenzana and Bernardo (2009) and Heffner et al. (2011) showed promising results of GS in plants.

In plants, several authors have used breeding data with individuals genotyped with intermediate- to high-density markers to show that traits such as grain yield, biomass yield, disease resistance and flowering evaluated under different environmental conditions can be predicted with varying levels of accuracy depending on, among other factors, the heritability of the trait, the size of the training population, the number of markers, the relationship between the training and testing sets, and genotype × environment interaction (GE) (de los Campos et al., 2009; Crossa et al., 2010, 2011; Pérez et al., 2010, 2012; Burgueño et al., 2012; Gonzalez-Camacho et al., 2012; Hickey et al., 2012; Riedelsheimer et al., 2012; Windhausen et al., 2012; Zhao et al., 2012).

The main results of most prediction studies carried out on maize and wheat trials at International Maize and Wheat Improvement Center (CIMMYT) show that when the aim is to predict the genetic values of individuals in a population (with unknown subpopulations), the use of intermediate- to high-density markers, along with pedigree information, produces diverse prediction accuracy of the genetic values of unobserved individuals, with pedigree accounting for a large proportion of predictive ability. Pedigree (when available) is the baseline model that considers family links (or breeders' structures) and, when used together with marker information, increases the prediction accuracy for all traits most of the time.

General findings of CIMMYT studies show that the accuracy of genotype imputation from low- to high-marker density is high for large training sets and for individuals who have close relatives in the training set even if the training set is relatively small; this offers a valuable economic option for imputing high-density markers to large sample populations from small sample populations that were genotyped with high-density markers. However, prediction accuracy between genetically unrelated populations (or families) is low, when using any marker density; likewise, when heritability is low, genomic information does not help prediction accuracy.

In terms of the algorithms used to make predictions in CIMMYT trials, no one prediction model fits all situations (trait–environment combinations), yet empirical evidence shows that models that include nonlinear functions of the markers, when used on complex traits (that is, grain yield), tend to increase prediction ability as compared with linear models. For less complex traits that are predominantly additive (that is, male and female flowering in maize and resistance to rust diseases in wheat), linear models gave the best prediction accuracy.

In a recent article using data from a highly structured CIMMYT maize population, Windhausen et al. (2012) showed that when predicting between unrelated subpopulations, accuracy was close to zero, and that almost all cross-validation accuracy achieved by marker-based prediction was essentially the result of assigning lines to subpopulations with differing trait means; identical accuracies were obtained when prediction was simply based on breeder knowledge of structural groupings, rather than on marker-based prediction. Windhausen et al. (2012) discussed several possible applications of GS to maize breeding programs, that is, prediction within progenies of the same cross and prediction of progenies of different crosses. Prediction within the same cross implies training and validating within, for example, F₂ individuals or doubled haploids or advanced inbred lines (that is, F₆) derived from one cross for which phenotyping in multi-environment trials is more expensive than genotyping. Another prediction problem that usually arises in practical breeding is predicting individuals within and between different crosses, that is, within and between F₂ individuals (or their doubled haploids). It is expected that factors such as the degree of relatedness of individuals between crosses, and whether the LD between markers and QTL is stable across different crosses, will affect the prediction accuracy between crosses.

A similar structural paradigm should be considered for genomic prediction in multi-environment plant breeding trials. GE produces environments that are structured into related or unrelated subsets that may increase or decrease prediction ability. In plants, prediction accuracy has been estimated by evaluating training and validation sets in single environments or in a subset of similar environments (within optimum or drought environments). Burgueño et al. (2012) studied the effect of modeling GE (or not) on genomic prediction ability when using marker and pedigree information. They found that multi-environment models benefit from borrowing information from correlated environments and from using information regarding pedigree and genetic markers. Thus, when the environmental structure (GE) was modeled, this increased the prediction ability of unobserved individuals by about 20% with respect to the single-environment prediction model. Windhausen et al. (2012) indicated that the impact on prediction accuracy of environmental structure in combination with population structure should be considered for further research.

Two basic applications of GS are being studied in CIMMYT's global maize and wheat breeding programs. One application consists of predicting the genotypic values of individuals for potential release as cultivars. In this application, both additive and non-additive effects are important for determining the final commercial value of the maize or wheat lines to be released in the near future. The other application is concerned with predicting the breeding value of candidates in rapid-cycle populations (that is, focusing on the precise prediction of additive effects in the breeding program's early generations).

The main purpose of this article is to describe and summarize the results of genomic prediction in CIMMYT's maize and wheat breeding programs starting from the initial assessment of the predictive ability of different models using pedigree and marker information to the present, when methods for implementing GS in practical global maize and wheat breeding programs are being studied and investigated. The article is organized as follows: first, we briefly summarize the genomic prediction results obtained using several CIMMYT maize and wheat breeding data sets and different models for predicting genetic values of lines in a breeding population in a single environment and/or across environments (drought or optimum). We studied the effect of modeling GE (structuring environments) on the prediction ability of a wheat multi-environment trial using pedigree and marker data. Second, we show the results of predicting between related and/or unrelated populations; predicting between unrelated populations in CIMMYT breeding populations has been unsuccessful. Third, we present prediction ability within two bi-parental F₂ crosses in maize when a small number of lines and markers are considered.

Materials and methods

Models for genomic prediction

The standard linear genetic model considers that the phenotypic response of the ith individual (y_i) is explained by a factor common to all individuals, a genetic factor specific to that individual (g_i) and the residual comprising all other non-genetic factors (ɛ_i), including environmental effects (temporal or spatial) and effects described by the design of the experiment, among others. Thus, the linear genetic model for n genotypes (i=1,...,n) is represented by y_i=g_i+ɛ_i. In this standard linear genetic model, the genetic factor g_i can be described by adding the molecular marker effects or by using pedigree, or both. When g_i is defined as a parametric linear regression on marker covariates x_ij (for example, 0, 1 and 2 for additive effects), then 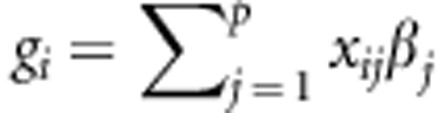, such that

where β_j is the effect of the the jth marker covariate on y_i (Meuwissen et al., 2001) (j=1,2,…p, markers). Assuming that the distribution of the residuals is normal with mean zero and variance 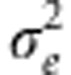, then the likelihood of model (1) is

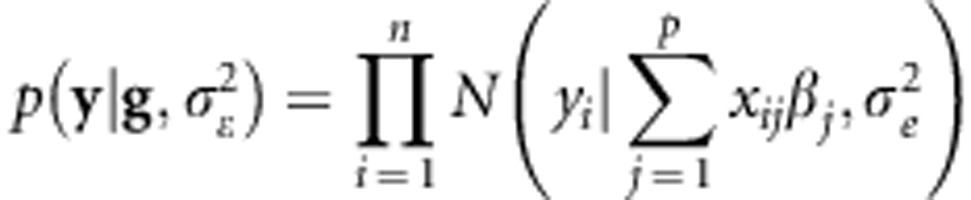where 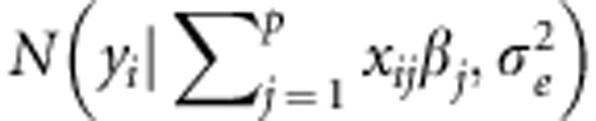denotes a normal density for random variable y_i centered at 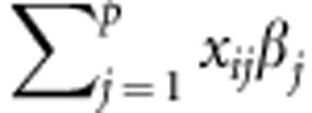and with variance .

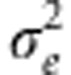The large variation resulting from hundreds of thousands of markers can be controlled by various shrinkage methods that can be formulated in frequentist or Bayesian models. Depending on how priors on the marker effects are assigned, different Bayesian linear regression models can also be derived. We considered models for GS that differ in the information used (pedigree, molecular markers or both) and in the way markers are incorporated into the model. We used parametric linear regression models, for example, the Bayesian LASSO (BL) and the GBLUP, as well as semiparametric nonlinear models, that is, Reproducing Kernel Hilbert space (RKHS) and the Neural Network methods with a Radial Basis Function (RBFNN) and Bayesian regularization. The pedigree model, BL and GBLUP are explained in detail in several articles, for example, de los Campos et al. (2009), Crossa et al. (2010, 2011) and Pérez et al. (2010). The GBLUP models using pedigree and genomic information while modeling GE using factor analytic (FA) model information are described in Burgueño et al. (2012). Detailed descriptions of the nonlinear models RKHS and RBFNN are given in de los Campos et al. (2009), Gonzalez-Camacho et al. (2012) and Pérez et al. (2012). A brief description of these and other models is given in the Appendix.

Models accounting for epistasis

There is concrete proof that the agglomeration of multiple gene × gene interactions (epistasis) having small effects and acting in small epistatic networks is important for explaining the heritability of complex traits in genome-wide association studies (McKinney and Pajewski, 2012). Epistasis networks and methods with connections based on gene × gene interactions can also be integrated for GS using statistical genetic models that consider these network complexities. Evidence from studies conducted at CIMMYT for complex traits, such as grain yield, shows that models that allow for nonlinear components consistently predicted the unobserved individuals better than linear models (Crossa et al., 2010, 2011; Gonzalez-Camacho et al., 2012; Pérez et al., 2012). In principle, epistasis can be incorporated when the number of markers is large, but the large number of epistatic effects (two-locus interaction) makes their use unfeasible. The RKHS regression approach and the RBFNN implicitly map marker effects into a high-dimensional feature space that utilizes non-additive genetic effects. Recently, Wang et al. (2012) developed an approach for incorporating the large number of markers used in GS into the adaptive mixed LASSO (Wang et al., 2011), which accounts for two-locus epistasis effects for predicting genetic values.

In a recent study, González-Camacho et al. (2012) analyzed real and simulated data by Zhang and Xu (2005). Simulated data have a sample size of 600 individuals and a genome with only a single chromosome (1800 cm long) and 121 evenly spaced markers with a 15 cm per marker interval. The authors simulated 9 main QTL effects and 13 interactions between different QTL effects; all QTL effects overlapped with markers. Each QTL made a contribution to phenotypic variance that varied from 0.5 to 20%. Results show that the prediction ability of RKHS and RBFNN was superior to that of the BL, indicating that RKHS and RBFNN are able to capture patterns (for example, gene × gene effects) that cannot be captured by a linear model. When marker main effects and two-marker interactions were fitted, the performance of the linear model increased sharply and that of the semiparametric methods decreased, indicating that, for nonlinear models, information on gene × gene interaction incorporated into the input space becomes redundant in the feature space, whereas for the linear models, information on gene × gene interaction incorporated in the input space is useful for predicting the feature space. The linear model was able to detect this via estimates of regression coefficients that weigh the contribution of each marker to the estimated conditional expectation. On the other hand, in both RBFNN and RKHS, each marker gets a similar weight in the basis function or kernel, and the effect of adding non-signal covariates reduces method performance.

Assessing the models' predictive ability

The predictive ability of the models was computed as a Pearson correlation between predicted and observed values. Commonly, phenotypic and genotypic data comprise inbred lines that are either breeders' candidates for selection or segregating populations at different levels of inbreeding. Phenotypic data may include candidates for selection from different years tested in different environments.

Two types of partition designs were used for the data sets (training and testing sets). The first partition design considered a cross-validation that divides the data into a training sample and a validation sample or testing set. The models are fitted using the training sample, and the fitted models are used to predict outcomes in the validation sample. Here, the data set is divided into k groups; this is done by assigning observations {i=1,..,n} to k disjoint sets {S₁,...,S_k}. Each of these sets can then be used to measure predictive ability. For example, using the first set, the data can be divided so that the training set contains all the observations in {S₂,...,S_k}, and the testing set those in S₁. Subsequently, models are fitted using data in {S₂,...,S_k}, and the fitted models are used to obtain predictions for observations in {S₁}, that is, {ŷ_i: i∈S₁}. Repeating this exercise for the second, third,.., kth sets yields a whole set of CV predictions 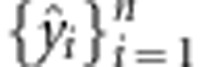that can be compared with actual observations 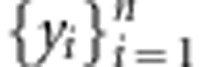to assess predictive ability. In general, we used a 10-fold cross-validation scheme.

In addition to using a k-fold cross-validation partition layout, we used a second partition design for splitting the data into training and testing sets that consists of 50 random partitions, with each partition randomly assigning 90% (or less) of the lines to the training set and the remaining 10% (or more) of the lines to the testing set. This partition scheme is similar to that used by Gonzalez-Camacho et al. (2012) and Gianola et al. (2011), and helps obtain a distribution of the correlations in the testing set for each tested model.

Results

Predicting genetic values of lines in a breeding population

The main objective of these initial studies was to compare the prediction ability of various parametric and semiparametric models using intermediate- to high-marker density for assessing the genomic prediction of genetic values in real plant breeding populations evaluated under different environmental conditions. The maize data used consist of diverse inbred lines (that is, tropical, subtropical, tolerant to acid soils, and so on) from CIMMYT's Global Maize Program that were evaluated for several traits in different environments and genotyped with low and high marker density. The wheat lines in one data set are selection candidates evaluated for grain yield and other traits in several site–year combinations (Pérez et al., 2012), whereas the other data set comprises a set of historical wheat lines from CIMMYT's Global Breeding Program evaluated in several mega environments (Crossa et al., 2010; Burgueño et al., 2012).

Maize

A summary of the results is presented in Table 1 for the mean correlation of 10-fold cross-validation (Crossa et al., 2010) and 50 random partitions (Gonzalez-Camacho et al., 2012), each with 90–100% for the training and testing sets using two-marker densities in a maize population of 284 inbred lines evaluated for various trait–environment combinations and genotyped with 1148 and 55 000 SNPs. Broad-sense heritabilities of the trait–environment combinations were relatively high for male and female flowering traits, and intermediate for grain yield; these estimates were consistently higher under well-watered (WW) conditions than under severe drought stress (SS). Results indicate that increasing the marker density increased the prediction ability of the models for most trait–environment combinations. It is clear that prediction for all traits under both marker densities is always more problematic under SS than under WW conditions. This effect is clearer for a complex trait such as GY under stress conditions (GY-SS or GY-LOW), compared with GY under optimum conditions (GY-WW or GY-HIGH). This result confirms the importance of improving field evaluations under stress conditions (that is, drought and/or heat) by using appropriate experimental designs and statistical models that account for uneven soil characteristics and other environmental trends occurring during the crop cycle.

Table 1. Mean correlations between predicted and observed values of the three models, BL, RKHS regression and RBFNN for four traits (female flowering, FFL; male flowering, MFL; grain yield, GY: anthesis-silking interval, ASI) measured in the following environments: WW, SS, HIGH and LOW in 284 maize inbred lines genotyped with 55 000 and 1148 SNPs.

Trait–environment (heritability)	BL	RKHS	RBFNN
55 000 SNPsa
FFL-WW (0.89)	0.814	0.836	0.834
FFL-SS (0.81)	0.754	0.763	0.757
MFL-WW (0.88)	0.817	0.841	0.832
MFL-SS (0.83)	0.776	0.782	0.780
ASI-WW (0.79)	0.582	0.586	0.594
ASI-SS (0.77)	0.612	0.621	0.605
GY-WW (0.49)	0.557	0.548	0.529
GY-SS (0.38)	0.326	0.330	0.288
GY-HI (0.50)	0.633	0.663	0.653
GY-LOW (0.40)	0.410	0.402	0.393
1148 SNPsb
FFL-WW	0.781	0.588	—
FFL-SS	0.774	0.648	—
MFL-WW	0.790	0.607	—
MFL-SS	0.778	0.674	—
ASI-WW	0.513	0.547	—
ASI-SS	0.517	0.572	—
GY-WW	0.525	0.514	—
GY-SS	0.415	0.453	—
GY-HI	—	—	—
GY-LOW	—	—	—

Abbreviation: BL, Bayesian LASSO; HI, optimum; LOW, stress; RBFNN, radial basis function neural network; RKHS, reproducing kernel Hilbert space; SNP, single-nucleotide polymorphism; SS, severe drought stress; WW, well-watered.

The best prediction model for each trait-environment combination in the data set is underlined.

^aExtracted from Gonzalez-Camacho et al. (2012).

^bExtracted from Crossa et al. (2010).

For more simple traits, such as male and female flowering, the effect of stress conditions decreased prediction ability, but this ability was higher when using higher marker density than with intermediate marker density. Another trend that emerged from these results is that with low-density markers and for simple traits (FFL and MFFL), the predictive ability of the linear model (BL) surpassed those of the nonlinear models (RKHS and RBFNN), whereas with high-density markers, nonlinear models always showed better prediction ability than the linear models. One can speculate that nonlinear models can capture small cryptic epistatic effects better with high marker density, and they cannot be captured with low marker density. Colinearity between high-density markers is another possible reason for the poorer prediction of the linear model compared with the nonlinear model. These results indicate that imputation from low marker density to high marker density, shown by Hickey et al. (2012) to be very accurate in maize, is important in the practical implementation of GS, because imputation from low to high marker density will generate economic savings during the breeding cycles while increasing prediction accuracy.

Wheat

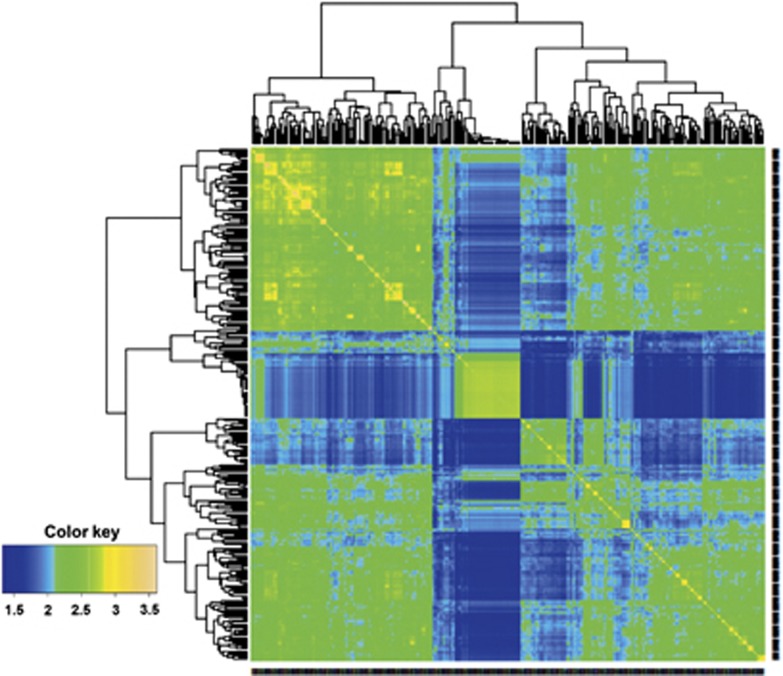
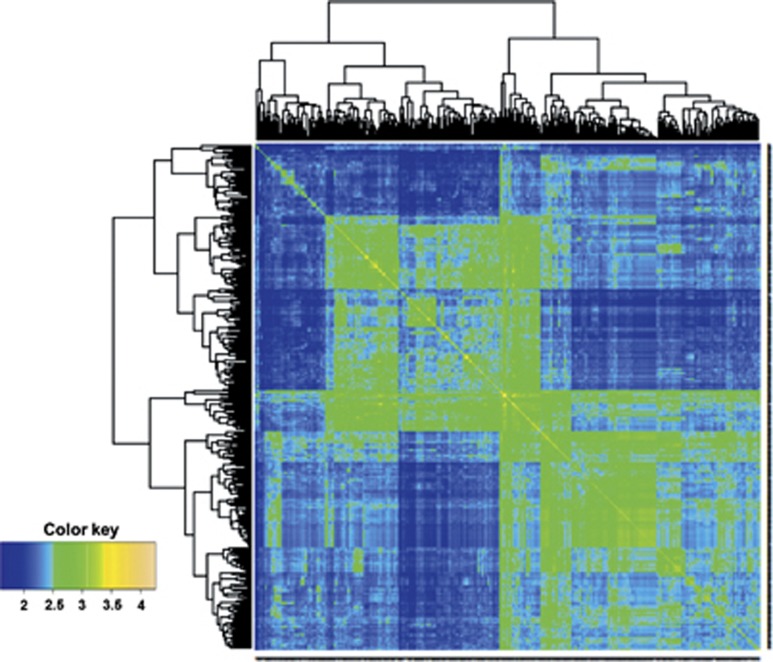
The summary in Table 2 shows the prediction ability of two wheat data sets for grain yield measured in various environments. Here, the number of genotypes in each data set is 306 and 599, and the number of markers is 1717 and 1279, respectively (Pérez et al., 2012; Burgueño et al., 2012). Prediction accuracies were highly consistent in both sets of experiments, with BL with markers and pedigree (PMBL), and RKHS with pedigree and markers (PMRKHS) giving the best predictions on the data set of 599 wheat lines and with models MRKHS and MRBFNN as the best predictors on the data set of 306 wheat lines. Figures 1 and 2 depict the heatmap of the genomic (G) matrix for data on 306 and 599 wheat lines, respectively. The 306 lines comprise three groups, one large population (top left), one small subset unrelated to either of the other two and another large population that is closely related to the first large one, apparently with two closely related subgroups (Figure 1). The 599 wheat lines formed two clear large groups, each with several subgroups closely related to each other (Figure 2); the two large subgroups overlap slightly.

Table 2. Mean correlations between observed and predicted values for GY using GBLUP; P; Bayesian LASSO with markers, and with markers + pedigree (MBL, PMBL, respectively); RKHS regression with markers, and with marker + pedigree (MRKHS and PMRKHS, respectively); MRBFNN, and MBRNN models in two data sets, one with 306 wheat lines genotyped with 1717 DArTs markers and evaluated in seven environments, and the other with 599 wheat lines genotyped with 1279 DArTs and evaluated in four environments.

		Model
Trait	Environment	GBLUP	MBL	MRKHS	MRBFNN	MBRNN
306 lines and 1717 DArT markersa
	1	0.43	0.48	0.51	0.51	0.50
	2	0.41	0.48	0.50	0.43	0.43
GY	3	0.29	0.20	0.37	0.42	0.32
	4	0.46	0.45	0.53	0.55	0.49
	5	0.56	0.59	0.64	0.66	0.63
	6	0.67	0.70	0.73	0.71	0.69
	7	0.50	0.46	0.53	0.54	0.50
		Model
Trait	Environment	P	MBL	MRKHS	PMBL	PMRKHS
599 lines and 1279 DArT markersb
	1	0.45	0.52	0.60	0.54	0.61
	2	0.42	0.49	0.49	0.50	0.49
GY	3	0.42	0.40	0.45	0.45	0.40
	4	0.45	0.46	0.52	0.50	0.46

Abbreviations: BRNN, Bayesian regularized neural networks; GBLUP, genomic best linear unbiased predictor; GY, grain yield; MBRNN, Bayesian regularized neural networks with markers; MRBFNN, radial basis function neural networks with markers; P, pedigree; RBFNN, radial basis function neural networks; RKHS, reproducing kernel Hilbert space.

The best prediction model for each environment in the data set is underlined.

^aExtracted from Pérez et al. (2012).

^bExtracted from Crossa et al. (2010).

Figure 1.

Heat map of the G matrix for the data set with 306 wheat lines genotyped with 1717 DArTs markers.

Figure 2.

Heat map of the G matrix for the data set with 599 wheat lines genotyped with 1279 DArTs markers.

The prediction problem addressed in this research concerned the prediction of the entire population. It is interesting to note that markers consistently increased prediction ability over the baseline pedigree-derived model in all environments of both data sets. Another clear result emerging from these two data sets is that considering markers and pedigree together consistently increased the prediction ability of all models, as compared with models with markers only or pedigree only. For other problems (such as prediction between subpopulations), a decrease in prediction ability was expected, especially for subpopulations that are not related, for example, those shown in Figure 1. When one of the large subpopulations in Figure 2 was predicted based on the other large subpopulation, prediction accuracy decreased, as expected (de los Campos, personal communication).

Predicting genetic values of lines between populations or subpopulations

Wheat

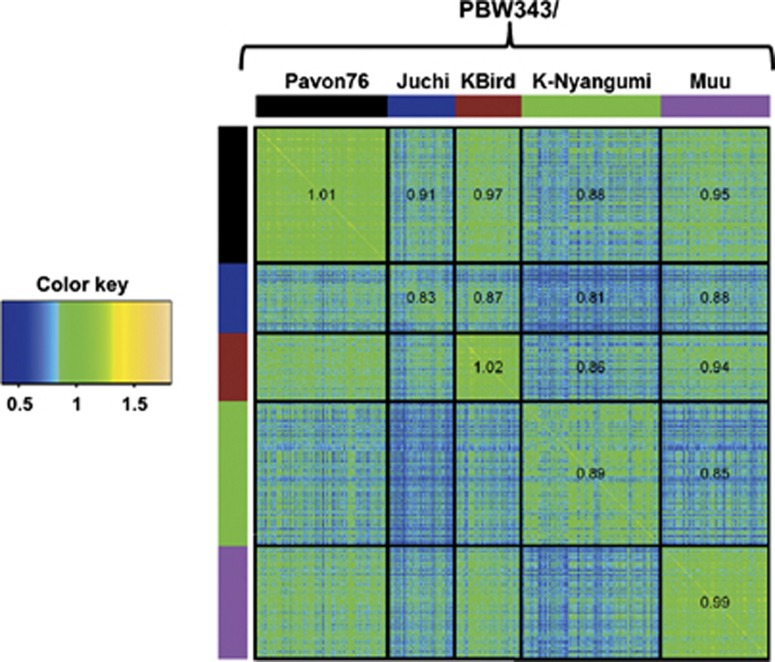
In a recent study, we used a stem rust data set from five wheat populations (PBW343/Juchi, PBW343/Pavon76, PBW343/Muu, PBW343/Kingbird and PBW343/K-Nyangumi) for genomic prediction (Ornella et al., 2012). Resistance to stem rust is known to be affected by several major genes and also influenced by slow-rusting genes with small additive effects. All populations were derived from crosses between resistant parents (Juchi, Pavon76, Muu, Kingbird and K-Nyangumi) and PBW343, a moderately susceptible parent. The parents and the F₆ generation recombinant inbred lines were evaluated for reaction to stem rust at different locations. The sample sizes of the five wheat populations were 92 genotypes in PBW343/Juchi, 176 individuals in PBW343/Pavon76, 148 genotypes in PBW343/Muu, 90 individuals in PBW343/Kingbird and 176 genotypes in PBW343/K-Nyangumi. Genotypes were molecularly characterized using 1400 Diversity Arrays Technology Pty. Ltd (http://www.diversityarrays.com/) (DArT markers).

As depicted in Figure 3, there are five clearly distinct yet related (half-sib) populations; however, lines in the Juchi population do not seem to be closely related. Results of the pairwise prediction of one population using the other are shown in Table 3. The accuracy of predictions of one population using another population was relatively high, except for PBW343/K-Nyangumi when predicted by PBW343/Juchi (using BL, 0.14) and PBW343/Juchi when predicted by PBW343/K-Nyangumi (using GBLUP, 0.14). Furthermore, Table 4 indicates that prediction of stem rust data in each individual populations using stem rust data from the other four populations gave relatively high correlations, except for population PBW343/Juchi, which, as shown by Ornella et al. (2012), does not have lines that are closely related among themselves or to lines in other populations.

Figure 3.

Heat map of the genomic relationship matrix G of five wheat populations: PBW343/Pavon76, PBW343/Juchi, PBW343/Kingbird, PBW343/K-Nyangumi and PBW343/Muu. The numbers indicate the average values of the corresponding elements of G within and between populations (from Ornella et al., 2012).

Table 3. Pair-wise correlations between observed and predicted stem rust values of two models, Bayesian LASSO and the GBLUP, trained in one population and evaluated in the other population for five populations (adapted from Ornella et al., 2012).

	Traininga
	PBW343/Juchi	PBW343/Kingbird	PBW343/K-Nyangumi	PBW343/Muu	PBW343/Pavon76
Testing
PBW343/Juchi	—	0.48	0.14	0.28	0.31	Bayes LASSO
PBW343/Kingbird	0.53	—	0.29	0.25	0.54
PBW343/K-Nyangumi	0.14	0.30	—	0.28	0.28
PBW343/Muu	0.18	0.30	0.33	—	0.29
PBW343/Pavon76	0.37	0.51	0.22	0.33	—
GBLUP

There are five related populations: PBW343/Juchi, PBW343/Kingbird, PBW343/K-Nyangumi, PBW343/Muu and PBW343/Pavon76.

^aThe triangle on the upper-right shows the prediction ability (correlation) of Bayes LASSO, with the rows indicating the training population (that is, PBW343/Juchi) and the columns the testing population (that is, PBW343/Kingbird, 0.48); the triangle on the lower-left gives the prediction ability of GBLUP, with the columns indicating the training population (that is, PBW343/Juchi) and the rows the testing population (that is, PBW343/Kingbird, 0.53).

Table 4. Correlations between predicted and observed stem rust values for five wheat populations, when four of them, with different numbers of individuals in the training set, predict each of the others in the testing set using the GBLUP and the Bayesian LASSO (BL) models.

Population	Number of lines in the training set	Number of lines in the testing test	GBLUP	BL
Four populations predicting one population
PBW343/Muu	534	148	0.59	0.60
PBW343/K-Nyangumi	506	176	0.52	0.53
PBW343/Kingbird	592	90	0.79	0.82
PBW343/Juchi	590	92	0.41	0.39
PBW343/F6Pavon	506	176	0.59	0.62
All populations 50 random partitions with 90:10
All populations	612	70	0.62	0.64

Mean correlations when considering all five populations combined with a prediction design that considers 50 random partitions with a split of 9:1 for the training set: testing set proportion.

It is interesting to point out that even under the population structure existing in this wheat data set, stem rust prediction between populations, and also within the meta-population comprising all five populations (Table 4), was relatively high. The architecture of the traits has an important role that may help to explain these results. For more complex traits, such as grain yield, this prediction result may not hold; thus population structure could become the main driving force for increasing the prediction accuracy of the meta-population, while prediction between populations significantly decreases.

Maize

Recently, Windhausen et al. (2012) investigated various aspects of genomic prediction within and between populations, and discussed the potential uses of genomic prediction in maize hybrid development. The authors used 255 diverse maize lines tested in six trials (almost all identical to those used by Crossa et al. (2010)), and classified them into eight breeding populations differing in mean performance. The authors examined the problem of separately predicting each breeding population based on marker effects estimated in the other populations; prediction ability was nearly zero. Results suggest that in the current study, prediction comes mainly from pedigree (subpopulation structure within the global set), with negligible contributions from the relationship between the training and validation sets or from LD between markers and causal variants underlying the predicted traits. Potential uses of genomic prediction in maize hybrid development are discussed, emphasizing the need to define the breeding scenario in which genomic prediction should be applied (that is, prediction across or within populations) and the size of the training sets with a strong genetic relationship to the validation set.

Prediction within breeding populations incorporating GE, pedigree and genomic information

Pedigree- and genomic-derived additive predictions

Previous results referred to genomic predictions of models for a single environment and did not consider correlated environmental structures due to GE. Crossa et al. (2010) evaluated the predictive ability of pedigree, genomics and pedigree+genomic information in single-environment models such as those used for the wheat multi-environment data set. Here, we summarize results from Burgueño et al. (2012), who, using the same data set as Crossa et al. (2010), were the first to evaluate the impact of modeling GE covariance structures for multi-environment trials. The data comprise 599 wheat lines genotyped with 1279 DArTs and evaluated in four wheat mega environments. Crossa et al. (2010) used pedigree, genomic and pedigree+genomic-derived models for a wheat multi-environment trial comprising four environments (E1–E4) with different genetic correlations, E1 not being genetically correlated with the others, and E2 and E4 with intermediate to high genetic correlations. Crossa et al. (2010) assessed prediction problems relevant to plant breeders: (1) predicting the performance of genotypes that have not been evaluated in any environment (assessed by cross-validation CV1), and (2) predicting the performance of genotypes that have been evaluated in some environments, but not in others (assessed by cross-validation CV2). Prediction was performed for lines within environments and across environments.

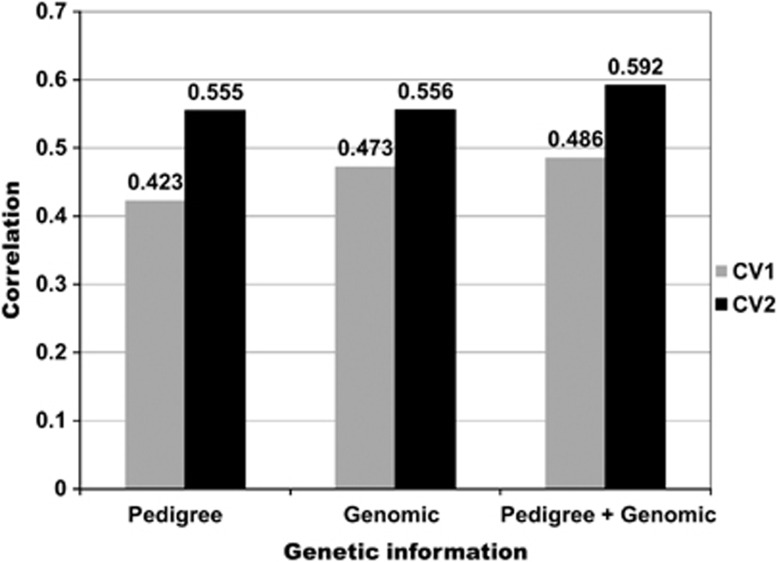
Burgueño et al. (2012) found that the predictive ability of genomic-based models was higher than that of pedigree-based models. Their results confirmed the superiority of pedigree+genomic models for GS over pedigree-based predictions or genomic-based predictions alone. Predicting the performance of newly developed lines that have never been evaluated in the field (CV1) is more challenging than predicting the performance of lines that have been evaluated in different but correlated environments (CV2). Figure 4 shows correlations obtained from multi-environment models that model GE using the FA model in two cross-validations schemes (CV1 and CV2). Correlations for CV1 do not change much and those in CV2 were 31, 17.5 and 21.8% greater than those obtained in CV1, indicating the importance of having information from correlated environments when predicting performance.

Figure 4.

Mean correlations (across four environments) between predicted and observed grain yield values derived from models using only pedigree, only genomics and pedigree+genomic for two cross-validation schemes (CV1 and CV2) (adapted from Burgueño et al., 2012). Cross-validation CV1 predicts genotypes that have never been evaluated in any environment, and cross-validation CV2 predicts genotypes that were evaluated in some environments but not in other environments.

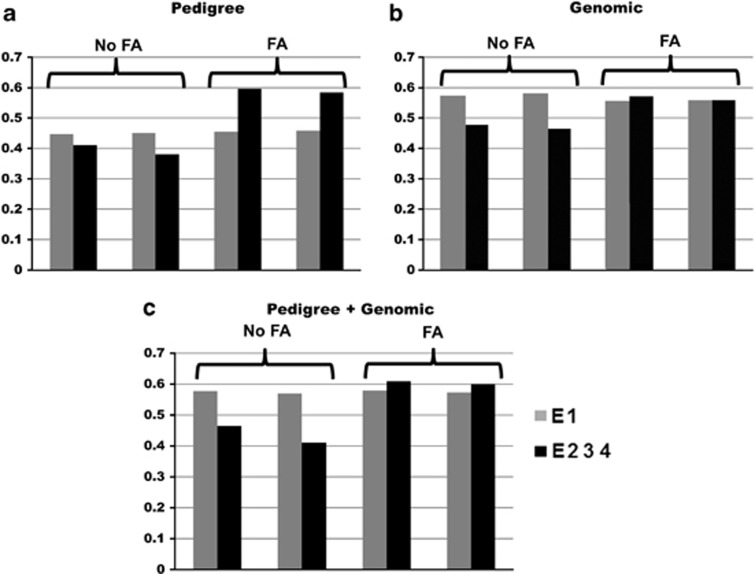
Figure 5 shows that the impact of modeling GE in CV2 is marked in environments E2–E4, but not in E1; this is because genetic values in E2–E4 have high genetic correlations, whereas genetic values in E1 exhibit low genetic correlations with those from E2–E4. For correlated environments E2–E4, the benefits in predictive ability come from borrowing information from correlated environments by modeling GE and by using information regarding pedigree and genomic relationships. Interestingly, Burgueño et al. (2012) also examined the predictive accuracy of models without using pedigree and genomic relationships, and showed that to predict the environments that cause a great deal of the GE, such as environment E1 (and E4), modeling GE using information on genomic relationships and/or pedigree gives better prediction accuracy than when the GE is not modeled and the information on genomic and pedigree is ignored.

Figure 5.

Correlations between predicted and observed performance in environment 1 (E1) and average of environments 2, 3 and 4 (E2 3 4) obtained in CV2 using only pedigree (a), only genomics (b) or using pedigree+genomics (c)-based models with different specifications for the residual and genetic covariance matrices (FA=GE modeled using the factor analytic model; no FA=GE not modeled) (adapted from Burgueño et al., 2012).

In general, these results also agree with those reported by Burgueño et al. (2011), who demonstrated, without any pedigree and genomic information, that modeling GE based solely on phenotypic data is a good thing, as it always gives better predictions than simple linear mixed models without modeling GE.

Pedigree- and genomic-derived additive and additive × additive predictions

As proposed by Burgueño et al. (2007), pedigree-derived additive and additive × additive relationship information can be combined into a single model that will model GE using the FA model with two random effects: one is a regression on pedigree additive relationships, and the other, a regression on pedigree epistasis additive × additive relationships (see Appendix). Thus, genomic-derived additive and additive × additive relationships can be combined into a single model by extending them into one with two random effects: one with regression on genomic additive relationships, and the other, regression on genomic epistasis additive × additive relationships. We have assessed these predictions to examine whether the inclusion of epistasis will improve prediction ability as compared with using additive effects alone.

Results in Table 5 are for cross-validation CV2 that predicts the genetic performance of 599 lines that were tested in some environments but not in others. Results show that including pedigree additive relationships and pedigree epistasis additive × additive relationships did improve prediction in some environments or combinations of environments. Also, genomic additive relationships and genomic epistasis additive × additive relationships did improve predictions in most environments (and their combinations), as compared with models that only include pedigree additive or genomic additive relationships. These results indicate that modeling additive × additive epistasis along with GE is important for increasing the accuracy of predictions in wheat breeding populations. These findings agree with those recently reported by Wang et al. (2012), who found that modeling epistasis did increase predictive ability.

Table 5. Mean correlations between the predicted and observed values of genotypes for individual environments (E1, E2, E3 and E4), and for three environments combined (E2, E3 and E4) using five different factor analytic models (FA) for a cross-validation scheme (CV2), each with 10-fold cross-validation.

	FA additive pedigree (G0P)	FA additive genomic (G0M)	FA pedigree additive (G0P), FA genomics additive (G0M)	FA pedigree additive (G0P), FA pedigree additive × additive (G0PP)	FA genomic additive (G0M), FA genomic additive × additive (G0MM)
E1	0.460	0.552	0.469	0.512	0.554
E2	0.623	0.609	0.638	0.612	0.637
E3	0.633	0.581	0.612	0.634	0.603
E4	0.533	0.513	0.448	0.540	0.465
E2, E3, E4	0.596	0.571	0.566	0.598	0.568

The best predictive model for each environment or environment combination is underlined. Data used were extracted from Crossa et al. (2010) and Burgueño et al. (2012).

Factor analytic-pedigree for G_0P; factor analytic-genomic for G_0M; factor analytic-pedigree (G_0P) and factor analytic-genomic (G_0M); factor analytic-pedigree additive (G_0P) and factor analytic-pedigree additive × additive (G_0PP); factor analytic-genomic additive (G_0M) and factor analytic-genomic additive × additive (G_0MM).

Prediction within bi-parental maize populations

One of the key ways in which GS can be used in a maize breeding program is to improve source populations from which candidate inbred lines can be predicted and selected as parents for the next generation; in this manner, genetic gains in a closed multi-parent population derived from three or more elite lines are maximized. It is important to know whether greater gains per year could be achieved at a lower cost and in less time using this approach than using the conventional pedigree breeding approach for the same investment. Prediction within full-sib families is the most favorable situation for GS, with very high LD and no pedigree, family or group structure; therefore, we consider the accuracies estimated for the bi-parental populations as the maximum obtainable in closed rapid-cycle marker-only selection.

In this study, we show results of two bi-parental populations comprising 249 and 250 F₂ test-cross individuals, respectively, that were genotyped with 238 and 271 SNPs, respectively, and evaluated under different drought and optimum environmental conditions. Table 6 shows the predictive ability for grain yield across environments measured as a Pearson correlation between the observed value (y) and the predicted value (ŷ) averaged over all 50 validation runs for each of the different combinations of number of individuals and number of markers for two maize bi-parental populations. Broad-sense heritability for grain yield was 0.57 for bi-parental population 1 and 0.28 for bi-parental population 2 when all drought and optimum environments were combined. Prediction accuracy in these bi-parental populations reached around 0.4 at most, when 90 individuals were randomly taken (50 times) as the training population from the entire sample of bi-parental population 2. When 50 individuals were sampled, prediction accuracy dropped to around 0.3. Although research is needed to balance the genotypic and phenotypic costs, it is possible to speculate that these accuracies can still be considered adequate, as they will save costs when large numbers of bi-parental populations are evaluated in the field, and have the additional benefit of potentially increasing selection intensity. Predictions in Table 6 indicate that decreasing the number of markers also has a negative impact on prediction accuracy. However, this effect is much more drastic in bi-parental population 1 (with a heritability for grain yield of 0.27) than in bi-parental population 2 (with a heritability for grain yield of 0.57). Prediction accuracy can be computed by dividing the prediction ability by the square root of the broad-sense heritability of the target trait evaluated in the respective set of environments.

Table 6. Mean correlations between the predicted grain yield values for three models (BL, RKHS regression and GBLUP) when the numbers of individuals in the training sets randomly taken from the entire population (50 different times) are 30, 40, 50, 70 and 90 for different numbers of SNPs.

Model_ number of individuals in the training population	Number of SNPs
	238 SNPs	100 SNPs	50 SNPs
Bi-parental population 1(249 F2individuals; 238 SNPs)
BL_30	0.1348	0.1009	0.0640
RKHS-KA_30	0.1520	0.1144	0.0703
GBLUP_30	0.1643	0.1173	0.0672
BL_40	0.1539	0.1286	0.0899
RKHS-KA_40	0.1685	0.1380	0.0925
GBLUP_40	0.1789	0.1441	0.0906
BL_50	0.2093	0.1598	0.0918
RKHS-KA_50	0.2004	0.1555	0.0944
GBLUP_50	0.2165	0.1612	—
BL_70	0.2236	0.1814	0.1152
RKHS-KA_70	0.2153	0.1756	0.1147
GBLUP_70	0.2338	0.1839	—
BL_90	0.2484	0.2000	0.1251
RKHS-KA_90	0.2386	0.1952	0.1284
GBLUP_90	0.2574	0.2024	—
Bi-parental population 2 (250 F2individuals; 271 SNPs)
	271 SNPs	100 SNPs	50 SNPs
BL_30	0.2994	0.2765	0.2165
RKHS-KA_30	0.2924	0.2725	0.2136
GBLUP_30	0.2982	0.2770	0.2161
BL_40	0.3367	0.3156	0.2447
RKHS-KA_40	0.3371	0.3172	0.2471
GBLUP_40	0.3378	0.3146	—
BL_50	0.3471	0.3264	0.2585
RKHS-KA_50	0.3486	0.3271	0.2621
GBLUP_50	0.3467	—	—
BL_70	0.3717	0.3549	0.2818
RKHS-KA_70	0.3770	0.3605	0.2866
GBLUP_70	0.3714	—	—
BL_90	0.3919	0.3725	0.2998
RKHS-KA_90	0.4066	0.3859	0.3199
GBLUP_90	0.3903	—	—

Abbreviations: BL, Bayesian LASSO; RKHS, reproducing kernel Hilbert space; SNP, single-nucleotide polymorphism.

For each bi-parental population and for each number of markers (columns) the best predictive model is underlined.

Discussion

GS has a number of uses in a breeding program; however, its greatest potential use is at points in the breeding program where selection using traditional methods (for example, through the generation of phenotypes via replicated trials) is too expensive, time consuming, or not biologically or logistically possible. The most important questions relating to the applicability of GS in the CIMMYT maize and wheat global breeding programs are which prediction problem will better help breeders predict: (1) breeding values of individuals for rapid selection cycling or (2) genotypic values of advanced lines that are in the last stages of testing. While predicting breeding values require a precise estimation of additive effects, predicting genetic values of advance lines requires using models that account for additive as well as epistatic genetic effects. Results of analyzing vast amounts of data in both CIMMYT breeding programs indicate that pedigree and markers offer opportunities for achieving prediction than can be exploited in the breeding pipeline. However, questions on where and how to use this information remain open. Questions that require further research are, among others, how many individuals and markers are needed per bi-parental population? And can related bi-parental families (half-sibs or quarter-sibs) increase prediction accuracy? The impact of these factors on the prediction accuracy of genomic breeding values on which selection decisions are made can be evaluated by computer simulation.

At CIMMYT, we are placing increasingly greater emphasis on the design of the validation population. In CIMMYT breeding programs, genomic information may be useful for (1) predicting the effect of an unknown population structure, (2) predicting unrecorded pedigree structure, (3) correcting incorrect pedigree and (4) making predictions about the genetic value of Mendelian sampling terms. Each of these four uses of genomics in the breeding programs has different economic value; therefore, design validation schemes should sometimes partition the overall accuracy of a genomic breeding value into the accuracy of these different components.

Genetic and environmental structure

Genetic structure (family or breeding populations) brings up questions such as which prediction problem needs to be assessed when applying GS in real plant breeding populations, predicting between families or within family, or both. Likewise, do distantly related (that is, quarter-half-sibs) families contribute (or not) to prediction ability compared with families (that is, half-sibs or full-sibs) that are more closely related and therefore can be better predicted? Experimental maize data indicate that prediction of unrelated lines has low accuracy, and that we can predict between families only if they have some degree of relatedness.

The initial prediction results of CIMMYT maize and wheat breeding trials indicate that promising accuracy can be achieved. In this prediction assessment case, all markers will inherently consider substructures (as the pedigree model does). De los Campos et al. (2010) showed that regressing phenotypic values on all available markers is equivalent to regressing phenotypic values on all principal components, thus considering all subpopulations. Furthermore, when combining data from different experiments and populations with different levels of performance, the mixed model will automatically adjust for differences in the mean of these populations and/or experiments. A different prediction problem arises when predicting between subpopulations that are not related. In this case, prediction accuracy dropped significantly and some becomes negligible. However, when all subpopulations are related and form one large global population with a clear structure, the prediction of one population based on the others can be done with relatively high accuracy, as shown by the prediction of stem rust in wheat. However, for a complex trait such as grain yield, these relatively high predictions may not be obtained. A different prediction assessment is concerned with predicting within bi-parental populations; in maize, a prediction ability of around 0.4 with low marker density was achieved. This could save resources during phenotyping.

Although GE has an important role in genomic prediction (Burgueño et al., 2012), genomic information can only be used if the G matrix from bi-parental populations consisting of an F₂ crossed with a tester (that has no structure) and obtained from around 200 SNP markers contains information that will allow borrowing genotypic information from other individuals in other environments. Increasing the number of markers and/or the sample size might further increase prediction ability. Initial results of bi-parental populations should be assessed in more F₂ populations that have been evaluated using different crosses (related and unrelated) tested in different environmental conditions.

Breeding value components in GS

Formally, a breeding value can be partitioned into two components: (1) the parent average (that is, one individual receives 50% of its genome from each of its two parents) and (2) Mendelian sampling, which is the random sampling of the genome of each parent. In efficient breeding programs, genetic progress is primarily driven by the time taken to evaluate the Mendelian sampling term accurately. In the absence of performance on an individual itself or on its descendants, traditional breeding value estimation methods have no ability to evaluate the Mendelian sampling term. Plant breeders have traditionally evaluated the genetic potential of the Mendelian sampling term using replicated field trials of the candidates for selection that are both expensive and time consuming.

Genomic information offers the possibility of accurately estimating the genetic potential of Mendelian sampling terms without having to evaluate individual candidates for selection in the field. This has a great time- and cost-saving potential. While the major benefit of genomic information in an efficient breeding program will likely be its ability to accurately evaluate the Mendelian sampling term, genomic information also has other valuable uses. For example, it can be used to overcome the effect of incorrectly recorded or unrecorded pedigree information, thereby helping to increase the ability to accurately evaluate the parent average component in a breeding value. In some breeding programs, such as those with very low levels of pedigree recording, there may be major population subgroups or structures hidden within the data that could be captured and revealed by the genomic information.

While making selection decisions based on breeding values that contain these pedigree or structure components (as well as some Mendelian sampling components) may be useful, breeders need to be cautious, as the family or population structure with the highest genetic merit could come to dominate the breeding population over time, and useful genetic variation within other families or population subgroups could be lost. These are well-known results using classic BLUP methodology, as BLUP uses both within- and between-family information, and with low heritability traits, between-family selection is dominant. For this reason, methods to control inbreeding in BLUP selection programs are used, so that individuals from more families are chosen.

Therefore, for the reasons mentioned above, when validating the performance of GS within breeding programs, one needs to be aware of the different components possibly contained within a genomic breeding value and evaluate the benefits of genomic information regarding these components. For example, when structure is known, genomic information may not be needed to evaluate its genetic merit; pedigree information is reasonably powerful for evaluating the genetic merit of the parent average component, yet only genomic information or field trials on the selection candidates or their descendants can evaluate the genetic potential of the Mendelian sampling term. Validation of the usefulness of genomic information should place major emphasis on the latter comparison.

Data Archiving

There were no data to deposit.

APPENDIX

Pedigree model (P)

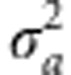In this model, the vector of genetic values g={g_i} was assumed to follow a multivariate normal density centered at zero and with a (co)variance matrix proportional to the numerator relationship matrix (A), computed from the pedigree, that is, . Here, is the variance of additive effects on the base population and the unknowns are 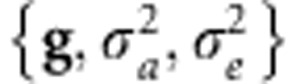. Independent scaled-inverse χ² densities, 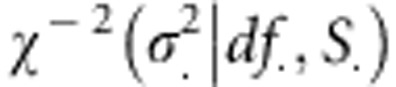, were assigned to variance parameters. Therefore, the joint posterior density of model unknowns is

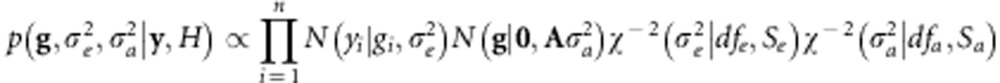where H denotes the collection of hyperparameters, and df and S are prior degree-of-freedom and scale parameters set to one and four, respectively. Inferences were based on samples from the above posterior density obtained using a Gibbs sampler.

Linear regression models

GBLUP

One of the first penalized regression methods used in genomic selection was Ridge Regression (RR). This marker-based model (RR-BLUP) is expressed as

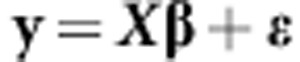where X is the genotype matrix for the bi-allelic markers (coded as 0, 1 and 2) and 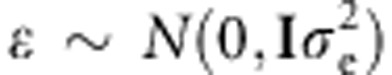. The marker effects are obtained by solving the optimization problem 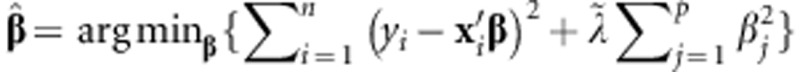, where 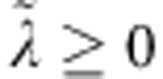is a regularization parameter. It can be shown that the solution to this problem is given by 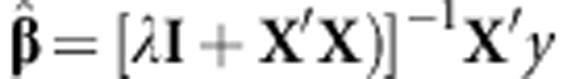. GEBV can be obtained from model (1A) by setting g=Xβ such that the equation 1A can be written as

Assuming that 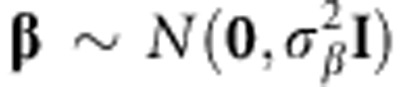, it can be shown that 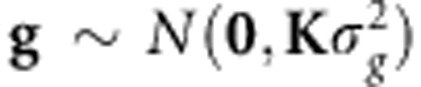, where K=XX′. When G=K/c=XX′/c with 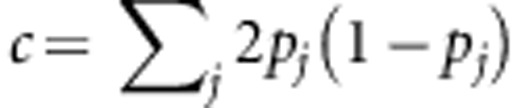and p_j being the minor allele frequency, then 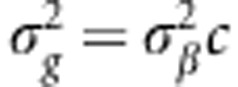and is called GBLUP, and the G matrix is the genomic-derived relationship matrix, with ĝ=XX′[XX′+λI]⁻¹y.

Linear mixed models with genotype × environment interaction

For simplicity, we will use the same notation as in Burgueño et al. (2012). The basic linear mixed model for the phenotypic response of g individuals evaluated in J environments is

with y=(y′₁,…,y′_J)′,g=(g′₁,…,g′_J)′, ɛ=(ɛ′₁,…,ɛ′_J)′, where y_j={y_ij} (i=1,2,…,g) is a column vector of g phenotypic records (or means) collected in each of the jth environments (j=1,…,J), X_j and Z_j are incidence matrices vectors of systematic effects, θ_j, and random genetic effects g_j, for each environment.

Pedigree and genomic linear mixed models

The vector of random effects had a covariance structure Cov(g,g′)=G₀⊗A, Cov(ɛ,ɛ′)=R₀⊗I and Cov(g,ɛ′)=0, where G₀ is a J × J variance–covariance of the genetic effect on environments, ⊗ is the Kronecker product, A={a(i,i′)} is a numerator relationship matrix, R₀={Cov(ɛ_ij,ɛ_i′j)} is a g × g covariance matrix (within-environments, across-genotypes) of model residuals and I is an identity matrix of size J. This model can easily be extended to accommodate heterogeneous residual variances.

The marginal density of the data is multivariate normal with mean and variance–covariances as

In the previous models, A={a(i,i′)} represents a matrix of additive relationships derived from a pedigree (A_P). Alternatively, this matrix can be derived from molecular marker information, that is, A_M=G (the genomic relationship matrix in GBLUP; see VanRaden (2008) for more details).

Burgueño et al. (2012) outlined how pedigree and marker information can be combined in a single model by extending (3A) to a model with two random effects, one of which, g_P∼N(0,G_0P⊗A_P), represents a regression on pedigree additive relationships, and the other represents a regression on marker additive relationships, g_m∼N(0,G_0M⊗A_M). Thus, (3A) and (4A) become

and

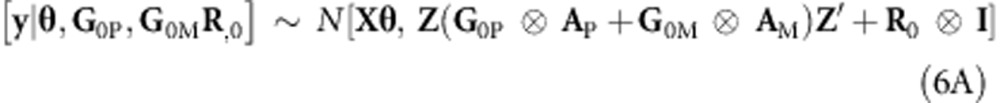Similar to Burgueño et al. (2007), pedigree-derived additive and additive × additive relationship information can be combined into a single model by extending (5A) to a model with two random effects, one of which, g_P∼N(0,G_0P⊗A_P), is a regression on pedigree additive relationships. The other represents a regression on pedigree epistasis additive × additive relationships, 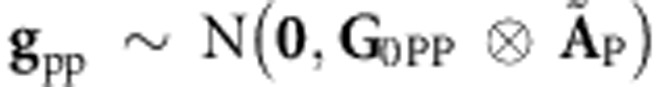, where Ã_P=A_P#A_P (where # is the element-wise multiplication operator, that is, Hadamard product). Therefore (5A) and (6A) become

and

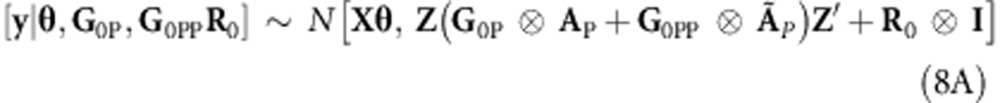Habier et al. (2007) have shown that A_M approaches A_P; therefore it is possible to assume that Ã_M tends to Ã_P. Thus, the genomic-derived additive and additive × additive relationships can be combined into a single model by extending (5A) to a model with two random effects, one with g_M∼N(0,G_0M⊗A_M), representing a regression on genomic additive relationships, and the other representing a regression on genomic epistasis additive × additive relationships, 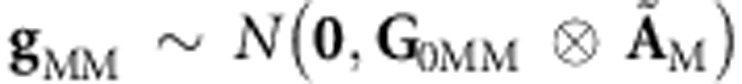. Thus (7A) and (8A) become

and

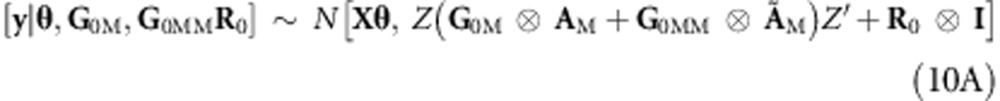Modeling genotype × environment covariance structures using the factor analytic model

The factor analytic (FA) model that defines matrices for g_P and g_M in (5A) and (6A) is 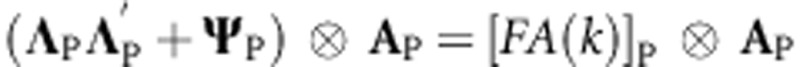for pedigree and 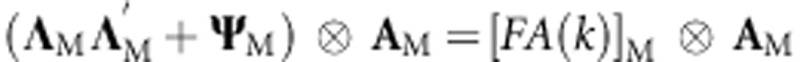for markers where Λ_P (or Λ_M) is a matrix of order J × k, with the kth column containing the environment loadings for the kth latent factor, and Ψ being a diagonal matrix (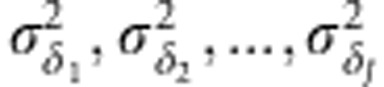) of the order J × J. When only one factor is considered, k=1, the model has one multiplicative term and is denoted as FA(1); for k=2, FA(2) has two multiplicative components, and so on.

The factor analytic model that defines (g_P+g_PP) in (7A) and (8A) is 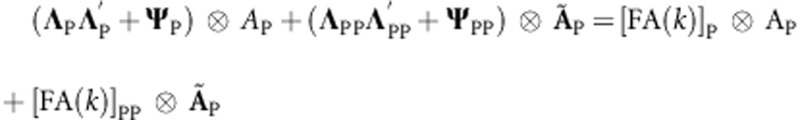. Similarly, the factor analytic model that defines (g_M+g_MM) in (9A) and (10A) is 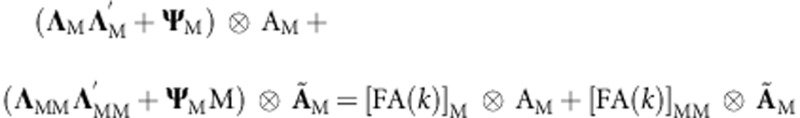. In this model, only one of Ψ_M or Ψ_MM(Ψ_P or Ψ_PP) can be estimated in order to make the parameter identifiable.

Bayesian LASSO (BL)

Marker effects in (1A) are assumed independent and identically distributed a priori. The BL assigns the same double exponential distribution to all marker effects (conditionally on a regularization parameter), that is 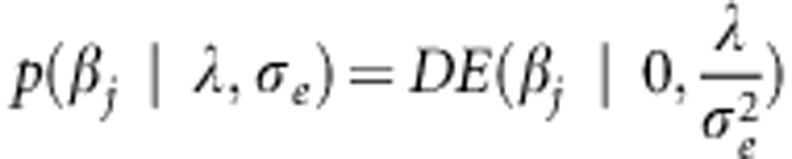, where λ⩾0 is a regularization parameter. Compared with the Normal distribution, the DE assigns a bigger mass near 0, shrinking small marker effects. The joint posterior density of models unknowns is given by:

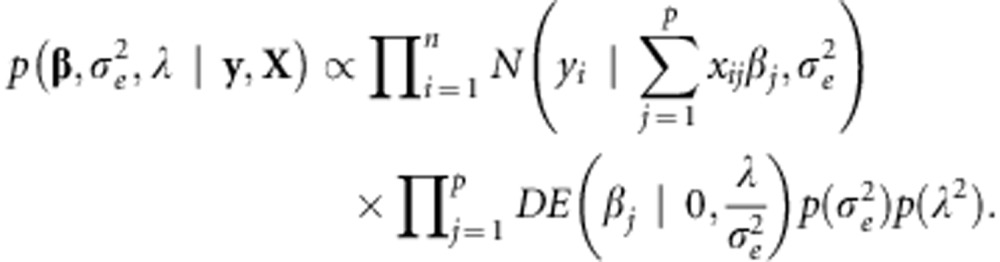It is usual to assign a prior distribution to the square of the regularization parameter (λ²); for example, it can be a beta or a gamma distribution (de los Campos et al., 2009) but it also can be estimated by using cross-validation (Park and Casella, 2008). It is also usual to assign a scaled-inverse χ² distribution, χ⁻²(df_e,S_e) to 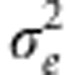. The DE distribution does not conjugate with the normal distribution, but it can be expressed as a mixture of scaled normal densities, which allows us to represent the original problem as a hierarchical model (Park and Casella, 2008) and then the posterior distributions can be obtained using a Gibbs sampler.

The BL is explained in detail in several articles, such as Park and Casella (2008), de los Campos et al. (2009), Crossa et al. (2010, 2011), Pérez et al. (2010) and Gonzalez-Camacho et al. (2012). Guidelines for setting the hyperparameters for the prior distributions for the regularization parameters and 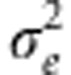are given in Pérez et al. (2010) and Gonzalez-Camacho et al. (2012).

Principal component regression––lower-dimension representation of matrices K and G

De los Campos et al. (2010) showed that the symmetric matrix K and the rectangular marker matrix X can be represented using spectral decomposition and singular value decomposition, respectively. Based on these eigen analyses, the authors show that the regression of the phenotypes on the markers is equivalent to the regression of the phenotypes on the principal components. Thus, a model that includes all the markers implicitly considers there may be potential population structures in the data.

A general prediction model can be represented as

where y is the phenotypic response (centered), K is an incidence matrix that could be the same as the realized relationship matrix (G), or the same as XX′ or the same as matrix X; 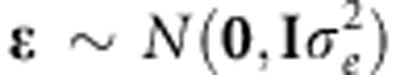, and α∼N(0,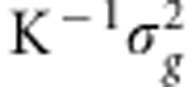). This last assumption helps obtain results related to the spectral decomposition and singular value decomposition of K and X (de los Campos et al., 2010). However, α, as previously defined, does not strictly denote the effects of the markers.

Defining g=Kα, de los Campos et al. (2010) showed that

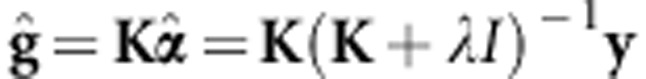Note that this is similar to equation. 2 of vanRaden (2008), that is, 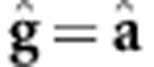( 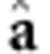denotes the GEBV according to vanRaden (2008) and, in this case, K=G. According to de los Campos et al. (2010), .

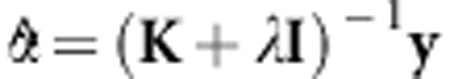Spectral decomposition

Following the previous line of reasoning, and as g=Kα, then equation. 11A can be written as y=g+ɛ. Owing to the fact that K=G is a symmetric matrix, it can be expressed as K=ΔΨΔ′, where Δ contains the eigenvectors of K(ΔΔ′=I), and Ψ={Ψ_j} is a diagonal matrix with the eigenvalues of K(with j=1,2,…,g). Then model y=g+ɛ can be reformulated as

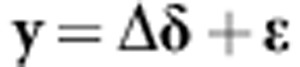where δ=ΨΔ′α∼N(0,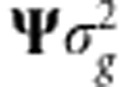) and 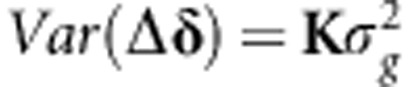. Evidently, as δ∼N(0,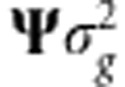), then Δδ∼N(0,).

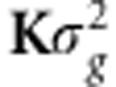Singular value decomposition

Note that y=Kα+ɛ, y=g+ɛ and y=Δδ+ɛ are not generally used in GS. Usually, in GS the model expressing the regression of phenotype on markers is defined in equation 1A, where X was already defined and β∼N(0,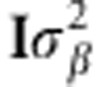) is the vector with the marker effects. Then, the singular value decomposition of X is X=UDV′, where U and V denote the left and right eigenvectors of matrix X, and 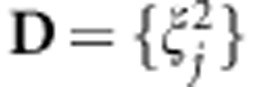is the diagonal matrix with the singular values of matrix X. Defining δ=DV′β, it can be shown that (1A) can be written as in de los Campos et al. (2010):

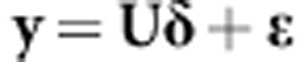where δ=DV′β∼N(0,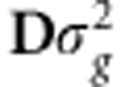). This indicates that regressing phenotypes on all markers is equivalent to regressing phenotypes on all principal components. This reparameterization of the original model based on eigenvalue decomposition accounts for possible unrevealed population structures existing in the training set.

Nonlinear models

Single hidden layer feed-forward neural network (NN)

We follow the symbols and sequence outlined by Pérez et al. (2012) with the structure of the NN depicted in Figure A1 (originally presented by Gonzalez-Camacho et al. (2012), and later adapted by Perez et al. (2012)) This NN can be thought of as a two-step regression (for example, Hastie et al., 2009). In the first step, in the hidden layer, input variables x_i= (x_i1,...,x_ip) (j=1,…,p markers) are combined for each neuron (k=1,…,S neurons), using a linear function, 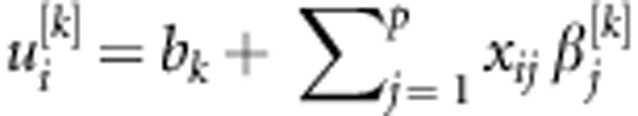, and subsequently transformed using a nonlinear activation function, yielding a set of inferred scores, 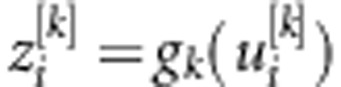, where g_k(.) is the activation function that maps the inputs into the real line in the closed interval [−1,1]. One computes 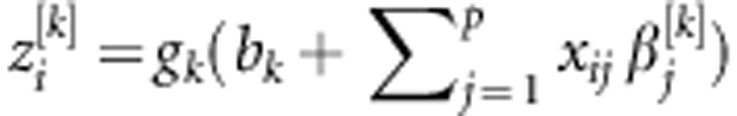, where b_k is an intercept, and (β₁^[1],…, β_p^[1];… β₁^[S],…, β_p^[S])' is a vector of regression coefficients or ‘weights' of each neuron k in the hidden layer. In the second step, these scores are used in the output layer as basis functions to regress the response using the linear activation function on the data-derived predictors, such that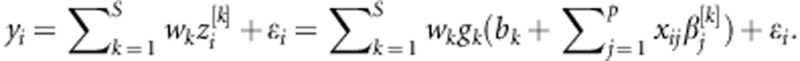

Radial Basis Function Neural Network (RBFNN)

The architecture of a single hidden layer RBFNN with S nonlinear neurons is similar to that of the single hidden layer feed-forward neural network. The only difference is that each nonlinear neuron in the hidden layer has a Gaussian RBF defined as 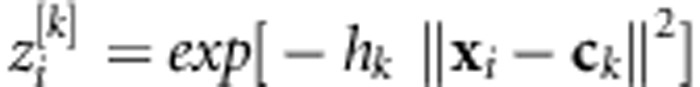, where 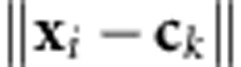is the Euclidean norm between the input vector, x_i, and the center vector, c_k, and h_k is the bandwidth of the Gaussian RBF. Then, in the linear output layer, phenotypes are regressed on the data-derived features, 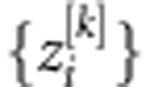; thus the response phenotype is 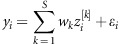, where ɛ_i is a model residual.

Reproducing Kernel Hilbert Spaces (RKHS) Regression

RKHS models have been suggested as an alternative to multiple linear regressions for capturing complex interaction patterns that may be difficult to account for in a linear model framework (Gianola et al., 2006). In a RKHS model, the regression function takes the following form:

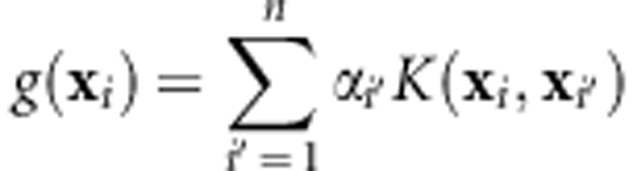where x_i=(x_i1,…x_ip)′ and x_i′=(x_i′1,…x_i′p)′ are input vectors of marker genotypes in individuals i and i', α_i are regression coefficients, and 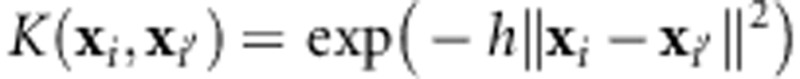is the reproducing kernel defined (here) with a Gaussian basis function, where h is a bandwidth parameter and 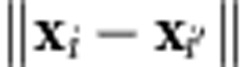is the Euclidean norm between pairs of input vectors. The strategy termed ‘kernel averaging' for selecting optimal values of h within a set of candidate values was implemented using the Bayesian approach described in de los Campos et al. (2010). Similarities and connections between the RKHS and the RBFNN are given in Gonzalez-Camacho et al. (2012).

The authors declare no conflict of interest.