LigandRNA: computational predictor of RNA–ligand interactions

LigandRNA is a novel program for scoring and ranking ligand poses in RNA 3D structures, based on a statistical potential. It is available free of charge as a web server at http://ligandrna.genesilico.pl. It can be run for a single RNA–ligand complex as well as for a list of ligand poses generated by any third-party docking program. For ligand poses generated by Dock6, it is possible to obtain a consensus score (Dock6 + LigandRNA).

Abstract

RNA molecules have recently become attractive as potential drug targets due to the increased awareness of their importance in key biological processes. The increase of the number of experimentally determined RNA 3D structures enabled structure-based searches for small molecules that can specifically bind to defined sites in RNA molecules, thereby blocking or otherwise modulating their function. However, as of yet, computational methods for structure-based docking of small molecule ligands to RNA molecules are not as well established as analogous methods for protein-ligand docking. This motivated us to create LigandRNA, a scoring function for the prediction of RNA–small molecule interactions. Our method employs a grid-based algorithm and a knowledge-based potential derived from ligand-binding sites in the experimentally solved RNA–ligand complexes. As an input, LigandRNA takes an RNA receptor file and a file with ligand poses. As an output, it returns a ranking of the poses according to their score. The predictive power of LigandRNA favorably compares to five other publicly available methods. We found that the combination of LigandRNA and Dock6 into a “meta-predictor” leads to further improvement in the identification of near-native ligand poses. The LigandRNA program is available free of charge as a web server at http://ligandrna.genesilico.pl.

INTRODUCTION

Functions of many RNAs depend on their interactions with other molecules in the cell (Rivas and Eddy 2001; Thomas and Hergenrother 2008; Fulle and Gohlke 2010; Dieterich and Stadler 2013). In particular, many regulatory RNA molecules exert their function by interacting with small molecule ligands. Examples include riboswitches, which are mRNA-embedded elements that can directly bind a ligand and thus regulate the gene function without the need for protein cofactors (Montange and Batey 2008). Ligands that bind to riboswitches range from very simple molecules, such as ions (Baker et al. 2012), to amino acids (Mandal et al. 2003) and to more complex metabolites like vitamin B₁₂ (Warner et al. 2007), thiamine pyrophosphate (TPP) (Mironov et al. 2002), flavine mononucleotide (FMN) (Winkler et al. 2002), and many others (Garst et al. 2011). The fact that riboswitches are common in bacterial cells and rarely occur in eukaryotic cells makes them particularly attractive as targets for antibacterial drugs (Blount and Breaker 2006).

Another well-studied group of bacterial RNAs that are drug targets (in particular antibiotics) are rRNAs, the molecules that form the active site of ribosomes. Many antibiotics act by binding specifically to the most important sites of the ribosome that are largely formed by the RNA: the peptidyl transferase center (PCT) in the large subunit, the decoding center in the small subunit, or the protein exit channel (for review, see Poehlsgaard and Douthwaite 2005). Viral RNA can also be a drug target; e.g., aminoglycosides can also act as inhibitors of the dimerization initiation site of HIV-1 RNA (Ennifar et al. 2006), self-splicing group I introns (Park et al. 2000), ribozymes of hepatitis delta virus (Chen et al. 1997), and hammerhead ribozymes of several plant viroids (Borda and Sigurdsson 2004). Considerable effort has been directed at finding compounds that target HIV-1 TAR RNA (Bannwarth and Gatignol 2005). Thus, RNA can be now considered an important class of potential therapeutic targets (for reviews, see Thomas and Hergenrother 2008; Aboul-ela 2010).

Another area of practical application of RNA–ligand interactions is the use of RNA aptamers as biosensors (Wang et al. 2011) and tools for imaging intracellular metabolites and signaling molecules (Paige et al. 2012).

The analysis of the atomic details of RNA–ligand interactions is greatly facilitated by the availability of high-resolution structures of RNA–ligand complexes. However, the experimental structure determination for RNA and its complexes is challenging and currently cannot be accomplished in a high-throughput manner. This has motivated the development of computer software for modeling of RNA–ligand complex structures based on the available structures of RNA receptors. Some of these developments were inspired by analogous methods created earlier for modeling of protein–ligand complexes (for review, see Bottegoni 2011).

Morley and Afshar (2004) were among the first who created a scoring function specific for RNA–ligand complexes. They expanded their proprietary high-throughput docking program by the empirical regression-based function RiboDock (or rDock) to deal with RNA–ligand complexes. However, this method was parameterized and tested on a limited set of only 10 RNA molecules. Moitessier et al. (2006) developed another scoring function dedicated exclusively to the prediction of interactions between RNA and aminoglycoside antibiotics. The function was implemented in the AutoDock program (Morris et al. 2009). An important feature of this method is that it allows for both ligand and RNA flexibility.

DrugScoreRNA is a general-purpose, knowledge-based function for scoring RNA–ligand complexes developed by the Gohlke group (Pfeffer and Gohlke 2007). It employs a distance-dependent potential calculated on the basis of contacts between ligand and receptor atoms, as in the DrugScore method for scoring protein–ligand complexes (Gohlke et al. 2000). This approach presumes that the relative strength of interactions between a ligand atom of type x and a nucleic acid atom of type y separated by the distance r can be predicted from the normalized radial pair-distribution function. The distribution function was derived from known complexes in the form of contact statistics. Ligand and nucleic-acid atom types were patterned following the Tripos atom types notation (SYBYL Molecular Modeling Software, 7.3).

Dock6 is a docking suite of programs originally developed for docking small molecule ligands to protein structures, but recently its functionalities were also extended to include RNA–ligand docking (Lang et al. 2009). Dock6 is a highly configurable program with many options, so expert knowledge is required to run calculations. There are several approaches to the sampling of the poses (e.g., using chemical matching), and there are nine built-in scoring functions, differing in speed and theoretical foundations. The default scoring function is a grid-based score, based on the nonbonded terms of the AMBER molecular mechanics force field (Kuntz et al. 1982). The force-field type is defined by the user, as both the receptor and the ligand require an initial preparation with external tools, e.g., Chimera (Pettersen et al. 2004).

Guilbert and James (2008) have also addressed the RNA–ligand docking problem by applying a classical molecular mechanics force field to the receptor and the ligand in their docking procedure MORDOR, similar to the methodology used by Dock6. Their method requires receptor and ligand preparation and allows for both ligand and receptor flexibility. The predictive power of both Dock6 and MORDOR was reported to be comparable, but Dock6 is three to 10 times faster (Lang et al. 2009).

Almost all of the aforementioned scoring methods (except DrugScoreRNA) are integrated with particular docking programs and cannot be easily used to evaluate RNA–ligand complexes generated by other methods. Researchers interested in RNA–ligand docking and modeling of RNA–ligand structures would benefit from the availability of a scoring function that is software-independent and can rank and validate models of RNA–ligand complexes regardless of the procedure used to generate them. The lack of a user-friendly method available as a web server capable of comparing RNA–ligand complexes generated by different modeling/docking methods motivated us to develop LigandRNA, a method for computational prediction of RNA–ligand interactions, based on methodology similar to that used successfully in our methods for predicting RNA–cation complexes, MetalionRNA (Philips et al. 2012), and RNA–protein complexes, DARS-RNP and QUASI-RNP (Tuszynska and Bujnicki 2011).

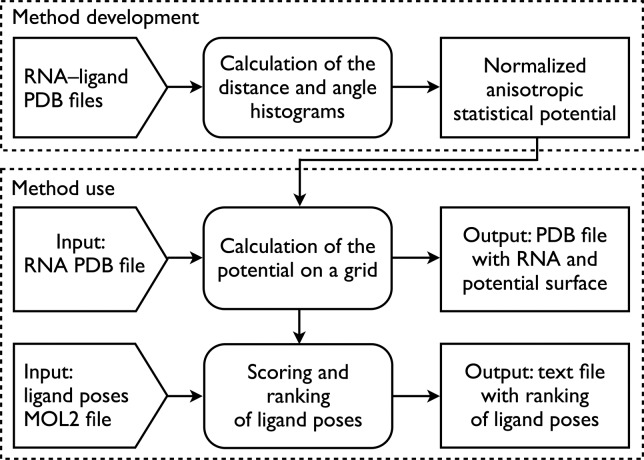
LigandRNA is based on a statistical potential derived from analysis of RNA–ligand contacts observed in 251 structures of RNA–ligand complexes. As an input, LigandRNA takes an RNA 3D structure in the Protein Data Bank (PDB) format and ligand poses in MOL2 format. It returns a ranking of ligand poses according to the scores and four variants of PDB files with the receptor structure, in which the B-factor values for surface-exposed atoms are replaced by values of the potential (for O, C, and N atoms of the ligand separately, and for all atoms combined), averaged for all cells of a grid within the distance of 2 Å form a given atom. These output files allow for visualization of relative preferences of different regions of RNA surface to interact with different atoms of the ligand, as well as to reveal regions that are potential “hotspots” for binding of small molecules in general. Figure 1 illustrates the main steps of our approach.

FIGURE 1.

The workflow of LigandRNA. Input data are indicated as arrows, calculations are indicated by boxes with rounded corners, and outputs are indicated by rectangular boxes. Contact statistics have been derived from a representative set of 251 RNA–ligand complexes. For a user-defined query RNA structure and ligand poses submitted to the LigandRNA server, the score of each ligand pose is calculated on the basis of potential distribution calculated for the query RNA structure.

RESULTS AND DISCUSSION

Statistical potential

LigandRNA is an independent grid-based program dedicated to scoring and ranking ligand poses in RNA 3D structures using a knowledge-based statistical potential. The potential is obtained using the inverse Boltzmann scheme, which presumes that only those ligand poses are favorable that exhibit interactions fitting the maxima of the statistical distribution of RNA–ligand atom contacts derived from experimentally determined structures of RNA–ligand complexes. We have used the same approach that we found successful in prediction of RNA–metal ion interactions with our method MetalionRNA (Philips et al. 2012). First, we defined a list of RNA atom pairs [a, b] in nucleotides, of which b is an atom that may directly interact with a ligand, and a is covalently bound to b (Table 1). For post-transcriptionally modified nucleotides in RNA molecules identified by ModeRNA (Rother et al. 2011), we took into account only those pairs [a, b] that were chemically identical to those in the unmodified “parent” nucleotides (for details of RNA modification pathways and relationships between the structures of modified residues and their unmodified counterparts, see the MODOMICS database) (Machnicka et al. 2013). This means that in the current version of the potential additional functional groups of modified residues (e.g., in the case of methylation) do not contribute directly to the potential, so they are only considered as steric hindrance.

TABLE 1.

RNA atom pairs used to derive RNA–ligand contacts

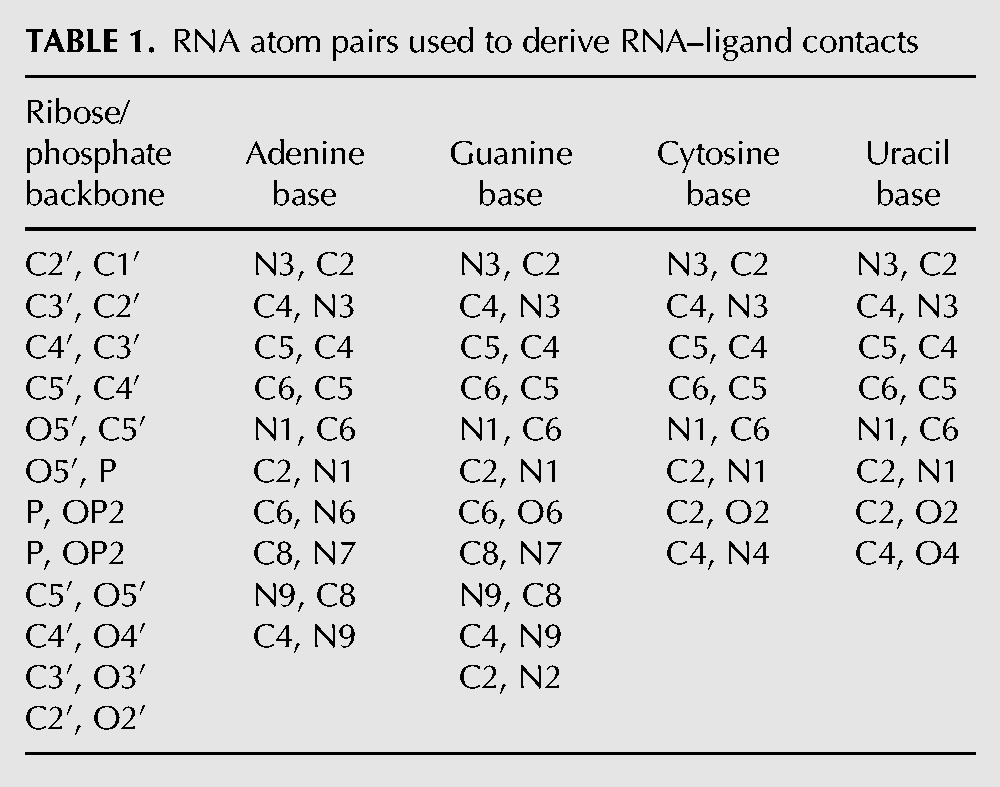
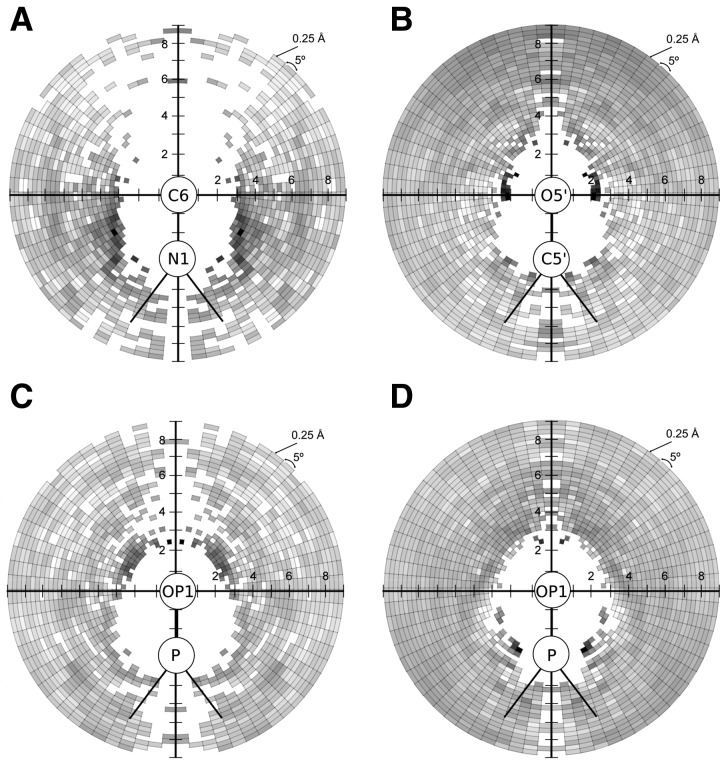
Second, we categorized ligand atoms into the following 21 Tripos atom types: carbon sp (C.1), carbon sp² (C.2), carbon sp³ (C.3), carbon in aromatic rings (C.ar), carbon in amidinium and guanidinium groups (C.cat), nitrogen sp (N.1), nitrogen sp² (N.2), nitrogen sp³ (N.3), nitrogen sp³ positively charged (N.4), nitrogen in aromatic rings (N.ar), nitrogen in amid bonds (N.am), nitrogen in amidinium and guanidinium groups (N.pl3), oxygen sp² (O.2), oxygen sp³ (O.3), oxygen in carboxylate and phosphate groups (O.co2), sulfur sp² (S.2), sulfur sp³ (S.3), sulfone sulfur (S.O2), phosphorus sp³ (P.3), fluorine (F), and chlorine (Cl). Finally, to obtain contact statistics, all the ligand atoms c were described by the distance d to the respective atom b and by the angle α (a, b, c) of an RNA pair [a, b]. To generate statistics from a set of measured values for d and α, they were discretized by statistical binning, using steps of 0.25 Å and 5°, which corresponded to a radial grid R. Next, the counts per bin were normalized since the spatial units defined by discrete steps of d and α had different sizes (the bin volume is dependent on the distance and angle). Accordingly, we divided the count of ligand atoms obtained from each d and α pair by the corresponding volume V of the radial grid R bin. Figure 3, below, illustrates the examples of potential distributions.

FIGURE 3.

The diagrams show the distribution of values for a normalized potential derived from contact statistics for the following: (A) RNA atom pair [N1, C6] from cytosine and ligand atom C.ar; (B) atom pair [C5′, O5′] from the RNA backbone and ligand atom O.3; (C) atom pair [P, OP1] from the RNA backbone and ligand atom N.3; and (D) atom pair [P, OP1] from the RNA backbone and ligand atom C.3. The darker the area, the smaller the value of the potential for the given bin. The grid used for counting uses radial steps of 0.25 Å and 5° around atom b (covalently bound to a).

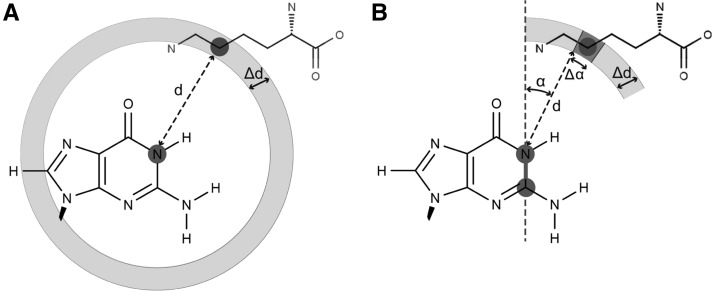
Our potential for predicting RNA–ligand interaction is to some extent similar to existing potentials such as DrugScoreRNA (Pfeffer and Gohlke 2007) in the use of a distance-dependent scoring system for groups of ligand atoms. However, it is more sophisticated, as it also takes into consideration the angles between atom pairs in RNA and individual atoms in ligands, thereby introducing anisotropy. Figure 2 illustrates the difference between the orientation-dependent potential in LigandRNA and orientation-independent potentials. In LigandRNA, the search space is divided into well-defined small regions, which enables the discrimination between different orientations of the ligand atoms that are located at the same distance with respect to the reference atom in RNA. On the other hand, in the orientation-independent potential, all such orientations are treated equally.

FIGURE 2.

Schematic representation of a distance-dependent statistical potential (A) and LigandRNA distance- and angle-dependent potential (B).

We calculated the LigandRNA statistical potential from selected 251 RNA–ligand complexes derived from the PDB. We chose complexes, in which a ligand was organic and interacted only with the RNA molecule. For RNAs with sequence identity >90% and interacting with the same ligand, only the structure with the highest resolution was taken. For tests, all previously selected RNA–ligand complexes were manually clustered according to their ligand's chemical structure class (e.g., kanamycin, tobramycin, or geneticin belong to the “kanamycin-like” cluster, arginine to the “amino acid” cluster, and adenine to the “purine” cluster). In total we defined 62 different clusters.

RNA–small molecule statistical preferences

The distribution of statistical potential values reflects the preferred interaction geometries. Figure 3 illustrates the preference for selected aromatic, polar, and charge–charge interactions. In Figure 3A, favorable binding geometries are shown for the cytosine atom pair [N1, C6] and the ligand atom C.ar. Here, long-distance interactions are preferable and are clearly orientation-dependent. The diagram shows that the preference for aromatic interaction starts at the distance of ∼3.5 Å, with the minimum blurred at the angle 90°–180°. The grid cells marked white around the RNA atoms [N1, C6] indicate the lack of RNA–ligand atoms’ contacts in the training set. The potential distribution function for the atom pair [C5′, O5′] from the RNA backbone and the ligand atom O.3 (Fig. 3B) has a peak tuple (the darkest areas), which corresponds to the favorable positions of a ligand atom O.3. The peak tuple is present at a distance of ∼2–2.5 Å, with an angle in the range of 60°–90°, which corresponds to a typical direct interaction involving a hydrogen bond. Dark gray areas on the plot indicate a general preference for indirect (e.g., water-mediated) interactions between the RNA O5′ atom and ligand O.3 atoms positioned at larger distances, however, without strong preference for any particular angle. Figure 3C shows the potential distribution for interactions between the atom pair [P, OP1] from RNA backbone and the ligand atom N.3. Here, the potential minimum is at a close distance to the RNA atoms, at ∼2.5–3 Å, with an angle of 20°–65°. In Figure 3D favorable binding geometries are shown for the atom pair [P, OP1] and the ligand atom C.3. The interaction is preferred at 2.25–2.75 Å with an angle of 10°–20° and at 3.25–3.75 Å with an angle of 145°–155°, while there are no specific preferences for long-range interactions.

LigandRNA predicts RNA–ligand interactions with high accuracy

To test the ability of LigandRNA to discriminate between native-like and non-native-like poses of small molecule ligands with respect to their RNA receptors and to compare its performance to other methods, we ran a benchmark with separate training and test data sets. We clustered ligands according to their chemical structure and applied a cross-validation procedure. We generated a series of leave-one-out data sets that contained all ligands except the group of small molecules belonging to the particular cluster. Then, we derived a series of LigandRNA potential variants, in which small molecules belonging to a particular cluster were excluded from training (so they could be used for testing that variant of the potential). Next, we selected representative structures from each cluster and generated a few hundred ligand poses with Dock6 (with the average of 798 per ligand). For our benchmark, we used 42 complexes, for which Dock6 was able to generate at least one pose with root mean square deviation of all atoms (RMSD) ≤2 Å to the reference experimental structure (this restriction results from the fact that LigandRNA and DrugScoreRNA are scoring functions for evaluation of ligand poses and would never find a near-native solution [RMSD ≤2 Å] in the data set, where such poses are not present). The poses generated by docking were then scored with LigandRNA, DrugScoreRNA, and combinations of the aforementioned potentials (including the Dock6 scoring function) (Tables 2, 3).

TABLE 2.

The results of test for 42 RNA–ligand complexes

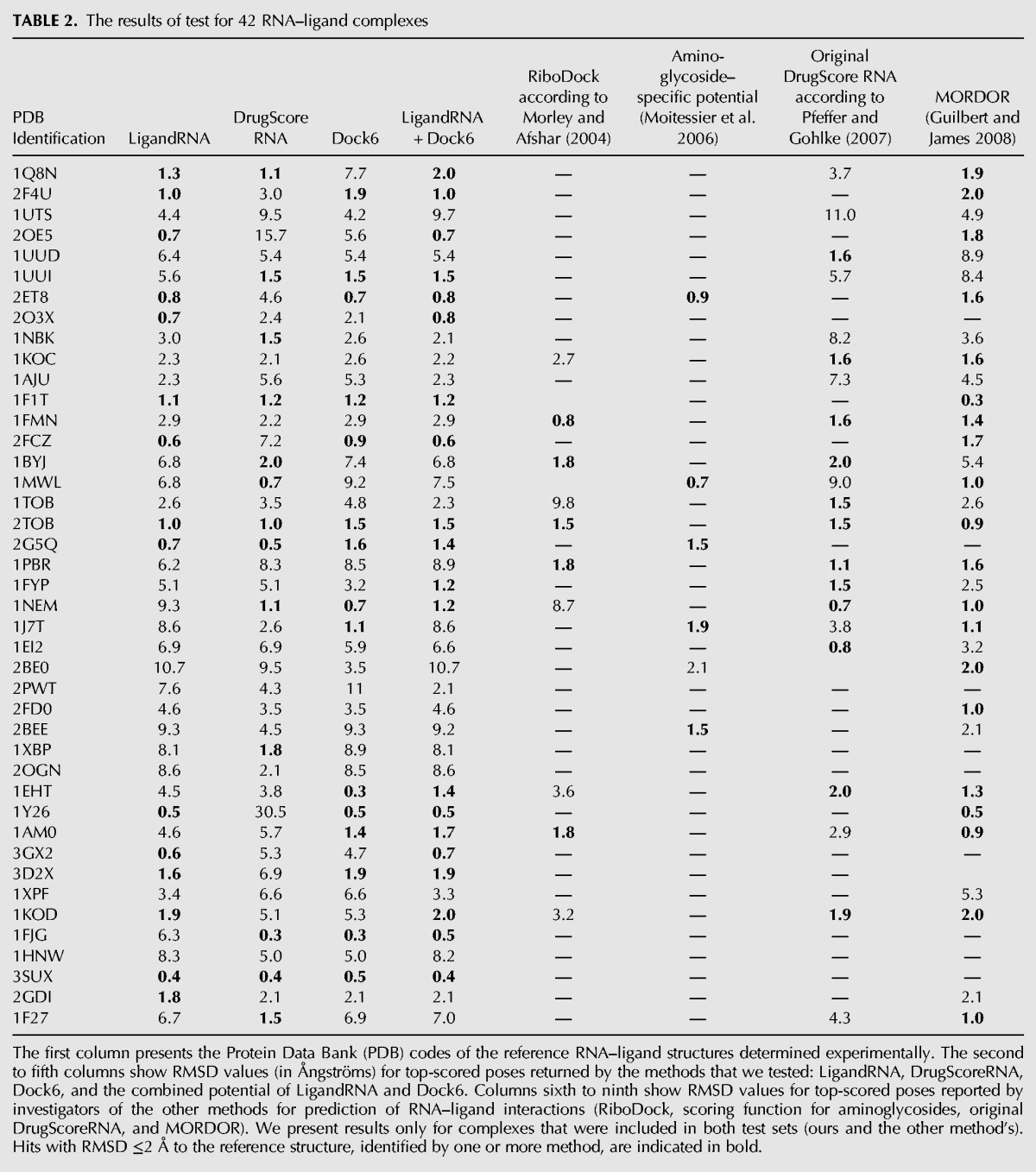
TABLE 3.

The results of test for 42 RNA–ligand complexes

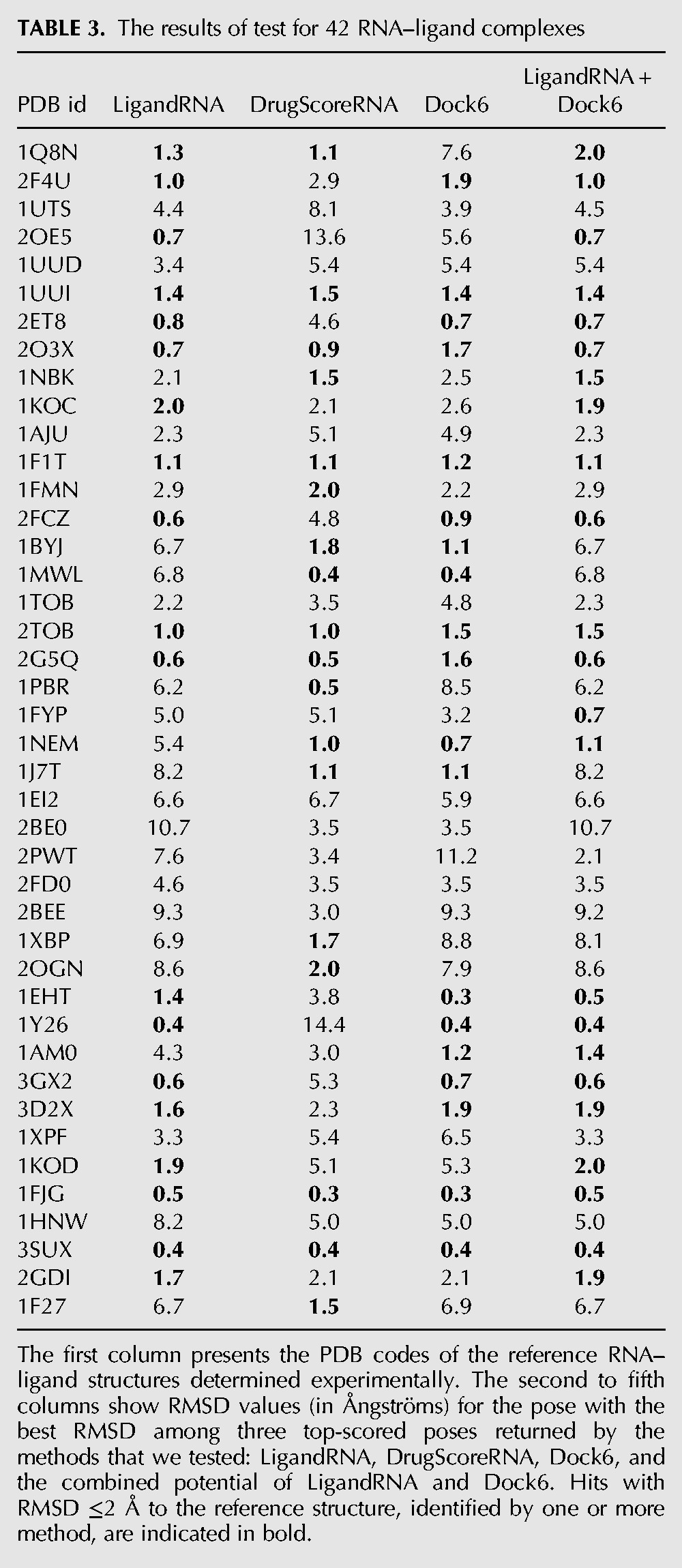
Users of docking methods are typically interested in obtaining a native-like model of a receptor–ligand complex, and for that purpose, a few top-scored poses are usually examined. We have therefore identified the three top-scoring poses reported for each RNA–ligand pair, and we identified the fraction of solutions, in which either the top-scoring pose or one among the three top-scoring poses exhibited a native-like structure.

If only the top-scoring pose was considered, LigandRNA found the best solution with RMSD ≤2 Å to the native structure in 15 cases, DrugScoreRNA in 13 cases, and Dock6 in 15 cases; the combined potential of LigandRNA and Dock6 gave the best result among all methods, as it found solutions with RMSD ≤2 Å to the reference structure in 20 cases (Table 2). Our test set comprises mostly complexes included in test sets of other methods described in the Introduction (RiboDock, scoring function for aminoglycosides, original DrugScoreRNA, and MORDOR), so we were able to compare the results obtained in our study for a subset of these complexes to the results reported for the aforementioned methods in original publications. RiboDock found solutions with RMSD ≤2 Å in five cases out of 10; Moitessier's potential for aminoglycosides returned a pose with RMSD ≤2 Å in five out of six cases; the original DrugScoreRNA potential found a near-native pose in 12 out of 21 cases; and MORDOR generated near-native poses in 20 out of 32 cases. If three top-scoring poses were considered, LigandRNA, DrugScoreRNA, and Dock6 performed similarly and found the near-native pose (with RMSD ≤2 Å to the reference structure) in 19, 18, and 19 cases, respectively. The combined potential of LigandRNA and Dock6 again gave the best result among all methods, as it found a solution with RMSD ≤2 Å to the reference structure in 23 cases (Table 3).

Further, we checked whether the top-ranked pose identified by LigandRNA, DrugScoreRNA, Dock6 and the combination of LigandRNA and Dock6 fulfilled the criterion of being “native-like,” i.e., whether its RMSD from the experimentally determined reference pose was below a threshold of 1.0, 1.5, or 2 Å, respectively. We performed calculations for two groups of targets: all cases, where Dock6 was able to generate at least one pose with RMSD to the reference experimental structure ≤2 Å (Table 4), and a subset of that group, in which at least one pose had RMSD to the reference ≤1 Å (Table 5).

TABLE 4.

The results of the test conducted for 42 RNA–ligand complexes with at least one ligand pose with RMSD ≤2 Å

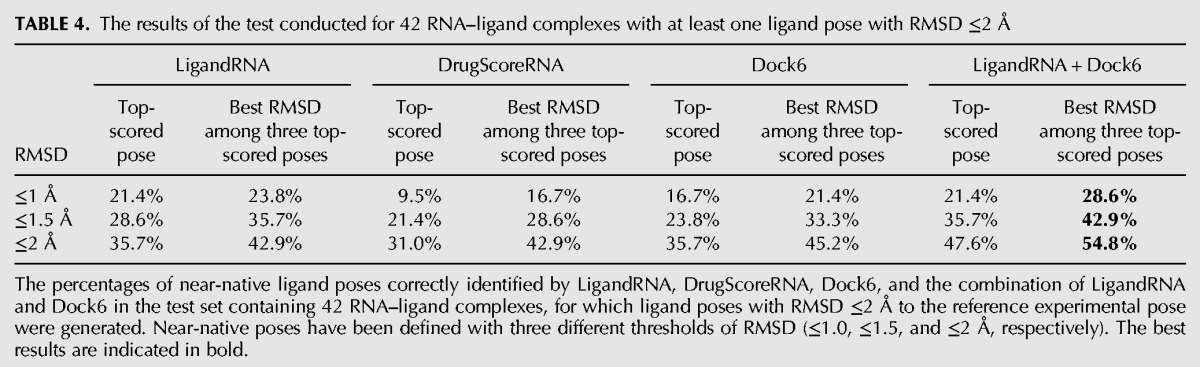
TABLE 5.

The results of the test conducted for 21 RNA–ligand complexes with at least one ligand pose with RMSD ≤1 Å

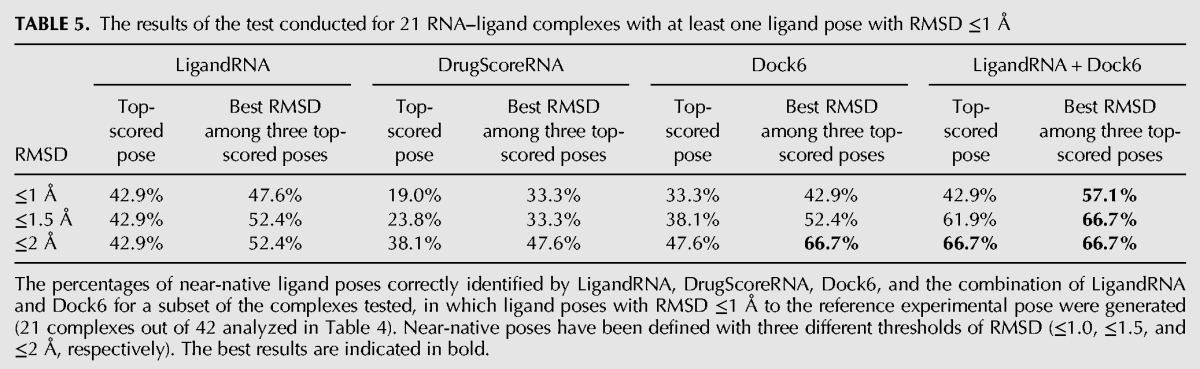
Our benchmarks show that individual potentials are moderately effective in identifying poses that are close to the experimentally determined structures. Among 42 structures of RNA–ligand complexes, for which the docking procedure was able to generate at least one pose with RMSD ≤2 Å to the native structure, top-scored solutions proposed by LigandRNA, DrugScoreRNA, and Dock6 had RMSD ≤2 Å in 35.7%, 31.0%, and 35.7% of the cases, respectively. If the criterion is relaxed to consideration of the best solution among three top-scoring poses, the percentage of successful solutions identified by the above-mentioned methods increases to 45.2%, 42.9%, and 45.2%. The number of top-scoring poses with RMSD to the reference structure ≤1 Å was lower, 21.4%, 9.5%, and 16.7%, respectively, and 23.8%, 16.7%, and 21.4% if three top-scoring solutions were considered. If only complexes for which the docking procedure was able to generate at least one pose with RMSD ≤1 Å to the native structure were considered, top-scoring solutions proposed by LigandRNA, DrugScoreRNA, and Dock6 had a RMSD ≤1 Å in 42.9%, 19%, and 33.3% of all cases and a RMSD ≤2 Å in 42.9%, 38.1%, and 47.6% of cases, respectively. If three top-scoring solutions were taken into consideration, one of them had RMSD ≤1 Å in 47.6%, 33.3%, and 42.9% of all cases and RMSD ≤2 Å in 52.4%, 47.6%, and 66.7% of all cases for LigandRNA, DrugScoreRNA, and Dock6, respectively. Thus, LigandRNA was generally better than DrugScoreRNA and comparable to Dock6.

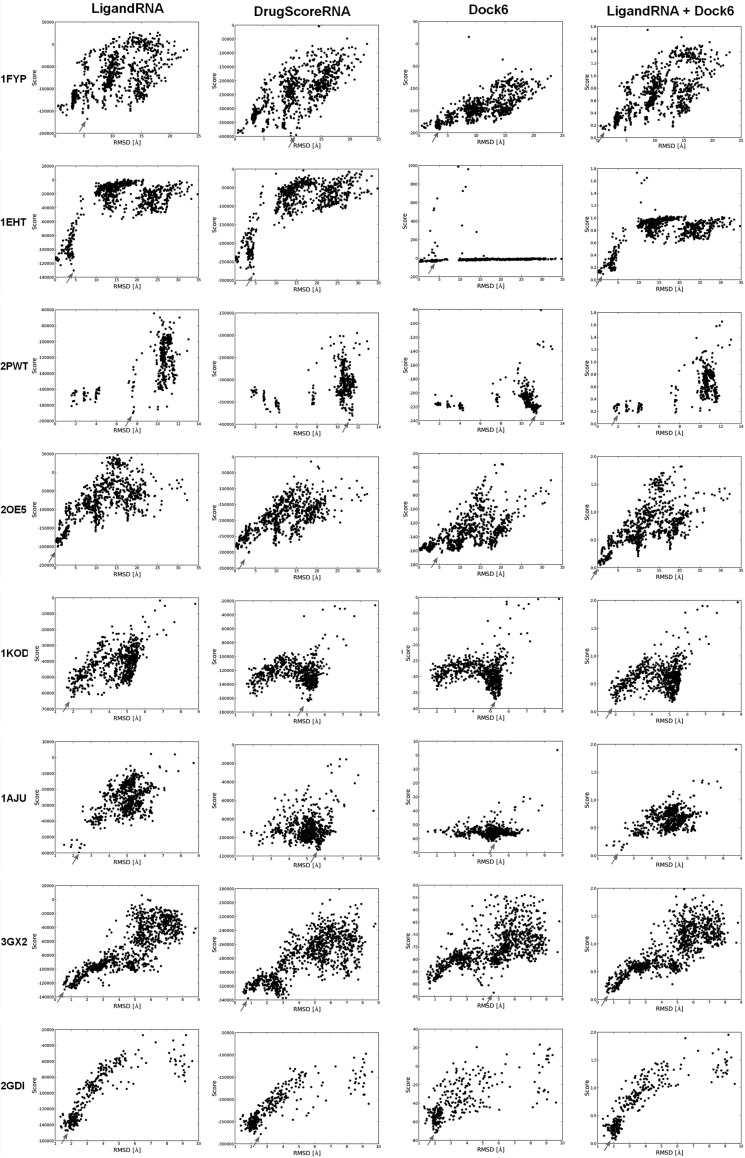
We tested various combinations of the individual scoring functions (data not shown), and we found that a “meta-predictor” comprising Dock6 and LigandRNA improves the accuracy of individual predictions. The combination of the Dock6 and LigandRNA scoring function achieves 47.6% correctly identified ligand poses (with RMSD ≤2 Å to the native structure) when all 42 structures are considered and achieves 66.7% correctly identified ligand poses for data sets where at least one pose exists with RMSD to the native structure ≤1 Å. If three top-scoring ligand poses are considered, the percentages are of 54.8% and 66.7%. As expected, the combination of the potentials not only increases the chances of the top-scoring pose to be close to the experimentally determined structure but also gives the best overall correlation coefficient between score and RMSD values of the corresponding ligand poses. Thus, the combination of LigandRNA and Dock6 scoring outperforms both individual methods alone. Figure 4 illustrates examples of eight complexes where the combined potential improved the correlation and identified a native-like ligand pose.

FIGURE 4.

Score-RMSD dependence for the selected RNA–ligand complexes from the test set. Each black dot corresponds to a single ligand pose. Arrows indicate top-scored poses according to each method.

Web server

To make our method available to the research community, we developed the LigandRNA web server available at http://ligandrna.genesilico.pl (server mirror is available at http://ligandrna.biol.amu.edu.pl). The server was implemented in Python using the Django web framework. The LigandRNA potential available on the server was derived from all 251 PDB structures used in this work for training and testing. The submission form accepts coordinates of an RNA receptor structure in the PDB format and a ligand conformers file in the MOL2 format. For Dock6 output files, it is possible to obtain a consensus score (combination of Dock6 and LigandRNA potentials); however, the current implementation of the server is unable to calculate Dock6 scores by itself, so poses generated with other methods are scored only with the LigandRNA potential. The results returned by the server are made available on a separate web page, which provides a file with the ranked ligand conformers in text format. Moreover, LigandRNA returns four PDB files containing the RNA receptor structure with the four variants of the LigandRNA potential mapped on individual atoms of the receptor (averaged for all grid cells within 2 Å from a given atom), for O, C, and N atoms of the ligand separately and for all atoms combined. With such modified PDB files, the distribution of LigandRNA potential values on surface atoms can be easily displayed in all commonly used structure visualization systems by coloring atoms according to the B-factor field.

The output files are kept on the server for 1 wk. The time required for LigandRNA to return predictions depends mainly on the size of the RNA molecule and the number of ligand poses to score. Currently we use a simple queuing system that allows running one prediction at a time. For a bacterial ribonuclease P RNA (PDB identification 2A64) that is 417 nucleotides long and has 236 paromycin poses to score, it takes ∼20 min to obtain the results. For comparison, the same number of poses for this complex can be scored by DrugScoreRNA in a few seconds and by Dock6 in a few minutes.

LigandRNA is a novel computational tool for scoring and ranking three-dimensional poses of small molecule ligands bound to RNA 3D structures. It uses an anisotropic statistical potential trained on a database of known RNA–ligand complexes. The current implementation is capable of making predictions for RNA structures in the PDB format and ligand poses in the MOL2 format. The LigandRNA scoring function was trained and tested on a representative set of 251 RNA–ligand complexes, using a leave-one-out cross-validation. The test proved the predictive power of LigandRNA, as the method successfully reproduced the experimentally determined positions of ligands in many different RNA molecules and the fraction of its best solutions was comparable to or better than other methods. LigandRNA was able to find correct docking solutions in two cases, where native-like solutions were missed by the other methods tested in this study: for citrulline bound to an RNA aptamer (PDB identification 1KOD; pose RMSD of 1.9 Å) and for the apramycin antibiotic bound to the ribosomal decoding center (PDB identification 2OE5; pose RMSD of 0.7 Å). Both structures are shown in Figure 5. Dock6 proposed poses with RMSD of 5.3 Å for citrulline and with RMSD of 5.6 Å for apramycin as the best solutions, DrugScoreRNA similarly proposed poses with RMSD of 5.1 Å and 15.7 Å for the two ligands, respectively. However, there are structures for which LigandRNA failed in finding a near-native ligand pose but other methods succeed (e.g., PDB identifications 1UUD and 1NEM). For that reason, we decided to score ligand poses with a combination of scores returned by two methods with very different scoring functions, i.e., LigandRNA and Dock6. Both scores were scaled to a range of <0,1> and added to each other with equal weights of 0.5, as their separate predictive powers were similar (Tables 4, 5). The number of best solutions identified by the combined potential was higher than the number of best solutions reported by either of the methods used separately. In our test set, we also found two cases where the combined potential identified a native-like pose that was missed by all potentials applied alone: for an aminoglycoside with the L-HABA group bound to the bacterial ribosomal decoding site (PDB identification 2PWT, pose RMSD of 2.0 Å) and for paromycin bound to the decoding region A-site (PDB identification 1FYP; pose RMSD of 1.2 Å) (Fig. 6).

FIGURE 5.

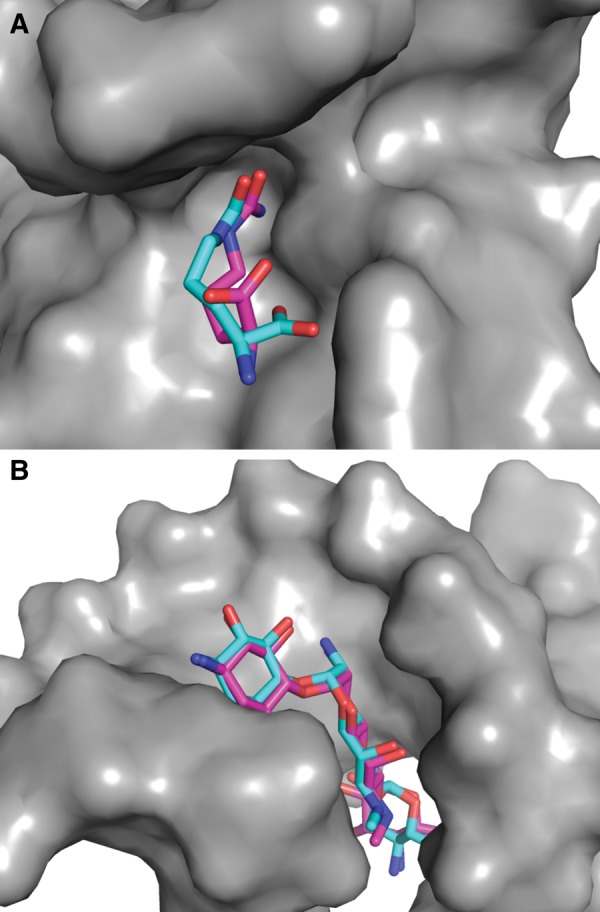
(A) The RNA aptamer structure in complex with citrulline (PDB identification 1KOD). (B) The ribosomal decoding center in complex with apramycin (PDB identification 2OE5). The experimentally identified ligand poses are shown in light blue, and the poses from computational docking identified as best-scored by LigandRNA are depicted in pink.

FIGURE 6.

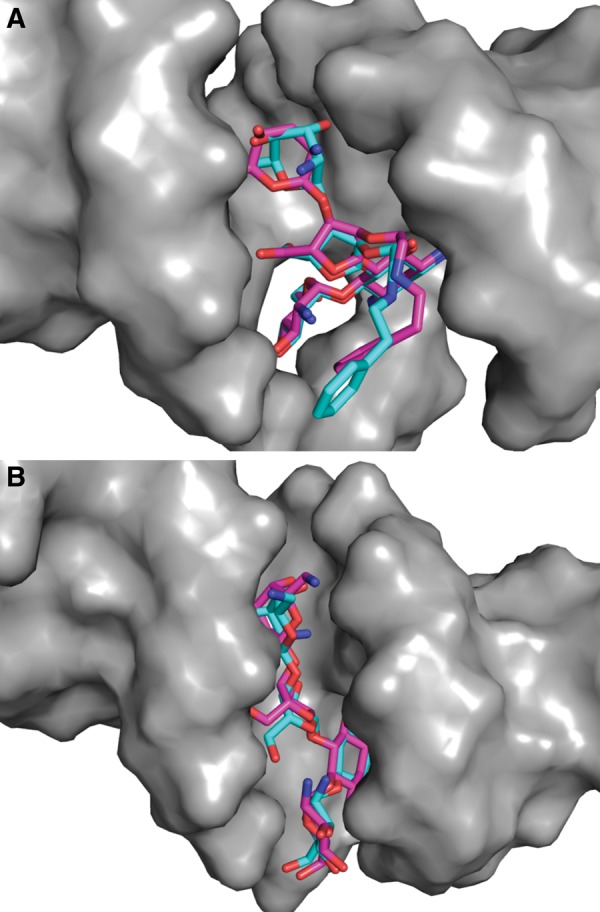
(A) The ribosomal decoding site in complex with aminoglycoside with the L-HABA group (PDB identification 2PWT). (B) The A-site decoding region in complex with paromycin (PDB identification 1FYP). The experimentally identified ligand poses are shown in light blue, and the poses from computational docking identified as best-scored by a combination of LigandRNA and Dock6 potentials are depicted in pink.

The added value of the combination of LigandRNA and Dock6 results most likely from the very different, and hence complementary, character of both scoring functions. LigandRNA is a knowledge-based statistical potential, while Dock6 scores ligand poses on the basis of a physics-based force field. The advantage of Dock6 is that it models the physical chemistry of the system; however, the use of this method is computationally costly and requires specialized expertise to set up and run the docking, and it is impossible to use Dock6 to score the poses obtained by other methods.

Conclusions

We have developed LigandRNA, a novel bioinformatics tool for the prediction of RNA–small molecule interactions. The anisotropic potential in LigandRNA contributes significant added value to the previously published scoring functions. In particular, the combination of the LigandRNA statistical potential and the Dock6 physics-based force field leads to much better identification of native-like poses. Thus, wherever it is possible to use Dock6 for RNA–ligand docking, we recommend using LigandRNA together with that method. LigandRNA is relatively fast and can be accessed via a freely available web server at http://ligandrna.genesilico.pl/ and at http://ligandrna.biol.amu.edu.pl. The input ligand poses are ranked according to their score, which can be used to infer the relative strength of binding.

One of the weaknesses of the statistical approach presented in this work is the relative paucity of RNA–ligand complexes. Thus, once per week (every Saturday at 1200 h Central European Time) the LigandRNA web server downloads structures of RNA–ligand complexes newly released in the PDB, which fulfill the conditions described in the section “Data set of RNA–ligand complex structures.” These structures are added to the original training set, and the statistical potential is recalculated. In time, the number of structures will increase, hopefully leading to a constant improvement of the potential. The LigandRNA website allows the user to select whether to perform predictions with the original potential described in this article or with the one that is being continually updated.

MATERIALS AND METHODS

Data set of RNA–ligand complex structures

To generate a knowledge-based potential, we used a representative set of 251 crystallographically determined and NMR-determined structures containing RNA and ligands (including structures of, e.g., protein–RNA complexes), available from the PDB. The list of PDB identifications and PDB files is provided on the LigandRNA server home page. Initially, we downloaded all the structures that contained an RNA molecule and a ligand and subsequently applied a series of criteria to select representative structures: For RNAs with sequence identity >90% containing the same ligand, we used only one structure with the highest resolution. For NMR structures, we always used the first model in the file. For residues with more than one alternative conformation, we used the first variant only. We excluded ligands closer than 6 Å to any atom other than RNA, water, or a cation, as we intended to take into account only ligands interacting exclusively with RNA atoms, whose binding is not caused by other molecules.

To test the predictive power of LigandRNA, we clustered ligands according to their chemical structure. Ligands were grouped manually according to the following criteria: (1) Ligands smaller than 13 atoms were classified into the “small organic” group; (2) ligands belonging to a major class of metabolites or organic species (pyranoses, amino acids, etc.) were grouped together according to that class; (3) antibiotics sharing a central chemical structure (e.g., tetracyclins) were grouped together; (4) compounds sharing a common substructure of at least six atoms were grouped together; and (5) the remaining compounds remained as single members of their respective classes. Next, we performed docking using Dock6 with default parameters with respect to the usage of the following: grid-score function, flexible ligand docking, all atom model, automated matching, internal energy calculation, with special options such as bump filter, chemical matching, secondary scoring, etc., disabled (for details, see Supplemental File 1). The standard all-atom CHARMM27 force field (MacKerell et al. 2000) for the RNA receptors and the general AMBER force field for ligands (Case et al. 2005) were used. We performed docking for at least one representative of each cluster of related ligands (more than one if their RNA targets were different) to guarantee the diversity of receptors and ligands. In our selection of representatives, we favored complexes that were previously used for training and testing RNA docking methods by other groups. In our test set, we included all 10 cases used by RiboDock (Morley and Afshar 2004), six out of 11 from a scoring function specific for aminoglycosides (Moitessier et al. 2006), 21 complexes out of 32 from the test set used by DrugScoreRNA (Pfeffer and Gohlke 2007), 32 out of 57 used by MORDOR (Guilbert and James 2008), and 30 out of 52 used by Dock6 (Lang et al. 2009). Our test set includes complexes used for the accuracy assessment with respect to how docking programs developed for protein–ligand complexes perform against RNA–ligand complexes (20 targets out of 36 used by Detering and Varani 2004 and 33 targets out of 60 used by Li et al. 2010). Altogether, we obtained between 69 and 1000 ligand poses (with the average of 798 per ligand) for 42 RNA receptors (for details, see Supplemental Table 1), for which we were able to generate at least one ligand pose with ≤2 Å RMSD to the experimentally determined one, which was regarded as a reference pose structure. All receptor–ligand complexes had their Dock6 score associated, and they were subjected to additional scoring using the LigandRNA and DrugScoreRNA scoring functions (we used all of the poses generated, regardless of their Dock6 scores).

Compilation of an anisotropic statistical potential

For the derivation of the statistical potential, we applied the same formalism as already described for MetalionRNA, a program for the prediction of RNA–metal ion binding sites (Philips et al. 2012). We developed a distance- and angle-dependent anisotropic potential describing interactions between ligand atoms and RNA atom pairs. An n-particle correlation function parametrized by interparticle distances and angles g⁽ⁿ⁾(d₁, α₁;… d_n, α_n) is translated into a knowledge-based potential W⁽ⁿ⁾(d₁, α₁;… d_n, α_n) via the following equation:

where g⁽ⁿ⁾ indicates the observed frequency of contacts of a ligand atom c with all adjacent atom pairs [a, b] (d is the distance between a ligand atom and atom b; α is the angle (a,b,c)), and W⁽ⁿ⁾ indicates the potential for a given position. We derived the function g⁽ⁿ⁾(d₁, α₁;… d_n, α_n) from 3D structures by sampling the frequencies of RNA atom pair and ligand atom contacts.

The maximum radius of interaction between an RNA atom pair and a ligand atom to be considered for the statistical potential was limited to 6 Å. This radius directly influences the specificity of the potential. A short distance emphasizes specific interactions between ligand and the atoms of its binding site.

Algorithm for scoring of ligand poses

We implemented a grid-based function for scoring ligand poses bound to a receptor structure. The most important advantage of using a grid is that the discretization of space obviates the need to solve the potential function analytically and allows mapping of the statistical data into well-defined portions of space. A grid-based approach has been successfully applied in our previous studies on RNA–metal ion interactions (Philips et al. 2012) and in small molecule docking, e.g., in the AutoDock program (Morris et al. 2009).

For each RNA atom pair [a, b], the LigandRNA program computes the potential values W⁽ⁿ⁾ in all cells of cubic grid C within the radius of 6 Å around the atom b. The potential values are computed for all of the atom types present in the ligand. The potential W⁽ⁿ⁾ is additive for cells of grid C at the distance of 6 Å from more than one RNA atom pair. Finally, all ligand poses are scored and ranked. The pose score is a sum of its atoms’ potentials. (All cells within the van der Waals radius of a certain ligand atom type are examined.)

SUPPLEMENTAL MATERIAL

Supplemental material is available for this article at http://ligandrna.genesilico.pl/site_media/supplementary/supp_mat.pdf.