Estimation and Selection via Absolute Penalized Convex Minimization And Its Multistage Adaptive Applications

Abstract

The ℓ₁-penalized method, or the Lasso, has emerged as an important tool for the analysis of large data sets. Many important results have been obtained for the Lasso in linear regression which have led to a deeper understanding of high-dimensional statistical problems. In this article, we consider a class of weighted ℓ₁-penalized estimators for convex loss functions of a general form, including the generalized linear models. We study the estimation, prediction, selection and sparsity properties of the weighted ℓ₁-penalized estimator in sparse, high-dimensional settings where the number of predictors p can be much larger than the sample size n. Adaptive Lasso is considered as a special case. A multistage method is developed to approximate concave regularized estimation by applying an adaptive Lasso recursively. We provide prediction and estimation oracle inequalities for single- and multi-stage estimators, a general selection consistency theorem, and an upper bound for the dimension of the Lasso estimator. Important models including the linear regression, logistic regression and log-linear models are used throughout to illustrate the applications of the general results.

1. Introduction

High-dimensional data arise in many diverse fields of scientific research. For example, in genetic and genomic studies, more and more large data sets are being generated with rapid advances in biotechnology, where the total number of variables p is larger than the sample size n. Fortunately, statistical analysis is still possible for a substantial subset of such problems with a sparse underlying model where the number of important variables is much smaller than the sample size. A fundamental problem in the analysis of such data is to find reasonably accurate sparse solutions that are easy to interpret and can be used for the prediction and estimation of covariable effects. The ℓ₁-penalized method, or the Lasso (Tibshirani, 1996; Chen et al., 1998), has emerged as an important approach to finding such solutions in sparse, high-dimensional statistical problems.

In the last few years, considerable progress has been made in understanding the theoretical properties of the Lasso in p ≫ n settings. Most results have been obtained for linear regression models with a quadratic loss. Greenshtein and Ritov (2004) studied the prediction performance of the Lasso in high-dimensional least squares regression. Meinshausen and Bühlmann (2006) showed that, for neighborhood selection in the Gaussian graphical models, under a neighborhood stability condition on the design matrix and certain additional regularity conditions, the Lasso is selection consistent even when p → ∞ at a rate faster than n. Zhao and Yu (2006) formalized the neighborhood stability condition in the context of linear regression as a strong irrepresentable condition. Candes and Tao (2007) derived an upper bound for the ℓ₂ loss of a closely related Dantzig selector in the estimation of regression coefficients under a condition on the number of nonzero coefficients and a uniform uncertainty principle on the design matrix. Similar results have been obtained for the Lasso. For example, upper bounds for the ℓ_q loss of the Lasso estimator has being established by Bunea et al. (2007) for q = 1, Zhang and Huang (2008) for q ∈ [1;2], Meinshausen and Yu (2009) for q = 2, Bickel et al. (2009) for q ∈ [1;2], and Zhang (2009) and Ye and Zhang (2010) for general q ≥ 1. For convex minimization methods beyond linear regression, van de Geer (2008) studied the Lasso in high-dimensional generalized linear models (GLM) and obtained prediction and ℓ₁ estimation error bounds. Negahban et al. (2010) studied penalized M-estimators with a general class of regularizers, including an ℓ₂ error bound for the Lasso in GLM under a restricted strong convexity and other regularity conditions.

Theoretical studies of the Lasso have revealed that it may not perform well for the purpose of variable selection, since its required irrepresentable condition is not properly scaled in the number of relevant variables. In a number of simulation studies, the Lasso has shown weakness in variable selection when the number of nonzero regression coefficients increases. As a remedy, a number of proposals have been introduced in the literature and proven to be variable selection consistent under regularity conditions of milder forms, including concave penalized LSE (Fan and Li, 2001; Zhang, 2010a), adaptive Lasso (Zou, 2006; Meier and Bühlmann, 2007; Huang et al., 2008), stepwise regression (Zhang, 2011a), and multi-stage methods (Hunter and Li, 2005; Zou and Li, 2008; Zhang, 2010b, 2011b).

In this article, we study a class of weighted ℓ₁-penalized estimators with a convex loss function. This class includes the Lasso, adaptive Lasso and multistage recursive application of adaptive Lasso in generalized linear models as special cases. We study prediction, estimation, selection and sparsity properties of the weighted ℓ₁-penalized estimator based on a convex loss in sparse, high-dimensional settings where the number of predictors p can be much larger than the sample size n. The main contributions of this work are as follows.

• We extend the existing theory for the unweighted Lasso from linear regression to more general convex loss function.

• We develop a multistage method to approximate concave regularized convex minimization with recursive application of adaptive Lasso, and provide sharper risk bounds for this concave regularization approach in the general setting.

• We apply our results to a number of important special cases, including the linear, logistic and log-linear regression models.

This article is organized as follows. In Section 2 we describe a general formulation of the absolute penalized minimization problem with a convex loss, along with two basic inequalities and a number of examples. In Section 3 we develop oracle inequalities for the weighted Lasso estimator for general quasi star-shaped loss functions and an ℓ₂ bound on the prediction error. In Section 4 we develop multistage recursive applications of adaptive Lasso as an approximate concave regularization method and provide sharper oracle inequalities for this approach. In Section 5 we derive sufficient conditions for selection consistency. In Section 6 we provide an upper bound on the dimension of the Lasso estimator. Concluding remarks are given in Section 7. All proofs are provided in an appendix.

2. Absolute Penalized Convex Minimization

In this section, we define the weighted Lasso for a convex loss function and characterize its solutions via the KKT conditions. We then derive some basic inequalities for the weighted Lasso solutions in terms of the symmetrized Bregman divergence (Bregman, 1967; Nielsen and Nock, 2007). We also illustrate the applications of the basic inequalities in several important examples.

2.1 Definition and the KKT Conditions

We consider a general convex loss function of the form

$$\ell (\mathrm{\beta })=\mathrm{\psi }(\mathrm{\beta })-\langle \mathrm{\beta },z\rangle ,$$ (1)

where ψ(β) is a known convex function, z is observed, and β is unknown. Unless otherwise stated, the inner product space is ℝ^p, so that {z,β} ⊂ ℝ^p and 〈β,z〉 = β′z. Our analysis of (1) requires certain smoothness of the function ψ(β) in terms of its differentiability. In what follows, such smoothness assumptions are always explicitly described by invoking the derivative of ψ. For any v = (v₁,…, v_p)′, we use ||v|| to denote a general norm of v and |v|_q the ℓ_q norm (Σ_j |v_j|^q)^1/q, with |v|_∞ = max_j |v_j|. Let ŵ ∈ ℝ^p be a (possibly estimated) weight vector with nonnegative elements ŵ_j, 1 ≤ j ≤ p, and Ŵ = diag(ŵ). The weighted absolute penalized estimator, or weighted Lasso, is defined as

$$\widehat{\mathrm{\beta }}=\underset{\mathrm{\beta }}{argmin}\left\{\ell (\mathrm{\beta })+\mathrm{\lambda }{\mid \widehat{W}\mathrm{\beta }\mid }_1\right\}.$$ (2)

Here we focus on the case where Ŵ is diagonal. In linear regression, Tibshirani and Taylor (2011) considered non-diagonal, predetermined Ŵ and derived an algorithm for computing the solution paths.

A vector β̂ is a global minimizer in (2) if and only if the negative gradient at β̂ satisfies the Karush-Kuhn-Tucker (KKT) conditions,

$$g=-\stackrel{.}{\ell }(\widehat{\mathrm{\beta }})=z-\stackrel{.}{\mathrm{\psi }}(\widehat{\mathrm{\beta }}),\{\begin{array}{cc}{g}_j={\widehat{w}}_j\mathrm{\lambda }sgn({\widehat{\mathrm{\beta }}}_j)\hfill & \text{if}{\widehat{\mathrm{\beta }}}_j\ne 0\hfill \\ g_j\in {\widehat{w}}_j\mathrm{\lambda }[-1,1]\hfill & \text{all}j,\hfill \end{array}$$ (3)

where ℓ̇(β) = (∂/∂β)ℓ(β) and ψ̇(β) = (∂/∂β)ψ (β). Since the KKT conditions are necessary and sufficient for (2), results on the performance of β̂ can be viewed as analytical consequences of (3).

The estimator (2) includes the ℓ₁-penalized estimator, or the Lasso, with the choice ŵ_j = 1, 1 ≤ j ≤ p. A careful study of the (unweighted) Lasso in general convex minimization (1) is by itself an interesting and important problem. Our work includes the Lasso as a special case since ŵ_j = 1 is allowed in our theorems.

In practice, unequal ŵ_j arise in many ways. In adaptive Lasso (Zou, 2006), a decreasing function of a certain initial estimator of β_j is used as the weight ŵ_j to remove the bias of the Lasso. In Zou and Li (2008) and Zhang (2010b), the weights ŵ_j are computed iteratively with ŵ_j = ρ̇_λ(β̂_j), where ρ̇_λ(t) = (d/dt)ρ_λ(t) with a suitable concave penalty function ρ_λ(t). This is also designed to remove the bias of the Lasso, since the concavity of ρ_λ(t) guarantees smaller weight for larger β̂_j. In Section 4, we provide results on the improvements of this weighted Lasso over the standard Lasso. In linear regression, Zhang (2010b) gave sufficient conditions under which this iterative algorithm provides smaller weights ŵ_j for most large β_j. Such nearly unbiased methods are expected to produce better results than the Lasso when a significant fraction of nonzero |β_j| are of the order λ or larger. Regardless of the computational methods, the results in this paper demonstrate the benefits of using data dependent weights in a general class of problems with convex losses.

Unequal weights may also arise for computational reasons. The Lasso with ŵ_j = 1 is expected to perform similarly to weighted Lasso with data dependent 1 ≤ ŵ_j ≤ C₀, with a fixed C₀. However, the weighted Lasso is easier to compute since ŵ_j can be determined as a part of an iterative algorithm. For example, in a gradient descent algorithm, one may take larger steps and stop the computation as soon as the KKT conditions (3) are attained for any weights satisfying 1 ≤ ŵ_j ≤ C₀.

The weight function ŵ_j can be also used to standardize the penalty level, for example with ŵ_j = {ψ̈_{j j}(β̂)}^1/2, where ψ̈_{j j}(β) is the j-th diagonal element of the Hessian matrix of ψ(β). When ψ(β) is quadratic, for example in linear regression, ŵ_j = {ψ̈_jj(β̂)}^1/2 does not depend on β̂. However, in other convex minimization problems, such weights need to be computed iteratively.

Finally, in certain applications, the effects of a certain set S_* of variables are of primary interest, so that penalization of β̂_S*, and thus the resulting bias, should be avoided. This leads to “semi-penalized” estimators with ŵ_j = 0 for j ∈ S_*, for example, with weights ŵ_i = I{j ∉ S_*}.

2.2 Basic Inequalities, Prediction, and Bregman Divergence

Let β^* denote a target vector for β. In high-dimensional models, the performance of an estimator β̂ is typically measured by its proximity to a target under conditions on the sparsity of β^* and the size of the negative gradient −ℓ̇(β^*) = z − ψ̇(β^*). For ℓ₁-penalized estimators, such results are often derived from the KKT conditions (3) via certain basic inequalities, which are direct consequences of the KKT conditions and have appeared in different forms in the literature, for example, in the papers cited in Section 1. Let D(β,β^*) = ℓ(β) − ℓ(β^*) − 〈ℓ̇(β^*), β − β^*〉 be the Bregman divergence (Bregman, 1967) and consider its symmetrized version (Nielsen and Nock, 2007)

$$\mathrm{\Delta }(\mathrm{\beta },{\mathrm{\beta }}^{\ast })=D(\mathrm{\beta },{\mathrm{\beta }}^{\ast })+D({\mathrm{\beta }}^{\ast },\mathrm{\beta })=\langle \mathrm{\beta }-{\mathrm{\beta }}^{\ast },\stackrel{.}{\mathrm{\psi }}(\mathrm{\beta })-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\rangle .$$ (4)

Since ψ is convex, Δ(β, β^*) ≥ 0. Two basic inequalities below provide upper bounds for the symmetrized Bregman divergence Δ(β̂, β^*). The sparsity of β^* is measured by a weighted ℓ₁ norm of β^* in the first one and by a sparse set in the second one.

Let S be any set of indices satisfying $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$ and let S^c be the complement of S in {1, …, p}. We shall refer to S as the sparse set. Let W = diag(w) for a possibly unknown vector w ∈ ℝ^p with elements w_j ≥ 0. Define

$$z_0^{\ast }={\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\mid }_{\infty },z_1^{\ast }={\mid W_{S^c}^{-1}{\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S^c}\mid }_{\infty },$$ (5)

$${\mathrm{\Omega }}_0=\{{\widehat{w}}_j\le w_j\forall j\in S\}\cap \{w_j\le {\widehat{w}}_j\forall j\in S^c\},$$ (6)

where for any p-vector v and set A, v_A = (v_j : j ∈ A)′. Here and in the sequel M_AB denotes the A × B subblock of a matrix M and M_A = M_AA.

Lemma 1

1. Let β^* be a target vector. In the event Ω₀ ∩ {|(z − ψ̇(β^*))_j| ≤ ŵ_jλ ∀j},

   $$\mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })\le 2\mathrm{\lambda }{\mid \widehat{W}{\mathrm{\beta }}^{\ast }\mid }_1\le 2\mathrm{\lambda }{\mid W{\mathrm{\beta }}^{\ast }\mid }_1.$$ (7)
2. For any target vector β^* and $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$, the error h = β̂ − β^* satisfies

   $$\begin{array}{l}\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })+(\mathrm{\lambda }-z_1^{\ast }){\mid W_{S^c}{h}_{S^c}\mid }_1\le \langle h_S,g_S-{\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\rangle \\ \le ({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }){\mid h_S\mid }_1\end{array}$$ (8)
   in Ω₀ for a certain negative gradient vector g satisfying |g_j| ≤ ŵ_jλ. Consequently, in ${\mathrm{\Omega }}_0\cap \{({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })/(\mathrm{\lambda }-z_1^{\ast })\le \mathrm{\xi }\}$, h ≠ 0 belongs to the sign-restricted cone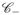 (ξ, S) = {b ∈ 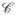(ξ, S) : b_j(ψ̇(β+ b) − ψ̇(β))_j ≤ 0 ∀ j ∈ S^c}, where

   $$\mathcal{C}(\mathrm{\xi },S)=\{b\in {ℝ}^p:{\mid W_{S^c}{b}_{S^c}\mid }_1\le \mathrm{\xi }{\mid b_S\mid }_1\ne 0\}.$$ (9)

Remark 2

Sufficient conditions are given in Subsection 3.2 for {|(z − ψ̇(β^*))_j| ≤ ŵ_j λ ∀j} to hold with high probability in generalized linear models. See Lemma 8, Remarks 10 and 11 and Examples 7, 8, and 9.

A useful feature of Lemma 1 is the explicit statements of the monotonicity of the basic inequality in the weights. By Lemma 1 (ii), it suffices to study the analytical properties of the penalized criterion with the error h = β̂ − β^* in the sign-restricted cone, provided that the event $({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })/(\mathrm{\lambda }-z_1^{\ast })\le \mathrm{\xi }$ has large probability. However, unless 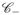(ξ, S) is specified, we will consider the larger cone in (9) in order to simplify the analysis. The choices of the target vector β^*, the sparse set $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$, weight vector ŵ and its bound w are quite flexible. The main requirement is that {|S|, $z_0^{\ast },z_1^{\ast }$} should be small. In linear regression or generalized linear models, we may conveniently consider β^* as the vector of true regression coefficients under a probability measure P_β^*. However, β^* can also be a sparse version of a true β, for example, ${\mathrm{\beta }}_j^{\ast }={\mathrm{\beta }}_{j}I\{\mid {\mathrm{\beta }}_j\mid \ge \mathrm{\tau }\}$for a threshold value τ under P_β.

The upper bound in Lemma 1 (i) gives the so called “slow rate” of convergence for the Bregman divergence. In Section 3, we provide “fast rate” of convergence for the Bregman divergence via oracle inequalities for |h_S|₁ in (8).

The symmetrized Bregman divergence Δ(β̂, β^*) has the interpretations as the regret in prediction error in linear regression, the symmetrized Kullback-Leibler (KL) divergence in generalized linear models (GLM) and density estimation, and a spectrum loss for the graphical Lasso, as shown in examples below. These quantities can be all viewed as the size of the prediction error since they measure distances between a target density of the observations and an estimated density.

Example 1 (Linear regression)

Consider the linear regression model

$$y_i=\sum _{j=1}^p{x}_{ij}{\mathrm{\beta }}_j+{\mathrm{\epsilon }}_i,i=1,\dots ,n,$$ (10)

where y_i is the response variable, x_{i j} are predictors or design variables, and ε_i is the error term. Let y = (y₁, …, y_n)′ and let X be the design matrix whose ith row is xⁱ = (x_i1,…, x_ip). The estimator (2) can be written as a weighted Lasso with $\mathrm{\psi }(\mathrm{\beta })={\mid X\mathrm{\beta }\mid }_2^2/(2n)$ and z = X′y/n in (1). For predicting a vector ỹ with E_β^*[ỹ|X, y] = Xβ^*,

$$n\mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })={\mid X\widehat{\mathrm{\beta }}-X{\mathrm{\beta }}^{\ast }\mid }_2^2={\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}[{\mid \stackrel{\sim }{y}-X\widehat{\mathrm{\beta }}\mid }_2^2\mid X,y]-\underset{\mathrm{\delta }(X,y)}{min}{\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}[{\mid \stackrel{\sim }{y}-\mathrm{\delta }(X,y)\mid }_2^2\mid X,y]$$

is the regret of using the linear predictor Xβ̂ compared with the optimal predictor. See Greenshtein and Ritov (2004) for several implications of (7).

Example 2 (Logistic regression)

We observe (X, y) ∈ ℝ^n×(p+1) with independent rows (xⁱ,y_i), where y_i ∈ {0,1} are binary response variables with

$${\mathrm{P}}_{\mathrm{\beta }}(y_i=1\mid x^i)={\mathrm{\pi }}_i(\mathrm{\beta })=exp(x^i\mathrm{\beta })/(1+exp(x^i\mathrm{\beta })),1\le i\le n.$$ (11)

The loss function (1) is the average negative log-likelihood:

$$\ell (\mathrm{\beta })=\mathrm{\psi }(\mathrm{\beta })-z^{\prime }\mathrm{\beta }\mathit{with}\mathrm{\psi }(\mathrm{\beta })=\sum _{i=1}^n\frac{log(1+exp(x^i\mathrm{\beta }))}{n},z=X^{\prime }y/n.$$ (12)

Thus, (2) is a weighted ℓ₁ penalized MLE. For probabilities {π′, π″} ⊂ (0,1), the KL information is K(π′, π″) = π′log(π′/π″) + (1 − π′)log{(1 − π′)/(1 − π″)}. Since $\stackrel{.}{\mathrm{\psi }}(\mathrm{\beta })={\sum }_{i=1}^n{x}^i{\mathrm{\pi }}_i(\mathrm{\beta })/n$ and logit(π_i(β^*)) − logit(π_i(β)) = xⁱ(β^* − β), (4) gives

$$\mathrm{\Delta }(\mathrm{\beta },{\mathrm{\beta }}^{\ast })=\frac{1}{n}\sum _{i=1}^n\left\{K({\mathrm{\pi }}_i({\mathrm{\beta }}^{\ast }),{\mathrm{\pi }}_i(\mathrm{\beta }))+K({\mathrm{\pi }}_i(\mathrm{\beta }),{\mathrm{\pi }}_i({\mathrm{\beta }}^{\ast }))\right\}.$$

Thus, the symmetrized Bregman divergence Δ(β^*,β) is the symmetrised KL-divergence.

Example 3 (GLM)

The GLM contains the linear and logistic regression models as special cases. We observe (X,y) ∈ ℝ^n×(p+1) with rows (xⁱ, y_i). Suppose that conditionally on X, y_i are independent under P_β with

$$y_i~f(y_i\mid {\mathrm{\theta }}_i)=exp\left(\frac{{\mathrm{\theta }}_i{y}_i-{\mathrm{\psi }}_0({\mathrm{\theta }}_i)}{{\mathrm{\sigma }}^2}+\frac{c(y_i,\mathrm{\sigma })}{{\mathrm{\sigma }}^2}\right),{\mathrm{\theta }}_i=x^i\mathrm{\beta }.$$ (13)

Let $f_{(n)}(y\mid X,\mathrm{\beta })={\prod }_{i=1}^{n}f(y_i\mid x^i\mathrm{\beta })$. The loss function can be written as a normalized negative likelihood ℓ(β) = (σ²/n)log f_(n)(y|X,β) with $\mathrm{\psi }(\mathrm{\beta })={\sum }_{i=1}^n\{{\mathrm{\psi }}_0(x^i\mathrm{\beta })+c(y_i,\mathrm{\sigma })\}/n$ and z = X′y/n. The KL divergence is

$$D\left(f_n(·\mid X,{\mathrm{\beta }}^{\ast })\Vert f_n(·\mid X,\mathrm{\beta })\right)={\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}log\left(\frac{f_{(n)}(y\mid X,{\mathrm{\beta }}^{\ast })}{f_{(n)}(y\mid X,\mathrm{\beta })}\right).$$

The symmetrized Bregman divergence can be written as

$$\mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })=\frac{{\mathrm{\sigma }}^2}{n}\left\{D\left(f_{(n)}(·\mid X,{\mathrm{\beta }}^{\ast })\Vert f_{(n)}(·\mid X,\widehat{\mathrm{\beta }})\right)+D\left(f_{(n)}(·\mid X,\widehat{\mathrm{\beta }})\Vert f_{(n)}(·\mid X,{\mathrm{\beta }}^{\ast })\right)\right\}.$$

Example 4 (Nonparametric density estimation)

Although the focus of this paper is on regression models, here we illustrate that Δ (β̂, β^*) is the symmetrised KL divergence in the context of non-parametric density estimation. Suppose the observations y = (y₁, …, y_n)′ are iid from f(·|β) = exp{〈β, T(·)〉 − ψ(β)} under P_β, where T(·) = (u_j(·), j ≤ p)′ with certain basis functions u_j(·). Let the loss function ℓ(β) in (1) be the average negative log-likelihood $n^{-1}{\sum }_{i=1}^{n}logf(y_i\mid \mathrm{\beta })$ with $z=n^{-1}{\sum }_{i=1}^{n}T(y_i)$. Since E_βT (y_i) = ψ̇(β), the KL divergence is

$$D\left(f(·\mid {\mathrm{\beta }}^{\ast })\Vert f(·\mid \mathrm{\beta })\right)={\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}log\left(\frac{f(y_i\mid {\mathrm{\beta }}^{\ast })}{f(y_i\mid \mathrm{\beta })}\right)=\mathrm{\psi }(\mathrm{\beta })-\mathrm{\psi }({\mathrm{\beta }}^{\ast })-\langle \mathrm{\beta }-{\mathrm{\beta }}^{\ast },\mathrm{\psi }({\mathrm{\beta }}^{\ast })\rangle .$$

Again, the symmetrized Bregman divergence is the symmetrised KL divergence between the target density f(·|β^*) and the estimated density f(·|β̂):

$$\mathrm{\Delta }(\mathrm{\beta },{\mathrm{\beta }}^{\ast })=D\left(f(·\mid {\mathrm{\beta }}^{\ast })\Vert f(·\mid \widehat{\mathrm{\beta }})\right)+D\left(f(·\mid \widehat{\mathrm{\beta }})\Vert f(·\mid {\mathrm{\beta }}^{\ast })\right).$$

van de Geer (2008) pointed out that for this example, the natural choices of the basis functions u_j and weights w_j satisfy ∫u_jdν = 0 and $w_k^2=\int u_k^{2}d\mathrm{\nu }$.

Example 5 (Graphical Lasso)

Suppose we observe X ∈ ℝ^n×p and would like to estimate the precision matrix β = (EX′X/n)⁻¹ ∈ ℝ^p×p. In the graphical Lasso, (1) is the length normalized negative likelihood with ψ(β) = −logdetβ, z = −X′X/n, and 〈β, z〉 = −trace(βz). Since the gradient of ψ is ψ̇(β) = E_βz = −β⁻¹, we find

$$\mathrm{\Delta }(\mathrm{\beta },{\mathrm{\beta }}^{\ast })=\text{trace}((\widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast })({({\mathrm{\beta }}^{\ast })}^{-1}-{\widehat{\mathrm{\beta }}}^{-1})=\sum _{j=1}^p{({\mathrm{\lambda }}_j-1)}^2/{\mathrm{\lambda }}_j,$$

where (λ₁, …, λ_p) are the eigenvalues of (β^*)^−1/2β̂(β^*)^−1/2. In graphical Lasso, the diagonal elements are typically not penalized. Consider ŵ_jk = I{j ≠ k}, so that the penalty for the off-diagonal elements are uniformly weighted. Since Lemma 1 requires |(z − ψ̇(β^*))_jk| ≤ ŵ_jkλ, β^* is taken to match X′X/n on the diagonal and the true β in correlations. Let S = {(j,k) : β_jk ≠ 0, j ≠ k}. In the event ${max}_{j\ne k}\mid z_{jk}-{\mathrm{\beta }}_{jk}^{\ast }\mid \le \mathrm{\lambda }$, Lemma 1 (i) gives

$$\mid S\mid \mathrm{\lambda }\underset{j\ne k}{max}\mid {\mathrm{\beta }}_{jk}^{\ast }\mid =o(1)\Rightarrow {\Vert {({\mathrm{\beta }}^{\ast })}^{-1/2}\widehat{\mathrm{\beta }}{({\mathrm{\beta }}^{\ast })}^{-1/2}-I_{p\times p}\Vert }_2=o(1)$$

where ||·||₂ is the spectrum norm. Rothman et al. (2008) proved the consistency of the graphical Lasso under similar conditions with a different analysis.

3. Oracle Inequalities

In this section, we extract upper bounds for the estimation error β̂ − β^* from the basic inequality (8). Since (8) is monotone in the weights, the oracle inequalities are sharper when the weights ŵ_j are smaller in $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$ and larger in S^c.

We say that a function φ(b) defined in ℝ^p is quasi star-shaped if φ(tb) is continuous and non-decreasing in t ∈ [0,∞) for all b ∈ ℝ^p and lim_b→0 φ(b) = 0. All seminorms are quasi star-shaped. The sublevel sets {b : φ(b) ≤ t} of a quasi star-shaped function are all star-shaped. Constant factors of the following form play a crucial role in our analysis.

Definition 3

For 0 ≤ η^* ≤ 1 and any pair of quasi star-shaped functions φ₀(b) and φ(b), define a general invertibility factor (GIF) over the cone (9) as follows:

$$F(\mathrm{\xi },S;{\mathrm{\phi }}_0,\mathrm{\phi })=inf\left\{\frac{\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+b,{\mathrm{\beta }}^{\ast })e^{{\mathrm{\phi }}_0(b)}}{{\mid b_S\mid }_1\mathrm{\phi }(b)}:b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)\le {\mathrm{\eta }}^{\ast }\right\},$$ (14)

where Δ(β, β^*) is as in (4).

The GIF extends the squared compatibility constant (van de Geer and Bühlmann, 2009) and the weak and sign-restricted cone invertibility factors (Ye and Zhang, 2010) from the linear regression model with φ₀(·) = 0 to the general model (1) and from ℓ_q norms to general φ(·). They are all closely related to the restricted eigenvalues (Bickel et al., 2009; Koltchinskii, 2009) as we will discuss in Subsection 3.1.

The basic inequality (8) implies that the symmetrized Bregman divergence Δ(β̂, β^*) is no greater than a linear function of |h_S|₁, where h = β̂ − β^*. If Δ(β̂, β^*) is no smaller than a linear function of the product |h_S|₁φ(h), then an upper bound for φ(h) exists. Since the symmetrized Bregman divergence (4) is approximately quadratic, Δ(β̂, β^*) ≈ 〈h, ψ̈(β^*)h〉, in a neighborhood of β^*, this is reasonable when h = β̂ − β^* is not too large and ψ̈ (β^*) is invertible in the cone. A suitable factor e^φ₀(b) in (14) forces the computation of this lower bound in a proper neighborhood of β^*.

We first provide a set of general oracle inequalities.

Theorem 4

Let { $z_0^{\ast },z_1^{\ast }$} be as in (5) with $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$, Ω₀ in (6), 0 ≤ η ≤ η^* ≤ 1, and {φ₀(b), φ(b)} be a pair of quasi star-shaped functions. Then, in the event

$${\mathrm{\Omega }}_1={\mathrm{\Omega }}_0\cap \left\{\frac{{\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }}{{(\mathrm{\lambda }-z_1^{\ast })}_{+}}\le \mathrm{\xi },\frac{{\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }}{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)}\le \mathrm{\eta }{e}^{-\mathrm{\eta }}\right\},$$ (15)

the following oracle inequalities hold:

$${\mathrm{\phi }}_0(\widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast })\le \mathrm{\eta },\mathrm{\phi }(\widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast })\le \frac{e^{\mathrm{\eta }}({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })}{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,\mathrm{\phi })},$$ (16)

and with φ_1,S(b) = |b_S|₁/|S|

$$\mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })+(\mathrm{\lambda }-z_1^{\ast }){\mid W_{S^c}{(\widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast })}_{S^c}\mid }_1\le \frac{e^{\mathrm{\eta }}{({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })}^2\mid S\mid }{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_{1,S})}.$$ (17)

Remark 5

Sufficient conditions are given in Subsection 3.2 for (15) to hold with high probability. See Lemma 8, Remarks 10 and 11 and Examples 7, 8, and 9.

The oracle inequalities in Theorem 4 control both the estimation error in terms of φ(β̂ − β^*) and the prediction error in terms of the symmetrized Bregman divergence Δ(β̂,β^*) discussed in Section 2. Since they are based on the GIF (14) in the intersection of the cone and the unit ball {b : φ₀(b) ≤ 1/e}, they are different from typical results in a small-ball analysis based on the Taylor expansion of ψ(β) at β = β^*. An important feature of Theorem 4 is that its regularity condition is imposed only on the GIF (14) evaluated at the target β^*; The uniformity of the order of Δ(β + b, β) in β is not required. Theorem 4 does allow φ₀(·) = 0 with F(ξ, S;φ₀, φ₀) = ∞ and η = 0 in linear regression.

3.1 The Hessian and Related Quantities

In this subsection we describe the relationship between the GIF (14) and the Hessian of the convex function ψ(·) in (1) and examine cases where the quasi star-shaped functions φ₀(·) and φ(·) are familiar seminorms. Throughout, we assume that ψ(β) is twice differentiable. Let ψ̈(β) be the Hessian of ψ(β) and Σ^* = ψ̈(β^*).

The GIF (14) can be simplified under the following condition.

Definition 6

Given a nonnegative-definite matrix Σ and constant η^* > 0, the symmetriized Bregman divergence Δ(β, β^*) satisfies the φ₀-relaxed convexity (φ₀-RC) condition if

$$\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+b,{\mathrm{\beta }}^{\ast })e^{{\mathrm{\phi }}_0(b)}\ge \langle b,\mathrm{\sum }b\rangle ,\forall b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)\le {\mathrm{\eta }}^{\ast }.$$ (18)

The φ₀-RC condition is related to the restricted strong convexity condition for the Bregman divergence (Negahban et al., 2010): ℓ(β^* + b) − ℓ(β^*) − 〈ℓ̇ (β^*), b〉 ≥ κ̃||b||² with a certain restriction b ∈ 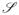and a loss function ||b||. It actually implies the restricted strong convexity of the symmetrized Bregman divergence with κ̃ = e^−η* and loss ||b||_* = 〈b,Σb〉^1/2. However, (18) is used in our analysis mainly to find a quadratic form as a media for the eventual comparison of Δ(β^* + b, β^*) with |b_S|₁φ(b) in (14), where φ(b) is the loss function. In fact, in our examples, we find quasi star-shaped functions φ₀ for which (18) holds for unrestricted b(η^* = ξ = ∞). In such cases, the φ₀-RC condition is a smoothness condition on the Hessian operator ψ̈(β) = ℓ̈(β), since $\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })={\int }_0^1\langle h,\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+th)h\rangle dt$ by (4).

In what follows, Σ = Σ^* = ψ̈ (β^*) is allowed in all statements unless otherwise stated. Under the φ₀-RC (18), the GIF (14) is bounded from below by the following simple GIF:

$$F_0(\mathrm{\xi },S;\mathrm{\phi })=\underset{b\in \mathcal{C}(\mathrm{\xi },S)}{inf}\frac{\langle b,\mathrm{\sum }b\rangle }{{\mid b_S\mid }_1\mathrm{\phi }(b)}.$$ (19)

In linear regression, F₀(ξ, S;φ) is the square of the compatibility factor for φ(b) = φ_1,S(b) = |b_S|₁/|S| (van de Geer, 2007) and the weak cone invertibility factor for φ(b) = φ_q(b) = |b|_q/|S|^1/q (Ye and Zhang, 2010). They are both closely related to the restricted isometry property (RIP) (Candes and Tao, 2005), the sparse Rieze condition (SRC) (Zhang and Huang, 2008), and the restricted eigenvalue (Bickel et al., 2009). Extensive discussion of these quantities can be found in Bickel et al. (2009), van de Geer and Bühlmann (2009) and Ye and Zhang (2010). The following corollary is an extension of an oracle inequality of Ye and Zhang (2010) from linear regression to the general convex minimization problem (1).

Corollary 7

Let η ≤ η^* ≤ 1. Suppose the φ₀-RC condition (18). Then, in the event

$${\mathrm{\Omega }}_0\cap \{{\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }\le min(\mathrm{\xi }(\mathrm{\lambda }-z_1^{\ast }),\mathrm{\eta }{e}^{-\mathrm{\eta }}{F}_0(\mathrm{\xi },S;{\mathrm{\phi }}_0))\},$$

the oracle inequalities (16) and (17) in Theorem 4 hold with the GIF F(ξ, S;φ₀, φ) replaced by the simple GIF F₀(ξ, S; φ) in (19). In particular, in the same event,

$${\mathrm{\phi }}_0(h)\le \mathrm{\eta },{\mid h\mid }_q\le \frac{e^{\mathrm{\eta }}({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }){\mid S\mid }^{1/q}}{F_0(\mathrm{\xi },S;{\mathrm{\phi }}_q)},\forall q>0,$$

with φ_q(b) = |b|_q/| S|^1/q and h = β̂ − β^*, and with φ_1,S(b) = |b_S|₁/|S|,

$$e^{-\mathrm{\eta }}\langle h,\mathrm{\sum }h\rangle \le \mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })\le \frac{e^{\mathrm{\eta }}{({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })}^2\mid S\mid }{F_0(\mathrm{\xi },S;{\mathrm{\phi }}_{1,S})}-(\mathrm{\lambda }-z_1^{\ast }){\mid W_{S^c}{h}_{S^c}\mid }_1.$$

Here the only differences between the general model (1) and linear regression (φ₀(b) = 0) are the extra factor e^η with η≤ 1, the extra constraint ${\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }\le \mathrm{\eta }{e}^{-\mathrm{\eta }}{F}_0(\mathrm{\xi },S;{\mathrm{\phi }}_0)$, and the extra φ₀-RC condition (18). Moreover, the simple GIF (19) explicitly expresses all conditions on F₀(ξ, S;φ) as properties of a fixed matrix Σ.

Example 6 (Linear regression: oracle inequalities)

For $\mathrm{\psi }(\mathrm{\beta })={\mid Xb\mid }_2^2/(2n)$ and Σ = X′X/n, F₀(ξ, S;φ_q) is the weak cone invertibility factor for q ∈ [1,∞] (Ye and Zhang, 2010), where a sharper version is defined as the sign restricted invertibility factor (SCIF):

$${\text{SCIF}}_q(\mathrm{\xi },S)=\underset{b\in {\mathcal{C}}_{-}(\mathrm{\xi },S)}{inf}{\mid \mathrm{\sum }b\mid }_{\infty }/{\mathrm{\phi }}_q(b),{\mathrm{\phi }}_q={\mid b\mid }_q/{\mid S\mid }^{1/q}.$$

For q = 1, $F_0^{1/2}(\mathrm{\xi },S;{\mathrm{\phi }}_{1,S})$ is the compatibility constant (van de Geer, 2007)

$${\mathrm{\kappa }}_{\ast }(\mathrm{\xi },S)=\underset{b\in \mathcal{C}(\mathrm{\xi },S)}{inf}\frac{{\mid S\mid }^{1/2}{\mid Xb\mid }_2}{{\mid b_S\mid }_1{n}^{1/2}}=\underset{b\in \mathcal{C}(\mathrm{\xi },S)}{inf}{\left(\frac{b^{\prime }\mathrm{\sum }b}{{\mid b_S\mid }_1^2/\mid S\mid }\right)}^{1/2}.$$ (20)

They are all closely related to the ℓ₂ restricted eigenvalues

$${\text{RE}}_2(\mathrm{\xi },S)=\underset{b\in \mathcal{C}(\mathrm{\xi },S)}{inf}\frac{{\mid Xb\mid }_2}{{\mid b\mid }_2{n}^{1/2}}=\underset{b\in \mathcal{C}(\mathrm{\xi },S)}{inf}{\left(\frac{b^{\prime }\mathrm{\sum }b}{{\mid b\mid }_2^2}\right)}^{1/2}$$

(Bickel et al., 2009; Koltchinskii, 2009). Since ${\mid b_S\mid }_1^2\le {\mid b\mid }_2^2\mid S\mid$, κ_*(ξ,S) ≥ RE₂(ξ, S) (van de Geer and Bühlmann, 2009). For the Lasso with ŵ_j = 1,

$${\mid \widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2\le \frac{{\mid S\mid }^{1/2}(\mathrm{\lambda }+z_0^{\ast })}{{\text{SCIF}}_2(\mathrm{\xi },S)}\le \frac{{\mid S\mid }^{1/2}(\mathrm{\lambda }+z_0^{\ast })}{F_0(\mathrm{\xi },S;{\mathrm{\phi }}_2)}\le \frac{{\mid S\mid }^{1/2}(\mathrm{\lambda }+z_0^{\ast })}{{\mathrm{\kappa }}_{\ast }(\mathrm{\xi },S){\text{RE}}_2(\mathrm{\xi },S)}$$ (21)

in the event $\mathrm{\lambda }+z_0^{\ast }\le \mathrm{\xi }(\mathrm{\lambda }-z_1^{\ast })$ (Ye and Zhang, 2010). Thus, cone and general invertibility factors yield sharper ℓ₂ oracle inequalities.

The factors in the oracle inequalities in (21) do not always have the same order for large |S|. Although the oracle inequality based on SCIF₂(ξ, S) is the sharpest among them, it seems not to lead to a simple extension to the general convex minimization in (1). Thus, we settle with extensions of the second sharpest oracle inequality in (21) with F₀(ξ, S;·).

3.2 Oracle Inequalities for the Lasso in GLM

An important special case of the general formulation is the ℓ₁-penalized estimator in a generalized linear model (GLM) (McCullagh and Nelder, 1989). This is Example 3 in Subsection 2.2, where we set up the notation in (13) and gave the KL divergence interpretation to (4). The ℓ₁ penalized, normalized negative likelihood is

$$\ell (\mathrm{\beta })=\mathrm{\psi }(\mathrm{\beta })-z^{\prime }\mathrm{\beta },\text{with}\mathrm{\psi }(\mathrm{\beta })=\frac{1}{n}\sum _{i=1}^n\{{\mathrm{\psi }}_0(x^i\mathrm{\beta })-c(y_i,\mathrm{\sigma })\}\text{and}z=\frac{X^{\prime }y}{n}.$$ (22)

Assume that ψ₀ is twice differentiable. Denote the first and second derivatives of ψ₀ by ψ̇₀ and ψ̈₀, respectively. The gradient and Hessian are

$$\stackrel{.}{\mathrm{\psi }}(\mathrm{\beta })=X^{\prime }{\mathrm{\psi }}_0(\mathrm{\theta })/n\text{and}\ddot{\mathrm{\psi }}(\mathrm{\beta })=X^{\prime }\text{diag}({\ddot{\mathrm{\psi }}}_0(\mathrm{\theta }))X/n,$$ (23)

where θ = Xβ and ψ̇₀ and ψ̈₀ are applied to the individual components of θ.

A crucial condition in our analysis of the Lasso in GLM is the Lipschitz condition

$$\underset{i\le n}{max}\left|log({\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }+t))-log({\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }))\right|\le M_1\mid t\mid ,\forall M_1\mid t\mid \le {\mathrm{\eta }}^{\ast },$$ (24)

where M₁ and η^* are constants determined by ψ₀. This condition gives

$$\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+b,{\mathrm{\beta }}^{\ast })={\int }_0^1\langle b,\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+tb)b\rangle dt\ge {\int }_0^1\sum _{{tM}_1\mid x^{i}b\mid \le {\mathrm{\eta }}^{\ast }}\frac{{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){(x^{i}b)}^2}{{ne}^{{tM}_1\mid x^{i}b\mid }}dt,$$

which implies the following lower bound for the GIF in (14):

$$F(\mathrm{\xi },S;{\mathrm{\phi }}_0,\mathrm{\phi })\ge \underset{b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)\le {\mathrm{\eta }}^{\ast }}{inf}\sum _{i=1}^n\frac{{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){(x^{i}b)}^2}{n{\mid b_S\mid }_1\mathrm{\phi }(b)}{\int }_0^{1}I\{{tM}_1\mid x^{i}b\mid \le {\mathrm{\phi }}_0(b)\}dt.$$

For seminorms φ₀ and φ, the infimum above can be taken over φ₀(b) = M₂ due to scale invariance. Thus, for φ₀(b) = M₂|b|₂ and seminorms φ, this lower bound is

$$F^{\ast }(\mathrm{\xi },S;\mathrm{\phi })=\underset{b\in \mathcal{C}(\mathrm{\xi },S),{\mid b\mid }_2=1}{inf}\sum _{i=1}^n\frac{M_2{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast })}{n{\mid b_S\mid }_1\mathrm{\phi }(b)}min\left(\frac{\mid x^{i}b\mid }{M_1},\frac{{(x^{i}b)}^2}{M_2}\right),$$ (25)

due to ${(x^{i}b)}^2{\int }_0^{1}I\{{tM}_1\mid x^{i}b\mid \le M_2\}dt=M_{2}min\{\mid x^{i}b\mid /M_1,{(x^{i}b)}^2/M_2\}$.

If (24) holds with η^* = ∞, $\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+b,{\mathrm{\beta }}^{\ast })\ge n^{-1}{\int }_0^1{\sum }_i{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){(x^{i}b)}^2{e}^{-{tM}_1\mid x^{i}b\mid }dt$, so that by the Jensen inequality (18) holds with Σ = Σ^* = ψ̈(β^*) and

$${\mathrm{\phi }}_0(b)=\frac{M_1{\sum }_{i=1}^n{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){\mid x^{i}b\mid }^3}{{\sum }_{i=1}^n{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){(x^{i}b)}^2}\le M_1{\mid Xb\mid }_{\infty }.$$ (26)

This gives a special F₀(ξ, S;φ₀) as

$$F_{\ast }(\mathrm{\xi },S)=\underset{b\in \mathcal{C}(\mathrm{\xi },S)}{inf}\frac{n{\langle b,{\mathrm{\sum }}^{\ast }b\rangle }^2/(M_1{\mid b_S\mid }_1)}{{\sum }_{i=1}^n{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){\mid x^{i}b\mid }^3}.$$ (27)

Since ${\mid Xb\mid }_{\infty }\le {\mid X_S\mid }_{\infty }{\mid b_S\mid }_1+{\mid X_{S^c}{W}_{S^c}^{-1}\mid }_{\infty }\mid W_{S^c}{b}_{S^c}\mid \le \{{\mid X_S\mid }_{\infty }+\mathrm{\xi }{\mid X_{S^c}{W}_{S^c}^{-1}\mid }_{\infty }\}\mid b_S\mid$ in the cone (ξ,S) in (9), for φ₀(b) = M₃|b_S|₁ with $M_3=M_1\{{\mid X_S\mid }_{\infty }+\mathrm{\xi }{\mid X_{S^c}{W}_{S^c}^{-1}\mid }_{\infty }\}$, the φ₀-RC condition (18) automatically implies the stronger

$$e^{-{\mathrm{\phi }}_0(b)}\langle b,{\mathrm{\sum }}^{\ast }b\rangle \le \mathrm{\Delta }({\mathrm{\beta }}^{\ast }+b,{\mathrm{\beta }}^{\ast })\le e^{{\mathrm{\phi }}_0(b)}\langle b,{\mathrm{\sum }}^{\ast }b\rangle ,\forall b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)<\infty .$$ (28)

Under the Lipschitz condition (24), we may also use the following large deviation inequalities to find explicit penalty levels to guarantee the noise bound (15).

Lemma 8

1. Suppose the model conditions (13) and (24) with certain {M₁, η^*}. Let x_j be the columns of X, ${\mathrm{\sum }}_{ij}^{\ast }$ be the elements of Σ^* = ψ̈(β^*). For penalty levels {λ₀, λ₁} define t_j = λ₀I{j ∈ S} + w_jλ₁I{j ∉ S}. Suppose the bounds w_j in (6) are deterministic and

   $$M_1\underset{j\le p}{max}({\mid x_j\mid }_{\infty }\mid t_j/{\mathrm{\sum }}_{jj}^{\ast })\le {\mathrm{\eta }}_0{e}^{{\mathrm{\eta }}_0}\mathit{and}\sum _{j=1}^{p}exp\left\{-\frac{{nt}_j^2{e}^{-{\mathrm{\eta }}_0}}{2{\mathrm{\sigma }}^2{\mathrm{\sum }}_{jj}^{\ast }}\right\}\le \frac{{\mathrm{\epsilon }}_0}{2}$$ (29)

   for certain constants η₀ ≤ η^* and ε₀ > 0. Then, ${\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}\left\{z_0^{\ast }\le {\mathrm{\lambda }}_0,z_1^{\ast }\le {\mathrm{\lambda }}_1\right\}\ge 1-{\mathrm{\epsilon }}_0$.

2. If c₀ = max_t ψ̈(t), then part (i) is still valid if (24) and (29) are replaced by

   $$\sum _{j=1}^{p}exp\left\{-\frac{n^2{t}_j^2}{2{\mathrm{\sigma }}^2{c}_0{\mid x_j\mid }_2^2}\right\}\le \frac{{\mathrm{\epsilon }}_0}{2}.$$ (30)

   In particular, if ${\mid x_j\mid }_2^2=n$, 1 ≤ j ≤ p, w_j = 1, j ∉ S and λ₀ = λ₁ = λ (so t_j = λ), then part (i) still holds if $\mathrm{\lambda }\ge \mathrm{\sigma }\sqrt{(2c_0/n)log(2p/{\mathrm{\epsilon }}_0)}$.

The following theorem is a consequence of Theorem 4, Corollary 7 and Lemma 8.

Theorem 9

1. Let β̂ be the weighted Lasso estimator in (2) with GLM loss function in (22). Let β^* be a target vector and h = β̂−β^*. Suppose that the data follows the GML model (13) satisfying the Lipschitz condition (24) with certain {M₁, η^*}. Let F^*(ξ,S;φ) be as in (25) with $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$ and a constant M₂. Let η ≤ 1 ∧ η^* and {λ, λ₀, λ₁} satisfy

   $${\mid w_S\mid }_{\infty }\mathrm{\lambda }+{\mathrm{\lambda }}_0\le min\{\mathrm{\xi }(\mathrm{\lambda }-{\mathrm{\lambda }}_1),\mathrm{\eta }{e}^{-\mathrm{\eta }}{F}^{\ast }(\mathrm{\xi },S;M_2{\mid ·\mid }_2)\}.$$ (31)
   Then, in the event ${\mathrm{\Omega }}_0\cap \{{max}_{k=0,1}(z_k^{\ast }/{\mathrm{\lambda }}_k)\le 1\}$ with the $z_k^{\ast }$ in (5) and Ω₀ in (6),

   $$\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })\le \frac{e^{\mathrm{\eta }}{({\mid w_S\mid }_{\infty }\mathrm{\lambda }+{\mathrm{\lambda }}_0)}^2\mid S\mid }{F^{\ast }(\mathrm{\xi },S;{\mathrm{\phi }}_{1,S})},\mathrm{\phi }(h)\frac{e^{\mathrm{\eta }}({\mid w_S\mid }_{\infty }\mathrm{\lambda }+{\mathrm{\lambda }}_0)}{F^{\ast }(\mathrm{\xi },S;\mathrm{\phi })}$$ (32)
   for any seminorm φ as the estimation loss. In particular, for φ(b) = M₂|b|₂, (32) gives |h|₂ ≤ η/M₂. Moreover, if either (29) or (30) holds for the penalty level {λ₀, λ₁} and the weight bounds w_j in (6) are deterministic, then

   $${\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}\{(\mathit{32})\mathit{holds}\mathit{for}\mathit{all}\mathit{seminorms}\mathrm{\phi }\}\ge {\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}({\mathrm{\Omega }}_0)-{\mathrm{\epsilon }}_0.$$

2. Suppose η^* = ∞ and (31) holds with F^*(ξ,S;M₂|·|₂) replaced by the special simple GIF F_*(ξ,S) in (27) for the φ₀ in (26). Then, the conclusions of part (i) hold with F^*(ξ,S;·) replaced by the simple GIF F₀(ξ, S;·) in (19). Moreover, φ₀(h) ≤ η and (32) can be strengthened with the lower bound Δ(β^* + h,β^*) ≥ e^−η〈h,Σ^*h〉.

3. For any η^* > 0, the conclusions of part (ii) hold for the φ₀(b) = M₃|b_S|₁ in (28), if F_*(ξ,S) is replaced by ${\mathrm{\kappa }}_{\ast }^2(\mathrm{\xi },S)/(M_3\mid S\mid )$ in (31), where κ_*(ξ,S) is the compatibility constant in (20).

Remark 10

If either (29) or (30) holds for the penalty levels {λ₀, λ₁} and the bounds w_j in (6) are deterministic, then (32) implies P_β^*{the noise bound (15) holds} ≥ P_β^*(Ω₀) − ε₀.

Remark 11

Suppose that max_{j ∉ S} 1/w_j, ${max}_{j}1/{\mathrm{\sum }}_{jj}^{\ast }$, max_j∈S w_j, ${max}_j{\mathrm{\sum }}_{jj}^{\ast }$, and M₁ are all bounded, and that $\{1+F_{\ast }^2(\mathrm{\xi },S)\}(logp)/n\to 0$. Then, (29) holds with the penalty level ${\mathrm{\lambda }}_0={\mathrm{\lambda }}_1=a\mathrm{\sigma }\sqrt{(2/n)log(p/{\mathrm{\epsilon }}_0)}$ for certain $a\le (1+o(1)){max}_j{({\mathrm{\sum }}^{\ast })}_{jj}^{1/2}/w_j$, due to max{λ₀, η, η₀} → 0+. Again, the conditions and conclusions of Theorem 9 “converge” to those for the linear regression as if the Gram matrix is Σ^*.

Remark 12

In Theorem 9, the key condition (31) is weaker in parts (i) and (ii) than part (iii), although part (ii) requires η^* = ∞. For Σ = Σ^* and M₁ = M₂ ≤ M₃/(1 + ξ),

$${\mathrm{\kappa }}_{\ast }^2(\mathrm{\xi },S)/(M_3\mid S\mid )\le min\left\{F_{\ast }(\mathrm{\xi },S),F^{\ast }(\mathrm{\xi },S;M_2{\mid ·\mid }_2)\right\},$$

since $n^{-1}{\sum }_{i=1}^n{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast }){\mid x^{i}b\mid }^3/\langle b,{\mathrm{\sum }}^{\ast }b\rangle \le {\mid Xb\mid }_{\infty }\le {\mid b_S\mid }_1{M}_3/M_1$ as in the derivation of (28) and |b|₂ ≤ |b|₁ ≤ (1 + ξ)|b_S|₁ in the cone (9). For the more familiar ${\mathrm{\kappa }}_{\ast }^2(\mathrm{\xi },S)/(M_3\mid S\mid )$ with the compatibility constant, (31) essentially requires a small $\mid S\mid \sqrt{(logp)/n}$. The sharper Theorem 9 (i) and (ii) provides conditions to relax the requirement to a small |S|(log p)/n.

Remark 13

For ŵ_j = 1, Negahban et al. (2010) considered M-estimators under the restricted strong convexity condition discussed below Definition 6. For the GLM, they considered iid sub-Gaussian xⁱ and used empirical process theory to bound the ratio Δ(β^* + b,β^*)/{|b|₂(|b|₂ − c₀|b|₁} from below over the cone (9) with a small c₀. Their result extends the ℓ₂ error bound ${\mid S\mid }^{1/2}(\mathrm{\lambda }+z_0^{\ast })/{\text{RE}}_2^2(\mathrm{\xi },S)$ of Bickel et al. (2009), while Theorem 9 extends the sharper (21) with the factor F₀(ξ, S;φ₂). Theorem 9 applies to both deterministic and random designs. Similar to Negahban et al. (2010), for iid sub-Gaussian xⁱ, empirical process theory can be applied to the lower bound (25) for the GIF to verify the key condition (31) with F^*(ξ,S;M₂|·|₂) ≳ |S|^−1/2, provided that |S|(log p)/n is small.

Example 7 (Linear regression: oracle inequalities, continuation)

For the linear regression model (10) with quadratic loss, ψ₀(θ) = θ²/2, so that (24) holds with M₁ = 0 and η^* = ∞. It follows that F^*(ξ,S;M₂|·|₂) = ∞ and (31) has the interpretation with η = 0+ and ηe^−ηF^*(ξ,S;M₂| · |₂) = ∞. Moreover, since M₁ = 0, η₀ = 0+ in (29). Thus, the conditions and conclusions of Theorem 9 “converge” to the case of linear regression as M₁ → 0+. Suppose iid ε_i ~ N(0,σ²) as in (13). For ŵ_j = w _j = 1 and ${\mathrm{\sum }}_{jj}^{\ast }={\sum }_{i=1}^n{x}_{ij}^2/n=1$, (29) holds with ${\mathrm{\lambda }}_0={\mathrm{\lambda }}_1=\mathrm{\sigma }\sqrt{(2/n)log(p/{\mathrm{\epsilon }}_0)}$ and (31) holds with λ = λ₀(1 + ξ)/(1 − ξ). The value of σ can be estimated iteratively using the mean residual squares (Städler et al., 2010; Sun and Zhang, 2011). Alternatively, cross-validation can be used to pick λ. For φ(b) = φ₂(b) = | b |₂/|S|^1/2, (32) matches the risk bound in (21) with the factor F₀(ξ, S;φ₂).

Example 8 (Logistic regression: oracle inequalities)

The model and loss function are given in (11) and (12) respectively. Here we verify the conditions of Theorem 9. The Lipschitz condition (24) holds with M₁ = 1 and η^* = ∞ since ψ₀(t) = log(1 + e^t) provides

$$\frac{{\ddot{\mathrm{\psi }}}_0(\mathrm{\theta }+t)}{{\ddot{\mathrm{\psi }}}_0(\mathrm{\theta })}=\frac{e^t{(1+e^{\mathrm{\theta }})}^2}{{(1+e^{\mathrm{\theta }+t})}^2}\ge \{\begin{array}{ll}{e}^{-\mid t\mid }\hfill & t<0\hfill \\ e^{-t}{(1+e^{\mathrm{\theta }})}^2/{(e^{-t}+e^{\mathrm{\theta }})}^2\ge e^{-\mid t\mid }\hfill & t>0.\hfill \end{array}$$

Since max_t ψ̈(t) = c₀ = 1/4 we can apply (30). In particular, if ${\widehat{w}}_j=w_j=1={\mid x_j\mid }_2^2/n,\mathrm{\lambda }=\{(\mathrm{\xi }+1)/(\mathrm{\xi }-1)\}\sqrt{(log(p/{\mathrm{\epsilon }}_0))/(2n)}$ and λ{2ξ/(ξ + 1)}/F_*(ξ,S) ≤ ηe^−η, then (32) holds with at least probability 1 − ε₀ under P_β^*. For such deterministic Ŵ and X, an adaptive choice of the penalty level is $\mathrm{\lambda }=\widehat{\mathrm{\sigma }}\sqrt{(2/n)logp}$ with ${\widehat{\mathrm{\sigma }}}^2={\sum }_{i=1}^n{\mathrm{\pi }}_i(\widehat{\mathrm{\beta }})\{1-{\mathrm{\pi }}_i(\widehat{\mathrm{\beta }})\}/n$, where π_i(β) is as in Example 2.

Example 9 (Log-linear models: oracle inequalities)

Consider counting data with y_i ∈ {0,1,2,…}. In log-linear models, it is assume that

$${\mathrm{E}}_{\mathrm{\beta }}(y_i)=e^{{\mathrm{\theta }}_i},{\mathrm{\theta }}_i=x^i\mathrm{\beta },1\le i\le n.$$

This becomes a GLM with the average negative Poisson log-likelihood function

$$\ell (\mathrm{\beta })=\mathrm{\psi }(\mathrm{\beta })-z^{\prime }\mathrm{\beta },\mathrm{\psi }(\mathrm{\beta })=\sum _{i=1}^n\frac{exp(x^i\mathrm{\beta })-log(y_i!)}{n},z=X^{\prime }y/n.$$

In this model, ψ₀(t) = e^t, so that the Lipschitz condition (24) holds with M₁ = 1 and η^* = ∞. Although (30) is not useful with c₀ = ∞, (29) can be used in Theorem 9.

4. Adaptive and Multistage Methods

We consider in this section an adaptive Lasso and its repeated applications, with weights recursively generated from a concave penalty function. This approach appears to provide the most appealing choice of weights both from heuristic and theoretical standpoints. The analysis here uses the results in Section 3 and an idea in Zhang (2010b).

We first consider adaptive Lasso and provide conditions under which it improves upon its initial estimator. Let ρ_λ(t) be a concave penalty function with ρ̇_λ(0+) = λ, where ρ̇_λ(t) = (∂/∂t)ρ_λ(t). The maximum concavity of the penalty is

$$\mathrm{\kappa }=\underset{0<t_1<t_2}{sup}\frac{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(t_2)-{\stackrel{.}{p}}_{\mathrm{\lambda }}(t_1)\mid }{t_2-t_1}.$$ (33)

Let (ξ,S) be the cone in (9). Let φ₀(b) be a quasi star-shaped function and define

$$F_2(\mathrm{\xi },S;{\mathrm{\phi }}_0)=inf\left\{\frac{e^{{\mathrm{\phi }}_0(b)}\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+b,{\mathrm{\beta }}^{\ast })}{{\mid b_S\mid }_2{\mid b\mid }_2}:0\ne b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)\le {\mathrm{\eta }}^{\ast }\right\}.$$ (34)

This quantity is an ℓ₂ version of the GIF in (14). The analysis in Section 3 can be used to find lower bounds for (34) in the same way simply by taking φ(b) = |b|₂ and replacing |b_S|₁ with |b_S|₂. For example, in generalized linear models (13) satisfying the Lipschitz condition (24), the derivation of (25) yields

$$F_2(\mathrm{\xi },S;M{\mid ·\mid }_2)\ge \underset{b\in \mathcal{C}(\mathrm{\xi },S),{\mid b\mid }_2=1}{inf}\sum _{i=1}^n\frac{M_2{\ddot{\mathrm{\psi }}}_0(x^i{\mathrm{\beta }}^{\ast })}{n{\mid b_S\mid }_2}min\left(\frac{\mid x^{i}b\mid }{M_1},\frac{{(x^{i}b)}^2}{M_2}\right).$$

Given 0 < ε₀ < 1, the components of the error vector z − ψ̇(β^*) are sub-Gaussian if for all $0\le t\le \mathrm{\sigma }\sqrt{(2/n)log(4p/{\mathrm{\epsilon }}_0)}$,

$${\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}\left\{\mid {(z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }))}_j\mid \ge t\right\}\le 2e^{-{nt}^2/(2{\mathrm{\sigma }}^2)}.$$ (35)

This condition holds for all GLM when the components of Xβ^* are uniformly in the interior of the natural parameter space for the exponential family.

Theorem 14

Let κ be as in (33), $S_0=\{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$, λ₀ > 0, 0 < η < 1, 0 < γ₀ < 1/κ, A > 1, and ξ ≥ (A+1 − κγ₀)/(A−1). Let φ₀ be a quasi star-shaped function, F(ξ, S;φ₀, φ₀) be the GIF in (14), and F₂(ξ, S;φ₀) its ℓ₂-version in (34). Suppose

$${\mathrm{\lambda }}_0\{1+A/(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)\}\le F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)\mathrm{\eta }{e}^{-\mathrm{\eta }},F_{\ast }\le F_2(\mathrm{\xi },S;{\mathrm{\phi }}_0),$$ (36)

for all S ⊇ S₀ with |S\S₀| ≤ ℓ^*. Let β̃ be an initial estimator of β and β̂ be the weighted Lasso in (2) with weights ŵ_j = ρ̇_λ(|β̃_j|)/λ and penalty level λ = Aλ₀/(1 − κγ₀). Then,

$${\mid \widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2\le \frac{e^{\mathrm{\eta }}}{F_{\ast }}\left\{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2+\left(\mathrm{\kappa }+\frac{1}{{\mathrm{\gamma }}_{0}A}-\frac{\mathrm{\kappa }}{A}\right){\mid \stackrel{\sim }{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2\right\}$$

in the event $\{{\mid {(\stackrel{\sim }{\mathrm{\beta }}-\mathrm{\beta })}_{S_0^c}\mid }_2^2\le {\mathrm{\gamma }}_0^2{\mathrm{\lambda }}^2{\ell }^{\ast }\}\cap \{{\mid z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\mid }_{\infty }\le {\mathrm{\lambda }}_0\}$. Moreover, if (35) holds and ${\mathrm{\lambda }}_0=\mathrm{\sigma }\sqrt{(2/n)log(2p/{\mathrm{\epsilon }}_0)}$ with 0 < ε₀ < 1, then P_β* {|z − ψ̈(β^*)| ≥ λ₀} ≤ ε₀.

Theorem 14 raises the possibility that β̂ improves β̃ under proper conditions. Thus it is desirable to repeatedly apply this adaptive Lasso in the following way,

$${\widehat{\mathrm{\beta }}}^{(k+1)}=\underset{\mathrm{\beta }}{argmin}\left\{\ell (\mathrm{\beta })+\sum _{j=1}^p{\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}({\widehat{\mathrm{\beta }}}_j^{(k)})\mid {\mathrm{\beta }}_j\mid \right\},k=0,1,\dots .$$ (37)

Such multistage algorithms have been considered in the literature (Fan and Li, 2001; Zou and Li, 2008; Zhang, 2010b). As discussed in Remark 16 below, it is beneficial to use a concave penalty ρ_λ in (37). Natural choices of ρ_λ include the smoothly clipped absolute deviation and minimax concave penalties (Fan and Li, 2001; Zhang, 2010a).

Theorem 15

Let {κ,S₀, λ₀, η, γ₀, A, ξ, ℓ^*, λ} be the same as Theorem 14. Let β̂⁽⁰⁾ be the unweighted Lasso with ŵ_j = 1 in (2) and β̂^(ℓ) be the ℓ-th iteration of the recursion (37) initialized with β̂⁽⁰⁾. Let ξ₀ = (λ + λ₀)/(λ − λ₀). Suppose (36) holds and

$$e^{\mathrm{\eta }}\{1+(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)/A\}/F({\mathrm{\xi }}_0,S_0;{\mathrm{\phi }}_0,{\mid ·\mid }_2)\le {\mathrm{\gamma }}_0\sqrt{{\ell }^{\ast }}.$$ (38)

Define r₀ = (e^η/F_*){κ + 1/(γ₀A) − κ/A}. Suppose r₀ < 1. Then,

$${\mid {\widehat{\mathrm{\beta }}}^{(\ell )}-{\mathrm{\beta }}^{\ast }\mid }_2\le \frac{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2}{e^{-\mathrm{\eta }}{F}_{\ast }(1-r_0)/(1-r_0^{\ell })}+\frac{r_0^{\ell }{e}^{\mathrm{\eta }}\mathrm{\lambda }\{1+(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)/A\}}{F({\mathrm{\xi }}_0,S_0;{\mathrm{\phi }}_0,{\mid ·\mid }_2)}$$ (39)

in the event

$$\left\{{\mid z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\mid }_{\infty }\le {\mathrm{\lambda }}_0\right\}\cap \left\{\frac{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2}{e^{-\mathrm{\eta }}{F}_{\ast }(1-r_0)}\le {\mathrm{\gamma }}_0\mathrm{\lambda }\sqrt{{\ell }^{\ast }}\right\}.$$ (40)

Moreover, if (35) holds and ${\mathrm{\lambda }}_0=\mathrm{\sigma }\sqrt{(2/n)log(4p/{\mathrm{\epsilon }}_0)}$ with 0 < ε₀ < 1, then the intersection of the events (40) and $\{{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2\le n^{-1/2}\mathrm{\sigma }\sqrt{2\mid S_0\mid log(4\mid S_0/{\mathrm{\epsilon }}_0\mid )}\}$ happens with at least P_β^*probability 1 − ε₀, provided that

$$\frac{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+n^{-1/2}\mathrm{\sigma }\sqrt{2\mid S_0\mid log(4\mid S_0\mid /{\mathrm{\epsilon }}_0)}}{e^{-\mathrm{\eta }}{F}_{\ast }(1-r_0)}\le \frac{{\mathrm{\gamma }}_{0}A{\mathrm{\lambda }}_0\sqrt{{\ell }^{\ast }}}{1-\mathrm{\kappa }{\mathrm{\gamma }}_0}.$$

Remark 16

Define R⁽⁰⁾ = λe^η{1 + (1 − κγ₀)/A}/F(ξ₀, S₀; φ₀, |·|₂) and

$$R^{(\infty )}=\frac{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2}{e^{-\mathrm{\eta }}{F}_{\ast }(1-r_0)},R^{(\ell )}=(1-r_0^{\ell })R^{(\infty )}+r_0^{\ell }{R}^{(0)}.$$

It follows from (39) that R^(ℓ) is an upper bound of |β̂^(ℓ) − β^*|₂ under proper conditions. This implies |β̂^(ℓ) − β^*| ≤ 2R^(∞) after ℓ = |logr₀|⁻¹ log(R^(∞)/R⁽⁰⁾) iterations of the recursion (37). Under condition (35),

$${\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}{R}^{(\infty )}\le \{\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+2\mathrm{\sigma }\sqrt{\mid S_0\mid /n}\}{e}^{\mathrm{\eta }}/\{F_{\ast }(1-r_0)\}.$$

Since ρ_λ(t) is concave in t, $\mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2\le {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(0+){\mid S_0\mid }^{1/2}=\mathrm{\lambda }{\mid S_0\mid }^{1/2}$. This component of E_β^*R^(∞)matches the noise inflation due to model selection uncertainty since $\mathrm{\lambda }\asymp {\mathrm{\lambda }}_0=\mathrm{\sigma }\sqrt{(2/n)log(p/{\mathrm{\epsilon }}_0)}$. This noise inflation diminishes when ${min}_{j\in S_0}\mid {\mathrm{\beta }}_j^{\ast }\mid \ge \mathrm{\gamma }\mathrm{\lambda }$ and ρ̇_λ(t) = 0 for |t| ≥ γλ, yielding the super-efficient ${\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}{R}^{(\infty )}\le \{2\mathrm{\sigma }\sqrt{\mid S_0\mid /n}\}{e}^{\mathrm{\eta }}/\{F_{\ast }(1-r_0)\}$ without the log p factor. The risk bound R^(∞) is comparable with those for concave penalized least squares in linear regression (Zhang, 2010a).

Remark 17

For log(p/n) ≍ log p, the penalty level λ in Theorems 14 and 15 are comparable with the best proven results and of the smallest possible order in linear regression. For log(p/n) ≪ log p, the proper penalty level is expected to be of the order $\mathrm{\sigma }\sqrt{(2/n)log(p/\mid S_0\mid )}$ under a vectorized sub-Gaussian condition which is slightly stronger than (35). This refinement for log(p/n) ≪ log p is beyond the scope of this paper.

5. Selection Consistency

In this section, we provide a selection consistency theorem for the ℓ₁ penalized convex minimization estimator, including both the weighted and unweighted cases. Let ||M||_∞ = max_|u|∞≤1 |Mu|_∞ be the ℓ_∞-to-ℓ_∞ operator norm of a matrix M.

Theorem 18

Let ψ̈(β) = ℓ̈(β) be the Hessain of the loss in (1), β̂ be as in (2), β^* be a target vector, $z_k^{\ast }$ be as in (5), Ω₀ in (6), $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$ and F(ξ,S;φ₀, φ) as in (14).

1. Let 0 < η ≤ η^* ≤ 1, ${\mathcal{B}}_0^{\ast }=\{\mathrm{\beta }:{\mathrm{\phi }}_0(\mathrm{\beta }-{\mathrm{\beta }}^{\ast })\le \mathrm{\eta },{\mathrm{\beta }}_{S^c}=0\}$ and S_β = { j: β_j ≠ 0}. Suppose

   $$\underset{\mathrm{\beta }\in {\mathcal{B}}_0^{\ast }}{sup}{\mid {\widehat{W}}_{S^c}^{-1}{\ddot{\mathrm{\psi }}}_{S^c,S_{\mathrm{\beta }}}(\mathrm{\beta }){\{{\ddot{\mathrm{\psi }}}_{S_{\mathrm{\beta }}}(\mathrm{\beta })\}}^{-1}{\widehat{W}}_{S_{\mathrm{\beta }}}sgn({\mathrm{\beta }}_{S_{\mathrm{\beta }}})\mid }_{\infty }\le {\mathrm{\kappa }}_0<1$$ (41)

   $$\underset{\mathrm{\beta }\in {\mathcal{B}}_0^{\ast }}{sup}{\Vert {\widehat{W}}_{S^c}^{-1}{\ddot{\mathrm{\psi }}}_{S^c,S_{\mathrm{\beta }}}(\mathrm{\beta }){\{{\ddot{\mathrm{\psi }}}_{S_{\mathrm{\beta }}}(\mathrm{\beta })\}}^{-1}\Vert }_{\infty }\le {\mathrm{\kappa }}_1.$$ (42)
   Then, {j: β̂_j ≠ 0} ⊆ S in the event

   $${\mathrm{\Omega }}_1^{\ast }={\mathrm{\Omega }}_0\cap \left\{{\mid {\widehat{w}}_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }\le \mathrm{\eta }{e}^{-\mathrm{\eta }}F(0,S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0),{\mathrm{\kappa }}_1{z}_0^{\ast }+z_1^{\ast }<(1-{\mathrm{\kappa }}_0)\mathrm{\lambda }\right\}.$$ (43)
2. Let 0 < η ≤ η^* ≤ 1 and = {β: φ₀(β − β^*) ≤ η,sgn(β) = sgn(β^*)}. Suppose (41) and (42) hold with ${\mathcal{B}}_0^{\ast }$ replaced by . Then, sgn(β̂) = sgn(β^*) in the event

   $${\mathrm{\Omega }}_1^{\ast }\cap \left\{\underset{\mathrm{\beta }\in {\mathcal{B}}_0}{sup}{\Vert {\{{\ddot{\mathrm{\psi }}}_S(\mathrm{\beta })\}}^{-1}\Vert }_{\infty }({\mid {\widehat{w}}_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })<\underset{j\in S}{min}\mid {\mathrm{\beta }}_j^{\ast }\mid \right\}.$$ (44)

3. Suppose conditions of Theorem 9 hold for the GLM. Then, the conclusions of (i) and (ii) hold under the respective conditions if F(0,S;φ₀, φ₀) is replaced by F^*(ξ,S;M₂|·|₂) or F_*(ξ,S) or ${\mathrm{\kappa }}_{\ast }^2(\mathrm{\xi },S)/(M_3\mid S\mid )$ with the respective φ₀ in Theorem 9.

For ŵ_j = 1, this result is somewhat more specific in the radius η for the uniform irrepresentable condition (41), compared with a similar extension of the selection consistency theory to the graphical Lasso by Ravikumar et al. (2008). In linear regression (10), ψ̈β) = Σ = X′X/n does not depend on β, so that Theorem 18 with the special w_j = 1 matches the existing selection consistency theory for the unweighted Lasso (Meinshausen and Bühlmann, 2006; Tropp, 2006; Zhao and Yu, 2006; Wainwright, 2009). We discuss below the ℓ₁ penalized logistic regression as a specific example.

Example 10 (Logistic regression: selection consistency)

Suppose $w_j=1={\mid x_j\mid }_2^2/n$ where x_j are the columns of X. If (43) and (44) hold with $z_0^{\ast }$ and $z_1^{\ast }$ replaced by $\sqrt{(log(p/{\mathrm{\epsilon }}_0))/(2n)}$, then the respective conclusions of Theorem 18 hold with at least probability 1 − ε₀ in P_β^*.

6. The Sparsity of the Lasso and SRC

The results in Sections 2, 3, and 4 are concerned with prediction and estimation properties of β̂, but not dimension reduction. Theorem 18 (i) and (iii) provide dimension reduction under ℓ_∞-type conditions (41) and (42). In this section, we provide upper bounds for the dimension of β̂ under conditions of a weaker ℓ₂ type. For this purpose, we introduce

$${\mathrm{\kappa }}_{+}(m)=\underset{\mid B\mid =m}{sup}\left\{{\mathrm{\lambda }}_{max}\left(W_B^{-2}{\int }_0^1{\ddot{\mathrm{\psi }}}_B({\mathrm{\beta }}^{\ast }+tb)dt\right):B\cap S=\varnothing ,b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)\le {\mathrm{\eta }}^{\ast }\right\}$$ (45)

as a restricted upper eigenvalue, where λ_max(M) is the largest eigenvalue of matrix M, B ⊆ {1,…, p}, and ψ̈_B(β) and W_B are the restrictions of the Hessian of (1) and the weight operator W = diag(w₁,…, w_p) to ℝ^B.

Theorem 19

Let β^* be a target vector, $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$, β̂ be the weighted Lasso estimator (2), and $z_k^{\ast }$ be the ℓ_∞-noise level as in (5). Let 0 ≤ η^* ≤ 1, φ_1,S(b) = |b_S|₁/|S|, φ₀ be a quasi star-shaped function, and F(ξ,S;φ₀, φ) be the GIF in (14). Then, in the event (15),

$$\#\{j:{\widehat{\mathrm{\beta }}}_j\ne 0,j\notin S\}<d_1=min\left\{m\ge 1:\frac{m}{{\mathrm{\kappa }}_{+}(m)}>\frac{e^{\mathrm{\eta }}{\mathrm{\xi }}^2\mid S\mid }{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_{1,S})}\right\}.$$

It follows from the Cauchy-Schwarz inequality that κ₊(m) is sub-additive, κ₊(m₁ + m₂) ≤ κ₊(m₁) + κ₊(m₂), so that m/κ₊(m) is non-decreasing in m. For GLM, lower bounds for the GIF and probability upper bounds for $z_k^{\ast }$ can be found in Subsection 3.2. For $S=\{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$. Theorem 19 gives an upper bound for the false negative.

In linear regression, upper bounds for the false negative of the Lasso or concave penalized LSE can be found in Zhang and Huang (2008) and Zhang (2010a) under a sparse Riesz condition (SRC). We now extend their results to the Lasso for the more general convex minimization problem (1). For this purpose, we strengthen (18) to

$$e^{-{\mathrm{\phi }}_0(b)}{\mathrm{\sum }}^{\ast }\le \ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+b)\le e^{{\mathrm{\phi }}_0(b)}{\mathrm{\sum }}^{\ast },\forall b\in \mathcal{C}(\mathrm{\xi },S),{\mathrm{\phi }}_0(b)\le {\mathrm{\eta }}^{\ast },$$ (46)

and assume the following SRC: for certain constants {c_*, c^*}, integer d^*, 0 < α < 1, 0 < η ≤ η^* ≤ 1, all A ⊃ S with |A| = d^*, and all u ∈ ℝ^A with |u| = 1,

$$c_{\ast }\le \langle u,{\ddot{\mathrm{\psi }}}_A({\mathrm{\beta }}^{\ast })u\rangle \le c^{\ast },\frac{\mid S\mid }{2(1-\mathrm{\alpha })}\left(\frac{e^{2\mathrm{\eta }}{c}^{\ast }}{c_{\ast }}+1-2\mathrm{\alpha }\right)\le d^{\ast }.$$ (47)

Theorem 20

Let β̂ be the Lasso estimator (2) with w_j = 1 for all j, β^* be a target vector, $S\supseteq \{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$, and $z_k^{\ast }$ be the ℓ_∞-noise level as in (5). Let φ₀ be a quasi star-shaped function, and F(ξ,S;φ₀,φ) be the GIF in (14). Suppose (46) and (47) hold. Let d₁ be the integer satisfying d₁ − 1 ≤ |S|(e^2ηc^*/c_* − 1)/(2 − 2α) < d₁. Then,

$$\#\{j:{\widehat{\mathrm{\beta }}}_j\ne 0,j\notin S\}<d_1$$

when $z_0^{\ast }+\mathrm{\xi }{z}_1^{\ast }\le (\mathrm{\xi }-1)\mathrm{\lambda },\mathrm{\lambda }+z_0^{\ast }\le \mathrm{\eta }{e}^{-\mathrm{\eta }}F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)$, and

$$\underset{A\supset S,\mid A\mid \le d_1}{max}{\mid {({\mathrm{\sum }}^{\ast })}_A^{-1/2}{\stackrel{.}{\ell }}_A({\mathrm{\beta }}^{\ast })\mid }_2\le e^{-\mathrm{\eta }}\mathrm{\alpha }\mathrm{\lambda }\sqrt{d_1/c^{\ast }}.$$

Theorems 19 and 20 use different sets of conditions to derive dimension bounds since different analytical approaches are used. These sets of conditions do not imply each other. In the most optimistic case, the SRC (47) allows d^* = d₁ +|S| to be arbitrary close to |S| when e^2ηc^*/c_* ≈ 1, while Theorem 19 requires d₁ ≥ |S| when κ₊(m) ≥ 1 and F(ξ,S;φ₀,φ_1,S) ≤ 1 (always true for Σ^* with 1 in the diagonal).

7. Discussion

In this paper, we studied the estimation, prediction, selection and sparsity properties of the weighted and adaptive ℓ₁-penalized estimators in a general convex loss formulation. We also studied concave regularization in the form of recursive application of adaptive ℓ₁-penalized estimators.

We applied our general results to several important statistical models, including linear regression and generalized linear models. For linear regression, we extend the existing results to weighted and adaptive Lasso. For the GLMs, the ℓ_q,q ≥ 1 error bounds for a general q ≥ 1 for the GLMs are not available in the literature, although ℓ₁ and ℓ₂ bounds have been obtained under different sets of conditions respectively in van de Geer (2008) and ]citeNegahbanRWY10. Our fixed-sample analysis provides explicit definition of constant factors in an explicit neighborhood of a target. Our oracle inequalities yields even sharper results for multistage recursive application of adaptive Lasso based on a suitable concave penalty. The results on the sparsity of the solution to the ℓ₁-penalized convex minimization problem is based on a new approach.

An interesting aspect of the approach taken in this paper in dealing with general convex losses such as those for the GLM is that the conditions imposed on the Hessian naturally “converge” to those for the linear regression as the convex loss “converges” to a quadratic form.

A key quantity used in the derivation of the results is the generalized invertibility factor (14), which grow out of the idea of the ℓ₂ restricted eigenvalue but improves upon it. The use of GIF yields sharper bounds on the estimation and prediction errors. This was discussed in detail in the context of linear regression in Ye and Zhang (2010).

We assume that the convex function ψ(·) is twice differentiable. Although this assumption is satisfied in many important and widely used statistical models, it would be interesting to extend the results obtained in this paper to models with less smooth loss functions, such as those in quantile regression and support vector machine.

Appendix A

Proof of Lemma 1

Since ψ̇(β̂) − ψ̇(β^*) = z − ψ̇(β^*) − g, (3) implies

$$\mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })=\langle \widehat{\mathrm{\beta }},z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\rangle -\mathrm{\lambda }{\mid \widehat{W}\widehat{\mathrm{\beta }}\mid }_1-\langle {\mathrm{\beta }}^{\ast },z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })-g\rangle$$

and |g_j| ≤ ŵ_jλ. Thus, (7) follows from |(z − ψ̇(β^*)_j| ≤ ŵ_jλ and ŵ_j ≤ w_j in S in Ω₀.

For (8), we have h_S^c = β̂_S^c and ${\mathrm{\beta }}_{S^c}^{\ast }=0$, so that in Ω₀ (3) gives

$$\begin{array}{l}\mathrm{\Delta }(\widehat{\mathrm{\beta }},{\mathrm{\beta }}^{\ast })=\langle {\widehat{\mathrm{\beta }}}_{S^c},{\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S^c}\rangle -\mathrm{\lambda }{\mid {\widehat{W}}_{S^c}{\widehat{\mathrm{\beta }}}_{S^c}\mid }_1-\langle h_S,{\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })-g\}}_S\rangle \\ \le {\mid W_{S^c}{\widehat{\mathrm{\beta }}}_{S^c}\mid }_1(z_1^{\ast }-\mathrm{\lambda })+\langle h_S,g_S-{\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\rangle \\ \le {\mid W_{S^c}{\widehat{\mathrm{\beta }}}_{S^c}\mid }_1(z_1^{\ast }-\mathrm{\lambda })+{\mid h_S\mid }_1(z_0^{\ast }+{\mid w_S\mid }_{\infty }\mathrm{\lambda }).\end{array}$$

This gives (8). Since Δ(β̂,β^*)>0, h ∈ (ξ,S) when $({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })/(\mathrm{\lambda }-z_1^{\ast })\le \mathrm{\xi }$. For j ∉ S, h_j(ψ̇(β + h) − ψ̇(β))_j = β̂_j(z − ψ̇(β^*) − g)_j ≤ |β̂_j|(w_jλ − g_j) ≤ 0.

Proof of Theorem 4

Let h = β̂ − β^*. Since ψ(β) is a convex function,

$$t^{-1}\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+th,{\mathrm{\beta }}^{\ast })=\frac{\partial }{\partial t}\left\{\mathrm{\psi }({\mathrm{\beta }}^{\ast }+th)-t\langle h,\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\rangle \right\}$$

is an increasing function of t. For 0 ≤ t ≤ 1 and in the event Ω₁, (8) implies

$$t^{-1}\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+th,{\mathrm{\beta }}^{\ast })\le \mathrm{\Delta }(h+{\mathrm{\beta }}^{\ast },{\mathrm{\beta }}^{\ast })<({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }){\mid h_S\mid }_1.$$

By (9) and (14), F(ξ,S;φ₀,φ₀) ≤ Δ(β^* + th,β^*)e^φ₀(th)/{t|h_S|₁φ₀(th)} for φ₀(th) ≤ η^*. Thus, for φ₀(th) ≤ min{η^*,φ₀(h)} and in the event Ω₁,

$${\mathrm{\phi }}_0(th)e^{-{\mathrm{\phi }}_0(th)}\le \frac{\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+th,{\mathrm{\beta }}^{\ast })}{t{\mid h_S\mid }_{1}F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)}\le \frac{{\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }}{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)}\le \mathrm{\eta }{e}^{-\mathrm{\eta }}.$$

If η^* < φ₀(h), the above inequality at φ₀(th) = η^* would give η^*e^−η*< ηe^−η, which contradicts to η ≤ η^* ≤ 1. Thus, η^* ≥ φ₀(h) and φ₀(th)e^−φ₀(th) ≤ ηe^−η for all 0 ≤ t ≤ 1. This implies φ₀(h) ≤ η ≤ η^*. Another application of (8) yields

$$\mathrm{\phi }(h)\le \frac{\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })e^{{\mathrm{\phi }}_0(h)}}{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,\mathrm{\phi }){\mid h_S\mid }_1}\le \frac{({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })e^{\mathrm{\eta }}}{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,\mathrm{\phi })}.$$

We obtain (17) by applying (16) with φ = φ_1,S to the right-hand side of (8).

Proof of Lemma 8

1. Since $\stackrel{.}{\mathrm{\psi }}(\mathrm{\beta })={\sum }_{i=1}^n{x}^i{\stackrel{.}{\mathrm{\psi }}}_0(x^i\mathrm{\beta })/n$ by (23),

   $$\begin{array}{l}{\mathrm{E}}_{\mathrm{\beta }}exp\left\{\frac{n}{{\mathrm{\sigma }}^2}\langle b,z-\stackrel{.}{\mathrm{\psi }}(\mathrm{\beta })\rangle \right\}=exp\left[\sum _{i=1}^n\frac{{\mathrm{\psi }}_0(x^i(\mathrm{\beta }+b))-{\mathrm{\psi }}_0(x^i\mathrm{\beta })-(x^{i}b){\stackrel{.}{\mathrm{\psi }}}_0(x^i\mathrm{\beta })}{{\mathrm{\sigma }}^2}\right]\\ =exp\left[\sum _{i=1}^n{\int }_0^1\frac{{(x^{i}b)}^2{\ddot{\mathrm{\psi }}}_0(x^i(\mathrm{\beta }+tb))}{{\mathrm{\sigma }}^2}(1-t)dt\right].\end{array}$$ (48)
   This and (24) imply that for M₁|Xb|_∞ ≤ η₀,

   $${\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}exp\left\{\frac{n}{{\mathrm{\sigma }}^2}\langle b,z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\rangle \right\}\le exp\left[\frac{{ne}^{{\mathrm{\eta }}_0}\langle b,{\mathrm{\sum }}^{\ast }b\rangle }{2{\mathrm{\sigma }}^2}\right].$$ (49)
   Since ${max}_{k=0,1}{z}_k^{\ast }/{\mathrm{\lambda }}_k={max}_j{t}_j^{-1}\mid z_j-{\stackrel{.}{\mathrm{\psi }}}_j({\mathrm{\beta }}^{\ast })$ by (5),

   $$\begin{array}{l}{\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}\left\{\underset{k=0,1}{max}{z}_k^{\ast }/{\mathrm{\lambda }}_k>1\right\}\le \sum _{j=1}^p{\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}\left\{\mid z_j-{\stackrel{.}{\mathrm{\psi }}}_j({\mathrm{\beta }}^{\ast })\mid >t_j\right\}\\ \le \sum _{j=1}^p{\mathrm{E}}_{{\mathrm{\beta }}^{\ast }}exp\left\{\frac{n}{{\mathrm{\sigma }}^2}{b}_j\mid z_j-{\stackrel{.}{\mathrm{\psi }}}_j({\mathrm{\beta }}^{\ast })\mid -\frac{n}{{\mathrm{\sigma }}^2}{b}_j{t}_j\right\}\end{array}$$
   with $b_j=e^{-{\mathrm{\eta }}_0}{t}_j/{\mathrm{\sum }}_{jj}^{\ast }$. Since M₁ max_ij|x_ij|b_j ≤ η₀, (49) gives

   $${\mathrm{P}}_{{\mathrm{\beta }}^{\ast }}\left\{\underset{k=0,1}{max}{z}_k^{\ast }/{\mathrm{\lambda }}_k>1\right\}\le \sum _{j=1}^{p}2exp\left(-\frac{{ne}^{-{\mathrm{\eta }}_0}{t}_j^2}{2{\mathrm{\sigma }}^2{\mathrm{\sum }}_{jj}^{\ast }}\right).$$

2. If (30) holds, we simply replace ¨₀(xⁱ(β + tb)) by c₀ in (48). The rest is simpler and omitted.

Proof of Theorem 9

(i) Since F^*(ξ,S;φ) in (25) is a lower bound of F(ξ,S;φ₀,φ) in (14), (32) follows from Theorem 4 with φ₀(b) = M₂|b|₂. The probability statement follows from Lemma 8. (ii) Since (18) holds for the φ₀(b) in (26), we are allowed to use F_*(ξ,S) = F₀(ξ,S;φ₀) in Corollary 7. The condition η^* = ∞ is used since φ₀(b) does not control M₁|Xb|_∞. (iii) We are also allowed to use φ₀(b) = M₃|b_S|₁ in (28) due to M₁|Xb|_∞ ≤ φ₀(b).

Proof of Theorem 14

Let h = β̂ − β^*, w_j = ŵ_j and S = {j : |β̂_j| > γ₀λ}∪ S₀. For j ∉ S, w_j = ρ̇_λ(|β̃_j|)/λ ≥ {ρ̇_λ(0+) − κγ₀λ}/λ = 1 − κγ₀, so that $z_1^{\ast }={\mid W_{S^c}^{-1}{\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S^c}\mid }_{\infty }\le {\mathrm{\lambda }}_0/(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)=\mathrm{\lambda }/A$. We also have $z_0^{\ast }\le {\mid z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\mid }_{\infty }\le {\mathrm{\lambda }}_0=(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)/\mathrm{\lambda }/A$. Since |ŵ|_∞ ≤ 1, these bounds for $z_0^{\ast }$ and $z_1^{\ast }$ yield

$$\frac{{\mid {\widehat{w}}_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }}{\mathrm{\lambda }-z_1^{\ast }}\le \frac{\mathrm{\lambda }+(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)\mathrm{\lambda }/A}{\mathrm{\lambda }-\mathrm{\lambda }/A}=\frac{A+1-\mathrm{\kappa }{\mathrm{\gamma }}_0}{A-1}\le \mathrm{\xi }.$$

Thus, since |g_j| ≤ ŵ_jλ in (8), Lemma 1 provides

$$h\in \mathcal{C}(\mathrm{\xi },S),\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })\le {\mid h_S\mid }_2({\mid {\widehat{w}}_S\mid }_2\mathrm{\lambda }+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\mid }_2)$$

Since $\mid S\backslash S_0\mid \le {\mid {(\stackrel{\sim }{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast })}_{S_0^c}\mid }_2^2/({\mathrm{\gamma }}_0^2{\mathrm{\lambda }}^2)\le {\ell }^{\ast }$, we have by (36)

$${\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast }\le \mathrm{\lambda }+{\mathrm{\lambda }}_0={\mathrm{\lambda }}_0\{1+A/(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)\}\le F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)\mathrm{\eta }{e}^{-\mathrm{\eta }}.$$

Thus, φ₀(h) ≤ η by (16), so that by (34) and (36),

$$e^{-\mathrm{\eta }}{F}_{\ast }{\mid h_S\mid }_2{\mid h\mid }_2\le \mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })\le {\mid h_S\mid }_2({\mid {\widehat{w}}_S\mid }_2\mathrm{\lambda }+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\mid }_2).$$

Since |h_S| = 0 implies h = 0 for h ∈ (ξ,S), we find

$$e^{-\mathrm{\eta }}{F}_{\ast }{\mid h\mid }_2\le {\mid {\widehat{w}}_S\mid }_2\mathrm{\lambda }+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\mid }_2.$$ (50)

Since ${\widehat{w}}_j\mathrm{\lambda }={\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\stackrel{\sim }{\mathrm{\beta }}}_j\mid )\le {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_j^{\ast }\mid )+\mathrm{\kappa }\mid {\stackrel{\sim }{\mathrm{\beta }}}_j-{\mathrm{\beta }}_j^{\ast }\mid$, we have

$${\mid {\widehat{w}}_S\mid }_2\mathrm{\lambda }\le \mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+\mathrm{\kappa }{\mid \stackrel{\sim }{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2.$$

Since |z − ψ̇(β^*)|_∞ ≤ λ₀ = (1 − κγ₀)λ/A and $\mid {\stackrel{\sim }{\mathrm{\beta }}}_j-{\mathrm{\beta }}_j^{\ast }\mid =\mid {\stackrel{\sim }{\mathrm{\beta }}}_j\mid \ge {\mathrm{\gamma }}_0\mathrm{\lambda }$ for j ∈ S\S₀,

$$\begin{array}{l}{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_S\mid }_2\le {\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2+{\mid S\backslash S_0\mid }^{1/2}(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)\mathrm{\lambda }/A\\ \le {\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2+{\mid \stackrel{\sim }{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2(1-\mathrm{\kappa }{\mathrm{\gamma }}_0)/({\mathrm{\gamma }}_{0}A).\end{array}$$

Inserting the above inequalities into (50), we find that

$$e^{-\mathrm{\eta }}{F}_{\ast }{\mid \widehat{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2\le \mid {\stackrel{.}{\mathrm{\rho }}}_{\mathrm{\lambda }}(\mid {\mathrm{\beta }}_{S_0}^{\ast }{\mid )\mid }_2+{\mid {\{z-\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\}}_{S_0}\mid }_2+\left(\mathrm{\kappa }+\frac{1}{{\mathrm{\gamma }}_{0}A}-\frac{\mathrm{\kappa }}{A}\right){\mid \stackrel{\sim }{\mathrm{\beta }}-{\mathrm{\beta }}^{\ast }\mid }_2.$$

The probability statement follows directly from (35) with the union bound.

Proof of Theorem 15

Let R^(ℓ) be as in Remark 16. For |z − ψ̇(β^*)|_∞ ≤ λ₀, (16) of Theorem 4 gives |β̂⁽⁰⁾ − β^*|₂ ≤ e^η(λ + λ₀)/F(ξ₀,S₀;φ₀, |·|₂) = R⁽⁰⁾. Under conditions (38) and (40), we have $R^{(\ell )}\le {\mathrm{\gamma }}_0\mathrm{\lambda }\sqrt{{\ell }^{\ast }}$ for all ℓ ≥ 0. We prove (39) by induction. We have already proved (39) for ℓ = 0. For ℓ ≥ 1, we let β̃ = β̂^(ℓ−1) and apply Theorem 14: |β̂^(ℓ) − β^*|₂ ≤ (1 − r₀)R^(∞) + r₀R^(ℓ−1) = R^(ℓ). The probability statement follows directly from (35) with the union bound.

Proof of Theorem 18

Let z̃ = z − ψ̇(β^*) and λ be fixed. Consider

$$\widehat{\mathrm{\beta }}(\mathrm{\lambda },t)=\underset{\mathrm{\beta }}{argmin}\left\{\mathrm{\psi }(\mathrm{\beta })-\langle \mathrm{\beta },\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })+t\stackrel{\sim }{z}\rangle +t\mathrm{\lambda }\sum _{j=1}^p{\widehat{w}}_j\mid {\mathrm{\beta }}_j\mid :{\mathrm{\beta }}_{S^c}=0\right\}$$ (51)

as an artificial path for 0 ≤ t ≤ 1. For each t, the KKT conditions for β̂(λ, t) are

$$g_S(\mathrm{\lambda },t)=t\mathrm{\lambda }{\widehat{W}}_S{u}_S(\mathrm{\lambda },t),u_j(\mathrm{\lambda },t)\{\begin{array}{ll}=sgn({\widehat{\mathrm{\beta }}}_j(\mathrm{\lambda },t))\hfill & \forall {\widehat{\mathrm{\beta }}}_j(\mathrm{\lambda },t)\ne 0\hfill \\ \in [-1,1],\hfill & \forall j\in S,\hfill \end{array}$$

where g(λ, t) = −ψ̇(β̂(λ, t)) + ψ̇(β^*) + tz̃. Since (51) is constrained to β_S^c= 0 and both the error z̃ and the penalty level λ are scaled with t, Theorem 4 with ξ = 0 yields

$${\mathrm{\phi }}_0(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t)-{\mathrm{\beta }}^{\ast })\le {\mathrm{\eta }}_t\to 0\text{with}{\mathrm{\eta }}_t{e}^{-{\mathrm{\eta }}_t}=t\mathrm{\eta }{e}^{-\mathrm{\eta }},\forall 0<t\le 1.$$ (52)

Let S_t = {j : β̂_j(λ, t) ≠ 0}. Applying the differentiation operator D = (∂/∂t) to the KKT conditions, we find that almost everywhere in t,

$${(Dg)}_{S_t}(\mathrm{\lambda },t)={\stackrel{\sim }{z}}_{S_t}-{\ddot{\mathrm{\psi }}}_{S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t)){\{(D\widehat{\mathrm{\beta }})(\mathrm{\lambda },t)\}}_{S_t}=\mathrm{\lambda }{\widehat{W}}_{S_t}{u}_{S_t}(\mathrm{\lambda },t).$$

It follows that

$${(D\widehat{\mathrm{\beta }})}_{S_t}(\mathrm{\lambda },t)={\{{\ddot{\mathrm{\psi }}}_{S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t))\}}^{-1}\{{\stackrel{\sim }{z}}_{S_t}-\mathrm{\lambda }{\widehat{W}}_{S_t}{u}_{S_t}(\mathrm{\lambda },t)\}$$ (53)

and with an application of the chain rule,

$${(Dg)}_{S^c}(\mathrm{\lambda },t)={\stackrel{\sim }{z}}_{S^c}-{\ddot{\mathrm{\psi }}}_{S^c,S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t)){\{{\ddot{\mathrm{\psi }}}_{S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t))\}}^{-1}\{{\stackrel{\sim }{z}}_{S_t}-\mathrm{\lambda }{\widehat{W}}_{S_t}{u}_{S_t}(\mathrm{\lambda },t)\}.$$

Since g(λ, t) is almost differentiabe and β̂(λ, 0+) = β^*, we have g(λ, 0+) = 0 and

$$g_{S^c}(\mathrm{\lambda },1-)={\int }_0^1\left[{\stackrel{\sim }{z}}_{S^c}-{\ddot{\mathrm{\psi }}}_{S^c,S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t)){\{{\ddot{\mathrm{\psi }}}_{S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t))\}}^{-1}\{{\stackrel{\sim }{z}}_{S_t}-\mathrm{\lambda }{\widehat{W}}_{S_t}{u}_{S_t}(\mathrm{\lambda },t)\}\right]dt.$$

Thus, (52), (41), and (42) imply

$${\mid {\widehat{W}}_{S^c}^{-1}{g}_{S^c}(\mathrm{\lambda },1-)\mid }_{\infty }\le {\mid {\widehat{W}}_{S^c}^{-1}{\stackrel{\sim }{z}}_{S^c}\mid }_{\infty }+{\mathrm{\kappa }}_1{\mid {\stackrel{\sim }{z}}_S\mid }_{\infty }+{\mathrm{\kappa }}_0\mathrm{\lambda }{\mid u_{S_t}(\mathrm{\lambda },t)\mid }_{\infty },$$

which is smaller than λ in the event in (43). Thus, since ¨_S(β̂(λ, 1−)) is of full rank, β̂(λ, 1−) is the unique solution of the KKT conditions (3) for β̂. This completes the proof of part (i).

For part (ii), we observe that (44) implies $S=\{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$. Since β̂(λ, 0+) = β^*, there exists t₁ > 0 such that $u_S(\mathrm{\lambda },t)=sgn({\mathrm{\beta }}_S^{\ast })$ for all 0 <t <t₁. By (52), β̂(λ, t) ∈ 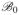for 0 <t <t₁. It follows from (53) and (44) that

$${\mid {(D\widehat{\mathrm{\beta }})}_S(\mathrm{\lambda },t)\mid }_{\infty }\le {\Vert {\{{\ddot{\mathrm{\psi }}}_{S_t}(\widehat{\mathrm{\beta }}(\mathrm{\lambda },t))\}}^{-1}\Vert }_{\infty }{\mid {\stackrel{\sim }{z}}_S-\mathrm{\lambda }{\widehat{W}}_{S}sgn({\mathrm{\beta }}_S^{\ast })\mid }_{\infty }<\underset{j\in S}{min}\mid {\mathrm{\beta }}_j^{\ast }\mid -{\mathrm{\epsilon }}_1$$

for 0 <t <t₁ and some ε₁ > 0. Since β̂(λ, 0+) = β^*, this implies ${\mid {\widehat{\mathrm{\beta }}}_S(\mathrm{\lambda },t)-{\mathrm{\beta }}_S^{\ast }\mid }_{\infty }<{min}_{j\in S}\mid {\mathrm{\beta }}_j^{\ast }\mid -{\mathrm{\epsilon }}_1$ for all 0 <t <t₁ ∧ 1. It follows that sgn(β̂(λ, t)) = sgn(β^*) for 0 < t ≤ 1 by the continuity of β̂(λ, t) in t, that is, t₁ = 1. Consequently, conditions (41), and (42) are only needed for the smaller class 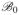in the proof of part (i). This gives β̂(λ, 1) = β̂ and completes the proof of part (ii).

Finally, in part (iii), F₀(ξ,S;φ₀,φ₀) is simply replaced by its lower bounds with the respective φ₀.

Proof of Theorem 19

Suppose the event Ω₁ in (15) happens, so that ŵ_j ≥ w_j for j ∉ S and the conclusion of Theorem 4 hold. Let h = β̂ − β^* and $\widehat{\mathrm{\sum }}={\int }_0^1\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+xh)dx$. It follows from (1) that Σ̂h = ψ̇(β^* + h) − ψ̇(β^*) = ℓ̇(β̂) − ℓ̇(β^*). By the KKT conditions (3),

$$\mid {(\widehat{\mathrm{\sum }}h)}_j\mid =\mid {(\stackrel{.}{\ell }(\widehat{\mathrm{\beta }})-\stackrel{.}{\ell }({\mathrm{\beta }}^{\ast }))}_j\mid \ge {\widehat{w}}_j\mathrm{\lambda }-z_j\ge w_j(\mathrm{\lambda }-z_1^{\ast })>0,j\notin S.$$

Let B ⊆ {j ∉ S : β̂_j ≠ 0} with |B| ≤ d₁. It follows from Theorem 4 that φ₀(h) ≤ η ≤ η^*, so that (45) implies ${max}_{{\mid u\mid }_2=1}{\mid {(W^{-1}{\widehat{\mathrm{\sum }}}^{1/2}u)}_B\mid }_2^2={\mathrm{\lambda }}_{max}(W_B^{-2}{\widehat{\mathrm{\sum }}}_B)\le {\mathrm{\kappa }}_{+}(d_1)$. Thus, by the definition of Δ(β, β^*) in (4),

$${(\mathrm{\lambda }-z_1^{\ast })}^2\mid B\mid \le {\mid {(W^{-1}\widehat{\mathrm{\sum }}h)}_B\mid }_2^2\le {\mathrm{\kappa }}_{+}(d_1)\langle h,\widehat{\mathrm{\sum }}h\rangle ={\mathrm{\kappa }}_{+}(d_1)\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast }).$$

This and the prediction bound in Theorem 4 yield

$$\mid B\mid \le \frac{{\mathrm{\kappa }}_{+}(d_1)\mathrm{\Delta }({\mathrm{\beta }}^{\ast }+h,{\mathrm{\beta }}^{\ast })}{{(\mathrm{\lambda }-z_1^{\ast })}^2}\le \frac{{\mathrm{\kappa }}_{+}(d_1)e^{\mathrm{\eta }}{({\mid w_S\mid }_{\infty }\mathrm{\lambda }+z_0^{\ast })}^2\mid S\mid }{{(\mathrm{\lambda }-z_1^{\ast })}^{2}F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_{1,S})}\le \frac{{\mathrm{\kappa }}_{+}(d_1)e^{\mathrm{\eta }}{\mathrm{\xi }}^2\mid S\mid }{F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_{1,S})}<d_1.$$

Since all subsets B ⊆ {j ∉ S : β̂_j ≠ 0} with |B| ≤ d₁ satisfies |B| < d₁, it must hold that #{j ∉ S : β̂_j ≠ 0} < d₁.

Proof of Theorem 20

Let z̃ = z − ψ̇(β^*) = −ℓ̇(β^*) and β̂(λ, t) be the artificial estimator in (51) with ŵ_j = 1, and h(λ, t) = β̂(λ, t) − β^*. Let λ_* ≤ λ^* be penalty levels satisfying

$$[{\mathrm{\lambda }}_{\ast },{\mathrm{\lambda }}^{\ast }]\subseteq {\cap }_{0<t\le 1}\left\{\mathrm{\lambda }:{\mathrm{\phi }}_0(h(\mathrm{\lambda },t))\le \mathrm{\eta },h(\mathrm{\lambda },t)\in \mathcal{C}(\mathrm{\xi },S),{\mid {({\mathrm{\sum }}^{\ast })}^{-1/2}\stackrel{\sim }{z}\mid }_2\le \frac{\mathrm{\alpha }\mathrm{\lambda }\sqrt{d_1}}{e^{\mathrm{\eta }}\sqrt{c^{\ast }}}\right\}.$$ (54)

We pick such an interval [λ_*,λ^*] containing the penalty level λ of concern in the theorem. This is allowed by Lemma 1 and Theorem 4. We first prove the stronger conclusion

$$\underset{{\mathrm{\lambda }}_{\ast }\le \mathrm{\lambda }\le {\mathrm{\lambda }}^{\ast }}{max}\underset{0<t\le 1}{max}\#\{j:{\widehat{\mathrm{\beta }}}_j(\mathrm{\lambda },t)\ne 0,j\notin S\}<d_1$$ (55)

under the additional assumption

$$\underset{{\mathrm{\lambda }}_{\ast }\le \mathrm{\lambda }\le {\mathrm{\lambda }}^{\ast }}{min}\underset{0<t\le 1}{min}\#\{j:{\widehat{\mathrm{\beta }}}_j(\mathrm{\lambda },t)\ne 0,j\notin S\}\le d_1.$$ (56)

Let g(λ, t) = tz̃ + ψ̇(β^*) − ψ̇(β̂(λ, t)) be the negative gradient at β̂(λ, t) in (51). By the KKT conditions for (51), sgn(β̂_j(λ, t±)) ≠ 0 implies |g(λ, t)| = tλ. Thus, (56) implies the existence of λ ∈ [λ_*,λ^*], t₁ ∈ (0, 1], and A₁ ⊂ {1, …, p} satisfying

$$\{j:sgn({\widehat{\mathrm{\beta }}}_j(\mathrm{\lambda },t_1))\ne 0\}\cup S\subseteq A_1\subseteq \{j:\mid g(\mathrm{\lambda },t_1)\mid =t_1\mathrm{\lambda }\}\cup S,\mid A_1\mid \le d_1+\mid S\mid .$$ (57)

Moreover, if max_{λ*≤λ≤λ^*} max_0<t≤1 #{j : β̂_j(λ, t) ≠ 0, j ∉ S} ≥ d₁, then by the continuity of β̂(λ, t), it would be possible to restrict (57) to |A₁| = d₁ + |S| with some different λ ∈ [λ_*,λ^*] and t₁ ∈ (0, 1]. Therefore, it suffices to deny this possibility by proving |A₁| < d₁ + |S| based on (57) and (54). Let A₀ = A₁\S. We prove |A₀| < d₁, which is equivalent to |A₁| < d₁ + |S|.

Let v_(A) =(v_jI{j ∈ A}, j ∈ A₁)′ ∈ ℝ^A₁ and v_A = (v_j, j ∈ A)′ ∈ ℝ^A for all vectors v = (v₁, …, v_p)′. Let h = h(λ, t₁), $\widehat{\mathrm{\sum }}={\int }_0^1\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+xh)dx$, and g = g(λ, t₁) =t₁z̃ + ψ̇(β^*) − ψ̇(β^* + h) =t₁z̃ − Σ̂h. Since $h_{A_1^c}=0,{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{g}_{(A_1)}=t_1{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{\stackrel{\sim }{z}}_{A_1}-{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{(\widehat{\mathrm{\sum }}h)}_{A_1}=t_1{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{\stackrel{\sim }{z}}_{A_1}-h_{A_1}$. Thus, since g_j =t₁λsgn(h_j) for j ∈ A₀ by the KKT conditions,

$$\langle g_{(A_0)},{\widehat{\mathrm{\sum }}}_{A_1}^{-1}g(A_1)\rangle =t_1\langle g_{(A_0)},{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{\stackrel{\sim }{z}}_{A_1}\rangle -\langle g_{(A_0)},h_{A_1}\rangle \le t_1\langle g_{(A_0)},{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{\stackrel{\sim }{z}}_{A_1}\rangle .$$

Since ${\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_0)}\mid }_2^2+{\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_1)}\mid }_2^2={\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(S)}\mid }_2^2+2\langle g_{(A_0)},{\widehat{\mathrm{\sum }}}_{A_1}^{-1}{g}_{(A_1)}\rangle$, we have

$${\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_0)}\mid }_2^2+{\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_1)}\mid }_2^2\le {\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}g(s)\mid }_2^2+2t_1{\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_0)}\mid }_2{\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{\stackrel{\sim }{z}}_{A_1}\mid }_2.$$

By (54) and (46), ${\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{\stackrel{\sim }{z}}_{A_1}\mid }_2\le e^{\mathrm{\eta }/2}{\mid {({\mathrm{\sum }}_{A_1}^{\ast })}^{-1/2}{\stackrel{\sim }{z}}_{A_1}\mid }_2\le \mathrm{\alpha }\mathrm{\lambda }\sqrt{\mid A_0\mid /(c^{\ast }{e}^{\mathrm{\eta }})}$, so that

$$(1-\mathrm{\alpha }){\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_0)}\mid }_2^2+{\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}{g}_{(A_1)}\mid }_2^2\le {\mid {\widehat{\mathrm{\sum }}}_{A_1}^{-1/2}g(s)\mid }_2^2+\mathrm{\alpha }{t}_1^2{\mathrm{\lambda }}^2\mid A_0\mid /(c^{\ast }{e}^{\mathrm{\eta }}).$$

Moreover, since |A₁| ≤ d₁ + |S| ≤ d^*, it follows from (54), (46), and (47) that the eigenvalues of Σ̂_A1all lie in the interval c_*e^−η and c^*e^η. Thus, since g_A0= t₁λsgn(β̂_A0),

$$\frac{(1-\mathrm{\alpha })t_1^2{\mathrm{\lambda }}^2\mid A_0\mid }{c^{\ast }{e}^{\mathrm{\eta }}}+\frac{t_1^2{\mathrm{\lambda }}^2\mid A_0\mid +{\mid g_S\mid }_2^2}{c^{\ast }{e}^{\mathrm{\eta }}}\le \frac{{\mid g_S\mid }_2^2}{c_{\ast }{e}^{-\mathrm{\eta }}}+\frac{\mathrm{\alpha }{t}_1^2{\mathrm{\lambda }}^2\mid A_0\mid }{c^{\ast }{e}^{\mathrm{\eta }}}.$$

Since |g|_∞ ≤ t₁λ, the above inequality gives by algebra the dimension bound

$$\mid A_0\mid \le \left(\frac{e^{2\mathrm{\eta }}{c}^{\ast }/c_{\ast }-1}{2-2\mathrm{\alpha }}\right)\frac{{\mid g_S\mid }_2^2}{t_1^2{\mathrm{\lambda }}^2}\le \left(\frac{e^{2\mathrm{\eta }}{c}^{\ast }/c_{\ast }-1}{2-2\mathrm{\alpha }}\right)\mid S\mid <d_1.$$

This proves (55) under the additional assumption (56).

Now we prove (56). In the special case of φ₀(b) = 0, the condition on λ in (54) is monotone so that we are allowed to pick λ^* = ∞. Since β̂(λ, 1) = 0 for very large λ, (56) holds automatically for φ₀(b) = 0. By (46), this special case is equivalent to linear regression since the Hessian does not depend on β. The difference of the general model (1) from linear regression is that the condition $\mathrm{\lambda }+z_0^{\ast }\le \mathrm{\eta }{e}^{-\mathrm{\eta }}F(\mathrm{\xi },S;{\mathrm{\phi }}_0,{\mathrm{\phi }}_0)$, which excludes large λ, is needed to prove φ₀(h(λ, t)) ≤ η by Theorem 4. To overcome this difficulty, we consider very small t > 0. Let b = (β − β^*)/t. By (51),

$$\begin{array}{l}{t}^{-1}\{\widehat{\mathrm{\beta }}(\mathrm{\lambda },t)-{\mathrm{\beta }}^{\ast }\}=\underset{b}{argmin}\left\{\mathrm{\psi }({\mathrm{\beta }}^{\ast }+tb)-\langle tb,\stackrel{.}{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })+t\stackrel{\sim }{z}\rangle +t\mathrm{\lambda }{\mid {\mathrm{\beta }}^{\ast }+tb\mid }_1\right\}\\ =\underset{b}{argmin}\left\{{\int }_0^1(1-x)\langle tb,\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+\mathit{xtb})tb\rangle dx-t^2\langle b,\stackrel{\sim }{z}\rangle +t\mathrm{\lambda }{\mid {\mathrm{\beta }}^{\ast }+tb\mid }_1\right\}\\ =\underset{b}{argmin}\left\{{\int }_0^1(1-x)\langle b,\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast }+\mathit{xtb})b\rangle dx-\langle b,\stackrel{\sim }{z}\rangle +\mathrm{\lambda }{\mid {\mathrm{\beta }}^{\ast }/t+b\mid }_1\right\}.\end{array}$$

Let $S_0=\{j:{\mathrm{\beta }}_j^{\ast }\ne 0\}$. Since $\mathrm{\lambda }{\mid {\mathrm{\beta }}^{\ast }/t+b\mid }_1-\mathrm{\lambda }{\mid {\mathrm{\beta }}^{\ast }\mid }_1/t\to \mathrm{\lambda }\langle sgn({\mathrm{\beta }}^{\ast }),b\rangle +\mathrm{\lambda }{\mid b_{S_0^c}\mid }_1$ as t → 0+, t⁻¹{β̂(λ, t) − β^*} converges (along a subsequence if necessary) to

$$\widehat{b}(\mathrm{\lambda })=\underset{b}{argmin}\left\{2^{-1}\langle b,\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })b\rangle -\langle b,\stackrel{\sim }{z}\rangle +\mathrm{\lambda }\langle sgn({\mathrm{\beta }}^{\ast }),b\rangle +\mathrm{\lambda }{\mid b_{S_0^c}\mid }_1\right\}.$$

Moreover, since z̃ − ¨(β^*)b̂(λ) is the negative gradient at b̂(λ), we have

$$\{j:\mid g_j(\mathrm{\lambda },t)\mid =t\mathrm{\lambda },j\notin S\}\to \{j\notin S:{(\stackrel{\sim }{z}-\ddot{\mathrm{\psi }}({\mathrm{\beta }}^{\ast })\widehat{b}(\mathrm{\lambda }))}_j=\mathrm{\lambda }sgn({\widehat{b}}_j(\mathrm{\lambda }))\}.$$ (58)

Since this limit does not depend on φ₀(·), the dimension bound (55) in the special case of linear regression implies that the right-hand side of (58) contains a smaller number of elements than d₁. This gives (56) in the general case by (58) and completes the proof.