Statistical Analysis of Notational AFL Data Using Continuous Time Markov Chains

Abstract

Animal biologists commonly use continuous time Markov chain models to describe patterns of animal behaviour. In this paper we consider the use of these models for describing AFL football. In particular we test the assumptions for continuous time Markov chain models (CTMCs), with time, distance and speed values associated with each transition. Using a simple event categorisation it is found that a semi-Markov chain model is appropriate for this data. This validates the use of Markov Chains for future studies in which the outcomes of AFL matches are simulated.

Key Points.

• A comparison of four AFL matches suggests similarity in terms of transition probabilities for events and the mean times, distances and speeds associated with each transition.

• The Markov assumption appears to be valid.

• However, the speed, time and distance distributions associated with each transition are not exponential suggesting that semi-Markov model can be used to model and simulate play.

• Team identified events and directions associated with transitions are required to develop the model into a tool for the prediction of match outcomes.

Introduction

Animal biologists frequently perform ethological studies creating models in order to provide an accurate description of animal behaviour. The effects of various factors can then be studied in terms of the parameters of these models. The data often consists of continuous time records of behaviour which can be described using Markov chain models which take into account both the duration and the sequence of acts. Using these models it is possible to determine whether behaviour is homogeneous during an observation period, and, when behaviour is not homogeneous, changes in the model parameters can be used to determine when and how behaviour changes. Sports can be studied in a similar manner, using notational analysis to collect the data as described in Forbes and Clarke, 2004 and Forbes, 2006. If changes in behaviour can be linked to successful outcomes we will have a valuable tool for player development.

Markov chains have been previously used to model sports events (Bellman, 1977; Bukiet et al., 1997; Forbes, 2006; Forbes and Clarke, 2004; Hirotsu, 2002; Hirotsu and Wright, 2003a; 2003a). Forbes and Clarke, 2004 and Forbes, 2006 created discrete Markov chains for AFL football, but this is probably the first time that an attempt has been made to model AFL football using CTMCs, because the data was not previously available. The model is similar to the above animal behaviour models; however, in addition to associating times with events we also have distances and speeds.

Methods

CTMC Assumptions

There are a number of assumptions associated with a continuous time Markov chain. The Markov property implies that transitions are independent of the time for previous transitions as well as the type of previous transitions. In addition it is assumed that the characteristics of the transitions have exponential distributions for each state. In animal behaviour it is commonly found that the times for behaviours (bouts) do have an exponential distribution.

In our analysis of AFL football we refer to the states of the Markov chain as events, such as a Kick. We have the times for each transition between events as well as the distance and speed associated with each transition, so we shall endeavour to include all three of these transition characteristics into our CTMC model. It is unlikely that these variables will have exponential distributions because these dimensions are confined by field size and shape and because there is a grouping of behaviours under each of the events (e.g. a Kick may be long, short, a ground kick, a clanger, a kick to advantage or an ineffective kick). Also it may be that we do not have a first-order Markov model in that the transition probabilities may not be independent of the previous sequence of events. This paper will investigate these issues in detail.

Processes which do not have exponentially distributed transition times are called Semi-Markov chains. A common distribution in the animal behaviour literature is a displaced exponential distribution which allows for a non-zero minimum value. The gamma distribution has also been used to describe the duration of animal behaviours, allowing for a mixture of exponential distributions. Log-normal distributions are also used and even normal distributions which have been censored at zero. All these possible distributions can be tested for our time, distance and speed variables. Of course, a multivariate distribution allowing for correlations between these three variables should also be considered.

Haccou and Meelis, 1992 recommend the following process for analysing behavioural data in animals.

1. Search for homogeneous periods in order to reduce the error variances in the model. In particular it is possible to determine whether changes are abrupt or gradual.

2. Analysis in the presence of gradual changes require special modelling but where there are abrupt changes the data should be divided into homogeneous subphases and analysed as indicated below for each subphase.

3. Determine suitable distributions for the time, distance and speed variables and test the sequential dependence properties of the process. Also search for outliers.

4. If the distributions are exponential and there is first-order sequential dependency a standard Markov chain analysis is possible.

5. If the distributions are a mixture of exponential or gamma distributions and there is first-order sequential dependency the behavioural categories (Markov states) may have to be subdivided before a standard Markov chain analysis is possible.

6. If the distributions are not exponential or mixtures of exponential or gamma distributions, but there is first-order sequential dependency, a semi-Markov chain analysis is possible.

7. If there is higher order sequential dependency ad hoc analysis methods are required.

We will follow this process, in the analysis below, using a data set derived from four AFL matches during the 2004 season.

The data

The data was collected by Champion Data, the official provider of AFL statistics, for four matches during the 2004 season. These matches, the venues and the results are described in Table 1. In this paper we apply the ideas of Haccou and Meelis, 1992 in this context using the event definitions shown in Table 2. These event definitions are over-simplistic in that they do not identify the teams involved in each transition. However, this simple event definition does allow us to test the assumptions of the CTMC. Forbes, 2006 and Forbes and Clarke, 2004 use a different set of event definitions in their work. Their definitions identify the teams involved in each transition; however, they do not differentiate between handballs and kicks, making the modelling of distances, times and speeds problematic for these events.

Table 1.

Description of data: 4 AFL matches in the 2004 season.

Venue	Home Team	Away Team	Winner	Home Team Score	Away Team Score
Kardinia Park, Geelong	Geelong	St Kilda	Geelong	101	94
Subiaco Oval, Perth	West Coast	Western Bulldogs	West Coast	106	57
Melbourne Cricket Ground	Melbourne	Hawthorn	Melbourne	107	63
Sydney Cricket Ground	Sydney	Kangaroos	Kangaroos	112	118

Table 2.

Description of event codes.

Event code	Event Description
BEHI	Behind
BUBO	Ball up bounce
CEBO	Centre ball up
HB	Hand ball
KI	Kick in
KK	Kick
THIN	Throw in

In the following analysis we start with an exploratory analysis in which we examine the assumption of an exponential distribution for time, distance and speed for each type of event. Thereafter we test for time inhomogeneity in our data and then test the nature of any time dependencies.

Results

Exploratory data analysis

A transition matrix was derived using the above event codes and the average times (sec), distances (m) and speeds (m·sec^-1) were calculated for each event as shown in Table 3. Clearly kicks (KK) are the most common event followed by handballs (HB). The mean times, distances and speeds vary markedly for the different types of events as expected.

Table 3.

Transition matrix and average event statistics.

	To Events
From Events	BEHI	BUBO	CEBO	HB	KI	KK	THIN	Total	Pct % (SD)
BEHI	0	0	0	0	85	0	0	85	2.93
BUBO	1	14	0	35	0	41	3	94	3.24
CEBO	0	16	0	61	0	49	0	126	4.34
HB	0	16	0	385	0	511	29	941	32.44
KI	0	0	0	20	0	64	0	84	2.90
KK	85	38	112	381	0	738	90	1444	49.78
THIN	0	11	0	61	0	48	7	127	4.38
Total	86	95	112	943	85	1451	129	2901	100.00
Mean Time	18.41	11.85	9.16	4.48	6.73	9.51	11.87	8.22	(8.66)
Mean Distance	36.22	9.33	9.45	13.37	7.37	37.51	18.40	25.80	(20.35)
Mean Speed	2.29	1.10	1.28	4.60	2.68	6.54	2.23	5.06	(4.87)

Abbreviations: see Table 1. Pct = Percentage, SD = standard deviation.

The histograms in Figure 1 show the distributions for time, distance and speed when all event types are combined. A right skew distribution is exhibited in all cases with skewness coefficients of 2.40 for time, 0.85 for distance and 2.51 for speed. In particular, the lumpiness of the distance distribution demonstrates the effect of the different events. Figure 2 shows a time plot for the events for each of the four matches. This plot shows obvious differences between the four matches. The Geelong match shows relatively few behinds except in the last quarter. The number of behinds peaked in the middle of the match for the Perth and in the first half of the Melbourne game. The number of goals is related to the number of centre bounces (CEBO), with three of the four games showing relatively few goals in the last few minutes of the match. Kicks were relatively rare for the Sydney game while Kick-Ins were relatively rare for the Geelong game.

Figure 1.

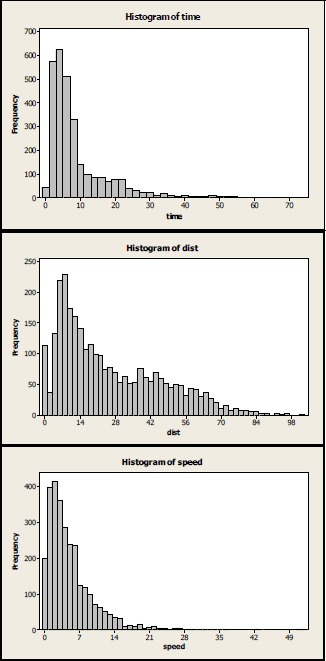
Distributions for event values: Time, Distance and Speed.

Figure 2.

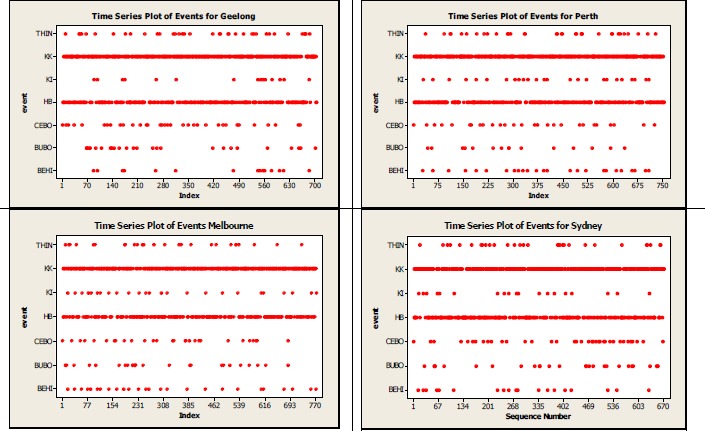
Event Sequences for each of the four venues.

Figure 3 compares the time, distance and speed distributions for each match using a 3 parameter LogLogistic distribution to describe each distribution. This is a versatile distribution shown below to describe the data well. There are obviously quite small differences between the matches, and the nonparametric Kruskal-Wallis tests in Table 4 suggest that there is a significant difference only for speed, with a slower game played in Sydney than in Melbourne.

Figure 3.

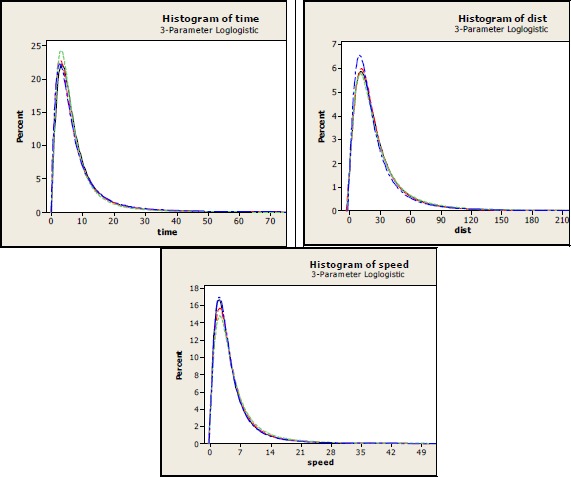
Distribution of event times, distances and speeds for the four venues.

Table 4.

Means (±SD) for each venue.

		Venue
Variable	Geelong	Melbourne	Perth	Sydney
Time (sec)	8.37 (.32)	7.70 (.28)	8.46 (.33)	8.84 (.37)
Distance (m)	26.06 (.76)	27.29 (.77)	25.49 (.72)	24.59 (.77)
Speed (m·sec-1)	4.99 (.19)	5.58 (.18)	5.14 (.17)	4.88 (4.76) *

* p < 0.05 compared with Melbourne.

Figure 4 compares the distribution of event times, durations and speeds for each type of event, again using a 3-parameter LogLogistic distribution. There are clearly very significant differences between the various types of events (Kruskal Wallis: p<0.001). Moreover it is clear that an exponential distribution is not appropriate in most cases.

Figure 4.

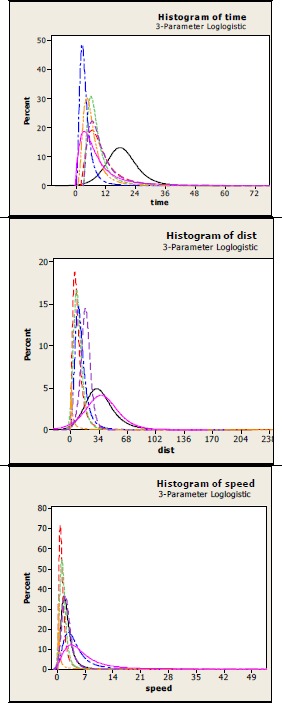
Distribution of event times, distances and speeds for the seven events.

The goodness of fit for a set of four common survival distributions was studied using the Anderson-Darling statistic. This statistic measures the area between the fitted distribution function and the nonparametric empirical distribution function. As shown in Table 5, the 3-parameter LogNormal distribution (LN) and the 3-parameter Loglogistic (LL) distributions gave the most consistently good results. The 3- parameter Gamma (G) and the 3-parameter Weibull (W) distributions were less appropriate in most instances.

Table 5.

Ranking of distributional fit using the Andersen-Darling statistic.

Event	Time				Distance				Speed
	LL	G	W	LN	LL	G	W	LN	LL	G	W	LN
THIN	1	3	4	2	1	3	4	2	1	3	4	2
KK	1	4	3	2	3	2	4	1	4	1	3	2
KI	2	3	4	1	3	2	1	4	3	2	1	4
HB	1	3	4	2	1	3	4	2	2	3	4	1
CEBO	1	3	4	2	4	2	1	3	4	3	1	2
BUBO	1	3	4	2	1	3	4	2	1	3	4	2
BEHI	4	2	1	3	1	3	4	2	1	3	4	2
Mean Rank	1.6	3.0	3.4	2.0	2.0	2.6	3.1	2.3	2.3	2.6	3.0	2.1

Table 6 shows the correlations between our time, distance and speed variables for each type of event. Spearman rank correlations were used on account of the lack of normality in most cases. The correlations are particularly interesting for Kick-Ins, with longer kicks apparently associated with shorter times, resulting in a much quicker speed. This is expected since a run with the ball is more likely before a short kick than before a long kick.

Table 6.

Spearman rank correlations for transition values (** p< 0.001).

	Correlations
Event	Time*Distance	Time*Speed	Distance*Speed
BEHI	.030	-.604 (**)	.717 (**)
BUBO	.072	-.577 (**)	.697 (**)
CEBO	.129	-.435 (**)	.798 (**)
HB	.213 (**)	-.659 (**)	.533 (**)
KI	-.248 (**)	-.265 (**)	.998 (**)
KK	.438 (**)	-.629 (**)	.356 (**)
THIN	.069	-.633 (**)	.415 (**)
All	.414 (**)	-.520 (**)	.520 (**)

Analysis for time inhomogeneity in the case of abrupt changes

Visual methods can be used for detecting inhomogeneity in time. Our time plots give some indication of inhomogeneity in time and between matches in that Figure 2 suggests that the frequency of events varies over time and between matches. However, Table 4 showed that the mean time and duration were similar for all the matches with a barely significant difference in the case of speed. This suggests that any inhomogeneity in our CTMCs will be confined to the transition probabilities. Hypothesis tests can be used to confirm whether this is true, using changes in mean termination rates or in the sequence of transitions to detect any time inhomogeneity.

If the number of change points is known a Kruskal-Wallis test can be used to test whether the distribution of values for a specific event differs between the differing periods. This test makes no assumption about the distribution of values for a specific event. We compared the time, distance and speed distributions for each event between the quarters in any match and found no significant differences for any event when the Bonferroni correction was applied (α= 0.05/28). This confirms that there is no time inhomogeneity in the time, distance and speed distributions.

Change points in the transition matrix can be tested using multinomial logistic regression. In animal behaviour studies it is not usual to allow a transition from a state to itself, however, we shall allow this in AFL football so that we can track the passage of the ball from player to player. On the other hand there are some transitions that are not possible in AFL football (e.g. a Kick-In is the only event that can follow a Behind), so we will ignore all transitions with a frequency of zero in Table 3.

For the sake of simplicity we again consider the end of each quarter as possible change points for each of the four matches. Our multinomial logistic regression analysis shows no significant match or quarter effect, suggesting that the transition matrix, like the transition variables, is homogeneous in time. As a result we shall use our complete data set for all four matches to test for sequential dependency.

Tests of sequential dependency

In a continuous time Markov chain (CTMC) a first-order dependency in the sequence of states is assumed. This means that the transition probability for states A and B in time ? is independent of the sequence of preceding states. This implies that the transition durations are independent for a given sequence of states. Dependencies may be short-term, long- term, or periodic in nature. They may relate to the sequence of states or dependencies between transition values and preceding and/or following states, or they may relate to correlations with transition values in subsequent transitions. In the case of animal behaviour transitions from state A to itself cannot occur, but as mentioned above this is not true in the case of AFL football. Instead there are several other transitions that are impossible as exhibited in Table 3.

Deviation from first-order dependency in a sequence of states is commonly tested with a chi-squared test. This test has reasonable power, however, it does not necessarily detect dependencies of higher than second order. Multinomial logistic regression was therefore used to model the occurrence of event Y based on the two previous events (X and A). It was found that only the most recent event had a significant influence [χ²(36) = 762.0, p<0.001] while the effect of the previous event was not significant [χ²(42) = 44.6, p = 0.384].

The next form of dependency occurs when the transition value distributions depend on the preceding state. This can be tested using a Kruskal-Wallis test, making no assumptions regarding the nature of the value distributions. Not unsurprisingly there was a strong relationship between the type of previous event and the values for time [χ²(6) = 20.7, p = 0.002], distance [χ²(6) = 186.7, p<0. 001] and speed [χ²(6) = 210.6, p<0.001].

Relations between subsequent transitions for the same and for different states produce a further form of dependency found in (semi-)Markov models, which can be measured using autocorrelation. Autocorrelations were initially calculated for all types of events simultaneously. For the time variable there was a very weak but significant positive autocorrelation of 0.05 for every second transition, suggesting that shorter events, such as handballs, would alternate with other types of event such as kicks. This theory is supported by the transition matrix in table 3. For the distance variable there was a weak but significant negative autocorrelation of 0.07 for successive events (lag one), again suggesting a tendency to alternate handballs and kicks, while for the speed variable there was a weak but significant negative autocorrelation of 0.05 for successive events and a stronger positive autocorrelation of 0.12 for every second event. Although all these correlations are weak they do tell us something interesting about the game. It is expected that these correlations will be automatically incorporated in the model through the transition matrix.

When autocorrelations are considered for each type of event separately, only in the case of Kicks do we obtain any significant autocorrelations. The time taken for consecutive kicks has a weak but significant negative correlation of 0.15, suggesting that short duration kicks alternate with longer duration kicks. However, the speed for consecutive kicks has a weak but significant positive correlation of 0.10. Although weak, these correlations probably need to be incorporate in the modelling process.

Discussion and Conclusion

Our analysis of four 2004 AFL football matches has shown that inhomogeneity is unlikely to be a problem within an AFL football match. There were similar processes for all four matches, perhaps on account of the similar scores for the four matches. However, for our definition of events there were marked differences in time, distance and speed requiring a separate analysis for each type of event. The distributions for the time, distance and speed variables varied for the different types of event, however, the 3- parameter LogLogistic and the 3-parameter LogNormal distributions tended to give the best fit. There were strong correlations between these variables for most of the events. Finally, it was confirmed that a first-order sequential dependency existed for the events, and that for successive kicks there was a weak correlation for the speed and time variables.

These results suggest that a semi-Markov model is appropriate since the distributions are not usually exponential or mixtures of exponential or gamma distributions, but there is first-order sequential dependency. This model could be used for simulation purposes. An initial centre bounce (CEBO) would result in Ball-up Bounce (BUBO) a handball (HB) or a kick (KK) with respective probabilities of 13%, 48% and 39%. The associated time, distance and speed could be generated using the appropriate CEBO three-parameter log-normal distributions, allowing appropriate correlations between the times, distances and speeds. Similarly, results for all ensuing game events could be simulated. Through changes to the transition matrix and/or other model parameters, the resulting model could be used in order to predict the effect of rules changes and changes in play strategy.

However, although the total number of goals and behinds would be known, the final score and the winner would not be known. In order to develop a more useful model all that is needed is a split of the events to identify the teams involved in each transition. The current work suggests that a semi-Markov model would be appropriate for this extended model, allowing a simulation similar to that described above, from which scores and the winning team could be determined for each simulated game.

In the above analysis we have associated distances, speeds and times with each transition in time. The addition of directions for each transition would make it possible for a spatial simulation to be performed. In this case it would make sense to define the events according to spatial zone (within the field) as well as activity. An alternative approach would have been to use the quarters of the field as the events, again using time, distance, speed and direction to describe each transition. This approach would also not allow the simulation of match outcomes but it would help coaches and players to better understand the spatial patterns of play. A further extension to this work could allow continuous changes in the model parameters over time with the possible inclusion of covariates in the models for the transition probabilities.

Biographies

Denny MEYER

Employment

Senior Lecturer, Swinburne University of Technology, Australia.

Degree

DBL, MBL, BSc(Hons)

Research interests

Sport statistics, time series analysis and data mining.

E-mail: DMeyer@swin.edu.au

Donald FORBES

Employment

Football Analyst, Champion Data, Australia.

Degree

PhD, LLB, GradDip(AppStats), BSc

Research interests

Modelling in sport, gambling.

E-mail: don@vicbet.com

Stephen R. CLARKE

Employment

Professor, Swinburne University of Technology, Australia.

Degree

PhD, M.A., BSc(Hons), Dip Ed

Research interests

Modelling in sport, gambling.