Patient-tailored prioritization for a pediatric care decision support system through machine learning

Abstract

Objective

Over 8 years, we have developed an innovative computer decision support system that improves appropriate delivery of pediatric screening and care. This system employs a guidelines evaluation engine using data from the electronic health record (EHR) and input from patients and caregivers. Because guideline recommendations typically exceed the scope of one visit, the engine uses a static prioritization scheme to select recommendations. Here we extend an earlier idea to create patient-tailored prioritization.

Materials and methods

We used Bayesian structure learning to build networks of association among previously collected data from our decision support system. Using area under the receiver-operating characteristic curve (AUC) as a measure of discriminability (a sine qua non for expected value calculations needed for prioritization), we performed a structural analysis of variables with high AUC on a test set. Our source data included 177 variables for 29 402 patients.

Results

The method produced a network model containing 78 screening questions and anticipatory guidance (107 variables total). Average AUC was 0.65, which is sufficient for prioritization depending on factors such as population prevalence. Structure analysis of seven highly predictive variables reveals both face-validity (related nodes are connected) and non-intuitive relationships.

Discussion

We demonstrate the ability of a Bayesian structure learning method to ‘phenotype the population’ seen in our primary care pediatric clinics. The resulting network can be used to produce patient-tailored posterior probabilities that can be used to prioritize content based on the patient's current circumstances.

Conclusions

This study demonstrates the feasibility of EHR-driven population phenotyping for patient-tailored prioritization of pediatric preventive care services.

Background and significance

Despite the acknowledged importance of preventive services and the abundance of authoritative guidelines for use in primary care,^1–3 rates of delivery of preventive services remain suboptimal. This is especially true in pediatric primary care settings⁴ where there are competing demands on physician’s time for addressing acute and chronic issues and for providing anticipatory guidance for normal child growth and development. Furthermore, as the body of evidence-based recommended guidelines keeps growing, it becomes extremely difficult to determine which guidelines may apply to a particular patient and which are of highest priority^5–8 within the time constraints of a typical office visit.

Computer decision support systems (CDSS) have been shown to improve rates of delivery of preventive services.^9–11 Over the past 8 years, we have developed and deployed an innovative pediatric CDSS—the child health improvement through computer automation (CHICA) system—that uses a scannable paper interface—for use in routine care in our busy primary care pediatric clinics.¹² CHICA integrates well into the high volume workflow of our practices by implementing age-appropriate screening of patients in the waiting room, and then combining this information with the patient’s electronic health record (EHR) to generate patient-specific reminders and recommendations for the physician. CHICA has been studied in a number of randomized trials and has been shown to improve rates of both delivery of preventive services as well as management of chronic conditions.^13–16 By automating the process of screening and appropriately alerting the physician, CHICA has significantly decreased the burden of screening families and identifying relevant practice guidelines.¹⁷

To select which recommendations apply to a patient at a specific encounter, CHICA employs a global static prioritization scheme based on the expected value of the recommendation,¹⁸ with priorities assigned by experts based on the product of risk of adverse outcome, severity of the outcome, and the effectiveness of the physician's action to prevent adverse outcome. Selected guidelines result in patient screening questions and (if appropriate) physician prompts.^{14 18} While this method has yielded good results, its primary limitation is that it relies only on known population risks. It does not adapt to patient-specific risks that may be inferred from data about their changing circumstances. For example, a particular patient may have a higher or lower risk of a health condition or outcome, such as anemia or developmental delay, based on other data in the EHR. This would alter the expected value of screening for these conditions, thus altering the prioritization for that individual. We previously described an alternative, patient-tailored prioritization scheme using Bayesian networks,¹⁸ which prioritizes based on all of the available context. The premise of this approach is predicated on the notion that the patient's medical record contains data that can significantly alter or predict the posterior probabilities of variables of interest. In this paper, we continue this work by studying the predictive power of data in the EHR.

Bayesian networks place each variable (eg, clinical information or a screening question) into a directed acyclic graph, in which vertices represent variable nodes and edges represent probabilistic relationships among variables, as in figure 1. Conditional probability tables underlying each node define these relationships. Such networks allow the articulation of complex multivariate associations. To use the network, one can instantiate evidence variables in the network (variables with known values), which revises the probability of each target variable (the variables one desires to predict).

Figure 1.

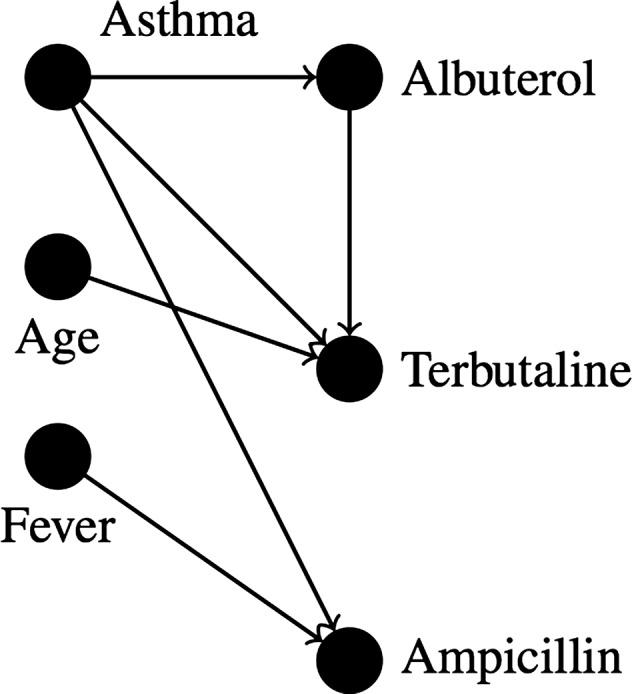
A Bayesian network for asthma treatment.

A Bayesian network can model complex relationships, such as those between the patient condition and relevant preventive care. They are appealing because of their multivariate approach and because relationships are modularly represented as probability distributions that require no a priori hypotheses. Patient screening prioritization could then be performed by instantiating variables known about the patient’s current state (ie, current condition along with past screening and behavior) and selecting the targets with the highest expected value of information. This type of approach expands on approaches used in a variety of systems for medical diagnosis¹⁹ and treatment.²⁰

One challenge to this approach is that it requires experts to articulate both the relationships among variables and the strength of those relationships. Not only is this time consuming and challenging,²¹ but the necessary data are often non-existent. Our previous work shows that relationships among some variables might be unknown even to the local experts.²² Therefore, in this paper we propose an approach that does not initially require any human input (although expert opinion can later be integrated). The approach uses a well-known, efficient method to discover a Bayesian network from an observational dataset.

Algorithms to perform this structure discovery have been developed relatively recently²³ and have become computationally tractable even more recently.²⁴ It is now possible to discover a Bayesian network of several hundred nodes from a relatively small dataset in a matter of hours on a desktop computer. While our previous work using association rule mining discovered meaningful patterns in a different pediatric dataset,²² this work extends this idea to create Bayesian networks that can be used to prioritize pediatric screening questions and interventions.

Objective

In this work, we describe a methodology for assessing individual patient risk of health threats or outcomes, using structure-discovery algorithms. We then evaluate this approach on a dataset of nearly 30 000 patients, analyzing both the discovered relationships and the predictive power of the derived model with the goal of determining its suitability for use in an expected value prioritization of relevant preventive care screening questions and interventions.

Materials and methods

Using data from previous encounters, we used a structure discovery algorithm to build a Bayesian network. We then evaluated the Bayesian network by instantiating the clinical variables with known values (called evidence) for a test set of patients and iteratively examining the posterior probability of each target value. This measures the network's ability to discriminate those patients with the highest probability of certain outcomes. This discriminative power is a sine qua non for the expected value calculations to prioritize questions and reminders. Here we describe the dataset preparation, model generation, and evaluation.

Dataset preparation

To build the model, we used observational data collected by CHICA during 2005–11 from 29 402 unique patients and 177 clinical variables that are recorded by CHICA as coded concept questions and answers. Approximately two-thirds of these patients are below 12 years of age and one-third are between 12 and 21 years of age. We produced a dataset appropriate for a structure-learning algorithm using structured query language.

The variables fell into five broad categories, shown in table 1. The vast majority of the coded concept questions were screening questions (eg, ‘Is there a smoker at home?’) or physician concerns (eg, concern about drug abuse). The remaining questions were as follows: 40 questions were exam and test results; 18 were anticipatory guidance (information on patient history or education—eg, have firearms been discussed?); two were demographic (preferred language and insurance status).

Table 1.

A breakdown of the 177 CHICA variables used in this study

CHICA variable category	Count
Patient screening question or physician concern	117
Anticipatory guidance	18
Exam	31
Test result	9
Demographic	2

The majority were patient screening questions or physician concerns. Eighteen were ‘anticipatory guidance’—information on patient history and education. The remaining 42 were demographics, exams, and test results.

CHICA, child health improvement through computer automation.

Some variables were binary, but many had several possible categorical values, which usually included one normal value and several gradations of abnormal (eg, in response to ‘Do any household members smoke?’ possible abnormal answers included ‘relapse’, ‘yes, ready to quit’, and ‘yes, not ready to quit’). To increase the discriminative power of our statistical methods, a CHICA expert recoded each variable into a binary response.

Next, we extracted the most recent known value of each variable for each patient, resulting in a dataset of 29 402 rows and 177 columns, with three possible values: ‘true’, ‘false’, and ‘missing’. All the algorithms we describe below (with the exception of edge orientation) ignore missing values, so our methods are minimally biased toward unrecorded information. We randomly permuted the rows of the dataset and split the permuted data into a training and test set (2/3 and 1/3, respectively). The training set was used for model generation and the test set for model evaluation.

Model generation

We generated a Bayesian network using Java and the freely available Tetrad toolkit,²⁵ in four steps.

First, we generated a ‘network skeleton’ from the training data using the max–min parents and children (MMPC) structure discovery algorithm,²⁴ which is included in Tetrad. A ‘network skeleton’ is an undirected Bayesian network without underlying probabilities. Skeleton generation is becoming a common first step in modern Bayesian structure learning on large datasets.^{24 26 27} It typically uses tests of statistical association to discover structure. This has performance advantages over graph heuristic methods, and the discovered relationships also usually have a logical meaning to a human viewer. MMPC is one of the best among these skeleton discovery algorithms, partly because it can construct a model ‘faithful to the data’ at small sample sizes.^{24 28} This means that if the data have no inconsistencies, the underlying structure is always detected. Of course, no real observational data are without inconsistency, but MMPC's small sample size requirement makes it resilient to noisy data. MMPC's underlying statistical test is the G² test, which is asymptotically equivalent to χ² but has preferable behavior for structure learning at small sample sizes.²⁷ This implementation of MMPC ignores missing values so that erroneous edges are avoided (eg, a correlation that occurs because edges are missing).

Second, to direct the graph, we implemented a simple greedy search to optimize a global heuristic (the BDeu statistic, also available in Tetrad), which estimates how well the graph explains the data. This follows the example of the max–min hill climbing algorithm,²⁴ which builds on MMPC. The graph-heuristic approach is more robust than other approaches on noisy data. Tetrad's BDeu statistic cannot ignore missing values. This might have unfairly biased edge direction when many values were missing, but studies show that the predictive power of most Bayesian networks is fairly insensitive to non-structural errors.²⁹ It does, however, mean that the resulting directionality might not reflect true causal direction, which must be considered in interpreting the actual graph structure.

Third, we estimated the probabilities in our model (again, with missing values ignored), using maximum likelihood estimation with Dirichlet hyperparameters initialized to α=1. This is a typical method, and it is equivalent to adding one case to each parameter, which can smooth out network parameters learned from noisy data.²⁶

Finally, we exported the graph to XDSL format using Java. XDSL is the preferred format for the SMILE framework,³⁰ a freely available toolkit for network inference.

Evaluation

To evaluate whether these networks could be used for dynamic prioritization, we used SMILE to compute the area under the receiver-operating characteristic curve (AUC) for all screening questions, concerns, and anticipatory guidance given our test set. We used a standard approach that relies on the Wilcoxon statistic's (W) equivalence to the AUC.³¹ The AUC measures the predictive power of the network. A higher AUC value corresponds to the probability that when an item is true, it is ranked higher than when it is not. To compute W, we performed the following steps: for each target variable, for each applicable test patient (ie, patients for whom this variable was not missing), we ‘instantiated’ that patient (setting values for all of the other known variables in the network for that patient) and measured the posterior probability of the target variable computed by the network. We used this information to compute W and the SE of W.³¹ Our set of target variables included all variables relevant to patient screening prioritization: the 135 variables in the first two rows of table 1.

Because a higher AUC represents greater ability to discriminate between true and false cases on a test set, it is a sine qua non for prioritization. If the network can accurately predict when a variable is true or false, then the posterior probability that the variable is true or false can be used in an expected value calculation to prioritize screening questions and prompts. The predictive power needed in an expected value calculation is dependent on several factors (see examples at the end of the Discussion section), so lesser predictive ability than is commonly needed may suffice for the proposed application. Furthermore, incorrect prioritization of screening questions is less catastrophic than incorrect prediction of disease. However, the system is unwieldy if it does not do much better than chance (AUC=0.5). We did not select a specific AUC threshold, but we analyzed portions of the network with AUC that were above average on our test set.

We also computed information about the graph structure using Gephi, an open-source graph visualization and manipulation tool.³² We calculated: the Markov blankets of target variables, the degree and betweenness centrality of problems and complaints, and the number of total subgraphs. The Markov blanket of a node is its parents, children, and siblings, and is frequently used as a heuristic for the set of most relevant variables in prediction.³³ This was computed by using Gephi's small-world analysis plug-in to count all variables less than three hops away from each target variable and manually removing nodes from this set that were not in the Markov blanket. All other measures were implemented directly by Gephi. The degree of a variable is simply the number of edges connecting it to other variables in the graph. Degree is a proxy of the variable's overall relevance in predicting other variables (because the more connected it is, the more of a role it is likely to play). Betweenness centrality is a somewhat more powerful measure of the variables’ relevance than degree. It is the number of shortest paths on which a variable lies between pairs of other variables.³⁴ Finally, the number of subgraphs are found by searching for components of the graph that have no edges touching other components.³⁵ The graph visualizations in the figures were also created with Gephi.

This retrospective analysis was approved by the institutional review board.

Results

Graph structure

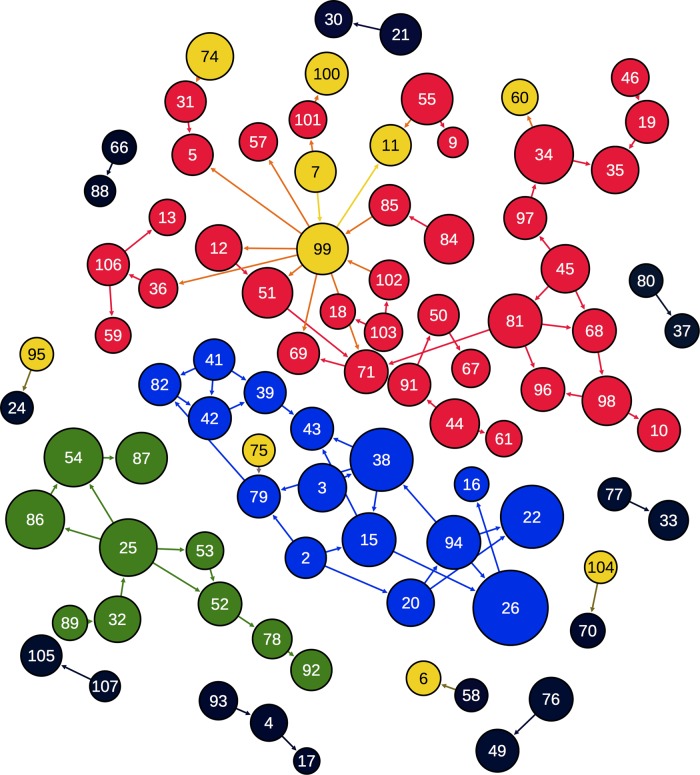
The final graph contained 107 variables (uncorrelated variables or those without predictive power are automatically removed by the algorithms described above). Seventy-eight variables were in the target set for prioritization (screening questions, physician concerns, and anticipatory guidance) and 10 non-target variables were in the Markov blanket of that target set. This filtered graph of 88 variables was made up of 13 subgraphs, of which 10 had three or fewer nodes.

The filtered graph can be seen in figure 2. Each variable is numbered; the number, name, degree, count, and AUC of each variable can be found in supplementary appendix A (available online only). The filtered graph is also included as a supplement in GEXF (graph exchange XML) format (available online only).

Figure 2.

Graph learned from a training set of approximately 30 000 patients, filtered to include only screening questions, anticipatory guidance, and their Markov blankets. It consists of 88 nodes (clinical variables) and 90 edges (relationships). Nodes are colored by subgraph and their size is determined by area under the receiver-operating characteristic curve (larger is higher). The three largest subgraphs are given a unique color; the smaller subgraphs are black. Non-target variables are yellow. Node numbers correspond to the node information table in supplementary appendix A (available online only).

Eight of 10 of the tiny subgraphs contained at least one node of AUC less than 0.60 (ie, not much more predictive than chance). The other two were: the year a home was renovated was predictive of the year it was built (AUC 0.65) and substance abuse in the family was predictive of engaging in high-risk activities under the influence of alcohol (AUC 0.60).

Summary statistics and analysis of most predictive nodes

Average AUC was 0.65 with an average SE of 0.020, and the 39 above-average (AUC ≥ 0.65) variables are listed, along with their SE, in table 2. High AUC tended to have smaller SE than those with low AUC (mean 0.028 vs 0.054). Table 3 shows the 10 non-target variables and their degree (the number of edges attaching that variable to the graph). Betweenness centrality is not shown, because the degree was highly correlated with it—only nodes of degree 2 and higher had a betweenness centrality score greater than zero.

Table 2.

The 39 target variables with above-average AUC (≥0.65, accounting for SE), alongside their SE

#	Variable	AUC	SE
26	Has used tobacco	0.90	0.017
22	Drunk in the past month	0.83	0.036
38	Friends use drugs	0.83	0.027
34	Firearms are kept unloaded	0.80	0.010
54	Looks both ways when crossing street	0.80	0.018
86	Knows what to do in response to a smoke alarm	0.80	0.011
25	Has an escape plan for house fire	0.79	0.015
15	Uses cigarettes or snuff with friends	0.76	0.019
81	Has safety latches installed	0.76	0.011
94	Uses illegal drugs	0.76	0.034
55	Uses low-iron infant formula	0.74	0.039
87	Stops at the curb before crossing	0.74	0.016
51	Knows how to save a choking child	0.73	0.011
44	Has a smoke detector	0.72	0.017
84	Sleeps on side or back	0.72	0.016
98	Wears sports protective gear	0.72	0.017
45	Has stairway gates	0.71	0.012
3	Abuses over-the-counter drugs	0.71	0.047
20	Has driven with a drunk	0.70	0.036
35	Visits homes with firearms	0.70	0.012
12	Knowledgeable about burns	0.69	0.011
32	Firearms have been discussed	0.69	0.017
52	Knows how to swim	0.66	0.011
68	Play area is fenced	0.66	0.009
71	Has the poison control number on phone	0.66	0.008
76	Lives in a pre-1978 home undergoing renovation	0.66	0.049
96	Wears a bike helmet	0.66	0.008
10	Bicycle has coaster breaks	0.65	0.046
19	Doors are secure for child	0.65	0.031
42	Happy with how things are going	0.65	0.023
43	Has had intercourse	0.65	0.023
49	Home was built before 1950	0.65	0.055
79	Had felt sad the past few weeks	0.65	0.026
91	Has tested smoke detector batteries	0.65	0.011
97	Wears a life jacket	0.65	0.020
39	Has had fun in the past 2 weeks	0.64	0.027
69	Play equipment is protected	0.64	0.020
82	School suspension in the past year	0.64	0.019
106	Has seen a dentist	0.64	0.014

AUC is the probability a true instance is correctly ranked higher than a false instance. SE is a measure of the SD of the AUC. The # is the variable number in Figure 2 and supplementary appendix A (available online only).

AUC, area under the receiver-operating characteristic curve.

Table 3.

The 10 non-target variables in the Markov blanket of target variables, alongside their degree

Variable	Degree
Standard 18-month developmental screening test	1
Vision screening	1
Normal oral exam	1
Sickle cell disease	1
Has asthma or symptoms of asthma	2
Family history: breastfed	2
Has medication allergies	1
Premature birth	1
English vs spanish speaker	11
ADHD diagnosis	1

Degree is the number of edges connected to this variable, and is related to that variable's importance in prediction.

ADHD, attention deficit hyperactivity disorder.

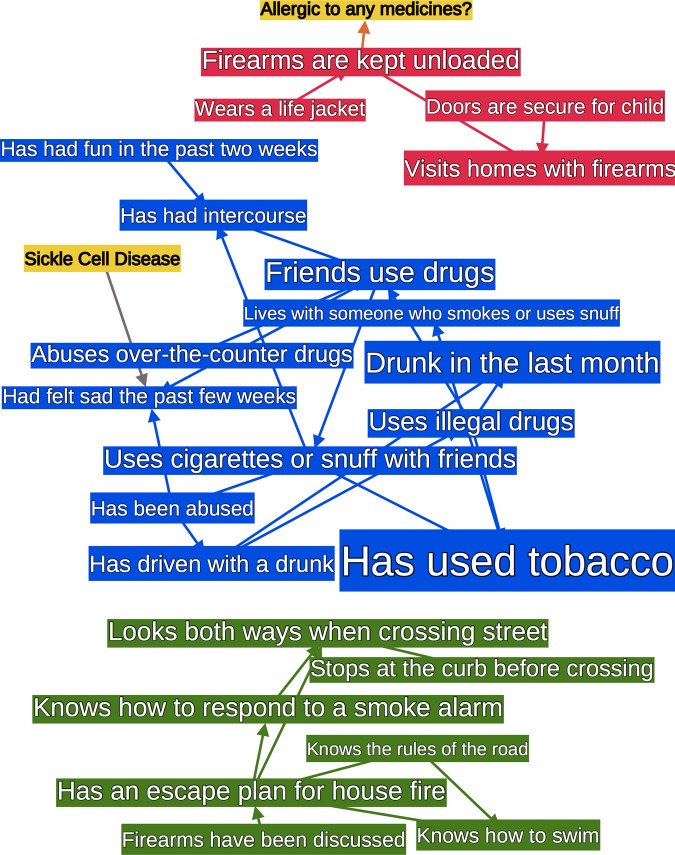
The top seven target variables had AUC of 0.8 or above. Figure 3 shows an extract of the graph containing these seven nodes and their Markov blankets. These graphs included almost the entirety of the two smaller subgraphs, and only a small portion of the largest one. The relationships between these top seven variables fell into two categories.

Figure 3.

The Markov blankets of high area under the receiver-operating characteristic curve (AUC) nodes from figure 2. Nodes are sized by AUC and the color matches figure 2. The Markov blanket of a node is its parents, children, and siblings, and is frequently used as a heuristic for the set of most relevant variables in prediction.²⁴

Category 1: intuitively correct relationships

Variables that seemed intuitively correlated were reflected in the graph; for example, drug use is correlated to both alcohol use and drug use of friends. One entire subgraph is predominantly alcohol and drug use (see the blue subgraph in figures 2 and 3).

Category 2: less-intuitive relationships

Some unexpected correlations arose. For example, knowing what to do in response to a smoke alarm is partly predicted by behavior at a crosswalk. Similarly, whether firearms are kept unloaded is related to wearing a life jacket (see green and red subgraphs in figures 2 and 3). Correlations with lower AUC were also frequently interesting, such as the relationships between mood, drug use, and sex in adolescents (lower AUC means that the test set did not consistently support the discovered relationship, but its existence in the graph means the training set supported it.).

Discussion

We have employed a statistical method to learn a Bayesian network of pediatric preventive care variables, including screening questions and physician observations, assessments and actions, entirely automatically from previously collected aggregate data, creating a phenotype of the population. We then evaluated the predictive power of the network, laying the groundwork for an expected value approach to prioritize risk assessments and physician prompts based on the current state of the patient. The average AUC (0.65) of the 78 target variables modeled was the same as an earlier expert-derived Bayesian network for childhood asthma detection on CHICA data.³⁶

The top seven of these (AUC≥0.8) fell into two categories. Category 1, teen high-risk behaviors, gives the system good face validity. These behaviors are known to be correlated.³⁷ Category 2 highlights an advantage of a statistically based system: less well recognized relationships (including local correlations that might be true in only the target population) are automatically captured by the system. For example, correlations among safety behaviors have been described in our work with other systems.²²

The ability to predict an individual patient's risk of a health state has myriad practical applications, but for the CHICA system, it supports an individualized approach to prioritizing risk assessments and services. The Bright Futures guidelines, the federally recognized authoritative source of preventive care guidelines for children, contain 574 pages of recommendations.³ In a single decade, American Academy of Pediatrics policies generated over 162 discrete, specific recommendations.⁸ This vastly exceeds what can be done in a typical visit. Without prioritization, the advice followed by pediatricians becomes arbitrary. When the probability of a patient having a particular health risk is known, it becomes possible to move it up or down in priority. For example, knowing a teen is likely to have used tobacco can increase the priority of smoking cessation counseling, and predicting that a family keeps loaded firearms in the home could raise the priority of discussing gun safety.

A demonstration of a full expected value approach to prioritizing questions and alerts in the CHICA system is beyond the scope of the present study because it requires the assessment of severity (utility) of the corresponding adverse outcome. Nonetheless, a couple of examples can illustrate the value of tailoring prioritization to the individual child. Our network offers an AUC of 0.9 for teen smoking. The posterior probability for an individual will vary, but this AUC can be thought of as including (approximately) the point 90% sensitivity and 90% specificity. The baseline rate of teen smoking in the USA is about 20%. This means that the network may distinguish teens with a 69% likelihood of smoking (who certainly would deserve screening and counseling) from those with a 3% likelihood of smoking whose visits might be better spent discussing school performance or asthma.

A less dramatic example might be lead risk (old housing stock); 3.4% of our patients have such risk.¹⁷ With an AUC of only 0.66, the network can still identify children with a risk of 6.4% from those with a risk of less than 2% who may not need screening at all.

Limitations and future directions

Like all machine-learning approaches, the model (network) can be negatively biased by the training set and can contain non-generalizable relationships (called over-fitting). The magnitude of this problem is reflected by the predictive power of the network. Ours was good on average but had weak areas—six variables were predicted no better than chance (AUC 0.5). Future work should improve: (1) the training data and (2) the use of those data. For (1), two problems are commonplace. One is that data in medical informatics are often noisy. This is actually unlikely here; our previous work has demonstrated that data collected using CHICA are reliable and meaningful.³⁸ Another problem is that not enough context is provided, leading to transitive relationships (ie, there is a valid statistical relationship but there is a hidden variable, ie, not accounted for). Such transitive relationships frequently occur in EHR data mining.³⁹ We can see this in our network: ‘sickle cell disease’ and ‘friends use drugs’ are connected, probably because both are more common in our African-American population. Although it is computationally intractable to learn networks of more than a few hundred variables, feature selection can be used on a broad dataset to choose relevant contextual variables for the structure-learning algorithm. Many feature selection algorithms exist.⁴⁰ Although they are commonly quite slow, we are developing fast feature selection methods that use network analysis in correlation graphs.⁴¹ For (2), many of the non-target variables were connected to each other rather than to screening questions. It would be preferable to force exam and test results to be linked to screening questions, which can be accomplished by specifying a priori knowledge to the structure-learning algorithm before processing.

The networks in our system are time agnostic. It would be optimal to model not just what was last known to be true but when it was true. For example, if the last concern about drug use was 10 years ago, it is likely not to be a concern now. We mitigate this problem by using the most recent value for each patient; presumably if drug use was a concern many years ago, there would be a more recent instance in which the patient no longer said they used drugs. However, true temporal modeling should be compared to the standard time-agnostic model. In particular, the modeling of temporal patterns, such as increasing values of a parameter or recurrence of a risk factor, may impart greater predictive power. A variety of approaches supports network learning with time, including dynamic Bayesian networks,⁴² continuous time Bayesian networks,⁴³ and a model we are developing.

Finally, as mentioned earlier, the full prioritization score we previously proposed includes the likelihood of a health risk, its severity (disutility), and the effectiveness of addressing it as a rational way of prioritizing assessment questions or physician reminders.¹⁸ By expanding our Bayesian networks into influence diagrams that include decision and value nodes, we can select risk questions and prompts based on their expected value. At that point, a clinical trial of the patient-tailored prioritized questionnaires will be appropriate.

Conclusion

This study demonstrates the feasibility of Bayesian structure learning and inference to build models for prioritizing pediatric screening questions and reminders in a patient-tailored manner, by using discriminative power as a sine qua non for future expected value calculations. These population-phenotype models are built automatically, using only previously collected data without human intervention. The outputs are easy-to-understand diagrams that can be edited by designers and researchers. This preliminary work used a dataset of 29 402 patients and 177 screening and preventive care variables to produce a dynamic model of 107 nodes and 143 edges. Structure analysis revealed groups of related nodes as well as some non-intuitive correlations (eg, firearms and life jackets). Average AUC on a test set was 0.65, with seven nodes above 0.8. Although we have outlined several future improvements to our methodology, we have also shown that even this average AUC can be discriminative enough to prioritize screening questions properly, depending on risk prevalence and the other factors in our previously developed expected value approach.