Abstract
Adaptive optics (AO) ophthalmoscopes have garnered increased clinical and scientific use for imaging the microscopic retina. Unlike conventional ophthalmoscopes, however, AO systems are commonly designed with spherical mirrors that must be used off-axis. This arrangement causes astigmatism to accumulate at the retina and pupil conjugate planes, degrading AO performance. To mitigate this effect and more fully tap the benefit of AO, we investigated a novel solution based on toroidal mirrors. Derived 2nd order analytic solutions along with commercial ray tracing predict performance benefit of toroidal mirrors for ophthalmoscopic use. For the Indiana AO ophthalmoscope, a minimum of three toroids is required to achieve performance criteria for retinal image quality, beam displacement, and beam ellipticity. Measurements with fabricated toroids and retinal imaging on subjects substantiate the theoretical predictions. Comparison to off-the-plane method is also presented.
OCIS codes: (010.1080) Active or adaptive optics, (110.4500) Optical coherence tomography, (080.4035) Mirror system design, (170.4460) Ophthalmic optics and devices, (330.5310) Vision - photoreceptors
1. Introduction
The advent of high-resolution ophthalmoscopes with adaptive optics (AO) has enabled cellular-resolution imaging of the living human retina [1]. This has led to exciting new directions to probe the normal and diseased retina for clinical and scientific use. In parallel to these applications, there have been considerable technological improvements in the ophthalmic AO, especially in its three key components: wavefront sensor, wavefront corrector, and control algorithm. Often overshadowed by advances in these areas are the many basic optical components – lenses and mirrors – that are necessary to relay the imaging beam from one active component to the next.
In the first AO retina camera, relay optics consisted of on-axis afocal telescopes formed by achromatic lenses [2]. Telescopes used in this manner provided diffraction-limited imaging and made the design straightforward to implement. Back reflections from the lenses, however, largely limited this approach to the flood-illumination modality where the undesirable effect of these reflections on the wavefront sensor could be avoided by injecting the light source close to the eye. Today, AO is commonly employed in other ophthalmoscopic modalities, most notably the scanning laser ophthalmoscope (SLO) and scanning optical coherence tomography (OCT) [3–20]. Rather than flood illuminating the retina, SLO and OCT raster scan a focused spot of light across the retina. Scanning in this manner requires the wavefront sensor beacon to pass through many optical elements of the system. Until recently [17], the only solution to avoid back reflections is the use of spherical mirrors in place of lenses. But, these must be used off axis, an arrangement that is well known to generate astigmatism in both pupil and image conjugate planes. Astigmatism not only blurs the retinal image, but also causes beam displacement (wobble) and beam ellipticity at pupil conjugate planes when the beam is scanned. Beam displacement is undesirable as it reduces temporal bandwidth performance of the closed-loop AO and compromises the fine spatial sampling of the AO wavefront sensor. Thus both high temporal and high spatial frequency aberrations risk being properly measured by the wavefront sensor and corrected by the AO system.
There have been recent efforts to address these unwanted spatial and temporal losses. These include strategic placement of the wavefront corrector close to the eye to decrease beam ellipticity [12] and off-the-plane designs to reduce all three effects: retinal blur, beam displacement and beam ellipticity [6, 7, 9, 21]. The off-the-plane approach extends earlier work on the first SLOs [22, 23]. In this approach, astigmatism generated by the first spherical mirror of each afocal telescope in the system is compensated by astigmatism purposely added to the second spherical mirror by physically tilting the mirror (or equivalently optical axis of the system) out of the plane. This off-the-plane strategy using spherical mirrors has proven highly effective, but results in a 3D optical path with vertically and horizontally slanting beams. Such beam arrangement adds complexity to the conversion of existing, in-the-plane systems (requires major system redesign) and complicates system alignment.
In this paper, we propose and validate an alternative approach based on the use of toroidal mirrors. First, we derive 2nd order analytic solutions for mirror-based afocal telescopes consisting of one and two toroids. The derivation parallels that of [21], but uses mirror surface shape (toroid), rather than mirror tilt, as the degree of freedom. Next, we use the analytic solutions along with commercial ray tracing to predict performance benefit of toroidal mirrors in a specific AO ophthalmoscope, the Indiana AO-OCT system. As this system shares many design attributes of other AO ophthalmic systems, the analysis and findings presented here are readily applicable to these other systems. For the Indiana system, three toroidal mirrors are predicted the minimum number needed to meet our performance criteria for retinal image quality, beam displacement, and beam ellipticity. Finally, we validate the three toroid design by fabricating and swapping in the customized toroids into the Indiana system and comparing measured system performance to that predicted by 2nd order theory and commercial ray tracing. Comparison to off-the-plane method is also presented.
2. Methods
Methods is divided in four parts. Section 2.1 describes the Indiana AO-OCT system, and in particular its layout of mirror-based afocal telescopes, the source of astigmatism to be corrected with toroidal mirrors. Section 2.2 derives theoretical expressions to predict performance of systems composed of spherical and toroidal mirrors, and applies these to the individual afocal telescopes of the Indiana system. Section 2.3 presents our method for predicting performance of the Indiana system for different numbers and locations of toroidal mirrors. Section 2.4 describes our protocol for experimental evaluation of the Indiana system with toroidal mirrors.
2.1 Description of Indiana AO-OCT system
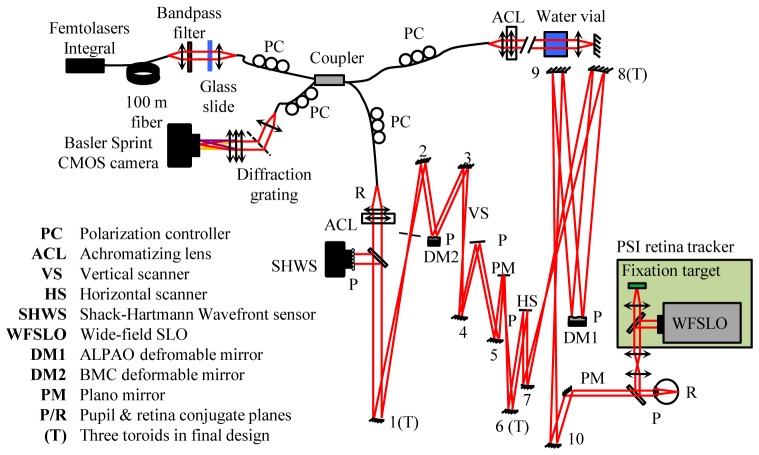
Figure 1 shows a schematic of the Indiana AO-OCT system. Important for this study is the system’s sample arm that consists of five off-axis afocal telescopes that conjugate the pupil of the eye with the lenslet array of the wavefront sensor, the two deformable mirrors in a woofer-tweeter configuration (ALPAO and Boston Micromachines Corporation (BMC) mirrors), and two galvanometer scanners (horizontal and vertical). The spherical mirrors, which are labeled from number 1 to 10, have focal lengths from 125 mm to 500 mm with incident beam angles of 2.38° to 11°. The system is designed for a 6.67 mm beam at the eye and a 3.6° × 3.6° (1.08 × 1.08 mm2) field of view (FOV) of the retina. Additional system details are provided in the figure caption and Table 1 as well as in Cense et al. [14], which presents an earlier version of the system. Relevant differences with the new system include larger diameter deformable mirrors, a 4.4 mm diameter BMC mirror with 140 actuators and a 13.5 mm diameter ALPAO membrane mirror with 97 electrodes.
Fig. 1.
Schematic of the Indiana AO-OCT system for retinal imaging. The sample arm contains a woofer-tweeter AO system for correction of ocular aberrations, two galvanometer scanners, and five relay afocal telescopes, each consisting of two spherical mirrors. The AO cascades a 97-actuator (1500 µm pitch) voice-coil actuated membrane mirror from ALPAO and a 140-discrete-actuator deformable mirror (400 µm pitch) from BMC. Wavefront measurements are obtained with a SHWS (20 × 20 lenslet array; 500 µm pitch). Pitch of the lenslet array at the BMC, ALPAO, and eye pupil planes is 200 µm, 667 µm and 334 µm, respectively. A Femtolaser Integral (λc ~800 nm, Δλ = 160 nm, bandpassed at λc ~809 nm, Δλ = 81 nm) provides the SHWS beacon as well as OCT imaging.
Table 1. Indiana AO-OCT sample arm.
| Optical element | Radii of curvature (mm) |
Incident angle, I
(deg) |
Pupil diameter (mm) |
|
|---|---|---|---|---|
| SHWS lenslet array | - | 0 | 10 | |
| SM # 1 | 750 | 4.5 | - | |
| SM # 2 | 300 | −8.33 | - | |
| MEMs-140 DM | - | 15 | 4 | |
| SM #3 | 300 | −10 | - | |
| SM # 4 | 300 | 5 | - | |
| Vertical scanner | - | −11 | 4 | |
| SM # 5 | 400 | 7.5 | - | |
| Plano mirror | - | −4 | - | |
| SM # 6 | 400 | 5 | - | |
| Horizontal scanner | - | −3.75 | 4 | |
| SM # 7 | 300 | 5.83 | - | |
| SM # 8 | 1000 | −3.75 | - | |
| ALPAO-97 DM | - | −4.13 | 13.33 | |
| SM # 9 | 1000 | 2.38 | - | |
| SM # 10 | 500 | 7.5 | - | |
| Eye pupil plane | - | 0 | 6.67 | |
Key: (SM) spherical mirror
2.2 Theory
2.2.1 Single toroidal mirror
The second-order performance of a single toroidal mirror in an off-axis configuration (Fig. 2 ) can be characterized with four equations. The first two are Coddington equations [24], written as
Fig. 2.
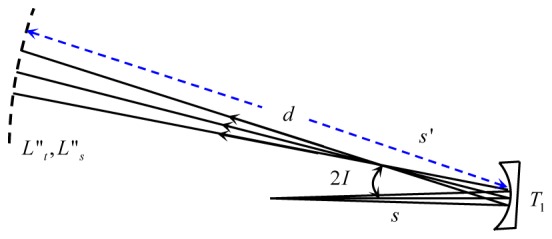
Off axis performance of a toroidal mirror, T1. Variables are defined in the text.
| (1) |
These relate the tangential and sagittal foci (ft and fs ) of the toroid to the principle surface radii (rt and rs) of the toroid and the incident angle I of the beam. For simplicity, I is assumed to lie in the tangential plane. Note that because I projects to a single point in the field, the derived solutions to follow are restricted to the same point. Third is the Gaussian equation for first-order image formation of a thin element, in this case the toroid, and expressed here in wavefront vergence
| (2) |
Using the notation in Fig. 2, is vergence of the object at the toroid, F is power of the toroid for a specified meridian ( or ), and is vergence of the image at the toroid. Refractive index of the medium in which the telescope resides is assumed one (air). To determine vergence at an arbitrary distance, d, downstream of the toroid requires a fourth equation, often referred to as the transfer equation
| (3) |
where is the downstream vergence at d. Astigmatism generated by the toroid at this location is simply the difference in vergence between tangential () and sagittal () meridians. General expressions for and are obtained by accounting for the toroid’s impact using Eqs. (1) and (2), and propagating the light after the toroid using Eq. (3), the result being
| (4) |
and
| (5) |
2.2.2 Afocal telescope with toroidal mirrors
In AO ophthalmic systems, spherical mirrors are used almost exclusively in pairs to form a cascade of afocal telescopes. To make a single afocal telescope out of toroidal mirrors requires adding a second toroid to the diagram in Fig. 2, in this case downstream of the first at a distance d equal to the sum of the equivalent spherical mirror focal lengths . and are nominally the equivalent focal lengths of the corresponding toroid, a somewhat loose constraint to maintain the original system magnification and system layout. As an additional constraint, AO ophthalmic systems are designed with pupil conjugate planes that are relayed from telescope to telescope by placement of the pupil planes one focal length in front of the first mirror of each telescope, in which case s becomes in Fig. 2. Here is the equivalent spherical radius of the first toroid, nominally .
Taken together, these changes result in the afocal telescope configuration shown in Fig. 3 . This configuration is referred to as the finite conjugate case owing to the proximity of the pupil planes to the telescope mirrors. With the addition of a second toroid, the constraints and , and the use of Eqs. (4) and (5), the tangential and sagittal vergences immediately exiting the telescope in this finite conjugate case can be expressed as
| (6) |
and
| (7) |
where M is defined as the magnification of the telescope, r 2/ r 1. To assure zero astigmatic blur at the pupil plane of the telescope, L't 2 and L's 2 must equal to 2/r 2. r 2 is the equivalent spherical radius of the second toroid, nominally . While solutions for , , , and rs 2 can be obtained from Eqs. (6) and (7), the equations do not fully capture the performance of afocal telescopes used in AO ophthalmoscope systems.
Fig. 3.
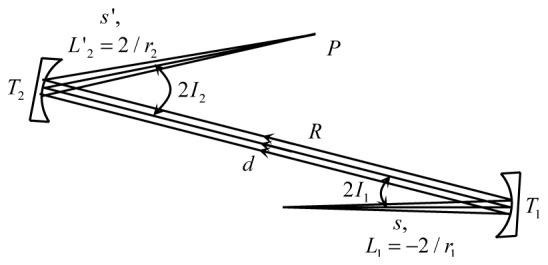
Finite conjugate case () for an in-the-plane afocal telescope formed by a pair of off-axis toroidal mirrors.
Specifically, ophthalmic systems place the retina conjugate plane at the common focal point between toroids of the same telescope, thus interleaved with the pupil planes. This arrangement is shown in Fig. 4 and is referred to as the infinite conjugate case () owing to the distal location of the retinal planes in the object and image spaces. The tangential and sagittal vergences immediately exiting the telescope in this infinite conjugate case can be expressed as Eqs. (8) and (9). To minimize astigmatism at the retinal conjugate planes requires both L't 2 and L's 2 to be zero.
| (8) |
and
Fig. 4.
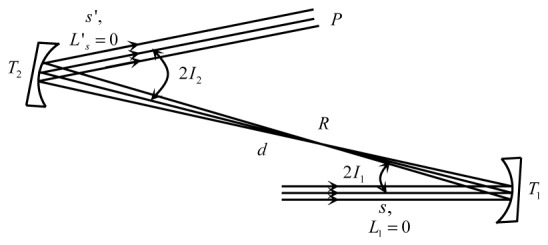
Infinite conjugate case (s =∞) for an in-the-plane afocal telescope formed by a pair of off-axis toroidal mirrors.
| (9) |
Thus to simultaneously compensate astigmatism of the afocal telescope at both pupil conjugate and retinal conjugate planes requires satisfying the conditions imposed by Eqs. (6) through (9). Two toroids provide enough degrees of freedom to do so and results in radii of curvature of the toroids being
| (10) |
| (11) |
| (12) |
and
| (13) |
Equations (10) through (13) assure zero system astigmatism at both pupil conjugate and retinal conjugate planes, accomplished while maintaining an in-the-plane configuration. Two toroidal mirrors in the telescope provide the best astigmatic correction, but practical constraints such as cost motivate interest in telescope performance with just one toroid, leaving the other mirror spherical.
For the case in which the second mirror is toroidal and the first spherical, r 1 is substituted for rt 1 and rs 1 in Eqs. (6) and (7). Using these equations, astigmatic blur at the pupil conjugate planes (finite conjugate case) is eliminated for radii of curvature of the second mirror, rt 2 and rs 2, given as
| (14) |
and
| (15) |
For the same telescope but for the infinite conjugate case, r 1 is substituted for rt 1 and rs 1 in Eqs. (8) and (9). Astigmatic blur at the retinal conjugate planes is eliminated for radii of curvature of the second mirror, rt 2 and rs 2, expressed as
| (16) |
and
| (17) |
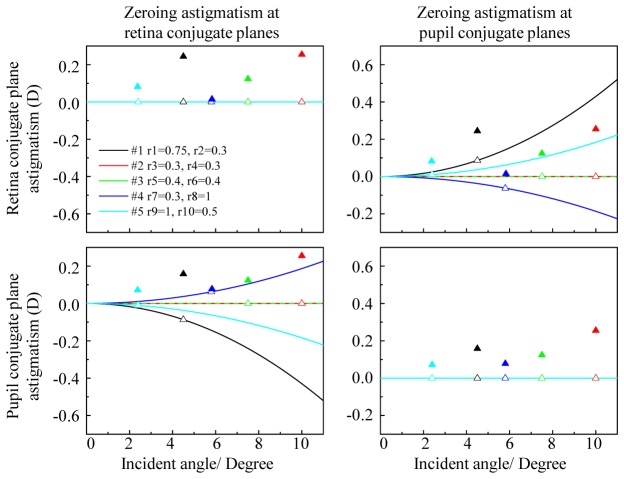
Evaluation of Eqs. (14) to (17) reveals that one toroidal mirror completely eliminates astigmatism at either the pupil conjugate plane or the retina conjugate plane, but not necessarily both. Equations (14) and (15) and Eqs. (16) and (17) do not have enough degrees of freedom to provide the same solution for rt 2 and rs 2. The one exception is when the telescope magnification is unity (M = 1). While not apparent from Eqs. (14) to (17), use of small angle approximation leads to identical expressions for this special case, thus eliminating astigmatism at both planes. We chose not to employ this approximation in Eqs. (14) to (17) as it is overly constraining with similar solutions found at much larger angles (see below). Interestingly even if M ≠ 1, zeroing astigmatism at one plane can also reduce astigmatism at the other, albeit not necessarily down to zero. These general findings are captured in the Fig. 5 plots. Shown is astigmatism – predicted by substituting Eqs. (14) and (15) into Eqs. (8) and (9) and substituting Eqs. (16) and (17) into Eqs. (6) and (7) – for each of the five afocal telescopes used in the Indiana AO-OCT sample arm (Fig. 1 and Table 1). Shown are pupil (finite) and retina (infinite) conjugate cases with and without the second mirror as a toroid in the telescope.
Fig. 5.
Predicted astigmatism at (top row) retina and (bottom row) pupil conjugate planes for each of the five afocal telescopes in the Indiana AO-OCT system. Two constraints are applied, zeroing astigmatism at (left column) retina conjugate planes and (right column) pupil conjugate planes. Filled triangles (▲) denote telescopes with all spherical mirrors. Unfilled triangles (Δ) denote telescopes with the second mirror toroidal. Solid curves generalize the five telescopes (with second mirror as toroid) to arbitrary incident angle, I1.
As evident in the figure, telescopes with unit magnification (#2 and #3) require only a single toroid to simultaneously eliminate astigmatism at both planes and achieve diffraction-limited imaging. This holds regardless of which plane astigmatism is explicitly zeroed and is robust at relatively large incident angles, I1. For example for these two unit-magnification telescopes, astigmatism less than 0.098 Diopters (corresponding to diffraction-limited performance for a pupil diameter of 4mm) is predicted at both conjugate planes for incident angles up to 27°, realized by extending the Fig. 5 plots to 30° (not shown). This latter property is important as telescopes #2 and #3 have the largest incident angles, I1 (10° and 7.5°) of the five. For the other three telescopes (M ≠ 1), astigmatism is fully eliminated at one of the two planes, and reduced at the other. This holds for all but one of the six cases: retina conjugate plane of telescope #4 with astigmatism zeroed at the pupil conjugate plane (compare filled and unfilled blue triangles in top right plot of Fig. 5).
Interestingly, the mathematical expressions for astigmatism derived from Eqs. (6) to (9) and Eqs. (14) to (17) indicate a sign reversal sensitive to telescope magnification. This is apparent in the Fig. 5 plots of these expressions that reveal two types of cases for sign reversal: (1) M < 1 and zeroing astigmatism at retina conjugate planes and (2) M > 1 and zeroing astigmatism at the pupil conjugate planes. These cases are the cyan and black triangles in bottom-left plot and blue triangle in top-right plot of Fig. 5. While not directly taken advantage of here in this study, this sign reversal can compensate the astigmatism generated by other telescopes in the system.
Solid traces in the plots generalize the five telescopes to arbitrary angle and clearly show that for M ≠ 1 smaller I1 generates less astigmatism and results in better performance.
While not shown here due to space limitation, a similar set of expressions can be derived with the first element of the telescope as toroid and the second spherical. This requires substituting r 2 for rt 2 and rs 2 in Eqs. (6) through (9), and solving for rt 1 and rs 1.
2.3 Determination of number and location of toroidal mirrors for Indiana AO-OCT system
From Fig. 5, 2nd order theory predicts that replacement of all spherical mirrors (10) in the Indiana AO-OCT system with toroidal ones of appropriate shape fully and simultaneously corrects astigmatism at all pupil and retinal conjugate planes. This guarantees best system performance, at least to 2nd order. Because two of the telescopes in the system have unit magnification, a maximum of eight toroids – not 10 – is actually predicted without loss in performance. Suggestive from Fig. 5, system performance should decrease with less than eight toroids, but performance may still be sufficient depending on the application criteria. For example a five toroid system can be created by combining the five telescopes in Fig. 5, each with one toroid. Using the five to fully correct astigmatism at the retina conjugate planes (infinite conjugate case; top-left plot of Fig. 5), astigmatism at the corresponding pupil conjugate planes (finite conjugate case; bottom-left plot of Fig. 5) results in an order of magnitude reduction of astigmatism at the eye pupil plane, from 0.79 D to 0.07 D. The latter is marginally worse than the diffraction limit for 6.67 mm diameter pupil (0.035 D).
The fewest toroids acceptable ultimately depend on the required system performance. For our study, we chose the following criteria, which are general enough to be applicable to most systems: (1) diffraction limited system performance (wavefront root-mean-square (RMS) error < λ/14 µm), (2) beam displacement at pupil conjugate planes less than the wavefront sensor sampling pitch, and (3) a circular beam cross section at pupil conjugate planes (ellipticity > 95%). The first must hold over the entire 3.6° × 3.6° FOV of the AO-OCT system and assures AO is expended only on correction of ocular aberrations. The second preserves fine spatial and temporal fidelity of the AO at the two DMs and the eye pupil. The third assures proper beam coverage by the DM actuators. Specifically, beam ellipticity (E) is defined as the ratio of the magnification in tangential (Mt) and sagittal (Ms) directions and for the AO-OCT system is expressed as
| (18) |
| (19) |
and
| (20) |
95% ellipticity corresponds to a width-to-height difference of half the pitch of the ALPAO actuators. Thus E>95% assures beam coverage of all ALPAO actuators. It also assures a symmetric system numerical aperture. As evident from Mt and Ms expressions, ellipticity is sensitive to toroid location in the telescope, requiring a balancing of even and odd positions to maintain a round beam.
As a practical constraint in our analysis, paraxial parameters of the AO-OCT system (e.g., equivalent mirror focal lengths, incident beam angles, and mirror separations) were nominally held fixed regardless of number and location of spherical mirrors replaced with toroidal ones. This avoided vignetting effects and preserved system magnification.
The most direct approach to determine the fewest number of toroids is to assess system performance for each possible combination of toroids. While rigorous, this approach does not take advantage of design principles that might eliminate certain combinations, hence every combination must be tested, the total for this system being 1023 (toroid number: 1 to 10; locations: 10). To greatly limit the number of combinations considered, we divided the AO-OCT sample arm into three subsystems based on function and then applied the 2nd order predictions in Section 2.2 as guidelines to converge on a subset of toroid combinations that showed most promise.
The first subsystem consists of the first two telescopes (mirrors #1 to #4), BMC mirror, and vertical scanner. Over this section, the beam is unaffected by the scanners and thus no beam wobble can occur. Likewise, the geometric size of the astigmatic blur at the BMC mirror is calculated to be less than the lenslet pitch. Taken together, these indicate little to no benefit is accrued by adding toroids to this first subsystem to correct astigmatism at pupil (finite) conjugate planes. Therefore, any toroid added should instead correct at the final retina (infinite) conjugate plane of the subsystem, realized by zeroing astigmatism (vergence) at the vertical scanner plane. The second subsystem includes the next telescope (mirrors #5 and #6) and the horizontal scanner. The telescope’s astigmatism and the motion of the beam created by the vertical scanner creates beam wobble at the horizontal scanner. This requires one toroid to correct, and because of unit magnification, both finite and infinite conjugate cases are fully and simultaneously corrected at a single point in the FOV. For convenience, we chose to explicitly keep astigmatism zero at the horizontal scanner plane. The third subsystem consists of the last two telescopes (mirrors #7 to #10), ALPAO mirror, and the eye pupil. Similar to the second subsystem, astigmatism of the telescopes and beam motion (now caused by both scanners) creates beam wobble and impacts retinal image quality. In addition, beam wobble must be controlled at both ALPAO and eye pupil planes. Because of the importance of AO stability, minimizing beam wobble at the ALPAO likely requires a toroid to be near it. Collectively, these constraints make the third subsystem the most demanding on the toroids.
Summarizing, each of the three subsystems imposes effectively one constraint with the last subsystem imposing possibly two. This indicates four toroidal mirrors (one for each constraint) may be necessary to achieve the defined performance criteria. Two or three toroids, however, may also prove effective, but depends on the demand of each constraint. One that is not overly demanding is beam wobble generated in the third subsystem at the ALPAO plane. Wobble generated here is attributed entirely by the first of the two telescopes (mirrors #7 and #8) in the subsystem. Fortunately, this telescope contains the least astigmatism (see filled blue triangle on left top plot in Fig. 5), and causes beam displacement that is less than the pitch of SH lenslet array at ALPAO plane. Thus fewer toroids might be possible.
Based on this synopsis, we evaluated via ray tracing toroid-based AO-OCT designs of zero (1), one (10), two (20), three (20), and ten (1) toroids. Note that we did not evaluate four toroids owing to the findings with two and three. The numbers in parentheses indicate the combinations evaluated. These were selected based on their promise from the 2nd order predictions and included combinations of similar number and arrangement. The latter (oversampling) helped to assure we did not miss an effective combination. Zero and ten toroids were included for comparison as they represent the original (worst) and best possible performing designs, respectively. While this strategy did not guarantee finding the optimal combination of toroids, it did provide a practical path to combinations that met the defined performance criteria.
For each combination, system performance was determined with ray trace modeling in Zemax (Zemax Development Corporation, Washington, USA). This included using Zemax’s built-in optimization for finding rt and rs of the toroids. Because of the overriding importance of diffraction-limited image quality at the retina, the infinite conjugate constraint was always applied to optimize the shape of the last toroidal mirror in the system, regardless of toroidal number considered. Thus for combinations with only one toroid, optimization included only this constraint. For the remaining combinations (two, three and ten), optimization also included finite and infinite constraints applied at other pupils planes in the system. Specifically for two toroids, finite and infinite constraints were separately applied at the vertical scanner. For three toroids, finite and infinite constraints were separately applied at both the vertical and horizontal scanners. For ten toroids, finite and infinite constraints were applied at each of the five telescopes in the system.
System performance for each combination of optimized toroids was then assessed based on the three criteria already established: (1) retinal image quality, (2) beam displacement, and (3) beam ellipticity. An additional implicit constraint was to preserve – within reason – the original mirror focal lengths and separations.
Advantages of ray trace modeling over 2nd order theory are a more accurate representation of the system (e.g., inclusion of higher order aberrations) and the ability to optimize over the full FOV (3.6° × 3.6°), which was done here. Nevertheless a comparison with 2nd order theory can reveal the importance of these effects as well as provide insight into the ray tracing. To do so, we compared the two approaches for a three-toroid design, the one ultimately selected for experimental validation. Protocol for determining the analytic solution was as follows. Expressions were derived for wavefront vergence at the last plane of each of the three subsystems for the infinite or finite conjugate case. Vergence was calculated for both tangential and sagittal planes L"t and L"s by applying Eqs. (1) to (3) successively to each telescope in the subsystem, similar to that for the single telescope examples in Section 2.2.1. Radii of curvature of the three toroids (one per subsection) were then solved. For the finite conjugate case, the radius of the toroidal mirror was determined by setting L"t and L"s to the optical power of the last mirror in the subsystem. For the infinite conjugate case, radius of the toroidal mirror was determined by setting L"t and L"s to zero.
2.4 Experimental validation of the Indiana AO-OCT with three toroidal mirrors
From the system analysis in section 2.3, a three-toroid design was determined as the best combination for satisfying the three performance criteria with the minimum number of toroids. To experimentally validate the design, three toroids were fabricated and swapped with spherical mirrors in the Indiana AO-OCT system. System performance was assessed by measuring image quality, beam displacement, and beam ellipticity. The custom toroids were fabricated by QED Technologies (Rochester, New York) with specified peak-to-valley surface quality of 63 nm and coated with protected silver. Toroids were placed in the AO-OCT system by replacement of the corresponding spherical mirrors, paying careful attention that distances and angles matched the original AO-OCT design (Fig. 1 and Table 1).
Next, a commercial Shack-Hartmann wavefront sensor (Imagine Optics, HASO3 128-GE), with 14.6 × 14.6 mm diameter aperture, 128 × 128 microlenses (pitch = 114 μm), and measurement accuracy of λ/100, was used to align each telescope in the system. This entailed real time aberration measurements at the telescope with the commercial SHWS, while fine axial and lateral adjustments were made to the second mirror of each telescope without changing the beam angle to the next telescope. Adjustment was made until the measured wavefront error was as close as possible (typically < 0.05 waves µm RMS) to the Zemax design for Zernike defocus and astigmatism RMS. This tedious process was repeated for each telescope, starting with the first where the beam enters the sample arm from the fiber coupler and ending at the pupil plane designated for the eye.
Beam displacement at the ALPAO and eye pupil planes were measured by slowly scanning – both vertically and horizontally – over the system’s ±1.8° FOV at the retina. To aid measurement, a plastic transparency with regularly spaced dark rings was inserted temporarily in the beam near the first pupil plane (adjacent to ACL) and a paper screen placed first at the ALPAO plane and then at the eye pupil plane. The former required removing the ALPAO mirror. As the scanners rotated, a digital camera captured videos of the ring pattern image formed at the screen. The camera’s 20 µm sampling at the screen and calibrated field of view enabled absolute measurement of beam motion.
Beam ellipticity was extracted from beam profile measurements captured with the Imagine Optics wavefront sensor at the ALPAO and eye pupil planes. Conservatively, the 114 µm lenslet pitch of the sensor generated an error in ellipticity no greater than 0.86% and 1.7% for the 13.3 mm and 6.67 mm beams at the ALPAO and eye pupil planes, respectively.
Finally, performance of the three-toroid AO-OCT system was demonstrated by capturing images of photoreceptors in human subjects. Retinal locations between fovea and 6° retinal eccentricity were recorded in the right eye of three subjects. All had best corrected visual acuity of 20/20 or better and were free of ocular disease. Age, refractive error, and axial length were 30, 46, and 57 years; 0, −2.5, and +1.75 D; and 23.6, 25.4, and 23.5 mm. Eye length was measured with the Zeiss IOLMaster®. Maximum power delivered to the eye was 400 µW, measured at the cornea and within safe limits established by ANSI [25]. Written informed consent was obtained after the nature and possible risks of the study were explained. The eye to be imaged was cyclopleged and dilated with one drop of Tropicamide 0.5%. The eye and head were aligned and stabilized using a bite bar mounted to a motorized XYZ translation stage.
Two imaging tests were conducted. First, cone images were acquired on the emmetropic subject without AO compensation. In this way the quality of the cone images (or lack thereof) gave a direct indication of the combined system and ocular aberrations without masking by the AO. To do this we replaced the BMC and ALPAO DMs with high quality planar mirrors. 1.5° × 1.5° volumes were acquired at 4° nasal 3° superior retinal eccentricity using an A-scan spacing and rate of 1 μm and 167,000 lines/s, respectively. Volumes were acquired at 0.82 vol/s.
For the second test, photoreceptor images were acquired on the two myopic subjects during dynamic AO compensation. This test examined the system’s ability to resolve fine granular structure in the photoreceptor mosaic, both near the fovea (0.2° to 0.3° retinal eccentricity) where cones are increasingly narrow and densely packed, and in the periphery (4.5° and 6° retinal eccentricity) where cones are larger and separated by densely packed rods. Here the ALPAO mirror was reinserted into the AO-OCT system and the AO operated in closed loop. Volumes approximately 0.5° × 0.5° in en face were acquired at a rate of 2.7 to 4.2 vol/s and at the three retinal locations. A-scan rate was 167,000 lines/s, and A-scan spacing was 0.6 to 0.75 μm.
A-scans were axially registered to each other to remove axial motion of the eye. En face images of the photoreceptor mosaic were then obtained by extracting the cone inner and outer segment reflections from the volumes and projecting along depth. Finally a low pass filter was applied to the en face images to remove spatial frequencies above the diffraction limit cutoff of the system, dictated by the 6.67 mm pupil at the eye.
3. Results
3.1 Toroid number and location – predicted performance
The Indiana AO-OCT system design was evaluated with a combination of toroidal mirrors. Performance was predicted by ray trace modeling and 2nd order theory, and assessed based on three criteria: retinal image quality, beam displacement, and beam ellipticity.
3.1.1 Retinal image quality
Figure 6 (left) shows the predicted image quality of the spherical-mirror-based AO-OCT system for scan angles over the system’s 3.6° × 3.6° FOV. The 25 spot diagrams generated with the AO off (wavefront correctors flat) revealed substantial blur intrinsic to the system and generated by the spherical mirrors of the five relay telescopes. Corresponding wavefront RMS error ranged from 0.48 to 0.55 waves (center to edge of field), substantially worse than the diffraction limit criteria (<λ/14). In contrast, Fig. 6 (right) shows the same spot diagrams, but with one of the spherical mirrors replaced with a toroidal one. Adding this one toroid dramatically improves retinal image quality, causing all rays to fall inside the solid circle denoting the diffraction-limited blur size. The corresponding wavefront RMS error ranged from 0.01 to 0.07 waves (center to edge of field) and provided diffraction-limited imaging across the entire FOV. While mirror #8 was selected as the toroid for the Fig. 6 results, selecting any of the other nine also provided diffraction-limited imaging. Thus only a single toroidal mirror placed at any of the 10 locations in the system meets the retinal image quality criteria.
Fig. 6.
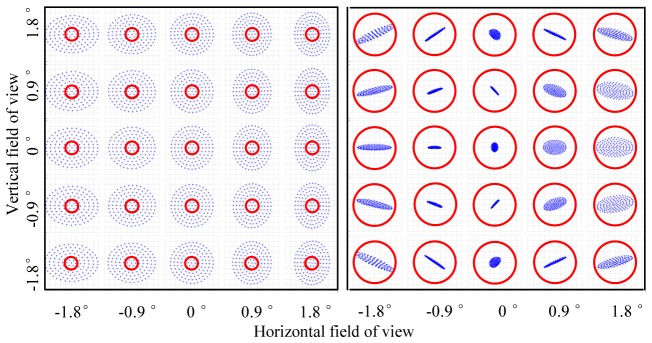
Predicted image quality of the Indiana AO-OCT sample arm as function of scan angle with perfect eye (aberration free). PSF spot diagrams at the retina were generated by ray trace modeling with (left) all spherical mirrors and (right) spherical mirror #8 (see Fig. 1 and Table 1) replaced with a toroidal one. Wavefront correctors were flat for both configurations. Shape of the toroid (rt and rs) was determined by ray trace optimization. Solid red circles denote diffraction-limited blur size. Note the left and right spot diagrams are on different spatial scales.
3.1.2 Beam displacement and ellipticity
Figure 7 illustrates displacement and ellipticity performance of the AO-OCT system with two combinations of toroidal mirrors: zero (original) and three. As shown, the introduction of three toroids noticeably reduces beam wobble at both the eye pupil and ALPAO planes. This combination of toroids also maintained – at least visually – the highly circular cross section of the beam.
Fig. 7.
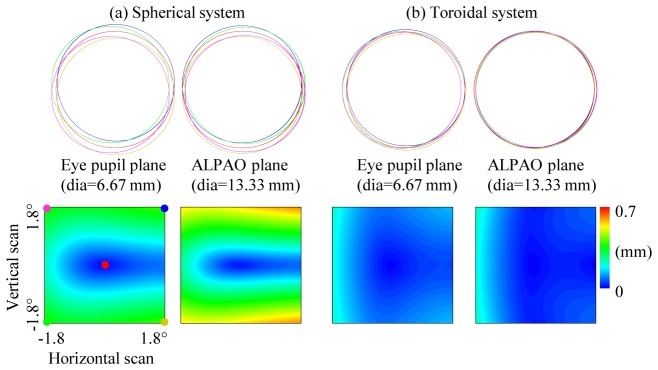
Illustration of beam displacement predicted by ray trace modeling for the Indiana AO-OCT system. Beam shape and location at the eye pupil and ALPAO planes are shown for two cases: (a) original system with all spherical mirrors and (b) system with three toroidal mirrors. Five beam locations at the retina are shown on top row: one centered on the system’s FOV (0°, 0°) and four at the corner edges (−1.8°, −1.8°), (−1.8°, 1.8°), (1.8°,-1.8°), and (1.8°, 1.8°). Locations in the FOV are color coded and depicted in the bottom left displacement plot. Note scaling of the eye pupil and ALPAO planes differ by a factor of two. False color maps in bottom row quantify beam displacement at ALPAO and eye pupil planes for arbitrary FOV (within ± 1.8°).
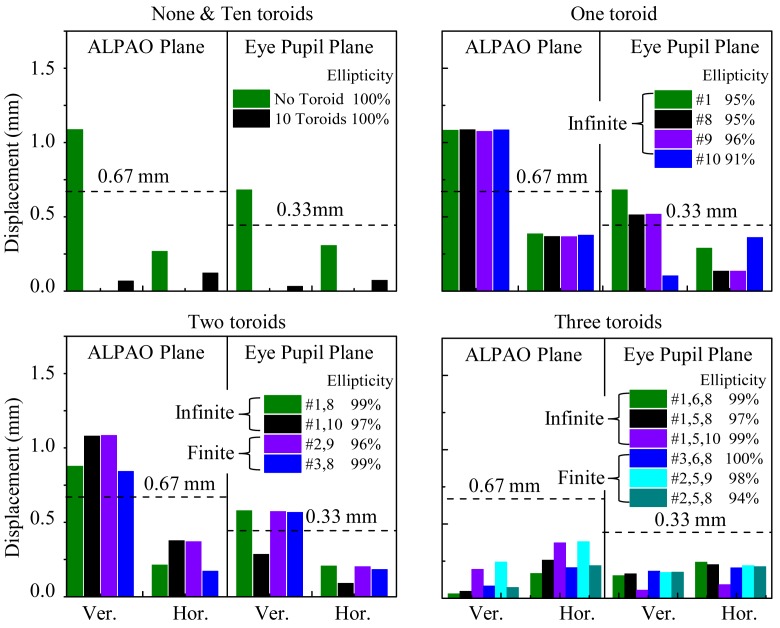
Figure 8 shows the best performing toroid combinations that we evaluated in this study. The results are distributed across toroid number, toroid location, and two optimization parameters (finite and infinite conjugate constraints). Best performance minimized predicted beam displacement and ellipticity at both ALPAO and eye pupil planes. Several important trends are present in the Fig. 8 data and are discussed below.
Fig. 8.
Predicted beam displacement and ellipticity at ALPAO and eye pupil planes for ± 1.8° vertical (Ver.) and horizontal (Hor.) scans. AO-OCT system performance is shown for various numbers of toroids: (a) zero and 10, (b) one, (c) two, and (d) three. Different combinations of toroids are specified by the numeric labels (1 through 10), which indicate mirror location (defined in Fig. 1). To the right of the numeric labels is the corresponding beam ellipticity, E. Infinite and finite labels refer to the conjugate constraint (finite or infinite) imposed on the first toroid of the two toroid system and the first two toroids of the three toroid system during optimization of toroid shapes. Dashed lines represent lenslet pitch at ALPAO and eye pupil planes.
First, the number of toroids directly impacts performance. More toroids generally mean less beam displacement and hence better system performance. Designs with zero and one toroids show unsatisfactory performance as vertical displacements exceed the SHWS lenslet pitch. Likely source is the uncorrected astigmatism generated by the telescope between the two scanners. Because the vertical scanner lies upstream of the telescope, more vertical than horizontal motion results. Two toroids provide better performance, but still do not reach the criteria set by the lenslet pitch at ALPAO and eye pupil planes. Three toroids improve performance still further with five of the six combinations shown meeting the displacement and ellipticity criteria. 10 toroids permits compensation at every retina and pupil conjugate plane in the system and as expected provides the most stable beam. However, 10 toroids performed only marginally better than three toroids (average displacement of best three-toroid combination and ten toroids are 0.15 mm and 0.07 mm in Fig. 8). In general, a minimum of three toroids (out of 10 possible) was found necessary to achieve the performance criteria for the AO-OCT system.
Second, location of toroids is also important. Both displacement and ellipticity performance varies appreciably depending on the combination chosen for a given number of toroids. For displacement, the most effective combinations distributed the toroids across the entire system targeting (1) parts that generated relatively large astigmatism (e.g., mirror #1), thus correcting astigmatism at its source and (2) locations that are most sensitive to the beam properties (e.g., ALPAO and eye pupil planes). While this is obviously influenced by the number of toroids that can be distributed, seemingly small differences in position can result in noticeable differences in performance. As an example we evaluated (not shown in Fig. 8) four combinations of three toroids that differed only by the location of their last toroid: (1, 6, 7), (1, 6, 8), (1, 6, 9), and (1, 6, 10). The worst performing combination was (1, 6, 7), which had its last toroid located furthest from the ALPAO and eye pupil planes. This additional separation resulted in noticeably poorer beam displacement that was actually comparable to the original no toroid case (displacement range = 0.27 to 1.1 mm). On the other extreme, combination (1, 6, 10) had its last toroid located closest to the eye pupil, and provided best beam displacement at this plane (displacement range = 0.07 to 0.1 mm at eye pupil). Combinations (1, 6, 8) and (1, 6, 9) fell in between with the former having its last toroid immediately upstream of the ALPAO mirror and the latter immediately downstream of it. Both gave comparable performance at the eye pupil plane, but (1, 6, 8) gave the best of any of the combinations at the ALPAO plane. Displacement range equals 0.03 to 0.17 mm for (1, 6, 8) at ALPAO plane.
In addition to the effect on beam displacement, location of the toroids also affected beam ellipticity. Combinations with toroids at both odd and even mirror locations (1st and 2nd mirrors of a telescope) provided markedly better beam cross section (larger E) than those at all odd or all even locations. As a representative example, the all even combination (2, 6, 8) gives an ellipticity of 88% compared to the average ellipicity of 98% in Fig. 8. In fact all of the best combinations (see Fig. 8) used both odd and even locations. This finding is consistent with our theoretical expectations that stem from Eqs. (18) to (20).
Third, Fig. 8 also reveals the potential influence of our optimization method. Specifically, our optimization procedure for the two and three toroid combinations included finite and infinite conjugate constraints applied at the two scanner planes of the system. While we had wanted to select the same mirror locations for each constraint in order to provide a more rigorous comparison, this was not possible. The finite constraint often resulted in toroid surfaces that diverted – noticeably – from the original mirrors’ focal lengths and separations in the system. To circumvent this, we selected adjacent mirror locations that were not susceptible to this effect. Assuming this location change negligible (not tested), solutions obtained with the two conjugate constraints yielded comparable performance. Examples of several combinations are shown in Fig. 8 for the two and three toroid cases.
Taken together, Fig. 8 results indicate that a minimum of three toroidal mirrors is necessary to meet our criteria for retinal image quality, beam displacement, and beam ellipticity for the AO-OCT system. Numerous three-toroid combinations met the criteria. From these we selected combination (1, 6, 8) for further experimental validation as it provided a strong balance in performance. It provided the best reduction in beam displacement at the ALPAO plane (critical for AO stability) and retained a highly circular beam (E = 99%).
3.2 Three toroid system - measured performance
Toroidal mirrors for the three-toroid design (1, 6, 8) were fabricated, validated, and integrated into the Indiana AO-OCT system. Retinal image quality, beam displacement, and beam ellipticity of the system were measured, and performance further substantiated with images of photoreceptor cells acquired with the system.
3.2.1 Toroid validation
Mirrors #1, #6, and #8 were selected as toroids with radii of curvature (rt and rs) shown in Fig. 9(a) determined by ray trace optimization. Also shown are estimates from 2nd order theory. The analytic approach gave consistently similar radii for all three toroids, being no greater than 0.06% from the ray trace predictions. This provided additional assurance in our ray tracing method. Of course exact agreement is not expected as ray trace optimization balanced performance across the entire FOV of the system and captured higher-order effects. Equivalent radii of curvature of the toroids was 750.1 mm, 399.6 mm, and 999.4 mm, which matched that of the original spheres in Table 1 and preserved system magnification. Figure 9(b) shows surface elevation maps for the three fabricated toroids. Evident in both design (top row) and measured (bottom row) surfaces is the characteristic astigmatic pattern with elevation along the vertical meridian (positive power) and depression along the horizontal one (negative power). The figure shows the fabricated toroids are in excellent agreement with design, yielding peak-to-valley differences no worse than 34 nm. This difference corresponds to a double pass optical path difference of λ/12 using the central wavelength of the Indiana AO-OCT system, thus meeting the design specifications provided to QED Technologies.
Fig. 9.
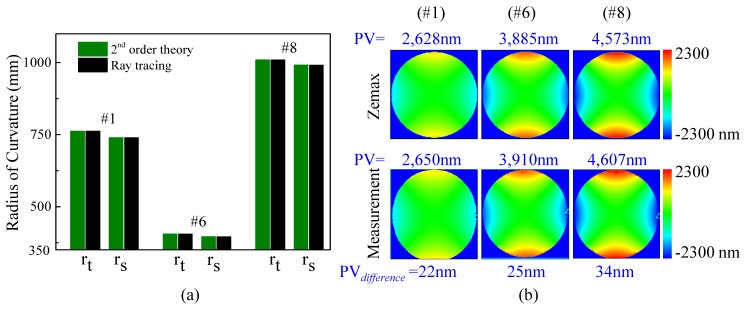
Comparison of surface shape for the three toroidal mirrors (#1, #6, and #8) fabricated for the AO-OCT system. (a) Radii of curvature of the three toroids were determined from ray trace modeling and compared to that predicted by 2nd order theory. (b) Ray trace and measured surface maps are compared for the three fabricated toroidal mirrors. Surface elevation is coded on a color scale. PV is the peak-to-valley surface elevation; PVdifference is the difference in PV between design and measurement.
3.2.2 Retinal image quality
Figure 10 shows measured image quality performance of the three-toroid AO-OCT system for five field positions. For comparison, also shown is predicted performance of the three-toroid design as well as that of the original system with all spherical mirrors. None of the cases included AO correction. For the all-spherical-mirror case, the wavefront error maps clearly reveal substantial astigmatism generated by the 10 spherical mirrors, regardless of field position. Corresponding wavefront RMS error is ~0.5 waves. The middle figure shows the predicted wavefront error for the three-toroid design. Here the RMS error is dramatically improved, ranging from 0.02 to 0.06 waves and providing diffraction-limited imaging (<λ/14) across the ± 1.8° field. The right figure shows the measured wavefront map for the same three-toroidal-mirror case, also without AO correction, which was realized by temporally replacing the ALPAO and BMC with high quality planar mirrors. While the pattern of the measured wavefront error is visually different from that of the design, the magnitude of these differences is quite small. Specifically, measured wavefront RMS error ranged from 0.05 to 0.06 waves, indicating performance is diffraction limited and consistent with the theoretical predictions. Small discrepancies between measurement and theory are likely due to exceedingly small errors in alignment and measurement. Note that the RMS values of the three-toroid case are a factor of ten better compared to the original all-spherical-mirror case.
Fig. 10.
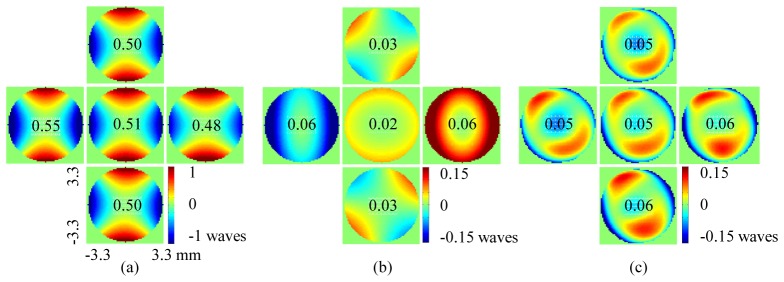
Comparison of image quality of AO-OCT system (a) predicted for all-spherical mirror design, (b) predicted for three-toroidal mirror design (#1, #6, #8) and (c) measured for three-toroidal mirror design using commercial HASO3 wavefront sensor. 6.67 mm wavefront error maps at the eye pupil plane are shown for five field locations: one centered on FOV (0°, 0°) and four at edge ( ± 1.8°, 0°), (0°, ± 1.8°). All cases are with a perfect eye (no ocular aberrations) and without AO correction (ALPAO and BMC flat). Numeric values denote wavefront RMS error in units of waves, defined as the center wavelength of the Indiana AO-OCT system.
3.2.3 Beam displacement and ellipticity
Figure 11 compares measured beam displacement of the three-toroid AO-OCT system to predictions from ray tracing optimization and 2nd order theory. As shown in the figure, measurements are consistent with predictions though on average somewhat higher. This is not unexpected given that laboratory measurements include all sources of imperfections and noise, some inevitably not part of the theory and modeling. In spite of these, the laboratory system still met our displacement criteria. It was well below the 0.67 mm threshold at the ALPAO plane; it also met the criteria at the eye pupil plane, albeit barely. Performance at the ALPAO is more critical for AO loop control, which requires stable registration of corrector actuators to SHWS lenslets. Interestingly, the variations between measurement and predictions are comparable to those between ray trace modeling and 2nd order theory. This suggests that the variations in Fig. 11 are perhaps fine subtleties in performance reflective of secondary rather than major differences in the three results.
Fig. 11.
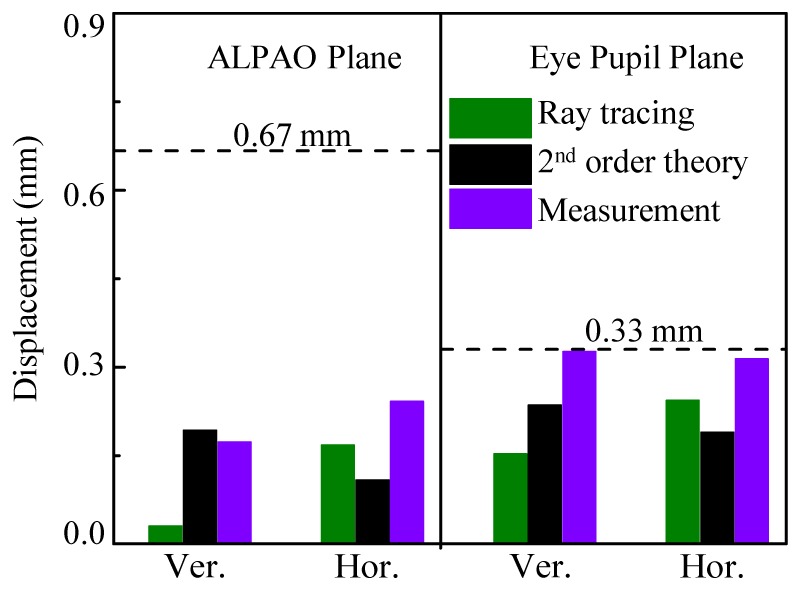
Comparison of measured and predicted beam displacement of the three-toroid AO-OCT system for ± 1.8° vertical (Ver.) and horizontal (Hor.) scans. Predictions were determined from ray trace optimization and 2nd order theory. Displacement is at ALPAO and eye pupil planes. Dashed lines represent the lenslet pitch.
Beam ellipticity was measured at 99% at ALPAO plane and 100% at eye pupil plane. Both are consistent with the ray trace predictions of Fig. 8 for this toroid combination (see green bar corresponding to toroid combination #1, #6, and #8 in right bottom plot of figure).
3.2.4 Photoreceptor imaging
Finally, performance of the three-toroid AO-OCT system was demonstrated by capturing images of photoreceptors in three human subjects. Two imaging tests were conducted. For the first, cone images were acquired on the emmetropic subject without AO compensation. Figure 12 shows a representative image acquired at 4° nasal 3° superior retina with focus at the photoreceptor layer. The image reveals a regular pattern of bright punctate reflections whose nominal spacing and overall appearance is consistent with that of cone photoreceptors at this location. The resolution and clarity of cones is direct confirmation that not only the subject’s ocular aberrations were sufficiently small, but the system’s aberrations were as well. With the original all-spherical-mirror AO-OCT system, the resolution of cones was never observed without the use of AO (unpublished observation), a result consistent with the poor image quality of the system as attested by the PSF spot diagrams in Fig. 6 (left).
Fig. 12.

En face image of cone photoreceptor mosaic extracted from AO-OCT volume acquired at a retinal eccentricity of 4° nasal 3° superior. BMC and ALPAO were removed and replaced with high quality planar mirrors. Scale bar is 50 μm.
For the second test, photoreceptor images were acquired on the two myopic subjects during dynamic AO compensation. The first part of this test examined the system’s ability to resolve cone photoreceptors near the fovea (0.2° to 0.3° retinal eccentricity) where these cells are increasingly narrow and densely packed. The left column of Fig. 13(a) shows a representative example. The two enlarged views (highlighted in green and red) reveal punctate reflections whose arrangement and spacing are consistent with cones at this small retinal eccentricity. Both myopic subjects were also imaged in an earlier study with the original all-spherical-mirror AO-OCT system [16] In that study, cones could not be resolved this close to the fovea center and in fact the cone imaging study had to be limited to retinal eccentricities no smaller than 0.5°.
Fig. 13.

Photoreceptor mosaics extracted from AO-OCT volumes acquired on myopic subjects. (a) En face projections confined to the photoreceptor layer is shown for volumes acquired at 0.2°~0.3° and 4.5° retinal eccentricity in the left and right columns, respectively. Scale bars are 25μm (b) OCT B-scan is shown at the top with corresponding en face images of (left) IS/OS and (right) PTOS reflections below at 6° retinal eccentricity. Inset shows individual cones that exhibit an IS/OS reflection characteristic of a TEM10–like mode. Superimposed boxes are color coded and 7.8 μm in width. Scale bars are 10 μm.
Additional evidence was found in the second part of the test that examined the system’s ability to resolve fine granular structure in the periphery (4.5° and 6° retinal eccentricity). Here cones are larger and separated by densely packed rods. Representative results are shown in Fig. 13(a-right column) and (b). The former shows regularly-spaced bright spots in en face that are characteristic of cones at this location and which have been extensively reported with previous AO-OCT systems [12, 13, 15, 16, 18]. Not previously reported are the finer reflections that are evident in the gaps between cones. The mottled appearance of these is suggestive of rod structure. While a detailed study is required to confirm, these findings are encouraging. In particular they point in the direction of recent rod imaging results obtained with AO-SLO systems that have incorporated the off-the-plane design to correct astigmatism [8, 9].
A key advantage of AO-OCT is its ability to axially resolve reflections within cones, namely those at the inner segment / outer segment junction (IS/OS) and the posterior tip of the outer segment (PTOS). Extending Fig. 13(a), Fig. 13(b) shows the separate contributions of the two reflections. As expected, both cone layers reveal the same regular pattern of bright punctate reflections, each originating from a single cone cell. In spite of the images being noisy, the IS/OS reflection exhibits a more irregular appearance. Assuming waveguide properties of the cone dominate these reflections, this irregular appearance could be interpreted as the presence of additional optical modes – various spatial distributions of light energy that propagate through the photoreceptor – beyond the most fundamental Gaussian mode. Color coded in the figure are specific cones whose IS/OS reflection exhibits a dominated (transverse electromagnetic) TEM10-like appearance. Proper interpretation of these reflections remains. Nevertheless, our ability to now resolve these fine details is additional supportive evidence that toroidal mirrors in the AO-OCT system have indeed improved resolution.
4. Discussion and conclusion
4.1 Summary of results
We introduced and validated a new solution based on toroidal mirrors to correct for astigmatism in spherical-mirror-based AO ophthalmoscopes. Our investigation resulted in three major areas of development: derivation of 2nd order theory, ray trace modeling, and experimental validation. First we derived 2nd order expressions for mirror-based afocal telescopes consisting of one and two toroids. Analytic expressions for the two cases, Eqs. (14) to (17) and Eqs. (10) to (13) respectively, predicted toroidal shapes (rt and rs) that minimized system astigmatism at finite and infinite conjugate planes for a single point in the field. The theory predicts that two toroidal mirrors are necessary to fully correct astigmatism at both retina (infinite) and pupil (finite) conjugate planes. A single toroid can fully correct astigmatism at one of the two and in many cases also reduces astigmatism at the other, but not necessarily to zero. The best telescope, however, is one with unit magnification as it requires only a single toroid (not two) to fully correct astigmatism at both conjugate planes simultaneously.
While our derived expressions are for single telescopes, they can be readily applied to more complicated systems that are composed of multiple telescopes. Here we illustrated their use for the Indiana AO-OCT system, a system that shares many common features with other AO ophthalmic systems in the field. 2nd order theory predicts that eight of the ten spherical mirrors of the Indiana system must be converted to toroids in order to fully correct astigmatism at all retina and pupil conjugate planes. Fewer toroids will still be beneficial, but not provide the ideal imaging performance predicted for eight. This raises the practical question then as to how much uncorrected astigmatism is acceptable and how many toroids is actually needed.
This question was addressed in the second part of the study. 2nd order theory, ray trace modeling, and performance criteria were combined to determine the number and location of toroidal mirrors for the Indiana AO-OCT system. Here we took a different tack from that of previous studies by explicitly establishing three performance criteria: retinal image quality (RMS<λ/14), beam displacement (<lenslet pitch), and beam ellipticity (width-to-height difference < 1/2 pitch of ALPAO actuators). The first is tied to diffraction-limited imaging at the retina and the latter two to fundamental parameters of the AO system whose performance is directly affected by beam quality at the pupil. These criteria are sufficiently general to be applicable to a broad range of ophthalmic AO systems, yet sufficiently explicit for optical design optimization. With these criteria we investigated over fifty toroid combinations, most with two and three toroids pre-selected largely on their promise from 2nd order predictions. Three-toroid combinations were found to meet our criteria, a toroid number substantially fewer than the predicted eight required for perfect astigmatic correction. Note this approach contrasts with some off-the-plane strategies in which the goal is to correct for astigmatism at each and every telescope of the system. Our results indicate this is unnecessary, at least as defined by our three performance criteria. Note also that even our strategy does not guarantee finding the optimal combination of toroids. Rather, it provides a path to combinations that meet the defined performance criteria and indeed we found numerous three-toroid combinations that did, indicating considerable flexibility in the toroidal system design.
The third part of our study validated the best performing three-toroid design (#1, #6, #8). This tedious and time consuming step was motivated by the lack of similar measurements in the AO ophthalmic literature. Validation of ophthalmic systems commonly centers on the quality of actual retinal images acquired with the system, with improved or higher quality images implying the modeling specifications were met. While certainly helpful, results of this type are often too gross to elucidate actual performance along the technical specifications that drove the original design. Here in this study we measured laboratory system performance for the three established performance criteria. We found to align our laboratory system to the Zemax design required a separate calibrated SHWS that was positioned sequentially after each telescope. This step was critical to match residual defocus and astigmatism of each telescope in the design. Measurements of retinal image quality, beam ellipticity, and beam displacement achieved the three performance criteria. Measured RMS wavefront error and beam ellipticity also closely matched Zemax predictions (Figs. 8 and 10). In contrast, measured beam displacement was consistently larger than predicted regardless of plane (ALPAO and eye pupil) and scanner type (vertical and horizontal) (Fig. 11). To better understand the significance of this difference, we wanted to compare our measured displacements to that of other AO ophthalmic systems, especially off-the-plane designs, but such measurements have not been reported.
4.2 Impact of vergence due to source spectrum and retinal thickness
OCT technology relies on light sources of broad spectra to achieve high axial resolution. The longitudinal chromatic aberration (LCA) of the eye, however, focuses each wavelength of the spectra to a different depth in the retina. Thus only one wavelength can have zero vergence. For the light source in the Indiana AO-OCT system (720-880 nm), the vergence range is about 0.34 D [26]. This dioptric amount is commonly corrected with an achromatizing lens (ACL) of equal but opposite LCA inserted at the first pupil conjugate plane (immediately downstream of the fiber collimator) in the system. This position is chosen because back reflections from the ACL cannot enter the SHWS. A consequence though is that the ACL-added vergence must propagate through the entire system with each wavelength passing through slightly different parts of each optical element before finally reaching the eye. Therefore system performance depends on wavelength. A second vergence factor is retinal thickness. To focus from the most anterior layer to the most posterior layer of the retina requires up to 1 D of vergence change. Because focus is controlled with the ALPAO DM, this second factor is restricted to the single telescope between the eye and ALPAO.
To examine how the Indiana system performance is effected by these two factors (light source spectrum and retina thickness), we incorporated both in our Zemax model. This consisted of adding ± 0.17 D vergence at the ACL plane and ± 0.5 D vergence at the ALPAO plane using Zernike phase surfaces. We assessed vergence of −0.67 D, 0 D, and +0.67 D by determining wavefront RMS error across the system FOV ( ±1.8°). For a specific vergence, axial length of a paraxial model eye was adjusted until best performance was achieved across the FOV. Then, RMS values were averaged across five FOV points, four at the corners ( ±1.8°, ±1.8°) and one at the center (0°, 0°). Modeling predicted the system preserves diffraction limited image quality at retina plane for all FOV and vergences considered. Average RMS of the system was 0.06, 0.05, and 0.05 waves with vergence of −0.67 D, 0 D, and 0.67 D, respectively. Thus the effect of vergence caused by the light source in the Indiana system and thickness of the retina is predicted to be negligible. Note that system performance at pupil plane is independent of beam vergence.
4.3 Comparison to off-the-plane method
As expected toroidal and off-the-plane methods have much in common. Both control astigmatism by manipulating mirrors in the system. 2nd order performance of both is derived from the same four equations (Coddington, Gaussian, and transfer equations) and impacted by the same system parameters (telescope magnification, mirror focal lengths, and beam incident and exit angles). While the two manipulate different mirror parameters (mirror shape versus mirror rotation) significant performance improvement is realized regardless of method. Both correct astigmatism at retinal and pupil conjugate planes and effectiveness to do so depends on the same number of degrees of freedom, either number of toroids or number of off-the-plane bends.
Underneath these overarching similarities, however, are theoretical differences in performance, two of which stand out. First, the toroidal method preserves global coordinates, meaning there is no rotation or tilting of the beam about its axis as it propagates through the system. Preservation in this way stems from the system lying in a single plane, a design feature of toroids. As a consequence, the orientation and orthogonality of horizontal and vertical scanning is maintained throughout the entire system and into the eye. Similarly aberrations generated in the system and eye also maintain their orientation. In contrast, off-the-plane method fundamentally induces rotation to the global coordinates at each and every off-axis telescope in the system. This culminates in tilting and in more severe cases arcs in the scanned pattern at the retina. Aberrations also rotate, but in a complex manner that depends on the telescope that generates it and the location of the telescope in the system.
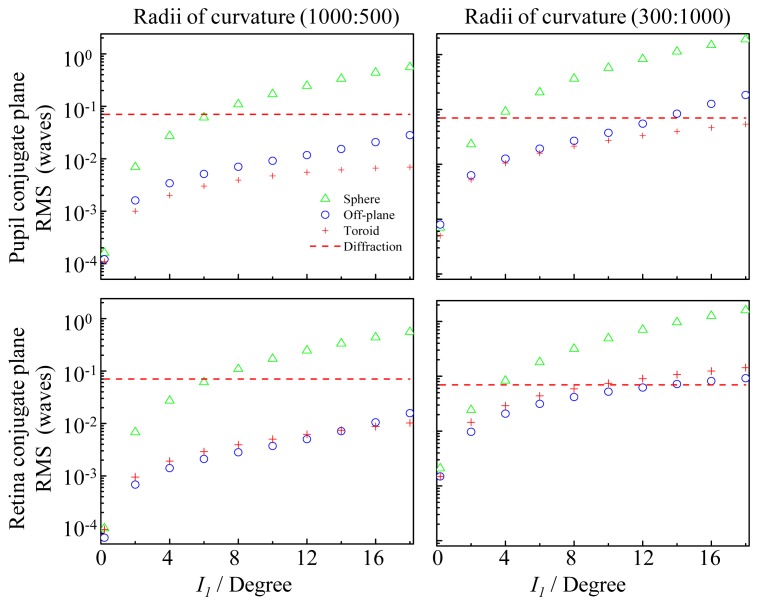
A second advantage of the toroidal method is improved image quality performance, in particular for the finite conjugate case that is most critical for optimized AO control. To examine this, we followed the ray trace modeling used by Gómez-Vieyra, et al. [21] for predicting off-the-plane performance for a single afocal telescope, results of which are shown in their Fig. 5. After replicating their Fig. 5 results, we applied the same modeling to the five telescopes of the Indiana system. Results were consistent across the five, and Fig. 14 shows two of these, selected because of their opposite magnification (1000:500 and 300:1000). The figure compares predicted performance for the original all-spherical-mirror, off-the-plane, and toroidal methods for optimized finite and infinite conjugate cases. Regardless of telescope or conjugate case, off-the-plane and toroidal methods provide substantially better RMS performance than the original all-spherical-mirror system. But, differences between off-the-plane and toroidal methods are also evident. For the finite conjugate case, toroidal method shows increasingly better performance with increased incident angle compared to off-the-plane. Over the angle range shown (0° to 18°), toroidal RMS is up to four times better. Zernike analysis reveals that the difference in performance lies with the 2nd order aberrations. While both methods provide comparable levels of higher order aberrations (3rd order and higher), the toroidal method provides superior correction of astigmatism and defocus.
Fig. 14.
Comparison of predicted image quality for three different designs of the same afocal telescope: (Δ) original, (o) off-the-plane, and ( + ) toroidal. The original has both mirrors spherical with beam confined to a single plane. Off-the-plane has both mirrors spherical with beam directed off the plane at 90° by the second mirror. Toroidal has the second mirror a toroid. Each plot shows the wavefront RMS error as a function of incident angle, I1, at the first mirror of the telescope. Left and right columns correspond to telescope #5 (1000:500) and #4 (300:1000), respectively, from the Indiana AO-OCT system (see legend of Fig. 5). Telescopes are optimized for (top row) pupil (finite) an (bottom row) retina (infinite) conjugate cases. Incident beam diameter was 6.67 mm. Wavelength was 809 nm, center of the AO-OCT system spectrum. Dashed lines represent diffraction-limited performance (RMS = λ/14).
For the infinite conjugate case, off-the-plane performs better (up to 1.6 times, RMS) except at large angles for the 1000:500 telescope. Like the finite conjugate case, the toroidal method is found more effective at correcting astigmatism and defocus. But unlike the finite conjugate case, the toroidal method provides somewhat worse correction of higher order aberrations.
Differences between toroidal and off-the-plane also extend to their implementation, some a direct consequence of the theoretical differences discussed above. The toroidal method allows in-the-plane designs and thus relatively easy conversion of an existing spherical-mirror-based system by direct exchange of spherical mirrors with appropriate toroidal ones. In-the-plane design also facilitates easy alignment. We found the extra degree of alignment (rotation) required of toroids was readily controlled by simply rotating the toroid in its mount while monitoring the downstream beam quality with the calibrated SHWS. Perhaps the two most significant attributes of the toroidal method are the considerable freedom it allows for the incident angles as well as correction of aberrations beyond 2nd order. The former provides considerable flexibility in the optical design to work around components in the sample arm such as wavefront correctors and scanners whose physical sizes are fixed. This flexibility combined with the insensitivity to large incident angles as shown in Fig. 14 may be particularly beneficial for commercial systems that must be compact and have short focal length optics, which contribute to large angles. As for the correction of additional aberrations, the magnetorheological technology used to fabricate our three toroids is capable of shaping the mirror with additional aberration correction. The theoretical RMS results of Fig. 14 reveal that 3rd and higher order aberrations limit the imaging performance of toroidal telescopes and so correction of these with a more complex mirror shape would benefit system performance.
The one major disadvantage of toroids is expense. Our toroids were customized mirrors whose specifications were driven almost entirely by other system constraints. We did this on purpose as one of the goals was to improve an existing all-spherical-mirror AO ophthalmic system, not create a new one in which toroids are part of the original design strategy. Expense of magnetorheological technology and other advanced technologies to fabricate these special surfaces will inevitably drop as they mature and become commonplace. Making toroids a part of the design process from the very beginning gives the best opportunity to reduce cost in other ways. Cost can be reduced – in some cases substantially – by selecting toroidal mirrors in the design that are of small diameter, determining actual toroidal surface quality required of the intended imaging (we used 63 nm peak-to-valley, but a less stringent quality may be acceptable), and when possible, selecting toroidal shapes that are available in stock or already on test plates at the fabrication facility.
Acknowledgments
The authors wish to thank Ravi Jonnal for assistance with the new AO system, and Qiang Wang and Timothy Turner for helpful discussions of the manuscript. The authors also thank William Monette, Thomas Kemerly, and Daniel Jackson for electronic and machining support. Financial support was provided by NEI grants 1R01 EY018339, 5R01 EY014743, and P30 EY019008.
References and links
- 1.J. Porter, H. M. Queener, J. E. Lin, K. Thorn, and A. Awwal, eds., Adaptive Optics for Vision Science Principles, Practices, Design, and Applications (John Wiley & Sons, Hoboken, NJ, 2006). [Google Scholar]
- 2.Liang J., Williams D. R., Miller D. T., “Supernormal vision and high-resolution retinal imaging through adaptive optics,” J. Opt. Soc. Am. A 14(11), 2884–2892 (1997). 10.1364/JOSAA.14.002884 [DOI] [PubMed] [Google Scholar]
- 3.Roorda A., Romero-Borja F., Donnelly III W., Queener H., Hebert T., Campbell M., “Adaptive optics scanning laser ophthalmoscopy,” Opt. Express 10(9), 405–412 (2002). 10.1364/OE.10.000405 [DOI] [PubMed] [Google Scholar]
- 4.Hammer D. X., Ferguson R. D., Bigelow C. E., Iftimia N. V., Ustun T. E., Burns S. A., “Adaptive optics scanning laser ophthalmoscope for stabilized retinal imaging,” Opt. Express 14(8), 3354–3367 (2006). 10.1364/OE.14.003354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang Y., Poonja S., Roorda A., “MEMS-based adaptive optics scanning laser ophthalmoscopy,” Opt. Lett. 31(9), 1268–1270 (2006). 10.1364/OL.31.001268 [DOI] [PubMed] [Google Scholar]
- 6.Burns S. A., Tumbar R., Elsner A. E., Ferguson D., Hammer D. X., “Large-field-of-view, modular, stabilized, adaptive-optics-based scanning laser ophthalmoscope,” J. Opt. Soc. Am. A 24(5), 1313–1326 (2007). 10.1364/JOSAA.24.001313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dubra A., Sulai Y., “Reflective afocal broadband adaptive optics scanning ophthalmoscope,” Biomed. Opt. Express 2(6), 1757–1768 (2011). 10.1364/BOE.2.001757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dubra A., Sulai Y., Norris J. L., Cooper R. F., Dubis A. M., Williams D. R., Carroll J., “Noninvasive imaging of the human rod photoreceptor mosaic using a confocal adaptive optics scanning ophthalmoscope,” Biomed. Opt. Express 2(7), 1864–1876 (2011). 10.1364/BOE.2.001864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Merino D., Duncan J. L., Tiruveedhula P., Roorda A., “Observation of cone and rod photoreceptors in normal subjects and patients using a new generation adaptive optics scanning laser ophthalmoscope,” Biomed. Opt. Express 2(8), 2189–2201 (2011). 10.1364/BOE.2.002189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hermann B., Fernández E. J., Unterhuber A., Sattmann H., Fercher A. F., Drexler W., Prieto P. M., Artal P., “Adaptive-optics ultrahigh-resolution optical coherence tomography,” Opt. Lett. 29(18), 2142–2144 (2004). 10.1364/OL.29.002142 [DOI] [PubMed] [Google Scholar]
- 11.Zawadzki R. J., Jones S. M., Olivier S. S., Zhao M., Bower B. A., Izatt J. A., Choi S., Laut S., Werner J. S., “Adaptive-optics optical coherence tomography for high-resolution and high-speed 3D retinal in vivo imaging,” Opt. Express 13(21), 8532–8546 (2005). 10.1364/OPEX.13.008532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang Y., Cense B., Rha J., Jonnal R. S., Gao W., Zawadzki R. J., Werner J. S., Jones S., Olivier S., Miller D. T., “High-speed volumetric imaging of cone photoreceptors with adaptive optics spectral-domain optical coherence tomography,” Opt. Express 14(10), 4380–4394 (2006). 10.1364/OE.14.004380 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zawadzki R. J., Choi S. S., Jones S. M., Oliver S. S., Werner J. S., “Adaptive optics-optical coherence tomography: optimizing visualization of microscopic retinal structures in three dimensions,” J. Opt. Soc. Am. A 24(5), 1373–1383 (2007). 10.1364/JOSAA.24.001373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cense B., Koperda E., Brown J. M., Kocaoglu O. P., Gao W., Jonnal R. S., Miller D. T., “Volumetric retinal imaging with ultrahigh-resolution spectral-domain optical coherence tomography and adaptive optics using two broadband light sources,” Opt. Express 17(5), 4095–4111 (2009). 10.1364/OE.17.004095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Torti C., Povazay B., Hofer B., Unterhuber A., Carroll J., Ahnelt P. K., Drexler W., “Adaptive optics optical coherence tomography at 120,000 depth scans/s for non-invasive cellular phenotyping of the living human retina,” Opt. Express 17(22), 19382–19400 (2009). 10.1364/OE.17.019382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kocaoglu O. P., Lee S., Jonnal R. S., Wang Q., Herde A. E., Derby J. C., Gao W., Miller D. T., “Imaging cone photoreceptors in three dimensions and in time using ultrahigh resolution optical coherence tomography with adaptive optics,” Biomed. Opt. Express 2(4), 748–763 (2011). 10.1364/BOE.2.000748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Felberer F., Kroisamer J. S., Hitzenberger C. K., Pircher M., “Lens based adaptive optics scanning laser ophthalmoscope,” Opt. Express 20(16), 17297–17310 (2012). 10.1364/OE.20.017297 [DOI] [PubMed] [Google Scholar]
- 18.Jonnal R. S., Kocaoglu O. P., Wang Q., Lee S., Miller D. T., “Phase-sensitive imaging of the outer retina using optical coherence tomography and adaptive optics,” Biomed. Opt. Express 3(1), 104–124 (2012). 10.1364/BOE.3.000104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Merino D., Dainty C., Bradu A., Podoleanu A. G., “Adaptive optics enhanced simultaneous en-face optical coherence tomography and scanning laser ophthalmoscopy,” Opt. Express 14(8), 3345–3353 (2006). 10.1364/OE.14.003345 [DOI] [PubMed] [Google Scholar]
- 20.Pircher M., Zawadzki R. J., Evans J. W., Werner J. S., Hitzenberger C. K., “Simultaneous imaging of human cone mosaic with adaptive optics enhanced scanning laser ophthalmoscopy and high-speed transversal scanning optical coherence tomography,” Opt. Lett. 33(1), 22–24 (2008). 10.1364/OL.33.000022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gómez-Vieyra A., Dubra A., Malacara-Hernández D., Williams D. R., “First-order design of off-axis reflective ophthalmic adaptive optics systems using afocal telescopes,” Opt. Express 17(21), 18906–18919 (2009). 10.1364/OE.17.018906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Webb R. H., Hughes G. W., Delori F. C., “Confocal scanning laser ophthalmoscope,” Appl. Opt. 26(8), 1492–1499 (1987). 10.1364/AO.26.001492 [DOI] [PubMed] [Google Scholar]
- 23.Webb R. H., Hughes G. W., “Scanning laser ophthalmoscope,” IEEE Trans. Biomed. Eng. 28(7), 488–492 (1981). 10.1109/TBME.1981.324734 [DOI] [PubMed] [Google Scholar]
- 24.J. M. Geary, ed., Introduction to Lens Design: With Practical ZEMAX Examples (Willmann-Bell, Inc., 2002). [Google Scholar]
- 25.A.N.S.I. Z136, 1, Safe Use of Lasers (Laser Institute of America, 2007). [Google Scholar]
- 26.Atchison D. A., Smith G., “Chromatic dispersions of the ocular media of human eyes,” J. Opt. Soc. Am. A 22(1), 29–37 (2005). 10.1364/JOSAA.22.000029 [DOI] [PubMed] [Google Scholar]