Abstract
Spectroscopic Optical Coherence Tomography (S-OCT) extracts depth resolved spectra that are inherently available from OCT signals. The back scattered spectra contain useful functional information regarding the sample, since the light is altered by wavelength dependent absorption and scattering caused by chromophores and structures of the sample. Two aspects dominate the performance of S-OCT: (1) the spectral analysis processing method used to obtain the spatially-resolved spectroscopic information and (2) the metrics used to visualize and interpret relevant sample features. In this work, we focus on the second aspect, where we will compare established and novel metrics for S-OCT. These concepts include the adaptation of methods known from multispectral imaging and modern signal processing approaches such as pattern recognition. To compare the performance of the metrics in a quantitative manner, we use phantoms with microsphere scatterers of different sizes that are below the system’s resolution and therefore cannot be differentiated using intensity based OCT images. We show that the analysis of the spectral features can clearly separate areas with different scattering properties in multi-layer phantoms. Finally, we demonstrate the performance of our approach for contrast enhancement in bovine articular cartilage.
OCIS codes: (170.4500) Optical coherence tomography; (300.0300) Spectroscopy; (290.5850) Scattering, particles; (180.0180) Microscopy; (170.3880) Medical and biological imaging
1. Introduction
Spectroscopic Optical Coherence Tomography (S-OCT) is an extension of OCT [1] that provides depth-resolved intensity-based backscattering information along with depth-resolved spectroscopic information. Due to wavelength dependent absorption and scattering, S-OCT enables detection of chromophores, as well as structural variations of tissue in the nanometer range [2,3]. Because of these unique capabilities, S-OCT fills a niche in medical molecular imaging and make this technique a promising method for detection of early stage cancer and other diseases that affect tissue structure [4,5]. Also the classification of arterial plaque in intravascular imaging according to the lipid distribution has been an interesting target for S-OCT [6,7].
There are a few near infrared (NIR) endogenous chromophores in biological tissue, from which hemoglobin is the most diagnostically relevant, since the state of blood oxygenation can be derived from NIR spectral features. Unfortunately detection of wavelength dependent absorption of most endogenous absorbers in the NIR region is challenging, because its effect is relatively weak and/or the spectra are featureless (e.g., melanins). Consequently, a significant amount of research has been focused on detection of exogenous contrast mechanisms with S-OCT, including absorbing dyes [8] and nanoparticles [9,10]. On the other hand, wavelength dependent scattering from small particles introduces unique features, which strongly depend on the shape, size, distribution and refractive index of the particles as well as the wavelength of light.
S-OCT can be performed in two different ways. Hardware based S-OCT systems typically employ two or three wavelength bands and combine the signals in a differential manner [11–14]. More commonly used are post processing based methods, which apply a time frequency distribution (TFD) like the short time Fourier transform (STFT) to the OCT data. The choice of the spectral analysis is an important consideration in S-OCT, since different methods have a strong impact on the results, which has been extensively explored previously [15–17]. The post processing methods work with any common OCT system, no matter whether it is operating in the time or frequency domain [1,18]. System and method-based error sources in S-OCT can be separated into three classes: (1) Stochastic errors arise from the random nature of biological tissue and system instabilities that introduce, for instance, speckle like noise on the spectroscopic signal [15,19]. (2) Systematic errors are caused by the wavelength dependent transfer function of the optical system, which depends on the axial and lateral position in the sample [20–23]. (3) Numerical errors occur from the choice of the method used to calculate the spectroscopic signal [15,16]. Additionally, S-OCT measures the total wavelength dependent extinction of the sample in an integrative manner (i.e., along the optical path length). The separation of absorptive and scattering contributions from the extinction signal has been demonstrated [24,25], while the cumulative manner of the signal still remains a problem in highly scattering media.
The various error sources make a quantitative analysis for highly scattering biological tissue challenging [20,26,27], though progress has been made for measuring the blood oxygenation level quantitatively in vivo using OCT in the visible range, albeit this comes along with limited penetration depth due to the choice of wavelength [2]. Similarly, Yi et al. obtained a full set of quantitative optical scattering properties of biological tissue ex vivo using Inverse Spectroscopic Optical Coherence Tomography (iSOCT) [28]. The properties were obtained using a standard OCT system in the NIR, but again with limited pentration depth. Quantitative measurements across the full axial measurement range of conventional S-OCT systems remain challenging and emphasize the need for reliable qualitative metrics.
Therefore spectroscopic information is typically qualitatively displayed as a color map, which is overlaid across the intensity based image [1,29]. We will use the term (digitally) ‘staining’ in analogy to histology, where slices are stained to enhance the contrast for specific features of the sample [1].
In this paper we introduce new concepts for visualization and analysis of the spectroscopic information, which were adapted from multispectral imaging for remote sensing [30,31] and general spectral analysis. A wide range of metrics has been presented for S-OCT, including the center of mass (COM) calculation for each spectrum [1], the bandwidth of the autocorrelation function (ACF) of the spectra [19] and the sub band (SUB) metric, where sub bands of the spectra are directly mapped into the three channels of the RGB color model. Furthermore several metrics have used fitting algorithms like least squares and specific models to analyze the depth resolved spectra (see for instance [3,32,33]).
We compare these new concepts with the established metrics, including the COM, ACF and SUB methods in a quantitative manner. To further demonstrate the results, we use phantom samples with varying scattering properties. Finally we present data of biological tissue consisting of cartilage/bone tissue in vitro, where the application of S-OCT leads to higher contrast in comparison to the pure intensity based OCT images.
2. Materials and methods
In this section we describe the general signal processing for S-OCT, as well as the OCT systems and samples used for the experiments.
2.1. System and samples
OCT data for the phantom samples were obtained using a Thorlabs® Callisto OCT system containing a lens with an effective focal length of 36mm. The system has a center wavelength of 930nm and a bandwidth of 130nm, which is spread over a 1024 pixel camera. The axial resolution and the lateral resolution are 7µm and 8µm, respectively. The raw spectral data were saved to the hard disc and further processed in Matlab®. The computer used for the processing was an Intel® Xeon®E5-2620 with 2.00GHz CPU built up with 64GB RAM with a Windows 7® 64bit and Matlab® 2011a installation.
The phantom samples in this study consist of silicone foils (RTV-2 silicone, silikonfabrik.de, Ahrensburg, Germany) with approximately 100µm thickness. Polybead® microspheres from Polyscienes (Warrington, PA, USA), dry form in 1.00µm and 3.00µm diameters, were embedded in the foils as scattering structures with concentrations ranging from 0.6% to 0.8% per weight. Note that the size of the scattering microspheres is well below the resolution limit of the system. The foils were used to form phantom samples with different structures, which will be described in the results paragraph.
For the cartilage tissue sample, a custom-built assembly was used, which allowed the exposure of a static mechanical load on a bovine articular osteochondral plug in a culture chamber. The cartilage side faces an optical window enabling an integrated OCT scan head to obtain images of the compressed sample, while the load is applied from the other side. Contrary to the OCT system used for the phantom studies, the integrated scan probe needs a larger working distance and is therefore equipped with a lens with an effective focal length of 54mm, resulting in a lateral resolution of 12µm. The scan head can be tilted by up to 4° with respect to the normal of the optical window to prevent specular reflections from entering the objective. The cartilage-bone cylinders for the experiments (7 mm high and 6 mm in diameter) were excised from the shoulder joint of a ten-month-old bull directly after slaughter. After excision the samples were deep frozen and stored. Before the experiments the sample was thawed out and stored in phosphate buffered saline, to avoid dehydration.
2.2. Signal processing
The general signal processing steps are displayed in Fig. 1 . As the figure illustrates signal processing for S-OCT splits up into four separate blocks: OCT data processing, spectral analysis, calculation of a spectroscopic metric and color mapping (‘staining’). In the next sections we review each block individually.
Fig. 1.

Signal processing for S-OCT. The signal processing chain for S-OCT splits up into four separate blocks: OCT data processing, spectral analysis, the calculation of a spectroscopic metric and the color map (‘staining’).
2.2.1. OCT processing
In a first step the raw interferometric spectra are re-sampled from the wavelength to the wavenumber domain. Also the DC component from the spectral domain data, which consists of the reference spectrum, is removed by subtraction, and then the spectra are normalized to the reference spectrum. For intensity based standard OCT processing the data is finally multiplied by a window function and Fourier transformed.
2.2.2. Spectral analysis
As a second step the spectral analysis is performed on the resampled and normalized spectra using the Dual Window method, which was introduced for S-OCT by Robles et al. [34]. We have chosen this methods as it has shown excellent results for extracting the spectroscopic information introduced by wavelength dependent scattering [5, 35], and absorption in-vivo [2]. In this method the spectra are analyzed by two STFTs with different window sizes. The results of the two STFTs are combined by multiplication. We shifted the windows pixel wise across the sample, to obtain one spectrum per pixel. Finally the absolute value from the complex valued data was calculated for further processing. The advantage of using two windows is that the resolution in the spatial and spectral domain can be independently tuned thus ameliorating the resolution trade-off associated with using a single window (i.e., STFT) [34]. Note that the choice of the window sizes is an important consideration in this method and has to be carefully chosen according to the technical parameters of the system and the type of sample that is investigated [34]. We adjusted the window sizes by optimizing the results of the different metrics used. Concrete numbers for the window sizes used are given in the results section. We also note that other methods are available for computing the depth resolved spectra in SOCT: for the interested reader, we refer them to reference [15].
2.2.3. Spectroscopic metric and color map
The calculation of the spectroscopic metric and the generation of the color map are closely related. Figure 2 shows a block diagram of the steps and methods involved in calculating the various spectroscopic metrics and the generation of the color map. There are four blocks: preprocessing, feature reduction, pattern recognition and display.
Fig. 2.
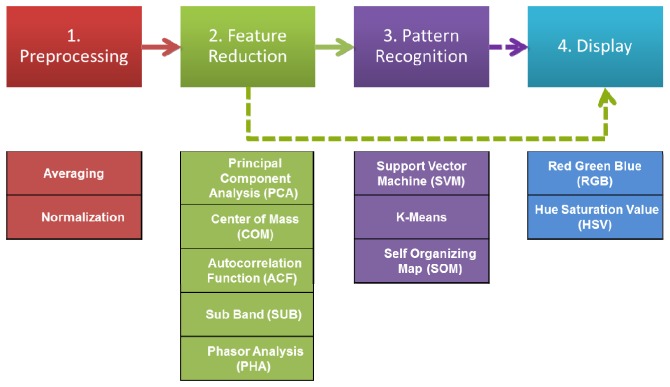
Signal processing steps to calculate the spectroscopic metric and display the data split into four blocks: (1) preprocessing that includes normalization and averaging of the data. (2) Feature reduction, which contains one of the following methods: Phasor Analysis (PHA), Center of Mass (COM), Autocorrelation Function (ACF), Principal Component Analysis (PCA) or Sub Band (SUB). (3) Pattern recognition, an optional step, which consists of one of the following methods K-Means clustering, Self Organizing Map (SOM) or Support Vector Machine (SVM). (4) Displaying the results from the different methods in a color map using the RGB or HSV color model. Alternatively the output of the feature reduction method can be displayed directly, without applying pattern recognition, using an appropriate color map.
Pre-processing is necessary in order to reduce the noise and to correct for system specific features. First, the depth-resolved spectra are averaged using a smoothing two dimensional Gaussian filter. The edges of the spectra, which are lower in intensity, are more susceptible to noise compared to the center spectral region. Hence we exclude this part of the data from the subsequent analysis. Finally we normalize the depth-resolved spectra by scaling them from zero to one. This preprocessing reduces speckle-like noise and excludes intensity information from subsequent analyses (thus only taking spectral fluctuations into account).
The aim of the spectroscopic metric is to reduce the dimensionality of the spectra and to highlight the relevant sample properties. Feature reduction is necessary for the visualization of the multidimensional data as a color map, which is the most intuitive way to display theinformation content of the spectroscopic analysis. Since the standard intensity analysis, which is performed in OCT, can give complementary information regarding to the spectroscopic analysis, it is useful to combine both, the results from intensity and spectral analysis, in one image. Therefor the intensity distribution can be encoded in the intensity of the image, while the spectroscopic metric is encoded in the color of the image. Typically the color map in S-OCT is used in two different ways: (1) one can encode continuous features, e.g. the center of mass, directly into color. In this case, the interpretation is done by the user, who is looking for areas in the color map with similar hues. (2) On the other hand, if one is only interested in differentiating a limited set of sample properties, a discrete staining can be used. Therefore, to classify the spectra according to the relevant sample properties, pattern recognition algorithms can be used and the results can be displayed in discrete colors, e.g. blue and red.
In pattern recognition one can distinguish between unsupervised and supervised methods. Unsupervised methods do not require a priori measurements, while supervised methods need a learning phase, where a set of labeled data needs to be available. The accuracy of pattern recognition approaches can considerably be better when the number of input variables is reduced by feature reduction. Thus we will use the feature reduction methods in two ways: (1) to reduce the dimensionality of the data in order to display the spectroscopic information directly using a color map and (2) to reduce the number of the features for the subsequent pattern recognition analysis.
The methods for “digital staining” and pattern recognition are briefly described below. For further detail, we refer the reader to the appendix, where a more rigorous mathematical description is included.
The first method we use for feature reduction is Principal Component Analysis (PCA), which is a simple and non-parametric tool for data analysis (e.g., feature reduction in NIR spectroscopy to analyze multi component spectra) [36]. We use PCA to reduce the number of features for the subsequent pattern recognition algorithms, as well as a tool to directly encode the relevant features of the spectra in the RGB color model (PCA-RGB), a method adapted from multispectral imaging [31]. The next feature reduction method is the SUB metric which is similar to the way the human eye detects colors. In this method the spectrum is divided into three sub-bands using weighting functions [2,29]. The integrated values of each sub band can be directly assigned to red, blue and green hue in the RGB color model. We also use the autocorrelation function (ACF) method [19,35]. Here the bandwidth or a combination of different bandwidths about the zero lag of the autocorrelation function (ACF) of the spectra is used as an indicator for the scattering properties of the sample. The COM metric calculates the center of mass for each spectrum, thus the whole spectrum is reduced to one single value [1]. This value can be used to calculate a color map according to the hue channel in the hue, saturation and value (HSV) color model. Finally, we use Phasor Analysis (PHA) where each spectrum is reduced to two parameters given by the real and imaginary parts of the demodulated (or depth resolved) spectrum’s Fourier transform at a particular frequency [37]. This method has been shown to be fast and effective for unmixing fluorescence microscopy spectral images [38].
Next, we introduce the pattern recognition methods used in this work. K-Means [39] is an unsupervised algorithm, which assigns the spectra to one of a predefined number of clusters. This number of clusters is not known for many applications of S-OCT. Thus we adapted a cluster shrinking algorithm, which reduces the number of clusters according to a sample independent threshold. One of the properties of the K-Means algorithm is that the ordering of the clusters can change in each run. This is a problem when a specific color is assigned to a specific cluster. To alleviate this problem, we use Multi-dimensional Scaling (MDS) [40] to transform the outcome from the clustering to a new, one dimensional data space. The random change in the ordering of the clusters will therefore be suppressed. Additionally the topology of the feature space of the sample properties is preserved. Therefore similar clusters, e.g. with small Euclidian distances in the feature space, are grouped together and are assigned to similar colors e.g. red and yellow, while clusters with relatively larger distances are assigned to colors with more contrast e.g. red and blue.
Self Organizing Maps (SOM) are based on artificial neural networks and can be applied to unsupervised pattern recognition problems [41]. We use a one dimensional SOM in the same way as K-Means for clustering. Furthermore we use a three dimensional SOM to encode the spectroscopic information directly into the three channels of the RGB color model (SOM-RGB) [42]. Lastly, we use Support Vector Machines (SVM) which are a powerful approach to classify data with supervised algorithms [39]. To test the ability of the SVM to classify unknown data sets, we use k-fold cross-validation [43].
A more detailed description of the methods discussed above is given in appendix A.
3. Results and discussion
3.1. Phantom samples
OCT images for the phantom samples were recorded with dimensions of 1.7mm in the lateral and axial directions. The processed B-Scans, which originally consisted of 512x512 pixels respectively 512 A-Scans, were reduced to the relevant cutout. The reduced B-Scans together with the particular phantom structure as insets are shown in Fig. 3 .
Fig. 3.

Standard intensity based OCT images of the microsphere phantoms. The insets show the structure of the particular phantom, blue indicates 3µm microspheres, while red indicates 1µm microspheres. Bar specifies 200µm.
For the spectral analysis the 3dB window sizes for the Dual Window method were set to approximately ~48nm and ~8nm. The signal outside the window was set to zero and a 1024 point zero padding was applied. The resulting depth-resolved spectra were smoothed using a Gaussian filter with a pixel width of 37x51 (123µm and 169µm) in axial and lateral dimension, respectively, and normalized as described above (section 2.2.3). Additionally we excluded 50 points of the edges from the spectra from the subsequent analysis. Finally the spectra were processed with the specific metric algorithm (PCA, COM, PHA, SUB or ACF). The spectra were reduced by PCA to the first three principal components (PCs) (which contain >78% of the data variance) for the PCA-RGB method and the subsequent pattern recognition. First we used continuous encoding of the metric into a color map to gain insightinto the phantom sample`s structure according to the spectral features. In Fig. 4 the imaging capabilities of the COM and SUB metrics as well as the PCA-RGB and SOM-RGB metrics for phantom 3 are shown. PCA-RGB encodes the normalized first three principal components into the three channels of the RGB color model. SOM-RGB uses a three dimensional Self Organizing Map with 10 units in each dimension, which is also directly encoded in the channel of the RGB color model. We have chosen phantom 3 as an example, because it has the most complicated structure. On the left side of this phantom a foil with 3µm microspheres is on top of a foil with 1µm microspheres and on the right side 1µm foil is on top of a 3µm microspheres foil. While the SUB and SOM-RGB metric only separate the top 3µm from the 1µm layer, but stain the bottom 3µm layer in a different color, the PCA-RGB and COM metric stain the areas of similar scattering properties with similar hue and thus depict the real sample structure best.
Fig. 4.

Continuous mapping of spectroscopic metrics for phantom sample 3. Bar indicates 200µm.
Next we combine unsupervised pattern recognition algorithms with the metrics, to separate the areas with the different microspheres to obtain a discrete staining. Figure 5 shows the results acquired from PCA combined with the extended K-Means clustering algorithm. The areas are stained according to the output of the clustering algorithm, which means that 1µm spheres are assigned to the blue color and 3µm spheres are assigned to the red color. We also delineate the areas for which the accuracies for the quantitative analysis were obtained. These areas were restricted to make sure that only one size of microspheres was present in each area. The images show the excellent capability of the K-Means algorithm to classify the spectra according to the relevant spectral features, which were introduced by the differently sized microspheres. Note that while in the intensity based images the areas appear quite homogeneous, the stained OCT images show clear contrast based on the scattering properties, even for the more complicated structured phantoms like e.g. phantom 3. In comparison to the continuous staining presented in Fig. 4 the contrast of the discrete staining is higher and the areas can be better separated. As a drawback the analysis is more sensitive to artifacts, which can for instance be seen in the right upper part of Fig. 5(b).
Fig. 5.

S-OCT analysis by PCA and K-Means clustering of phantoms 1-4. Blue staining indicates 1µm microspheres, red staining 3µm microspheres. Rectangles indicate areas which were chosen for accuracy calculation. Bar indicates 200 µm.
To compare the different metrics in a quantitative manner, we clustered all metrics with K-Means and calculated the accuracy, sensitivity and specificity. The accuracy reflects the number of correct classified outcomes, while the sensitivity is true positives rate and specificity is the true negative rate.
Additionally, we used a one dimensional SOM, as another unsupervised pattern recognition approach, with two units to cluster the PCA metric (results in the last line of Table 1 ). Phasor Analysis was performed with a frequency of 7.88µm. For the ACF metric the bandwidth was calculated at 19 amplitude levels and the output was reduced to three PCs by PCA. Tay et al. demonstrated that the use of multiple bandwidths can improve the performance of the ACF method [35], therefore multiple bandwidth instead of a single bandwidth (e.g. the full width at half maximum) were chosen. The SUB metric was calculated using rectangular shaped weighting functions with equal widths, resulting in approximately 40nm bandwidth of each channel.
Table 1. Cluster accuracies for microsphere phantoms for the different metrics combined with a K-Means algorithm and a Self Organizing Map for two clusters.
|
|
Phantom 1
|
Phantom 2
|
Phantom 3
|
Phantom 4
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K-Means + | Accuracy | Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | |
| ACF | 62.4 | 98.9 | 41.9 | 76.7 | 85.7 | 71.3 | 69.3 | 88.0 | 62.9 | 87.4 | 99.4 | 80.1 | |
| PHA | 81.4 | 99.8 | 59.6 | 89.5 | 92.1 | 87.3 | 95.6 | 99.9 | 92.1 | 94.0 | 96.8 | 91.6 | |
| SUB | 88.7 | 99.8 | 70.9 | 92.3 | 92.5 | 92.1 | 86.2 | 96.1 | 79.8 | 93.4 | 96.2 | 90.9 | |
| COM | 90.7 | 99.5 | 75.1 | 92.4 | 93.0 | 91.8 | 91.0 | 93.7 | 88.6 | 95.1 | 96.4 | 93.9 | |
| PCA | 87.4 | 99.7 | 68.6 | 93.4 | 94.2 | 92.6 | 95.4 | 99.9 | 91.7 | 98.6 | 99.9 | 97.4 | |
| PCA + SOM | 79.4 ± 1.6 | 100 ± 0.0 | 57.0 ± 1.7 | 90.1 ± 0.7 | 92.4 ± 0.5 | 88.0 ± 1.5 | 91.6 ± 1.5 | 98.4 ± 0.8 | 86.5 ± 2.4 | 98.6 ± 0.5 | 99.4 ± 0.2 | 97.9 ± 1.1 |
|
Table 1 gives the results for the different metrics and the four phantom samples, while the overall performance (average of all phantoms) is listed in Table 2 . In general nearly all methods give very good results with accuracies better than 90%, headed by the PCA metric with almost 94%. The ACF method shows the weakest performance, with an overall accuracy of only ~74%. A further analysis of the detailed results given in Table 1 indicates that the layered structure of phantoms 1-3 is maybe not well suited for this metric; however the performance improves for the side by side structure of phantom 4, giving an accuracy of ~87%. This is comparable to the results of Kartakoullis et al. [17], who published a similar approach using side by side structured phantom samples. The group used the pure ACF, instead of the bandwidth for the PCA and compared two different clustering algorithms and the performance of two TFDs.
Table 2. Average cluster performance overall phantom samples.
| Method | Accuracy | Sensitivity | Specificity |
|---|---|---|---|
| PCA K-Means | 93.7 | 98.4 | 87.6 |
| PHA K-Means | 90.2 | 97.1 | 82.6 |
| COM K-Means | 92.3 | 95.6 | 87.4 |
| SUB K-Means | 90.2 | 96.2 | 83.4 |
| ACF K-Means | 73.9 | 93.0 | 64.1 |
| PCA SOM | 89.9 | 97.6 | 82.4 |
The reported standard deviation for the SOM method is given by the standard deviation of 100 repetitions of the computation, since we observed that due to the random initialization of the algorithm variations for the accuracy of up to 10% appeared.
We also analyzed the processing times for the different metrics. Most algorithms require a short time for the processing using our computer system, and are therefore after optimization suited for real time imaging. This has already been demonstrated for the PCA and K-Means method by the use of General Purpose Graphics Processing Unit programming by Jaedicke et al. [44].
So far we have only used unsupervised methods; however the accuracy can be improved vastly by using the available a priori information. Since the class (the size of the microspheres) for each spectrum is known for the phantom samples, a labeled data set can be constructed and used to train a classifier. We selected SVMs for supervised pattern recognition and used k-fold cross validation to search for the best kernel and penalty factor. The used SVM for the analysis had a third order polynomial kernel and a C penalty factor of 0.05. During the testing phase we found that the number of principal components used for training had a significant influence on the performance–this was not the case for the unsupervised methods. For example, with the K-Means approach, using 11 PCs instead of 3 improved the performance by <1%. In contrast the SVM performed significantly better with 11 PCs or 22 PCs compared to 3 PCs (performance improved by 20%, see Table 4). For phantom 4, the first 3 PCs contain ~78% of the data variance, whereas 11 PCs contain 95% and 22 PCs contain 99%. For the analysis all data were transformed to the principal component space using the loadings of phantom 4, which served as a template because the differently sized microspheres are arranged using a side by side structure and thus the spectra are just affected by microspheres of one size. First each phantom was treated individually and a 10 fold cross validation was conducted. The SVM was able to classify the data with nearly 100% using 11 PCs and 22 PCs, which is shown in detail for all phantom samples in Table 3 .
Table 3. Accuracies for the Support Vector Machine supervised pattern recognition algorithm and microsphere phantoms. Each phantom is classified separately.
|
|
Phantom 1
|
Phantom 2
|
Phantom 3
|
Phantom 4
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | Accuracy | Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | Sensitivity | Specificity | Accuracy | Sensitivity | Specificity |
| 3 PCs | 85.7 | 82.8 | 86.4 | 72.0 | 90.3 | 65.1 | 76.4 | 83.3 | 71.9 | 84.4 | 99.7 | 76.3 |
| 11 PCs | 100 | 100 | 100 | 99.79 | 100 | 99.58 | 100 | 100 | 100 | 99.98 | 100 | 99.96 |
| 22 PCs | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
The results for an overall classification of all phantom samples are listed in Table 4 . Here, one large data set containing all phantom samples was used to train and test the SVM by 10-fold cross validation. Again the performance is nearly perfect with an accuracy of more than 99% for both, 11 PCs and 22 PCs. These results demonstrate the exceptional potential of the combination of supervised pattern recognition and S-OCT. It has to be emphasized that this approach is different from the K-Means algorithm. While the latter only searches for dissimilarities in one specific sample or data set, the SVM approach looks for similarities between a known sample or data set and an unknown sample.
Table 4. Accuracies for the Support Vector Machine supervised pattern recognition algorithm and microsphere phantoms. Overall classification performance for microspheres phantom samples.
| SVM | Accuracy | Sensitivity | Specificity |
|---|---|---|---|
| 3 PCs | 84.76 | 76.90 | 93.99 |
| 11 PCs | 99.40 | 99.61 | 99.24 |
| 22 PCs | 99.92 | 99.99 | 99.85 |
3.2. Biological tissue
We demonstrated in the previous section that the PCA extended K-Means algorithm is an excellent approach to enhance the contrast using spectroscopic features, based on wavelength dependent scattering in phantom samples. As wavelength dependent scattering is a far stronger effect in the wavelength range covered by our OCT system, we believe that the underlying physical principle is similar for microsphere based samples and biological tissue. Based on this fact and the lack of available training data for a supervised pattern recognition algorithm, the PCA extended K-Means approach was chosen for analysis of the cartilage/bone sample.
In the experiment, static loading was applied to the sample by exerting a force of 50N on its bone side, which was generated by a 5kg weight placed on top of the culture chamber.
OCT images were taken from the opposite side of the chamber through the glass window every 5 minutes, starting from the application of the load. The reflection of the window can be seen at the top of the images. Each recorded frame of the OCT images consisted of 500 A-Scans and had a scanning width of 1.5mm. Figure 6 illustrates the intensity based OCT images, which appear relatively homogenous over the course of the experiment. Cartilage tissue has a layered structure, which is of great interest due to its correlation to mechanical properties [45–47]. In Fig. 7 a histological image of a similar bovine cartilage sample, which was stained by Safranin O and Fast Green, is shown. Here the 4 zones of the cartilage (namely the superficial, the middle, the deep and the calcified zone, which is connected to the subchondral bone) can be identified. The tidemark is the visible border of the connection between the deep zone and the calcified zone [48]. Although three layers can be seen after 45 minutes in the images, there is not enough contrast in the intensity based images to clearly identify different zones during the compression.
Fig. 6.

OCT images of cartilage/bone sample after application of a static load for of 50N after 0minutes, 15minutes and 45minutes (from left to right).
Fig. 7.
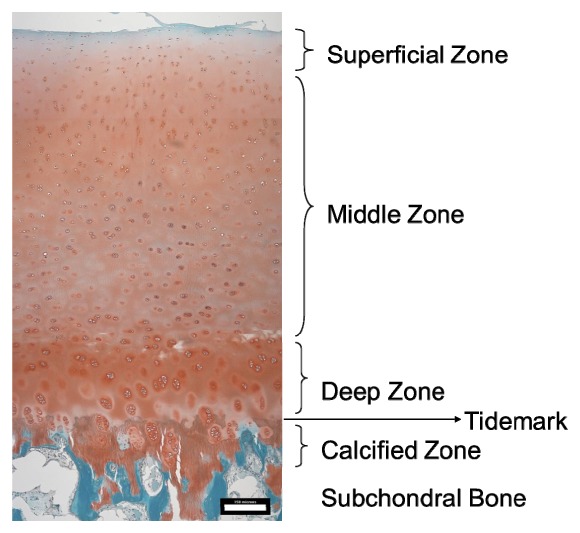
Histological image of articular bovine cartilage tissue. Scale bar is 150µm.
Therefore the DW method in combination with the PCA and extended K-Means algorithm was applied to obtain depth resolved spectra and enhance the contrast due to spectroscopic features. The same parameters for processing as described in the previous paragraph were used to obtain a TFD for each recorded frame. Subsequently, the spectra from all frames were processed together by use of the PCA extended K-Means metric using 5 clusters. The results of the digitally stained OCT images are shown in Fig. 8 .
Fig. 8.
Cartilage sample under mechanical load after 0 minutes, 5 minutes, 10 minutes, 20 minutes, 30 minutes and 45 minutes analyzed by S-OCT using the PCA extended K-Means metric. Bar indicates 200µm.
Before the load is placed on the chamber, the cartilage image looks quite homogeneous in the digitally stained OCT image. After applying the force to the sample for 5 minutes, there are no zoned layers recognizable in the upper part of the tissue, while two layers can be clearly distinguished at the bottom (blue and turquois). After 10 minutes, an additional layer (stained red) appears at the top with increasing thickness as time progresses. This behavior is not visible using conventional OCT imaging, where layers appear later and have a different distribution. The colors of the spectroscopic staining indicate the similarities of the clusters, therefore three different layers can be identified (red, green-yellow-turquois and blue). We compared the thickness of these three layers with the values for the first three cartilage zones given in the literature [49] and found a good accordance. Although no quantitative conclusions can be drawn from these preliminary results, the change of the collagen fiber composition in the different zones [49] could be a reasonable explanation for the enhanced contrast due to spectroscopic features. The enhanced contrast of the zones after application of the load can maybe explained by the effect of optical clearing. During static compression of the cartilage, water is expelled out of the tissue [50]. Xu et al. measured reflectance spectra for gastric tissues and reported a correlation of optical clearing, which is connected to reduced scattering, with dehydration [51]. We believe that the water content varies throughout the cartilage depth and the applied load affects the ratio of solid components to contained fluid unevenly. This, in turn, changes the scattering properties and thus also the spectra between the particular cartilage zones. The correlation between NIR spectra and cartilage properties under load was also demonstrated by Hoffmann et al. [52]. However, because validation against conventional methods (e.g. histology) is difficult, since such methods significantly change the samples’ structure, control measurements remain an objective for future studies. Additionally, it would be interesting to use model based metrics, for example, iSOCT [28] or Fourier-domain low-coherence interferometry (fLCI) [53], in combination with pattern recognition to improve the physical interpretation of the results.
4. Conclusion
In this paper we compared different metrics derived from the depth resolved spectroscopic information afforded by S-OCT to visualize scattering properties. We demonstrated that the combination of the Dual Window spectral analysis with the different metrics leads to high performance clustering of areas with different scattering properties in microsphere phantoms. The use of Self Organizing Maps and Principal Components Analysis based RGB imaging was introduced and evaluated as a new metric for S-OCT. Our results indicate that the use of these metrics can help to increase contrast compared to the sub band RGB metric.
We also quantitatively compared the clustering accuracies of the K-Means algorithm for different metrics. The most promising method is Principal Component Analysis with an overall clustering accuracy for our phantoms of nearly 94%. In K-Means clustering, the number of clusters has to be estimated in advance, which means that a priori information has to be known about the sample. Therefore we adapted a cluster shrinking algorithm, which reduces the number of clusters. Additionally we further extended K-Means and used Multi Dimensional Scaling to suppress the fluctuating ordering of clusters and transfer the topology of the cluster outcome to the color map. Furthermore, we demonstrated the effectiveness of supervised pattern recognition algorithms for application in S-OCT, which can be applied when a labeled training set is available. Here, we used a Support Vector Machine, which could classify the data of the phantom samples with almost 100% accuracy. Finally we demonstrated the application of our method for spectroscopic contrast enhancement in biological tissue. Specifically, we imaged articular bovine cartilage tissue and showed a layered structure of cartilage, likely resulting from changes in scattering and due to optical clearing. A validation against conventional imaging methods will be a future task. In conclusion, we have shown that reliable metrics for visualization in S-OCT can be obtained by pattern recognition techniques. These results will help to pave the way to establish S-OCT as a future diagnostic tool.
Acknowledgments
This work was supported by the RW TÜV Stiftung, the European Space Agency and the Research School + , which is the graduate school of the Ruhr-University. The authors thank Marita Kratz for preparation of the phantom and tissue samples and the histological cartilage image and Adam Wax for supplying a Dual Window spectral analysis algorithm implementation.
Appendix A
A.1. Non parametric data analysis methods
Principal Component Analysis projects data onto an orthogonal basis such that the variance of each projection is maximized. The new representations of the data, which are called principal components or scores are ordered in descending orders of variance [39]. The transformation matrix contains the so called loadings (i.e., the projection of the data vector onto each orthogonal vector). Typically most of the variance of the data can be described by the first few principal components. Thus the number of features which describe most of the variance of the data can be minimized with this method.
Multi-dimensional scaling (MDS) is a technique which can be used with a similar aim as PCA. MDS is a technique that rescales the data to a lower dimensional data space by preserving the pairwise distances of the data as close as possible [54]. While metric MDS preservers the pairwise distance, non-metric MDS only maintains the ordering of the data [40].
A.2. Spectroscopic metrics
The mathematical model behind the metrics that are directly mapped into the RGB model can be described by the following formulas, where WR,B,G describe weighting functions:
| (1) |
| (2) |
| (3) |
The SUB method uses rectangular weighing functions and integrates the values for each sub band, while other methods use more sophisticated weighting functions (e.g., Commission Internationale d’Eclairage or CIE, for short). In our analysis, we use rectangular weighting functions with equal widths.
Phasor analysis is a method which has been applied to analyze the time decay of signals from fluorescence lifetime imaging microscopy or nonlinear pump-probe microscopy [37,55]. This method is related to Fourier-domain low-coherence interferometry spectroscopy, where a correlation plot is obtained by Fourier transforming the depth resolved spectrum [53]. It has been shown that peaks in the correlation plots allow the separation of different sized scatterers [32]. In Phasor analysis, the signals are represented in frequency space using the signal’s real and imaginary part at a given frequency. This process is able to separate signals with small life-time differences without utilizing complicated or computationally expensive nonlinear fitting algorithms. We use the following equations to calculate the real and imaginary part, g and s respectively [37]:
| (4) |
| (5) |
We used the frequency ω as a free parameter to optimize the analysis. Using these formulas and an appropriate frequency the spectra are mapped into the first quadrant of the unit circle.
A.3. Pattern recognition
In K-Means each observation is assigned to a cluster. The concept behind this unsupervised pattern recognition method is to minimize the distances between the K cluster means and the representation of the observations in the feature space. Thus the output consists of the coordinates of K cluster means µk,k=1…K and a vector which assigns each observation (e.g. spectrum) to one of the cluster labels 1…K. The algorithm works in an iterative manner, where each observation is assigned to its nearest cluster mean and new cluster means are calculated in a second step. The algorithm stops after a predefined number of iterations or when no significant chance of the cluster means is detected. To initialize the algorithm commonly all cluster means are set to a random position in the feature space. Therefore the cluster labels 1…K are not fixed to a certain position in the feature space and their ordering can change from run to run. To obtain consistent color maps and to preserve the feature space we therefore use MDS to project the clusters means on a new one dimensional data space, as described above.
In order to use K-Means clustering without a priori information (e.g. the number of clusters), we adapted the shrinking algorithm from Jee et al. [56]. The aim of this algorithm, which is displayed in Fig. 9
Fig. 9.
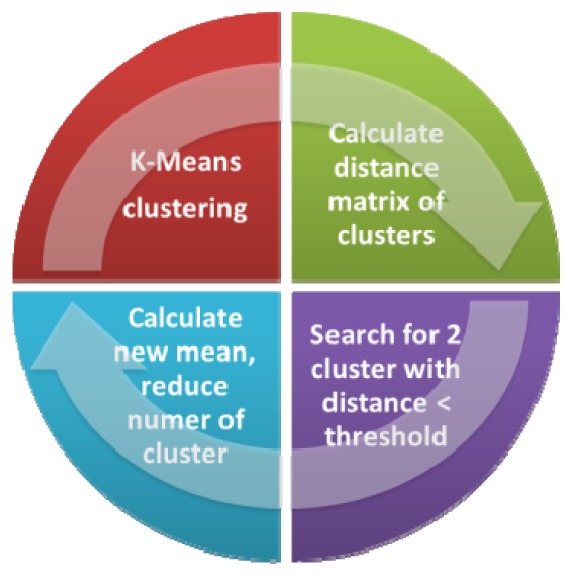
Shrinking algorithm to automatically reduce the number of cluster in K-Means. In an iterative manner adjacent cluster are merged and the data is clustered again until no cluster distances below the threshold are existing.
, is to reduce the number of clusters based onto their pair wise distances in the feature space. In a first step the distance matrix is calculated for the coordinates of the cluster means. Then MDS is used to project the data onto a two dimensional feature space. This feature space is normalized and two clusters with a distance below the threshold are summarized. Next the K-Means algorithm is performed again with a reduced cluster number and with the cluster means of the first iteration as starting points. The merged new cluster has an initial starting point, which is the mean of the coordinates of both prior clusters. This procedure is repeated iteratively until no more cluster, which have a distance below the threshold, are found. Because the algorithm works in a normalized feature space, the threshold parameter gives a sample independent scaling factor, which defines the maximum number of clusters. Hence the algorithm is an effective way to estimate the number of clusters expected in an individual sample.
Self-organizing maps (SOM) are based on neural networks and preserve the topological structure of the data, which means that observations with similar features are mapped closer together in the output space than those with dissimilar features. The output space can have one or more dimensions depending on the specific application, using the so called neurons or units to represent the input data. Typically the map is two dimensional to display the inner structure of the data in a convenient way. The weights of the SOMs, which connect the units with the input space, are initialized randomly. Therefore the results from the SOM can vary based on the initial random conditions.
Support Vector Machines (SVM) are based on well understood theory in machine learning. The idea of the SVM is to transform the data (non)linearly into a higher dimensional feature space, where the classes can be separated by hyperplanes. Essential for the SVMs is the so called kernel trick, which avoids the computational expensive mapping of the data in the higher dimensional feature space. The SVM algorithm maximizes the margin which separates the classes, therefore only a small number of vectors is needed to construct the margins, the support vectors [57]. Outliers of the data can be tolerated using the penalty factor C. To estimate the performance of the SVM we use k-fold cross validation. Here the data set is randomly split into k sub sets. One of these sub sets serves as test data, while the remaining sub sets are used to train the classifier. This is repeated k times for each sub set serving as a test set. Finally the calculated performance values of the iterations are averaged. According to Kohavi et al., this is a good estimate of the performance of a classifier to classify unknown, new observations [43].
References and links
- 1.Morgner U., Drexler W., Kärtner F. X., Li X. D., Pitris C., Ippen E. P., Fujimoto J. G., “Spectroscopic optical coherence tomography,” Opt. Lett. 25(2), 111–113 (2000). 10.1364/OL.25.000111 [DOI] [PubMed] [Google Scholar]
- 2.Robles F. E., Wilson C., Grant G., Wax A., “Molecular imaging true-colour spectroscopic optical coherence tomography,” Nat. Photonics 5(12), 744–747 (2011). 10.1038/nphoton.2011.257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yi J., Radosevich A. J., Rogers J. D., Norris S. C. P., Çapoğlu İ. R., Taflove A., Backman V., “Can OCT be sensitive to nanoscale structural alterations in biological tissue?” Opt. Express 21(7), 9043–9059 (2013). 10.1364/OE.21.009043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Backman V., Wallace M. B., Perelman L. T., Arendt J. T., Gurjar R., Müller M. G., Zhang Q., Zonios G., Kline E., McGilligan J. A., Shapshay S., Valdez T., Badizadegan K., Crawford J. M., Fitzmaurice M., Kabani S., Levin H. S., Seiler M., Dasari R. R., Itzkan I., Van Dam J., Feld M. S., “Detection of preinvasive cancer cells,” Nature 406(6791), 35–36 (2000). 10.1038/35017638 [DOI] [PubMed] [Google Scholar]
- 5.Graf R. N., Robles F. E., Chen X., Wax A., “Detecting precancerous lesions in the hamster cheek pouch using spectroscopic white-light optical coherence tomography to assess nuclear morphology via spectral oscillations,” J. Biomed. Opt. 14(6), 064030 (2009). 10.1117/1.3269680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.M. Tanaka, M. Hirano, T. Hasegawa, and I. Sogawa, “Lipid distribution imaging in in-vitro artery model by 1.7-μm spectroscopic spectral-domain optical coherence tomography,” in Proc. SPIE 8565, Photonic Therapeutics and Diagnostics IX (2013), p. 85654F–85654F–7. [Google Scholar]
- 7.Fleming C. P., Eckert J., Halpern E. F., Gardecki J. A., Tearney G. J., “Depth resolved detection of lipid using spectroscopic optical coherence tomography,” Biomed. Opt. Express 4(8), 1269–1284 (2013). 10.1364/BOE.4.001269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xu C., Ye J., Marks D. L., Boppart S. A., “Near-infrared dyes as contrast-enhancing agents for spectroscopic optical coherence tomography,” Opt. Lett. 29(14), 1647–1649 (2004). 10.1364/OL.29.001647 [DOI] [PubMed] [Google Scholar]
- 9.Oldenburg A. L., Hansen M. N., Ralston T. S., Wei A., Boppart S. A., “Imaging gold nanorods in excised human breast carcinoma by spectroscopic optical coherence tomography,” J. Mater. Chem. 19(35), 6407–6411 (2009). 10.1039/b823389f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lee T. M., Oldenburg A. L., Sitafalwalla S., Marks D. L., Luo W., Toublan F. J.-J., Suslick K. S., Boppart S. A., “Engineered microsphere contrast agents for optical coherence tomography,” Opt. Lett. 28(17), 1546–1548 (2003). 10.1364/OL.28.001546 [DOI] [PubMed] [Google Scholar]
- 11.Sacchet D., Moreau J., Georges P., Dubois A., “Simultaneous dual-band ultra-high resolution full-field optical coherence tomography,” Opt. Express 16(24), 19434–19446 (2008). 10.1364/OE.16.019434 [DOI] [PubMed] [Google Scholar]
- 12.Spöler F., Kray S., Grychtol P., Hermes B., Bornemann J., Först M., Kurz H., “Simultaneous dual-band ultra-high resolution optical coherence tomography,” Opt. Express 15(17), 10832–10841 (2007). 10.1364/OE.15.010832 [DOI] [PubMed] [Google Scholar]
- 13.Cimalla P., Walther J., Mehner M., Cuevas M., Koch E., “Simultaneous dual-band optical coherence tomography in the spectral domain for high resolution in vivo imaging,” Opt. Express 17(22), 19486–19500 (2009). 10.1364/OE.17.019486 [DOI] [PubMed] [Google Scholar]
- 14.Storen T., Royset A., Svaasand L. O., Lindmo T., “Measurement of dye diffusion in scattering tissue phantoms using dual-wavelength low-coherence interferometry,” J. Biomed. Opt. 11(1), 014017 (2006). 10.1117/1.2159000 [DOI] [PubMed] [Google Scholar]
- 15.Xu C., Kamalabadi F., Boppart S. A., “Comparative performance analysis of time-frequency distributions for spectroscopic optical coherence tomography,” Appl. Opt. 44(10), 1813–1822 (2005). 10.1364/AO.44.001813 [DOI] [PubMed] [Google Scholar]
- 16.Graf R. N., Wax A., “Temporal coherence and time-frequency distributions in spectroscopic optical coherence tomography,” J. Opt. Soc. Am. A 24(8), 2186–2195 (2007). 10.1364/JOSAA.24.002186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kartakoullis A., Bousi E., Pitris C., “Scatterer size-based analysis of optical coherence tomography images using spectral estimation techniques,” Opt. Express 18(9), 9181–9191 (2010). 10.1364/OE.18.009181 [DOI] [PubMed] [Google Scholar]
- 18.Leitgeb R., Wojtkowski M., Kowalczyk A., Hitzenberger C. K., Sticker M., Fercher A. F., “Spectral measurement of absorption by spectroscopic frequency-domain optical coherence tomography,” Opt. Lett. 25(11), 820–822 (2000). 10.1364/OL.25.000820 [DOI] [PubMed] [Google Scholar]
- 19.Adler D. C., Ko T. H., Herz P., Fujimoto J. G., “Optical coherence tomography contrast enhancement using spectroscopic analysis with spectral autocorrelation,” Opt. Express 12(22), 5487–5501 (2004). 10.1364/OPEX.12.005487 [DOI] [PubMed] [Google Scholar]
- 20.Kasseck C., Jaedicke V., Gerhardt N. C., Welp H., Hofmann M. R., “Substance identification by depth resolved spectroscopic pattern reconstruction in frequency domain optical coherence tomography,” Opt. Commun. 283(23), 4816–4822 (2010). 10.1016/j.optcom.2010.06.073 [DOI] [Google Scholar]
- 21.Z. Hu and A. M. Rollins, “Optical Design for OCT,” in Optical Coherence Tomography - Technology and Applications (2008), pp. 379–404. [Google Scholar]
- 22.Leitgeb R. A., Drexler W., Povazay B., Hermann B., Sattmann H., Fercher A. F., “Spectroscopic Fourier domain optical coherence tomography: principle, limitations, and applications,” Proc. SPIE 5690, 151–158 (2005). 10.1117/12.592911 [DOI] [Google Scholar]
- 23.Hermann B., Hofer B., Meier C., Drexler W., “Spectroscopic measurements with dispersion encoded full range frequency domain optical coherence tomography in single- and multilayered non-scattering phantoms,” Opt. Express 17(26), 24162–24174 (2009). 10.1364/OE.17.024162 [DOI] [PubMed] [Google Scholar]
- 24.Robles F. E., Wax A., “Separating the scattering and absorption coefficients using the real and imaginary parts of the refractive index with low-coherence interferometry,” Opt. Lett. 35(17), 2843–2845 (2010). 10.1364/OL.35.002843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Xu C., Marks D. L., Do M., Boppart S., “Separation of absorption and scattering profiles in spectroscopic optical coherence tomography using a least-squares algorithm,” Opt. Express 12(20), 4790–4803 (2004). 10.1364/OPEX.12.004790 [DOI] [PubMed] [Google Scholar]
- 26.Faber D. J., van Leeuwen T. G., “Are quantitative attenuation measurements of blood by optical coherence tomography feasible?” Opt. Lett. 34(9), 1435–1437 (2009). 10.1364/OL.34.001435 [DOI] [PubMed] [Google Scholar]
- 27.Hermann B., Bizheva K., Unterhuber A., Považay B., Sattmann H., Schmetterer L., Fercher A. F., Drexler W., “Precision of extracting absorption profiles from weakly scattering media with spectroscopic time-domain optical coherence tomography,” Opt. Express 12(8), 1677–1688 (2004). 10.1364/OPEX.12.001677 [DOI] [PubMed] [Google Scholar]
- 28.Yi J., Backman V., “Imaging a full set of optical scattering properties of biological tissue by inverse spectroscopic optical coherence tomography,” Opt. Lett. 37(21), 4443–4445 (2012). 10.1364/OL.37.004443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xu C., Vinegoni C., Ralston T. S., Luo W., Tan W., Boppart S. A., “Spectroscopic spectral-domain optical coherence microscopy,” Opt. Lett. 31(8), 1079–1081 (2006). 10.1364/OL.31.001079 [DOI] [PubMed] [Google Scholar]
- 30.Jacobson N., Gupta M., “Design goals and solutions for display of hyperspectral images,” IEEE Trans. Geosci. Rem. Sens. 43(11), 2684–2692 (2005). 10.1109/TGRS.2005.857623 [DOI] [Google Scholar]
- 31.Tyo J. S., Konsolakis A., Diersen D. I., Olsen R. C., “Principal-components-based display strategy for spectral imagery,” IEEE Trans. Geosci. Rem. Sens. 41(3), 708–718 (2003). 10.1109/TGRS.2003.808879 [DOI] [Google Scholar]
- 32.Robles F. E., Wax A., “Measuring morphological features using light-scattering spectroscopy and Fourier-domain low-coherence interferometry,” Opt. Lett. 35(3), 360–362 (2010). 10.1364/OL.35.000360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yi J., Gong J., Li X., “Analyzing absorption and scattering spectra of micro-scale structures with spectroscopic optical coherence tomography,” Opt. Express 17(15), 13157–13167 (2009). 10.1364/OE.17.013157 [DOI] [PubMed] [Google Scholar]
- 34.Robles F. E., Graf R. N., Wax A., “Dual window method for processing spectroscopic optical coherence tomography signals with simultaneously high spectral and temporal resolution,” Opt. Express 17(8), 6799–6812 (2009). 10.1364/OE.17.006799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Tay B. C., Chow T. H., Ng B. K., Loh T. K., “Dual-window dual-bandwidth spectroscopic optical coherence tomography metric for qualitative scatterer size differentiation in tissues,” IEEE Trans. Biomed. Eng. 59(9), 2439–2448 (2012). 10.1109/TBME.2012.2202391 [DOI] [PubMed] [Google Scholar]
- 36.H. W. Siesler, Y. Ozaki, S. Kawata, and H. M. Heise, Near Infrared Spectroscopy (WILEY-VCH Verlag GmbH, 2005). [Google Scholar]
- 37.Digman M. A., Caiolfa V. R., Zamai M., Gratton E., “The phasor approach to fluorescence lifetime imaging analysis,” Biophys. J. 94(2), L14–L16 (2008). 10.1529/biophysj.107.120154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fereidouni F., Bader A. N., Gerritsen H. C., “Spectral phasor analysis allows rapid and reliable unmixing of fluorescence microscopy spectral images,” Opt. Express 20(12), 12729–12741 (2012). 10.1364/OE.20.012729 [DOI] [PubMed] [Google Scholar]
- 39.C. M. Bishop and N. M. Nasrabadi, Pattern Recognition and Machine Learning (Springer New York, 2006). [Google Scholar]
- 40.Sammon J., “A nonlinear mapping for data structure analysis,” IEEE Trans. Comput. C-18(5), 401–409 (1969). 10.1109/T-C.1969.222678 [DOI] [Google Scholar]
- 41.Kohonen T., “The self organizing map,” Proc. IEEE 78(9), 1464–1480 (1990). 10.1109/5.58325 [DOI] [Google Scholar]
- 42.Groß M., Seibert F., “Visualization of multidimensional image data sets using a neural network,” Vis. Comput. 10(3), 145–159 (1993). 10.1007/BF01900904 [DOI] [Google Scholar]
- 43.Kohavi R., “A study of cross-validation and bootstrap for accuracy estimation and model selection,” Int. Jt. Conf. Artifical Intell. 14, 1137–1145 (1995). [Google Scholar]
- 44.V. Jaedicke, S. Ağcaer, S. Goebel, N. C. Gerhardt, H. Welp, and M. R. Hofmann, “Spectroscopic optical coherence tomography with graphics processing unit based analysis of three dimensional data sets,” in Proc. SPIE 8592, Biomedical Applications of Light Scattering VII, Adam P. Wax; Vadim Backman, ed. (2013), 859215. [Google Scholar]
- 45.Cernohorsky P., de Bruin D. M., van Herk M., Bras J., Faber D. J., Strackee S. D., van Leeuwen T. G., “In-situ imaging of articular cartilage of the first carpometacarpal joint using co-registered optical coherence tomography and computed tomography,” J. Biomed. Opt. 17(6), 060501 (2012). 10.1117/1.JBO.17.6.060501 [DOI] [PubMed] [Google Scholar]
- 46.Li X., Martin S., Pitris C., Ghanta R., Stamper D. L., Harman M., Fujimoto J. G., Brezinski M. E., “High-resolution optical coherence tomographic imaging of osteoarthritic cartilage during open knee surgery,” Arthritis Res. Ther. 7(2), R318–R323 (2005). 10.1186/ar1491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jeffery A. K., Blunn G. W., Archer C. W., Bentley G., “Three-dimensional collagen architecture in bovine articular cartilage,” J. Bone Joint Surg. Br. 73(5), 795–801 (1991). [DOI] [PubMed] [Google Scholar]
- 48.Zhang L., Hu J., Athanasiou K. A., “The role of tissue engineering in articular cartilage repair and regeneration,” Crit. Rev. Biomed. Eng. 37(1-2), 1–57 (2009). 10.1615/CritRevBiomedEng.v37.i1-2.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kasaragod D. K., Lu Z., Jacobs J., Matcher S. J., “Experimental validation of an extended Jones matrix calculus model to study the 3D structural orientation of the collagen fibers in articular cartilage using polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 3(3), 378–387 (2012). 10.1364/BOE.3.000378 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang L., Hu J., Athanasiou K. A., “The role of Tissue Engineering in Articular Cartilage Repair and Regeneration,” Crit. Rev. Biomed. Eng. 37(1-2), 1–57 (2009). 10.1615/CritRevBiomedEng.v37.i1-2.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Xu X., Wang R., Elder J. B., “Optical clearing effect on gastric tissues immersed with biocompatible chemical agents investigated by near infrared reflectance spectroscopy,” J. Phys. D Appl. Phys. 36(14), 1707–1713 (2003). 10.1088/0022-3727/36/14/309 [DOI] [Google Scholar]
- 52.Hoffmann M., Lange M., Meuche F., Reuter T., Plettenberg H., Spahn G., Ponomarev I., “Comparison of Optical and Biomechanical Properties of Native and Artificial Equine Joint Cartilage under Load using NIR Spectroscopy,” Biomed. Tech. (Berl.) 57, 1059–1061 (2012).22945094 [Google Scholar]
- 53.Wax A., Yang C., Izatt J. A., “Fourier-domain low-coherence interferometry for light-scattering spectroscopy,” Opt. Lett. 28(14), 1230–1232 (2003). 10.1364/OL.28.001230 [DOI] [PubMed] [Google Scholar]
- 54.R. O. Duda, P. E. Hart, and D. G. Stork, Pattern Classification (John Wiley & Sons, 2012). [Google Scholar]
- 55.Robles F. E., Wilson J. W., Fischer M. C., Warren W. S., “Phasor analysis for nonlinear pump-probe microscopy,” Opt. Express 20(15), 17082–17092 (2012). 10.1364/OE.20.017082 [DOI] [Google Scholar]
- 56.T. Jee, H. Lee, and Y. Lee,G. Tummarello, P. Bouquet, and O. Signore, eds., “Shrinking Number of Clusters by Multi-Dimensional Scaling.,” in SWAP 2006 - Semantic Web Applications and Perspectives, Proceedings of the 3rd Italian Semantic Web Workshop, G. Tummarello, P. Bouquet, and O. Signore, eds. (CEUR-WS.org, 2006). [Google Scholar]
- 57.Cortes C., Vapnik V., “Support-vector networks,” Mach. Learn. 20(3), 273–297 (1995). 10.1007/BF00994018 [DOI] [Google Scholar]



