Strategic Treatment Interruptions During Imatinib Treatment of Chronic Myelogenous Leukemia

Abstract

Although imatinib is an effective treatment for chronic myelogenous leukemia (CML), and nearly all patients treated with imatinib attain some form of remission, imatinib does not completely eliminate leukemia. Moreover, if the imatinib treatment is stopped, most patients eventually relapse (Cortes et al. in Clin. Cancer Res. 11:3425–3432, 2005). In Kim et al. (PLoS Comput. Biol. 4(6):e1000095, 2008), the authors presented a mathematical model for the dynamics of CML under imatinib treatment that incorporates the anti-leukemia immune response. We use the mathematical model in Kim et al. (PLoS Comput. Biol. 4(6):e1000095, 2008) to study and numerically simulate strategic treatment interruptions as a potential therapeutic strategy for CML patients. We present the results of numerous simulated treatment programs in which imatinib treatment is temporarily stopped to stimulate and leverage the anti-leukemia immune response to combat CML. The simulations presented in this paper imply that treatment programs that involve strategic treatment interruptions may prevent leukemia from relapsing and may prevent remission for significantly longer than continuous imatinib treatment. Moreover, in many cases, strategic treatment interruptions may completely eliminate leukemic cells from the body. Thus, strategic treatment interruptions may be a feasible clinical approach to enhancing the effects of imatinib treatment for CML. We study the effects of both the timing and the duration of the treatment interruption on the results of the treatment. We also present a sensitivity analysis of the results to the parameters in the mathematical model.

1 Introduction

Chronic myelogenous leukemia (CML) results from the uncontrolled growth of white blood cells due to increased and unregulated growth of predominantly myeloid cells in the bone marrow and the accumulation of these cells in the blood (Sawyers 2000). The standard treatment for CML is the tyrosine kinase inhibitor imatinib mesylate (marketed as Gleevec or Glivec) (Angstreich et al. 2004). Although imatinib is an effective treatment for CML and most patients attain some form of remission, imatinib does not completely eliminate all leukemia cells, and if the imatinib treatment is stopped, most patients eventually relapse (Cortes et al. 2005; Michor et al. 2005) (though we do note that in some recent clinical findings, e.g., (Rousselot et al. 2007; Mahon et al. 2009), several patients have demonstrated relapse-free survival after imatinib discontinuation). There are three standard types of remission: hematologic, cytogenetic, and molecular. Each layer corresponds to a 2-log, or 100-fold, difference from the previous layer. According to (Lowenberg 2003), each patient typically has approximately 10¹² leukemia cells prior to imatinib treatment. Hence, hematologic remission corresponds to 10¹⁰ cells, cytogenetic remission corresponds to 10⁸ cells, and molecular remission corresponds to 10⁶ cells. Assuming that the average person has approximately 6 liters of blood, these remission levels correspond to the concentration levels given in Table 1. With imatinib treatment, nearly all patients achieve hematologic remission (Lee 2000), and approximately 75% of patients achieve cytogenetic remission (Cortes et al. 2005).

Table 1.

Leukemia cell concentrations (in k/μL) corresponding to hematologic, cytogenetic, and molecular remission levels

Remission level	Hematologic	Cytogenetic	Molecular
Concentration (k/μL)	1.67	1.67 × 10−2	1.67 × 10−4

Several recent mathematical models have been developed to study the dynamics of CML under imatinib treatment, including (Komarova and Wodarz 2005; Michor et al. 2005; Kim et al. 2008), and (Roeder et al. 2006). In all of these studies, the authors conclude that imatinib does not completely eliminate the leukemia cell population, and propose that imatinib therapy should be combined with an additional form of treatment. In (Michor et al. 2005), the authors develop a four-compartment differential equations model based on the known biology of the hematopoietic system to model the dynamics of CML with imatinib treatment. In (Kim et al. 2008), the authors incorporate the anti-leukemia immune response in CML patients on imatinib therapy to the model proposed in (Michor et al. 2005) by adding interactions with anti-leukemia T-cells. The authors of (Kim et al. 2008) formulate their mathematical model as a system of delay-differential equations (DDEs), and demonstrate that the immune response may play a critical role in determining the length of time that CML patients on imatinib treatment remain in remission.

In this paper, we present a strategic treatment interruption treatment strategy for CML based on the delay differential equation model proposed in (Kim et al. 2008). We use the model in (Kim et al. 2008) to numerically determine an optimal time period during which imatinib treatment should be temporarily stopped in order to leverage the anti-leukemia immune response. Although the leukemia load initially suppresses the T-cell immune response, a small number of T-cells remain and can eventually be leveraged to potentially eradicate leukemia. We demonstrate that such a strategic treatment interruption significantly improves the efficacy of imatinib treatment for CML patients. In particular, the results of our simulations suggest that, in many cases, leukemia can be completely eliminated with a strategic treatment interruption timed during the patient’s own anti-leukemia immune response. In (Kim et al. 2008), the authors consider total leukemia elimination to be complete if the total cancer population in the body is below 1 cell, i.e.,

$$\text{Total}\text{cancer}\text{concentration}<{10}^{-10}k/\mathrm{\mu }\mathrm{L},$$

assuming that the average patient has about 6 L of blood. Since the mathematical model presented in (Kim et al. 2008) is a continuous deterministic system, in reality, the model never allows the total cancer population to actually reach 0. Since a total cancer concentration of 10⁻¹⁰k/μL corresponds to less than one cancer cell in the blood, this is a reasonable indicator for total cancer elimination.

This paper is organized in the following way. In Sect. 2, we provide an overview of the delay-differential equation model for the dynamics of CML, imatinib, and the anti-leukemia immune response presented in (Kim et al. 2008). In Sect. 3, we propose several strategic treatment interruption treatment programs for CML patients based on the anti-leukemia immune response described in (Kim et al. 2008), and we present and analyze the results of these simulated treatment plans. In particular, we study the effects of changing the timing and duration of the treatment interruption on the time required for the patient to achieve cytogenetic remission and (in many cases) the time required for total cancer elimination. In Sect. 4, we study the sensitivity of the results to the universal and patient-specific parameters used in the mathematical model. We discuss conclusions, drawbacks of the mathematical model used for our numerical analysis, and areas for further research in Sect. 5. In Appendix A, we derive an explicit, closed-form solution for the mathematical model for CML presented in (Michor et al. 2005).

2 A Mathematical Model for CML with Imatinib Treatment

Michor et al. (2005), used data from 169 patients to develop and analyze a mathematical model for CML. In this model, leukemia cells are assumed to develop through four stages of differentiation. The different cell populations at time t are denoted as follows: y₀(t), leukemia stem cells; y₁(t), progenitor cells; y₂(t), differentiated cells; and y₃(t), terminally differentiated cells. Leukemia cells progress through the various stages in the following way. Stem cells regenerate themselves at rate r_y. Stem cells expand and progress to become progenitor cells at rate a_y and die at rate r₀. Progenitor cells become differentiated cells at rate b_y and die at rate d₁. Differentiated cells expand and progress to become terminal cells at rate c_y and die at rate d₂. Terminal cells die at rate d₃. With imatinib treatment, the rate at which leukemia cells pass from one stage to the next is greatly reduced, thus causing a rapid drop in the leukemia population. In particular, according to this model, imatinib treatment reduces the parameters a_y and b_y by 100-fold and 750-fold, respectively. For the initial conditions, it is assumed that all four leukemia compartments are in steady state relative to one another.

In addition, Michor et al. included a second set of leukemia cells to incorporate the possibility of imatinib-resistant mutations. It was assumed that the only cells that can acquire imatinib-resistant mutations are stem cells, and they mutate at a rate u per division. In this paper, we will assume that there are no imatinib-resistant mutations (i.e., u = 0), so we do not include the second set of differential equations here. However, we describe them in Appendix A. The system of ODEs that describes the model for the leukemia cell populations is given below. Although Michor et al. did not derive an explicit solution for this system of differential equations in their original work, the system can be solved exactly using diagonalization and we present the solution in Appendix A:

$$\begin{array}{l}\frac{{dy}_0}{dt}\left(r_y(1-u)-d_0\right)y_0,\\ \frac{{dy}_1}{dt}=a_y{y}_0-d_1{y}_1,\\ \frac{{dy}_2}{dt}=b_y{y}_1-d_2{y}_2,\\ \frac{{dy}_3}{dt}=c_y{y}_2-d_3{y}_3.\end{array}$$

In (Kim et al. 2008), the authors modified this model to incorporate an anti-leukemia immune T-cell response into the ODE model. The motivation for their model is based on experimental data taken from (Chen et al. 2008), in which the authors conducted TNF-α and IFN-γ ELISPOT analyses at multiple time points to measure the evolution of the anti-leukemia T-cell responses of CML patients undergoing imatinib treatment. To incorporate the dynamics of the imatinib-induced T-cell immune response in the system of equations governing the CML dynamics, the authors of (Kim et al. 2008) added interactions with T-cells and a delay-differential equation to model the T-cell population. In the modified system, each equation contains an added term which accounts for the death of leukemia cells as a result of an interaction with T-cells. In addition, a delay-differential equation is included for the population T of anti-leukemia T-cells. The leukemia cell death rates d_i, 0 ≤ i ≤ 3, in (Michor et al. 2005) correspond to the natural death rates of the leukemia populations under imatinib treatment. In the DDE model of (Kim et al. 2008), the authors distinguish between the natural death rate of leukemia and the death rate due to the cytotoxic T-cell response. Thus, the death rates d_i in the DDE model are a fraction, λ, of the combined death rates estimated in (Michor et al. 2005). The parameter λ represents the fraction of the leukemia cell deaths that results from nonimmune (versus immune) causes. It is assumed that λ is greater than 0.5, so that the anti-leukemia immune response contributes to less than half of the decline in leukemia under imatinib treatment (Kim et al. 2008). In (Kim et al. 2008), the authors set λ = 0.75; we include a discussion of the sensitivity of our results on the choice of λ. Following (Kim et al. 2008), we assume that u = 0 and that there are no imatinib-resistant leukemia cells. In Sect. 5, we discuss the possibility of acquired imatinib resistance. The mathematical model which includes the immune response is given by the following:

$$\begin{array}{l}\frac{{dy}_0}{dt}=(r_y-d_0)y_0-q_{C}p(C,T)y_0,\\ \frac{{dy}_1}{dt}=a_y{y}_0-d_1{y}_1-q_{C}p(C,T)y_1,\\ \frac{{dy}_2}{dt}=b_y{y}_1-d_2{y}_2-q_{C}p(C,T)y_2,\\ \frac{{dy}_3}{dt}=c_y{y}_2-d_3{y}_3-q_{C}p(C,T)y_3,\end{array}$$ (1)

$$\frac{dT}{dt}=s_T-d_{T}T-p(C,T)C+2^{n}p(C_{n\tau },T_{n\tau })q_T{C}_{n\tau },$$ (2)

where

$$\begin{array}{c}p(C,T)=p_0{e}^{-c_{n}C}kT,C=\sum _{i=0}^3{y}_i,\\ C_{n\tau }=C(t-n\tau ),T_{n\tau }=T(t-n\tau ).\end{array}$$

The variables in this model are the same as those in the model of Michor et al. (2005), with the exception of the new variables C and T. The variable C represents the total concentration of all leukemia cells. The variable T represents the concentration of anti-leukemia T cells. The final terms q_C p₀e^−c_nCkTy_i follow the law of mass action. The kTy_i is the rate of interaction between anti-leukemia T-cells and the leukemia cell subpopulation y_i, where k is the mixing coefficient. The coefficient p₀ is the probability that a T-cell engages the cancer cell upon interaction, and q_C is the probability that the cancer cell dies from the T-cell response. Moreover, leukemia cells suppress the anti-leukemia T-cell immune response, and although the precise mechanism is unknown, this model assumes that the level of down-regulation depends on the current cancer population. The probability that a T-cell engages a cancer cell is modeled as an exponential decay as a function of the cancer concentration. Thus, the probability of a productive T-cell interaction with a cancer cell is p₀e^−c_nC, where c_n is the rate of exponential decay due to negative pressure. We note that the authors of Kim et al. (2008) model T-cell dynamics in particular because T-cells are the main mediators of the anti-leukemia response, as has been demonstrated by the major role that cytotoxic T-cells play in curing leukemia after an allogenic stem cell transplant. By extension, they are hypothesizing that autologous T-cells will also be the key players in the anti-leukemia immune response.

In the delay-differential equation (2) for modeling the anti-leukemia T-cell response, the parameter s_T denotes the constant supply rate of T-cells into the system from stem cells. The parameter d_T represents the natural death rate of T-cells, and p(C, T)C is the rate at which T-cells engage leukemia cells and commit to n rounds of division. The final term represents the population increase due to n divisions of stimulated T-cells, where τ is the average duration of one division, and C_nτ and T_nτ are the time delayed cancer and T-cell concentrations, respectively. The coefficient q_T is the probability that a T-cell survives the encounter with an activated leukemia cell. Once a T-cell is stimulated, it exits the collection of interacting T-cells and re-enters the system nτ time units later after n divisions.

The estimated universal and patient-dependent parameter values for this system are given in Table 2 (and are taken from (Michor et al. 2005) and (Kim et al. 2008)). The parameters n, s_T, d_T, and c_n are patient-dependent parameters, and in (Kim et al. 2008) the authors use experimental data for CML patients on imatinib treatment published by Chen et al. (2008) to estimate values for these parameters for particular patients. It is our goal here to demonstrate numerically that strategically timed treatment interruptions may lead to total eradication of cancerous cells, and we wish to study here the activation of T-cells as a general feature, rather than to focus on particular patient-dependent data sets. Thus, we will present detailed numerical results here for simulations using the parameter values in Table 2, which are representative of the parameter values for all patient data in (Chen et al. 2008). To study the impact of the particular numerical values of the parameters on our results, we present an extensive sensitivity analysis in Sect. 4, and we vary the parameters to include the ranges of the parameter values for all patients analyzed in (Chen et al. 2008).

Table 2.

Estimates of parameters (Kim et al. 2008; Michor et al. 2005)

Parameter	Description	Estimate
λ	Fractional adjustment constant	0.75
d0	Stem cell death rate	0.003 λ/day
d1	Progenitor cell death rate	0.008 λ
d2	Differentiated cell death rate	0.05 λ
d3	Terminal cell death rate	λ
ry	Stem cell regeneration rate	0.008/day
ay	Stem cell growth rate	1.6 (without imatinib treatment) 1.6/100 (with imatinib treatment)
by	Progenitor cell growth rate	10 (without imatinib treatment) 10/750 (with imatinib treatment)
cy	Differentiated cell growth rate	100
rz	Imatinib resistant mutation stem cell regeneration rate	0.023/day
az	Imatinib resistant mutation stem cell growth rate	1.6
bz	Imatinib resistant mutation progenitor cell growth rate	10
cz	Imatinib resistant mutation differentiated cell growth rate	100
k	Kinetic (mixing) coefficient	1 (k/μL)−1/day
p0	Probability that T-cell engages cancer cell	0.8
qC	Probability that cancer cell dies from encounter with T-cell	0.75
qT	Probability that T-cell survives encounter with cancer cell	0.5
τ	Duration of one T-cell division	1 day
n	Average number of T-cell divisions	1.2
dT	Anti-leukemia T-cell death rate	0.001/day
sT	Anti-leukemia T-cell supply rate	1.2 × 10−6 (k/μL)/day
cn	Decay rate of immune responsivity	1 (k/μL)−1
y0(0)	Initial leukemia stem cell concentration	1.8 × 10−5k/μL

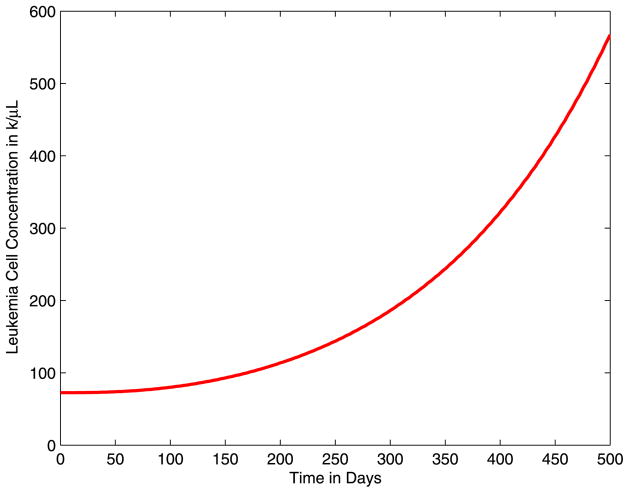
In Fig. 1, we illustrate the results of simulating the delay-differential equations model presented in (Kim et al. 2008) without imatinib treatment, i.e., a_y = 1.6 and b_y = 10. We plot the total leukemia cell concentrations ${\sum }_{i=0}^3{y}_i$ for 0 ≤ t ≤ 500 days. We observe that without imatinib treatment, the cancer population grows rapidly. Moreover, we note that without treatment, the immune response is fully suppressed and the T-cell concentration remains at the initial steady state s_T/d_T.

Fig. 1.

Total leukemia concentration without imatinib treatment for 0 ≤ t ≤ 500 days

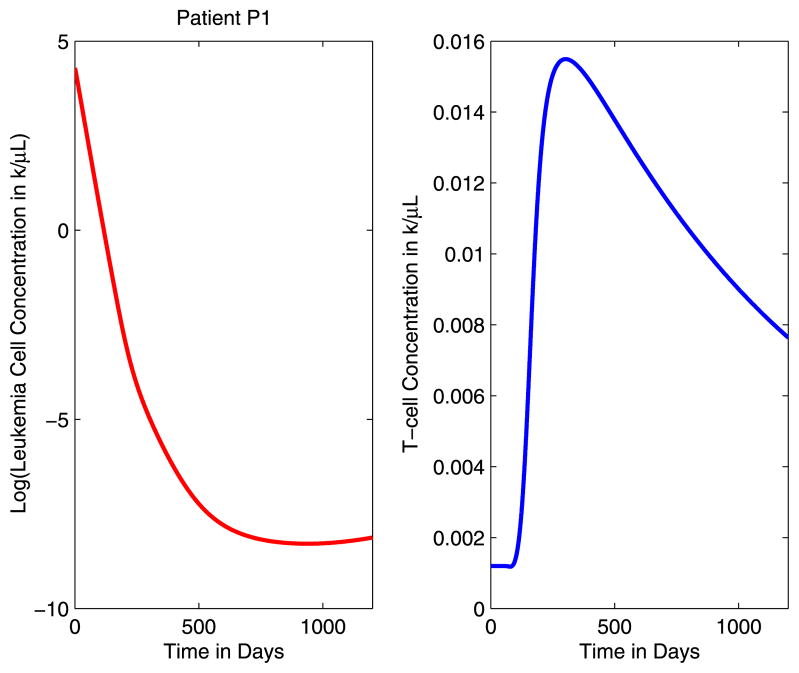
Next, in Fig. 2, we illustrate the results of simulating the delay-differential equations model of Kim et al. (2008) with continuous imatinib treatment, i.e., a_y = 1.6/10 and b_y = 10/750. We plot the base-10 logarithm of the total leukemia cell concentrations ${\sum }_{i=0}^3{y}_i$ and the T-cell concentrations T(t) for 0 ≤ t ≤ 1200 days. In (Kim et al. 2008), it has been demonstrated that this model that includes the anti-leukemia T-cell response provides a closer fit to the immunological data than the Michor model (Michor et al. 2005) that does not include the immune response. In particular, we note that the 2005 model of Michor et al. (2005) predicts that leukemia relapses after 15 to 24 months, despite continued imatinib treatment. However, this contradicts clinical observations in imatinib-treated patients, who generally remain in remission well beyond 30–40 months, as described in Piazza et al. (2006). With the addition of the T-cell response in the model of Kim et al. (2008), persistence of anti-leukemia T-cells even at low levels prevents leukemia from relapsing for up to 50 months.

Fig. 2.

The logarithm of the leukemia concentration and the T-cell concentration with continuous imatinib treatment

The graphs in Fig. 2 illustrate several important points about the dynamics of CML under imatinib treatment and the imatinib-induced immune response as described by the DDE model of Kim et al. (2008). As soon as imatinib treatment begins, there is a sharp decline in the leukemia cell concentrations. Although imatinib drives the cancer population to low levels, it does not completely eliminate the leukemia stem cells, and the result is a situation in which leukemia is never completely eliminated. In particular, we note that the minimum total cancer concentration predicted by the model before cytogenetic relapse is 1.1 × 10⁻⁴ k/μL. Assuming that an average person has approximately 6 liters of blood, this concentration level corresponds to a total leukemia cell population of half a million to a million cells. We also observe that the model predicts that with continuous imatinib treatment, the patient will eventually relapse. These observations demonstrate an important point, namely that the model does not predict that CML is eliminated by imatinib treatment alone. However, the model does predict that it takes significantly more time for the disease to relapse when compared with the Michor model that does not include the immune response.

In addition, we observe fluctuations in the anti-leukemia T-cell concentrations that correspond to changes in the leukemia cell concentrations. Initially, the T-cell concentrations remain low, close to the steady-state level, as the immune response is fully suppressed by leukemia. As the leukemia cell concentrations decrease, the patient’s immune response is eventually stimulated and the T-cell concentrations increase accordingly. When the leukemia cell populations become sufficiently low, the T-cells are no longer stimulated and begin to contract. As a result, the immune response does not expand sufficiently to eliminate the leukemia cells. It is clear from these observations that there is a critical time period during which the anti-leukemia immune response is activated. If the leukemia cell concentration is too high, the immune response is fully suppressed. On the other hand, if the leukemia cell concentration is too low, the immune response will not be sufficiently stimulated. For reference, we note that the T-cell population begins increasing at t = 90 days, and the maximum T-cell concentration is 3.09 × 10⁻²k/μL at t = 206 days.

3 Strategic Treatment Interruptions

Strategic treatment interruptions (STIs), also known as “structured treatment interruptions” or “supervised treatment interruptions” are planned interruptions of drug treatment designed to reduce and/or relieve the side effects of the drugs, to reduce drug resistance, and/or to stimulate the immune response. In this section, we study several treatment interruption plans for imatinib treatment of CML based on the mathematical model for CML discussed in Sect. 2. In particular, we attempt to improve the effectiveness of treatment by strategically interrupting imatinib treatment in order to leverage the patient’s own anti-leukemia immune response.

Strategic treatment interruptions have been studied extensively for patients with chronic HIV infection being treated with highly active antiretroviral therapy (HAART) (Adams et al. 2004; Bajaria et al. 2004; Koup 2004; Maserati et al. 2007). In this context, strategic treatment interruptions were motivated primarily by the development of drug resistance, evolution of viral strains, detrimental short- and long-term side effects, and patient complications (Bajaria et al. 2004). Numerous studies have been conducted to explore the benefits of strategic treatment interruptions for HIV treatment, but the results vary widely and are highly dependent on treatment schedules, starting times, and patient-specific factors.

In this work, however, we are primarily interested in the use of strategic treatment interruptions as a technique for leveraging the patient’s own anti-leukemia immune response to combat CML. In this first study, we perform several simulations in which we temporarily stop imatinib treatment once. We vary the length of the interruption and the starting time of the interruption, and measure the time required for the patient to achieve cytogenetic remission and the time required for total cancer elimination (if total elimination occurs). We assume that when imatinib is stopped, the stem cell and progenitor cell growth rates (a_y and b_y, respectively) immediately return to their values without imatinib treatment (1.6 and 10, respectively). Similarly, we assume that when imatinib is restarted, a_y returns to 1.6/100 and b_y returns to 10/750 immediately.

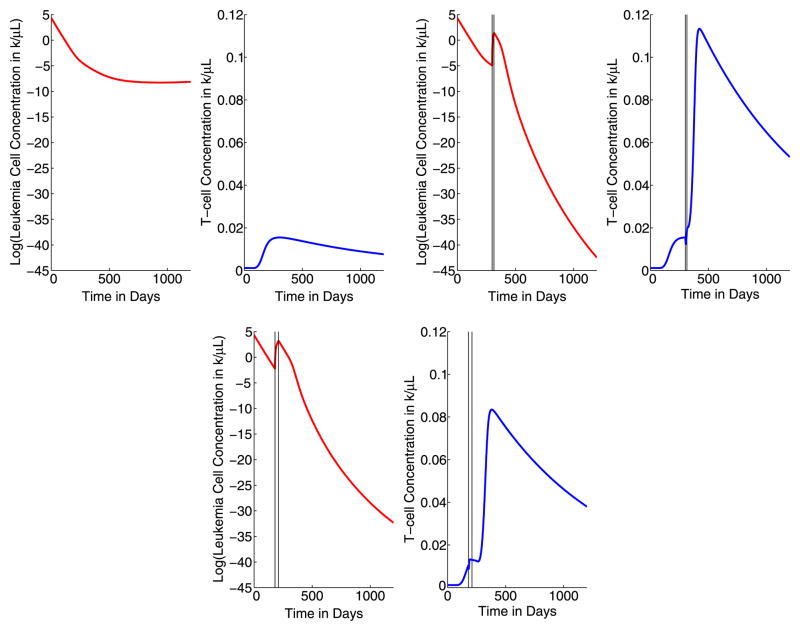
In Tables 3 and 4, we present the results of several 15-day and 30-day strategic treatment interruption simulations. In each of these studies, we simulate a single treatment interruption in an attempt to leverage the first immune response increase. Imatinib treatment is temporarily stopped on a specified day for either 15 or 30 days. In Fig. 3, we plot the base-10 logarithm of the total leukemia cell concentration and the T-cell concentrations for 0 ≤ t ≤ 1200 days with continuous imatinib treatment (upper left), with a 15-day strategic treatment interruption from t = 300 days until t = 315 days (upper right), and with a 30-day strategic treatment interruption from t = 180 days until t = 210 days (lower). In each graph, the timing of the treatment interruption is marked with vertical lines. These graphs demonstrate the general dynamics of the leukemia and T-cell concentrations for all the simulations described in Tables 3 and 4, so we include only these illustrative cases here. For ease of comparison amongst the scenarios, the axis scales (minimum and maximum values) are the same for each of the three treatment strategies presented in Fig. 3. With the start of imatinib treatment at time t = 0, the leukemia cell concentration begins decreasing rapidly, and at approximately 90 days, the leukemia cell concentration is small enough that the immune response is no longer significant and the T-cell concentration begins increasing. As a result of the strategic treatment interruption, there is a small, fast rise in the concentration of leukemia cells while the imatinib treatment is stopped. However, this increase does not reach the initial level of leukemia cells present in the patient. Eventually, after imatinib treatment is restarted, the leukemia cell concentration falls below the level of cytogenetic remission. For the second case (treatment interruption for 300 ≤ t ≤ 315 days) illustrated in Fig. 3, the leukemia concentration first falls below the level of cytogenetic remission 408 days after the start of treatment, and after 627 days, cancer has been completely eliminated.

Table 3.

Results of several 15-day strategic treatment interruption (abbreviated as STI above) plans. For each simulation, we report the first day of the 15-day treatment interruption, the maximum leukemia concentration that occurs after the interruption, the time required for the patient to achieve cytogenetic remission, and the time required for total cancer elimination (i.e., concentration < 10⁻¹⁰k/μL)

Treatment plan: First day of 15-day STI	Maximum leukemia concentration (k/μL) after interruption	Time until cytogenetic remission (days)	Time until total cancer elimination (days)
No STI	n/a	251	n/a
90	20.6 at t = 106	312	n/a
120	17.25 at t = 136	313	n/a
150	14.58 at t = 166	316	879
180	11.71 at t = 196	329	665
210	8.96 at t = 226	346	616
240	6.75 at t = 256	365	606
270	5.14 at t = 286	386	611
300	4.01 at t = 316	408	627
330	3.21 at t = 346	433	655
360	2.64 at t = 376	459	693
390	2.23 at t = 406	487	739

Table 4.

Results of several 30-day strategic treatment interruption (abbreviated as STI above) plans. For each simulation, we report the first day of the 30-day strategic treatment interruption, the maximum leukemia concentration that occurs after the interruption, the time required for the patient to achieve cytogenetic remission, and the time required for total cancer elimination (i.e., concentration < 10⁻¹⁰k/μL)

Treatment plan: First day of 30-day STI	Maximum leukemia concentration (k/μL) after interruption	Time until cytogenetic remission (days)	Time until total cancer elimination (days)
No STI	n/a	251	n/a
90	34.6 at t = 121	342	n/a
120	31.35 at t = 151	345	n/a
150	28.30 at t = 181	350	929
180	24.33 at t = 211	364	711
210	19.92 at t = 241	382	662
240	16.07 at t = 271	404	654
270	13.06 at t = 301	426	656
300	10.77 at t = 331	449	666
330	9.05 at t = 361	473	681
360	7.75 at t = 391	498	699
390	6.75 at t = 421	524	722

Fig. 3.

Logarithm of the leukemia concentrations and the T-cell concentrations for 0 ≤ t ≤ 1200 days with continuous imatinib treatment (upper left), with a 15-day treatment interruption (STI) from t = 300 to t = 315 days (upper right), and with a 30-day treatment interruption from t = 180 to t = 210 (lower). The treatment interruption is indicated with vertical lines

In each table, we present the first day of the treatment interruption, the maximum leukemia cell concentration that occurs after the treatment interruption occurs, the time required for the patient to achieve cytogenetic remission, and the time required for total cancer elimination (i.e., total concentration <10⁻¹⁰k/μL). In almost all cases, the strategic treatment interruption strategies that we consider result in total cancer elimination within the first 3 years of treatment. For reference, we note that the minimum total cancer concentration predicted by the mathematical model with a 15-day treatment interruption beginning at t = 300 is 1.52 × 10⁻²⁶k/μL, which corresponds to a total cancer cell count of 9.12 × 10⁻¹⁷ cells (assuming 6 L of blood). This minimum concentration is significantly lower than (several orders of magnitude) the cancer elimination criterion of 10⁻¹⁰k/μL.

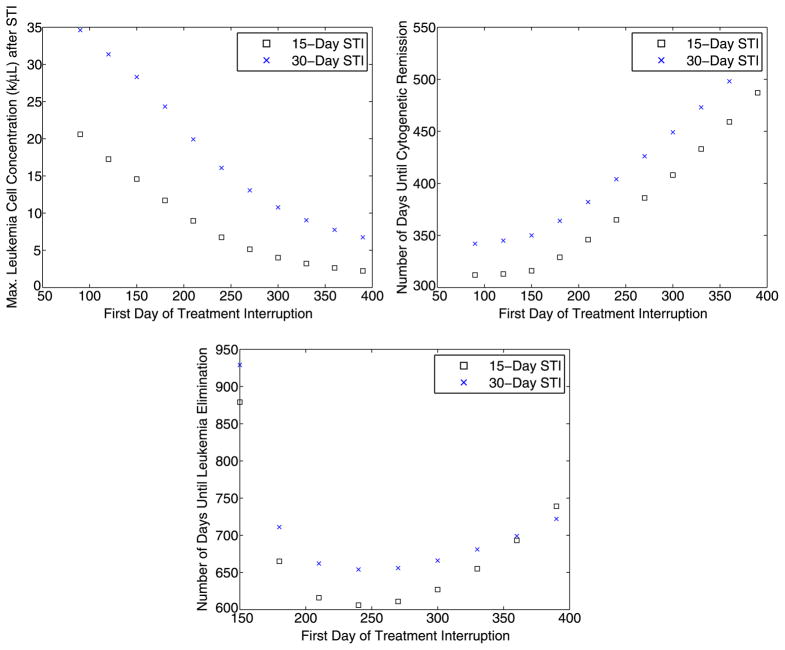
We summarize the results presented in Tables 3 and 4 with a series of graphs. In Fig. 4, we plot the maximum leukemia concentration (k/μL) that occurs after the interruption vs. starting day of the treatment interruption (upper left); the time (in days) until cytogenetic remission vs. starting day of the treatment interruption (upper right); and the time (in days) until complete leukemia elimination vs. starting day of the treatment interruption (lower).

Fig. 4.

Summary of the results of several 15-day and 30-day strategic treatment interruptions. Upper left: The maximum leukemia concentration (k/μL) that occurs after the interruption vs. starting day of the treatment interruption. Upper right: Time (in days) until cytogenetic remission vs. starting day of the treatment interruption. Lower: Time (in days) until complete leukemia elimination vs. starting day of the treatment interruption

In Sect. 4, we perform several hundred simulations in which we vary the parameters in Tables 2 over a wide range that includes the biologically relevant values determined by the data presented in (Chen et al. 2008).

The results presented in Tables 3 and 4 demonstrate that there is a tradeoff between the starting time of the treatment interruption, the maximum cancer concentration observed after the interruption, and the time required for the patient to achieve cytogenetic remission and total cancer elimination. As the starting time of the interruption increases, the maximum cancer concentration observed due to the spike after imatinib is stopped decreases, and the time required until cytogenetic remission and total cancer elimination increases. Thus, before clinical implementation of strategic treatment interruptions for CML patients, these issues should be studied in more detail, and the individual treatment goals of each patient should be taken into consideration when devising a treatment plan.

4 Sensitivity Analysis

In this section, we conduct a sensitivity analysis of the model parameters with respect to the effectiveness of the strategic treatment interruption strategies. We apply the Latin Hypercube sampling (LHS) method described in (McKay et al. 1979). The LHS technique provides a method for simultaneously sampling a wide range of parameters and statistically determining the correlation between the values of the parameters and various outcomes. We simulate the delay-differential equation model with various strategic treatment interruptions several thousand times with randomly sampled sets of parameters; using LHS, the values of the parameters are chosen in such a way that each parameter is well distributed over its range of possible values. In particular, the parameters are sampled uniformly over the ranges given in Table 5. We vary every parameter and initial condition used in the model.

Table 5.

Sensitivity analysis of the parameters used in the DDE model for a 15-day strategic treatment interruption from t = 300 to t = 315. For each parameter, we report the estimate of the parameter, the range used for Latin Hypercube sampling, and the Pearson product-moment correlation (PPMC) and Spearman rank-order correlation (SROC) coefficients between the parameter and the minimum cancer concentration. To obtain the correlation coefficients, we performed 1000 simulations in which every parameter was varied over the given range

Parameter	Estimate	Range	PPMC	SROC
λ	0.75	0.5 to 1	−0.1438	−0.0866
d0	0.003 λ/day	±25%	−0.0217	0.0158
d1	0.008 λ	±25%	−0.0135	0.0625
d2	0.05 λ	±25%	−0.1238	0.0566
d3	λ	±25%	0.0364	0.0718
ry	0.008/day	±25%	0.0342	0.0195
ay	1.6 without imatinib 1.6/100 with imatinib	±25%	0.0224	−0.0235
by	10 without imatinib 10/750 with imatinib	±25%	0.0218	0.0077
cy	100	±25%	0.0668	−0.0708
rz	0.023/day	±25%	−0.0319	−0.0323
az	1.6	Same as ay	0.0224	−0.0235
bz	10	Same as by	0.0218	0.0077
cz	100	Same as cy	0.0668	−0.0708
u	0/division	4 × 10−8 – 8 × 10−8	−0.0854	−0.0889
k	1 (k/μL)−1/day	±25%	−0.0871	−0.1246
p0	0.8	±25%	−0.0981	−0.1298
qC	0.75	±25%	−0.0307	−0.0526
qT	0.5	±25%	−0.1174	−0.2229
τ	1 day	12–24 hours	0.0732	0.1217
n	1.17 to 2.2	1 to 3	−0.2534	−0.4543
dT	1 – 7 × 10−3/day	1 × 10−3 to 1 × 10−2	0.1444	0.0372
sT	1 × 10−5 to 1 × 10−6 k/μL/day	1 × 10−5 to 1 × 10−6	−0.0499	−0.0852
cn	0.8 to 7/day	0 to 10	0.1637	0.3921
C(0)	23.1–116.8 k/μL	20 to 200	0.0947	0.0414

We provide in Table 5 the Pearson product-moment correlation (PPMC) and Spearman rank-order correlation (SROC) coefficients between each parameter and the minimum cancer concentration attained during the course of treatment before the model predicts a relapse above the level of cytogenetic remission. To obtain the correlation coefficients in Table 5, we performed 1000 LHS simulations with a strategic treatment interruption from t = 300 to t = 315 days after the start of treatment, but we note that the correlation coefficients obtained with all other strategic treatment interruption strategies considered in Sect. 3 are comparable. We also note that the relationship between the parameter values and the minimum cancer concentration is monotonic.

As indicated in Table 5, the most sensitive parameters are n (the average number of T-cell divisions per stimulation), q_T (the probability that a T-cell survives an encounter with a leukemia cell), and c_n (the rate of exponential decay in the probability of a productive T-cell interaction with a cancer cell, or the level of immune down-regulation). Since we are specifically timing the interruption to leverage the patient’s own immune response, it makes sense that the parameters that are most sensitive to the effectiveness of treatment are those that are directly related to T-cell activity. We note that as a potential clinical application for treatment of CML, these parameters should be measured before and during treatment so that the strategic treatment interruption plan can be constructed to optimize the anti-leukemia immune response. In addition, in Table 6 we present the results of several thousand strategic treatment interruption simulations using the parameter ranges described in Table 5. In particular, for each strategic treatment interruption, we perform 500 simulations in which every parameter is randomly varied over the ranges given in Table 5. In Table 6, we report the fraction of these simulations that result in a successful treatment. Here, a successful treatment is a simulation in which the total cancer population falls below the total elimination criterion.

Table 6.

Results of LHS sensitivity analysis of the parameters in Table 5. For each strategic treatment interruption (abbreviated as STI above) plan, 500 simulations are performed in which every parameter is randomly varied over the ranges given in Table 5. We report the fraction of LHS samples that result in a successful treatment. A success is defined as a simulation in which the total cancer population falls below 10⁻¹⁰k/μL

Treatment plan: STI days	Fraction of successful treatments	Treatment plan: plan: STI days	Fraction of successful treatments
90 ≤ t ≤ 105	0.488	120 ≤ t ≤ 135	0.544
150 ≤ t ≤ 165	0.568	180 ≤ t ≤ 195	0.450
210 ≤ t ≤ 225	0.544	240 ≤ t ≤ 255	0.546
270 ≤ t ≤ 285	0.468	300 ≤ t ≤ 315	0.650
330 ≤ t ≤ 345	0.512	360 ≤ t ≤ 375	0.486
390 ≤ t ≤ 405	0.474	90 ≤ t ≤ 120	0.434
120 ≤ t ≤ 150	0.458	150 ≤ t ≤ 180	0.480
180 ≤ t ≤ 210	0.516	210 ≤ t ≤ 240	0.542
240 ≤ t ≤ 270	0.566	270 ≤ t ≤ 300	0.588
300 ≤ t ≤ 330	0.624	330 ≤ t ≤ 360	0.578
360 ≤ t ≤ 390	0.550	390 ≤ t ≤ 420	0.542
90 ≤ t ≤ 135	0.450	150 ≤ t ≤ 195	0.524
210 ≤ t ≤ 255	0.578	270 ≤ t ≤ 315	0.624
330 ≤ t ≤ 375	0.528	390 ≤ t ≤ 435	0.536
450 ≤ t ≤ 495	0.530	510 ≤ t ≤ 555	0.544
570 ≤ t ≤ 615	0.528	630 ≤ t ≤ 675	0.526
690 ≤ t ≤ 735	0.518	750 ≤ t ≤ 795	0.494

5 Discussion and Concluding Remarks

In this paper, we have presented the results of numerous strategic treatment interruption simulations for CML patients being treated with imatinib. This study used the mathematical model presented in (Kim et al. 2008), which models the dynamics between CML, imatinib, and the patient’s own immune response, to simulate strategic treatment interruption programs designed to leverage the anti-leukemia immune response. Mathematical modeling is an important tool for investigating the dynamics of this complex system, and it provides the ability to simulate and investigate treatment interruption therapy techniques as a possible treatment for CML patients. We have demonstrated numerically that strategically-timed imatinib treatment interruptions could lead to a potential cure for CML, and that the effectiveness of the treatment depends on the starting time of the treatment interruption and the length of time that imatinib treatment is stopped.

In this first study, we have used numerical results (such as the time required for total cancer elimination) to make general observations about the effectiveness of different start times and durations for various treatment interruption programs. In the future, we plan to study this optimization problem in more detail; we also plan to consider treatment interruption programs in which treatment is stopped more than once. In (Kim et al. 2008), the authors presented a vaccination strategy as a possible immunotherapy treatment for CML, and in a future work, we plan to study combinations of strategic treatment interruptions and vaccinations as a possible treatment for CML.

There are two major drawbacks to the delay differential equations model of Kim et al. (2008) that we have used to perform numerical simulations of strategic treatment interruption plans. First, the model does not consider competition among hemapoetic stem cells. In (Dingli and Michor 2006), Dingli and Michor presented a mathematical model for cancer stem cell development that assumes that normal stem cells and tumor stem cells compete for a common resource. Similarly, in (Roeder and Glauche 2008), Roeder and Glauche presented a mathematical model which assumes a stochastic competition between normal stem cells and tumor stem cells. Although there is not sufficient quantitative data on the growth dynamics of stem cells in patients before diagnosis to validate one of these models over another, the models that consider competition among hemapoetic stem cells are consistent with current clinical data (Roeder and Glauche 2008), and in a future work, we plan to numerically simulate strategic treatment interruptions using the mathematical models presented in (Dingli and Michor 2006) and (Roeder and Glauche 2008). Generally, we hypothesize that the inclusion of such a competition process would actually improve the results of strategic treatment interruptions. During imatinib treatment of CML, competition between normal and tumor cells has the effect of increasing the time that CML remains in remission. During a treatment interruption, on the other hand, CML is expected to relapse, and the leukemia cell population will quickly overpower the normal cell population during a relapse. Thus, the relatively small population of normal cells present during a relapse will provide little competition.

Second, we have not considered here the possibility of imatinib-resistant mutations. In (Komarova and Wodarz 2005), the authors presented a mathematical framework for the emergence of cancers treated with targeted drugs, and for the specific case of CML, the authors estimate that imatinib-resistant stem cells are generated maximally at a rate of 10⁻⁹–10⁻⁸ mutations per division. In future work, we plan to study in detail the effects of imatinib-resistant mutations on strategic treatment interruptions. In particular, we plan to add a set of imatinib-resistant leukemia cells to the delay differential equations model of Kim et al. (2008), and to derive new parameter values with resistant cells using the patient data presented in (Chen et al. 2008) and (Kim et al. 2008). We note that a treatment interruption may potentially impose an increased risk of mutations, as drug resistant mutations may be more likely to emerge when the patient stops taking imatinib and only low levels remain. For example, in (Koup 2004), the author observed that although researchers were initially enthusiastic about the possibility of successfully treating HIV with strategic treatment interruptions (primarily to give patients a respite from side effects), several clinical trials demonstrated that patients developed an increased amount of drug resistance while receiving strategic treatment interruptions. This observation has since been repeated in several other studies on the use of treatment interruptions during antiretroviral therapy for HIV patients. Thus, the potential effects of treatment interruptions on the resistance mutation rate for CML patients should be thoroughly investigated.

Appendix A: Exact Solution of the Michor Model

The system of ODEs that describes the mathematical model of Michor et al. (2005) is given below. We include here the second set of differential equations which describe the dynamics of the imatinib-resistant leukemia cells. These populations are denoted z₀, z₁, z₂, z₃ (imatinib-resistant stem cells, progenitor cells, differentiated cells, and terminally differentiated cells, respectively).

$$\begin{array}{l}\frac{{dy}_0}{dt}=\left(r_y(1-u)-d_0\right)y_0,\frac{{dz}_0}{dt}=(r_z-d_0)z_0+r_{y}u{y}_0,\\ \begin{array}{cc}\frac{{dy}_1}{dt}=a_y{y}_0-d_1{y}_1,& \frac{{dz}_1}{dt}=a_z{z}_0-d_1{z}_1,\\ \frac{{dy}_2}{dt}=b_y{y}_1-d_2{y}_2,& \frac{{dz}_2}{dt}=b_z{z}_1-d_2{z}_2,\\ \frac{{dy}_3}{dt}=c_y{y}_2-d_3{y}_3,& \frac{{dz}_3}{dt}=c_z{z}_2-d_3{z}_3.\end{array}\end{array}$$ (A.1)

To find the exact solution of this system of ODE’s given, we first write the system in matrix form x′ = Ax, where

$$\mathbf{x}={\left[\begin{array}{cccccccc}{y}_0& y_1& y_2& y_3& z_0& z_1& z_2& z_3\end{array}\right]}^T$$

and A is the coefficient matrix of the system. The eigenvalues of the coefficient matrix A are given by

$$\begin{array}{l}{\lambda }_0=r_y(1-u)-d_0,{\lambda }_4=r_z-d_0,\\ \begin{array}{cc}{\lambda }_1=-d_1,& {\lambda }_5=-d_1,\\ {\lambda }_2=-d_2,& {\lambda }_6=-d_2,\\ {\lambda }_3=-d_3,& {\lambda }_7=-d_3,\end{array}\end{array}$$ (A.2)

and we obtain the following explicit solution of the Michor model for CML:

$$\begin{array}{l}{y}_0(t)={\alpha }_0{e}^{(r_y(1-u)-d_0)t},\\ y_1(t)={\alpha }_1{e}^{-d_{1}t}-\frac{a_y{\alpha }_0}{r_y(u-1)+d_0-d_1}{e}^{(r_y(1-u)-d_0)t},\\ y_2(t)={\alpha }_2{e}^{-d_{2}t}+\frac{b_y(-{\alpha }_1{r}_y+{\alpha }_1{ur}_y+{\alpha }_1{d}_0-{\alpha }_1{d}_1)}{(-r_y(1-u)+d_0-d_1)(d_2-d_1)}{e}^{-d_{1}t}\\ -\frac{{\alpha }_0{b}_y{a}_y}{(-r_y(1-u)+d_0-d_1)(r_y(1-u)-d_0+d_2)}{e}^{(r_y(1-u)-d_0)t},\\ y_3(t)={\alpha }_3{e}^{-d_{3}t}-\frac{{\alpha }_0{a}_y{b}_y{c}_y}{(r_y(1-u)+d_3-d_0)(r_y(u-1)+d_0-d_2)(r_y(1-u)+d_1-d_0)}\\ \times e^{(r_y(1-u)-d_0)t}\\ +\frac{{\alpha }_2{c}_y}{d_3-d_2}{e}^{-d_{2}t}-\frac{{\alpha }_1{b}_y{c}_y}{(d_3-d_1)(d_1-d_2)}{e}^{-d_{1}t},\\ z_0(t)={\beta }_0{e}^{(r_z-d_0)t}-\frac{{\alpha }_0{r}_{y}u}{r_y(u-1)+r_z}{e}^{(r_y(1-u)-d_0)t},\\ z_1(t)={\beta }_1{e}^{-d_{1}t}+\frac{{\beta }_0{a}_z(r_y(u-1)+r_z)}{(r_y(u-1)+r_z)(r_z-d_0+d_1)}{e}^{(r_z-d_0)t}\\ -\frac{{\alpha }_0{ur}_y{a}_z}{(r_y(u-1)+r_z)(r_y(1-u)-d_0+d_1)}{e}^{(r_y(1-u)-d_0)t},\\ z_2(t)={\beta }_2{e}^{-d_{2}t}+\frac{{\alpha }_0{r}_y{ua}_z{b}_z}{(r_y(1-u)-d_0+d_2)(r_y(u-1)+r_z)(r_y(u-1)+d_0-d_1)}\\ \times e^{(r_y(1-u)-d_0)t}\\ +\frac{{\beta }_0{a}_z{b}_z}{(r_z-d_0+d_2)(r_z-d_0+d_1)}{e}^{(r_z-d_0)t}+\frac{{\beta }_1{b}_z}{d_2-d_1}{e}^{-d_{1}t},\\ z_3(t)={\beta }_3{e}^{-d_{3}t}+\frac{{\beta }_1{b}_z{c}_z}{(d_2-d_1)(d_3-d_1)}{e}^{-d_{1}t}+\frac{{\beta }_2{c}_z}{d_3-d_2}{e}^{-d_{2}t}\\ +\frac{{\alpha }_0{r}_y{ua}_z{b}_z{c}_z·e^{(r_y(1-u)-d_0)t}}{(r_y(u-1)+d_0-d_1)(r_y(1-u)-d_0+d_2)(r_y(1-u)-d_0+d_3)(r_y(u-1)+r_z)}\\ +\frac{{\beta }_0{a}_z{b}_z{c}_z}{(r_z-d_0+d_1)(r_z-d_0+d_2)(r_z-d_0+d_3)}{e}^{(r_z-d_0)t},\end{array}$$

where the α_i and β_i are arbitrary constants of integration that are determined by the initial conditions of the leukemia cell populations. Since the solutions y_i and z_i are all linear combinations of exponential functions, it is clear that the long-term behavior of the system depends only on the relative sizes of the eigenvalues λ_i, i = 0..7. For the particular values of the parameters given in Table 2, the only positive eigenvalues are r_y(1 − u) − d₀ and r_z − d₀, so the leukemia stem cell populations y₀ and z₀ dominate the dynamic of this system.