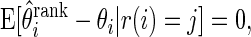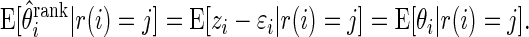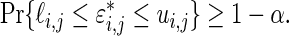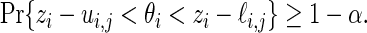Abstract
Empirical Bayes methods have been extensively used for microarray data analysis by modeling the large number of unknown parameters as random effects. Empirical Bayes allows borrowing information across genes and can automatically adjust for multiple testing and selection bias. However, the standard empirical Bayes model can perform poorly if the assumed working prior deviates from the true prior. This paper proposes a new rank-conditioned inference in which the shrinkage and confidence intervals are based on the distribution of the error conditioned on rank of the data. Our approach is in contrast to a Bayesian posterior, which conditions on the data themselves. The new method is almost as efficient as standard Bayesian methods when the working prior is close to the true prior, and it is much more robust when the working prior is not close. In addition, it allows a more accurate (but also more complex) non-parametric estimate of the prior to be easily incorporated, resulting in improved inference. The new method’s prior robustness is demonstrated via simulation experiments. Application to a breast cancer gene expression microarray dataset is presented. Our R package rank.Shrinkage provides a ready-to-use implementation of the proposed methodology.
Keywords: Bayesian shrinkage, Confidence intervals, Ranking bias, Robust multiple estimation
1. Introduction
Large-scale technologies, which measure many similar entities in parallel, have emerged as an important tool in biomedical research. For example, the expression level of thousands of genes is compared between cancer and normal tissues in microarray experiments. In genome-wide association studies, the log odds ratio of the association of disease status (disease vs. control) and single-nucleotide polymorphism (SNP) frequency is estimated for thousands or millions of SNPs in a single case–control study. There are two prominent features in large-scale data. First, different parameters (e.g. difference in expression levels between cancer and normal tissues for different genes) are often studied with the same set of subjects and using the same design. Second, a large majority of the underlying parameters are 0. Because of this, the unknown parameters can be profitably modeled as random effects in an empirical Bayes framework. A popular model is to treat the large number of parameters as draws from a spike-and-slab prior distribution that is a mixture of a large mass at 0 and a non-zero component. The parameters in the spike-and-slab prior can be estimated from the many parallel measurements, resulting in an empirical Bayes analysis that borrows information across different genes or SNPs. The empirical Bayes framework automatically adjusts for the large number of hypothesis tests or effect estimates. The application of empirical Bayes to large-scale testing naturally leads to the false discovery rate (FDR) and the local FDR (Benjamini and Yekutieli, 2005; Efron and others, 2001; Newton and others, 2004; Efron, 2008). The application to parallel estimation (e.g. of the log fold changes in expression level) in the microarray context includes Newton and others (2001), Kendziorski and others (2003), and Smyth (2004). There is substantial literature in this area and the reader is referred to Efron (2010) for a summary of the state of the art in the empirical Bayes approach to large-scale inference and for complete references.
This paper focuses on estimating the effect sizes, the log fold change in gene expression level in microarray data, for example. We show that a popular empirical Bayes random effects model can lead to poor performance if the form of the prior is mis-specified; this has important practical implications because in real applications we are never certain of the correct distributional form, especially in the tails of the distribution, which often produce the most interesting observations. Motivated by this sensitivity to the form of the random effects model, we propose a new rank-conditioned inference in which shrinkage and confidence intervals are based on the distribution of the measurement error conditioned on the rank of the data instead of on the data themselves as in a traditional Bayesian posterior. The primary advantage of the rank-conditioned method is that it is almost as efficient as standard Bayesian methods when the working prior is close to the true prior, and it is much more robust when the working prior is not close. In particular, the proposed method provides efficient and valid inference even when the working random effects model substantially deviates from the true model in location. The proposed method can, therefore, substantially improve empirical Bayes inference for microarray studies as well as other large-scale data such as for genome-wide association studies and flow cytometry.
To put the rank-conditioned method in the context of the broader literature, we note the following. First, we condition on rank of the observed data in order to obtain more robust estimation of effect size. This is different from Noma and others (2010), whose aim is to better rank the effect sizes. Second, the idea of combining a Bayes formulation with rank-based likelihood has previously been proposed and studied in other context; for example, Dunson and Taylor (2005) use the idea for estimating quantiles, Gu and Ghosal (2009) for estimating receiver operating characteristic curves, and Hoff (2007) in estimating semi-parametric copula. Large-scale data is an area where this idea can be more profitably used because rank of the observed data and the observed data themselves are closely correlated. We are, therefore, able to take advantage of the robust property of the rank method with little loss of efficiency compared with standard empirical Bayes. Third, improved robustness can also be achieved through a more diffuse prior for the random effects. For example, Do and others (2005) and Kim and others (2009) combine Dirichlet process with spike-and-slab prior in a non-parametric Bayes model for random effects. A more diffuse prior, however, necessarily weakens the effectiveness of shrinkage and information borrowing as seen in the simulation study in Section 4.2.
The paper is organized as follows. Section 2 describes a model for large-scale microarray data analysis. Section 3 presents our proposed ranked-conditioned inference. Section 4 consists of simulation studies assessing the performance of rank-conditioned inference. Section 5 applies the proposed method to a breast cancer microarray dataset. Section 6 is discussion.
2. Empirical Bayes model for large-scale data
For concreteness, throughout the remainder of the paper, we focus on estimating the standardized effect size in case–control microarray experiments; application of our method in other large-scale data, such as genome-wide association studies, is similar.
We begin by describing an empirical Bayes model for the log fold change in gene expression. Let 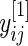 and
and 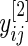 be the log expression level of the
be the log expression level of the 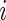 th gene for the
th gene for the 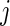 th subject in the cancer and normal group, respectively. The total number of genes is
th subject in the cancer and normal group, respectively. The total number of genes is 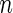 so that
so that 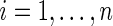 . We start with the model
. We start with the model
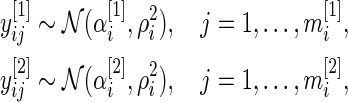 |
where 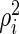 is the variance of the
is the variance of the 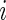 th gene expression common for the cancer and normal groups, and
th gene expression common for the cancer and normal groups, and 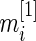 and
and 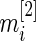 are the respective sample sizes. The quantity
are the respective sample sizes. The quantity 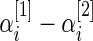 is the average (log) fold change (Guo and others, 2006; Choe and others, 2005). Let
is the average (log) fold change (Guo and others, 2006; Choe and others, 2005). Let 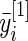 be the mean of
be the mean of 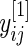 over
over 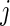 , and similarly let
, and similarly let 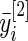 be the mean of
be the mean of 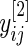 . It then follows that
. It then follows that
 |
where
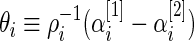 |
is the standardized log fold change and 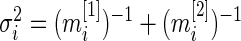 . Note that
. Note that 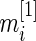 and
and 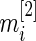 typically do not vary much from gene to gene in a microarray experiment so that variance
typically do not vary much from gene to gene in a microarray experiment so that variance 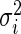 should be relatively constant across
should be relatively constant across 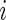 .
.
The first stage of our empirical Bayes model is
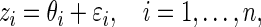 |
(2.1) |
where  independently for
independently for 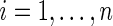 . In application, the
. In application, the 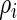 in the definition of
in the definition of 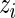 will be replaced by its pooled estimate using
will be replaced by its pooled estimate using 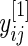 and
and 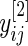 and
and 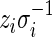 will then follow a
will then follow a 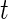 -distribution. For simplicity, we shall use normal error model (2.1), since the
-distribution. For simplicity, we shall use normal error model (2.1), since the 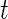 degrees of freedom,
degrees of freedom, 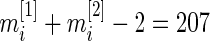 , is large for the breast cancer data in Section 6. For a smaller
, is large for the breast cancer data in Section 6. For a smaller 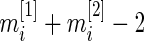 , a modified version of (2.1) based on a non-central
, a modified version of (2.1) based on a non-central 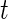 -distribution can be used instead. For a genome-wide association study,
-distribution can be used instead. For a genome-wide association study, 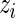 can be the estimated log odds ratio from a logistic regression for the association between disease status and the
can be the estimated log odds ratio from a logistic regression for the association between disease status and the 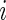 th SNP,
th SNP, 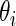 be the unknown true log odds ratio and
be the unknown true log odds ratio and 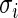 be the standard error of estimate
be the standard error of estimate  . Next, we will model
. Next, we will model 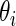 as independent random draws from a prior
as independent random draws from a prior 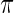 . Given prior
. Given prior 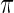 , the Bayesian inference for
, the Bayesian inference for 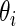 is based on the posterior distribution of
is based on the posterior distribution of 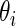 given
given 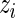 with density
with density
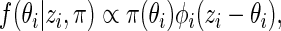 |
(2.2) |
where 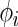 is a
is a 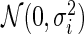 density. The posterior mean
density. The posterior mean 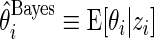 is a standard Bayes estimator of
is a standard Bayes estimator of 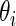 and the
and the 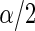 and
and 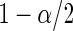 quantiles of the posterior distribution provide the
quantiles of the posterior distribution provide the  confidence limits
confidence limits  and
and 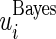 .
.
The prior 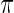 , however, is unknown. Empirical Bayes analysis uses a working prior
, however, is unknown. Empirical Bayes analysis uses a working prior  in place of
in place of 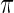 with the parameters in
with the parameters in 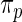 estimated from data
estimated from data 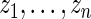 usually via maximum likelihood (Morris, 1983). Our parametric working prior
usually via maximum likelihood (Morris, 1983). Our parametric working prior 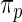 is a three-component mixture
is a three-component mixture
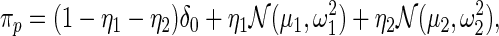 |
(2.3) |
where 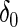 is the delta function (point mass) at 0, and
is the delta function (point mass) at 0, and 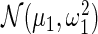 and
and 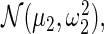 respectively, model the up- and down-regulated genes. This working prior is the same as that in Noma and others (2010) with one important difference: we use (2.3) to model the distribution of the standardized differences
respectively, model the up- and down-regulated genes. This working prior is the same as that in Noma and others (2010) with one important difference: we use (2.3) to model the distribution of the standardized differences 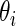 instead of the raw differences
instead of the raw differences 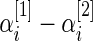 . We show in Section 5 that modeling the standardized differences
. We show in Section 5 that modeling the standardized differences 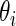 as draws from a common prior leads to a much better fit to a breast cancer microarray dataset.
as draws from a common prior leads to a much better fit to a breast cancer microarray dataset.
An important practical advantage of working prior (2.3) is that the posterior distribution 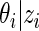 is also a mixture of the same form as (2.3) (see Noma and others, 2010; Muralidharan, 2010) for analytical formula), which makes programming much easier and computing time manageable for large-scale problems. Spike-and-slab priors such as (2.3) have been used in variable selection and shrinkage estimation (see, e.g. Ishwaran and Rao, 2005) and have played a prominent role in multiple testing (Efron and others, 2001).
is also a mixture of the same form as (2.3) (see Noma and others, 2010; Muralidharan, 2010) for analytical formula), which makes programming much easier and computing time manageable for large-scale problems. Spike-and-slab priors such as (2.3) have been used in variable selection and shrinkage estimation (see, e.g. Ishwaran and Rao, 2005) and have played a prominent role in multiple testing (Efron and others, 2001).
3. Rank-conditioned inference
3.1. Rank-conditioned shrinkage
For our basic model (2.1), we have
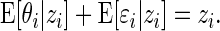 |
The Bayesian estimate 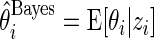 can also be written as
can also be written as
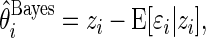 |
which reflects the fact that the conditional mean of 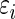 , given the observed
, given the observed 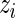 , is no longer 0.
, is no longer 0.
For the dataset 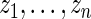 , let
, let 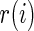 be the rank of
be the rank of 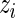 among
among 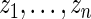 . Our rank-conditioned inference for
. Our rank-conditioned inference for 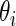 is based on the conditional distribution
is based on the conditional distribution
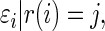 |
(3.1) |
where  is the realized value of rank
is the realized value of rank 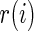 . The rank-conditioned shrinkage estimator is defined as
. The rank-conditioned shrinkage estimator is defined as
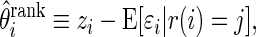 |
(3.2) |
where 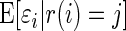 is the conditional mean of the error
is the conditional mean of the error 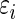 , given that
, given that 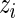 has rank
has rank 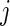 among
among 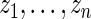 . Given prior
. Given prior 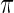 , a draw from (3.1),
, a draw from (3.1), 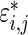 , which is error
, which is error 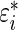 conditional on
conditional on 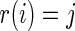 , can be generated using the following three steps:
, can be generated using the following three steps:
Step 1: Generate 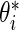 from density
from density  independently for
independently for 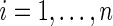 . Let
. Let 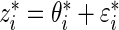 , where
, where 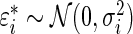 .
.
Step 2: Let 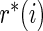 be the rank of
be the rank of 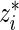 among
among 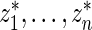 .
.
Step 3: Repeat Steps 1–2 until 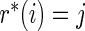 . Then output
. Then output  .
.
Theorem 3.1 —
Let
and
independently for
. Let
be defined as in model (2.1). then
is unbiased in the sense that
for any given
and
, when the expectation is evaluated with respect to the joint distribution of
and
.
Proof. —
Theorem 3.1 follows directly from definition (3.2) and (2.1):
Theorem 3.1 says that
corrects the ranking bias, a concept discussed as in Jeffries (2009).
In addition to point estimate
, the proposed method provides a natural confidence interval for
. Let
and
satisfy
(3.3) It follows that
We have, therefore, shown that the interval
(3.4) contains the realized
with
probability, given
when
and
are drawn as in Theorem 3.1.
Conditioning on 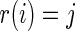 in the rank-conditioned shrinkage estimator (3.2) and confidence limits (3.4) is in fact closely related to conditioning on
in the rank-conditioned shrinkage estimator (3.2) and confidence limits (3.4) is in fact closely related to conditioning on 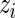 itself in standard Bayes, as a larger
itself in standard Bayes, as a larger 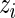 generally corresponds to a higher rank. More specifically, let
generally corresponds to a higher rank. More specifically, let 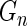 be the empirical distribution of
be the empirical distribution of 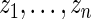 . Suppose that
. Suppose that 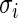 ,
, 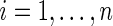 , can be modeled as draws from some distribution
, can be modeled as draws from some distribution 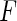 . It then follows from Glivenko–Cantelli theorem that
. It then follows from Glivenko–Cantelli theorem that 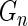 converges uniformly to
converges uniformly to  , the distribution of
, the distribution of 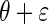 with
with 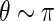 ,
, 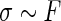 , and
, and 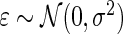 . In such a case, conditioning on
. In such a case, conditioning on 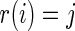 is almost the same as conditioning on
is almost the same as conditioning on 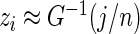 so long as
so long as 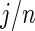 is not close to 0 or 1 (the difference can be more substantial for
is not close to 0 or 1 (the difference can be more substantial for 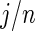 close to 0 or 1). The proposed rank-conditioned inference, however, can be much more robust than standard empirical Bayes against mis-specification of
close to 0 or 1). The proposed rank-conditioned inference, however, can be much more robust than standard empirical Bayes against mis-specification of 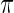 . For this, we have the following result.
. For this, we have the following result.
Theorem 3.2 —
Let
and
independently for
. Let
be defined as in model (2.1). In the case where the
are equal, conditional distribution (3.1) and consequently rank-conditioned estimator (3.2) and confidence limits (3.4) remain the same (and valid) when the true prior density
is replaced by density
for any given constant
.
Proof. —
The proof is straightforward. Let
and
+
as in the three steps above. When the
are equal, the rank of
is not changed when
are all translated by a constant
, so the distribution of
does not change. Theorem 3.2 then follows.
For unequal
, Theorem 3.2 remains approximately valid so long as the variation in
is small. Section 5 demonstrates that the rank-based shrinkage is in general more robust, not just against location shift. This is a unique feature of rank-conditioned shrinkage: the ranking bias
is negative for lower ranked
and positive for higher ranked
even when evaluated under a badly specified prior. In the three steps for generating
at the beginning of this section, the prior
determines which
will be output as
. As such, the effect of a grossly mis-specified
on
remains limited. A grossly mis-specified
can, however, have a much larger distorting impact on Bayes shrinkage estimator
.
Finally, a confidence interval such as (3.4) that adjusts for ranking
can be crucial for valid inference; Benjamini and Yekutieli (2005) show that the unadjusted marginal confidence interval of
can have coverage probability that differs substantially from the nominal coverage for top-ranked parameters selected based on the same data. They propose the false coverage rate controlled confidence interval as a solution to this problem. As shown in Efron (2010, pp. 230–233) however, this interval can differ markedly from the corresponding Bayes interval and can be frighteningly wide. Westfall (2005) suggests constructing empirical Bayes confidence intervals centered at the shrunken estimators; the same idea is used and further developed in Qiu and Gene Hwang (2007) and in Ghosh (2009). Our interval is similar, but is instead based on rank-conditioned shrinkage. It is generally very close to the corresponding Bayes interval when the working prior is close to the true prior.
3.2. Non-parametric update of the parametric prior
In Section 2, a parametric working prior 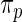 is used in empirical Bayes to capture the primary structure of
is used in empirical Bayes to capture the primary structure of 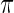 . For the rank-conditioned method, we propose a non-parametric update of density
. For the rank-conditioned method, we propose a non-parametric update of density 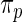 to density
to density 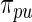 by formula
by formula
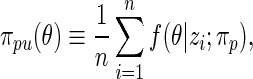 |
where the posterior density 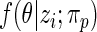 is given by (2.2) with
is given by (2.2) with 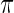 replaced by
replaced by 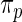 and with
and with 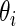 replaced by a generic
replaced by a generic 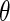 . The parameters in
. The parameters in 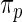 will take the values of their maximum likelihood estimates.
will take the values of their maximum likelihood estimates. 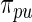 can be interpreted as the average of the posterior densities for
can be interpreted as the average of the posterior densities for 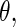 given
given 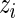 with prior
with prior 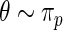 . Vardi and others (1985) use a similar update to improve the estimated image density in positron emission tomography. They show that it is one expectation-maximization iteration and therefore always increases the (marginal) likelihood of
. Vardi and others (1985) use a similar update to improve the estimated image density in positron emission tomography. They show that it is one expectation-maximization iteration and therefore always increases the (marginal) likelihood of 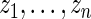 . See also Eggermont and LaRiccia (1997). The use of
. See also Eggermont and LaRiccia (1997). The use of 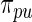 in place of
in place of 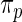 does not significantly increase the computational burden for rank-conditioned inference. The density
does not significantly increase the computational burden for rank-conditioned inference. The density 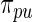 could potentially be further updated but the analytical complexity and computational cost will increase drastically.
could potentially be further updated but the analytical complexity and computational cost will increase drastically.
3.3. Algorithm and implementation
The three-step algorithm for drawing 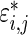 in Section 3.1 is greatly simplified for the special case of
in Section 3.1 is greatly simplified for the special case of 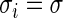 for all
for all 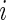 because the distribution of
because the distribution of 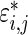 depends only on the rank
depends only on the rank 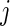 and not on
and not on 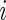 . Under this condition, Steps 2 and 3 become
. Under this condition, Steps 2 and 3 become
Let
be the order statistics of
. Let
be the
that corresponds to
. Output
for
.
In this way, one round of Steps 1–3 generates a complete and independent set of 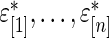 . The
. The 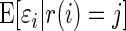 in (3.2) is now simply
in (3.2) is now simply 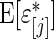 and the
and the  and
and 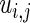 in (3.3) are defined by
in (3.3) are defined by 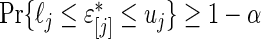 irrespective of the value of
irrespective of the value of 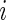 .
.
For most large-scale problems, the values of error standard deviation 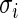 may not be constant but they are not far apart (say within a factor of 3 or 4) because of the inherent common design structure. For the microarray example in Section 2,
may not be constant but they are not far apart (say within a factor of 3 or 4) because of the inherent common design structure. For the microarray example in Section 2, 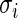 for standardized difference
for standardized difference 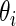 depends only on sample size
depends only on sample size 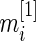 and
and 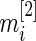 . Therefore,
. Therefore, 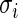 does not differ too much unless the number of missing data points varies dramatically between genes. Similarly, in genome-wide association study, each SNP is compared between the same set of cases and controls. For such dataset, we can partition the
does not differ too much unless the number of missing data points varies dramatically between genes. Similarly, in genome-wide association study, each SNP is compared between the same set of cases and controls. For such dataset, we can partition the 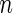 observations,
observations, 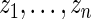 , into several sub-groups so that
, into several sub-groups so that 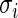 for observations within each sub-group varies within a factor of 1.5, for example. The simplified algorithm above can then be applied to each subgroup separately as an approximation. Monte Carlo Markov chain type of algorithm is under investigation to efficiently sample from the rank-conditioned distribution (3.1) without requiring
for observations within each sub-group varies within a factor of 1.5, for example. The simplified algorithm above can then be applied to each subgroup separately as an approximation. Monte Carlo Markov chain type of algorithm is under investigation to efficiently sample from the rank-conditioned distribution (3.1) without requiring 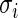 to be constant.
to be constant.
4. Assessing performance of rank-conditioned inference
4.1. Simulation study 
This example is adapted from Efron (2010, pp. 230–233). Let 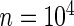 and
and 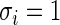 for all
for all 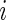 for model (2.1). The true
for model (2.1). The true 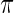 for random effects
for random effects 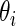 is (2.3) with
is (2.3) with 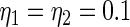 ,
,  ,
, 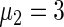 ,
, 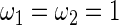 . These parameter values are chosen to have a moderate Bayes shrinkage effect. Monte Carlo simulation is conducted to compare the Bayes shrinkage estimates
. These parameter values are chosen to have a moderate Bayes shrinkage effect. Monte Carlo simulation is conducted to compare the Bayes shrinkage estimates 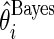 and rank-conditioned shrinkage estimates
and rank-conditioned shrinkage estimates 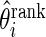 under five different specifications of working prior
under five different specifications of working prior 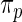 . These working priors
. These working priors 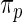 have the same parametric form of (2.3) but with possibly different values of
have the same parametric form of (2.3) but with possibly different values of 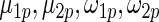 as given in various rows of Table 1. Parameters not listed are the same as in true prior. For example,
as given in various rows of Table 1. Parameters not listed are the same as in true prior. For example, 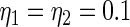 for all the five working priors. Our simulation study is conducted as follows:
for all the five working priors. Our simulation study is conducted as follows:
Table 1.
Mean square error of the three methods under different model mis-specification
| Working prior |
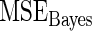 with with 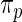
|
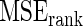 with with 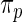
|
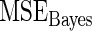 with with 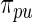
|
|---|---|---|---|
| Same as true prior | 0.675 | 0.677 | 0.677 |
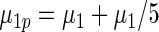 |
0.763 | 0.710 | 0.681 |
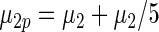 |
|||
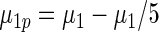 |
0.762 | 0.685 | 0.683 |
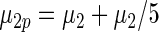 |
|||
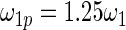 |
0.702 | 0.686 | 0.683 |
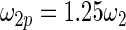 |
|||
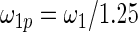 |
0.699 | 0.681 | 0.679 |
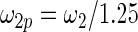 |
Step 1: Generate 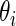 ,
, 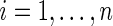 , from prior
, from prior 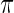 . Let
. Let 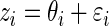 as in model (2.1).
as in model (2.1).
Step 2: Let 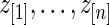 be the order statistics of
be the order statistics of 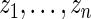 . Let
. Let 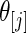 be the
be the 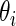 corresponding to
corresponding to 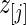 . The
. The 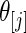 can, therefore, refer to different
can, therefore, refer to different 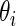 for different realizations of
for different realizations of 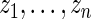 .
.
Step 3: Compute empirical Bayes estimate 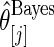 under working model
under working model 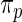 . Compute the rank-conditioned estimate
. Compute the rank-conditioned estimate 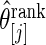 under working model
under working model 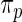 and its non-parametric update
and its non-parametric update 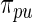 , respectively.
, respectively.
Step 4: Let 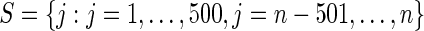 . Calculate the mean square loss
. Calculate the mean square loss
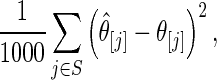 |
for estimator 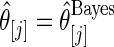 and estimator
and estimator 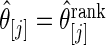 for both
for both 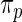 and
and 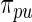 . We only include the 500 lowest and 500 highest
. We only include the 500 lowest and 500 highest 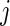 in
in 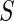 because these
because these 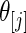 are most interesting in large-scale data analysis.
are most interesting in large-scale data analysis.
Steps 1–4 are replicated 1000 times and the mean square error 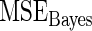 for Bayes method and mean square error
for Bayes method and mean square error 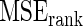 for rank-conditioned inference are estimated by averaging the squared error loss over these replications. The estimated
for rank-conditioned inference are estimated by averaging the squared error loss over these replications. The estimated 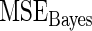 and
and 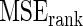 values are given in Table 1. In row 1, the working prior is the same as the true prior and the standard Bayes is therefore optimal. The rank-conditional inference under both
values are given in Table 1. In row 1, the working prior is the same as the true prior and the standard Bayes is therefore optimal. The rank-conditional inference under both 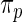 and
and 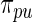 shows little loss of efficiency with almost the same mean square error. In rows 2 and 3,
shows little loss of efficiency with almost the same mean square error. In rows 2 and 3, 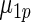 and
and 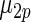 in the working prior are shifted away from
in the working prior are shifted away from 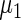 and
and 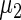 in the true prior. The
in the true prior. The 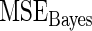 increases noticeably with this model mis-specification. The rank-conditioned inference, especially under
increases noticeably with this model mis-specification. The rank-conditioned inference, especially under 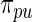 , proves robust with a much smaller change in
, proves robust with a much smaller change in 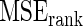 from row 1. In rows 4 and 5,
from row 1. In rows 4 and 5, 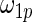 and
and 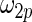 in the working prior are inflated or shrunk from
in the working prior are inflated or shrunk from 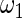 and
and 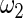 in the true prior. Again, rank-conditioned inference is more robust.
in the true prior. Again, rank-conditioned inference is more robust.
4.2. Simulation study 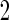
For simulation 2, we continue to let 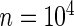 and
and 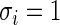 for all
for all 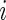 in model (2.1). The true prior
in model (2.1). The true prior 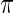 of
of 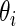 now has the form
now has the form
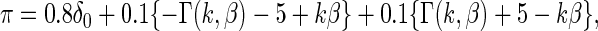 |
(4.1) |
where 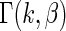 is the Gamma distribution with shape
is the Gamma distribution with shape 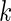 and scale
and scale 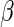 . We take
. We take 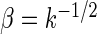 so that
so that 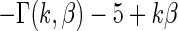 always has mean
always has mean  5 and variance 1 and
5 and variance 1 and  always has mean 5 and variance 1 for any
always has mean 5 and variance 1 for any 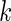 . For the simulation study, we generate
. For the simulation study, we generate 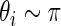 and
and 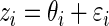 ,
, 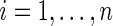 , as specified by (2.1) and (4.1). Let
, as specified by (2.1) and (4.1). Let 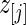 be the
be the 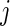 th order statistic of
th order statistic of 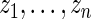 and let
and let 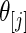 be the corresponding
be the corresponding 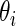 . For every dataset
. For every dataset 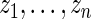 , we compute a point estimate and 90% confidence limits for
, we compute a point estimate and 90% confidence limits for 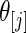 ,
, 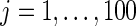 , using three different methods. Method 1 is Bayes estimate
, using three different methods. Method 1 is Bayes estimate 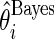 and confidence limits
and confidence limits 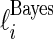 and
and 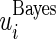 in Section 2 using
in Section 2 using 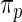 in (2.3) as the working prior. In accordance with empirical Bayes, parameters
in (2.3) as the working prior. In accordance with empirical Bayes, parameters 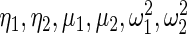 in
in 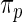 are substituted by their maximum likelihood estimates using data
are substituted by their maximum likelihood estimates using data 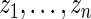 under models (2.1) and (2.3). We shall call this parametric Bayes method. Method 2 is also based on Bayes posterior but with a more diffuse prior using Dirichlet process mixture. Let
under models (2.1) and (2.3). We shall call this parametric Bayes method. Method 2 is also based on Bayes posterior but with a more diffuse prior using Dirichlet process mixture. Let 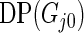 be the Dirichlet process with base distribution
be the Dirichlet process with base distribution 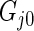 and scaling parameter 1 and let
and scaling parameter 1 and let 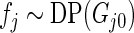 be a (random) distribution drawn from this Dirichlet process. Following Do and others (2005) and Dunson (2010), we take the more diffuse prior,
be a (random) distribution drawn from this Dirichlet process. Following Do and others (2005) and Dunson (2010), we take the more diffuse prior, 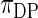 , as
, as
 |
where 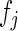 ,
,  is generated as
is generated as
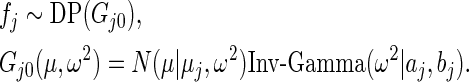 |
To be consistent with Method 1, 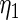 and
and 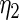 in
in  and
and 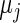 in
in 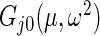 are substituted by their maximum likelihood estimates under models (2.1) and (2.3) as in Method 1. For the inverse gamma distribution, we choose shape parameter
are substituted by their maximum likelihood estimates under models (2.1) and (2.3) as in Method 1. For the inverse gamma distribution, we choose shape parameter 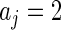 and scale parameter
and scale parameter 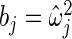 , where
, where 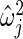 is maximum likelihood estimate of variance
is maximum likelihood estimate of variance 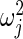 in (2.3), so that the mean of the inverse gamma equals
in (2.3), so that the mean of the inverse gamma equals 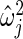 . Note that the prior
. Note that the prior 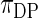 is considerably more diffuse and less informative than
is considerably more diffuse and less informative than 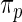 due to the extra variation in
due to the extra variation in 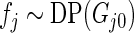 . We call Method 2 non-parametric DP Bayes. Method 3 is the proposed rank-conditioned inference under
. We call Method 2 non-parametric DP Bayes. Method 3 is the proposed rank-conditioned inference under 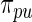 , the non-parametric update of
, the non-parametric update of  . Again, the parameters in
. Again, the parameters in 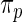 are substituted by their maximum likelihood estimates. Let
are substituted by their maximum likelihood estimates. Let 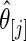 be the point estimate and
be the point estimate and 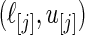 be the confidence limits of
be the confidence limits of 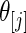 from one of the three methods. Let 1(
from one of the three methods. Let 1( ) be the indicator function. The mean square error and actual coverage rate for parameter
) be the indicator function. The mean square error and actual coverage rate for parameter 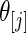 ,
, 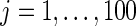 , are estimated by averaging
, are estimated by averaging
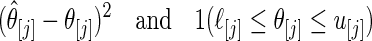 |
over 1000 replications of 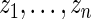 .
.
The simulation study is conducted for 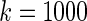 ,
, 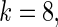 and
and 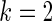 with prior
with prior 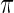 given by (4.1); the results are given in Figures 1–3, respectively. In each figure, the left panel shows the estimated root MSE for the lowest 100 ranked genes,
given by (4.1); the results are given in Figures 1–3, respectively. In each figure, the left panel shows the estimated root MSE for the lowest 100 ranked genes, 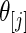 for
for  , and the right panel shows the estimated actual coverage rate of nominal 90% confidence intervals for
, and the right panel shows the estimated actual coverage rate of nominal 90% confidence intervals for 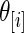 . Figure 1 shows the case where
. Figure 1 shows the case where 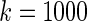 ; when
; when 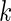 is large, the normal distribution in the working prior
is large, the normal distribution in the working prior 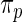 approximates
approximates 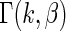 in true prior
in true prior 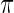 extremely well. As expected, the parametric Bayes performs the best among the three methods with the smallest mean square errors and close (to nominal) actual coverage rates for all
extremely well. As expected, the parametric Bayes performs the best among the three methods with the smallest mean square errors and close (to nominal) actual coverage rates for all 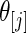 ,
, 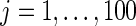 . The non-parametric Bayes with Dirichlet process prior performs poorly as the mean square errors are large and the actual coverage rates are far off. This is not surprising because an overly diffuse prior
. The non-parametric Bayes with Dirichlet process prior performs poorly as the mean square errors are large and the actual coverage rates are far off. This is not surprising because an overly diffuse prior 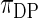 does not bring the needed shrinkage. Figure 3 shows the case for
does not bring the needed shrinkage. Figure 3 shows the case for 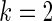 , in which the working prior deviates substantially from the true prior. The parametric Bayes performs poorly with huge MSE and far off actual coverage rates, while the non-parametric Bayes is much superior in both MSE and coverage rates. Figure 2 is for
, in which the working prior deviates substantially from the true prior. The parametric Bayes performs poorly with huge MSE and far off actual coverage rates, while the non-parametric Bayes is much superior in both MSE and coverage rates. Figure 2 is for  , an intermediate case between
, an intermediate case between 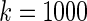 and
and 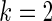 . Neither of the two methods works well especially for
. Neither of the two methods works well especially for 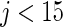 . Our proposed rank-based inference, however, performs well for all the three cases. In particular, it is only slightly worse than the parametric Bayes for
. Our proposed rank-based inference, however, performs well for all the three cases. In particular, it is only slightly worse than the parametric Bayes for 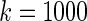 when the prior is correctly specified. When the prior is mis-specified as in
when the prior is correctly specified. When the prior is mis-specified as in  and
and  , its mean square errors are the smallest among the three methods and its actual coverage rates are not too far off from the nominal 90%. The rank-conditioned inference therefore achieves robustness against mis-specified prior with minimal loss of efficiency under correctly specified prior. While not shown in the graphs, the superior performance of the rank-conditioned inference is similarly observed for the highest ranked
, its mean square errors are the smallest among the three methods and its actual coverage rates are not too far off from the nominal 90%. The rank-conditioned inference therefore achieves robustness against mis-specified prior with minimal loss of efficiency under correctly specified prior. While not shown in the graphs, the superior performance of the rank-conditioned inference is similarly observed for the highest ranked 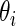 such as
such as 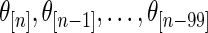 . The difference between the methods is small for middle-ranked
. The difference between the methods is small for middle-ranked 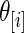 as their inference are primarily determined by the large mass at 0 which is present in both the true prior
as their inference are primarily determined by the large mass at 0 which is present in both the true prior 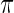 and working prior
and working prior 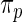 . Finally, our implementation of Method 2 is based on R package DPpackage (Jara and others, 2011). Two additional simulation studies are included in supplementary material available at Biostatistics online.
. Finally, our implementation of Method 2 is based on R package DPpackage (Jara and others, 2011). Two additional simulation studies are included in supplementary material available at Biostatistics online.
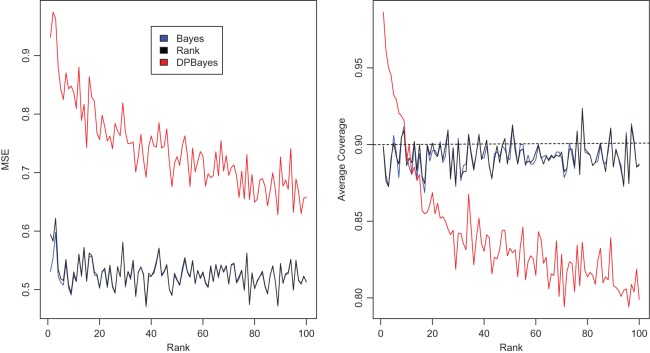
Figure 1.
Simulation study of Section 4.2 with the correct prior in (4.1) and parameter 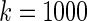 . The left panel is the root mean square error for parameter estimate
. The left panel is the root mean square error for parameter estimate 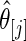 ,
, 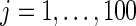 , and the right panel is the actual coverage rate of confidence intervals for
, and the right panel is the actual coverage rate of confidence intervals for 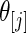 at the 90% nominal level. Parametric empirical Bayes and rank-conditional inference perform similarly in this case with smaller mean square error and correct actual coverage rates. The non-parametric Bayes model with Dirichlet prior performs considerably worse compared with the other two methods in both mean square error and actual coverage rate.
at the 90% nominal level. Parametric empirical Bayes and rank-conditional inference perform similarly in this case with smaller mean square error and correct actual coverage rates. The non-parametric Bayes model with Dirichlet prior performs considerably worse compared with the other two methods in both mean square error and actual coverage rate.
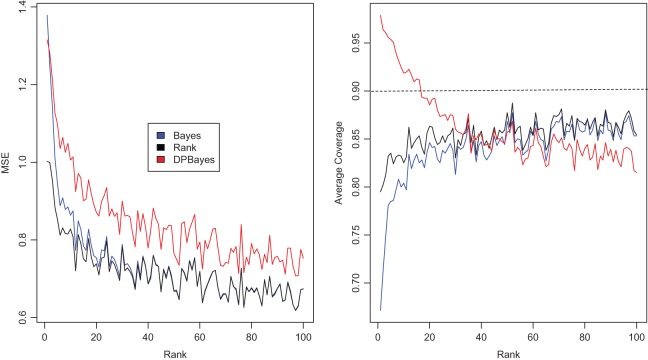
Figure 3.
Simulation study of Section 4.2 with the correct prior in (4.1) and parameter 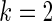 . The rank-conditional inference is the best in terms of MSE and non-parametric Bayes with Dirichlet prior is the close second best. The parametric Bayes is the distant third, with much larger MSE for
. The rank-conditional inference is the best in terms of MSE and non-parametric Bayes with Dirichlet prior is the close second best. The parametric Bayes is the distant third, with much larger MSE for 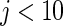 . For the actual coverage rates, non-parametric Bayes method with Dirichlet prior is the best and the rank-conditioned inference is the close second. The parametric Bayes again is the distant third due to its much lower actual coverage rates.
. For the actual coverage rates, non-parametric Bayes method with Dirichlet prior is the best and the rank-conditioned inference is the close second. The parametric Bayes again is the distant third due to its much lower actual coverage rates.
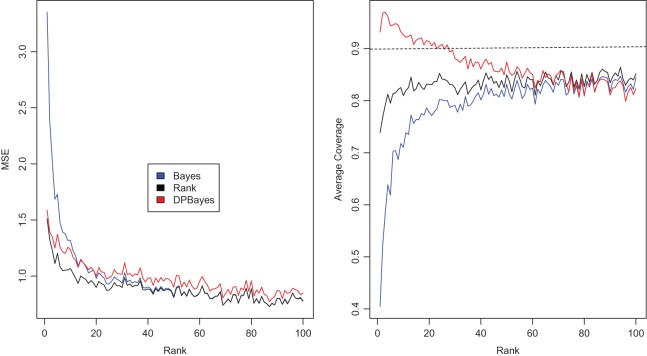
Figure 2.
Simulation study of Section 4.2 with the correct prior in (4.1) and parameter  . The rank-conditioned method has the smallest root mean square errors and close actual confidence rates. The parametric Bayes and non-parametric Bayes with Dirichlet prior perform badly due to the large mean square error especially for
. The rank-conditioned method has the smallest root mean square errors and close actual confidence rates. The parametric Bayes and non-parametric Bayes with Dirichlet prior perform badly due to the large mean square error especially for 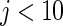 .
.
5. Application to breast cancer microarray dataset
We now apply our proposed method to the breast cancer data in Wang and others (2005). This was a large Affymetrix-based gene expression profiling study of 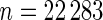 genes on 286 untreated patients with lymph node-negative primary breast cancer. The data are available at http://www.ncbi.nlm.nih.gov/geo/ as dataset GSE2034. We will compare gene expression level between patients who developed distant metastasis (74 subjects) and patients who were relapse-free at 5 years (135 subjects) among the 209 estrogen receptor positive patients. These data were also analyzed in Noma and others (2010). We use the gene expression model described in Section 2 with
genes on 286 untreated patients with lymph node-negative primary breast cancer. The data are available at http://www.ncbi.nlm.nih.gov/geo/ as dataset GSE2034. We will compare gene expression level between patients who developed distant metastasis (74 subjects) and patients who were relapse-free at 5 years (135 subjects) among the 209 estrogen receptor positive patients. These data were also analyzed in Noma and others (2010). We use the gene expression model described in Section 2 with 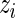 being the standardized sample mean difference in log gene expression level and
being the standardized sample mean difference in log gene expression level and 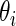 being the true standardized mean difference for the
being the true standardized mean difference for the 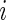 th gene. We have
th gene. We have 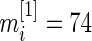 and
and 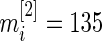 for all
for all  as there are no missing values for any gene. It then follows that
as there are no missing values for any gene. It then follows that 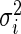 in (2.1) is
in (2.1) is 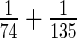 for all
for all 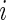 .
.
The maximum likelihood estimates of the parameters in the working prior  obtained by assuming models (2.1) and (2.3) for
obtained by assuming models (2.1) and (2.3) for 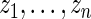 are
are
| η1 | μ1 | ω1 | η2 | μ2 | ω2 |
|---|---|---|---|---|---|
| 0.0856 | 0.258 | 0.0426 | 0.315 | −0.159 | 0.0470 |
which suggests about 40% of non-zero 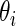 among
among 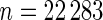 genes. In order to check the fit of the parametric prior
genes. In order to check the fit of the parametric prior 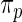 , we simulated new data from the fitted
, we simulated new data from the fitted 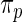 and compared its distribution to that of the original data through the following algorithm. Let
and compared its distribution to that of the original data through the following algorithm. Let 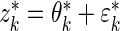 , where
, where 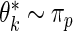 and
and 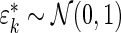 . The percentiles of
. The percentiles of 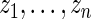 and
and 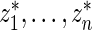 are given in the table below, which shows excellent fit of model
are given in the table below, which shows excellent fit of model  to data
to data 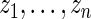 . As comparison, we also fit the model used in Noma and others (2010), which formulates in terms of the unstandardized log fold change
. As comparison, we also fit the model used in Noma and others (2010), which formulates in terms of the unstandardized log fold change 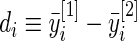 . Using notation of this paper, their model is
. Using notation of this paper, their model is
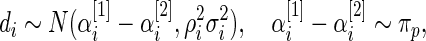 |
where 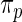 has form (2.3). The discrepancy between the percentiles of the original data
has form (2.3). The discrepancy between the percentiles of the original data  and the simulated new data
and the simulated new data 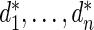 is much larger here. Modeling the standardized log fold change therefore provides much better fit to this dataset.
**
is much larger here. Modeling the standardized log fold change therefore provides much better fit to this dataset.
**
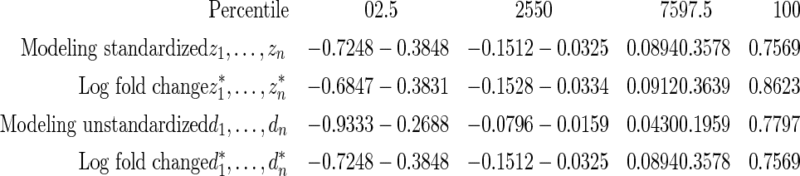 |
Coming back to the model in Section 2 and using the maximum likelihood estimates for 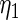 ,
, 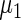 ,
, 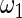 ,
, 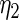 ,
, 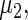 and
and 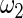 obtained above, the standard empirical Bayes estimates
obtained above, the standard empirical Bayes estimates 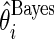 and the corresponding 90% confidence interval for all
and the corresponding 90% confidence interval for all 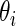 are then computed under
are then computed under 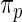 . Rank-conditioned estimates
. Rank-conditioned estimates 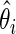 and 90% intervals are also calculated under both
and 90% intervals are also calculated under both  and the non-parametric update
and the non-parametric update 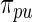 . Results for
. Results for 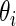 that correspond to the five lowest ranked
that correspond to the five lowest ranked 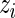
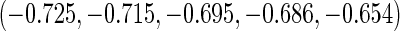 and to the five highest ranked
and to the five highest ranked 
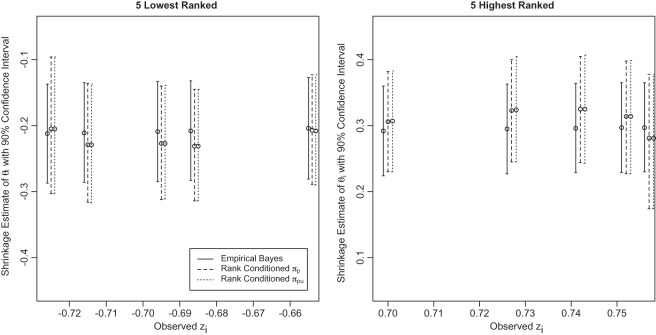
 are given in Figure 4 for the three methods. We make three observations. First, the three methods have a huge shrinkage effect on the raw estimate
are given in Figure 4 for the three methods. We make three observations. First, the three methods have a huge shrinkage effect on the raw estimate  for these top genes. For example,
for these top genes. For example, 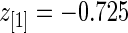 but
but 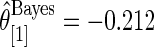 and
and 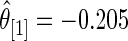 (under both
(under both  and
and 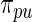 ). Second, results from empirical Bayes and rank-conditioned inference under
). Second, results from empirical Bayes and rank-conditioned inference under 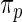 and
and 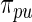 are very similar although the rank-conditioned confidence intervals are a little wider. The same is true for other
are very similar although the rank-conditioned confidence intervals are a little wider. The same is true for other 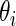 not shown in Figure 4. This is not surprising, given the excellent fit of working prior
not shown in Figure 4. This is not surprising, given the excellent fit of working prior  to
to 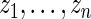 as discussed above. The agreement of the three methods and the robustness properties of the rank-conditioned inference should give us more confidence in the result. Third, an oddity of the rank-conditioned inference is that
as discussed above. The agreement of the three methods and the robustness properties of the rank-conditioned inference should give us more confidence in the result. Third, an oddity of the rank-conditioned inference is that 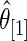 can be slightly larger than
can be slightly larger than 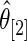 even though
even though  by definition. This happens when the difference in rank-conditioned bias for
by definition. This happens when the difference in rank-conditioned bias for 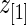 and
and 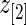 as random variables exceeds their observed difference in the observed
as random variables exceeds their observed difference in the observed 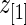 and
and  . The same can happen to estimates of other ranks. This is generally a small peculiarity that is appropriately accounted for by the wide confidence intervals.
. The same can happen to estimates of other ranks. This is generally a small peculiarity that is appropriately accounted for by the wide confidence intervals.
Figure 4.
Parametric empirical Bayes and rank-conditional inference of 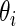 for the five lowest ranked and the five highest ranked
for the five lowest ranked and the five highest ranked 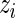 for the breast cancer dataset in Section 5.
for the breast cancer dataset in Section 5.
6. Discussion
We have proposed a rank-conditioned inference that can substantially improve the prior robustness of empirical Bayes inference with little loss of efficiency. More research is needed, however, to further develop and establish the proposed method. For example, in the simulations presented in Section 4, the actual coverage rates for the rank-conditioned intervals, in spite of being a substantial improvement over standard empirical Bayes, are still below the nominal 90% rate for 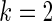 and
and  . We expect that it is possible to further improve the actual coverage rate by drawing on similar research in the empirical Bayes literature, such as in Morris (1983), Laird and Louis (1987), He (1992), Qiu and Gene Hwang (2007), and Gene Hwang and others (2009). Second, model (2.1) assumes that errors
. We expect that it is possible to further improve the actual coverage rate by drawing on similar research in the empirical Bayes literature, such as in Morris (1983), Laird and Louis (1987), He (1992), Qiu and Gene Hwang (2007), and Gene Hwang and others (2009). Second, model (2.1) assumes that errors 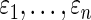 are independent, which can be unrealistic in many applications. We are currently working to relax this requirement to accommodate a more general correlation structure. Preliminary results show that the method in this paper continues to work well if the correlation of
are independent, which can be unrealistic in many applications. We are currently working to relax this requirement to accommodate a more general correlation structure. Preliminary results show that the method in this paper continues to work well if the correlation of 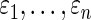 is mild. Details will be reported in a future manuscript. We hope this paper will stimulate more research in robust Bayes inference for large-scale data to meet the pressing analytical need in genomics and genetics.
is mild. Details will be reported in a future manuscript. We hope this paper will stimulate more research in robust Bayes inference for large-scale data to meet the pressing analytical need in genomics and genetics.
7. Software
Our R package rank.Shrinkage provides a ready-to-use implementation of the proposed methodology. The R code for the simulation studies is available at https://sites.google.com/site/jiangangliao/.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
L.G.L.’s and T.M.'s work was supported by Penn State Cancer Institute internal grant. Berg's work was supported by Grant Number UL1 TR000127 from the National Center for Advancing Translational Sciences (NCATS). The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
Supplementary Material
Acknowledgements
We are grateful for the extremely thorough review and suggestions by an anonymous reviewer and an associate editor, which led to a greatly improved manuscript. Conflict of Interest: None declared.
References
- Benjamini Y., Yekutieli D. False discovery rate-adjusted multiple confidence intervals for selected parameters. Journal of the American Statistical Association. 2005;100(469):71–81. [Google Scholar]
- Choe S. E., Boutros M., Michelson A. M., Church G. M., Halfon M. S. Preferred analysis methods for affymetrix genechips revealed by a wholly defined control dataset. Genome Biology. 2005;6(2):16. doi: 10.1186/gb-2005-6-2-r16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do K. A., Müller P., Tang F. A Bayesian mixture model for differential gene expression. Journal of the Royal Statistical Society. 2005;54(3):627–644. [Google Scholar]
- Dunson D. B. Nonparametric Bayes applications to biostatistics. Bayesian Nonparametrics. 2010;28:223. [Google Scholar]
- Dunson D. B., Taylor J. A. Approximate Bayesian inference for quantiles. Nonparametric Statistics. 2005;17(3):385–400. [Google Scholar]
- Efron B. Microarrays, empirical Bayes and the two-groups model. Statistical Science. 2008;23(1):1–22. [Google Scholar]
- Efron B. Large-Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction. Volume 1. Cambridge: Cambridge University Press; 2010. [Google Scholar]
- Efron B., Tibshirani R., Storey J. D., Tusher V. Empirical Bayes analysis of a microarray experiment. Journal of the American Statistical Association. 2001;96(456):1151–1160. [Google Scholar]
- Eggermont P. P. B., LaRiccia V. N. Nonlinearly smoothed EM density estimation with automated smoothing parameter selection for nonparametric deconvolution problems. Journal of the American Statistical Association. 1997;92(440):1451–1458. [Google Scholar]
- Gene Hwang J. T., Qiu J., Zhao Z. Empirical Bayes confidence intervals shrinking both means and variances. Journal of the Royal Statistical Society. 2009;71(1):265–285. [Google Scholar]
- Ghosh D. Empirical Bayes methods for estimation and confidence intervals in high-dimensional problems. Statistica Sinica. 2009;19(1):125. [Google Scholar]
- Gu J., Ghosal S. Bayesian ROC curve estimation under binormality using a rank likelihood. Journal of Statistical Planning and Inference. 2009;139(6):2076–2083. [Google Scholar]
- Guo L., Lobenhofer E. K., Wang C., Shippy R., Harris S. C., Zhang L., Mei N., Chen T., Herman D., Goodsaid F. M. Rat toxicogenomic study reveals analytical consistency across microarray platforms. Nature Biotechnology. 2006;24(9):1162–1169. doi: 10.1038/nbt1238. [DOI] [PubMed] [Google Scholar]
- He K. Parametric empirical Bayes confidence intervals based on James-Stein estimator. Statistics and Decisions. 1992;10(1–2):121–132. [Google Scholar]
- Hoff P. D. Extending the rank likelihood for semiparametric copula estimation. The Annals of Applied Statistics. 2007;1(1):265–283. [Google Scholar]
- Ishwaran H., Rao J. S. Spike and slab variable selection: frequentist and Bayesian strategies. The Annals of Statistics. 2005;33(2):730–773. [Google Scholar]
- Jara A., Hanson T. E., Quintana F. A., Müller P., Rosner G. L. DPpackage: Bayesian non-and semi-parametric modelling in R. Journal of Statistical Software. 2011;40(5):1. [PMC free article] [PubMed] [Google Scholar]
- Jeffries N. O. Ranking bias in association studies. Human Heredity. 2009;67(4):267–275. doi: 10.1159/000194979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kendziorski C. M., Newton M. A., Lan H., Gould M. N. On parametric empirical Bayes methods for comparing multiple groups using replicated gene expression profiles. Statistics in Medicine. 2003;22(24):3899–3914. doi: 10.1002/sim.1548. [DOI] [PubMed] [Google Scholar]
- Kim S., Dahl D. B., Vannucci M. Spiked Dirichlet process prior for Bayesian multiple hypothesis testing in random effects models. Bayesian Analysis. 2009;4(4):707–732. doi: 10.1214/09-BA426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird N. M., Louis T. A. Empirical Bayes confidence intervals based on bootstrap samples. Journal of the American Statistical Association. 1987;82(399):739–750. [Google Scholar]
- Morris C. N. Parametric empirical Bayes inference: theory and applications. Journal of the American Statistical Association. 1983;78(381):47–55. [Google Scholar]
- Muralidharan O. An empirical Bayes mixture method for effect size and false discovery rate estimation. The Annals of Applied Statistics. 2010;4(1):422–438. [Google Scholar]
- Newton M. A., Kendziorski C. M., Richmond C. S., Blattner F. R., Tsui K. W. On differential variability of expression ratios: improving statistical inference about gene expression changes from microarray data. Journal of Computational Biology. 2001;8(1):37–52. doi: 10.1089/106652701300099074. [DOI] [PubMed] [Google Scholar]
- Newton M. A., Noueiry A., Sarkar D., Ahlquist P. Detecting differential gene expression with a semiparametric hierarchical mixture method. Biostatistics. 2004;5(2):155–176. doi: 10.1093/biostatistics/5.2.155. [DOI] [PubMed] [Google Scholar]
- Noma H., Matsui S., Omori T., Sato T. Bayesian ranking and selection methods using hierarchical mixture models in microarray studies. Biostatistics. 2010;11(2):281–289. doi: 10.1093/biostatistics/kxp047. [DOI] [PubMed] [Google Scholar]
- Qiu J., Gene Hwang J. T. Sharp simultaneous confidence intervals for the means of selected populations with application to microarray data analysis. Biometrics. 2007;63(3):767–776. doi: 10.1111/j.1541-0420.2007.00770.x. [DOI] [PubMed] [Google Scholar]
- Smyth G. K. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Statistical Applications in Genetics and Molecular Biology. 2004;3(1):3. doi: 10.2202/1544-6115.1027. [DOI] [PubMed] [Google Scholar]
- Vardi Y., Shepp L. A., Kaufman L. A statistical model for positron emission tomography. Journal of the American Statistical Association. 1985;80(389):8–20. [Google Scholar]
- Wang Y., Klijn J. G. M., Zhang Y., Sieuwerts A. M., Look M. P., Yang F., Talantov D., Timmermans M., Meijer-van Gelder M. E., Yu J. and others. Gene-expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer. The Lancet. 2005;365(9460):671–679. doi: 10.1016/S0140-6736(05)17947-1. [DOI] [PubMed] [Google Scholar]
- Westfall P. H. Comment. Journal of the American Statistical Association. 2005;100(469):85–89. doi: 10.1198/016214504000001817. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.