Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Nov 11;13(12):5880–5885. doi: 10.1021/nl402722n

The Electronic Structure of CdSe/CdS Core/Shell Seeded Nanorods: Type-I or Quasi-Type-II?

Hagai Eshet †, Michael Grünwald ‡, Eran Rabani †,*
PMCID: PMC3862461  PMID: 24215466

Abstract

graphic file with name nl-2013-02722n_0006.jpg

The electronic structure of CdSe/CdS core/shell seeded nanorods of experimentally relevant size is studied using a combination of molecular dynamics and semiempirical pseudopotential techniques with the aim to address the transition from type-I to a quasi-type-II band alignment. The hole is found to be localized in the core region regardless of its size. The overlap of the electron density with the core region depends markedly on the size of the CdSe core. For small cores, we observe little overlap, consistent with type-II behavior. For large cores, significant core-overlap of a number of excitonic states can lead to type-I behavior. When electron–hole interactions are taken into account, the core-overlap is further increased. Our calculations indicate that the observed transition from type-II to type-I is largely due to simple volume effects and not to band alignment.

Keywords: Seeded nanorods, core/shell nanorods, electronic structure

Rod-shaped semiconductor nanocrystals1 represent a class of nanostructures in which the optical and electronic properties can be tuned by changing the composition, dimensions, and shape, offering an ideal model system to study fundamental properties and in particular, the transition between zero- and one-dimensional confinement. Recent developments in the fabrication of core/shell seeded nanorods2−6 have provided an additional knob by which the electrons/holes can either be confined to the core region or the shell. This leads in some cases to a desired intrinsic charge separation7 useful for optocatalytic devices.8,9 In other cases, where both electrons and holes are confined to the same region, the nanostructures show remarkable bright and stable fluorescence.3,4 These unique features of semiconductor nanorod heterostructures hold the promise to advance future light-harvesting devices.

Perhaps the most studied of the core/shell nanorod structures is that of CdSe core with a CdS shell.2 The hole is known to be localized at the CdSe core due to the large valence band offsets between CdSe and CdS. On the other hand, the conduction band offsets are quite small in the bulk, and thus, the electron can either be localized at the core or at the shell, depending on the size of the core, leading to a possible transition from a type-I to a quasi-type-II band alignment. This has been the focus of numerous experimental and theoretical studies.

Early work using lifetime measurements combined with model calculations hinted to a flat band alignment in which case the electron is confined to the CdS shell and the system is considered to be a quasi-type-II, regardless of the size of the CdSe core.10,11 More recent experiments based on scanning tunneling spectroscopy (STS) analyzed by a simple effective mass model suggested a conduction band offset of 0.3 eV, which in principle, would lead to a transition from type-I to quasi-type-II band alignment as the size of the CdSe core decreases.12 This apparent controversy has been addressed using multiexciton spectroscopy (MES) for nanorods with different core sizes, confirming that a transition from type-I (where the electron is localized at the core) to a quasi-type-II (where it is localized at the shell) occurs for a core diameter of 2.8 nm.13

Of course, a direct comparison between the STS and MES measurements must be done with care, as the former ignores the interactions between the electron and the localized holes, and thus may lead to a more diffuse electronic state compared to the excitonic state. In fact, the magnitude of this effect has not been addressed so far and will be discussed herein. To add more confusion, this debatable problem has been revisited very recently using time-resolved photoluminescence and transient absorption spectroscopies,14 showing that the radiative recombination rate is independent of the CdSe core size, consistent with a quasi-type-II band alignment for all the system sizes studied (i.e., cores above 2 nm). Other recent experimental studies have also revealed the spatial distribution of the wave function15,16 and long-lived exciton states in CdSe/CdS dot-in-rod structures.17

This controversy has also attracted numerous theoretical and computational studies. Using first-principle calculations, Luo and Wang18 have examined the band alignment of a CdSe/CdS core/shell seeded nanorod (dimensions 4.3 × 15.5 nm) for a core diameter of 3.4 nm, finding that the hole is localized inside the CdSe core and the electron in the CdS shell. Because the core size is larger than the expected transition (2.8 nm) it contradicts some measurements and calls for a systematic study of the band alignment with the core size.

An alternative approach based on an effective mass model was recently developed by Shabaev et al.19 for “giant” CdSe/CdS core/shell nanostructures. They find that the Coulomb potential created by strongly confined holes plays an important role in the electron confinement, a point overlooked by previous studies. Shabaev et al. also examined the effects of core size and CdSe/CdS conduction band offset dependencies on the electronic properties of the nanorod. They found that depending on the band offset, a transition from type-I to quasi-type-II may occur. However, their approach does not provide a quantitative prediction of the actual band offset in CdSe/CdS nanostructures.

In this work, we calculate the electronic structure of CdSe/CdS core/shell nanorods of 20 nm length. We consider two different values of rod diameter, 4 and 6 nm, and a number of different core sizes (2–4.5 nm). The rods are faceted, and the spherical CdSe core was placed at one-third of the length of the rod. The configurations used for the calculations are equilibrium structures relaxed with molecular dynamics runs of 100 ps duration at a temperature of 300 K. For these runs, interactions between atoms were described by a recently developed force-field,20 which has been shown to accurately describe CdSe/CdS heterostructures.20,21 The final configuration was quenched to remove structural effects of thermal fluctuations. (See Supporting Information for a detailed description of simulation methods.)

The electronic structure calculations of the seeded nanorods were performed within the local version of the semiempirical pseudopotential model,22−24 where the local screened pseudopotentials were fitted to reproduce the experimental bulk band structure, band gaps, effective masses, and so forth. Furthermore, ligand potentials were used to represent the passivation layer.25 For cadmium and selenium atoms, we have used the pseudopotential developed for CdSe25 while for sulfur atoms we have fitted the bulk properties of CdS using the existing pseudopotential for cadmium atoms.26 The pseudopotential for CdS gives a flat band alignment with CdSe in the bulk.27 The filter-diagonalization technique28 was then employed to filter nearly 40 single particle states near the bands edge. These states were then used to solve the Bethe-Salpeter equation. In order to compare the results to the non-interacting case, we used only one hole state, such that all excitations are associated with electron transitions. We verified that including more hole states does not affect the electron density but adds more excitations associated with hole transitions.

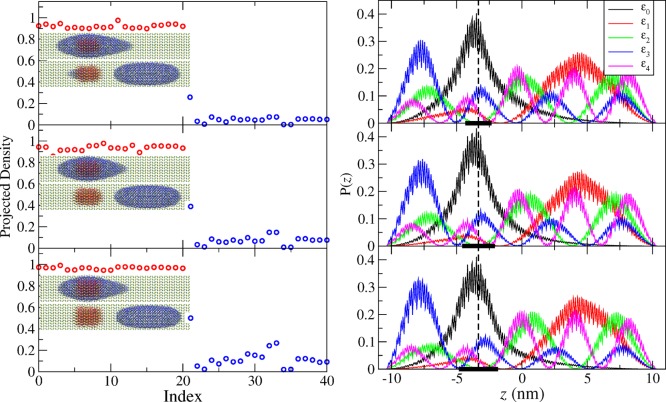
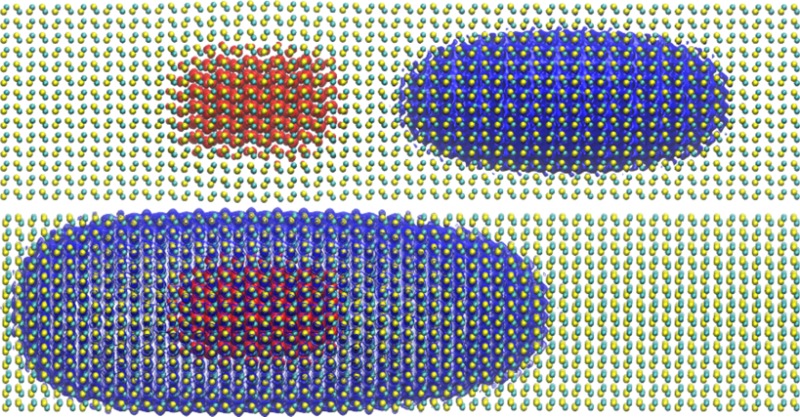
In the left panels of Figure 1 we plot the integrated projected valence (red circles) and conduction (blue circles) densities onto the core for ∼20 levels below the valence band maximum and ∼20 levels above the conduction band minimum. The results are shown for a fixed shell size (4 × 20 nm) and for core diameters that vary between 2 and 3 nm from top to bottom. The inset in each panel shows the hole density of the top of the valence band (red isosurface) and electron density of the two lowest states of the conduction band (blue isosurface), all superimposed on the nanorod frame.

Figure 1.

Figure 1

Open in a new tab

Integrated projected hole (red circles) and electron (blue circles) densities onto the core (left panels) and the corresponding electron density for the five lowest electron levels (right) for a 4 × 20 nm CdSe/CdS seeded nanorod. The seed diameters (from top to bottom) are 2, 2.5, and 3 nm. The dashed vertical line shows the position of the center of the core and the solid black line superimposed in the x-axis represents the core region, which is centered at z = −6.67 nm. Insets (left panels) show the hole (red) and electron (blue) density isosurfaces for the valence band maximum and the two lowest conduction band states.

We find that for all valence states calculated, the value of the integrated projected density of the hole is close to unity, implying that the hole is localized in the core with a small probability to leak into the shell region. By contrast, the overlap of the lowest conduction states with the core region depends markedly on core size. For the smallest core considered here (2 nm), we find appreciable, but minor, core-overlap of electron density only for the lowest conduction state. All higher states are delocalized in the shell region. With increasing core size, the core-overlap of the lowest state, as well as of a number of higher states, increases markedly, as could be expected from a transition from type-II to type-I band alignment.

The observed increase in core-overlap, however, is not primarily caused by a substantial change in band alignment. In the right panels of Figure 1, we plot the electron densities of the five lowest conduction states, projected onto the nanorod axis. As the core size increases, these densities change only slightly, as can also be seen in the insets of the left panels of Figure 1. The biggest contribution to the observed increase in core-overlap thus stems from the increasing core-volume itself. This result indicates that the transition between type-I and type-II behavior is a gradual one. The threshold value of core size at which different behavior is observed will therefore likely depend on the nature of the experimental measurement.

We obtain similar results for a thicker nanorod of the same length (6 × 20 nm) with core sizes ranging from 2.5 to 4.5 nm (see Figure 2). Like in the case of the thinner nanorod, all calculated valence states are highly localized in the core region. Conduction states show an increase in core-overlap with increasing core size. Comparing rods of different diameter, we find that the overlap of the lowest conduction state with the core decreases as the shell diameter increases, consistent with the decrease of the conduction level with increasing nanorod diameter.

Figure 2.

Figure 2

Open in a new tab

Same as Figure 1 but for a 6 × 20 nm CdSe/CdS seeded nanorod with seed diameters (from top to bottom) of 2.5, 3.5, and 4.5 nm.

This quasi-particle picture is consistent with recent low-temperature STS measurements, suggesting that the electron is somewhat delocalized in the nanorod with a notable amplitude in the core region.12 However, a direct comparison of our predictions with results from STS should be carried out with care. Because the typical broadening in the scanning tip (∼100 meV) is larger than the level spacing in the conduction band (∼30 meV), the transmission is likely to occur through a combination of conduction states rather than a single state. This makes a direct comparison of the degree of localization quite hard. Yet, our results for the lowest conduction state agree well with the experimental observation that tunneling through the lowest conduction state diminishes as one moves the tip away from the region of the core.12

The single-particle picture discussed in Figures 1 and 2 might be substantially modified when electron–hole interactions are taken into account.19 In fact, most experimental studies on the band alignment of CdSe/CdS core/shell nanorods are based on optical measurements in which an exciton is formed and the magnitude of the electron–hole interactions provides a measure of the degree of localization. This is particularly important for situations when the hole is localized at the core and can bind strongly the electron, thereby increasing its overlap with the core.19 Furthermore, this effect will be strongest for small cores and might therefore be expected to substantially shift the value of core size at which the type-I/type-II transition is observed.

Including the interactions between the electron and the hole is a subtle issue for nanorods, since perturbative techniques that work well for spherical nanocrystals often fail in nanorods as a result of small level spacing.19,29 Here, we resort to the Bethe–Salpeter approach30 within the static screening approximation, where excited states are obtained by diagonalizing the Bethe–Salpeter equation (BSE) with an exciton Hamiltonian give by31

graphic file with name nl-2013-02722n_m001.jpg

where |ϕt⟩ are the single particle states with energies εt; a,b label virtual states and i,j label occupied states; W and V are the screened and bare Coulomb potentials, respectively.

In Figure 3, we show the results for the projected electron density onto the core obtained from the BSE (green circles) for the 4 × 20 nm (left panel) and 6 × 20 nm (right panel). For comparison, we also include the integrated projected valence (red circles) and conduction (blue circles) densities onto the core for the non-interacting case shown in Figure 1 and Figure 2.

Figure 3.

Figure 3

Open in a new tab

Projected electron densities obtained from the BSE for a CdSe/CdS seeded nanorod (green circles) along with the projected valence (red circles) and conduction (blue circles) densities for the non-interacting case. Left and right panels show results for 4 × 20 and 6 × 20 nm rods, respectively. The core diameter (from top to bottom) is 2.5, 3, and 3.5 nm for the left panels and 2.5, 3.5, and 4.5 nm for the right panels. Corresponding insets show the hole density (red) and the electron density (blue) for the two lowest excitonic states associated.

Comparing the maximal value of the electron projected density for the lowest excitonic state, it is clear that including the electron–hole interactions leads to an increase of the overlap of the electron wave function with the core, as one might expect. A pronounced effect is also seen for higher excited states. We find two additional excitonic states that are highly localized near the core region (particularly for the larger seeds). These states may well be associated with recent reports on spatially separated long-lived exciton states in CdSe/CdS nanorods.17

The observed changes in the degree of core-overlap are partly due to marked changes in the shape of electronic densities. The insets for each panel in Figure 3 show the hole density of the top of the valence band (red isosurface) and electron density of the two lowest states of the conduction band (blue isosurface), all superimposed on the nanorod frame. Similar to the non-interacting cases shown in the insets of Figures 1 and 2, the isosurface of the lowest state is centered around the core region. The inclusion of electron–hole interactions via the BSE leads to a somewhat tighter electron density around the seed. The density of the second lowest state, however, is profoundly modified from the non-interacting cases, where the electron is mostly confined to the shell region away from the core. In the interacting case, we observe a dumbbell-like shape of the isosurface, centered around the core region.

The general trend of increasing core-overlap with core-size remains unchanged by introducing electron–hole interactions. Like in the non-interacting case, the main contribution to this increase is the increasing core-volume itself, rather than a substantial shift in band alignment. Furthermore, we do not observe a strong effect of core-size on the strength of electron–hole interactions, which would lead to increased localization of electrons in the core primarily for small cores.

In Table 1, we summarize the relevant energies calculated for the relaxed nanorods configurations. The quasi-particle gaps and the exciton energies for the seeded nanorods are slightly lower (∼0.1 eV) compared to experimental results.13 This is likely because the pseudopotential used in the electronic structure calculations was optimized for a perfect lattice configuration in the neat CdSe and CdS bulk systems, while our calculations were performed for a relaxed heterostructure. The small overall change in the band gap with the core size (roughly 0.2 eV going from Dcore = 2.5–4.5 nm) is in agreement with the photoluminescence experiments.13 The shift in the position of the hole level is larger than that of the electron since the latter overlaps the shell, which is kept fixed in this process. This is also consistent with STS measurements.12 We find that the conduction band minimum is always below that of a neat CdSe NC (results not shown here)25 for all sizes studied, confirming a very shallow band offset between the core and the shell for the electrons.

Table 1. Energies, Lifetimes, and Oscillator Strengths for CdSe/CdS Seeded Nanorodsa.

Dshell Dcore Ev Ec Eg Eex ΔEex τ (ns) f
4 0 –6.60 –4.01 2.59        
4 2 –6.38 –4.10 2.28 2.14 0.46 33 0.94
4 2.5 –6.31 –4.10 2.21 2.05 0.35 31 1.24
4 3 –6.25 –4.10 2.15 2.00 0.23 30 1.50
6 2.5 –6.35 –4.20 2.15 2.00 0.39 39 0.88
6 3.5 –6.25 –4.21 2.04 1.90 0.27 37 1.28
6 4.5 –6.15 –4.21 1.94 1.82 0.23 36 1.66
Open in a new tab
a

Calculated energies (in eV) for the top of the valence band (Ev), bottom of the conduction band (Ec), quasi-particle band gap (Eg), first exciton energies obtained within the BSE (Eex), and the energy difference between the first exciton in the core-only and core/shell structures (ΔEex) for CdSe/CdS core/shell seeded nanorods of different dimensions (in nm).f = [(4meE0)/(3ℏ2e2)]μ2 is the oscillator strength for the lowest exciton transition of energy E0 with transition dipole μ and τ is the radiative lifetime (assuming that for the lowest transition the index of refraction is close to 1).32

Table 1 also shows the energy difference between the first exciton in the core-only and core/shell structures (ΔEex) and the radiative lifetime (τ). These are also plotted in Figure 4. These quantities depend weakly on the length of the nanorod but show a pronounced effect with the core diameter and rod diameter. The calculated values are compared with the experimental results for the shift in the absorption peak and the radiative lifetime,15 a comparison that can serve to further assess the accuracy of the model. The experimental energy shifts vary from 0.34 to 0.16 eV when the core size increases from 2.2 to 3.3 nm in diameter. The theoretical values are slightly larger than the corresponding experimental results. However, our model captures the general trends with core size and the slope of ΔEex is similar. The comparison is complicated by the fact that experimental values were obtained for nanorods with different (shell) diameters, and no uncertainties are provided in ref (15) for the values of core diameter (or how these values were determined). Assuming a standard deviation of 0.5 nm, as quoted for the values of shell diameter, our results agree quantitatively with experiments.

Figure 4.

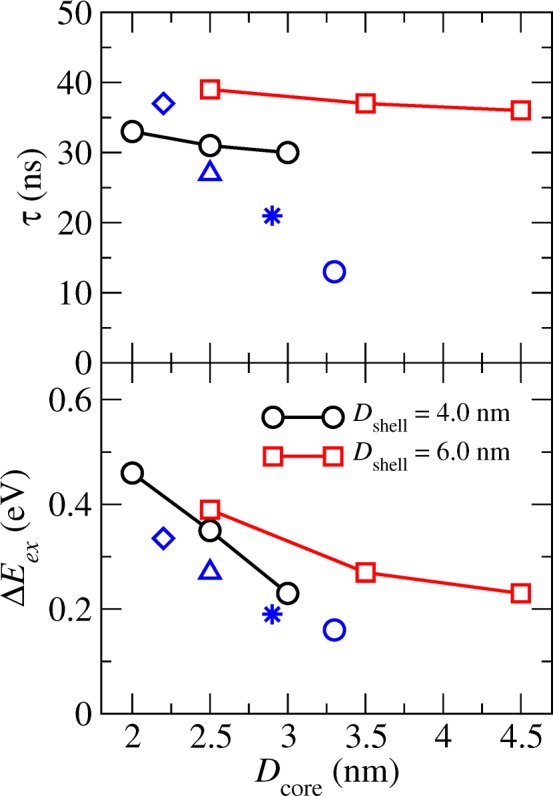
Figure 4

Open in a new tab

Plots of ΔEex (lower panel) and τ (upper panel) versus core diameter. Blue symbols are experimental results taken from ref (15). The shell thickness is 4.7 ± 0.5, 4.8 ± 0.5, 4.5 ± 0.5, and 4.1 ± 0.4 nm for the blue diamond, triangle, star, and circle, respectively.

Comparing the radiative lifetimes to the experimental values, we find that in both cases τ decreases with increasing core diameter. The lifetimes are very similar for the smaller cores (on the order of 30 ns), while for the larger cores, we overestimate the lifetimes by more than 50%. The discrepancy may indicate that for larger cores there are defects located at the interface between the two semiconductors that are not included in our model and may affect the slope of the lifetime with core diameter. Alternatively, the experimental lifetimes may include contributions from non-radiative decay, again not included in the theory. The non-radiative decay is expected to be more significant for large cores as the density of phonons changes with the core volume.

Finally, Table 1 also provides the values of the oscillator strength, which increases rapidly with the core size and decreases with the nanorod diameter. The dependence on the core and rod diameters can be explained in terms of the extent of electron localization and the effect of the core and nanorod dimensions on the overlap of the electron wave function with the core, as reported above.

In summary, we have used a combination of molecular dynamics and electronic structure simulation techniques to study the electronic properties of CdSe/CdS core/shell seeded nanorods. For all system sizes considered here, we find strong localization of the hole in the core of the nanorod. The overlap of conduction states with the core region depends on core size. For small cores, minor overlap occurs for the lowest conduction state only; for larger cores, sizable overlap is observed for a number of conduction states. When electron–hole interactions are taken into account, the core-overlap of conduction states increases but the same trend with core size is observed, which is consistent with experimental observations of a transition from type-I to quasi-type-II behavior with decreasing core size. Our results indicate that this transition is not primarily driven by a change in band-alignment, but rather by the change in core volume itself.

Acknowledgments

We would like to thank Uri Banin for insightful discussions. H.E. is grateful to The Center for Nanoscience and Nanotechnology at Tel Aviv University for a postdoctoral fellowship. M.G. was supported by the Austrian Science Fund (FWF) under Grant J 3106-N16. This work was supported by the Israel Science Foundation (Grant 611/11). E.R. thanks the Marko and Lucie Chaoul Chair.

Supporting Information Available

Additional information and figure. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

nl402722n_si_001.pdf (303.8KB, pdf)

References

  1. Peng X.; Manna L.; Yang W.; Wickham J.; Scher E.; Kadavanich A.; Alivisatos A. P. Shape control of CdSe nanocrystals. Nature 2000, 404, 59. [DOI] [PubMed] [Google Scholar]
  2. Talapin D.; Koeppe R.; Gotzinger S.; Kornowski A.; Lupton J.; Rogach A.; Benson O.; Feldmann J.; Weller H. Highly Emissive Colloidal CdSe/CdS Heterostructures of Mixed Dimensionality. Nano Lett. 2003, 3, 1677–1681. [Google Scholar]
  3. Carbone L.; et al. Synthesis and Micrometer-Scale Assembly of Colloidal CdSe/CdS Nanorods Prepared by a Seeded Growth Approach. Nano Lett. 2007, 7, 2942–2950. [DOI] [PubMed] [Google Scholar]
  4. Talapin D. V.; Nelson J. H.; Shevchenko E. V.; Aloni S.; Sadtler B.; Alivisatos A. P. Seeded Growth of Highly Luminescent CdSe/CdS Nanoheterostructures with Rod and Tetrapod Morphologies. Nano Lett. 2007, 7, 2951–2959. [DOI] [PubMed] [Google Scholar]
  5. Dorfs D.; Salant A.; Popov I.; Banin U. ZnSe quantum dots within CdS nanorods: A seeded-growth type-II system. Small 2008, 4, 1319–1323. [DOI] [PubMed] [Google Scholar]
  6. Sitt A.; Salant A.; Menagen G.; Banin U. Highly Emissive Nano Rod-in-Rod Heterostructures with Strong Linear Polarization. Nano Lett. 2011, 11, 2054–2060. [DOI] [PubMed] [Google Scholar]
  7. Costi R.; Cohen G.; Salant A.; Rabani E.; Banin U. Electrostatic Force Microscopy Study of Single Au-CdSe Hybrid Nanodumbbells: Evidence for Light-Induced Charge Separation. Nano Lett. 2009, 9, 2031–2039. [DOI] [PubMed] [Google Scholar]
  8. Costi R.; Saunders A. E.; Elmalem E.; Salant A.; Banin U. Visible Light-Induced Charge Retention and Photocatalysis with Hybrid CdSe-Au Nanodumbbells. Nano Lett. 2008, 8, 637–641. [DOI] [PubMed] [Google Scholar]
  9. Amirav L.; Alivisatos A. P. Photocatalytic Hydrogen Production with Tunable Nanorod Heterostructures. J. Phys. Chem. Lett. 2010, 1, 1051–1054. [Google Scholar]
  10. Muller J.; Lupton J.; Rogach A.; Feldmann J.; Talapin D.; Weller H. Monitoring surface charge movement in single elongated semiconductor nanocrystals. Phys. Rev. Lett. 2004, 93, 167402. [DOI] [PubMed] [Google Scholar]
  11. Muller J.; Lupton J.; Lagoudakis P.; Schindler F.; Koeppe R.; Rogach A.; Feldmann J.; Talapin D.; Weller H. Wave Function Engineering in Elongated Semiconductor Nanocrystals with Heterogeneous Carrier Confinement. Nano Lett. 2005, 5, 2044–2049. [DOI] [PubMed] [Google Scholar]
  12. Steiner D.; Dorfs D.; Banin U.; Della Sala F.; Manna L.; Millo O. Determination of Band Offsets in Heterostructured Colloidal Nanorods Using Scanning Tunneling Spectroscopy. Nano Lett. 2008, 8, 2954–2958. [DOI] [PubMed] [Google Scholar]
  13. Sitt A.; Della Sala F.; Menagen G.; Banin U. Multiexciton Engineering in Seeded Core/Shell Nanorods: Transfer from Type-I to Quasi-Type-Ii Regimes. Nano Lett. 2009, 9, 3470–3476. [DOI] [PubMed] [Google Scholar]
  14. She C.; Demortiére A.; Shevchenko E. V.; Pelton M. Using Shape To Control Photoluminescence from CdSe/CdS Core/Shell Nanorods. J. Phys. Chem. Lett. 2011, 2, 1469–1475. [Google Scholar]
  15. Raino G.; Stöferle T.; Moreels I.; Gomes R.; Kamal J. S.; Hens Z.; Mahr R. F. Probing the Wave Function Delocalization in CdSe/CdS Dot-in-Rod Nanocrystals by Time- and Temperature-Resolved Spectroscopy. ACS Nano 2011, 5, 4031–4036. [DOI] [PubMed] [Google Scholar]
  16. Kunneman L. T.; Zanella M.; Manna L.; Siebbeles L. D. A.; Schins J. M. Mobility and Spatial Distribution of Photoexcited Electrons in CdSe/CdS Nanorods. J. Phys. Chem. C 2013, 117, 3146–3151. [Google Scholar]
  17. Wu K.; Rodriguez-Cordoba W. E.; Liu Z.; Zhu H.; Lian T. Beyond Band Alignment: Hole Localization Driven Formation of Three Spatially Separated Long-Lived Exciton States in CdSe/CdS Nanorods. ACS Nano 2013, 7, 7173–7185. [DOI] [PubMed] [Google Scholar]
  18. Luo Y.; Wang L.-W. Electronic Structures of the CdSe/CdS Core-Shell Nanorods. ACS Nano 2010, 4, 91–98. [DOI] [PubMed] [Google Scholar]
  19. Shabaev A.; Rodina A. V.; Efros A. L. Fine structure of the band-edge excitons and trions in CdSe/CdS core/shell nanocrystals. Phys. Rev. B 2012, 86, 205311. [Google Scholar]
  20. Gruenwald M.; Zayak A.; Neaton J. B.; Geissler P. L.; Rabani E. Transferable pair potentials for CdS and ZnS crystals. J. Chem. Phys. 2012, 136, 234111. [DOI] [PubMed] [Google Scholar]
  21. Grünwald M.; Lutker K.; Alivisatos A. P.; Rabani E.; Geissler P. L. Metastability in Pressure-Induced Structural Transformations of CdSe/ZnS Core/Shell Nanocrystals. Nano Lett. 2013, 13, 1367–1372. [DOI] [PubMed] [Google Scholar]
  22. Wang L. W.; Zunger A. Electronic Structure Pseudopotential Calculations of Large (∼1000 atoms) Si Quantum Dots. J. Phys. Chem. 1994, 98, 2158. [Google Scholar]
  23. Zunger A.; Wang L. W. Appl. Surf. Sci. 1996, 350, 636. [Google Scholar]
  24. Williamson A. J.; Zunger A. Phys. Rev. B 2000, 61, 1978. [Google Scholar]
  25. Rabani E.; Hetényi B.; Berne B. J.; Brus L. E. Electronic Properties of CdSe Nanocrystals in the Absence and Presence of a Dielectric Medium. J. Chem. Phys. 1999, 110, 5355–5369. [Google Scholar]
  26. We use the following form for the local pseudopotential in momentum space: V(q) = (a1(q2 – a2))/(a3ea4q2 + 1) . The parameters for cadmium are a1 = 0.219, a2 = 0.936, a3 = 0.196, and a4 = 1.68. For selenium: a1 = −0.0291, a2 = 4.40, a3 = −1.20, and a4 = 0.318. For sulfur: a1 = −0.0321, a2 = 4.366, a3 = −1.21, and a4 = 0.282 in atomic units.
  27. Peng X.; Schlamp M. C.; Kadavanich A. V.; Alivisatos A. P. Epitaxial Growth of Highly Luminescent CdSe/CdS Core/Shell Nanocrystals with Photostability and Electronic Accessibility. J. Am. Chem. Soc. 1997, 119, 7019–7029. [Google Scholar]
  28. Toledo S.; Rabani E. Very Large Electronic Structure Calculations Using an Out-of-Core Filter-Diagonalization Method. J. Comput. Phys. 2002, 180, 256–269. [Google Scholar]
  29. Shabaev A.; Efros A. 1D Exciton Spectroscopy of Semiconductor Nanorods. Nano Lett. 2004, 4, 1821–1825. [Google Scholar]
  30. Bethe H.; Salpeter E. A Relativistic Equation for Bound-State Problems. Phys. Rev. 1951, 84, 1232. [Google Scholar]
  31. Rohlfing M.; Louie S. G. Phys. Rev. B 2000, 62, 4927. [DOI] [PubMed] [Google Scholar]
  32. Jain P. K.; Ghosh D.; Baer R.; Rabani E.; Alivisatos A. P. Near-Field Manipulation of Spectroscopic Selection Rules on the Nanoscale. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 8016–8019. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl402722n_si_001.pdf (303.8KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES