Origin of parameter degeneracy and molecular shape relationships in geometric-flow calculations of solvation free energies

Abstract

Implicit solvent models are important tools for calculating solvation free energies for chemical and biophysical studies since they require fewer computational resources but can achieve accuracy comparable to that of explicit-solvent models. In past papers, geometric flow-based solvation models have been established for solvation analysis of small and large compounds. In the present work, the use of realistic experiment-based parameter choices for the geometric flow models is studied. We find that the experimental parameters of solvent internal pressure p = 172 MPa and surface tension γ = 72 mN/m produce solvation free energies within 1 RT of the global minimum root-mean-squared deviation from experimental data over the expanded set. Our results demonstrate that experimental values can be used for geometric flow solvent model parameters, thus eliminating the need for additional parameterization. We also examine the correlations between optimal values of p and γ which are strongly anti-correlated. Geometric analysis of the small molecule test set shows that these results are inter-connected with an approximately linear relationship between area and volume in the range of molecular sizes spanned by the data set. In spite of this considerable degeneracy between the surface tension and pressure terms in the model, both terms are important for the broader applicability of the model.

INTRODUCTION

Implicit solvent models have received much attention in the past two decades due to their low computational cost and relatively high accuracy. Such models consist of a “nonpolar” free energy functional that accounts for cavity creation and dispersive interactions and a polar free energy functional that accounts for the difference in charging free energies of the solute between vacuum and solvent. While both of these terms depend on the solute-solvent boundary position and the resulting position-dependent dielectric, the polar and nonpolar functionals are often optimized independently. For example, different arbitrary choices of the boundary (e.g., the van der Waals surface¹ or molecular surface²) may be used for calculating solvent-accessible surface area (SASA) and the position-dependent local dielectric coefficient, respectively. To address this problem, some groups have recently developed methods that couple formalisms for the two functionals so that a single, optimal solvent-solute boundary can be estimated. For example, Dzubiella et al. proposed minimization of the solvation free energy with respect to a solvent volume exclusion function^{3, 4} and Bates et al. introduced surface definitions via surface free energy minimization.⁵ Recently, we have developed an approach to describe the solute-solvent interface using a potential-driven geometric flow model.^{6, 7} The key parameters in the geometric flow approach, such as solute and solvent dielectric constants ɛ, solvent internal pressure p, and surface tension γ can be systematically optimized for any training set of small molecules.⁸ However, such parameters would ideally be based on experimental measurements to provide more physical relevance and to remove unnecessary free parameters from the model to improve robustness and generalizability. Optimal choices for parameters such as solvent pressure and surface tension have been shown to vary significantly over a range of possible parameters with strong anti-correlation between these two quantities.⁸

Although a wide range of values are used in practice, a reasonable value of the solute dielectric constant ɛ_m has been estimated at 1.8 based on the high-frequency contributions to molecular polarizability.⁹ As explained by Marcus,¹⁰ the solvent internal pressure p is a nebulous concept that represents incremental isothermal stretching of local interactions, but without breaking the solvent intermolecular attractive forces. In particular, the internal pressure is defined as $p={\left(\frac{\partial U}{\partial V}\right)}_T$, the rate of change of the internal energy U with respect to the volume V at given temperature T. Experimental measurements estimate the solvent internal pressure at 172 MPa (0.0248 kcal mol⁻¹ Å⁻³) which is about 2000 times higher than atmospheric pressure.¹⁰ Surface tension γ is characterized by the energy required to change the area of an interface and is often associated with the energetics of hydrogen bonding structure of water molecules near the solute/solvent interface. The experimental measurement for the water-air interface at 25 °C is 72 mN/m (0.103 kcal mol⁻¹ Å⁻²).¹¹ Because of water's high number and strength of hydrogen bonds, its surface tension is larger relative to its internal pressure than for organic liquids.¹⁰

While models considering only the area of the cavity have been traditionally popular,^{12, 13} the recent inclusion of solute volume and nonpolar dispersive interactions in implicit solvation models is an important improvement.^{3, 4, 6, 14, 15} Considerations from scaled particle theory^{16, 17} and multiple recent studies concerning the solute size-dependence of the hydrophobic effect^{18, 19, 20} motivated this innovation which improves predictions of solvation forces and energies.^{3, 4, 15, 21, 22} In the present work, we combine these improvements with the use of realistic experiment-based parameters in the context of the geometric flow solvation model. We find that the experimental parameters of solvent internal pressure p = 172 MPa and surface tension γ = 72 mN/m produce solvation free energies within 1 RT of the global minimum root-mean-squared deviation from experimental data over a set of 58 molecules. Our results demonstrate that experimental values can be used for geometric flow solvent model parameters, thus eliminating the need for additional parameterization. It is worth noting that we focus on the applicability of the experimental-based solvation parameters with relevant physics in the geometric flow solvation model; the optimization of the force-field charge and radius parameters is not pursued.

METHODS

The geometric flow solvation model

The geometric flow based solvation model is briefly summarized below; more details are provided in previous publications.^{6, 7, 8, 23, 24} The total free energy functional for the solute-solvent system (G) can be written as the sum, G[χ, ϕ] = G_p[χ, ϕ] + G_np[χ, ϕ], of the polar free energy functional (G_p) and a nonpolar free energy functional (G_np). In the absence of mobile ions, the polar free energy functional is described by

$$\begin{array}{ccc}\hfill G_{\text{p}}[\chi ,\varphi ]& =& {\int }_{\Omega }\left(\chi \left({\varrho }_f\varphi -\frac{1}{2}{\varepsilon }_m{‖\nabla \varphi ‖}^2\right)\right.\hfill \\ & & +\left.(1-\chi )\left(-\frac{1}{2}{\varepsilon }_s{‖\nabla \varphi ‖}^2\right)\right)d\mathbf{x},\hfill \end{array}$$ (1)

where Ω is the problem domain, χ is a solvent accessibility indicator or characteristic function varying smoothly from 1 at the solute van der Waals surface to 0 in the bulk solvent. More specifically, χ defines a smooth interface between van der Waals and solvent accessible surfaces in a thermodynamically self-consistent manner, coupled with the local charges and electrostatic potential. The distribution function ϱ_f denotes the fixed charge distribution of the fixed solute molecule, the scalars ɛ_m and ɛ_s are the dielectric constants of the solute and solvent, respectively, and ϕ is the electrostatic potential. The nonpolar free energy functional is described by

$$G_{\text{np}}[\chi ,\varphi ]=\gamma A+pV+{\rho }_0{\int }_{\Omega }(1-\chi )U_{\text{vdW}}^{\text{att}}d\mathbf{x},$$ (2)

where γ is the solvent surface tension, A is the surface area of the solute, p is the solvent pressure, V is the volume of the solute, and ρ₀ is the solvent bulk density. The function $U_{\text{vdW}}^{\text{att}}$ is the attractive potential of the van der Waals dispersion interaction between the solute and the solvent, which can be represented by a summation of the attractive interaction potential (using a Weeks-Chandler-Anderson decomposition²⁵) for each atom. The area and volume can be calculated directly from the characteristic function χ via

$$\begin{array}{ccc}\hfill A& =& {\int }_{\Omega }\Vert \nabla \chi \Vert d\mathbf{x},\hfill \end{array}$$ (3)

$$\begin{array}{ccc}\hfill V& =& {\int }_{\Omega }\chi d\mathbf{x}.\hfill \end{array}$$ (4)

The polar and the nonpolar free energy functionals are coupled via the characteristic function χ. Therefore, extremizing the total free energy G with respect to ϕ and χ leads to two coupled partial differential equation. The first equation is a generalized Poisson equation which governs ϕ,

$$-\nabla ·\left(\epsilon \left(\chi \right)\nabla \varphi \right)=\chi {\varrho }_f,$$ (5)

where the dielectric function ɛ(χ) is defined as

$$\epsilon \left(\chi \right)={\varepsilon }_m\chi +{\varepsilon }_s(1-\chi )$$ (6)

such that it achieves the solute dielectric constant value ɛ_m in the solute interior and the solvent dielectric constant value ɛ_s in the exterior. The second equation resulting from variation of G is the generalized geometric flow equation which governs χ,

$$-\nabla ·\left(\gamma \frac{\nabla \chi }{\Vert \nabla \chi \Vert }\right)+w\left(\varphi \right)=0,$$ (7)

where w is a driving potential for the flow

$$w\left(\varphi \right)=p-{\rho }_0{U}_{\text{vdW}}^{\text{att}}+{\varrho }_f\varphi -\frac{1}{2}({\varepsilon }_m-{\varepsilon }_s){\Vert \nabla \varphi \Vert }^2.$$ (8)

Solving Eqs. 5, 7 together provide a self-consistent definition of both the electrostatic potential ϕ and the solvent density, defined via the solvent accessibility indicator function as 1 − χ. The solvation energy can be determined from these functions,

$$\Delta G_{\text{solv}}[\chi ,\varphi ]=G[\chi ,\varphi ]-{\int }_{\Omega }{\varrho }_f\psi d\mathbf{x},$$ (9)

where ψ is the electrostatic potential in the presence of a medium with the same dielectric constant as that of the solute.

Numerical methods

A grid-based optimization was carried out in (p, γ) space with p ranging from 0.001 to 0.055 kcal mol⁻¹ Å⁻³ and γ ranging from 0.055 to 0.165 kcal mol⁻¹ Å⁻², and a spacing of 0.005 along both of these axes. ɛ_m was held constant at 1.8 per the work of Leontyev and Stuchebrukhov,⁹ ɛ_s (solvent dielectric) at 80, solvent density at 0.0334 Å⁻³, and the minimum molecule-box edge distance at 3.8 Å. The equations were solved using the second-order central finite difference scheme discussed in Chen et al.,⁶ and the solver grid spacing was set at 0.25 Å. The experimental solvent internal pressure at 172 MPa¹⁰ converts to 0.0248 kcal mol⁻¹ Å⁻³, and the experimental surface tension of 72 mN/m¹¹ converts to 0.103 kcal mol⁻¹ Å⁻². Linear regression fits of γ_min(p) vs. p were performed with scipy (www.scipy.org).

Small molecule test sets

We investigate three different sets of molecules to provide a diverse range of molecular sizes and chemical properties. First, we re-examine the SAMPL0 set compiled originally by Nicholls et al.²⁶ that was analyzed by Thomas et al.⁸ Second, the linear, branched, and cyclic alkane set of Levy and Gallicchio²⁷ provides a basic set of nonpolar molecules with a range of geometries. Third, the SAMPL2 set²⁸ provides twice as many molecules as SAMPL0, with a broader range of experimental solvation energies, from −25 to +5 kcal/mol, for more robust testing of the methods. Prominent types of molecules in this set include uracils, parabens, and carboxylic acids.

For alkane and SAMPL0 sets, the charges, van der Waals radii, and well depth parameters were taken directly from the OPLS-AA (Optimized Potentials for Liquid Simulations - All Atom) force field.²⁹ For SAMPL2, these parameters were taken directly from Klimovich and Mobley,²⁸ who used Generalized Amber Forcefield (GAFF)^{30, 31} van der Waals parameters and computed charges using AM1-BCC.^{32, 33} We used the same approach to generate GAFF parameters for the SAMPL0 set molecules in Antechamber.³⁰

Although the ZAP-9 forcefield performed well in our previous analysis of SAMPL0,⁸ the OPLS-AA force field was chosen because it employs van der Waals interactions between solvent and solute, and thus experimental p and γ are likely to produce reasonable solvation free energies given the importance of the van der Waals term in the nonpolar free energy functional (Eq. 2).

RESULTS AND DISCUSSION

Overall performance of the geometric flow method for a range of pressures and surface tensions

To test the hypothesis that the geometric flow solvation model can predict reasonable solvation free energies with experimental or near-experimental parameters, we analyzed the root-mean-squared error (RMSE) for small molecule solvation energy in the space of p and γ parameter values for different sets of molecules. Figure 1 shows that there is a linear “valley” region in (p, γ) space along which the RMSE varies by less than RT by comparison to the minimum value for the entire surface. This linear valley covers a wide range of pressures, (0.001 < p < 0.055) kcal mol⁻¹ Å⁻³, but a narrow range of surface tensions ±0.01 kcal mol⁻¹ Å⁻² for γ at any given p.

Figure 1.

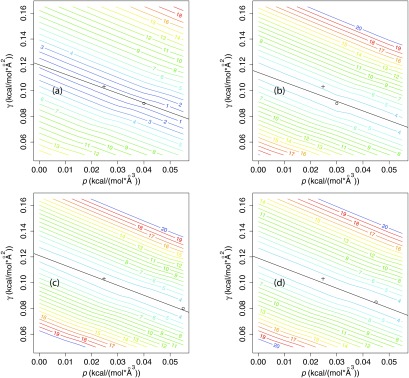
Root-mean-squared error (RMSE) in solvation free energy for different sets of molecules as a function of solvent internal pressure p and surface tension γ for a solute dielectric constant ɛ_m = 1.8 using the OPLS-AA force field.²⁹ (a) Linear, branched, and cyclic alkane set of Levy and Gallicchio;²⁷ (b) SAMPL0 set;²⁶ (c) SAMPL2 set;²⁸ (d) pooled set. The RMSE is normalized by RT = 0.592 kcal mol⁻¹ at 298 K, shown as contours. The linear regression fit of γ_min(p) vs. p is indicated in black, where γ_min(p) is the choice of γ at any given p which minimizes the RMSE (values provided in Table 1). The experimental values for the pressure¹⁰p = 0.0248 kcal mol⁻¹ Å⁻³ and surface tension¹¹ γ = 0.103 kcal mol⁻¹ Å⁻² are indicated with a cross on each plot and the minimum (γ, p) values are indicated with a circle.

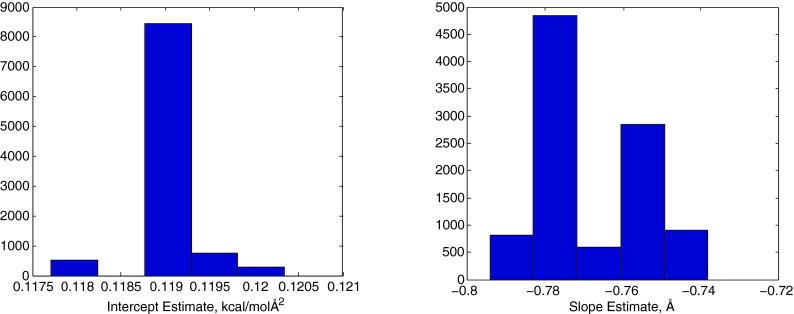
For a more quantitative analysis, we calculated linear fits for γ_min(p), the value of γ which minimizes the RMSE at a given p, for each set of molecules. Table 1 shows that the resulting slopes are −0.74 to −0.78 Å, while the intercepts range from 0.11 to 0.12 kcal mol⁻¹ Å⁻². The Pearson correlation coefficient was R² > 0.98 for all three sets and the pooled set. As described below, we also analyzed linear correlations for random subsets of the pooled set. Figure 2 shows that these parameter estimates are robust in cross-validation tests. Specifically, we examined fitting parameter distributions among a large number (10 000) of random subsamples of n molecules from the pooled set of N = 58 compounds, at varying levels of n. For n = N − 5 = 53, among the 10 000 random samples, the intercept estimate varies by less than 0.001 from the pooled-set value of 0.119 and the slope varies by less than 0.04 from the pooled-set value of −0.78. Pearson R² values for the γ_min(p) vs. p fits vary from 0.985 to 0.991 among the 10 000 subsamples of size n = 53. Even for n = N/2 = 29, the estimated intercept and slope vary by less than 0.005 and less than 0.05, respectively, relative to the full set (Figure S1 of the supplementary material³⁴). Furthermore, the R² for γ_min(p) vs. p is 0.94 or higher for each molecule in the pooled set, with the intercept ranging from 0.09 to 0.14 (see Table S1 of the supplementary material³⁴). These high R² values indicate that the negative linear correlation between p and γ is an inherent property of small molecule solvation in water and not merely an average phenomenon.

Table 1.

Solvent pressure and surface tension relationships. The intercept and slope were determined from a linear regression fit of γ_min(p) vs. p, where γ_min(p) is the value of γ which minimizes the RMSE at a given p. R² is the Pearson correlation coefficient value for the linear fit. Numbers in brackets indicate the 95% confidence interval for calculated values. RMSE_exp is the solvation energy error in units of RT = 0.592 kcal mol⁻¹ when using experimental values¹⁰ for p = 0.0248 kcal mol⁻¹ Å⁻³ and surface tension γ = 0.103 kcal mol⁻¹ Å⁻². RMSE_min is the error found when scanning the space of (p, γ) parameters and choosing the p_min and γ_min values which minimize the error.

Set	Alkanes	SAMPL0 (OPLS)	SAMPL0 (GAFF)	SAMPL2	Pooled
R2	0.99	0.99	0.99	0.98	0.99
Slope	−0.74	−0.75	−0.74	−0.77	−0.78
(Å)	[−0.80, −0.68]	[−0.80, −0.69]	[−0.80,−0.68]	[−0.84, −0.70]	[−0.83,−0.72]
Intercept	0.120	0.114	0.118	0.121	0.119
(kcal mol−1 Å−2)	[0.118, 0.122]	[0.112, 0.116]	[0.116, 0.120]	[0.119, 0.123]	[0.117, 0.121]
pmin	0.040	0.030	0.025	0.055	0.045
(kcal mol−1 Å−3)
γmin	0.090	0.090	0.100	0.080	0.085
(kcal mol−1 Å−2)
RMSEexp	1.03	4.69	4.12	3.61	3.72
(RT)
RMSEmin	0.32	3.47	4.12	3.27	3.21
(RT)

Figure 2.

Histograms of the intercept (left panel) and slope (right panel) for linear fits of the optimal surface tension γ_min and p based on 10 000 random sets of 53 small molecule compounds drawn randomly and without replacement from the set of 58 compounds.

Table 1 also presents the errors RMSE_exp for solvation free energy using experimental values for the pressure, p = 0.025 kcal mol⁻¹ Å⁻³, and surface tensio,n γ = 0.103 kcal mol⁻¹ Å⁻², parameters.¹⁰ For the pooled set, RMSE_exp = 3.72RT which is very close to the global minimum error, RMSE_min = 3.21RT at (p, γ) = (0.045, 0.085). The difference between RMSE values is denoted by ΔRMSE = RMSE_exp − RMSE_min; the largest ΔRMSE is 1.15 RT for the SAMPL0 set. In addition, Figure S2 of the supplementary material³⁴ shows that the small ΔRMSE is robust in cross-validation tests. In 10 000 size n = 53 samplings, ΔRMSE ranges from 0.35 to 0.75 for the majority of subsets and is less than 1RT for all sets. Even when the sample size is decreased from n = 53 to n = 38, ΔRMSE never exceeds 1.5RT, and n has to be reduced to 18 (0.31N) to find any subset for which ΔRMSE exceeds the approximate thermal noise level of 2RT.

Furthermore, our results are consistent with several previous investigations which estimated optimal water internal pressures of 0.03–0.09 kcal mol⁻¹ Å⁻³ for fitting implicit solvent models with a pressure-volume energy term to molecular dynamics (MD) simulation predictions of solvation forces on proteins.^{15, 22, 35} These observations, and our optimal surface tension and pressure estimates, are well explained by an internal pressure of p = 0.025 kcal mol⁻¹ Å⁻³ but poorly explained by the use of atmospheric pressure.¹⁰

In addition to statistical validation, we can demonstrate that these results are robust to the choice of force field used to model the small molecules. For the SAMPL0 set, we generate GAFF^{30, 31} parameters and compare the solvation free energy predictions from these parameters to those obtained from OPLS parameters. The resulting RMSE vs. (p, γ) landscape is shown in Figure S3 of the supplementary material,³⁴ and Table 1 shows that, for the SAMPL0 set, the slope and intercept of γ_min(p) vs. p are very similar regardless of whether OPLS or GAFF charges and radii are used. In addition, RMSE_exp and ΔRMSE are lower for SAMPL0-GAFF than SAMPL0-OPLS, which suggests that the auto-generated GAFF parameters are actually superior to OPLS parameters when used in the geometric flow model. These results show that the geometric flow results are robust to minor variations in force field. More detailed cross-validations of the optimal pressure and surface tension values can also be found in the supplementary material.³⁴

Performance of the geometric flow solvation model for individual molecules

While the RMSE differences between experimental (p, γ) and the global minimum are small, Table S1 of the supplementary material³⁴ shows that for individual molecules, RMSE difference between experimental (p, γ) and the global minimum averages 2.96 RT and can be as high as 10 RT for N, N-4-trimethylbenzamide and N, N-dimethyl-p-methoxybenzamide. Many molecules with RMSE differences above 3 RT are nitrogen-rich compounds, including imidazole, uracils, caffeine, cyanuric acid, and benzamides. One unusual property of such molecules is that they form very strong hydrogen bonds with water; this may be poorly approximated by geometric flow and warrant further investigation. In another study,²³ it was shown that errors for benzamides can be reduced with different charged assignments obtained from the density functional theory on a different set of atomic coordinates. Molecules with ether linkages (e.g., diethoxyethane) also tend to perform poorly, with the exception of dimethoxymethane.

Scaling relationships between small molecule volumes and areas

Figures 3a and S1 of the supplementary material³⁴ illustrate the relationships between volumes and areas calculated using the geometric flow models described above. Below, we offer two complementary interpretations of the observed strong correlation between volume and area.

Figure 3.

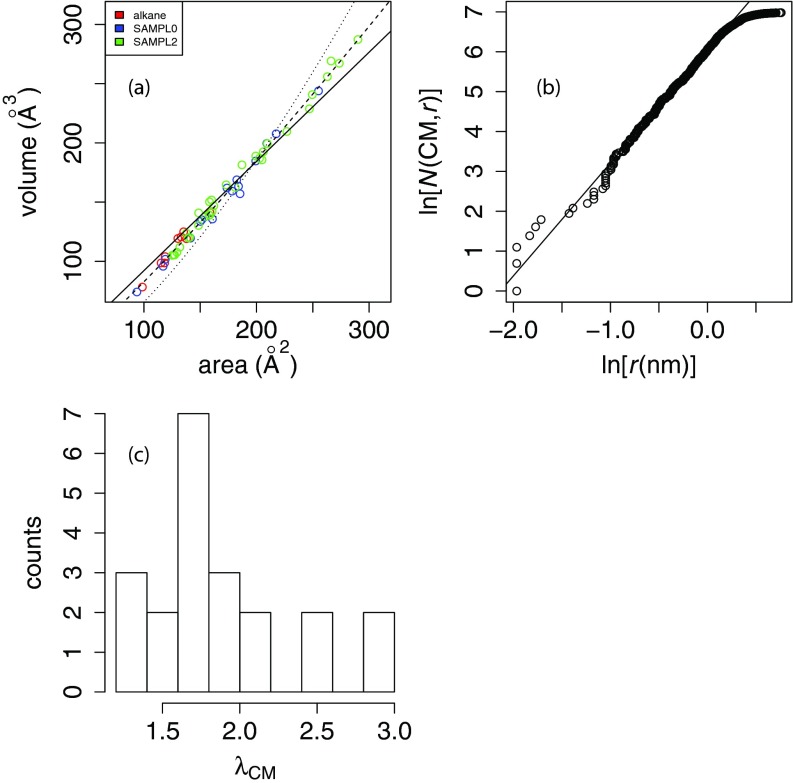
Area/volume relationship for small molecule test sets. In panel (a), the solid line indicates a linear least-squares fit with a slope of 1.1 ± 0.014 Å, an intercept of −27.3 ± 2.44 ų and a Pearson correlation coefficient of R² = 0.99. The dotted line indicates a nonlinear least-squares “spherical” fit (V = αA^3/2), where α = 0.066 ± 0.001, and the dashed line indicates a “free exponent” fit V = αA^β where α = 0.38 ± 0.03 and β = 1.17 ± 0.02. The nonlinear least-squares fits were performed with the nls function in R (www.R-project.org). Panel (b) shows the natural log of the radial counting function about the center of mass vs. log (r) for the protein villin. The first 2/3 of the points, representing the “interior volume,” can be fit with a slope of 2.83, which is the fractal density dimension λ_CM.³⁸ Panel (c) shows the distribution of fractal density dimensions λ_CM for small molecules in the pooled set for which the correlation coefficient of log atom count vs. log (r) is greater than 0.9. 38 of the 58 molecules in the unified set met this criterion.

A linear model with no intercept fits poorly to the data with a slope of 0.92 ± 0.01 Å, RMSD residuals of 74 ų, and Pearson correlation coefficient R² = 0.997. With a floating intercept, the model fits much better with a slope of 1.07 ± 0.01 Å, RMSD = 23 ų, and Pearson correlation coefficient R² = 0.990; however, the intercept obtained is −27 ų, or more than 10% of the median volume for the unified set. Additionally, a strictly “spherical” model (V∝A^3/2 with no intercept) also performs badly (RMSD = 219 ų). Thus, we perform a nonlinear least-squares fit with a floating exponent, fitting to the model V = αA^β and obtain α = 0.383 ± 0.030 and β = 1.17 ± 0.015 with a resulting RMSD of 22 ų. Analysis of variance (ANOVA) shows that the floating-exponent model outperforms both the linear and spherical models with p-values of 10⁻¹⁵ or less (see Table S2 of the supplementary material³⁴). Furthermore, the 95% confidence interval around β is [1.14,1.20], indicating that the exponent is statistically distinct from either 1 or 1.5.

In addition, we examine the area/volume relationship more broadly and its force field dependence using data from Gong and Yang³⁶ (see Figure S4 of the supplementary material³⁴). Four other types of molecular area/volume calculations (molecular face, van der Waals area/volume, solvent-accessible surface area and volume, and solvent-excluded area/volume) show a scaling behavior of V∝A^1.2, suggesting this shape behavior is general across different small molecules and different molecular area/volume calculation methods.

Geometric interpretation of volume-area correlation

In Figures 3b, 3c, we use the concept of density dimension to further explore the origin of the volume-area scaling relationships. For a given molecule, the “fractal” density dimension λ_CM(x) about a point x is the best-fit slope of log (N(x, r)) vs. log (r) according to a linear least squares regression, where N(x, r) is the “radial counting function”; i.e., the number of atoms within radius r of x.^{37, 38} If a molecule has an “interior volume,” then its radial counting function should scale with approximately r³ except for the rough surface region. We use the protein villin, which is large enough to have an interior volume, as a reference case. To exclude contributions from the non-flat surface, we perform a linear regression of log (N(x, r)) vs. log (r) over the inner 2/3 of atoms to estimate λ_CM of 2.83 (Figure 3b), but that beyond r ≈ 1 nm, the radial counting function, and thus V, scales with a smaller power of r. By comparison, we fit log (N(x, r)) vs. log (r) over the inner 2/3 of atoms for the small molecules in this work, which reveal density dimensions averaging about 1.84 and ranging from 1.05 to 3.71 (Figure 3c).

For the interior volume (V) of an idealized spherical molecule, V∝r³ and area A∝r², thus V∝A^3/2; i.e., the “density dimension” is 3.³⁷ In practice, molecules such as proteins have dimensions closer to 2.9 for the interior volume due to imperfect packing.^{37, 38} However, the surface region of a large molecule does not behave as a three-dimensional object since rather than being flat-surfaced like a sphere, the surface region has many crevices and protrusions.³⁷ Similarly, in a small molecule, the surface is only a few atomic diameters from the center of mass and there may not be a proper “interior volume”; this likely explains why we estimate an average fractal density dimension of about 1.67 for small molecules. Thus, most small molecules behave more like the protein surface than the protein interior, with the exception of d-xylose (λ_CM = 2.98) and diethyl propanedioate (λ_CM = 3.71). Since glucose also has a relatively high λ_CM = 2.58, this may be a property of sugars due to their compact ring structure. By contrast, the molecules with the lowest λ_CM like pentachloronitrobenzene and the parabens are primarily aromatic and thus flat, so that the radial counting function will only scale in two dimensions with r. Given the large differences in V/A scaling between small and large molecules, our results suggest that for broad applicability, both γA and pV terms are important.

Thermodynamic interpretation of volume-area correlation

The observed volume-area correlation can also be interpreted based on thermodynamic arguments.³⁹ For simplicity, we will focus only on the nonpolar contribution, assuming that this is the energetic contribution primarily associated with the anti-correlation between p and γ, without loss of generality. Consider a small nonpolar solute inserted into a solvent where a differential Gibbs energy (dG) can be described by

$$\begin{array}{c}\hfill dG=-SdT+VdP+\sum _i{\mu }_{i}d{N}_i+\gamma dA+{\rho }_0{\int }_{{\Omega }_s}{U}_{\text{vdW}}^{\text{att}}d\mathbf{x},\end{array}$$ (10)

where T, S, and V denote the temperature, entropy, and volume of the solvent, respectively, and Ω_s is the region of space in the solvent outside of the solute. Here, μ_i and N_i are the chemical potential and number of moles for ith component of the solvent. Consider a cavity in a homogeneous solvent at constant temperature and assume that the solute-solvent van der Waals interactions give a negligible contribution to the overall energy. Under this approximation, Eq. 10 becomes dG = γdA + Vdp and a simple Maxwell relationship gives

$${\left(\frac{\partial \gamma }{\partial p}\right)}_A={\left(\frac{\partial V}{\partial A}\right)}_p.$$ (11)

The total amount of volume resulting from both solvent (V) and cavity (V_m) is V_total = V_m + V and the change due to cavity insertion is dV = −dV_m. Furthermore, the created surface area in the solvent due to insertion is dA = dA_m if there is no significant deformation of the cavity upon the insertion. Given the assumptions above, the Maxwell relationship can be rewritten as

$${\left(\frac{\partial \gamma }{\partial p}\right)}_{A_s}=-{\left(\frac{\partial V_m}{\partial A_m}\right)}_p,$$ (12)

which provides a simple relationship between the variation of surface tension with respect to pressure and that of solute volume with respect to solute surface area. To test the applicability of Eq. 12, we examined the relation between ${\left(\frac{\partial {\gamma }_{\min }}{\partial p}\right)}_{A_s}$ and ${\left(\frac{\partial V_m}{\partial A_m}\right)}_p$ over all three sets with van der Waals energetics set to zero to be consistent with the conditions for Eq. 12 (see Figure S5 of the supplementary material for details³⁴). The two derivatives were linearly correlated with a slope of −1.00 ± 0.08, intercept of −0.22 ± 0.08 Å, and a Pearson correlation coefficient of R² = 0.72. This relationship implies that our data are qualitatively consistent with Eq. 12. The assumptions of constant area and pressure in the two respective derivatives are approximately justified since the calculated areas and volumes vary from the mean by less than 3% and 9%, respectively, for each set of molecules over the entire (p, γ) space examined in this study.

Furthermore, our results suggest that ${\left(\frac{\partial \gamma }{\partial p}\right)}_{A_s}$ varies over a small range from −0.9 to −0.7 Å. This small variation in the rate of change is supported by past work which investigated the pressure dependence of the interfacial tension between two immiscible fluid phases with a planar interface³⁹ and concluded that the dependence comes from the coupling of the pressure to differences in the partial molar volumes of two fluids between the two phases. The study also showed that the dependence also varies slightly for the interface of several hydrocarbon molecules with experimental measurements of ${\left(\frac{\partial \gamma }{\partial p}\right)}_A$ in the range of approximately −0.7 to 0.3 Å. This range is similar to the range we obtained in our analysis of optimal computed surface tensions and pressures using the geometric flow method.

CONCLUSIONS

The geometric flow approach provides a physically realistic solvation model without considering explicit solvent and has previously compared well to experimental data in limited tests. In this work, calculated solvation energies for multiple sets of small molecules with the OPLS-AA force field and showed that the geometric flow model has good accuracy for most molecules. More importantly, we demonstrated that experimental values can be used the solvent internal pressure and surface tension model parameters, thus eliminating the need for additional ad hoc parameterization of the model. With a set of 58 molecules and a solute dielectric constant of ɛ_m = 1.8, we find that the experimental parameters for the air-water interface, pressure p = 172 MPa (0.0248 kcal mol⁻¹ Å⁻³) and surface tension γ = 72 mN/m (0.103 kcal mol⁻¹ Å⁻²), produce solvation free energies within 1 RT of the global minimum root mean square deviation over the set. Thus, it is possible that the previously reported need to use a different “microscopic” surface tension closer to 0.03 kcal mol⁻¹ Å⁻² for small molecules^{12, 13} may result not from the curvature of small molecules,⁴⁰ but rather from the neglect of pressure-volume work and of a correct definition of internal pressure.¹⁰ Future work investigating geometric flow solvation predictions for a wider size range of small molecules is required for a detailed test of this hypothesis. The ability of geometric flow to make reasonable predictions of solvation free energy with experimentally derived parameters argues for the physical relevance of the model and its broad applicability. The reduction in the number of free parameters will also facilitate the extension of geometric flow to multi-conformational systems, proteins, and other more complicated cases where solvation is important to function. This adds to the existing benefit that the geometric flow formulation allows for simultaneous optimization of the polar and nonpolar components of solvation free energy.

In our previous work,⁸ we found that the optimal values for γ and p are strongly anti-correlated for all molecules. Thomas et al. rationalized this anti-correlation based on the fact that γ increases with stronger water/water interactions, while water/water interactions become weaker as p increases.⁸ While the p and γ terms of the solvation model are linearly correlated, our data on the interior volumes of proteins and small molecules suggest that this correlation only holds over a small range of molecular sizes, and that these terms are thus not redundant.

In summary, the geometric flow approach not only provides unambiguous coupled development of nonpolar and polar free energy functionals but also provides excellent results using experimental values for p and γ. This reduction in the number of free parameters will also facilitate the extension of geometric flow to blind predictions of solvation free energy and its use as a complement for interpreting related experiments. Future work should investigate the scalability of the geometric flow model to larger systems such as host-guest or protein-ligand binding energies where a broader range of solvation phenomena, including cavity de-wetting, influences the energetics of the system.