Abstract
Radiation therapy is an established method of cancer treatment. New technologies in cancer radiotherapy need a more accurate computation of the dose delivered in the radiotherapy treatment plan. This study presents some results of a Geant4-based application for simulation of the absorbed dose distribution given by a medical linear accelerator (LINAC). The LINAC geometry is accurately described in the Monte Carlo code with use of the accelerator manufacturer's specifications. The capability of the software for evaluating the dose distribution has been verified by comparisons with measurements in a water phantom; the comparisons were performed for percentage depth dose (PDD) and profiles for various field sizes and depths, for a 6-MV electron beam. Experimental and calculated dose values were in good agreement both in PDD and in transverse sections of the water phantom.
Keywords: Monte Carlo simulation, Geant4, Radiotherapy, Linear accelerator, Depth-dose curve
1. Introduction
In recent years, the accuracy of dose calculation has improved together with the computing power available for radiotherapy. The Monte Carlo method has been considered as an alternative to analytical methods for treatment planning in cancer radiotherapy.1,2
The feasibility of beam modelling for radiotherapy planning has to be demonstrated by calculation of dose distributions and their comparison to measurements. Simple beam models are used as an effective and rapid way of calculating dose distributions in an irradiated medium.
In the present work, the depth-dose distribution was reproduced based on a Geant4 (Geometry And Tracking, Version 4) Monte Carlo method. The Geant4 Simulation Toolkit3,4 was first used in 1994 in a research project for a new general purpose simulation code for high energy physics. As one of the first large object-oriented software applications in physics, Geant4 has become the standard simulation package for most HEP experiments, including three of the four experiments at the Large Hadron Collider (LHC).
However, the use of Geant4 is increasing rapidly. For medical physics applications, this code has some advantages over other codes such as EGSNRC, XVMC, MCNP, PENELOPE, and FLUKA.4
Geant4 can handle all types of particles, and it is able to handle complex geometries. Geant4 offers the most flexible geometry description among all Monte Carlo codes. Another appealing characteristic of Geant4 is its use of modern programming techniques (object-oriented, C++); all other codes currently in use are in FORTRAN. Another unique aspect of Geant4 is that it can model sources and geometries in motion, such as the rotating parts of an IMRT (intensity modulated radiation therapy) beam line, dynamic MLCs (multi-leaf collimators), a brachytherapy source moving through a catheter, moving parts of imaging systems, and even the motion of patient organs due to respiration, etc.5
Geant4 has the ability to handle both electric and magnetic fields. This can be helpful in simulation of novel, real-time imaging and treatment modalities where the treatment is performed in the presence of a magnetic field. Finally, Geant4 is open access and the source code is freely available.6 It is distributed to the user who is welcome not only to add a user code, but to modify the source code and even to repackage, redistribute or sell the modified source code.
2. Materials and methods
In this study, we simulated the head of a clinical linear accelerator (Siemens Primus) based on the manufacturer's detailed information by use of Geant4 Monte Carlo code.
Geant4 was developed at CERN for use with the LHC and is an object-oriented7,8 Monte Carlo simulation toolkit. Geant4 was developed to simulate the passage of particles through matter. It contains a large variety of physics models, covering the interactions of electrons, muons, hadrons, and ions with matter from 250 eV up to several peta-electron volts (1 PeV = 1015 eV).8,9
In the present study we developed a dedicated program in C++ language using Geant4 libraries that enables us to simulate the gantry of a Siemens Primus LINAC.
2.1. Simulation of the Siemens Primus accelerator gantry
The components of a linear accelerator for a 6-MV photon beam are shown in Fig. 1. In external radiotherapy, the X-ray treatment fields are usually delivered by a medical linear accelerator. Electrons are accelerated inside a waveguide up to the desired treatment energy, in this case approximately 6 MeV.
Fig. 1.
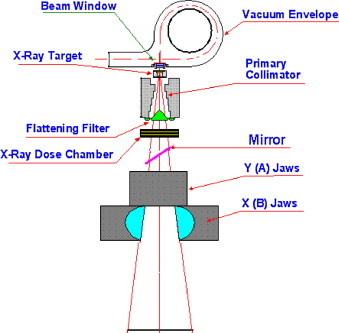
Structure of gantry in Siemens Primus linear accelerator, for 6-MV beam.
Target: The target creates Bremsstrahlung X-rays with a thin tungsten disk of approximately 1 mm height. The remaining primary electrons are absorbed in a graphite absorber inside the target. The target is of cylindrical design with a height of about 1.5 cm and a diameter of approximately 3 cm. The parameters of the primary electron beam hitting the target, including its energy, angular distribution, and spatial distribution, were chosen in order to minimize the discrepancies between simulation results and measured data. For the Geant4 code, we chose a parallel electron beam hitting the target with a Gaussian energy distribution with variance σ = 0.127 MeV.
Primary collimator: The primary collimator was made of tungsten. Basically it is a cylinder with cylindrical holes drilled into it. The primary collimator absorbs photons that are scattered outside the clinically used treatment field. Located directly beneath the target, its height is about 6.2 cm, and the outer diameter is about 7 cm.
Flattening filter: The flattening filter was made of stainless steel. It was attached to the lower end of the primary collimator. It is conically shaped and ends in a flat disk. Because the spectral distribution of the Bremsstrahlung has an angular dependence, the dose distribution has a strong peak at the central axis. The flattening filter is used to create a flat dose profile. Flattening filters have a major influence on the photon field. They scatter photons, they reduce the mean photon energy by pair production and Compton scattering, they absorb low-energy photons and therefore harden the beam, they reduce the overall intensity of the photon beam, and they contaminate the photon field with secondary electrons. The overall height of the 6-MV flattening filter of the Primus LINAC is close to 1.8 cm.
Jaws: Jaws are used for field shaping. The pair of jaws was made of tungsten. The jaws had a thickness of 7.8 cm.
2.2. Simulation of dose distribution in the water phantom
A water phantom with dimensions of 30 cm × 30 cm × 30 cm was simulated under the gantry with a source-surface distance (SSD) of 100 cm. The phantom was divided into voxels, with each voxel's dimensions being 1 mm × 1 mm × 1 mm, in which we collected the energy deposited to calculate the relative dose absorbed in the phantom. The percentage depth dose (PDD) and beam profiles were calculated in a water phantom for different field sizes. We then compared them with measurements for validation of our Monte Carlo model. All calculations were performed by two quad core CPU (8 CPU) servers composed of eight 3.2 GHz INTEL processors. The approximate run time was 140 h for 109 photons. The measurements of both depth-dose curves and lateral dose profiles for the square fields were made with a diode (Si–P) type detector (PFD3G, Scanditronix/Wellhofer) with thickness of active volume 0.06 mm and diameter of active area 2 mm. The diode was mounted on a computer controlled scanning system (RFA300-System, Scanditronix/Wellhofer). The uncertainty of the position accuracy of the scanning system provided by the manufacturer was ±1 mm. All of the measurements were obtained at SSD of 100 cm. For all measurements with the water tank scanning system, a Scanditronix electrometer was used, and the data collection was governed by OmniPro-Accept (Medical Physics Tool) software from Scanditronix/Wellhofer.
The LINAC was simulated for 6-MV X-rays and PDD curves, and beam profiles with different field sizes were calculated and compared with measurements.
To obtain accurate results from Monte Carlo simulations in radiotherapy calculations, precise modelling of the LINAC gantry and a sufficiently large number of particles are required. In order to obtain similar standard deviations the number of primary events needed for fields of larger size is smaller than that for narrow fields: 4 × 109 primary electrons for a 5 × 5 cm2 field, 3 × 109 electrons for a 10 × 10 cm2 field, 2 × 109 primary electrons for a 20 × 20 cm2 field and 109 primary electrons for a 30 × 30 cm2 field.
The most common variance reduction method is energy cut-off. Cut-off energy is the energy at which the Monte Carlo simulation stops transport of the particle if the particle's energy falls below the cut-off value. In all simulations, the energy cut-offs were 0.7 MeV for electrons and 0.01 MeV for photons.
3. Results
Data concerning the depth-dose curves were normalized to their maximum value at a depth Z = 15 mm and lateral profiles obtained with experimental measurements were normalized to the mean value in the flat zone of the lateral dose at depth Z = 50 mm.
In Fig. 2, experimental measured data and Geant4 Monte Carlo simulation results are shown. Fig. 2(a) shows the depth-dose curves, and in Fig. 2(b), the lateral dose profiles at 50, 100, and 200 mm depth, for the 5 cm × 5 cm field, are shown for the 6-MV beam and SSD = 100 cm.
Fig. 2.
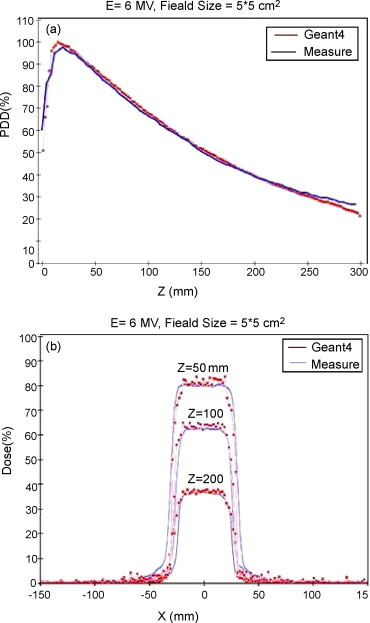
(a) Depth-dose profile. (b) Lateral dose profiles at 50, 100, and 200 mm depth for the 5 cm × 5 cm field, with the 6-MV beam. The blue lines refer to measured data; red dots refer to Geant4 Monte Carlo results.
In Fig. 3, we show experimentally measured data and Geant4 Monte Carlo simulation results. Fig. 3(a) shows the depth-dose curves, and Fig. 3(b) shows lateral dose profiles at 50, 100, and 200 mm depth, for the 10 cm × 10 cm field, with the 6-MV beam (SSD = 100 cm).
Fig. 3.
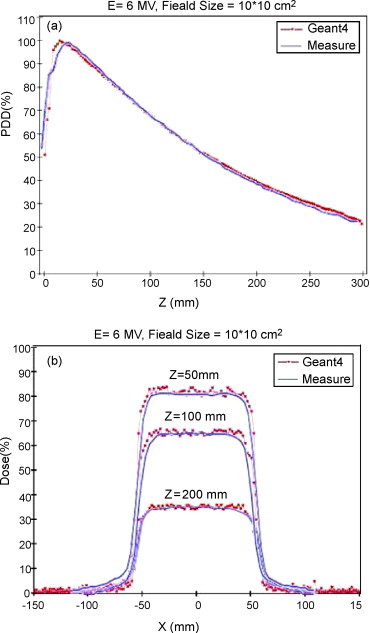
(a) Depth-dose profile. (b) Lateral dose profiles at 50, 100, and 200 mm depth for 10 cm × 10 cm field with a 6-MV beam. The blue lines refer to measured data, and red dots refer to Geant4 Monte Carlo results.
In Fig. 4, we show experimentally measured data and Geant4 Monte Carlo simulation results. Fig. 4(a) shows the depth-dose curves, and Fig. 4(b) shows lateral dose profiles at 50, 100, and 200 mm depth, for the 10 cm × 10 cm field, with the 6-MV beam (SSD = 100 cm).
Fig. 4.
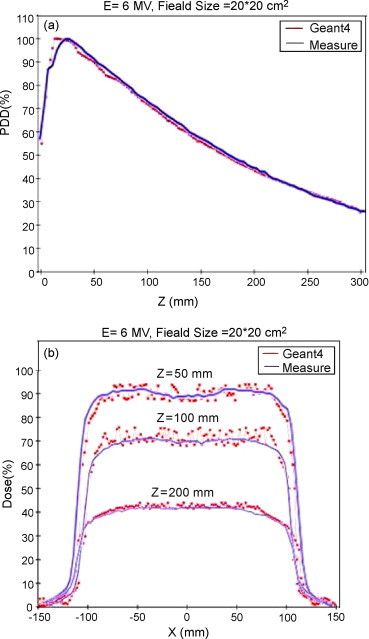
(a) Depth-dose profile. (b) Lateral dose profiles at 50, 100, and 200 mm depth for 20 cm × 20 cm field, with 6-MV beam. The blue lines refer to measured data, red dots refer to Geant4 Monte Carlo results.
In Fig. 5, we show experimentally measured depth-dose curves data and Geant4 Monte Carlo simulation results for the 30 cm × 30 cm field, with the 6-MV beam (SSD = 100 cm).
Fig. 5.
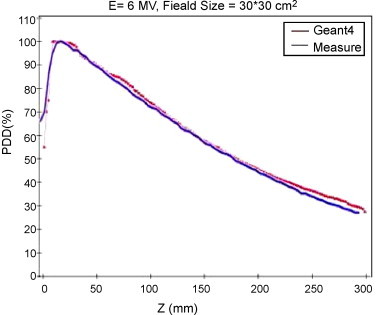
Depth-dose curve for the 30 cm × 30 cm field, with a 6-MV beam. The blue line refers to measured data, the red line refers to Geant4 Monte Carlo results.
4. Discussion
There is good agreement between computed and measured PDD, especially for depths less than 200 mm. This agreement fails around the dose build-up point. The uncertainty in computations amounts to 20% for locations deeper than 250 mm and around the dose build-up point. Usually, for larger field size the agreement between measurement and computation in Z direction becomes better. With increasing depth, the uncertainty of computed dose distribution in the lateral direction decreases from 10% to 5%. As a whole, the computational results are satisfactory at depths between 50 and 200 mm. The results in the penumbra of the radiation field are not reliable and are far from the measured results. In a previous study,8 the results of Geant4 were benchmarked against experiments up to the depth of 100 mm. In the present work it is shown that the agreement extends up to 250 mm depth.
5. Conclusions
In this study, a medical linear accelerator was simulated based on Siemens Primus manufacturer's information. The results obtained with Geant4 simulation, such as percentage depth-dose curves and beam profiles for different field sizes in a water phantom, show excellent agreement with the measured dose data for 6-MV photons produced by the LINAC, and there is only a minor statistical difference between the experimental measurements and the data obtained with the Geant4 simulations. This method of dose calculation can be an alternative dosimetric tool in addition to the traditional analytical treatment planning systems. By adjusting the parameters in the modelling of the geometry, this simulation might be used for the study of other medical LINACs’ gantries.
References
- 1.Verhaegen F., Seuntjens V. Monte Carlo modeling of external radiotherapy photon beams. Phys Med Biol. 2003;48:R107–R164. doi: 10.1088/0031-9155/48/21/r01. [DOI] [PubMed] [Google Scholar]
- 2.Nederlandse Commissie Voor Stralings dosimetrie, Monte Carlo Treatment Planning: An introduction NCS Delft The Netherlands, Report 16; 2006.
- 3.Agostinelli S., Allison J., Amako K., Apostolakis J., Araujo H., Arce P. GEANT4—simulation toolkit. Nucl Instr Meth Phys Res A. 2003;506:250–303. [Google Scholar]
- 4.Allison J., Amako J., Apostolakis K., Araujo J., Dubois H., Asai P.A. Geant4 developments and applications. IEEE Trans Nuc Sci. 2006;53:270–278. [Google Scholar]
- 5.Carrier J.F., Archambault L., Beaulieu L. Validation of GEANT4 (an object-oriented Monte Carlo toolkit) for simulations in medical physics. Med Phys. 2004;31:484–492. doi: 10.1118/1.1644532. [DOI] [PubMed] [Google Scholar]
- 6.The Geant4 web site and Manual, http://geant4.web.cern.ch/geant4/UserDocUserDocUse/UsersGuides/ForApplication.
- 7.Wellisch J.P. Geant4 physics validation for large HEP detectors. Nucl Instr Meth Phys Res A. 2003;502:669–672. [Google Scholar]
- 8.Foppiano F., Mascialino B., Pia M.G., Piergentili M. A Geant4 based simulation of an accelerator head for intensity modulated radiation therapy. Nuclear Science Symposium Conference Record, IEEE, vol. 4; 16–22 October; 2004. pp. 2128–2132. [Google Scholar]
- 9.Chauvie S., Depaola G., Ivanchenko V., Longo F., Nieminen P., Pia M.G. Geant4 low energy electromagnetic physics. Proceedings of CHEP; Beijing, China; 2001. pp. 337–340. [Google Scholar]


