Abstract
Aim
The aim of the paper is to examine the relation between the increase of the photon dose in water in the region of electronic disequilibrium – so-called build-up region – and the distance of the bolus from the water surface for the applied parameters of X-ray beams.
Materials and methods
PDD measurements were carried out using the plane-parallel ionization chamber Markus in the automatic water phantom IBA BluePhantom with OmniPro-Accept V7 (IBA Dosimetry GmbH, Schwarzenbruck, Germany). All measurements were performed for different field sizes and for 6 MV and 15 MV X-ray beams, respectively. A water-equivalent RW3 slab (Goettingen White Water) produced by PTW was used as a bolus.
Results
Placing a bolus in an irradiated field changes the shape of the PDD curve in the build-up region in comparison with the one obtained for an open field. All results has been inserted in tables and figures.
Conclusion
The closer the bolus is to the water surface, the smaller the depth of the maximum dose in the phantom for all investigated fields and energies. The changes in the build-up region are important, even if the bolus does not touch the surface of the water phantom. The influence of the bolus can be ignored when the bolus-surface distance equals 25 cm for 6MV X-ray beams and 39 cm for 15 MV X-ray beams.
Keywords: PDD, Bolus, Depth of the dose maximum, Build-up region
1. Introduction and the aim of the work
In radiation therapy with high energy photon beams, different types of boluses are used to modify the dose delivered to superficial tissues and the dose distribution near the irradiated surface. Such modifications have been investigated for both neck and head cancer treatment1–3 and breast radiation therapy.4–6 In those papers a beam spoiler (a piece of material, such as 1–2 cm thick lucite or polystyrene plate, placed in the path of the photon beam) was used for matching the dose to superficial tissues. The spoiler thickness and its distances from the irradiated surface in the applied techniques were established. Boluses are also applied in the Total Body Irradiation (TBI). In this technique a large SSD is applied and a tissue-equivalent slab is used to counteract the lack of electronic equilibrium near the irradiated surface.7,8 Kassae et al.8 studied separately the contribution of the electrons generated in air, vacuum and in the spoiler material to the dose at shallow depths in phantom by means of Monte Carlo simulations but for a large SSD (300–500 cm). With regard to the spoiler, these simulations of the depth dose changes were carried out only for three different spoiler-to-surface distances.
The applied bolus does not need to be in contact with the patient's body, hence the question arises: to what extent do the changes in the dose distribution within the irradiated area depend on the distance of the bolus from the surface for the standard SSD? Therefore, the authors decided to examine the relation between the increase of the photon dose in water in the region of electronic disequilibrium – so-called build-up region – and the distance of the bolus from the water surface for the applied parameters of X-ray beams. For that purpose, the percentage depth doses (PDDs) were investigated.
2. Materials and methods
6 MV and 15 MV X-ray beams generated by Siemens Primus™ Linear Accelerator (Siemens Medical Systems, Inc., Concord, USA) were selected for this study. Percentage depth doses (PDDs) were measured with the Markus fixed-separation parallel plate ionization chamber (PTW FREIBURG, Freiburg, Germany) shifted in the automatic phantom IBA BluePhantom with OmniPro-Accept V7 (IBA Dosimetry GmbH, Schwarzenbruck, Germany) from the depth of 100 mm to the surface with a 1 mm step. Marcus chamber has a 1 mm water-proof protective plastic cap that prevents measurements in water phantom, so the central axis depth doses were measured up to 1 mm below the surface. The value of the dose on the phantom surface was determined, because of the small distance, by linear extrapolation. Markus chamber is commonly used for depth dose measurements in the build-up region.1,9–11 A bolus made of a water-equivalent RW3 slab (Goettingen White Water) produced by PTW was placed on the surface of the phantom in an irradiated field. The bolus plates of 30 cm × 30 cm and thicknesses of 15 mm and 25 mm were fitted into photon beams of 6 MV and 15 MV, respectively. The choice of such thicknesses of slabs was determined by the depth of the dose maximum for a 10 cm × 10 cm field size at SSD = 100 cm for 6 MV and 15 MV X-ray beams, respectively. A tissue-equivalent slab was placed on hangers propping it up on the surface of the water. Subsequently the PDD measurements were carried out in water for the square fields: 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm and 20 cm × 20 cm for both 6 MV and 15 MV photon beams.
The bolus was moved up from the surface at a 1 cm step and then the PDD measurements were repeated.
The PDD values for open photon beams constituted a point of reference for the measured PDDs with the use of the RW3 slab. For square field sizes ranging from 5 cm × 5 cm to 20 cm × 20 cm as well as for both megavoltage beams the appropriate plate was moved up from the water phantom surface until the depth of the dose-rate maximum (dmax) was the same as the one for open beam.
The Levenberg–Marquart nonlinear least squares method in the OriginPro 7,5 (OriginLab Corporation, Northampton, USA) was used to fit all the curves.
3. Results
Fig. 1a and b shows the chosen measured percentage depth dose (PDD) curves for the field size of 10 cm × 10 cm and for 6 MV and 15 MV X-ray beams, respectively, just to illustrate the changes in the area of the build-up. Individual curves refer to measured data performed at different distances of the bolus from the surface of the phantom. The chosen bolus-surface distances (BSD) are given in both figures. The PDD curves measured without the bolus in the irradiated field are indicated with a black line in both graphs.
Fig. 1.
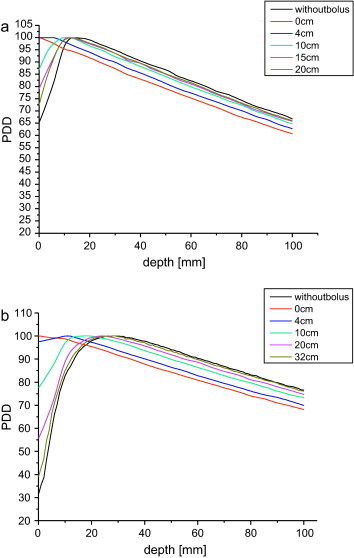
(a) Percentage depth dose for 6 MV photon beam and field size: 10 cm × 10 cm for different bolus-surface distances. (b) Percentage depth dose for 15 MV photon beam and field size: 10 cm × 10 cm for different bolus-surface distances.
The relations between the depth of the maximum dose (dmax) and the bolus-surface distance (BSD) for 6 MV and 15 MV photon beams are shown in Fig. 2a–d. These relations are presented for the following irradiated field sizes: 5 cm × 5 cm, 10 cm × 10 cm, 15 cm × 15 cm and 20 cm × 20 cm.
Fig. 2.
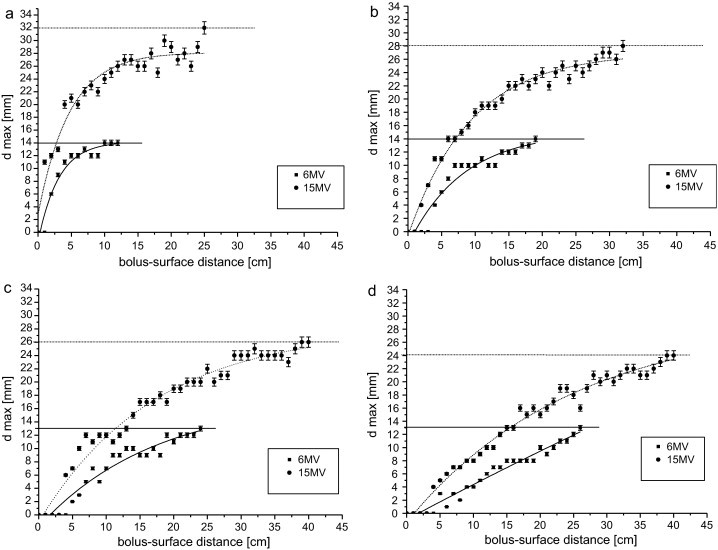
(a) Relation between the dmax and the BSD (bolus-surface distance) for field size 5 cm × 5 cm for 6 MV and 15 MV X-ray beams. (b) Relation between the dmax and the BSD (bolus-surface distance) for field size 10 cm × 10 cm for 6 MVand 15 MV X-ray beams. (c) Relation between the dmax and the BSD (bolus-surface distance) for field size 15 cm × 15 cm for 6 MVand 15 MV X-ray beams. (d) Relation between dmax and the BSD (bolus-surface distance) for field size 20 cm × 20 cm for 6 MV and 15 MV X-ray beams.
Solid and dotted curves in subsequent graphs represent the function fitted to the data series for the studied fields and for 6 MV and 15 MV photon beams, respectively. Measurement errors of the dmax were estimated as the deviations of the square root of the sum of squares of the obtained dose (about 3%) and in respect to the accuracy of the position of the ionization chamber (tolerance of detector's position amounts to 0.2 mm). Expansion factor for error bars amount to 3%.
In each graph the dmax values measured for an open photon beam are indicated with horizontal solid and dotted straight lines for 6 MV and 15 MV X-ray beams, respectively. Additionally, in all graphs the dmax values measured without the bolus in an irradiated field are indicated with straight lines.
Table 1 shows the compiled parameters of the equations of the fitted functions to data points both for the investigated fields and the 6 MV and 15 MV X-ray beams. A fitted function is given by Eq. (1):
| (1) |
Table 1.
Parameters of the fitted function (Eq. (1)) and correlation coefficients for the studied fields and two megavoltage beams.
| Field (cm × cm) | Accelerating voltage | Parameters of fitted function |
R2 | ||
|---|---|---|---|---|---|
| y0 | A | t | |||
| 5 × 5 | 6 MV | 14.19 | −15.65 | 3.07 | 0.94 |
| 15 MV | 28.16 | −25.26 | 4.78 | 0.94 | |
| 10 × 10 | 6 MV | 15.02 | −16.99 | 8.22 | 0.93 |
| 15 MV | 26.97 | −27.59 | 9.38 | 0.98 | |
| 15 × 15 | 6 MV | 17.47 | −19.24 | 17.46 | 0.94 |
| 15 MV | 28.04 | −29.11 | 17.19 | 0.97 | |
| 20 × 20 | 6 MV | 112.02 | −112.97 | 206.96 | 0.98 |
| 15 MV | 29.59 | −30.95 | 24.8 | 0.97 | |
Furthermore, the results inserted in Table 1 present the correlation coefficients R2, which served as a measure of the accuracy of the fit.
4. Discussion
By placing a bolus in an irradiated field the PDD curve changes in the build-up region in comparison to the results obtained without the use of a bolus (Fig. 1a–b). When the thickness of the bolus and the depth of the build-up region for a relevant photon energy are equal and at the same time the bolus lies directly on the surface of the phantom, the build-up region does not appear and the depth of maximum dose moves to the surface of the phantom (dmax = 0 mm). If the tissue-equivalent slab is moved up from the water surface, the maximum dose shifts to greater depth in the phantom until dmax for the appellative bolus-surface distance (BSD) reaches the value obtained for the open beam.
Fig. 2a–d shows that the BSD value depends both on the field size and on the photon energy (see also Table 1). For example, as BSD = 10 cm, in case of 6 MV X-ray and field size: 5 cm × 5 cm (Fig. 2a), the PDD curve is similar to the PDD curve obtained for open photon beam (solid line in Fig. 2a). However, for identical field parameters in the case of 15 MV X-ray, the PDD curve for BSD = 25 cm is similar to the PDD measured without the bolus. In order to fulfill the above mentioned conditions for larger irradiated fields – e.g. 20 cm × 20 cm – the BSD increases to the value of 26 cm for 6 MV and 39 cm for 15 MV photon beams. It is worth stressing that an analogous influence of the bolus was observed for all studied fields and both photon energies.
This outcome can be explained by photon interactions with atoms of the bolus. When a bolus is inserted in the beam's way, the electrons generated by photon interactions in the bolus appear in the beam. There is a larger fraction of low energy electrons present near the bolus.8 These low energy electrons dissipate energy and are lost to the beam at larger bolus phantom surface distance.
Electrons originated from a bolus can even interact with atoms of the phantom already on its surface. As a result the absorbed dose deposited in the region between the surface (d = 0 mm) and the depth of d = dmax increases. When a bolus is moved up more and more from the surface of the water, the influence of the electron stream formed in the bolus on the absorbed dose in the phantom decreases. It is caused partially by attenuation of these particles in the air gap and also by decrease of their fluence at the phantom surface.9 The depth of dmax is shifted to higher depth in the phantom for 15 photons beam, because the range of secondary electrons in the air is nearly threefold higher for 15 MV than for 6 MV photon beams. The values of dmax presented as a function of the BSD in Fig. 2a–d depict this dependence. Moreover, the exponential function given by Eq. (1) is fitted to the data series. Initially this function increases rapidly and then reaches a plateau, which is equal to the value of dmax measured without a bolus in an irradiated field. Parameters of this function are presented in Table 1. The fitting quality was assessed by using Pearson's correlation coefficients R2. Values of R2 are included in the interval: [0.93; 0.98] for all fittings (Table 1).
5. Conclusion
-
(i)
It noticed that the closer the bolus to the water surface is, the smaller the depth of the maximum dose in the phantom for all investigated fields and energies.
-
(ii)
On moving the bolus up from the phantom surface, the build-up region in the phantom rebuilds faster for smaller fields.
-
(iii)
The influence of the bolus can be ignored when the bolus-surface distance equals 25 cm for 6 MV and 39 cm for 15 MV X-ray beams.
References
- 1.Kassae A., Bloch P., Yorke E., Altsculer M.D., Rosenthal D.I. Beam spoilers versus bolus for 6 MV photon treatment of head and neck cancers. Med Dosim. 2000;25(Fall (3)):127–131. doi: 10.1016/s0958-3947(00)00038-8. [DOI] [PubMed] [Google Scholar]
- 2.Chu J.C.H., Coia L.R., Aziz D., Stafford P.M. Dose to superficial node for patients with head and neck cancer treated with 6 MV and 60 Co photons. Radiother Oncol. 1991;21(4):257–260. doi: 10.1016/0167-8140(91)90050-q. 8/91. [DOI] [PubMed] [Google Scholar]
- 3.Niroomand-Rad A., Javedan K., Rodgers J.E., Harter K.W. Effects of beam spoiler on radiation dose for head and neck irradiation with 10 MV photon beam. Int J Radiat Oncol Biol Phys. 1997;37(4):935–940. doi: 10.1016/s0360-3016(96)00538-x. [DOI] [PubMed] [Google Scholar]
- 4.Klein E.E., Michalet-Lorenz M., Taylor M.E. Use of a Lucite beam spoiler for high-energy breast irradiation. Med Dosim. 1995;20(Summer (2)):89–94. doi: 10.1016/0958-3947(95)00006-i. [DOI] [PubMed] [Google Scholar]
- 5.Lief E.P., Hunt M.A., Hong L.X., Amols H.I. Radiation therapy of large intact breasts using a beam spoiler or photons with mixed energies. Med Dosim. 2007;32(Winter (4)):246–253. doi: 10.1016/j.meddos.2007.02.002. [DOI] [PubMed] [Google Scholar]
- 6.Wittych J., Kukołowicz P. Wpływ płyty rozpraszającej na rozkład dawki od wiązki promieniowania × o energii 6 MeV. Rep Pract Oncol Radiother. 2003;8(1) [Google Scholar]
- 7.Kawa-Iwanicka A., Dybek M., Iwanicki T., Łobodziec W., Radkowski A. The technique of Total Body Irradiation applied in the St. Leszczyński Memorial Hospital in Katowice. Rep Pract Oncol Radiother. 2001;6(1):29–129. [Google Scholar]
- 8.Kassaee A., Xiao Y., Bloch P., Goldwein J., Rosenthal D.I., Bjarngard D.I. Doses near the surface during total-body irradiation with 15 MV X-ray. Med Dosim. 2000;25(Fall (3)):127–131. doi: 10.1002/ijc.10349. [DOI] [PubMed] [Google Scholar]
- 9.Hatice B., Aydın C., Murat O., Hilal A. Surface dose measurements with GafChromic film for 6 and 18 MV photon beams. Phys Med. 2009;25:101–104. doi: 10.1016/j.ejmp.2008.05.001. [DOI] [PubMed] [Google Scholar]
- 10.Hatice B., Nurdan O., Murat O., Aydın C., Hilal A. Surface dose and build-up region measurements with wedge filters for 6 and 18 MV photon beams. Jpn J Radiol. 2010;28:110–116. doi: 10.1007/s11604-009-0393-5. [DOI] [PubMed] [Google Scholar]
- 11.McKenna M., Gen Chen X., Altschuler M., Bloch P. Calculation of the dose in the build-up region for high energy photon beam. Treatment planning when beam spoilers are employed. Radiother Oncol. 1995;34:63–68. doi: 10.1016/0167-8140(95)01504-a. [DOI] [PubMed] [Google Scholar]


