Skip to main content
PMC home page
Reports of Practical Oncology and Radiotherapy logoLink to Reports of Practical Oncology and Radiotherapy
. 2012 Mar 6;17(2):115–118. doi: 10.1016/j.rpor.2012.01.011

Monte Carlo simulation for Neptun 10 PC medical linear accelerator and calculations of output factor for electron beam

Mohammad Taghi Bahreyni Toossi a,⁎, Mehdi Momennezhad b, Seyed Mohammad Hashemi a
PMCID: PMC3863207  PMID: 24377010

Abstract

Aim

Exact knowledge of dosimetric parameters is an essential pre-requisite of an effective treatment in radiotherapy. In order to fulfill this consideration, different techniques have been used, one of which is Monte Carlo simulation.

Materials and methods

This study used the MCNP-4Cb to simulate electron beams from Neptun 10 PC medical linear accelerator. Output factors for 6, 8 and 10 MeV electrons applied to eleven different conventional fields were both measured and calculated.

Results

The measurements were carried out by a Wellhofler-Scanditronix dose scanning system. Our findings revealed that output factors acquired by MCNP-4C simulation and the corresponding values obtained by direct measurements are in a very good agreement.

Conclusion

In general, very good consistency of simulated and measured results is a good proof that the goal of this work has been accomplished.

Keywords: Simulation, Monte Carlo, Linear accelerator, Dosimetry

1. Background

Application of Monte Carlo simulation in medical physics is back dated to the end of the 1970s.1

From those days till now, Monte Carlo techniques have been widely used in different areas of medical physics, in particular in physics of radiotherapy. Some of these applications are as follows: simulation of teletherapy sources, measurement of different dosimetric parameters in various environments, assessment of the effects of many factors on dose distribution in unisotropic tissues, studying dose distribution in different tissue interfaces, as well as modification of treatment systems.2–4

Nowadays, a number of Monte Carlo codes are available to be applied in medical physics to simulate different geometry in order to study particle transport and radiation interaction with matter. In radiotherapy, the Monte Carlo methods have been verified to be the most accurate techniques of predicting dose distribution and large number of investigations have been done on external teletherapy of electron and photon.5,6 The history and achievements of accelerator heads have been discussed in several reviews.7,8 Initially, most studies were devoted to photon beams.9,10 In the late 1980s, the simulation of electron beams started to attract the interest of researchers.11–15

The results revealed that dosimetric properties of electron beams, generated by linear accelerators, show significant difference between companies. Even machines produced by the same manufacturer have dissimilar beam characteristics due to small differences in the treatment head design.16 This is the reason why all centers confide on beam data measured by a medical physicist. In this study the electron beams from Neptun-10PC (IPJ-ZdAJ, Świerk, Poland) linear accelerator were evaluated using MCNP-4C (Los Alamos National Laboratory, RSICC, Oak Ridge, USA). This code is a general purpose Monte Carlo radiation transport code which can be used for single or coupled neutron, photon and electron transport in 3D geometry.17 It permits to simulate a variety of radiation sources and utilize several tallies to determine beam parameters.

Simulation works in radiotherapy are mainly focused on two parts: (a) simulation of radiation sources, e.g. X-ray beam line of Linac or 60CO of the older systems, which is very important and should be performed for individual systems; (b) patient's simulation and evaluation of various parameters affecting dose distribution in the body.18–21

The important feature of MCNP which paves the way for its easy application is the ability to define:

  • -

    General, critical, volume and surface sources.

  • -

    Proper definition of geometry.

  • -

    A wide range of variance reduction methods.

  • -

    Incorporating tallies to execute all required applications defined by operator an extensive library incorporating a wide range of cross sections.

2. Materials and methods

In this work the linear accelerator Neptun 10PC was simulated. Nearly 10 Neptun 10PC Linac have been installed in different centers around the country and are in operation (Tehran, Esfahan, Mashhad, …). Therefore, in this circumstance, to improve the accuracy of treatment planning, Monte Carlo simulation for Neptun 10 PC was recognized as a necessity. Electron mode of this Linac was simulated with MCNP-4C code and dosimetric parameters calculated.

The details of simulation and results are demonstrated elsewhere.22 When excellent agreement was obtained between the Monte Carlo simulated and dose distributions measured in a water phantom, in this study output factors for 6, 8 and 10 MeV electrons applied to eleven different conventional fields were both measured and calculated. Output factor for a given electron energy is the ratio of the dose for any specific field size (applicator size) to the dose for reference applicator, both measured at Zmax in a water phantom at SSD of 100 cm.

This unit is a standing-wave linear accelerator with a 270° bending magnet. It provides electron beams with nominal energies of 6, 8, 10 MeV and photon beam with 9 MV energy.

The main difference between electron and photon modes of this Linac is applicators. Applicators are composed of 10 pairs of blades, 0.8 cm in thickness, specially designed. They are placed after the secondary collimator.

Applicators are connected to a secondary collimator, therefore, they are moved together. By means of these applicators radiation fields ranging in area from 3 cm × 3 cm up to 25 cm × 25 cm can be formed Fig. 1.

Fig. 1.

Fig. 1

Open in a new tab

Applicators are installed on the head of accelerator.

A schematic design of all simulated parts of the Neptun 10 PC, including initial collimator, exit window, primary collimator, scattering foil, steel plate, ionization chamber, secondary collimator and applicators are shown in Fig. 2.

Fig. 2.

Fig. 2

Open in a new tab

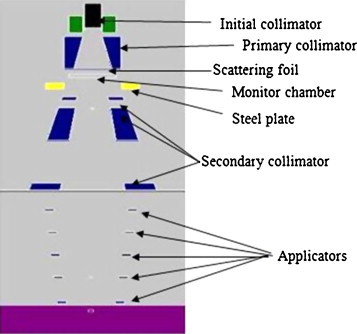
Schematic design of Neptun's simulated components.

This is a representation of the Linac head, and a water phantom in X = 0 plane in the default coordinate system. The water phantom dimensions were 50 cm × 50 cm × 20 cm .All interspaces were filled with air. The source was positioned at 100 cm from the phantom surface. It should be emphasized that the source energy distribution was a non-symmetrical Gaussian, but spatial distribution of particles was symmetrical Gaussian. The output factors were measured and calculated in a water phantom. For this objective a cubic cell (1 cm3) was defined at Zmax.

All dosimetric quantities generated by simulation were also experimentally measured. For this purpose, RFA-300 dosimetry system (Scanditronix-Wellhoffer, Schwarzenbruck, Germany) in conjunction with parallel plate chamber (Scanditronix-Wellhoffer, Schwarzenbruck, Germany) “(NACP) and diode detectors (Hi-Psi) (Scanditronix-Wellhoffer, Schwarzenbruck, Germany)” were employed.

The variance reduction techniques were used in this study to improve the speed and efficiency of simulation. These techniques include geometry truncation and cut-off energy. The low-energy cut-off for photon and electron was 10 and 500 keV, respectively. It should be emphasized that implementation of these limitations did not affect the final results produced by simulation. SPSS and excel software were employed for grouping and all other necessary statistical examination of our results. All computations were performed by a Pentium 4 PC (CPU = 3.2 GHz, RAM = 1024 MB).

3. Results

In this study, output factors for 3 cm × 3 cm, 4 cm × 4 cm, 6 cm × 6 cm, 8 cm × 8 cm, 10 cm × 10 cm, 12 cm × 12 cm, 15 cm × 15 cm, 18 cm × 18 cm, 20 cm × 20 cm, 22 cm × 22 cm, 25 cm × 25 cm field sizes were obtained by simulation and measurement. 10 cm × 10 cm field size was taken as a standard field. Output factor for a given electron energy is the ratio of the dose for any specific field size (applicator size) to the dose for reference applicator, both measured at Zmax in a water phantom at SSD of 100 cm. The Zmax is the depth of maximum dose of electron beam in a water phantom. The output factors were estimated for 6, 8 and 10 MeV electrons.

The system is nominally capable of generating electron beams of 6, 8 and 10 MeV, however measured dosimetric quantities indicated that the actual energy of the average output electron beams corresponded to 7.25, 8.8 and 10.68 MeV.

Measured and computed values of output factors with percentage difference for 6, 8 and 10 MeV electron beam applied to various field sizes are demonstrated in Table 1 and Figs. 3–5.

Table 1.

Measured and computed values of output factor for 6, 8 and 10 MeV electron beam applied to various field sizes.

6 MeV
 8 MeV
 10 MeV
Field size cm2 Computed Measured Difference (%) Computed Measured Difference (%) Computed Measured Difference (%)
3 × 3 0.93 0.941 1.17 0.967 0.971 0.41 0.976 0.973 0.31
4 × 4 0.96 0.963 0.31 0.997 1.002 0.5 0.998 1.01 1.19
6 × 6 0.971 0.975 0.41 1.007 1.01 0.3 1.012 1.016 0.39
8 × 8 0.983 0.988 0.51 1.003 1.005 0.2 1.009 1.006 0.3
10 × 10 1 1 0 1 1 0 1 1 0
12 × 12 1.004 1.005 0.1 0.997 0.998 0.1 0.993 0.998 0.5
15 × 15 1.011 1.014 0.3 0.99 0.987 0.3 0.968 0.968 0
18 × 18 0.992 0.999 0.7 0.976 0.968 0.83 0.933 0.946 1.37
20 × 20 0.993 0.995 0.2 0.966 0.959 0.73 0.937 0.939 0.21
22 × 22 0.991 0.992 0.1 0.95 0.948 0.21 0.926 0.923 0.33
25 × 25 0.977 0.976 0.1 0.955 0.95 0.53 0.901 0.909 0.88
Open in a new tab

Fig. 3.

Fig. 3

Open in a new tab

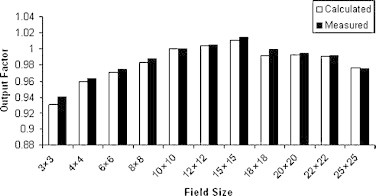
Measured and computed values of output factor for 6 MeV electron beam applied to various field sizes.

Fig. 4.

Fig. 4

Open in a new tab

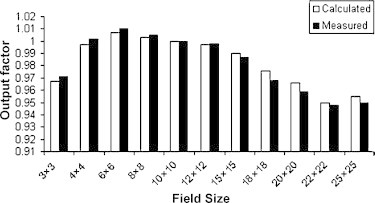
Measured and computed values of output factor for 8 MeV electron beam applied to various field sizes.

Fig. 5.

Fig. 5

Open in a new tab

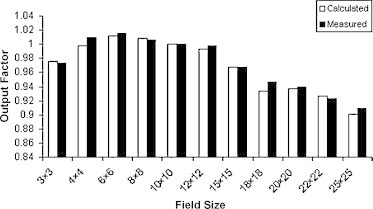
Measured and computed values of output factor for 10 MeV electron beam applied to various field sizes.

4. Conclusion and discussion

In this study, MCNP-4C code was employed to simulate electron mode of the Neptun 10PC Linac.

Our findings revealed that output factors, acquired by MCNP-4C simulation and the corresponding values obtained by direct measurements are in a very good agreement, with slight discrepancies between measured and calculated results, which may be related to little differences between the stated and actual dimensions of linear accelerator components as well as their composition. Also, there are some approximation techniques for speeding up simulation which can produce undesirable results.

Conflict of interest

None.

Footnotes

b

Monte Carlo N-Particle Transport Code – Version 4C.

References

  • 1.Udale-Smith Mary. Monte Carlo calculations of electron beam parameters for three Philips linear accelerators. Phys Med Biol. 1992;37(1):85–105. [Google Scholar]
  • 2.Ali Nedaie Hassan, Mosleh-Shirazi M.A., Shariary M., Gharaati H., Allahverdi M. Monte Carlo study of electron dose distributions produced by the elekta precise linear accelerator. Rep Pract Oncol Radiother. 2006;11(6):287–292. [Google Scholar]
  • 3.Ali Nedaie Hassan, Mosleh-Shirazi M.A., Gharaati H., Shariary M., Allahverdi M. Assessment of different MCNP Monte Carlo codes in electron absorbed dose. Rep Pract Oncol Radiother. 2006;11(6):293–298. [Google Scholar]
  • 4.Sanchez-Doblado F., Leal A., Perucha M., Arràns R., Núñez L., Rosellò J.V., Sànchez-Nieto B., Carrasco E., Gonzales A., Medrano J.C., Errazquin L., Sànchez-Calzado J.A. Monte Carlo clinical dosimetry. Rep Pract Oncol Radiother. 2002;7(2) [Google Scholar]
  • 5.Bahreyni Toossi M.T., Ghorbani M., Mowlavi A.A., Taheri M., Layegh M., Makhdoumi Y., Meigooni S.A. Air kerma strength characterization of a GZP6 Cobalt-60 brachytherapy source. Rep Pract Oncol Radiother. 2010;15(6):190–194. doi: 10.1016/j.rpor.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Bahreyni Toossi M.T., Abdollahi M., Ghorbani M. Monte Carlo dose calculation of GZP6 60Co stepping source based on a matrix shift technique. Rep Pract Oncol Radiother. 2011;16(1):10–13. doi: 10.1016/j.rpor.2010.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Andreo P. Monte Carlo techniques in medical radiation physics, (Review study) Phys Med Biol. 1991;36(7):861–920. doi: 10.1088/0031-9155/36/7/001. [DOI] [PubMed] [Google Scholar]
  • 8.Ma C.-M., Jiang S.B. Monte Carlo modeling of electron beams from medical accelerators. Phys Med Biol. 1999;44:R157–R189. doi: 10.1088/0031-9155/44/12/201. [DOI] [PubMed] [Google Scholar]
  • 9.Petti P.L., Goodman M.S., Sisterson J.M., Biggs P.J., Gabrial T.A., Mohan R. Sources of electron contamination for the Clinac-35 25-MV photon beam. Med Phys. 1983;10:856–861. doi: 10.1118/1.595348. [DOI] [PubMed] [Google Scholar]
  • 10.Mohan R., Chui C.S., Lidofsky L. Energy and angular distributions of photons for medical linear accelerator. Med Phys. 1985;12:592–597. doi: 10.1118/1.595680. [DOI] [PubMed] [Google Scholar]
  • 11.Udale M. A Monte Carlo investigation of surface doses for broad electron beams. Phys Med Biol. 1988;33:939–954. [Google Scholar]
  • 12.Ding G.H., Rogers D.W.O., Mackie T.R. Mean energy, energy–range relationship and depth-scalling factors for clinical electron beams. Med Phys. 1996;23:361–376. doi: 10.1118/1.597788. [DOI] [PubMed] [Google Scholar]
  • 13.Ma C.-M., Faddegon B.A., Rogers D.W.O., Mackie T.R. Accurate characterization of Monte Carlo calculated electron beams for radiotherapy. Med Phys. 1997;24:401–416. doi: 10.1118/1.597908. [DOI] [PubMed] [Google Scholar]
  • 14.Sempau J., Sanchez-Reyes A., Salvat F., Oulad ben Tahar H., Jiang S.B., Fernandez-Varea J.M. Monte Carlo simulation of electron beams from an accelerator head using PENELOPE. Phys Med Biol. 2001;46(4):1163–1186. doi: 10.1088/0031-9155/46/4/318. [DOI] [PubMed] [Google Scholar]
  • 15.Darko LALIC, Radovan D.ILIC, Srboljub J. STANKOVIC. Comparison of measured and Monte Carlo calculated electron beam central axis depth dose in water. Arch Oncol. 2001;9(2):83–87. [Google Scholar]
  • 16.Ding George X. Using Monte Carlo simulations to commission photon beam output factors—a feasibility study. Phys Med Biol. 2003;48(4):3865–3874. doi: 10.1088/0031-9155/48/23/005. [DOI] [PubMed] [Google Scholar]
  • 17.Los Alamos National Laboratory . Radiation Safety Information Computational Center; Los Alamos NM: 2000. Rsicc computer code collection MCNP4C Monte Carlo N-Particle Transport Code System. [Google Scholar]
  • 18.Lewist R.D., Ryde S.J.S., Hancock D.A., Evans C.J. An MCNP-based model of linear accelerator X-ray beam. Phys Med Biol. 1999;44:1219–1230. doi: 10.1088/0031-9155/44/5/010. [DOI] [PubMed] [Google Scholar]
  • 19.Helen H., Rock Mackie T., Edvin C. A dual source photon beam model use in convolution/superposition dose calculation for clinical megavoltage X-ray beam. Med Phys. 1997;24(12):1960–1974. doi: 10.1118/1.598110. [DOI] [PubMed] [Google Scholar]
  • 20.Lin S.Y., Chu T.C., Lin J.P. Monte Carlo simulation of a clinical linear accelerator. Appl Radiat Isot. 2001;(55):759–765. doi: 10.1016/s0969-8043(01)00130-0. [DOI] [PubMed] [Google Scholar]
  • 21.Chetty I., DeMarco J.J., Solberg T.D. A virtual source model for Monte Carlo modeling of arbitrary intensity distributions. Med Phys. 2000;27(1):166–172. doi: 10.1118/1.598881. [DOI] [PubMed] [Google Scholar]
  • 22.Bahreyni Toossi M.T, Momennezhad M, Hashemi S.M. Monte Carlo simulation of linear accelerator and electron beams used in radiotherapy. Iran. J. Radiat. Res., in press. [DOI] [PMC free article] [PubMed]

Articles from Reports of Practical Oncology and Radiotherapy are provided here courtesy of Via Medica sp. z o.o. sp. k.

RESOURCES