A new analytical formula for neutron capture gamma dose calculations in double-bend mazes in radiation therapy

Abstract

Background

Photoneutrons are produced in radiation therapy with high energy photons. Also, capture gamma rays are the byproduct of neutrons interactions with wall material of radiotherapy rooms.

Aim

In the current study an analytical formula was proposed for capture gamma dose calculations in double bend mazes in radiation therapy rooms.

Materials and methods

A total of 40 different layouts with double-bend mazes and a 18 MeV photon beam of Varian 2100 Clinac were simulated using MCNPX Monte Carlo (MC) code. Neutron capture gamma ray dose equivalent was calculated by the MC method along the maze and at the maze entrance door of all the simulated rooms. Then, all MC resulted data were fitted to an empirical formula for capture gamma dose calculations. Wu–McGinley analytical formula for capture gamma dose equivalent at the maze entrance door in single-bend mazes was also used for comparison purposes.

Results

For capture gamma dose equivalents at the maze entrance door, the difference of 2–11% was seen between MC and the derived equation, while the difference of 36–87% was found between MC and the Wu–McGinley methods.

Conclusion

Our results showed that the derived formula results were consistent with the MC results for all of 40 different geometries. However, as a new formula, further evaluations are required to validate its use in practical situations. Finally, its application is recommend for capture gamma dose calculations in double-bend mazes to improve shielding calculations.

1. Background

High energy photon beams are widely employed in modern radiation therapy techniques to improve the quality of treatments for deeply-seated tumors.^1–4 On the other hand, it is associated with unwanted photonuclear reaction between high energy photons and linac head materials, patient body and treatment room walls.^2–18 Production of photoneutrons occurs through photonuclear reactions, and consequently high energy gamma rays can be generated in the maze, following the capture process of thermalized neutrons.¹⁶ Both photoneutrons and neutron capture gamma rays are considered as undesirable radiations from radiation protection point of view, because they increase the patient and staff whole body radiation dose.^6,8,14,19

In a (n, γ) photonuclear reaction, an uncharged neutron penetrates a nucleus and then the nucleus releases its extra energy in the form of γ rays to reach the stable state. The cross-section of this reaction becomes high when a thermal neutron interacts with low Z materials found in concrete compositions according to the report of the National Commission on the Radiation Protection and Measurement.^17,18 In other words (n, γ) interactions occur mainly in H, Si and Ca atoms, those being the main components in an ordinary concrete composition. On the other hand, low Z materials can moderate fast neutrons and reduce their energy to thermal range and consequently capture gamma rays can be produced from thermalized neutrons interaction with concrete. Prompt capture gamma ray emissions within the maze have been studied by several researchers and the energy range from 2 MeV to 8 MeV has been reported for these gamma rays.^15,21 A study showed that in the mazes with 2 in. of borated polyethylene, most of (n, γ) interactions occurred with Boron atoms and gamma rays with average energy of 0.4 MeV released in the process.¹⁵ In another study by Tochilin and LaRiviere, average energy of 3.6 MeV was reported for capture gamma rays.²⁰ Finally, capture gamma rays are found at the maze entrance door and their effect on maze entrance door shielding should be considered in radiation therapy facilities. McGinley et al. reported that the major photon field at the end of a typical high energy accelerator facility is due to capture gamma rays.¹²

For calculation of capture gamma ray dose equivalent in single-bend mazes, Wu and McGinley²¹ studied seven different vaults and linac models and proposed the following analytical method:

$$D_{\text{g}}=5.7\times {10}^{-16}\times {\phi }_{\text{A}}\times {10}^{(-d_2/6.2)}$$ (1)

where D_g is capture gamma ray dose equivalent in Gy per Gy X-ray at the isocenter, φ_A is total neutron fluence at the inner maze entrance in terms of n⁰ m⁻² Gy⁻¹ and d₂ is the distance from point A in m (Fig. 1). Also, φ_A is given by the following equation:

$${\phi }_{\text{A}}=\frac{Q_{\text{N}}}{4\pi d^2}+\frac{5.4Q_{\text{N}}}{2\pi S}+\frac{1.26Q_{\text{N}}}{2\pi S}$$ (2)

where Q_N is the neutron source strength in n/Gy X-ray at the isocenter, d is the distance from the isocenter to point A in m and S is the total room inner surface in m². Recently, the International Atomic Energy Agency (IAEA) report No. 47⁷ and NCRP No. 151 has recommended the Wu–McGinley method for capture gamma rays dose calculations in radiation therapy with high energy photons. In a MC study, Mesbahi et al. simulated four different room and maze layouts to calculate capture gamma ray dose equivalent at the maze entrance door.¹³ They reported that although Wu–McGinley method results were in good agreement (16–17% difference) with MC results for single-bend mazes, considerable differences up to 95% were seen for a double-bend maze vault.

Fig. 1.

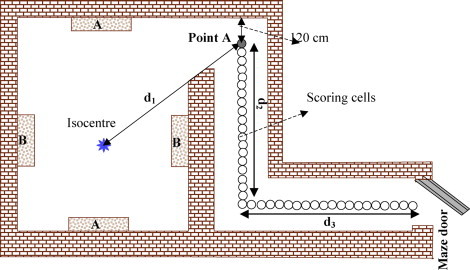
Top view of the simulated layouts, A and B show the type of simulated primary barrier in two different configurations.

2. Aim

As far as we know, there is no proposed analytical method for neutron capture gamma dose at the maze entrance door for double-bend mazes in the literature. Thus, in the current study we tried to develop a new analytical method to calculate the neutron capture gamma ray dose equivalent in double bend mazes.

3. Materials and methods

3.1. Monte Carlo simulations

The MCNPX Monte Carlo code and cross-section library for neutrons including ENDF/B-VII photonuclear data, and IAEA photonuclear data were used for MC simulations in the current study.^9–11 The MCNPX is a Monte Carlo code for transport simulation of electron, photon, and neutron and coupled electron–photon–neutron in different materials. Using the code, it is possible to simulate the first, second and fourth degree tori surfaces and complex geometries. Additionally, it is possible to simulate the photo-nuclear reactions using the MCNP code. A validated MC model of the 18 MeV photon beam of Varian 2100 linac was used for MC calculation. The MC model of the linac head had been benchmarked versus measured percent depth doses and dose profiles and had been used in previous studies.^5,13 Main components of the fully described 18 MeV photon beam of Varian 2100 Clinac head were simulated according to the manufacturer provided data. Primary electron beam, target, electron stopper, bending magnet, primary collimator, flattening filter, movable jaws and massive head shielding assembly were the simulated components of the linac. A 30 cm × 30 cm × 30 cm water phantom was positioned at the source-to-surface distance of 100 cm to resemble the patient body interactions with high energy photons. In all irradiations the beam direction was downward. To speed up photoneutron production, forth entry of phys:card in data card of MC input file was set to 1 to enable the biased photoneutron production. Neutron capture gamma ray dose was calculated in water cells with 10 cm diameter located at the height of 100 cm above the floor, every 20 cm along the maze. F6 tally (scores deposited energy per gram of absorbing material in MeV) was used in data card for neutron capture gamma ray dose calculation.

3.2. Simulated geometries

A total of 40 different vaults were simulated in terms of length and width and maze dimensions, with the wall material of ordinary concrete according to NCRP No. 144 recommended composition and density.¹⁷ The layout dimensions are shown in Table 1. All of the simulated geometries had double-bend mazes (Fig. 1). Four different groups of layouts were considered for MC calculations according as follows:

• (1)It is seen from Eq. (2) that the total inner surface of room affects the photoneutron fluence at point A. To study the room surface effect, different mazes were simulated with two types of room with inner surface of 295 and 240 m².
• (2)In some studied cases, the room dimensions remained constant but the length of the mazes was changed. The simulated mazes were composed of first and second legs with various lengths. In some cases, the first leg = 6 m, and second leg changed from 1 to 5 m. In the other cases the first leg = 7 m, and the second leg = 1–6 m. To investigate the relation between maze legs length and capture gamma dose equivalent, 22 different maze dimensions with the same room dimensions were simulated.
• (3)Constant room and maze dimensions with different maze cross-sectional area. The widths of the simulated mazes were considered as 2 m, 2.25 m, 2.5 m, 2.75 m, 3 m and the height of rooms remained constant for all configurations as 4 m.
• (4)The constant room and maze cross-section area with a difference in primary barriers positions. To study the effect of the primary barriers position on the capture gamma ray dose equivalent at the maze entrance door, two directions for gantry rotation were simulated. These two configurations of primary barriers are indicated with A and B in Fig. 1.

Table 1.

The geometric data of the simulated rooms and results of calculations with three methods for neutron capture gamma ray dose equivalent in Sv/Gy. The difference was calculated by the following formula: (MC-analytical method/MC) × 100.

Room	Inner room surface (m2)	d2 (m)	d3 (m)	Maze width (m)	Capture gamma ray dose equivalent (MC) (Sv/Gy)	Capture gamma ray dose equivalent Wu–McGinley method (Sv/Gy)	Capture gamma ray dose equivalent derived equation (Sv/Gy)	Difference between MC and Wu–McGinley methods (%)	Difference between MC and the derived equation (%)
1	258	6	1	2	4.89E−7	3.14E−7	4.80E−7	36	1.8
2	258	6	2	2	3.79E−7	2.17E−7	3.71E−7	75	2.1
3	258	6	3	2	2.97E−7	1.49E−7	2.88E−7	87	3.0
4	258	6	4	2	2.35E−7	1.03E−7	2.23E−7	56	5.1
5	258	6	5	2	1.81E−7	7.11E−8	1.72E−7	61	5.0
6	258	7	1	2	4.14E−7	8.04E−7	3.71E−7	49	10.4
7	258	7	2	2	3.20E−7	1.49E−7	2.99E−7	53	6.6
8	258	7	3	2	2.59E−7	1.03E−7	2.43E−7	60	6.2
9	258	7	4	2	1.90E−7	7.11E−8	1.79E−7	63	5.8
10	258	7	5	2	1.35E−7	4.90E−8	1.28E−7	65	5.2
11	258	7	6	2	1.08E−7	3.38E−8	1.03E−7	68	4.6
12	258	7	5	2	1.35E−7	4.90E−8	1.28E−7	64	5.2
13	258	7	5	2.25	1.42E−7	4.90E−8	1.34E−7	66	5.6
14	258	7	5	2.5	1.53E−7	4.90E−8	1.40E−7	68	8.5
15	258	7	5	2.75	1.58E−7	4.90E−8	1.46E−7	69	7.6
16	258	7	5	3	1.61E−7	4.90E−8	1.52E−7	70	5.6
17	258	6	4	2	2.39E−7	1.03E−7	2.23E−7	57	6.7
18	258	6	4	2	2.31E−7	1.03E−7	2.23E−7	56	3.5
19	258	7	4	2	1.85E−7	7.11E−8	1.72E−7	62	7.0
20	258	7	4	2	1.81E−7	7.11E−8	1.72E−7	61	5.0
21	279	6	1	2	5.27E−7	2.90E−7	5.18E−7	45	1.7
22	279	6	2	2	4.11E−7	2.06E−7	4.01E−7	50	2.4
23	279	6	3	2	3.20E−7	1.42E−7	3.11E−7	56	2.8
24	279	6	4	2	2.55E−7	9.79E−8	2.41E−7	62	5.5
25	279	6	5	2	2.02E−7	6.75E−8	1.86E−7	67	7.9
26	279	7	1	2	4.13E−7	2.06E−7	4.01E−7	50	2.9
72	279	7	2	2	3.22E−7	1.42E−7	3.11E−7	56	3.4
28	279	7	3	2	2.61E−7	9.79E−8	2.41E−7	63	7.7
29	279	7	4	2	1.95E−7	6.75E−8	1.86E−7	65	4.6
30	279	7	5	2	1.59E−7	4.66E−8	1.44E−7	71	9.4
31	279	7	6	2	1.21E−7	3.21E−8	1.12E−7	73	7.4
32	279	7	5	2	1.59E−7	4.66E−7	1.44E−7	71	9.4
33	279	6	4	2.25	2.20E−7	9.79E−8	2.13E−7	56	3.2
34	279	6	4	2.5	2.31E−7	9.79E−8	2.22E−7	58	3.9
35	279	6	4	2.75	2.39E−7	9.79E−8	2.32E−7	59	2.9
36	279	6	4	3	2.52E−7	9.79E−8	2.41E−7	61	4.4
37	279	6	4	2	2.65E−7	9.79E−8	2.41E−7	63	9.1
38	279	7	4	2	2.57E−7	9.79E−8	2.41E−7	62	6.2
39	279	7	4	2	2.01E−7	6.75E−8	1.86E−7	66	7.5
40	279	7	4	2	1.98E−7	6.75E−8	1.86E−7	66	6.1

For capture gamma dose calculation using the analytical method, Eqs. (1) and (2), and the neutron source strength of 1.3 × 10¹² n/Gy were applied according to the previous study on the MC model used.¹³ The values of φ_A were obtained from Eq. (2) for all geometries and then it was applied in Eq. (1) for capture gamma dose calculations.

3.3. Derivation of a new analytical formula

To derive a new formula from MC results, all data from 40 geometries was entered into a single work sheet and a polynomial was fitted to all data points using the MINITAB²¹ software. The R² value of fitting was 99.2% with P value of 5 × 10⁻⁴ (Fig. 3).

Fig. 3.

Results of MC calculations for all geometries used in the present study. Points are indicating the capture gamma dose equivalent along the maze. The fitted curve is shown with the solid line.

Then, using the fitted polynomial, an empirical relation was derived between gamma dose equivalent at any point along the maze and distance (d₂ + d₃) from inner maze entrance, point A. It is noteworthy to point out that the calculations for the rooms of the third group revealed that neutron capture gamma ray along the maze changed with cross-sectional area of mazes. So, the effect of cross-sectional area of the maze (S) in the gamma ray dose equivalent was considered in the derived equation. The following equation was obtained:

$$D_{\text{g}}=1.114\times {10}^{-16}\times {\phi }_{\text{A}}\times (\sqrt{S}\times e^{-((d_2+d_3)/3.89)}+e^{-((d_2+d_3)/4.00)})$$ (3)

where D_g is neutron capture gamma ray dose equivalent along the maze in terms of Sv/Gy. Parameters d₂ and d₃ denote the length of the first and second legs, respectively.

4. Results and discussion

Capture gamma ray dose equivalent was calculated at the maze entrance door by the MC method and derived equation. Also, the Wu–McGinley method with consideration of sum of two legs as a straight maze was used. The results of the three calculation methods and the differences between MC and two other analytical methods are shown in Table 1.

Fig. 2 shows the neutron spectra of simulated linac. It was consistent with the previous study using the same MC model.

Fig. 2.

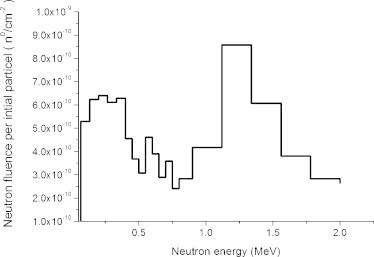
Monte Carlo calculated neutron spectra around the linac head at the distance of 1 m from electron target.

Fig. 3 shows MC calculated dose equivalent along the maze of all simulated geometries and also the fitted curve. The fitted curve is depicted as a solid line. It can be seen that the fitted curve is very close to a few cases in points along the first leg and there are large deviations from some studied cases. However, the difference between the fitted curve and MC calculated points within the second leg is not as large as the first leg and the fitted curve values get closer to MC data of all studied cases toward the maze entrance door. Consequently, if the derived equation is used for the second leg and maze entrance door the difference between the derived formula and MC calculated will be less than 11% in its worst case at the maze entrance door. The results are shown in Table 1. The capture gamma dose values along the maze for one of the simulated geometry, maze with d₂ = 7, d₃ = 6 (case = 11) is depicted in Fig. 4. As can be seen, capture gamma dose decreases with distance from point A, and a slight change occurs in the curve shape at the bending region of the maze and the slope of the curve decreases at this point. A relatively flat area of the curve at the bending region is the result of increase in the number of neuron interactions with the wall material. Consequently, there is a rise in the number of capture gamma rays at the bending. After the bending point, the capture gamma dose decreases with the same slope. This pattern is seen for all cases.

Fig. 4.

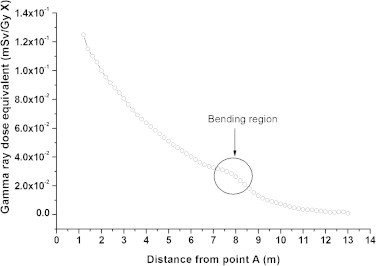
An example of MC calculated capture gamma dose along the maze with d₂ = 7, d₃ = 6 (case = 11).

Fig. 5 shows the results of capture gamma dose equivalent calculation with the proposed formula, MC and Wu–McGinley methods for case = 10 where the best match between MC and proposed equation was achieved (Fig. 5). It can be seen that there is good agreement between MC and derived equation results at all points along the maze. Whereas, the Wu–McGinley method underestimates the dose values considerably with respect to the MC method. Another previous investigation also showed differences of 86–95% in a long double-bend maze case between the Wu–McGinley and MC methods.¹³

Fig. 5.

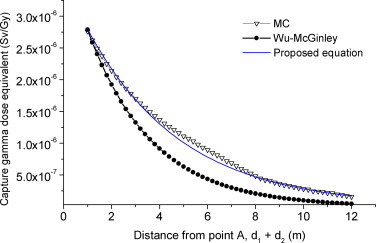
Comparison of calculated capture gamma dose equivalents for the maze with d₂ = 7 m and d₃ = 5 m legs with three studied methods.

Fig. 6 depicts the spectra of capture gamma rays and scattered and leaked photons from linac. As can be seen, the capture gamma rays maximum energy is higher than the scattered photon maximum energy and it reaches up to around 10 MeV while the maximum energy of scattered photons locates at 1 MeV. The first peak of gamma rays and linac photons occurs at 0.2–0.5 MeV, but there is another peak for capture gamma rays at 8–9 MeV. The figure shows that the maximum energy of capture gamma rays can be 10 times as high as that of scattered radiation reaching the maze entrance door. Consequently, in shielding calculations for maze entrance door against capture gamma rays, their higher energy relative to scattered photons should be considered.

Fig. 6.

MC calculated scattered photon and capture gamma spectra at the maze entrance door.

According to Table 1, the difference between the MC and Wu–McGinley methods for capture gamma dose at the maze entrance door are between 36% and 87%. However, the difference between the derived equation and MC ranges from 2% to 11% for all 40 geometries. The large differences of up to 11% are attributable to the fitting process that we used for equation derivation. In other words, the geometries whose capture gamma curves were far from the fitted curve showed large differences with MC results. It seems that reduction in differences between derived equation and MC results occurs because of including the effect of neutron attenuation with inserting maze cross-section area in the relation and also using more different dimensions and layouts for deriving Eq. (3).

5. Conclusion

The results of our derived formula showed good agreement with MC calculation results for 40 different maze layouts studied in the current research. However, further experimental investigations are needed to confirm its reliability in other cases. On the other hand, we think that its application can significantly improve shielding calculations in double-bend mazes.

Conflict of interest

None declared.