Multiple-source models for electron beams of a medical linear accelerator using BEAMDP computer code

Abstract

Aim

The aim of this work was to develop multiple-source models for electron beams of the NEPTUN 10PC medical linear accelerator using the BEAMDP computer code.

Background

One of the most accurate techniques of radiotherapy dose calculation is the Monte Carlo (MC) simulation of radiation transport, which requires detailed information of the beam in the form of a phase-space file. The computing time required to simulate the beam data and obtain phase-space files from a clinical accelerator is significant. Calculation of dose distributions using multiple-source models is an alternative method to phase-space data as direct input to the dose calculation system.

Materials and methods

Monte Carlo simulation of accelerator head was done in which a record was kept of the particle phase-space regarding the details of the particle history. Multiple-source models were built from the phase-space files of Monte Carlo simulations. These simplified beam models were used to generate Monte Carlo dose calculations and to compare those calculations with phase-space data for electron beams.

Results

Comparison of the measured and calculated dose distributions using the phase-space files and multiple-source models for three electron beam energies showed that the measured and calculated values match well each other throughout the curves.

Conclusion

It was found that dose distributions calculated using both the multiple-source models and the phase-space data agree within 1.3%, demonstrating that the models can be used for dosimetry research purposes and dose calculations in radiotherapy.

1. Background

Accurate calculation of absorbed dose distribution in patients irradiated by clinical electron beams is very important in radiotherapy treatment.¹ The most accurate method of radiation therapy dose calculation is based on Monte Carlo simulation of radiation transport. The Monte Carlo method is a numerical technique based on random number sampling to simulate a stochastic process, in this case, transport of photon and electron particles through a medium.² The major advantage of this method is that one can score many quantities of interest. For example, one can score not only energy deposition in a water phantom, but also the number of particles scattered in a particular region before depositing energy in a small volume of the water phantom. To achieve the full accuracy of a Monte Carlo dose calculation, detailed information on the character of the beam is required, which includes the energy, angular and spatial distributions of all particles in the clinical beam.^3,4 This phase-space information which is stored in a phase-space file imposes very high requirements for disk space and CPU time.

Beam modeling represents an alternative to phase-space information as direct input to the dose calculation code. Multiple-source model is a beam model based on the fact that particles from the same components of a linear accelerator have very similar characteristics in terms of energies and incident directions, and that particles from different components have different energy, angular and spatial distributions.^5–7

There are several published studies which are based on multiple-source models that appear to be attractive because of significant reduction in calculation time and data storage.⁷ For example: hybrid commissioning approach based on multiple-source model for Monte Carlo treatment planning as a time saving method for commissioning of the same type of accelerators based on models developed from only one simulated phase-space, and application in narrow beam radio-surgery.^8,9 Thus, full Monte Carlo simulation of the beam shows a very poor efficiency with a great limitation in time and storage capacity. One approach to reduce the time and storage capacity is to use a multiple-source model containing a set of physical parameters.¹⁰

2. Aim

The purpose of this study was to develop the accurate multiple-source models for the electron beams of the NEPTUN 10PC medical linear accelerator using the BEAMDP (BEAM Data Processor) computer code. This program can be used to analyze the phase-space parameters of a clinical electron beam generated using BEAMnrc and to derive the data required by a multiple-source model for representation and reconstruction of the electron beam for use in Monte Carlo radiotherapy treatment planning.¹¹ In this work, multiple-source models were developed based on a detailed modeling of the accelerator in our previous work.¹² With these models, the phase-space information of the electron beams can be precisely reconstructed and the dose distribution in a water phantom can be accurately calculated.

3. Materials and methods

3.1. Medical linear accelerator

In this work, all experimental measurements and Monte Carlo calculations were performed on a NEPTUN 10PC medical linear accelerator.¹³ This linac produces one photon beam quality at 9 MV, and electron beams with three selectable energies at 6, 8, and 10 MeV. For the electron beam mode, the primary electrons impinge on one of two available scattering foils (one scattering foil for 6 and 8 MeV electron beams and the other for 10 MeV). These are made from different thicknesses of lead.

An appropriate scattering foil is automatically selected for a particular nominal energy. The X-ray jaws provide the first collimation for the broad electron beam. The electron beams coming through the X-ray jaws are of uniform intensity distribution.¹⁴ The electron beam applicators of the NEPTUN 10PC linac consist of five scrappers, each of them being constructed from 3 layers with different thicknesses and materials. The distances between all the scrapers, except the last one, are the same. Therefore, the applicators have only to progressively collimate the beam using a set of five aperture plates without the use of any wall scatter. These aperture plates have decreasing dimensions downstream. The bottom aperture plate defines the treatment field size. The combination of applicators with photon jaws provides electron beams with field sizes from 3 cm × 3 cm up to 25 cm × 25 cm.

3.2. Experimental measurements

Central axis depth–dose curves and dose profiles for electron beams were measured in water using a radiation field analyzer computerized water phantom (RFA-300, IBA Scanditronix Medical AB, Uppsala, Sweden), which is a dosimetry system for 3D radiation field analysis. A waterproof high-doped p-type silicon diode (Scanditronix Medical AB, EFD-3G) was used to measure the percentage depth doses and dose profiles. The thickness of the silicon chip was 0.5 mm, and the diameter of the active area was 2 mm. A reference diode detector (IBA Scanditronix Medical AB) was placed in the periphery of the radiation field during scanning. Because the stopping power ratio of silicon to water is almost constant over the energies measured in radiotherapy (1–5% changes in 1–20 MeV energy range), the depth ionization can be directly used as the depth doses.¹⁵

The PDD curves for 6, 8 and 10 MeV electron beams were measured for three field sizes (3 cm × 3 cm, 10 cm × 10 cm, 25 cm × 25 cm) at SSD = 100 cm using the IAEA protocol.¹⁶ In addition, the dose profiles were measured for the reference field (10 cm × 10 cm) at the d_max for each electron beam. All the curves were plotted from the average values obtained from three separate measurements made for every situation.

The most probable electron energy at the phantom surface (E_p0) determined from the depth of the practical range R_p in water phantom using the following equation.^4,12

$$E_{\text{p}0}=0.22+1.98R_{\text{p}}+0.0025R_{\text{p}}^2$$ (1)

In addition, the mean energy on the phantom surface (E₀) determined from the R₅₀, the depth at which the dose falls to 50% of the maximum dose, using the following equation.^4,12

$$E_0=2.33R_{50}$$ (2)

3.3. Monte Carlo modeling of NEPTUN 10PC linac

In this study the NEPTUN 10PC linac was modeled using the BEAMnrc¹⁷ system based on EGSnrc code.¹⁸ For the Monte Carlo modeling of the Linac machine, the vendor provided us with detailed information regarding the geometry and material of various components of the treatment head. The model based on BEAMnrc code consists of a series of component modules. Each component is contained between two planes which are perpendicular to the z-axis and which cannot overlap. A schematic representation of the linac head and its components is shown in Fig. 1.

Fig. 1.

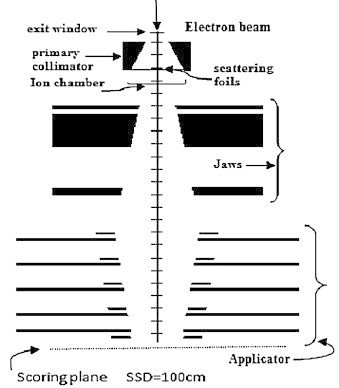
Schematic representation of the simulated geometry including linac head and position of the scoring plane for phase space file generation.

The head components, including exit window, primary collimator, scattering foils, monitor chamber, secondary collimator Jaws and applicators, were simulated based on manufacturer provided information. Modeling of electrons prior to exiting the vacuum tube is usually not done as part of Monte Carlo simulation. In the present study, constant values of the global electron cutoff energy (AE = ECUT = 0.7 MeV) and the global photon cutoff energy (AP = PCUT = 0.01 MeV) were used for all component modules in the BEAMnrc simulations.

The BEAMnrc code was run under the Microsoft Windows XP^® operating system using a dual processor (3800 GHz, ADM Athlon™, 64 × 2 Dual Core Processor, 1 GB RAM) computer. In the BEAMnrc code, the particles, after transporting, were scored at a scoring plane placed after the last scraper. The information of this scoring plane, which is named the phase-space file, was used as the source input for the simulations of the dose distributions in a rectilinear voxel geometry water phantom using the DOSXYZnrc system, which is also based on the EGSnrc code.¹⁹

3.4. Monte Carlo modeling of electron beams

Generally, the development of source models is performed in two steps. First, the commissioning, in which the source model is tuned in order to match a certain set of measurements. Second, the validation of the source model. For the second step the calculated dose distributions from models have to be compared with measurements, which have not been used for the commissioning. The BEAMnrc MC code was used to calculate the raw beam and create the phase-space file at the scoring plane located at the end of the last component of the treatment head at SSD = 100 cm. The phase-space file contained all of the particles in the simulated beam that reached the scoring plane.

A rectilinear voxel geometry water phantom with dimensions of 50 × 50 × 50 cm³ was simulated to provide full scatter conditions using the DOSXYZnrc code. The dose resolution of this water phantom for depth dose and dose–profile was 2 mm. The depth dose and dose–profile values from the phase-space files for three electron beams at the reference field were calculated in the simulated water phantom.

Electron beam energy tuning was performed by comparing calculated and measured PDD curves to the reference field size. To compare calculation and measurements, the value of each depth was normalized to the maximum value of energy deposited in the central axis. The electron beam energies were adapted to give depth–dose curves having the same depth at the 50% dose level.

After benchmarking of the simulated linac, the three electron beam models were used for calculating central axis depth–dose curves for the smallest and largest field sizes (3 cm × 3 cm and 25 cm × 25 cm). Then, the measured and calculated values of the PDD curves were compared with each other for validating of the provided models. In this study, we used the provided phase-space files from our previous work¹² for creating multiple-source models using the BEAMDP (BEAM Data Processor) code.¹¹

3.5. Multiple – source model

A multiple-source model is built from the phase-space file of a Monte Carlo simulation. It is required that each physical component in the treatment head has an associated LATCH bit during the full Monte Carlo simulation (LATCH is a 32-bit variable used to track the particle's history), and it is necessary to use inherited LATCH bit setting.^7,17

The multiple-source model is based on the observation that particles from different components of an accelerator can be treated as if they were from different sub-sources. Each sub-source represents a critical component in the treatment head and its geometrical dimensions are determined by the component dimensions. Each sub-source has its own energy spectrum and planar fluence distribution derived from the simulated phase-space data.^6,7

In the present study, the BEAMDP program is used to analyze the phase-space data and create the model. For model verification purposes, the DOSXYZnrc code was used for dose distribution calculations from the phase-space files, multiple-source models in a rectangular voxel based phantom. Dose distribution curves obtained from the multiple-source models were compared against dose distribution curves from the simulated phase-space file to validate the model.

The multiple-source models, not only validated against calculated dose distributions using the phase space files as input, but also every multiple-source model was validated directly against measurements. The calculated values, estimated by the multiple-source models were compared and tested against the measured values and calculated values by phase-space files using the Kolmogorov–Smirnov statistical test.

To evaluate the effects of multiple-source models on the saving in CPU time for the treatment head simulation and reducing disk space, simulations were done with BEAMnrc of a NEPTUN 10PC electron beams, to generate phase-apace data. Using the multiple-source models, each of these beams was used to calculate the parameters of the beam representation and a set of beams reconstructed based on these parameters.⁶ Then the simulation time and disk space required to store the original phase-space files were compared with the CPU time to reconstruct the phase-space and the amount of disk space needed to store of them.

3.6. Types of source models

“Each commonly used component of clinical linear accelerator has a simplified 2-dimensional type of sub-source in the plane perpendicular to the z-axis which has the same dimensions along the x and y-axes as the modeled component. The distance of the sub-source from the scoring plane is calculated from the mid-point of the component thickness. There are a variety of sub-sources with respect to the components in an accelerator. They are classified as rings, cones and point sources, applicators, collimators, rectangular plane sources and circular plane sources”.⁷

The full model, electron–photon sub-sources has been developed as multiple-source model in this work. We used a variety of sub-sources with respect to the components of the NEPTUN 10PC linac. A point source corresponds to the “direct” particles, particles coming directly from the exit window, and traversing components such as scattering foils, monitor chamber, without hitting any of the beam defining components such as collimator jaws or applicators. Source to surface distance (SSD) for a virtual point source is evaluated using a ‘pin-hole’ method.⁶ Primary collimators are modeled as a ring with zero height. The radial dimension of the sub-source is the same as that of the actual ring at the mid-point of the ring thickness. The distance from the sub-source to the scoring plane is calculated from the mid-point of the collimator thickness to the scoring plane. When the radius of this sub-source is set to zero the sub-source can be considered as a point source.⁷

Scattering foils and monitor ionization chambers are modeled as circular and rectangular planar sources respectively. Planar sub-sources are used for bremsstrahlung photons as they are created directly in these components. For charged particles planar sub-sources replaced by a virtual point source.⁷

“Collimator jaws are modeled as parallel-bars with zero height. The X and Y dimensions of the sub-source are the same as those of the actual collimator at its mid-point thickness. The distance from the sub-source to the scoring plane is calculated from the mid-point of the collimator thickness to the scoring plane”.⁷

Applicators are modeled as surfaces (rectangular rings) on the (x, y) plane with zero thickness.⁷ “The dimensions of the applicator opening should be exactly the same as that of the applicator being modeled. It is not necessary, however, that the applicator model for charged particles have the same outer dimensions as those of the applicator”.¹¹ “The outer dimensions can be considered to be equal to the inner opening dimensions plus a 0.5–2.0 cm margin. For bremsstrahlung photons, the outer dimensions of the applicator should correspond to the area “exposed” to the electron beam, but in most cases, the actual outer dimensions can be used for the photon sources. The distance from the sub-source to the scoring plane is calculated from the mid-point of the applicator thickness to the scoring plane”.⁷

4. Results

Our previous study results¹² showed that the PDD and dose–profile curves calculated by the MC method using the phase-space data files matched well with the measured values. Previous study also demonstrated that the MC phase-space data files can be used to generate accurate MC dose distributions for electron beams from NEPTUN 10PC medical linac.

We showed the validity of the electron beam modeling in our previously published report.¹² So, we focused only on the results of multiple-source models development in this study. In the present work, we used the provided phase-space files as input source files for the BEAMDP program to develop multiple-source models for the electron beams of the NEPTUN 10PC linac.

Fig. 2 shows the PDD curves measured and calculated using the phase-space files and multiple-source models for the 6, 8, and 10 MeV electron beams in the reference field (10 cm × 10 cm).

Fig. 2.

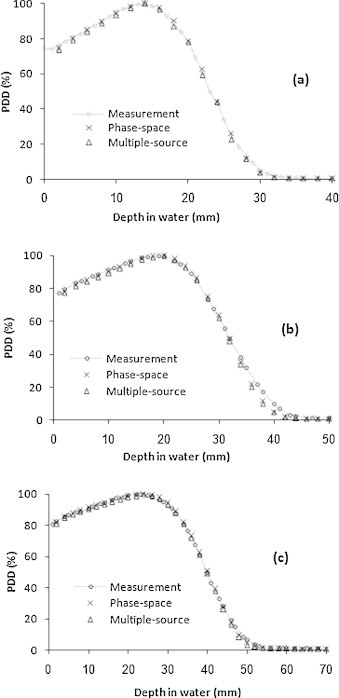
Central axis PDD curves of the measurements and MC calculations using the phase-space files and multiple-source models for different electron beam energies: 6 MeV (a), 8 MeV (b) and 10 MeV (c), at the reference field size (10 cm × 10 cm).

Fig. 3 shows the measured and calculated cross line dose profiles at depth of dose maximum d_max using the phase-space files and multiple-source models for three electron beam energies at the reference field.

Fig. 3.

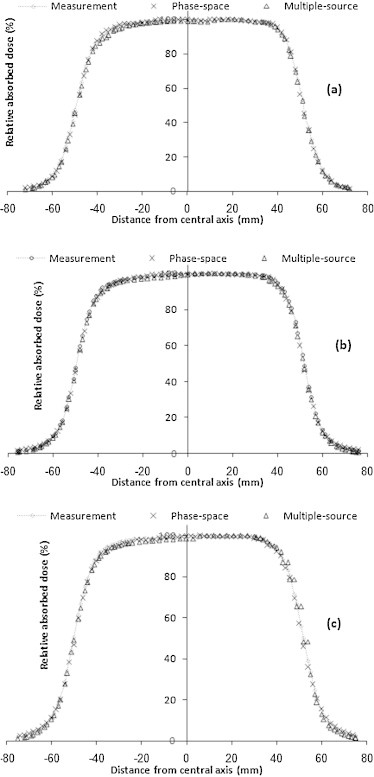
Measured and calculated cross line dose profiles at depth of dose maximum d_max using the phase-space files and multiple-source models for different electron beam energies: 6 MeV (a), 8 MeV (b) and 10 MeV (c), at the reference field size (10 cm × 10 cm).

Table 1 shows the measured and calculated electron beam PDD parameters using phase-space file (PSF) and multiple-source model (MSM) for three electron beam energies of the linac at the reference field size (10 cm × 10 cm).

Table 1.

Parameterized measured and calculated (using PSF and MSM) depth–dose curves from three electron beam energies at the 10 cm × 10 cm field size.

PDD parameters	6 MeV			8 MeV			10 MeV
	Measured	PSFa	MSMb	Measured	PSF	MSM	Measured	PSF	MSM
EP0 (MeV)	6.21	6.20	6.16	8.24	8.25	8.23	9.94	9.92	9.88
E0 (MeV)	5.68	5.67	5.62	7.43	7.45	7.39	9.29	9.30	9.24
R100 (mm)	14.00	14.00	14.00	18.00	18.00	18.00	24.00	24.00	24.00
R85 (mm)	18.60	18.80	18.50	25.80	26.20	26.00	32.70	33.00	32.80
R50 (mm)	24.40	24.30	24.10	31.90	32.00	31.70	39.87	39.91	39.65
Rq (mm)	17.80	18.30	18.10	24.00	24.6	24.20	30.40	30.80	31.00
Rp (mm)	30.10	30.01	29.60	40.30	40.35	40.25	48.80	48.70	48.50

^aPhase-space file.

^bMultiple-source model.

Fig. 4 shows the PDD curves measured and calculated using the phase-space files and multiple-source models for the 6, 8, and 10 MeV electron beams in the smallest field (3 cm × 3 cm).

Fig. 4.

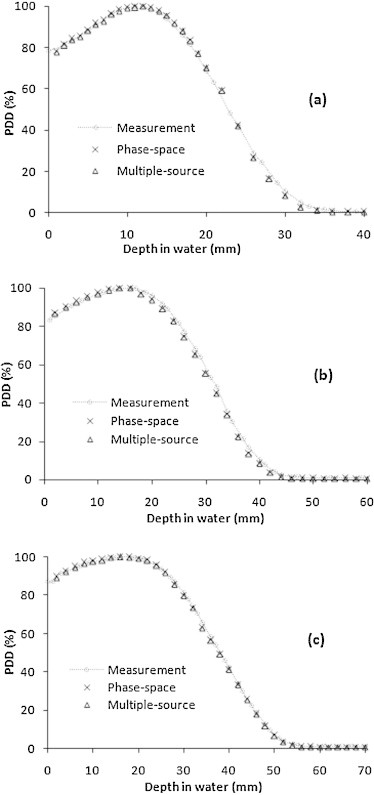
Central axis PDD curves of the measurements and MC calculations using the phase-space files and multiple-source models for different electron beam energies: 6 MeV (a), 8 MeV (b) and 10 MeV (c), at the smallest field size (3 cm × 3 cm).

Fig. 5 shows the PDD curves measured and calculated using the phase-space files and multiple-source models for the 6, 8, and 10 MeV electron beams in the largest field (25 cm × 25 cm).

Fig. 5.

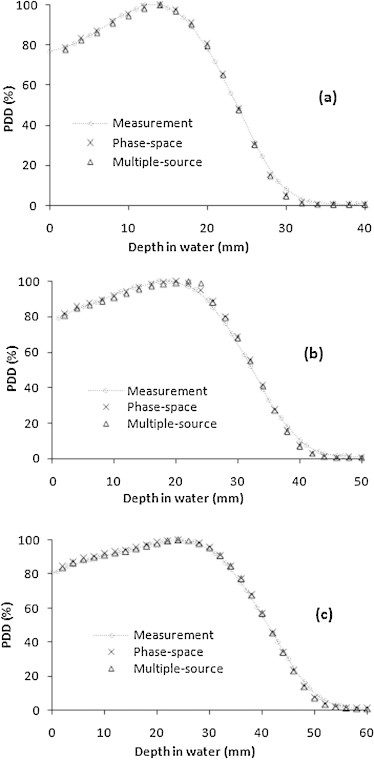
Central axis PDD curves of the measurements and MC calculations using the phase-space files and multiple-source models for different electron beam energies: 6 MeV (a), 8 MeV (b) and 10 MeV (c), at the largest field size (25 cm × 25 cm).

Table 2 shows the P-values of the Kolmogorov–Smirnov test resulted from the comparison between multiple-source models depth dose and beam profile calculations and water phantom measurements for various electron beam energies and field sizes.

Table 2.

The P-values of the K–S test obtained from the comparison of the data derived from the experimental measurements and the multiple-source models calculations for various electron beam energies and field sizes.

Electron beam energy (MeV)	3 cm × 3 cm	10 cm × 10 cm		25 cm × 25 cm
	PDD P-values	PDD P-values	Dose profile P-values	PDD P-values
6	0.512	0.743	0.327	0.362
8	0.234	0.203	0.633	0.166
10	0.821	0.256	0.588	0.124

Table 3 shows the P-values of the Kolmogorov–Smirnov test resulted from the comparison between multiple-source models depth dose and beam profile calculations and phase-space files calculations for various electron beam energies and field sizes.

Table 3.

The P-values of the K–S test obtained from the comparison of the multiple-source models depth dose and beam profile calculations versus phase-space files calculations for various electron beam energies and field sizes.

Electron beam energy (MeV)	3 cm × 3 cm	10 cm × 10 cm		25 cm × 25 cm
	PDD P-values	PDD P-values	Dose profile P-values	PDD P-values
6	0.739	0.831	0.504	0.562
8	0.443	0.411	0.722	0.349
10	0.879	0.396	0.658	0.241

Comparison of the measured and calculated dose distributions using the phase-space files and multiple-source models for three electron beam energies showed that the measured and calculated values match well each other throughout the curves. We showed that the agreement in dose calculations between the models and phase-space files was well within 1.3% for all models.

Table 4 shows how many particle histories are simulated and the size of phase-space file for each electron beam energy and field size. It is clear that lower number of histories is required for higher energies and larger field sizes to get the same statistics in dose calculation.

Table 4.

Number of particles (in millions), size of phase-space files (PSF) in MB for various electron beam energies and field sizes to create phase-space data at SSD = 100 cm.

Energy (MeV)	Field size (cm × cm)	Number of particles (106)	PSF size (MB)
			Full MC	MSM
6	3 × 3	160	39.6	0.032
	10 × 10	100	237	0.21
	25 × 25	60	712	0.63
8	3 × 3	140	46.3	0.043
	10 × 10	100	272	0.23
	25 × 25	60	741	0.69
10	3 × 3	140	51.7	0.047
	10 × 10	100	308	0.28
	25 × 25	60	773	0.71

The chart in Fig. 6 compares the required time (hours) for the treatment head simulation using full MC versus time of head simulation using multiple-source model for three electron beam energies at the 10 cm × 10 cm field size.

Fig. 6.

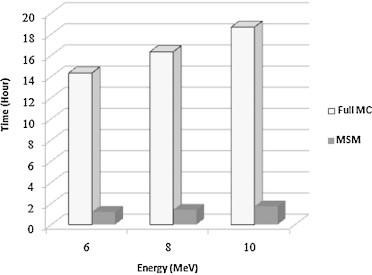
Time requirements (in hours) for treatment head simulation using full MC versus head simulation using multiple-source model for three electron beam energies at the 10 cm × 10 cm field size.

It was found that the dose calculation using the phase-space data requires millions of particles in order to achieve the desired statistical precision. In this case, the storage requirements for the phase-space data may reach tens or hundreds GB of disk space. While the multiple-source models require generally a few KB of data, which is negligible compared to the phase-space data. It must be noted that modeling of a simulated beam requires 10% or less particles compared to full Monte Carlo simulations. Meanwhile, the use of beam models does not provide any time savings for dose calculations.

5. Discussion

The aim of this project was to develop multiple-source models for the electron beams of the NEPTUN 10PC linac so that the models can be used for dosimetry research purposes and dose calculations in radiation therapy. In this regard, the models were developed and directly verified for electron beams from a NEPTUN 10PC linac.

Several multiple-source models for electron and photon beams of an Elekta Precise SL25 linear accelerator were developed by simulating radiation transport through the accelerator by the National Research Council of Canada (NRC).⁷ In this regard, the Sego study showed that the agreement in dose calculations between the models and original phase-space files was well within 1.0% for all sub-source models.⁷

In this work, the Kolmogorov–Smirnov test indicated that the PDDs and the dose profiles calculated values with the multiple-source models match well with those measured and calculated with original phase-space files, throughout the curves for all the linac electron beams (P-values > 0.1).

It is well accepted that the only accurate and practical way to obtain detailed information on a clinical electron beam is the Monte Carlo simulation of the treatment head.² Accurate Monte Carlo treatment planning cannot be performed without accurate beam phase-space data.²⁰ Optimistically, accurate accelerator simulation and accurate dose calculation algorithms will result in accurate dose calculation.^21,22

New technologies in cancer radiotherapy need a more accurate computation of dose delivered in the radiotherapy treatment plan.²³ Treatment plans optimized on the basis of over-simplified dose calculation algorithms can become non-physical due to the uncertainties in the beam profiles. In addition, detailed information about radiotherapy beams has a wide variety of applications in clinical physics and radiation dosimetry. The phase-space data can contain very detailed information about a clinical electron beam. However, the simulation of the phase space of a clinical beam can be time-consuming and require a large amount of disk space.²

The number of particles stored in the phase-space file depends on the field size, number of histories, electron beam energy and scoring field size. Sufficient particles transported to achieve better than 1% precision in the calculation of PDD for three electron beam energies at different field sizes are listed in Table 2. The radius of scoring field size in the x–y plane was 20 cm which centered about the beam axis.

Well-designed beam models can accurately represent the beam characteristics and reconstruct the beam phase-space information.⁶ In accordance with Sego and Mesbahi studies,^7,24 we showed that by using beam models rather than the raw beam phase-space data, one can save accelerator simulation time and reduce the disk storage requirement.This study emphasized electron beams of one accelerator design. Our findings indicated that dose distributions calculated using both the phase-space data and the multiple-source models agree within 1.3%, demonstrating that the model is adequate for the purpose of Monte Carlo treatment planning for the beams studied as stated by Ma et al.^6–8

6. Conclusion

This study demonstrates that the multiple-source models can be used to generate accurate MC dose distributions for electron beams from a NEPTUN 10PC linac. Thus, it is possible to model a simulated electron beam with 10% or less particles required for MC dose simulations, without significantly affecting the accuracy of dose calculation. This indicates that by these models the time for treatment head simulation can be reduced at least by a factor of 10 in comparison to full MC simulation. In addition, the disk space requirement for data saving is significantly reduced, in comparison to the straight forward approach of storing phase-space data for subsequent use in dose calculation. Thus, similar to other study results, we have shown that the advantages of beam multiple-source models over phase-space data for dose calculation include shorter computation time in the linac head simulation and a smaller disk space requirement. It is clear that both of them can impact clinical practice of MC treatment planning. It is concluded that this method can provide a quick, inexpensive and effective model for dosimetry research purposes and dose calculations in radiotherapy.

Conflict of interest

None declared.