Abstract
Background
As a routine method for stepping source simulation, a Monte Carlo program is run according to the number of steps and then the summation of dose from each run is taken to obtain total dose distribution. This method is time consuming.
Aim
As an alternative method, a matrix shift based technique was applied to simulate a stepping source for brachytherapy.
Materials and methods
The stepping source of GZP6 brachytherapy unit was simulated. In a matrix shift method, it is assumed that a radiation source is stationary and instead the data matrix is shifted based on the number of steps. In this study, by running MCNPX program for one point and calculation of the dose matrix using the matrix shift method, the isodose curves for the esophageal cancer tumor lengths of 4 and 6 cm were obtained and compared with the isodose curves obtained by running MCNPX programs in each step position separately (15 and 23 steps for esophageal cancer tumor lengths of 4 and 6 cm, respectively).
Results
The difference between the two dose matrixes for the stepping and matrix shift methods based on the average dose differences are 3.85 × 10−4 Gy and 5.19 × 10−4 Gy for treatment length of 4 cm and 6 cm, respectively. Dose differences are insignificant and these two methods are equally valid.
Conclusions
The matrix shift method presented in this study can be used for calculation of dose distribution for a brachytherapy stepping source as a quicker tool compared to other routine Monte Carlo based methods.
Keywords: Brachytherapy, Co-60, Stepping source, Monte Carlo simulation, Matrix shift based technique
1. Background
Brachytherapy consists in the positioning of sealed radioactive sources very close to or in contact with the target tissue. Because the absorbed dose falls off rapidly with the distance from the source, high doses may be delivered safely to a localized target region over a short time.1 The application of Monte Carlo simulation in medical physics is dates back to the end of the 1970s.2 From those days till now, Monte Carlo techniques have been widely used in different areas of medical physics, in particular in physics of radiotherapy. Several calculation methods, especially Monte Carlo methods, have been employed to assess the absorbed dose near brachytherapy sources.3–9 Stepping source in brachytherapy systems is used to treat a target lesion longer than the effective treatment length of the source, such as cancerous lesions in cervix, esophagus and rectum.10 Monte Carlo dosimetry on HDR brachytherapy stepping sources have been studied widely.10–14
2. Aim
In this study, a Co-60 stepping source (channel 6) of GZP6 afterloading intracavitary brachytherapy system made by (Nuclear Power Institute of China) has been simulated by Monte Carlo N-Particle (MCNPX) code.15 The routine method employed to simulate a stepping source is the running of Monte Carlo programs based on the number of steps and then summation of the data acquired following successive running of the program. For example, for treatment of a 6 cm tumor by GZP6 brachytherapy unit, the size of each step is 2.5 mm and Monte Carlo programs should be run 23 times which requires a long time. To overcome this problem, a matrix based method was developed to obtain dose distributions of stepping sources. In the matrix based method we assumed that the position of the source is fixed and instead the data matrix is shifted based on the number of steps. This method has been evaluated by comparing the dose distributions obtained by the conventional Monte Carlo based stepping method and the matrix shift method for two clinically important treatment lengths of esophagus cancer.
3. Materials and methods
3.1. HDR Co-60 source
HDR Co-60 GZP6 afterloading unit has six channels including one stepping and five non-stepping Co-60 sources for intracavitary treatment such as cervix, rectum, esophagus and nasopharynx malignancies. The GZP6 stepping source consists of a Co-60 active cylinder (length = 2 mm, diameter = 1 mm). The source has a very thin Nickel plating and a Titanium capsule (length = 3.5 mm, diameter = 1.5 mm). There are a number of inactive steel balls in the source braid (diameter = 1.5 mm). The active and non active pellets are covered by a steel spring. A schematic representation of the GZP6 stepping source channel is demonstrated in Fig. 1.
Fig. 1.

Schematic diagram of stepping source channel of GZP6 brachytherapy unit.
3.2. Monte Carlo simulations
To calculate dose distribution of a stepping source for intracavitary brachytherapy, the stepping source (channel 6) of GZP6 afterloading intracavitary brachytherapy system was simulated by employing the MCNPX code.15 This code is capable of simulating complicated geometrical structures to a greater extent than other widely used Monte Carlo programs.9 A cylindrical water phantom (length = 80 cm, diameter = 50 cm) was simulated for dose calculation. The source was located at the centre of the water phantom. Two photons with emission probabilities of 0.5 and energies of 1.17 and 1.33 MeV were defined in a source definition card.
The pedep mesh tally (Type 1) was employed for the absorbed dose calculation in each mesh cell. The rectangular mesh dimensions for the stepping method were 280 cells × 280 cells × 1 cell. The rectangular mesh dimensions for the mesh shift method were 600 cells × 280 cells × 1 cell in which 600 mesh cells and 280 mesh cells spatially are equivalent to 30 cm and 14 cm, respectively. The resolution of rectangular mesh in both methods was 0.05 cm. The conversion program gridconv was used for converting the mesh tally output file data into a text file. The pedep mesh tally scores the average energy deposition per unit volume (MeV/cm3/source-particle) for the particle type P. The outputs were converted to dose (Gy) by corresponding conversion factors. For both methods, a total number of 5 × 108 photon histories were scored to acquire less than 0.2% statistical uncertainty in the Monte Carlo calculations. In the stepping method, 15 and 23 MCNPX programs were run for esophageal tumor length of 4 and 6 cm, respectively, and dose distribution was calculated in each step position separately and then the summation of dose from each run was taken to obtain the total dose distribution.
In the matrix shift method, a Monte Carlo program was run for one point and the data matrix was shifted based on the number of steps (15 and 23 steps for esophageal cancer tumor lengths of 4 and 6 cm, respectively). The isodose curves for two clinically important treatment lengths of 4 and 6 cm for esophagus cancer were obtained by both methods and were compared with each other. The treatment lengths and the step size (2.5 mm) were selected according to a practical treatment plan by the GZP6 treatment planning system.
3.3. Matrix shift technique
As an alternative method, a matrix shift technique was developed to simulate the stepping source for intracavitary brachytherapy. In this method we assumed that the position of the radiation source is stationary and instead of the stepping movement of the source, the data matrix is shifted based on the number of steps. This process is similar to a situation where the source is fixed and the cylindrical water phantom is shifted. The resolution for the Monte Carlo mesh grids is considered at 0.05 cm in both Monte Carlo simulation methods. Matrix shifting was performed by a MATLAB (version 7.2.0.232) program. To simulate the stepping movement, first zero matrixes of 600 cells × 280 cells in dimensions were assumed corresponding to the size of data matrix. The data were shifted based on the step size and put in the zero matrixes. Through this data shifting, considering the step size (2.5 mm) and the mesh resolution (0.05 cm), the data were shifted in over 5 mesh cells in Z direction. As it is showed schematically in Fig. 2 for a 7 cells × 5 cells matrix, the quantity of Ak,j is put in Ak+5,j. This process was repeated according to the number of steps that corresponds to the treatment length. For example, assuming the step size of 2.5 mm, the matrix was shifted in 23 steps for getting the isodose curves of 6 cm tumor length. Finally, all matrixes were summed up and the isodose contours were plotted. A schematic representation of the matrix shift method is shown in Fig. 2.
Fig. 2.
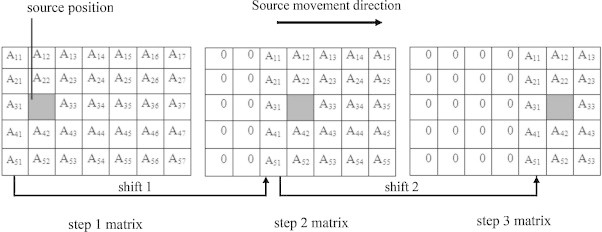
Schematic figure of matrix shift technique.
As Fig. 2 shows, after shifting a matrix, equal to the step size, a number of mesh cell data will be equal to zero and a number of them will be omitted. Finally, when the matrixes are summed up with each other, these zero cells reduce the quantity of the dose. To avoid this problem, the mesh size defined in Monte Carlo input program should be large enough for the isodose contours to be far from these cells. Therefore, depending on the treatment length and the region for which the isodose curves are plotted, the mesh size in the matrix shift method should be larger than the stepping method. For this purpose, it was suggested that the mesh size be considered at the most, 3 times greater than the stepping movement length. It was also suggested that the mesh cells should be at a suitable distance from the phantom edges to obtain a full scatter situation. In this study, the rectangular mesh dimensions for the mesh shift method were 600 cells × 280 cells × 1 cell in which 600 mesh cells and 280 mesh cells spatially are equivalent to 30 cm and 14 cm, respectively. According to the mesh size in the Monte Carlo simulation, the data were put on a 600 pixels × 280 pixels matrix in MATLAB software. The isodose curves for the esophageal cancer tumor lengths of 4 and 6 cm were obtained by running MCNPX for one point and then the final dose matrix was calculated by summing all of the shifted matrixes. In this stage for comparing the isodose curves obtained by two methods, the dose matrix was cut and transformed to a 280 pixels × 280 pixels matrix. Through this process the zero matrix cells were omitted.
4. Results
Dose distributions for the stepping source of GZP6 unit in water, acquired by two methods of stepping and matrix shift, are presented in Fig. 3. This Figure shows the contours corresponding to doses of 7.5, 6.25, 5, 3.75, 2.5, 1.25 Gy prescribed for treatment of 4 cm esophageal tumor length. The matrix shift method and stepping method contours are shown by Lines colormap and Jet colormap, respectively.
Fig. 3.
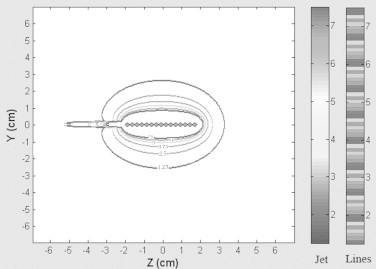
The isodose curves acquired by the stepping method and matrix shifted method for treatment length of 4 cm. The matrix shift method and stepping method contours are shown by Lines colormap and the colormap, respectively. Contours correspond to doses of 7.5, 6.25, 5, 3.75, 2.5, 1.25 Gy.
The difference between two dose values resulting from the stepping and matrix shift methods on the basis of the average dose difference is 3.85 × 10−4 Gy for the treatment length of 4 cm. The dose difference is insignificant and these two methods are equivalent.
In Fig. 4, the contours corresponding to doses of 7.5, 6.25, 5, 3.75, 2.5, 1.25 Gy acquired from the treatment length of a 6 cm tumor length were plotted. The matrix shift method and stepping method contours are presented by Lines colormap and Jet colormap, respectively. The differences between the two dose matrixes for stepping and matrix shift methods on the basis of the average dose difference is 5.19 × 10−4 Gy. The difference is small and these two methods are equivalent.
Fig. 4.
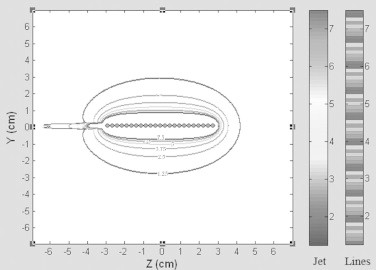
The isodose curves obtained by the stepping method and matrix shift method for treatment length of 6 cm. The matrix shift method and stepping method contours are shown by Lines colormap and Jet colormap, respectively. Contours correspond to doses of 7.5, 6.25, 5, 3.75, 2.5, 1.25 Gy.
5. Discussion and conclusions
In this study, a matrix shift technique was developed as an alternative method for dose calculation of a brachytherapy stepping source. The isodose curves for two clinically important treatment lengths of 4 and 6 cm for esophagus cancer were obtained by both the stepping and matrix shift methods and were compared with each other. As shown in Figs. 2 and 3, two sets of isodose curves are practically equal to each other and the results of the matrix based method are in good agreement with the result that we have obtained by running MCNPX programs in each step position separately. It can be concluded that this new technique can be an alternative method for simulating a stepping source movement with desirable steps. As a final result, the Monte Carlo based matrix shift method presented in this study can be used for calculation of dose distribution for a brachytherapy stepping source as a quicker tool compared to the other routine Monte Carlo stepping method. The new method also has the same accuracy as the stepping method.
Acknowledgements
The authors would like to thank the research council and the office of vice president for research affairs of Mashhad University of Medical Sciences for their financial support of this work. Also the authors would like to thank Dr. Ali Asghar Mowlavi and Dr. Ali Soleimani Meigooni for their assistance.
References
- 1.Halperin E.C., Perez C.A., Brady L.W. 5th ed. Lippincott Williams & Wilkins Publishers; 2007. Principles and practice of radiation oncology [book online] [Google Scholar]
- 2.Udale-Smith Mary. Monte Carlo calculations of electron beam parameters for three Philips linear accelerators. Phys Med Biol. 1992;37(1):85–105. [Google Scholar]
- 3.Mesbahi A., Naseri A. In-air calibration of new high dose rate 60Co brachytherapy sources: results of measurements on a GZP6 brachytherapy afterloading unit. Rep Pract Oncol Radiother. 2008;13(2):69–73. [Google Scholar]
- 4.Mesbahi A. Radial dose functions of GZP6 intracavitary brachytherapy 60Co sources: treatment planning system versus Monte Carlo calculations. Iran J Radiat Res. 2008;5(4):181–186. [Google Scholar]
- 5.Karaiskos P., Angelopoulos A., Baras P., Rozaki-Mavrouli H., Sandilos P., Vlachos L. Dose rate calculations around 192Ir brachytherapy sources using a Sievert integration model. Phys Med Biol. 2000 Feb;45(2):383–398. doi: 10.1088/0031-9155/45/2/309. [DOI] [PubMed] [Google Scholar]
- 6.Gifford K.A., Mourtada F., Cho S.H., Lawyer A., Horton J.L. Monte Carlo calculations of the dose distribution around a commercial gynecologic tandem applicator. Radiother Oncol. 2005 Nov;77(2):210–215. doi: 10.1016/j.radonc.2005.09.006. [DOI] [PubMed] [Google Scholar]
- 7.Papagiannis P., Angelopoulos A., Pantelis E., Sakelliou L., Karaiskos P., Shimizu Y. Monte Carlo dosimetry of 60Co HDR brachytherapy sources. Med Phys. 2003 Apr;30(4):712–721. doi: 10.1118/1.1563662. [DOI] [PubMed] [Google Scholar]
- 8.Mowlavi A.A., Cupardo F., Severgnini M. Monte Carlo and experimental relative dose determination for an Ir-192 source in water phantom. Iran J Radiat Res. 2008;6(1):37–42. [Google Scholar]
- 9.WatanabeY, Roy J., Harrington P.J., Anderson L.L. Experimental and Monte Carlo dosimetry of the Henschke applicator for high dose-rate 192 Ir remote afterloading. Med Phys. 1998 May 5;25(5):736–745. doi: 10.1118/1.598255. [DOI] [PubMed] [Google Scholar]
- 10.Li X.A., Suntharalingam M., Yu C. Dosimetry of source stepping for intravascular brachytherapy. Cardiovasc Radiat Med. 2001 Jul;2(3):165–172. doi: 10.1016/s1522-1865(01)00082-8. [DOI] [PubMed] [Google Scholar]
- 11.Miften M.M., Das S.K., Shafman T.D., Marks L.B. Optimization of a 90Sr/90Y radiation source train stepping for intravascular brachytherapy. Med Phys. 2002 Dec;29(12):2891–2896. doi: 10.1118/1.1524169. [DOI] [PubMed] [Google Scholar]
- 12.Wong T., Wallace S., Fernando W., Schumer W., Quong G. Dose errors in the near field of an HDR brachytherapy stepping source. Phys Med Biol. 1999 Feb;44(2):357–363. doi: 10.1088/0031-9155/44/2/005. [DOI] [PubMed] [Google Scholar]
- 13.Wong T., Fernando W., Johnston P.N., Bubb I.F. Transit dose of an Ir-192 HDR brachytherapy stepping source. Phys Med Biol. 2001;46:323–331. doi: 10.1088/0031-9155/46/2/304. [DOI] [PubMed] [Google Scholar]
- 14.Williamson J.F., Li Z., Monte Carlo aided dosimetry of the microselectron pulsed and high dose-rate 192 Ir sources. Med Phys. 1995 Jun;22(6):809–819. doi: 10.1118/1.597483. [DOI] [PubMed] [Google Scholar]
- 15.Waters LS. MCNPX User's manual, version 2.4.0. Report LA-CP-02-408. Los Alamos National Laboratory; 2002.


