Empirical estimation of beam-on time for prostate cancer patients treated on Tomotherapy

Abstract

Background and aim

This study proposed a method to estimate the beam-on time for prostate cancer patients treated on Tomotherapy when FW (field width), PF (pitch factor), modulation factor (MF) and treatment length (TL) were given.

Material and methods

The study was divided into two parts: building and verifying the model. To build a model, 160 treatment plans were created for 10 patients. The plans differed in combination of FW, PF and MF. For all plans a graph of beam-on time as a function of TL was created and a linear trend function was fitted. Equation for each trend line was determined and used in a correlation model. Finally, 62 plans verified the treatment time computation model – the real execution time was compared with our estimation and irradiation time calculated based on the equation provided by the manufacturer.

Results

A linear trend function was drawn and the coefficient of determination R² and the Pearson correlation coefficient r were calculated for each of the 8 trend lines corresponding to the adequate treatment plan. An equation to correct the model was determined to estimate more accurately the beam-on time for different MFs. From 62 verification treatment plans, only 5 disagreed by more than 60 s with the real time from the HT software. Whereas, for the equation provided by the manufacturer the discrepancy was observed in 16 cases.

Conclusions

Our study showed that the model can well predict the treatment time for a given TL, MF, FW and it can be used in clinical practice.

1. Background

Helical Tomotherapy (HT) is one of the novel approaches that enable intensity-modulated radiation therapy (IMRT) delivery technique. HT can provide a high conformity and homogeneity at the target volume and at the same time spare organs at risk (OAR).^1–7 This is achieved by a different dose delivery in reverse to a classic linear accelerator.⁸ In HT, the gantry rotates in a helical manner around the patient, while the couch moves toward the gantry. Fan beam is modulated by a binary multileaf collimator that generates an enormous number of beam elements that irradiate the target volume.^9,10 Treatment planning parameters in HT, namely field width (FW), pitch factor (PF) and modulation factor (MF), are also different. They are chosen individually for each treatment plan, based on the shape and volume of the planning target volume (PTV). Moreover, those parameters influence not only the dose distribution but also the beam-on time.¹¹

FW determines the size of the beam in the longitudinal axis and can have three discreet values: 1.05, 2.5 and 5 cm. The larger FW, the worse dose gradient in cranial–caudal direction but the shorter beam-on time.

PF is defined as the axial couch distance traveled for one gantry rotation divided by FW.¹² Contrary to the helical computed tomography (CT), in HT the PF should be less than 1. Another aspect worth considering when choosing PF is the thread effect. This effect occurs due to the helical junctioning of the divergent fan beam used in HT. Kissick et al.¹² proposed a solution to minimize the thread effect. They suggested to use a PF of 0.86/n, where n is an integer. The more complex PTV, the lower PF should be used to sculpt the dose distribution in the cranial–caudal direction.

MF is defined as the ratio of the maximum leaf open time to the mean leaf open time for all non-zero projections.¹³ It modulates the beam by limiting leaf open times. Higher MF increases the spectrum of beam modulation; however, it also increases the beam-on time.

In routine practice, the quality of dose distribution is very important.^14–16 The aim is always to spare OARs and at the same time to irradiate the target volume very conformally and homogeneously.¹⁷ However, the treatment time is also a very important issue.¹⁸ Prolonged beam-on time influences patient's comfort and increases the possibility of intra- and inter-fraction movements. Another important issue is that it decreases the number of patients irradiated per day. Taking all these facts into account, we usually have to make compromise between the quality of the treatment plan and the treatment time. It has been shown¹¹ that for prostate cancer patients the most optimal treatment planning parameters are: FW = 2.5, PF = 0.215, MF = 2.5. However, the MF value of up to 3.5 may also be considered.

Treatment time depends not only on the above mentioned treatment planning parameters but also on dose per fraction, target length in the longitudinal direction and average dose rate. Taking all these issues into account, one can see that estimation of the beam-on time is difficult. Moreover, the irradiation time is not known to the planner (for versions of up to 3.x) until final dose is calculated, that is at the end of treatment planning. In case where the dose distribution is not acceptable or the treatment time is too long, one needs to change the treatment planning parameters (FW, MF, PF) and start the whole procedure from the beginning. This is cumbersome since the optimization of the plan takes more than 2 h and it is not possible to make a copy of a plan (except the newest version of the Tomotherapy software (VoLO Technology) introduced in May 2012) or compare two versions of the plan.¹⁹ It would be useful to know the beam-on time in advance because it would reduce the workload of the treatment planning unit. According to the manufacturer, the irradiation time can be calculated based on the equation:

$$t=\frac{\text{MF}\cdot (\text{TL}+\text{FW})\cdot D_{\text{f}}}{\text{FW}\cdot \dot{D}}$$ (1)

where MF – modulation factor, FW – field width, TL – target length, D_f – dose per fraction, and $\dot{D}$ – average dose rate.

However, one does not know the exact dose rate during plan optimization. Mackie et al.²⁰ proposed a constant value. For example, for prostate treatment it would be 4.8 Gy/min, assuming exponential decay from an effective depth of 12 cm and an effective attenuation coefficient of 0.04 cm⁻¹. This can lead to some inconsistencies.

2. Aim

The aim of this study was to propose a method of treatment time computation based on empirical data gathered in our institution. This analysis was performed for three cases – a target volume covering the prostate alone, prostate with seminal vesicles and that including prostate, seminal vesicles and lymph nodes.

3. Materials and methods

3.1. Patients

This study included 10 patients treated for prostate cancer on Tomotherapy in our institution in order to develop a correlation model of beam-on time estimation. Then, 40 (treated on Tomotherapy version 3.1.5.3) and 22 (treated on Tomotherapy version 4.0.4.17) randomly chosen patients were used to verify this model.

For all 72 patients, CT images (Somatom Sensation Open, Siemens Corp.) were performed with slice reconstruction of 5 mm. Ten patients for whom the model was built were scanned only in a supine position with a knee-fix (Sinmed Corp.) immobilization system. However, the group of patients that verified our model was scanned both in a supine (49 patients) and prone position (13 patients) with a belly-board stand (Sinmed Corp.) The procedure before the CT was always the same – patients were asked to empty the bladder 30 min before the scanning and then to drink 500 ml of water. No preparations to empty the rectum (endorectal balloon or enema) were used. All OARs and target contours were created in the Eclipse 7.3.10 (Varian Corp.) treatment planning system. CT scans as well as structure sets were exported in DICOM format to the Hi-Art Tomotherapy planning system. Prostate gland, seminal vesicles and pelvic lymph nodes were delineated as a clinical target volume (CTV). For patients from the correlation model, a margin of 1 cm was always added to CTV to create a planning target volume (PTV). For patients who verified the model, margins from 0.7 cm to 1 cm were used. The correlation model was based on two cases: the first (PTV1) included the prostate gland, seminal vesicles, pelvic lymph nodes and a 1 cm margin; the other one (PTV2) included only the prostate gland with a 1 cm margin. However, in this study we verified our model for three groups of patients who had: only prostate (10 patients), prostate and seminal vesicles (38 patients) or prostate gland, seminal vesicles and pelvic lymph nodes (14 patients) irradiated.

3.2. Treatment plans and correlation model

To build a correlation model of treatment time, the authors performed 160 treatment plans for 10 patients. Each patient was considered twice – once PTV1 was a target volume, than PTV2. For each of these cases, eight treatment plans, which varied in combination of planning parameters (FW = 1.05, 2.5, 5 cm; PF = 0.107, 0.215, 0.43; MF = 1.5, 2.5, 3.5), were created. The exact specification of each plan is shown in Table 1. These data gave the information of how much the FW, PF and MF influence the beam-on time. The specific and detailed description of patients and the methodology of generating treatment plans for a correlation model was described in our previous publication.¹¹ On the basis of these data, a correlation model was built.

Table 1.

Values of planning parameters used to create eight different treatment plans. FW – field width, PF – pitch factor, and MF – modulation factor.

Plan name	FW	PF	MF planned	MF actual PTV1 Mean ± SD	MF actual PTV2 Mean ± SD
Reference	1.05	0.107	3.5	2.47 ± 0.32	2.26 ± 0.39
Default	2.5	0.215	2.5	2.01 ± 0.14	1.94 ± 0.22
FW = 1.05	1.05	0.215	2.5	2.05 ± 0.28	2.17 ± 0.14
FW = 5	5	0.215	2.5	1.86 ± 0.14	1.88 ± 0.13
PF = 0.107	2.5	0.107	2.5	1.89 ± 0.16	1.77 ± 0.15
PF = 0.43	2.5	0.43	2.5	2.10 ± 0.13	2.02 ± 0.16
MF = 1.5	2.5	0.215	1.5	1.25 ± 0.06	1.31 ± 0.05
MF = 3.5	2.5	0.215	3.5	2.80 ± 0.21	2.64 ± 0.22

It is well known, that due to a helical irradiation in Tomotherapy one of the most significant parameter determining the beam-on time is the target length (TL).²¹ Taking this into account, a graph of beam-on time as a function of TL was plotted for all 160 treatment plans. A linear trend function was drawn and the coefficient of determination R² and the Pearson correlation coefficient r were calculated for each of the 8 trend lines corresponding to the adequate treatment plan. Equations for each trend line were also determined and afterwards used in a correlation model. However, this model was not complete since PF and MF may be chosen continuously, contrary to FW that is a discrete parameter. It should be noted that, to minimize the thread effect,¹² it is advisable to use discrete values of 0.43, 0.287, 0.215 or 0.107, …. It has been shown¹¹ that for prostate cancer patients the treatment time for PF = 0.215 and PF = 0.43 is almost the same. For this reason, those patients who are planned with PF = 0.287 may be considered as those with PF = 0.215. Due to this fact, correction in the correlation model was only introduced for MF. For this purpose, a graph of mean beam-on time as a function of MF was plotted and a quadratic trend line was determined. This was done only for the data gathered for PTV1 plans since the trend line for PTV2 was analogical. Afterwards, an equation that corrected the beam-on time for MF values (different than 1.5, 2.5 and 3.5) was calculated.

All verifying 62 treatment plans were prepared in the same manner – the dose to OARs was reduced to a minimum, while the dose homogeneity in the PTV maintained between 95% and 107%, according to the ICRU 50 and 62 reports.^22,23 The dose constraint for OARs was chosen individually for each patient, based on their anatomical conditions. Some effort was made to keep the dose to PTV as homogeneous and conformal as possible, however, without violating DVH constraints stated in the QUANTEC paper.²⁴ Since we used in this study a Hi-Art Tomotherapy planning system version 3.1.5.3 (that has only 1 DVH point for optimization), we changed the constraint point during the whole process of optimization – starting from high doses toward low doses. The calculation grid size used for the dose calculation was 0.254 cm × 0.254 cm × 0.50 cm (fine). The correlation model was built for the conventional 2 Gy per day scheme of prostate cancer radiotherapy. Hence, in this study the authors included only prostate cancer patients treated in a single prescription dose level.

The authors tested two groups of patients treated on different versions of Tomotherapy software: 3.1.5.3 (40 patients) and 4.0.4.17 (22 patients). This was a must since the newer version of HT has the minimum gantry period for treatment mode equal to 12 rather than 15 s (as for the previous version). Due to this fact, the irradiation time can be shorter. An attempt was made to find a simple solution of scaling the estimated irradiation time in order to match the faster version of HT.

All treatment plans (62 in total) that were gathered to verify the treatment time computation model were compared with our estimation and with irradiation time calculated based on Eq. (1) provided by the manufacturer.

4. Results and discussion

A total of 222 plans were created, of which 160 were created to build a model that predicts a treatment time for prostate cancer patients when FW, PF, MF and TL were stated; and 62 plans were generated to verify this model.

4.1. Building a correlation model

In Fig. 1, a relationship of beam-on time as a function of TL is presented for all treatment plans created with parameters stated in Table 1. In this figure, linear trend functions were also marked and the exact equation, the coefficient of determination R² and the Pearson correlation coefficient r are presented in Table 2. From these data, it can be seen, that the coefficient of determination is very high for most of the treatment plans. Only for FW = 1.05, PF = 0.43 and MF = 3.5 is R² below 0.99. This means that, for example, for treatment plan MF = 3.5, 96.98% of the variation in beam-on time is due to the variation in TL. Whereas, the Pearson correlation coefficient r is interpreted as a measure of the strength of linear dependence between these two variables. A value of +1 or −1 implies that there is a perfect linear correlation between the two variables. In this study, the worst correlation was obtained for MF = 3.5 since r = 0.9848. Based on the data gathered in Table 2 one may notice that for all treatment plans the strength of linear dependence is very high.

Fig. 1.

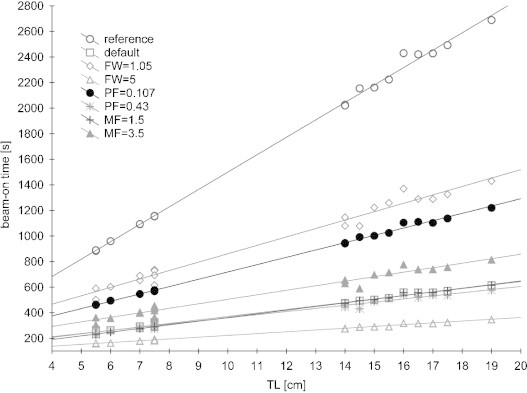
Beam-on time as a function of treatment length (TL) for each treatment plan. FW – field width, MF – modulation factor, and PF – pitch factor.

Table 2.

Equation of the linear trend function, the coefficient of determination R² and the Pearson correlation coefficient r for different treatment plan. TL – target length and t – beam-on time.

Plan name	Linear trend function	R2	r
Reference	t = 136.22·TL + 137.340	0.9975	0.9987
Default	t = 27.278·TL + 97.906	0.9933	0.9966
FW = 1.05	t = 65.782·TL + 203.200	0.9781	0.9890
FW = 5	t = 14.037·TL + 82.225	0.9953	0.9976
PF = 0.107	t = 57.301·TL + 145.490	0.9977	0.9988
PF = 0.43	t = 24.551·TL + 114.300	0.9780	0.9889
MF = 1.5	t = 28.646·TL + 75.739	0.9976	0.9988
MF = 3.5	t = 35.294·TL + 151.800	0.9698	0.9848

Equations of linear trend functions can be used to estimate the beam-on time for given treatment planning parameters and TL. For example, the patient with a very small bladder had to be irradiated on HT for the prostate and seminal vesicles, where TL = 7.5 cm. The plan was prepared for typical treatment planning parameters used in our institution: FW = 2.5, PF = 0.215 and MF = 2.5, and the beam-on time obtained for these data was approximately 5 min. However, for this plan the dose to the bladder was very high, due to its small volume. As shown,¹¹ the most significant reduction in dose to OARs can be obtained for FW = 1.05, although this is combined with the increase of irradiation time. With our simple method, one does not have to make another plan to find out what the beam-on time will be for new planning parameters. One needs only put TL into the formula from Table 2 for FW = 1.05 and calculate the treatment time. From this formula, it follows that the time will increase up to approximately 12 min. From these calculations, one has to make the decision whether to keep a short irradiation time with dose to the bladder compromised or to spare bladder keeping in mind that the longer beam-on time the more intrafraction motion. With this simple method, one may save time needed to optimize the treatment plan for new FW parameter. Moreover, when a change of FW is made the beamlets have to be calculated one more time, which also takes additional time. In our institution, the beamlets are calculated only during the night due to a large number of patients that need to be optimized during working hours. Thus, in our case the plan for FW = 1.05 could not be optimized until the next day.

It is well known that increasing MF leads to a better sparing of OARs. Thus, a correction in the model was introduced to estimate more accurately the beam-on time for MF different than: 1.5, 2.5 and 3.5. Based on the relationship of mean beam-on time as a function of MF, a quadratic function was fitted:

$$t=48.19\cdot {(\text{MF})}^2-179.5\cdot \text{MF}+432.6$$ (2)

where t – treatment time and MF – modulation factor. However, to find a correction value for MF an equation should be used:

$$\Delta t=t_{\text{MF}}-t_x=48.19\cdot [{(\text{MF})}^2-{({\text{MF}}_x)}^2]+179.5\cdot ({\text{MF}}_x-\text{MF})$$ (3)

where t_MF – treatment time estimated for MF: 1.5, 2.5 or 3.5, t_x – treatment time estimated for MF different than: 1.5, 2.5 or 3.5, MF – modulation factor equal to: 1.5, 2.5 or 3.5, and MF_x – modulation factor different than: 1.5, 2.5 or 3.5.

Correction factor calculated based on Eq. (3) should be added to the treatment time estimated according to the data from Table 2. An exception should be made only for patients in whom the prostate, seminal vesicles and lymph nodes were irradiated and a low MF was used in the treatment plan. This follows from the fact that for such a long PTV there is no difference in treatment time between MF = 1.5 and MF = 2.5.¹¹

4.2. Verification of the correlation model

All patients that were used to verify the model were usually planned with FW = 2.5 (54 patients) and only 8 patients were planned with FW = 1.05. This is a common FW used for prostate cancer patients^25,26 and Whitelaw et al.²⁷ stated that for most cases a FW of 2.5 is the most suitable one. However, plans for FW = 1.05 are also found in the literature.²⁸ Whereas, for PF most patients were treated with PF = 0.287 (56 patients) and only 6 plans were generated for PF = 0.215. In the literature, most patients are also treated with PF = 0.287,^25,26 although PF = 0.5 is also mentioned.²⁸ In the case of MF, there is a larger spectrum of values. Mean MF for a group of verification plans was 2.54 (SD = 0.24) with a range from 2.1 to 3.0. Those values agree with the ones found in the literature. Langen et al.²⁵ used 2.5 as did Grigorov et al.,²⁸ and Yuen et al.²⁹ used 3, whereas Fiorino et al.²⁶ used MF 2–2.5 for single dose-level plans. Based on this knowledge, the verification group was appropriate to verify the model, since it covered the most suitable clinically used range of treatment planning parameters.

The first part of the verification was based on the patients planned on the same version of Tomotherapy software (version 3.1.5.3) on which the correlation model was build. For this purpose, 40 randomly chosen patients treated in our institution were analyzed in terms of beam-on time. The authors estimated the treatment time based on the correlation model as well as on the basis of Eq. (1) given by the manufacturer. These data were than compared with the real time executed on the HT unit. Fig. 2 presents histograms of the time difference, in seconds and percentage, for each method. These data showed that the estimation suggested by the manufacturer tended to underestimate the beam-on time on average by 52 s (Fig. 3). However, differences of up to 154 s were observed. Whereas, the estimation based on the correlation model overestimated the treatment time on average by 14 s (Fig. 3). In Fig. 2B, an advantage of the correlation model might be observed, since the most frequent beam-on time differences were below 10% and the data were distributed almost symmetrically (skewness = −0.08), which might suggest a good assessment of our model.

Fig. 2.

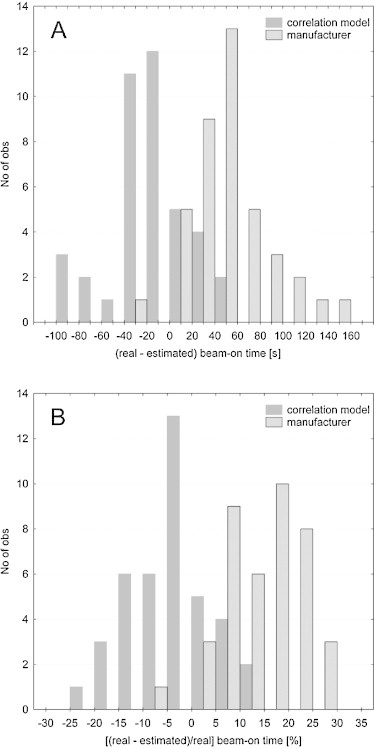
Histogram of differences between real (from HT system) and estimated (from correlation model) beam-on time in seconds (A) and percentage (B) for the first verification group of treatment plans.

Fig. 3.

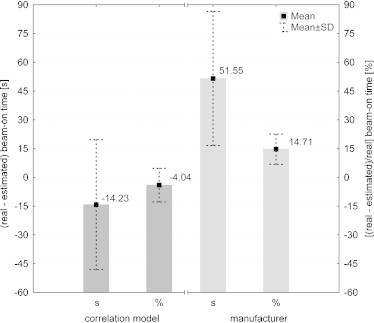
Mean differences between real (from HT system) and estimated (from correlation model) beam-on time in seconds and percentage for the first verification group of treatment plans.

The second part of the verification was based on the patients planned on the newer version of Tomotherapy software (version 4.0.4.17) which has the minimum gantry period for treatment mode equal to 12. This modernization shortens the beam-on time. This can be observed in Fig. 4, since the time differences for the correlation model were shifted toward larger discrepancies. The estimation based on the correlation model overestimated the treatment time on average by 87 s (Fig. 4). Whereas, the estimation suggested by the manufacturer underestimated the beam-on time on average by 8 s (Fig. 4). Due to the fact that the model overrated the beam-on time approximately by 23%, the authors concluded that it must be because of lower minimum gantry period and scaled all the data from the model by this value. Corrected values were presented in the form of histogram in Fig. 5A and B and as a mean difference in treatment time with standard deviation (SD) in Fig. 4. The above mentioned figures showed that after the introduction of a correction factor of 23% (because the estimated execution time was decreased by 23%) both methods (correlation model vs. manufacturer's equation) were more or less similar. However, in the model the SD for a mean treatment time difference is shorter. Knowing that SD may be a measure of uncertainty, one could conclude that a correlation model better predicts the beam-on time.

Fig. 4.

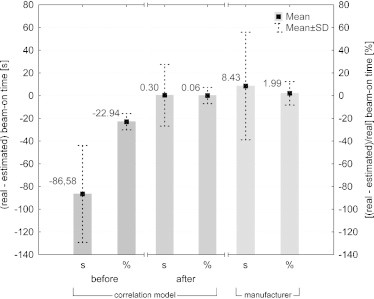
Mean differences between real (from HT system) and estimated (from correlation model) beam-on time in seconds and percentage for the second verification group of treatment plans. For correlation model presented results are before and after applying a correction factor.

Fig. 5.

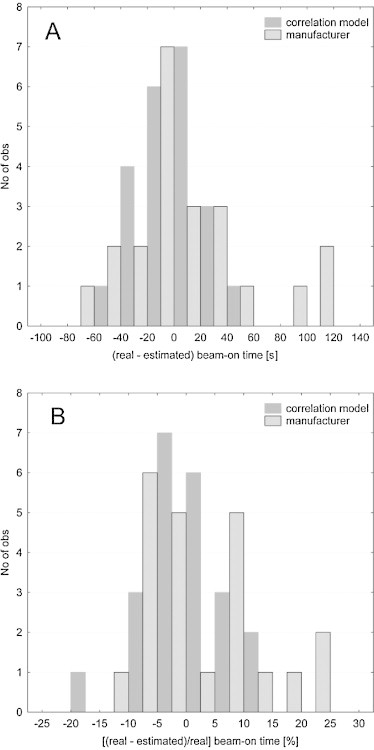
Histogram of differences between real (from HT system) and estimated (from correlation model) beam-on time in seconds (A) and percentage (B) for the second verification group of treatment plans.

The authors found one publication related to the estimation of the treatment time for patients treated on HT unit. This study³⁰ presented a method for estimation of the scaling factor for prostate cancer patients, which is a patient-specific parameter used to calculate the rotational period of the gantry and, as a result, the treatment time. The results obtained in this research are acceptable since the differences between real beam-on time and the estimation were from −2.8% to +7.1%. Those differences are smaller than in our study; however, Grigorov and Chow³⁰ tested the methodology only on 10 patients. Moreover, this study included only patients irradiated for prostate and seminal vesicle (without lymph nodes). Whereas, our study is designed to estimate the treatment time regardless of irradiated volume.

5. Conclusions

This study proposed a novel method to estimate the beam-on time for prostate cancer patients treated on Tomotherapy. The methodology was based on empirical data and was suited for 2 versions of HT unit – with minimum gantry rotation periods of 12 s and 15 s. The results are satisfying since for 62 treatment plans our model disagreed with the HT software in 5 plans – the disagreement of beam-on time was higher than 1 min. Whereas, for the equation provided by the manufacturer the discrepancy above 1 min was observed in 16 cases. From the data, one may conclude that the model can better predict the treatment time for a given TL, MF, FW and PF. This approach is easy in use since all one needs to do is to apply the equations from the model into a spreadsheet, enter the treatment planning parameters and the length of the PTV to immediately obtain the estimation. This may save a lot of time when one hesitates which treatment planning parameters to use. The authors think that it may be a useful tool in clinical practice.

Conflict of interest

None declared.

Financial disclosure

This study was supported by the Greater Poland Cancer Centre (grant no.1 dated 20 May 2009).