Abstract
Accurate quantification of cell specific rates and their uncertainties is of critical importance for assessing metabolic phenotypes of cultured cells. We applied two different methods of regression and error analysis to estimate specific metabolic rates from time-course measurements obtained in exponentially growing cell cultures. Using simulated data sets to compute specific rates of growth, glucose uptake, and lactate excretion, we found that Gaussian error propagation from prime variables to the final calculated rates was the most accurate method for estimating parameter uncertainty. We incorporated this method into a MATLAB-based software package called Extracellular Time-Course Analysis (ETA), which automates the analysis workflow required to (i) compute cell specific metabolic rates and their uncertainties, (ii) test the goodness-of-fit of the experimental data to the regression model, and (iii) rapidly compare the results across multiple experiments. ETA was used to estimate the uptake or excretion rate of glucose, lactate, and 18 different amino acids in a B-cell model of c-Myc-driven cancer. We found that P493-6 cells with High Myc expression increased their specific uptake of glutamine, arginine, serine, lysine, and branched-chain amino acids by 2- to 3-fold in comparison to Low Myc cells, but exhibited only modest increases in glucose uptake and lactate excretion. By making the ETA software package freely available to the scientific community, we expect that it will become an important tool for rigorous estimation of specific rates required for metabolic flux analysis and other quantitative metabolic studies.
Keywords: metabolic flux analysis, propagation of errors, MATLAB software, exponential growth, regression analysis
INTRODUCTION
Metabolic fluxes represent quantitative measures of material flow within a biochemical network and are thus considered fundamental determinants of in vivo cell physiology (Nielsen 2003; Sauer 2006; Stephanopoulos 1999; Wiechert 2001). Measurements of cell specific rates of nutrient uptake and product formation (i.e., normalized to cell density) provide the basis for intracellular flux calculations using flux balance analysis (FBA) or metabolic flux analysis (MFA) (Quek et al. 2010). The measured extracellular rates are critical inputs to these methods because they constrain the solution space of feasible intracellular fluxes. Therefore, accurate estimation of cell specific extracellular rates, and their associated uncertainties, is an essential task in the reconstruction of accurate metabolic flux maps. In addition, cell specific rates are intensive properties that do not depend on the size of the system under investigation, which facilitates comparisons between different experimental platforms.
Under balanced growth conditions, where the culture attains an internal metabolic steady state, all cell specific metabolic rates are considered constant and the extracellular rates can be determined by measuring changes in medium composition over time. This is not as trivial as it may seem since the observed rates of change are proportional to the mathematical product of specific rate (v) and cell density (X), with the latter continuously increasing as the culture grows. Therefore, the calculation procedure must account for the combined effects of both variables on the measured time courses, as well as random errors introduced by the various measurements of extracellular metabolite and cell concentrations. The preferred method involves regression analysis to estimate the specific growth rate of the culture (μ) and specific production rate (v) of each measured extracellular metabolite, using integrated balance equations that describe the rates of concentration change over time.
Several prior articles have applied regression analysis to determine metabolic rates from extracellular time courses of substrate depletion or product accumulation (Glacken et al. 1988; Goudar 2012; Kim and Forbes 2007; Zupke et al. 1995). However, these articles did not undertake a detailed error analysis of their regression approach and did not attempt to validate their approach using simulated data sets. Accurate assessment of uncertainty is critical for MFA because it provides the proper weighting of each measured rate in the sum-of-squares objective function that defines the best-fit solution. Furthermore, quantifying the uncertainty in each measurement enables rigorous statistical comparisons to be made between experiments. Recently, Goudar et al. (2009) assessed the propagation of uncertainty from prime variables into specific rates using both a Gaussian error propagation approach and Monte Carlo analysis. Their analysis, however, was limited to perfusion culture where cell concentrations are largely time invariant, and they did not provide a comparison to the more traditional approach of simply averaging the regressed rate parameters derived from replicate experiments. Furthermore, none of these prior studies have led to the development of publically available software tools that automate the estimation of metabolic rates and their uncertainties based on experimental time course measurements.
In this contribution, we compare two methods of error analysis applied to the problem of estimating metabolic rates from extracellular time-course measurements: (i) “Gaussian” error propagation from prime variables and (ii) “Sampling” the regressed parameters from multiple replicate experiments to estimate their standard deviation. Uncertainties obtained from the Gaussian and Sampling approaches were compared to the “true” Monte Carlo error estimate, which provides an asymptotically correct value but is more expensive to compute. We found that the Gaussian approach was the best choice for estimating uncertainty when using a small number of experimental replicates (n=3), which is typical of cell culture experiments. To automate the determination of specific rates and their uncertainties, we developed a MATLAB software package called Extracellular Time-Course Analysis (ETA). This software facilitates the import and selection of data points for regression, calculation of cell specific metabolic rates (or yields) and their uncertainties using either Gaussian error propagation or Monte Carlo analysis, and assessment of the goodness-of-fit of the exponential (or linear) growth model. The model can also account for first-order degradation of metabolites due to non-biological effects. The software provides an intuitive graphical user interface and documentation so that non-experts can readily implement these statistical features to analyze their own experimental data sets.
Using our newly developed ETA software package and a B-cell model of c-Myc-driven cancer, we assessed metabolic phenotypes under both High and Low Myc expression based solely upon extracellular metabolite and cell density measurements. We conducted time-course growth experiments and used ETA to estimate the specific uptake or excretion rate of glucose, lactate, and 18 different amino acids based on the exponential growth model. We found that the faster-growing High Myc cells globally upregulated their consumption of amino acids relative to glucose. In particular, specific uptake rates of glutamine, arginine, serine, lysine, and branched-chain amino acids were substantially increased in High Myc cells relative to Low Myc cells. Rates of glucose uptake and lactate excretion were also increased in High Myc cells, but the relative changes were modest in comparison to growth rate and amino acid fluxes. This study provides an example of how ETA can be applied to assess metabolic phenotypes of mammalian cells as a prelude to flux balance analysis, metabolic flux analysis, or more comprehensive metabolic profiling studies.
METHODS
Balance equation for cell growth
Balanced exponential growth in batch culture is a key underlying assumption of these calculations. This assumption is generally valid for cells that are not experiencing nutrient or spatial growth limitations. The exponential growth equation is
| (1) |
where μ is the specific growth rate, X is the cell density (i.e., cell mass or number per unit volume of culture medium), t is time, and X0 is the initial cell density at the onset of exponential growth. Transformation of the equation into a form suitable for linear regression results in
| (2) |
This equation can be used to determine the specific growth rate from linear regression of cell density measurements over time.
Balance equations for substrate uptake and product formation
The general balance equation that relates changes in medium composition to extracellular metabolic fluxes under batch growth conditions is
| (3) |
where C is metabolite concentration, k is the first-order degradation rate constant, v is the specific metabolite production rate, and X is the cell density determined from Equation (1). The sign of the specific rate is defined to be negative for substrates and positive for products. The decay term is necessary to account for spontaneous first-order degradation or accumulation of metabolites. Glutamine is the best example of a metabolite that is subject to degradation, since it is known to spontaneously degenerate to ammonia and pyrrolidonecarboxylic acid under typical culture conditions (Ozturk and Palsson 1990). The degradation rate constant is assumed to be independent of cellular metabolism and can be determined empirically by measuring the disappearance rate of glutamine in the absence of cells.
Substituting for X in Equation (3) using Equation (1) and integrating with respect to t gives
| (4) |
When the decay rate constant k is zero, this equation reduces to
| (5) |
Equations (4) and (5) are both in a linear form y = ax+ b that can be used to determine the slope parameter a by regression analysis, which can be subsequently used to calculate the specific rate v.
Data Simulation
Noise-free time courses for cell density and glucose and lactate concentrations were simulated using the rate parameters in Table I. Equations (2) and (5) were used to simulate 8 measurement time points separated by 12-hour intervals. Normally distributed random errors were introduced to the noise-free data using MATLAB’s normrnd random number generator to simulate 9999 replicate data sets. The data sets were separated into 3333 groups with n = 3 replicates.
TABLE I. Parameters used to generate simulated data sets.
The values are representative of those found in our prior experiments and in the literature. Equations (2) and (5) were used to simulate noise-free time courses for cell density (X), glucose concentration (S), and lactate (P). Normally distributed random errors with zero mean and standard deviation (SD) of σln(X), σs, or σp were added to the noise-free time courses of ln(X), S, or P, respectively.
| Parameter | Variable | Value | Units |
|---|---|---|---|
| Initial Log Cell Density | ln(X0) | ln(2×105) | |
| Log Cell Density Measurement SD | σ ln(X) | 0.1 | |
| Growth Rate | M | 0.02888 | h−1 |
| Initial Glucose Concentration | S | 20 | mM |
| Glucose Measurement SD | σs | 2 | mM |
| Glucose Uptake Flux | vs | 150 | nmol/106 cells/h |
| Initial Lactate Concentration | P | 2 | mM |
| Lactate Measurement SD | σp | 2 | mM |
| Lactate Excretion Flux | vp | 300 | nmol/106 cells/h |
| Time step | Δt | 12 | h |
Least-squares Regression and Error Analysis
Two separate methods were used for least-squares regression and error analysis (Fig 1). The Gaussian approach averaged the n replicate measurements at each time point and performed a single regression using the mean time-course data {m1, m2, …, mN}. The sample variance si2 of each data point was calculated and used to determine a pooled sample variance sp2 over the entire time course according to the equation
Figure 1. Overview of study design.
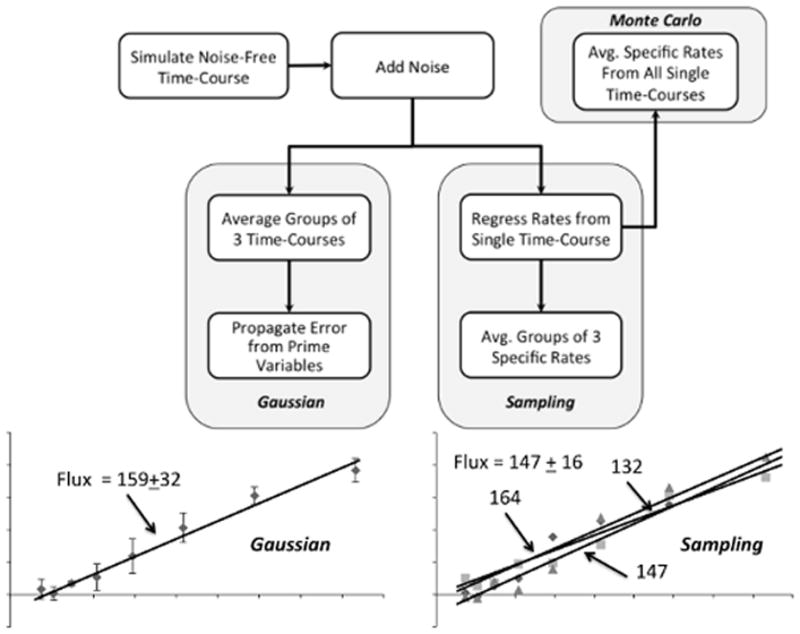
A noise-free time course was simulated using the parameter values listed in Table I. Normally distributed random errors were added to the noise-free time course to generate 9999 replicates. The replicates were grouped into 3333 simulated experiments, each with n=3. The simulated experiments were analyzed using either the Gaussian or Sampling approach to estimate specific rates and uncertainties. Monte Carlo estimates of the true parameter values and uncertainties were determined by computing the average and standard deviation of specific rates regressed from all 9999 time courses. An example is provided to illustrate how the Gaussian approach applies a single regression based on the average measurements from each simulated experiment, whereas the Sampling approach averages the rate parameters from n replicate regressions to estimate the final specific rate and its associated uncertainty.
| (6) |
where N is the total number of time points included in the regression. The standard error of the mean (SEM) was used to represent the uncertainty of each prime variable measurement, given by
| (7) |
Errors were propagated from directly measured prime variables, such as cell density or metabolite concentration, to each calculated variable q = f (m1, m2, …) using the equation (Taylor 1997)
| (8) |
where the sum is over all prime variables that influence the calculated value of q. Numerical finite differencing was applied to estimate the partial derivatives with respect to prime variables (Gardenier et al. 2011). Least-squares linear regression was performed based on Equations (2) and (5), using the propagated uncertainties δxi and δyi associated with x- and y-axis variables, respectively, to determine the weight wi of each data point in the sum-of-squared residuals (SSR) objective function
| (9) |
where
| (10) |
MATLAB’s lscov command was used to obtain the weighted least-squares estimate of the best-fit line. The iterative re-weighting method of York et al. (2004) was applied to regressions where errors were simultaneously present in both the x- and y-axis variables.
Alternatively, the Sampling approach did not average the raw data prior to regression. Each replicate time course was regresssed in an unweighted manner and rates were calculated based on Equations (2) and (5) without estimating the uncertainties of prime variables. The average and SEM of specific rates were then determined within each group of n replicates. Because uncertainties were calculated directly from sampling replicate rate estimates, this method required no error propagation.
Monte-Carlo Estimation
Monte Carlo (MC) parameter estimates provided “true” values to which the Gaussian and Sampling methods were compared. MC estimates were determined by averaging the specific rates derived from unweighted regression of all 9999 replicate time courses. The standard deviation σ of all 9999 replicates was used to estimate the true uncertainty of each rate parameter.
Goodness-of-Fit Assessment
We applied an F-test to assess the goodness-of-fit of our mathematical model to each experimental data set. This test is appropriate when the measurement variances are estimated from sample replicates (Bevington and Robinson 2003). The null hypothesis (H0) is that the model provides an adequate description of the data and that any lack-of-fit can be attributed to normally distributed random errors in the measurements. The F-test uses the degrees of freedom due to lack of fit (DOFLOF), the degrees of freedom due to pure error (DOFPE), and the sum-of-squared residuals (SSR) to determine a p-value. The DOFLOF is N−M, where N is the number of regressed data points and M is the number of fitted parameters (e.g., M=2 in the case of a linear model). The DOFPE is given by N(n−1). The p-value of the F-test is defined as
| (11) |
or the probability that the SSR exceeds a particular value of the F distribution with corresponding values of DOFLOF and DOFPE.
Cell Culture
The human P493-6 B-cell line expresses an EBNA2-estrogen receptor fusion protein and contains a tetracycline (Tet)-repressible human MYC construct (Schuhmacher et al. 1999). Addition of 1 μg/mL Tet completely represses MYC expression, while the co-addition of 1 μM beta-estradiol (BES, MP Biomedicals, Solon, OH) induces a low level of endogenous MYC expression driven by the EBNA2 viral protein (Yustein et al. 2010). This allows for three distinct levels of Myc expression: High (no addition), Low (Tet + BES), and None (Tet alone). (Only High and Low Myc expression levels were examined in this study.) Cells were cultured in RPMI 1640 medium (2 g/L glucose and 2 mM glutamine) supplemented with 10% fetal bovine serum (FBS) and 1% penicillin and streptomycin (PS) at 37°C and 5% CO2. All cell culture supplies were purchased from Invitrogen (Carlsbad, CA).
Cell Density and Metabolite Concentration Measurements
Extracellular uptake and excretion rates of P493-6 cells were determined in triplicate growth experiments. Three separate T-75 tissue culture flasks were seeded at a density of 150,000 cells/mL. Every 12–16 hours, 300 μL of cell suspension was removed from each flask after gentle mixing using a pipettor. 50 μL were used for counting on a hemacytometer while the remainder was centrifuged to remove cells, and the conditioned cell-free medium was frozen at −80°C. Concentrations of medium glucose and lactate were determined using a YSI 2300 Stat Plus Glucose and Lactate Analyzer (YSI, Yellow Springs, OH). Medium amino acid concentrations were determined using high-performance liquid chromatography (HPLC, Agilent 1200 series) with a gradient elution method on a reverse-phase column (Greene et al. 2009). Briefly, samples were derivatized immediately prior to injection with orthophthalaldehyde (OPA) and injected onto a ZORBAX Eclipse PLUS C18 column (Agilent Technologies, 4.6 × 150 mm, 3.5 μm). Mobile phase A was composed of 10 mM Na2HPO4, 10 mM Na2B4O7, and 8 ppm NaN3. Mobile phase B was a 9:9:2 mixture of methanol:acetonitrile:water. The gradient profile was as follows: 2% B for 0.5 minutes, ramp linearly to 47% for 15.5 minutes, ramp linearly to 100% B in 0.1 minutes, hold at 100% B for 3.4 minutes, ramp linearly to 2% B in 0.1 minutes, and hold for 1.4 minutes for a total time of 21 minutes. The flow rate was 1.5 mL/min, and the column was held at 40°C for the duration of the run.
The spontaneous degradation of glutamine to ammonia and pyrrolidonecarboxylic acid was included in the specific rate calculations (Ozturk and Palsson 1990). The degradation rate was determined to be 0.0031 h−1 by measuring glutamine disappearance in control experiments performed in the absence of cells. Evaporation rates determined in control T-75 flasks without cells were found to be negligible in comparison to cell specific metabolic rates.
T-test for comparison of flux estimates
A two tailed t-test was applied to compare specific rate estimates between two experimental groups. The t-statistic is calculated as
| (11) |
where
| (12) |
and
| (13) |
Here, sp2 is the pooled sample variance, di is the degrees of freedom defined as (Ni − 2), and N1 and N2 are the total number of data points used in each regression.
MATLAB Program – Extracellular Time-Course Analysis (ETA)
Using the MATLAB programming environment, custom m-files were coded to perform all calculations required to implement the Gaussian, Sampling, and Monte Carlo methods of rate and uncertainty estimation. A user interface was implemented to facilitate data input and analysis. Documentation included with the software details program usage and functionality. Briefly, cell density and metabolite concentration data can be imported from Microsoft Excel or manually entered by the user. Individual time points can be selected interactively to achieve an acceptable fit to the exponential growth model, based on both graphical displays and the p-value of the F-statistic. A first-order decay rate can be entered to correct for spontaneous metabolite degradation. Calculated specific rates (or yields) and their uncertainties are tabulated automatically and plotted in an accompanying figure window. The software is freely available at http://mfa.vueinnovations.com/.
In addition to proliferating cell cultures, the exponential growth model can be readily applied to cultures in stationary or decline phase, in which case the specific growth rate will be estimated as near zero or negative, respectively. Furthermore, specifying the dead cell density (Xd) as an accumulating product formed from first-order death of viable cells can then be used to estimate the death rate constant (kd) of the culture if measurements of cell viability are available (i.e., replace C with Xd and v with kd in Equation 3). ETA is also capable of applying a linear growth model, which is known to occur in some instances of diffusion-limited or contact-inhibited growth of cultures (Freshney 2000; Rizzi et al. 1989). Although advanced growth models involving logistic or Gompertz equations have been previously used to describe more complicated growth curves, these models are explicitly intended to describe unbalanced growth conditions where growth rate and metabolism are changing over time. Therefore, we have chosen to include only two growth models in ETA (i.e., exponential and linear), because they are applicable to the vast majority of typical cell cultures undergoing balanced growth. Since balanced growth is also a key underlying assumption of FBA and MFA, we do not expect that this limitation will severely restrict the applicability of the program for the purposes it is intended.
RESULTS
Comparison of Simulated Data Sets
We applied the Gaussian, Sampling, and Monte Carlo approaches to determine specific growth and metabolite production rates by regressing 9999 simulated time courses generated using the parameter values in Table I. We hypothesized that Gaussian error propagation from prime variables would provide more precise rate and uncertainty estimates in comparison to the Sampling approach, which involves simply averaging the regressed rate parameters derived from replicate experiments, when the number of replicates is small. To test this hypothesis we compared 3333 rate estimates derived from the Gaussian and Sampling approaches (each with n=3) to the “true” Monte Carlo estimates determined by averaging rate estimates from all 9999 simulated data sets. The calculated growth, glucose uptake, and lactate excretion rates returned by the Gaussian and Sampling methods exhibited normal distributions over the 3333 simulated experiments (data not shown). The mean of each distribution was nearly identical to the Monte Carlo estimate (Table II), and approximately 68% of the calculated rates fell within one standard error of the MC estimate in each case. As a result, we concluded that averaging experimental replicates either before or after regression analysis provides an equally valid approach to estimate the value of each specific rate parameter.
TABLE II. Rate estimations based on simulated data sets.
Values for both Gaussian and Sampling approaches are shown as M ± SEM, where M is the population mean over all 3333 simulated experiments (each with n=3) and SEM is the standard error of the population mean. (The Monte Carlo estimates represent the means over all 9999 replicates).
| Growth (h−1) | Glucose nmol/106 cells/h | Lactate nmol/106 cells/h | |
|---|---|---|---|
| Gaussian | 0.028878 ± 0.000013 | 150.1 ± 0.3 | 299.9 ± 0.3 |
| Sampling | 0.028878 ± 0.000013 | 150.1 ± 0.3 | 300.0 ± 0.3 |
| Monte Carlo | 0.028878 ± 0.000013 | 150.1 ± 0.3 | 300.0 ± 0.3 |
In contrast to the rate values, the two methods did not produce equally accurate estimates of parameter uncertainties. When comparing the distribution of uncertainties returned by each method, we found that Gaussian error propagation resulted in an approximately normal distribution that was centered on the true value while the uncertainties determined by the Sampling approach had a non-normal distribution that was not centered around the true value (Fig 2). In order to assess the accuracy of the two methods quantitatively, we calculated root-mean-square (RMS) errors based on the residuals between estimated uncertainties returned by the Gaussian or Sampling approach and the true values determined by Monte Carlo analysis. The RMS errors for Gaussian error propagation were nearly 3-fold lower than the Sampling approach, indicating less variability and greater accuracy (Table III). As a result, we concluded that the Gaussian approach provides more accurate and precise uncertainty estimates when the number of experimental replicates is small (e.g., n=3) and is therefore the preferred method.
Figure 2. Distribution of estimated uncertainties determined from simulated data sets.
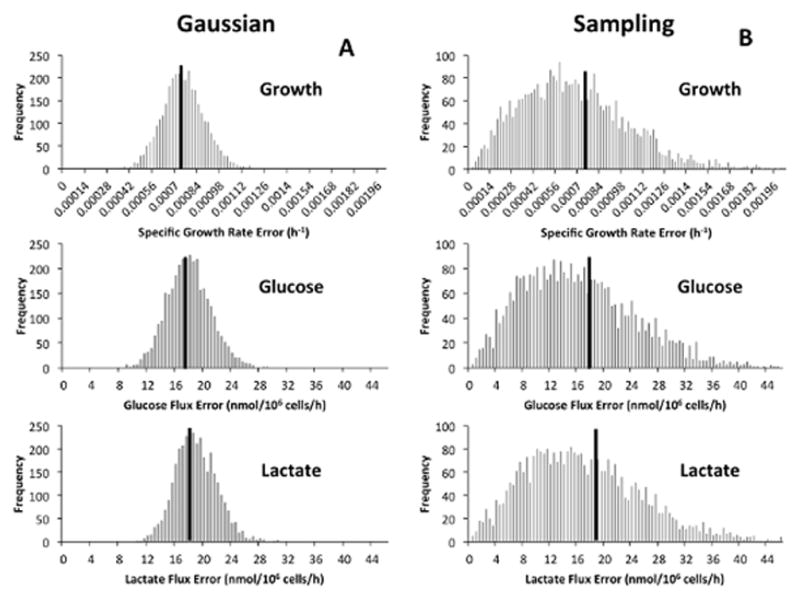
Histograms describing the distribution of uncertainties for specific growth, glucose uptake, and lactate excretion rates are shown for both (A) Gaussian error propagation and (B) Sampling rate estimates from replicate experiments. The solid black lines represent the Monte Carlo estimate of the true uncertainty of the estimated rates, which is given by .
TABLE III. Root-mean-square (RMS) errors of estimated uncertainties.
RMS errors were calculated for both the Gaussian and Sampling approaches by first computing the residuals between estimated uncertainties and the true values determined by Monte Carlo analysis. The residuals for all simulated experiments were then combined by taking the square root of the sum of squared residuals divided by the total number of simulated experiments (3333).
| Growth (h−1) | Glucose (nmol/106 cells/h) | Lactate (nmol/106 cells/h) | |
|---|---|---|---|
| Gaussian | 1.3×10−4 | 3.1 | 2.9 |
| Sampling | 3.5×10−4 | 8.6 | 9.0 |
P493-6 Rate Estimation with ETA
Using our custom ETA software, we estimated specific metabolic rates for High and Low Myc P493-6 cell cultures. We estimated specific growth rate as well as uptake and excretion rates of glucose, lactate, and 18 of 20 amino acids (Table IV). ETA enabled us to select the most appropriate points for analysis based on the goodness-of-fit F-test and visual inspection (Fig 3). For glutamine, we included an empirically determined degradation rate constant of 0.0031 h−1, which significantly improved the p-value of the model fit from 0.0044 to 0.9329. As shown in Fig. 4, the data fall along a straight line when corrected for degradation effects using Equation (4), but have a curved profile when uncorrected.
TABLE IV. Metabolic rates for High and Low Myc P493-6 cell cultures.
Rates have units of nmol/106 cells/h except for cell growth, which has units of h−1. P-values based on the goodness-of-fit F-test are listed for each rate parameter. Significance is indicated for the comparison between Low and High Myc conditions based on a two-tailed Student’s t-test with p < 0.05.
| High Myc | Low Myc | ||||
|---|---|---|---|---|---|
|
| |||||
| Metabolite | Specific Rate (nmol/106 cells/h) | Fit p-value | Specific Rate (nmol/106 cells/h) | Fit p-value | Sig. Diff. (p < 0.05) |
| Biomass (h−1) | 0.0290 ± 0.0010 | 0.1477 | 0.0176 ± 0.0010 | 0.7419 | ✔ |
|
| |||||
| Uptake Fluxes | |||||
| Glucose | 73 ± 7 | 0.9177 | 58 ± 7 | 0.5981 | ✖ |
| Arginine | 4.6 ± 0.6 | 0.4751 | 1.9 ± 0.3 | 0.0387 | ✔ |
| Asparagine | 0.9 ± 0.4 | 0.2923 | 0.9 ± 0.3 | 0.1637 | ✖ |
| Cystine | 0.73 ± 0.13 | 0.7364 | 0.88 ± 0.09 | 0.3990 | ✖ |
| Glutamine | 11.5 ± 0.7 | 0.9329 | 5.9 ± 0.40 | 0.2089 | ✔ |
| Histidine | 0.78 ± 0.12 | 0.903 | 0.17 ± 0.05 | 0.5644 | ✔ |
| Isoleucine | 2.5 ± 0.2 | 0.9694 | 1.3 ± 0.30 | 0.7093 | ✔ |
| Leucine | 3.3 ± 0.3 | 0.8483 | 1.02 ± 0.14 | 0.2334 | ✔ |
| Lysine | 2.1 ± 0.2 | 0.9233 | 0.26 ± 0.08 | 0.3271 | ✔ |
| Methionine | 0.7 ± 0.1 | 0.9807 | 0.11 ± 0.04 | 0.6590 | ✔ |
| Phenylalanine | 0.1 ± 0.3 | 0.9951 | 0.3 ± 0.11 | 0.9754 | ✖ |
| Serine | 4.1 ± 0.2 | 0.8515 | 1.34 ± 0.10 | 0.3054 | ✔ |
| Threonine | 0.27 ± 0.06 | 0.8198 | 0.57 ± 0.09 | 0.0520 | ✔ |
| Tyrosine | 0.57 ± 0.09 | 0.9797 | 0.14 ± 0.05 | 0.5471 | ✔ |
| Valine | 1.41 ± 0.12 | 0.9193 | 0.54 ± 0.07 | 0.4526 | ✔ |
|
| |||||
| Excretion Fluxes | |||||
| Lactate | 138 ± 9 | 0.2805 | 119 ± 7 | 0.9953 | ✖ |
| Alanine | 1.63 ± 0.14 | 0.8557 | 0.44 ± 0.09 | 0.1483 | ✔ |
| Aspartate | 0.36 ± 0.14 | 0.8772 | −0.38 ± 0.05 | 0.0072 | ✔ |
| Glutamate | 2.7 ± 0.4 | 0.6521 | 2.9 ± 0.2 | 0.4787 | ✖ |
| Glycine | 0.8 ± 0.2 | 0.3028 | 0.01 ± 0.08 | 0.3727 | ✔ |
Figure 3. Features of the ETA software package.
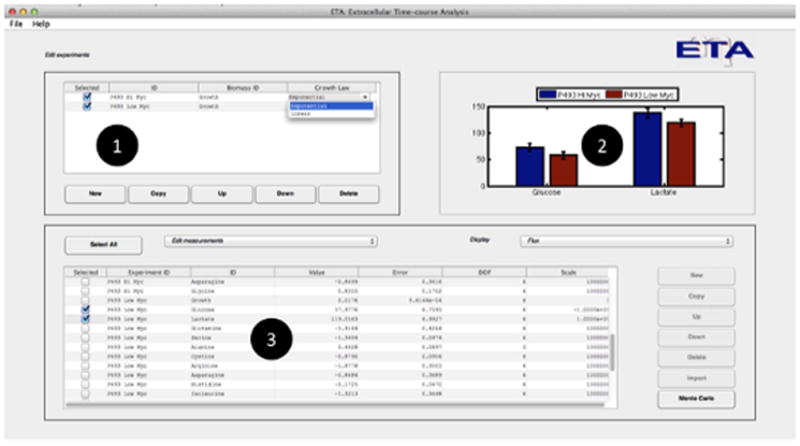
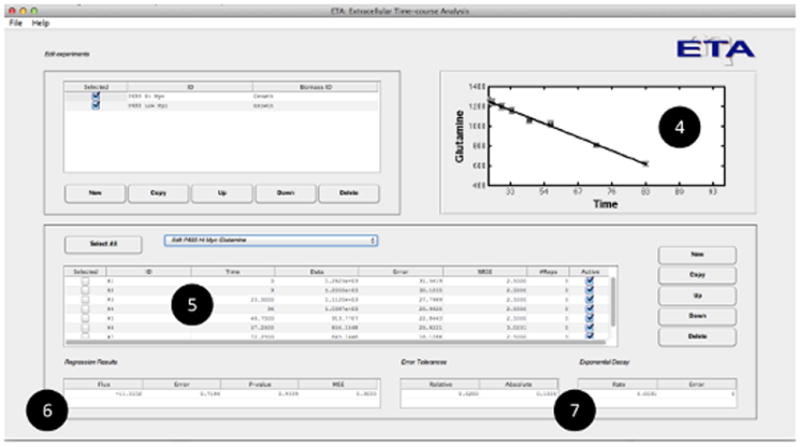
(A) Users are able to (1) create new experimental time courses and view the calculated rate (or yield) estimates and associated uncertainties in both (2) graphical and (3) tabular formats for either exponential or linear growth models. (B) When a single measurement is selected, the program allows the user to (4) graphically assess the goodness-of-fit, (5) enter and select raw data for regression, and (6) view the calculated rates along with the p-value and mean-square error of the fit. Adjustable error tolerances and first-order degradation parameters can also be supplied by the user (7).
Figure 4. Effects of spontaneous degradation on glutamine rate estimation.
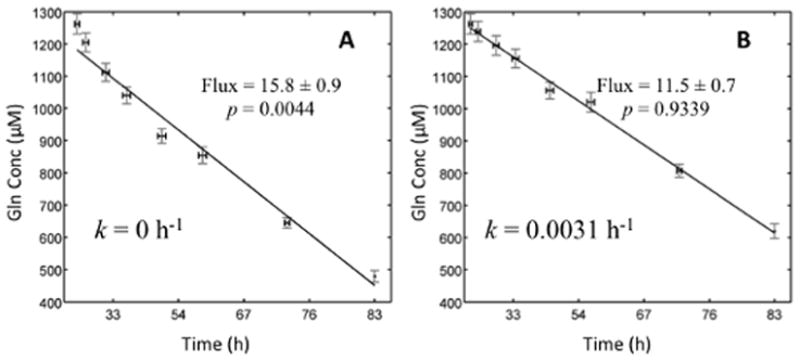
(A) When first-order degradation of glutamine is not accounted for, the data do not fit the exponential growth model. (B) When the correct degradation constant is included, Equation (4) provides an acceptable fit to the raw concentration measurements. Flux is measured in units of nmol/million cells/hour.
Growth of Low Myc cells was 40% slower than High Myc cells, while glucose uptake was reduced by only 21%. Both High and Low Myc cells exhibited a highly glycolytic phenotype, with the majority of incoming carbon excreted as lactate. This was most clearly indicated by the high lactate-to-glucose (L/G) ratios of 1.9 ± 0.2 and 2.1 ± 0.3 for High and Low Myc cells, respectively. Besides glucose, glutamine is the other major carbon substrate for mammalian cell cultures (Vander Heiden et al. 2009). Glutamine uptake was elevated nearly 2-fold in High Myc cells relative to Low Myc cells, supplying 9% of total carbon to High Myc cells and 7% to Low Myc cells. The uptake rates of most other amino acids were similarly elevated in High Myc cells (Table IV).
DISCUSSION
Accurate quantification of cell specific metabolic rates and their uncertainties is of critical importance for assessing metabolic phenotypes of cultured cells. Using rigorous parameter regression approaches, we have shown that Gaussian error propagation is the most accurate and precise method for estimating the uncertainty of specific rates when the number of experimental replicates is small. This analysis uses finite differencing to compute the derivatives in Equation (8), which allows the uncertainties in all prime variables to be propagated into calculated variables. The Sampling approach, however, attempts to estimate uncertainties based solely on the standard deviation of estimated rates determined from replicate experiments. When n is sufficiently large, this is an acceptable method that asymptotically approaches the accuracy of the Monte Carlo result. However, when n is small, uncertainty estimates become less reliable than those determined by Gaussian error propagation. A further practical consideration is that some experiments do not allow for repeated sampling of the same cell culture, which means that each time point must be derived from a separate culture plate or flask. Because there is no logical way to group these data points into individual time courses without first averaging the data from separate experimental replicates, the Sampling approach is not applicable to this scenario and Gaussian error propagation is the only approach that can be used to obtain meaningful uncertainty estimates.
We applied the Gaussian approach coded within our custom ETA software to analyze time-course experiments conducted on High Myc and Low Myc P493-6 B-cells. These cells contain a tetracycline-repressible Myc construct, which enables different levels of Myc expression to be studied on an isogenic background (Pajic et al. 2001; Pajic et al. 2000). High Myc cells are tumorigenic and resemble human Burkitt lymphoma cells, whereas Low Myc cells are nontumorigenic (Yustein et al. 2010). Therefore, comparison of metabolic phenotypes between High and Low Myc cells is expected to reveal differences between normal proliferating cells and cancerous cells.
Measurements of cell density and extracellular nutrient concentrations were obtained throughout exponential phase and biological replicates were averaged. This was followed by regression analysis to estimate specific rates of growth, substrate consumption, and product excretion. Based on these specific rates, we observed that High Myc cells significantly increased their growth rate and the magnitude of most nutrient uptake and excretion rates in comparison to Low Myc cells. These results are consistent with previous reports of the general stimulating effect of Myc on cell growth and metabolism (Fan et al. 2010; Morrish et al. 2009; Morrish et al. 2008). Studies in Rat1a fibroblasts and P493-6 cells have shown that Myc enhances flux through the glycolytic pathway by direct transactivation of several glycolytic genes (Kim et al. 2004; Osthus et al. 2000; Shim et al. 1997). However, ectopic Myc expression only modestly increased glucose consumption and lactate production in our system, and the relative changes in these rates were sub-proportional to the change in specific growth rate we observed. In contrast, most amino acid uptake fluxes were increased 2- to 3-fold in High Myc cells relative to Low Myc cells, which exceeded the 1.6-fold change in specific growth rate. Therefore, ectopic Myc expression impacted amino acid fluxes more strongly than glycolytic fluxes in P493-6 cells.
It has been previously shown that Myc exerts direct control over glutamine metabolism and that Myc-overexpressing cells are acutely sensitive to glutamine withdrawal or inhibition of anaplerotic glutamine flux entering the TCA cycle (Fan et al. 2010; Wise et al. 2008; Yuneva et al. 2007). Our data support these findings, as we observed a significant increase in glutamine uptake in High Myc cells as compared to Low Myc cells. However, our results also indicate that High Myc cells simultaneously increased most other amino acid fluxes in addition to glutamine. Nearly half of the incoming amino acids were consumed in excess of their biosynthetic requirements, which indicates that they were partially catabolized to meet the energetic or redox demands of P493-6 cells. Aside from one study that identified serine hydroxymethyltransferase (SHMT2) as a direct Myc target gene (Nikiforov et al. 2002), little is known about how Myc stimulates metabolism of other amino acids besides glutamine. Based on these results, further work to unravel the mechanisms by which Myc influences global patterns of amino acid utilization in tumor cells could have significant therapeutic or diagnostic implications.
One distinct advantage of using Gaussian error propagation for specific rate determination is the ability to rigorously assess the goodness-of-fit of the exponential growth model to the experimental data. In addition to accurate uncertainty estimation, the ETA software enables the user to interactively include or exclude individual data points based on the p-values of the goodness-of-fit F-test and graphical displays. This would not be possible without measurement of full time-course data, which enables confirmation of the underlying assumptions implying balanced growth and constant metabolic rates. Several recent articles have appeared in the biotechnology literature that rely on rate estimates computed from only two measurement time points (Jain et al. 2012; Mullen et al. 2012). While this may be suitable for initial screening experiments, it does not lend itself to the type of rigorous error analysis and statistical treatment that is necessary for quantitative flux studies. Therefore, collection of multiple sample time points under balanced growth conditions followed by regression analysis and Gaussian error propagation are prerequisite for precise determination of metabolic fluxes.
We determined p-values for the P493-6 data set which describe the confidence level in each fitted parameter based on an F-test. The goodness-of-fit p-value reflects the probability that any disagreements between the model and the experimental measurements are due to random errors rather than systematic errors. Based on this test, we should conclude that the fit is inadequate if the calculated p-value is unreasonably low. A low p-value can result from a few possible causes. First, it can indicate that the model is inadequate (e.g., balanced exponential growth assumption does not hold) or there are gross measurement errors in the data. Second, it can indicate that the true measurement errors are larger than what was specified in the regression analysis. If both of these can be excluded, the final possibility is that the measurement errors are not normally distributed. This can lead to p-values that seem small (e.g., 0.001) but may still be justifiable in practical cases where the errors have some non-Gaussian component. Fits that are grossly incorrect will often give very small p-values (e.g., 10−18) and should be summarily rejected (Press et al. 1992). In all cases, the p-values of the P493-6 rate estimates were greater than 0.001, indicating that the exponential model was acceptable.
One limitation of our approach is that it assumes balanced exponential growth with constant specific rates of nutrient uptake or product excretion. If the culture exhibits multiple distinct growth phases (e.g., exponential, stationary, decline, etc.) or metabolic shifts during the experiment, the full time course can be divided into separate subintervals in which growth and metabolism are approximately constant. This will allow for each subinterval to be separately analyzed and subsequently compared. Obviously, this is not possible if growth and metabolism are changing continuously over time or if distinct transition points cannot be readily identified within the overall time course. Both Leighty and Antoniewicz (2011) and Niklas et al. (2011) have developed sophisticated approaches for addressing such fully time-dependent scenarios by combining extracellular measurements with stoichiometric balance constraints that enable dynamic MFA calculations. Leighty and Antoniewicz used piece-wise linear functions to approximate the time-dependence of extracellular concentration measurements, whereas Niklas et al. applied polynomial splines to smooth and differentiate the extracellular measurements. Although these methods provide powerful alternative approaches that can be applied more generally to either metabolically transient or steady-state conditions, the underlying growth equations do not reduce to the canonical exponential growth model under steady-state growth conditions and therefore do not lend themselves readily to the analysis of standard growth experiments. Furthermore, the increased parameterization of these models can lead to elevated flux uncertainties in situations where the additional complexity is not warranted. This is especially evident during the initial period of batch or fed-batch growth when extracellular concentrations change slowly and therefore signal-to-noise ratios are small, as noted by Niklas et al. (2011).
In summary, the application of regression analysis and Gaussian error propagation provides a rigorous approach to compare the metabolic phenotypes of different cell lines and growth conditions. While many types of experimental assays have been developed to facilitate the rapid collection of metabolic measurements, software tools that automate the analysis and statistical assessment of these data have been lacking. Therefore, ETA has been developed to streamline the analysis workflow required to (i) compute cell specific metabolic rates and their uncertainties based on an exponential or linear growth assumption, (ii) test the goodness-of-fit of the experimental data to the regression model, and (iii) rapidly compare the results across multiple experiments. Although our approach does not involve the complexity of some recently introduced dynamic MFA algorithms, we expect that it will be applicable to most typical batch or intermittent fed-batch experiments where metabolic steady state is achieved for extended intervals punctuated by infrequent metabolic transitions caused by the onset of nutrient depletion, oxygen limitation, or accumulation of some inhibitory factor (Deshpande et al. 2009). The rates calculated by ETA can then serve as inputs for a wide range of more advanced stoichiometric or kinetic modeling approaches, including FBA or MFA.
Acknowledgments
This work was supported by NIH R21 CA155964 and a Vanderbilt Discovery Award. The authors thank Dr. Chi V. Dang for providing the P493-6 cell line used in this study.
References
- Bevington P, Robinson D. Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill; 2003. [Google Scholar]
- Deshpande R, Yang TH, Heinzle E. Towards a metabolic and isotopic steady state in CHO batch cultures for reliable isotope-based metabolic profiling. Biotechnol J. 2009;4(2):247–63. doi: 10.1002/biot.200800143. [DOI] [PubMed] [Google Scholar]
- Fan Y, Dickman K, Zong W. Akt and c-Myc differentially activate cellular metabolic programs and prime cells to bioenergetic inhibition. J Biol Chem. 2010;285(10):7324. doi: 10.1074/jbc.M109.035584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freshney RI. Culture of animal cells : a manual of basic technique. New York: Wiley; 2000. p. xxvi.p. 577. [Google Scholar]
- Gardenier GH, Gui F, Demas JN. Error Propagation Made Easy-Or at Least Easier. Journal of Chemical Education. 2011;88(7):916–920. [Google Scholar]
- Glacken MW, Adema E, Sinskey AJ. Mathematical descriptions of hybridoma culture kinetics: I. Initial metabolic rates. Biotechnol Bioeng. 1988;32(4):491–506. doi: 10.1002/bit.260320412. [DOI] [PubMed] [Google Scholar]
- Goudar CT. Computer programs for modeling mammalian cell batch and fed-batch cultures using logistic equations. Cytotechnology. 2012 doi: 10.1007/s10616-011-9425-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudar CT, Biener R, Konstantinov KB, Piret JM. Error propagation from prime variables into specific rates and metabolic fluxes for mammalian cells in perfusion culture. Biotechnology progress. 2009;25(4):986–998. doi: 10.1002/btpr.155. [DOI] [PubMed] [Google Scholar]
- Greene J, Henderson JW, Jr, Wikswo JP. Rapid and Precise Determination of Cellular Amino Acid Flux Rates Using HPLC with Automated Derivatization with Absorbance Detection. Agilent Technologies; 2009. pp. 1–8. [Google Scholar]
- Jain M, Nilsson R, Sharma S, Madhusudhan N, Kitami T, Souza AL, Kafri R, Kirschner MW, Clish CB, Mootha VK. Metabolite profiling identifies a key role for glycine in rapid cancer cell proliferation. Science. 2012;336(6084):1040–4. doi: 10.1126/science.1218595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim BJ, Forbes NS. Flux analysis shows that hypoxia-inducible-factor-1-alpha minimally affects intracellular metabolism in tumor spheroids. Biotechnol Bioeng. 2007;96(6):1167–82. doi: 10.1002/bit.21205. [DOI] [PubMed] [Google Scholar]
- Kim JW, Zeller KI, Wang Y, Jegga AG, Aronow BJ, O’Donnell KA, Dang CV. Evaluation of myc E-box phylogenetic footprints in glycolytic genes by chromatin immunoprecipitation assays. Mol Cell Biol. 2004;24(13):5923–36. doi: 10.1128/MCB.24.13.5923-5936.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leighty RW, Antoniewicz MR. Dynamic metabolic flux analysis (DMFA): a framework for determining fluxes at metabolic non-steady state. Metab Eng. 2011;13(6):745–55. doi: 10.1016/j.ymben.2011.09.010. [DOI] [PubMed] [Google Scholar]
- Morrish F, Isern N, Sadilek M, Jeffrey M, Hockenbery DM. c-Myc activates multiple metabolic networks to generate substrates for cell-cycle entry. Oncogene. 2009;28(27):2485–91. doi: 10.1038/onc.2009.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrish F, Neretti N, Sedivy JM, Hockenbery DM. The oncogene c-Myc coordinates regulation of metabolic networks to enable rapid cell cycle entry. Cell Cycle. 2008;7(8):1054–66. doi: 10.4161/cc.7.8.5739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mullen AR, Wheaton WW, Jin ES, Chen PH, Sullivan LB, Cheng T, Yang Y, Linehan WM, Chandel NS, DeBerardinis RJ. Reductive carboxylation supports growth in tumour cells with defective mitochondria. Nature. 2012;481(7381):385–8. doi: 10.1038/nature10642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen J. It is all about metabolic fluxes. J Bacteriol. 2003;185(24):7031–5. doi: 10.1128/JB.185.24.7031-7035.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikiforov MA, Chandriani S, O’Connell B, Petrenko O, Kotenko I, Beavis A, Sedivy JM, Cole MD. A functional screen for Myc-responsive genes reveals serine hydroxymethyltransferase, a major source of the one-carbon unit for cell metabolism. Mol Cell Biol. 2002;22(16):5793–800. doi: 10.1128/MCB.22.16.5793-5800.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niklas J, Schrader E, Sandig V, Noll T, Heinzle E. Quantitative characterization of metabolism and metabolic shifts during growth of the new human cell line AGE1.HN using time resolved metabolic flux analysis. Bioprocess Biosyst Eng. 2011;34(5):533–45. doi: 10.1007/s00449-010-0502-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osthus RC, Shim H, Kim S, Li Q, Reddy R, Mukherjee M, Xu Y, Wonsey D, Lee LA, Dang CV. Deregulation of glucose transporter 1 and glycolytic gene expression by c-Myc. J Biol Chem. 2000;275(29):21797–800. doi: 10.1074/jbc.C000023200. [DOI] [PubMed] [Google Scholar]
- Ozturk SS, Palsson BO. Chemical decomposition of glutamine in cell culture media: effect of media type, pH, and serum concentration. Biotechnol Prog. 1990;6(2):121–128. doi: 10.1021/bp00002a005. [DOI] [PubMed] [Google Scholar]
- Pajic A, Polack A, Staege MS, Spitkovsky D, Baier B, Bornkamm GW, Laux G. Elevated expression of c-myc in lymphoblastoid cells does not support an Epstein-Barr virus latency III-to-I switch. J Gen Virol. 2001;82(Pt 12):3051–5. doi: 10.1099/0022-1317-82-12-3051. [DOI] [PubMed] [Google Scholar]
- Pajic A, Spitkovsky D, Christoph B, Kempkes B, Schuhmacher M, Staege MS, Brielmeier M, Ellwart J, Kohlhuber F, Bornkamm GW. Cell cycle activation by c-myc in a Burkitt lymphoma model cell line. International journal of cancer Journal international du cancer. 2000;87(6):787–793. doi: 10.1002/1097-0215(20000915)87:6<787::aid-ijc4>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Press W, Teukolsky S, Vetterling W, Flannery B. Numerical Recipes in C: The Art of Scientific Computing. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- Quek L-E, Dietmair S, Krömer JO, Nielsen LK. Metabolic flux analysis in mammalian cell culture. Metab Eng. 2010;12(2):161–171. doi: 10.1016/j.ymben.2009.09.002. [DOI] [PubMed] [Google Scholar]
- Rizzi M, Klein C, Schulze C, Bui-Thanh NA, Dellweg H. Xylose fermentation by yeasts. 5. Use of ATP balances for modeling oxygen-limited growth and fermentation of yeast Pichia stipitis with xylose as carbon source. Biotechnol Bioeng. 1989;34(4):509–14. doi: 10.1002/bit.260340411. [DOI] [PubMed] [Google Scholar]
- Sauer U. Metabolic networks in motion: 13C-based flux analysis. Mol Syst Biol. 2006;2:62. doi: 10.1038/msb4100109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuhmacher M, Staege MS, Pajic A, Polack A, Weidle UH, Bornkamm GW, Eick D, Kohlhuber F. Control of cell growth by c-Myc in the absence of cell division. Curr Biol. 1999;9(21):1255–8. doi: 10.1016/s0960-9822(99)80507-7. [DOI] [PubMed] [Google Scholar]
- Shim H, Dolde C, Lewis BC, Wu CS, Dang G, Jungmann RA, Dalla-Favera R, Dang CV. c-Myc transactivation of LDH-A: implications for tumor metabolism and growth. Proc Natl Acad Sci U S A. 1997;94(13):6658–63. doi: 10.1073/pnas.94.13.6658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephanopoulos G. Metabolic Fluxes and Metabolic Engineering. Metab Eng. 1999;1:1–11. doi: 10.1006/mben.1998.0101. [DOI] [PubMed] [Google Scholar]
- Taylor JR. An introduction to error analysis : the study of uncertainties in physical measurements. Sausalito, Calif: University Science Books; 1997. p. xvii.p. 327. [Google Scholar]
- Vander Heiden MG, Cantley LC, Thompson CB. Understanding the Warburg effect: the metabolic requirements of cell proliferation. Science. 2009;324(5930):1029–1033. doi: 10.1126/science.1160809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiechert W. 13C metabolic flux analysis. Metab Eng. 2001;3(3):195–206. doi: 10.1006/mben.2001.0187. [DOI] [PubMed] [Google Scholar]
- Wise DR, DeBerardinis RJ, Mancuso A, Sayed N, Zhang XY, Pfeiffer HK, Nissim I, Daikhin E, Yudkoff M, McMahon SB, et al. Myc regulates a transcriptional program that stimulates mitochondrial glutaminolysis and leads to glutamine addiction. Proc Natl Acad Sci U S A. 2008;105(48):18782–7. doi: 10.1073/pnas.0810199105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- York D, Evensen NM, Martínez ML, De Basabe Delgado J. Unified equations for the slope, intercept, and standard errors of the best straight line. American Journal of Physics. 2004;72(3):367. [Google Scholar]
- Yuneva M, Zamboni N, Oefner P, Sachidanandam R, Lazebnik Y. Deficiency in glutamine but not glucose induces MYC-dependent apoptosis in human cells. J Cell Biol. 2007;178(1):93–105. doi: 10.1083/jcb.200703099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yustein JT, Liu Y-C, Gao P, Jie C, Le A, Vuica-Ross M, Chng WJ, Eberhart CG, Bergsagel PL, Dang CV. Induction of ectopic Myc target gene JAG2 augments hypoxic growth and tumorigenesis in a human B-cell model. Proc Natl Acad Sci U S A. 2010;107(8):3534–3539. doi: 10.1073/pnas.0901230107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zupke C, Sinskey AJ, Stephanopoulos G. Intracellular flux analysis applied to the effect of dissolved oxygen on hybridomas. Applied microbiology and biotechnology. 1995;44(1–2):27–36. doi: 10.1007/BF00164476. [DOI] [PubMed] [Google Scholar]


