Automated Algorithm for GI Spike Burst Detection and Demonstration of Efficacy in Ischemic Small Intestine

Abstract

We present a novel, fully-automated gastrointestinal spike burst detection algorithm. Following pre-processing with SALPA [45] and a Savitzky-Golay filter to remove unwanted low and high frequency components, candidate spike waveforms are detected utilizing the non-linear energy operator. Candidate waveforms are classified as spikes or artifact by a support vector machine. The new method achieves highly satisfactory performance with > 90% sensitivity and positive prediction value. We also demonstrate an application of the new method to detect changes in spike rate and spatial propagation patterns upon induction of mesenteric ischemia in the small intestine. Spike rates were observed to transiently increase 10–20 fold for a duration of ≈ 600 s, relative to baseline conditions. In ischemic conditions, spike activity propagation patterns included retrograde-longitudinal wavefronts with occasional spontaneous conduction blocks, as well as self-terminating concentric-circumferential wavefronts. Longitudinal and circumferential velocities were 6.8–8.0 cm/s and 18.7 cm/s, respectively.

Introduction

The small intestine exhibits an electrical activity that coordinates the contractions that mix and propel digestive contents. This electrical activity is composed of two major patterns, a rhythmic electrical “slow wave” (SW) activity, generated by the interstitial cells of Cajal (ICC), and smooth muscle action potentials, commonly termed “spikes” [39]. Spike activity is typically categorized as being comprised of individual events propagating in self-limiting “patches” which can be coordinated by the SW [24], or of a rapid succession of multiple electrical discharges (“bursts”) which have been associated with more broadly propagating peristaltic waves independent of the SW [25]. Several disease states have been associated with abnormal intestinal electrical activity, including diabetic enteropathy, post-operative dysmotility, and intestinal ischemia [23, 41, 27].

The use of extracellular electrodes to study the presence and pattern of intestinal electrical activity is a fundamental tool in gastrointestinal motility. Recently, multi-electrode high-resolution (HR) electrical mapping has resulted in the ability to record from hundreds of sites simultaneously in order to accurately map spatial patterns of electrical activity propagation [20, 7]. However, the large number of electrodes associated with HR mapping results in a massive data volume, necessitating fast and reliable automated methods to facilitate analysis. Accurate automated algorithms were recently developed for identifying and spatially mapping SW events [10, 9, 35], and have been incorporated into a unifying framework [47]. This framework has been successfully applied to experimental and clinical translation studies [8, 33]. However, no accurate, robust and widely available method yet exists to detect gastrointestinal (GI) spike bursts.

Spike detection is a commonly encountered problem in GI electrophysiology. In fact, some small intestine spike detection algorithms have been described previously [43, 36, 14, 21]. However, they have not yet reached an equal state of maturity as neural [30] and electromyogram [37] spike detection algorithms or ECG beat detection [11], in terms of accuracy and research/clinical utility. It is well known that extracellular in vivo intestinal recordings are subject to motion and cardiac artifacts, which complicates automated spike detection. The SW waveform can further complicate the issue, as typical spike recordings share a significant amount of spectral overlap with the fast downward deflection typically observed in SW recordings [46]. As these challenges with GI spike detection have not yet been fully and adequately addressed, in this work we aimed to develop a new, more robust automated method for detecting spike bursts in extracellular intestinal recordings.

Materials and Methods

Data acquisition

Serosal multi-electrode recordings were acquired from the small intestines of weaner pigs. Ethical approval for the studies was obtained from the Vanderbilt University and University of Auckland animal use and care committees. Data recorded from both of these institutions was used to demonstrate generalizability of the novel spike detection method in methods between laboratories. Animals were prepared and anesthetized as previously described [8]. Briefly, a midline laparotomy was performed to gain access to context of supporting mesenteric artery (SMA) vasculature. For the studies conducted at The University of Auckland laboratory, a flexible printed circuit board (PCB) array [7] was applied to the proximal jejunum ≈5–10 cm distal to the ligament of Treitz, as previously explained [1]. Each PCB array had 256 gold electrodes (32×8 array), of 0.3 mm diameter and 4 mm inter-electrode spacing. For studies conducted at Vanderbilt, a total of 48 silver-wire electrodes were distributed in subsets of 4 (2 × 2 array) or 16 (4 × 4 array) channels, spanning the length of the small intestine (15 cm distal to the Ligament of Treitz to 20 cm proximal to the ileocecal junction).

The intestine was immediately replaced inside the abdominal cavity, the wound edges approximated, and a baseline recording period of 15–30 minutes commenced prior to induction of ischemia. Only preparations which showed clear evidence of slow wave activity during baseline conditions were considered for further experiment and analysis. Both total localized ischemia and progressive total SMA ischemia were performed, simulating clinical patterns of thrombotic and embolic disease [32]. For the total ischemia experiments, arteries arising from the SMA vascular arcade that supplied the segments of mapped intestine were identified, isolated, and ligated. The intestine was immediately replaced inside the abdominal cavity and the wound edges were approximated, allowing nearly continuous data acquisition across baseline and ischemic periods. Tying off local arteries produced a highly localized ischemic section of bowel (indicated by dark purple color and vigorous contractions) approximately 10-15 cm in length. Ischemic segment recordings were performed for 10–30 minutes, long enough to clearly track the spike burst rate versus time (see Results). For progressive ischemia experiments, a pressure-driven occlusion cuff (In Vivo Metric; Healdsburg, CA) placed around the SMA was used to reduce the blood flow to a desired rate, as monitored by an ultrasonic flow probe (Transonic Systems Inc.; Ithaca, NY). Data was acquired in successive ≈30 minute periods during which the total blood flow to the intestine was reduced by 50, 75, 90, and 100%. The total duration of the progressive SMA ischemia experiment was about 3.5 hours. Body temperature was monitored and maintained for the duration of all experiments, as described in [42].

A Biosemi ActiveTwo system, modified for passive recordings, was used for acquisition of all recordings (Biosemi, Netherlands), with reference electrodes applied as previously described [8]. Data were acquired at either 256 or 512 Hz, both of which were observed to be sufficiently fast to cleanly record spike waveforms. A testing and validation dataset was collated from five experimental datasets taken across five animals (2 from Auckland; 3 from Vanderbilt). Manual analysis and classification of this data (comprising around 5000 spike waveforms) was performed independently by three investigators with significant prior experience in analyzing small intestine electrical recordings to generate a reference dataset. A waveform was deemed to be a “true” spike only when all investigators' classifications were in agreement. Of the 5000 waveforms assessed manually, about 25% were classified as spikes.

Spike burst detection algorithm

The spike detection algorithm described herein integrates a collection of established signal processing methods in a novel way. Each step is specifically adapted for the problem of reliably detecting spike bursts recorded extracellularly from the serosa of the small intestine. Spike bursts are characterized by a series of positive and negative deflections in rapid succession [12]. Details of the three main stages of signal processing are described below. These stages are: 1) Filtering / pre-processing; 2) Detection of “candidate” spike waveforms using the non-linear energy operator (NEO) with simple thresholding; and 3) Classification of candidate waveforms as spikes (or not) using a support vector machine (SVM).

1. Pre-processing with SALPA + SG filter

SWs, baseline wander, and other low frequency components (e.g. respiration) of the raw recordings were removed using the Subtraction of Artifacts by Local Polynomial Approximation (SALPA) algorithm [45]. In addition, the value of any point in the time series with magnitude exceeding a user-defined threshold (empirically set at 3 mV) was explicitly set to zero. Doing so removes large artifacts, such as irregularly occurring movement artifacts, while leaving the remainder of the time series intact. SALPA works by iteratively fitting a cubic polynomial to a sliding window of data, and is particularly well-suited for real-time applications [45]. A cubic polynomial is a high enough order to accurately fit SW and wandering baseline waveforms, but is low enough order to avoid over fitting to spikes. The 300 ms time window was empirically determined to be an optimal value for removing low frequency components without distorting spike waveforms (Fig. 1, top panel). A Savitzky-Golay (SG) [40] smoothing filter of order 9 and a window size of 100 ms was utilized to reduce high-frequency noise. Both parameter values were empirically determined by trial-and-error to be optimal for reducing high frequency noise without distorting spike waveforms (Fig. 1, top panel). SG filtering has previously been shown to act as an effective low pass filter applied to extracellular gastric and intestinal recordings [1, 34]. Removal of high-frequency noise is an important pre-processing step for spike detection because it helps prevent high-frequency, low-amplitude signals from falsely triggering the NEO spike detector (described below).

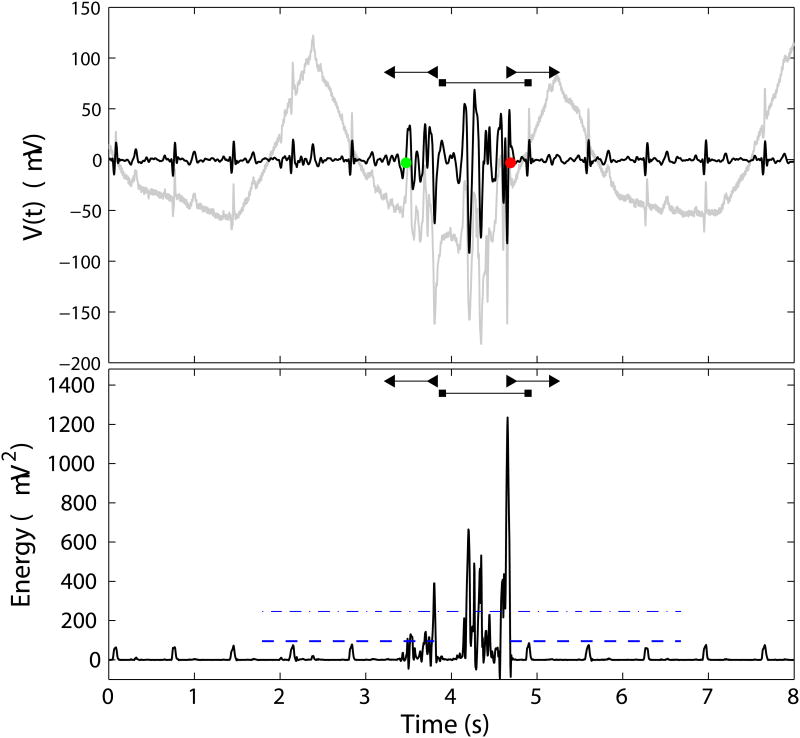
Figure 1.

Top: Representative raw electrode signal (gray trace) and SALPA + SG filtered signal (black trace). Bottom: Energy signal. The dash-dotted line marks the energy detection threshold. The window in which SVM features are computed is demarcated by the horizontal line terminating in squares. The lower threshold is indicated by the dotted line, and the horizontal bars terminating in left and right triangles demarcate the on and off time search windows, respectively. A spike burst occurs from ≈ 3.4 - 4.7 s. Regular cardiac artifacts are seen in the signals at approximately 0.75 s intervals.

2. Identification of candidate spike burst waveforms using NEO

The non-linear energy operator (NEO; [19]) was utilized for detection of candidate spike waveforms (Figure 1, bottom panel). The NEO transform (“energy signal”) was computed in the digital domain and centered about the median in a two-step process:

1. E[x(n)] = x(n)x(n) − x(n+1)x(n−1)

2. E[x(n)] ← E[x(n)] − Med(E[x(n)])

where Med(·), denotes the median. The NEO accentuates high amplitude, high frequency waveforms—i.e., spike bursts—as its magnitude is proportional to A²f², where A and f are the instantaneous amplitude and frequency [18, 19]. All points in the energy signal exceeding a threshold value were identified. Successive suprathreshold points representing an individual candidate spike burst waveform were clustered if the temporal distance between them was < δt, a user-selectable parameter. We tested a range of δt = 0.3 – 1.5 s. The NEO candidate spike detector marked the (integer indexed) mean time of each cluster of points representing a candidate spike burst waveform, N_c, for further analysis (see SVM classification). The energy signal threshold was computed as E_thresh = η σ̂_E, where σ̂_E estimates the noise level of the energy signal, and was computed as the median of the absolute deviation [29]. The noise threshold multiplier, η, was implemented as user-selectable; we tested a range of values for η from 1–18. Centering the NEO about the median helped properly set the detection threshold, and helped minimize the occurrence of low amplitude, high frequency signals — such as those observed by electrodes with no viable data — from falsely triggering the spike detector.

3. SVM Classification

The NEO detection stage tags all candidate spike waveforms, some of which may actually be spikes, and some of which may be artifacts. A support vector machine (SVM) was used to automate this binary classification task [6]. A total of five SVM input features were computed. For the first four SVM features described below, the mathematical operations are performed over window 1 s wide, expanded about the center point N_c, integer-indexed as n = {N_c − N_w, …, N_c + N_w}, where N = 2N_w + 1 is the number of data points in a 1 s window.

1. Integrated Energy. This feature attempts to capture spike waveforms which typically have sustained consecutive upward and downward deflections, and is defined as the sum of the energy signal averaged over a 1 s window: $\mathit{\text{IE}}=\frac{1}{N}{\sum }_{n}E[x(n)]$.

2. Crossing Rate. This feature is defined as the number of times the energy signal crosses the detection threshold in either direction per unit time: $\mathit{\text{CR}}=\frac{1}{N}{\sum }_{n}u(n)$ , where u(n) = 1 if E[x(n)] > E_thresh and E[x(n − 1)] < E_thresh, or vice versa; and u(n) = 0 otherwise. The SG filter step minimizes the number of spurious crossings due to noise alone.

3. Energy Signal-to-noise ratio. This feature represents the maximum instantaneous energy relative to a baseline level, and was designed to capture shorter-duration spike bursts.

   SNR_E = max(E[x(n)]/E_thresh.

4. Variance of the windowed electrode signal time series x(n). A data segment with high-variance might be indicate of a spike waveform: ${\sigma }_x^2=\mathit{\text{var}}(x(n))$

5. Duration of the candidate spike waveform. Spike bursts typically have longer durations than artifacts (motion, cardiac). This feature was computed by extending a 0.5 s wide window from the most exterior suprathreshold points in the windowed energy signal (E[x(n)] ≥ η σ̂_E), then searching for the outer-most points in the expanded windowed for which the energy signal amplitude exceeded a user-defined lower threshold of λ σ̂_E. We tested a range of λ = 1–3. These outermost points define the “on” (T_ON) and “off” (T_OFF) times of the candidate spike waveform (see Figure 1, bottom panel). The duration is computed as: δT = |T_ON − T_OFF|.

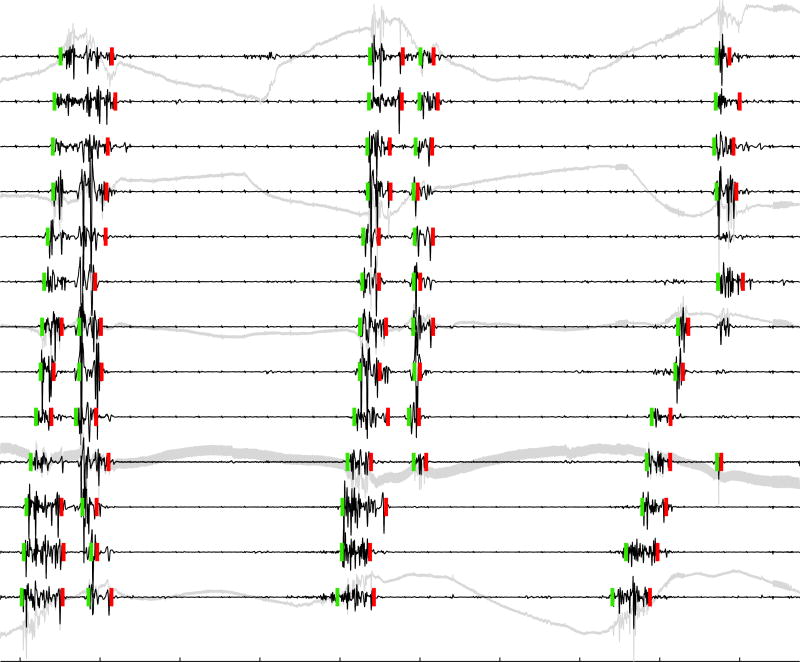
Spike burst waveform morphology varied substantially across electrodes and data sets (Figure 2), and each input feature was designed to help detect a variety of the ones most commonly observed. Features 1 and 2 were motivated by the observation that spike bursts typically consist of several relatively large amplitude (typically 100–1000 μV), fast deflections (≈50 ms), closely spaced in time. Features 3 and 4 were implemented to help identify shorter-duration spike bursts (≤ 300 ms) with a relatively low average power in a 1 s window, but a high SNR in the energy signal. Feature 5 was used to aid proper classification of longer duration spike bursts with slower rise and fall times, as well as short-duration non-spikes. The relative importance of these features was determined by training the SVM using all possible subset combinations of these features (see Relative Importance of SVM Features).

Figure 2.

Spike bursts with automated marks for on and off times (green and red vertical dashes). SALPA + SG-filtered traces are shown in black, with selected raw signals shown in gray. Tick marks on the abscissa are spaced at 2 s. Green and red vertical dashes indicate a 70 μV scale. Three successive waves of spike activity occur at intervals of approximately 8 s. All marks are validated as true positives, except two false negatives occurred during the 3rd wave of activity on 5th and 7th traces from top, likely due to their relatively small amplitude. The effect of the SALPA filter removing the baseline wander and (possibly) SWs indicated by sharper transients (e.g. 1st and 3rd traces, 2 s prior to 2nd wave of activity) is evident. The effect of the SG removing high frequency noise is illustrated in the 10th trace. Spike burst detection results shown are for δt = 0.5 s.

SVM Implementation and cross-validation

We implemented an SVM with radial basis functions, which are generally the best a priori choice for classification [16]. The feature space was normalized prior to the training phase. A 10-fold leave-one-out cross-validation was used to assess the accuracy of the SVM in discriminating spikes from artifacts. The SVM training set consisted of 5000 waveforms collated and manually classified from five experimental animals as detailed above. For automated analysis, candidate spike waveforms were first tagged by the NEO detector, and SVM input features were computed defined above. To quantify the performance of the SVM separating spikes and non-spikes, we computed the overall accuracy metric, A_roc, via the sensitivity (Sens.) and positive-prediction value (PPV) as follows:

$$\begin{array}{ccc}\mathit{\text{Sens}}.=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}+\mathit{\text{FN}}}& \mathit{\text{PPV}}=\frac{TP}{TP+FP}& A_{\mathit{\text{roc}}}=\mathit{\text{Sens}}.\times \mathit{\text{PPV}}.\end{array}$$

In the context of SVM validation, a true positive (TP) indicates the manual and SVM classification were in agreement; a false negative (FN) indicates a waveform identified as a spike by manual marking but not the SVM; and vice-versa for a false positive as (FP). The range of each Sens., PPV, and A_roc is 0-1; a value of 1 indicates perfect performance.

Validation and Performance Metrics of Automated Pipeline

Accurately determining the on and off times of spike burst activity are important for evaluating the propagation of intestinal spike activity [22]. Therefore, to fully validate the complete automated pipeline, we imposed a more stringent time criteria beyond binary classification alone. We quantified the overall performance of our full automated system using the Sens., PPV, and A_roc metrics as described above. For an automated marking to be considered a true positive (TP), we required that the on and off times must lie within 0.5 s on either side of the corresponding time-averaged manual reference marks. Any automated mark not meeting this criterion was deemed a false positive (FP). A false negative (FN) occurred when a manually marked spike was not properly identified by the automated system. The 0.5 s time tolerance was justified on the basis of approximating the natural variation between independent manual markers [10]. Manually marking the exact spike burst on and off times can be challenging due to the typical time-varying amplitude envelope that was observed (see Figure 2)—an effect likely due measuring the spatial average of the time-varying electrical potential in the surrounding intestinal tissue.

Results

SVM Accuracy and Relative Importance of Features

Table 1 lists the best results achieved for subsets of 1–5 features. (Supplemental Figure 1 shows results for all 31 possible subset combinations). With all 5 features input, SVM classification achieved an A_roc value of 0.90 ± 0.01. In general, using more input features resulted in better classification accuracy. The classification accuracy of SVM utilizing all 5 features was 7.6% superior to the optimal classification result inputting the single feature SNR_E (A_roc = 0.90 ± 0.01 vs. 0.84 ± 0.02). The largest jump in performance was noted between using 1 and 2 input features with maximum A_roc values of 0.84 ± 0.02 and 0.89 ± 0.01, respectively (see also Supplemental Figure 1). Smaller increases in classification accuracy were observed adding more features thereafter.

Table 1.

SVM performance dependence on input features. Performance increased with the number of features. The largest increase in performance was noted between using 1 and 2 features. The two most important features for proper classification were the SNR of the energy signal and the duration of the waveform. Table 1: ABME erickson et al.

Nfeat	Optimal subset	Aroc × 100
1	SNRE	83.9 ± 1.8
2	SNRE, ΔT	88.8 ± 1.1
3	SNRE, ΔT,	89.5 ± 1.3
4	All except IE	90.1 ± 1.4
5	All features.	90.3 ±1.3

Complete Automated System Performance

Figure 2 shows representative final on and off marks generated by our automated method over three successive waves of spike burst activity using parameter values η = 3, λ = 1.5, and δt = 0.5 s. Some of the multiphasic waveforms exhibited a noticeable quiescent period in between spiking and could plausibly have constituted two separate bursts (e.g. bottom three traces during first ≈ 2 s). Given this interpretation, all marks in this figure were validated as true positives, even with spike bursts waveforms exhibiting variable amplitude and duration. The two false negatives noted were attributed to the relatively small amplitude of the last burst waveform. Alternatively, multiphasic waveforms may plausibly be considered to arise from an ordered sequence of longitudinal-then-circular muscle contraction [13, 15], thus constituting a single bursting event. Using a value for δt = 1.5 s fused together individual events occurring within a single wave of activity for all traces shown in Figure 2, essentially removing the “inner” (first red off time and second green on time) spike marks. The main point is that algorithm parameter values could be easily tuned to provide results consonant with the investigators' interpretation of the electrograms.

Table 2 lists the optimal outcomes and corresponding parameter values defined for each of five data sets. The sensitivity generally ranged between 0.90–0.96, and the PPV ranged between 0.88–0.97. These metrics indicate highly satisfactory performance, being comparable with, or superior to, optimized automated SW detection algorithms, enabling accurate mapping of electrical activation patterns [10, 9]. For one particularly noisy data set (Auck 2), the maximum Sens. and PPV achieved were only 0.80 and 0.87, respectively. These results reflected a challenging dataset, for which all manual markers also commented there was ambiguity in determining when and where some spike events occurred.

Table 2.

Optimal performance and parameter values for each of 5 data sets, three of which were acquired at Vanderbilt University (Vb), and two at The University of Auckland (Auck.). The parameters η = 3, δt = 1.5, and λ = 2 serve as a good starting point, but may be tuned to the particular data set. N_cands and N_spikes indicate the number of candidate waveforms identified by the NEO spike detector, and N_spikes indicates the number of these classified as spikes by the SVM. See text for description of all other parameters. Table 2: ABME Erickson et al.

Data Set	η	δt	λ	Aroc	Sens.	PPV	Ncands	Nspikes
Vb 1	3	0.5	2	0.83	0.94	0.89	295	154
Vb 2	3	1.5	2	0.93	0.96	0.97	146	112
Vb 3	3	1.5	1	0.85	0.96	0.88	251	151
Auck 1	3	1.3	2	0.88	0.90	0.98	297	248
Auck 2	3	1.5	1	0.70	0.80	0.87	227	126

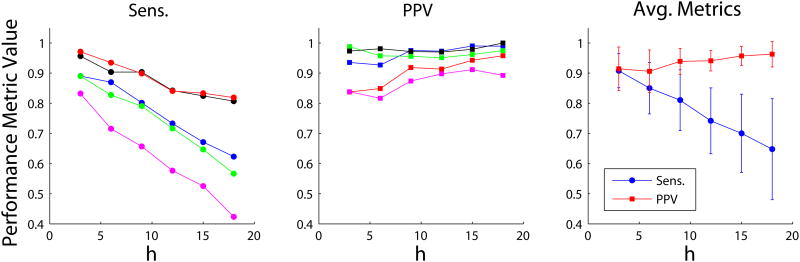
Figure 3 illustrates the algorithm's performance (Sens. and PPV) for each of five data sets analyzed vs. η, as well as the results averaged across all data sets. Comparing results for Vanderbilt and Auckland data sets, no discernible systematic difference in PPV was noted. However, a modest decrease in sensitivity was observed for the Auckland data sets, attributed to the lower SNR recordings inherent with flexible PCBs compared to traditional electrode platforms [7]. Optimal performance was achieved at a detection threshold of η = 3. As expected, the sensitivity decreased for larger values of η because as the NEO detection step produces more false negatives at a higher threshold. We observed that Sens. sharply decreased for η < 3, which was attributed to the fact that the clustering process defining an individual spike burst clusters an inappropriately large number of points at such low thresholds. Notably, the PPV remains relatively constant over a wide range of η, attributed to SVM properly classifying some (typically about 25-50%; see Table 2) candidate waveforms tagged by the NEO detector as non-spikes.

Figure 3.

Sensitivity (Sens.) and positive prediction value (PPV) vs. NEO detection threshold parameter, η, for the five data sets (Vanderbilt: blue, red, and black; Auckland: green and magenta). Only results for η ≥ 3 are shown for clarity. Sens. decreases with increasing η due to an increasing rate of false negatives. PPV remains fairly constant with increasing η due to SVM classification. Data shown for δt = 1.5, λ = 2. The metrics averaged across all 5 data sets are also shown (right-most panel). Mean ± s.d. are plotted.

The temporal clustering parameter δt was generally found to have little effect on the performance of the automated system (for η ≥ 3), except for when spike bursts were observed to occur in quick succession. In practice, the recommended value for the temporal clustering parameter δt was identified as 1.5 s, which provides for better performance in properly marking the on and off times of multi-phasic spike burst waveforms. However, a smaller value of δt = 0.5 s may be well-advised for recordings exhibiting closely timely bursts (for example, see Figure 6). The empirically determined optimal range for λ was 1.5–2. A lower value for λ made the algorithm more sensitive to low-amplitude artifacts typically cardiac in nature (Figure 1). A higher value made the algorithm less sensitive to the relatively small-amplitude spikes at the beginning and end of a spike burst.

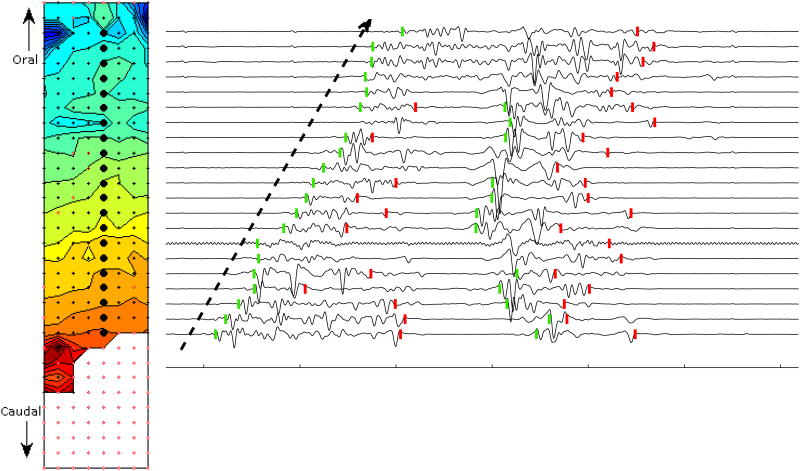
Figure 6.

Isochrone activation map and representative electrograms. During the experiment, the 32×128 mm array (4 mm inter-electrode spacing), shown here in planar projection, was wrapped around the circumference of the small intestine such that the left and right borders were nearly adjacent, positioned on either side of the mesenteric blood supply arcade. Red and blue colors indicate the earliest and latest spike activity on times, respectively. Isochrone contours are drawn at 100 ms intervals. A longitudinal wave propagates in the retrograde direction with an average velocity of about 8 cm/s over a segment ≈ 92 mm in length. Electrode sites are marked by a black dot if a spike burst was detected at that location, or colored white with red perimeter if no spike was detected. Larger black circles indicate sites corresponding to SALPA + SG-filtered electrograms shown at right. Tick marks on abscissa indicate 500 ms intervals. Spike burst on and off times are marked with green and red vertical dashes. The dashed arrow highlights the retrograde propagation pattern.

Demonstration of Automated System Utility—Total and Progressive SMA Ischemia

Total Ischemia

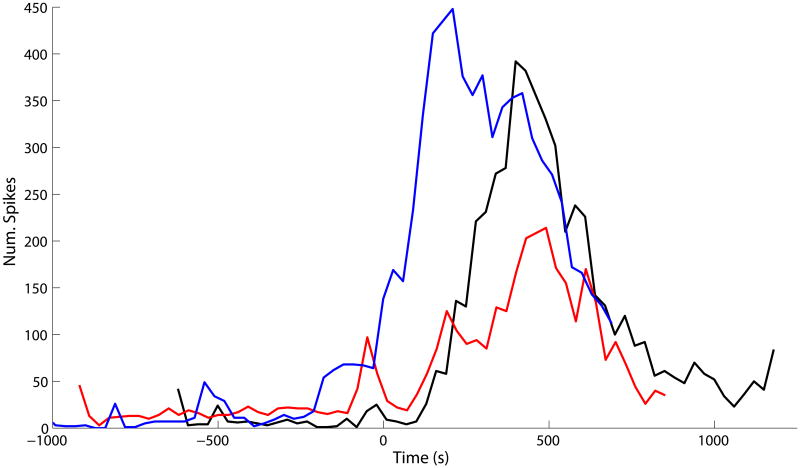
Once validated, the optimized algorithm was applied to define changes in spike activity occurring in a fully (100%) ischemic segment of intestine, in order to demonstrate practicability and experimental utility. The spike rate vs. time was quantified by counting the spike bursts array-wide in successive 30 s windows (Figure 4). Array-wide spike rates increased from 0.67 spikes/s (averaged over the 30 s window) during baseline to a peak rate during ischemia in the range of 7.2–14.9 spikes/s. The significant increase in spike activity levels (defined as being 5× greater than the baseline rate) lasted about 500–700 s. The typical lag before the spike rate began to markedly increase was about 120–150 s. In one experiment (Figure 4, blue trace), there was no time lag, possibly reflecting early occlusion of the artery prior to actual ligation. This could have occurred due to arterial kinking by the suture thread during intestinal manipulations prior to ligation, as suggested by the modest increase in spike rate at approximately -200 s. Overall, these results indicate that a readily observed transient increase (11–22×) in spike rate relative to baseline is a common electrical signature of the onset of total ischemia.

Figure 4.

Array-wide spike burst rate for localized total ischemia demonstration study. Results for three separate experiments are shown. The ordinate values (“Num. Spikes”) indicate the total number spike bursts observed across the entire electrode array during a 30 s window. Results are aligned on the abscissa such that, following a baseline period, 100% ischemia was induced at 0 s. Typically, the spike rate showed a marked increase followed by a decrease to near-baseline levels. For two experiments (red and black traces), there was a delay time of about 150 s before the spike rate started to increase; no such lag was observed for the other experiment (blue trace).

Progressive SMA Ischemia

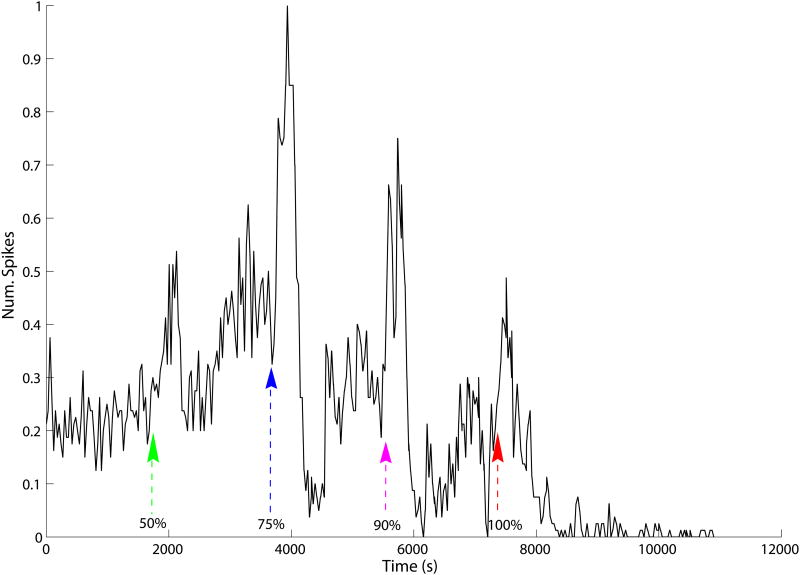
Our new automated system was also applied to a progressive ischemia demonstration study. A transient increase in spike rate was observed shortly after each incremental increase in ischemia severity (Figure 5). Following induction of 50% and 100% ischemia, the spike rate was transiently increased nearly 2-fold relative to baseline conditions for a duration of about 300 s. A pronounced (≈ 4-fold) transient increase in the spike rate was observed for both the 75 and 90% levels, also lasting about 300 s. Spike rates were depressed relative to baseline following 75 and 90% ischemia, and spikes essentially ceased 20 minutes after induction of 100% ischemia. In summary, the results for the partial ischemia study showed a transiently increased spike rate with each step-change in blood flow rate.

Figure 5.

Array-wide spike burst rate for progressive ischemia, normalized to the maximum spike rate observed (at about 3900 s). Baseline period: 0–1800s. Arrowheads indicate times at which 50, 75, 90, 100% ischemia were induced, respectively. A 2 to 4-fold transient increase in spike rate lasting about 210 s was observed for upon inducing each successively more severe level of ischemia.

Spatiotemporal Spike Propagation Analysis

As a final demonstration study, we used spike burst on-times marked with our new automated method to generated isochronal activation maps as well as animated sequences illustrating spatiotemporal propagation of spike burst activity in fully ischemic intestine. The validated interpolation scheme described in [9] was also implemented to more more completely color isochronal maps. Figure 6 illustrates spike activity propagating about 84 mm, primarily in the longitudinal-retrograde direction with average velocity of about 8 cm/s. This spike activity propagated in relatively uniform fashion as a wavefront extending around the circumference of the intestinal segment (the width of the electrode array) over the middle segment of the electrode array (about 56 mm). At the oral end of the array near the centerline (the side opposite the mesenteric arcade), spike activity appeared to propagate anisotropically with relatively higher velocity, in a somewhat elliptical manner. This wave of spike activity possibly self-terminated near the proximal boundary of the array. No spikes were detected along many of the most proximal electrode sites, however, spike times have been interpolated at these sites to color in the propagation map. Another possibility was that this area of the array was not in good electrical contact with the small intestine. Supplemental Figure 2 shows the corresponding sequence of frames illustrating the longitudinally propagating spike activity. Such animations can be useful to more readily observe some of the details of the propagation pattern.

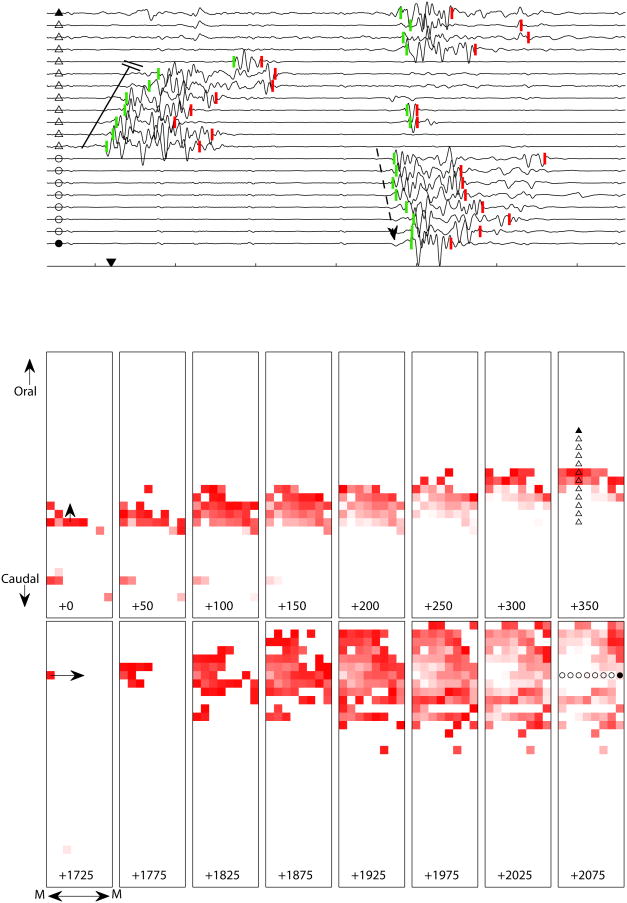
Figure 7 illustrates the situation in the same segment of intestine starting about 16 s later. The propagation pattern was more complex consisting of multiple distinct propagation events (See Supplementary Video 1 on-line for full animated sequence). Following some spiking activity at isolated sites toward the bottom of the array, a broad retrograde-longitudinal wavefront similar to the one illustrated in Figure 6 propagated in organized fashion with an average velocity of about 6.8 cm/s (Figure 7, top 8 frames). However, this wave of activity spontaneously terminates after reaching a line of conduction block after traveling 24 mm in 350 ms. A second retrograde wave re-initiated just above this block a few hundred ms later, but terminated after propagating only 8 mm (see full animated sequence). Following a ≈1 s quiescent period, spike burst activity re-initiated at a focal pacemaker adjacent to the mesenteric vasculature (top-left of the array) and propagated in somewhat concentric fashion around the circumference of the intestine (Figure 7, bottom 8 frames), with a velocity of about 18.7 cm/s. The circumferential activity appeared to be limited to a segment of intestine ≈52 mm in longitudinal length (see also Supplemental Figure 3). Interestingly, this higher velocity concentric activity occurred in the same region where the elliptic-longitudinal activity was noted just two bouts of spike activity earlier (Figure 6).

Figure 7.

Longitudinal and circumferential propagation of spike burst activity in fully ischemic small intestine and representative electrograms. Tick marks on abscissa indicate 500 ms intervals. Triangle and circle symbols at left of each electrogram are keyed to the electrode locations marked in the right most frames of the animation sequence. Downward-pointing arrowhead on abscissa marks the first spike burst on-time; numeric values at bottom of each frame indicate relative elapsed time in units of ms. Line of conduction block and dotted arrow correspond to two main waves of spike activity illustrated in frame sequences below. The on-time of a spike burst at a single electrode is indicated by a bright red pixel, set to progressively fade to white in 250 ms, in order to help visualize the propagation pattern. Square edge length represents 4 mm. Top row of frames (0–350 ms) shows a longitudinal wave of spike activity that propagated at 6.8 cm/s in the retrograde direction, self-terminating after covering a distance of 24 mm. Corresponding line of conduction block is indicated in electrograms 5–12, toward left. Bottom row of frames (1725–2075 ms) illustrates concentric-circumferentially propagating spike activity initiated on the edge of the electrode array adjacent to the mesenteric blood supply arcade (denoted by “M”) traveling around the entire electrode array (outer diameter of a intestinal segment) with a velocity of 18.7 cm/s. Dotted arrow overlaid on bottom 8 electrograms highlights this propagation pattern.

Discussion

Previous and Related Spike Detection Methods

The problem of small intestine spike burst detection is not new and has been approached previously by several other investigators [43, 36, 14, 21, 46]. However, our new system offers several key improvements and advantages over previous efforts. Almost all previous spike detection methods relied on hardware and/or digital band-pass filters, typically with a 20 Hz pass-band. However, Wang and Chen showed that band-pass filters cannot sufficiently discriminate the sharp downward deflection of SWs from spikes because they spectrally overlap to a significant degree [46]. Hence, SALPA is proposed here as a practical alternative, implemented with parameters optimized for application to small intestine recordings. The main advantage of SALPA over conventional high-pass filters is minimal/negligible phase-shift distortion in the spike waveforms to be isolated. SALPA was originally developed to suppress the electrical stimulation artifact in extracellular multi-channel array recordings from in vitro neural networks [45]. Our motivation for adapting SALPA for the purposes of GI applications was based on the observation that detecting small intestine spike bursts in the presence of SWs and other low frequency components presents a similar situation to neural spikes riding on relatively slowly time-varying stimulus artifacts.

Wang and Chen [46] used an ICA-based blind-source separation approach to separate spikes from SWs. Their approach helped solve the problem inherent with band-pass filters. However, this blind-source method alone could not discern sources representing spikes versus non-spikes. Thus, the end-user was tasked with manually determining which of the separated sources represented actual spikes. Previously, Ponti et al used a linear discriminant with 6 input features—all relating to the amplitude, rise and fall time of the electrode signal and its first time derivative— to automate detection of individual GI spike waveforms within bursts [36]. However, their method appeared to not be fully automated, requiring the laborious manual identification of candidate spike bursts waveforms. By contrast, our system is fully automated by virtue of using NEO to detect candidates, which are then classified by the SVM.

We utilized a SVM with (up to) five input features. SVM classification performance was significantly better when using multiple input features, demonstrating that our new method is more accurate than previously described methods which used only a single feature for spike detection. One such input feature utilized here was the integrated energy, which is related to Groh's spike detection method utilizing the averaged second derivative [14, 28], as well as Summer's method utilizing the “average power” [43]. Using all five SVM input features yielded a 10.2% increase in overall performance compared to inputting the integrated energy feature alone (A_roc = 0.90 ± 0.01 vs. 0.82 ± 0.03). It is also worth noting that, during development of the algorithm, we considered using a continuous wavelet transform (CWT) for estimating the energy content, e.g., as described in [29]. However, we ultimately decided against a CWT approach because we empirically found it to difficult to choose an appropriate mother wavelet and proper set of scales (“frequencies”) due to natural variations in GI spike waveforms.

We found that the spike duration feature, ΔT, was among the most important features for SVM classification. This finding may be explained by the observation that cardiac and motion artifacts with rise and fall times similar to that of a single spike may still contaminate a data set after preprocessing with SALPA and SG filtering. Thus, the SVM was trained to recognize these very short duration events as non-spikes. Other investigators have applied a boxcar smoothing procedure to reduce such short-duration artifacts [21]. However, this is a not an attractive approach because shorter-duration spike bursts may also smoothed away leading to an increase in false negatives (decreased sensitivity).

We note that Kim and Kim [19] used the NEO in addition to an artificial neural network (ANN) classifier for spike detection from in vivo extracellular neural recordings. Our adaptation of NEO for GI spike detection was inspired, in part, by their work in a separate field. Importantly, our implementation of a machine classifier diverged from the technique described in [19]. Whereas Kim and Kim directly input a window of data points from a candidate spike (detected by NEO) into the ANN, we computed five features based on the candidate spike waveform as input for the SVM. During construction of our algorithm, we also directly tested using a windowed time series x(n) as input to the SVM, but ultimately found that approach to be unsuccessful, due to the high variability of GI spike waveforms. In addition, during algorithm development, we determined that a fixed-length window for computing features provided slightly better overall performance (+7.8% Sens; -2.4% PPV) compared to a variable length window whose size was determined by the candidate waveform's on and off times.

While the performance of our automated system has been found in practice to achieve highly satisfactory results, generalizing well across all experimental preparations carried out in two separate laboratories, no automated system is perfect and some potential limitations deserve further remarks: 1) Investigators have employed electrodes of different sizes (e.g., 0.13 mm [4]) than the ones used for our validation experiments. The diameter effects the tissue-electrode impedance and determines the area of tissue in electrical contact over which the recorded potential is averaged, thus it is expected that spike burst waveforms recorded by others may vary in morphology, to a modest degree, from those used in our validation study. Because the SVM classifier was trained on a wide-ranging spike burst morphologies utilizing data sets from two separate preparations, it is expected that our automated method will be robust to electrode-specific variations in similar experimental preparations; 2) Our mapping results and previous work by Lammers et al [24] indicated that temporal accuracy at the ≈10 ms level may be required to properly map propagation of spike activity with high resolution electrode arrays. Given that our algorithm relies on a statistical measure to define the on and off times, and in light of variety of spike burst waveforms noted, millisecond accuracy cannot always be ensured. However, based on the demonstration study above (Figures 6 and 7), as well as detailed observations of the on and off time marks, it appears that our system can in fact mark spike bursts with sufficient temporal accuracy to properly track the spatial propagation patterns; and 3) Data sets with large cardiac artifacts can interfere with the clustering process such that the duration of candidate spikes is inaccurately measured, ultimately leading to false negatives. Further research may investigate techniques for specifically eliminating large cardiac artifact sets as a pre-processing step.

Validity of Findings from Total and Progressive Ischemia Demonstration Studies

Our results for spike rates versus time following induction of total ischemia are in accord with several previous studies. Meissner, Bowes, Sarna [26] noted a ≈210 s period of elevated spike activity immediately after occluding the canine superior mesenteric artery, followed by a long-lived period of diminished activity. The elevated spike activity we observed in a porcine subject lasted about twice that duration. Cabot and Kohatsu [4] previously observed a similar increase in spike rate, with a 60 s time lag after inducing ischemia in mongrel dogs. Similarly, we noted a delay in the onset of the spike rate increase, albeit with a somewhat longer lag time. The delay-time discrepancy could possibly be attributed to having used different animal models as well as differences in locations along the small intestine at which electrical activity was recorded (proximal vs. mid-jejunum).

The results presented herein for progressive ischemia are also in accord with those of previous investigators. At 75% ischemia (induced by hypoxia as opposed to arterial ligation), Chou noted a transient increase in spike activity and contractions lasting about 1–5 minutes [5]. Thereafter, the contractions and spike activity progressively diminished for a period 1–15 minutes, terminating in complete disappearance of spikes. By contrast, we did not observe a sustained disappearance of spike activity until inducing 100% ischemia, however, the overall patterns of spike behavior were similar.

On the whole, the spike rate changes induced by ischemia observed during our experiments were consonant with all previous reports. It is worth noting that the majority of the surface of the small intestine does not show spikes in the fasted state, but this can change on stimulation [22]. The increase in spike activity after the onset of ischemia is likely to be neurally mediated, because the response in intestine is abolished by tetrodotoxin [5]. It is also worth mentioning that contractions can cause artifacts in electrical recordings, however these can be distinguished from spike activity by their morphology [31, 2]. Due to the disparate time scales of mechanical vs. electrical events [3, 15], discrimination is automatically aided by the filtering methods applied herein.

We mapped the spatiotemporal propagation of spike burst activity in the pathological condition of ischemia, thus definitive comparisons to individual spike patch or spike burst activity mapped under normal physiological conditions cannot be drawn. Nonetheless, the results using our automated method do show some concordance with previous studies. Lammers et al have previously mapped spike bursts associated with peristaltic propagation using in vitro feline small intestine [25]. Such activity was observed to conduct along complete tubal segments, sometimes propagating for a relatively long distances (≥ 40 mm) in the oral (retrograde) direction. We also observed a similar behavior, as illustrated in Figure 6. Spontaneous conduction block of both spike burst [25] and individual spike (“patch”) [24] activity has been previously observed using in vitro feline and canine preparations. Similarly, in our in vivo ischemic porcine model, in some instances we observed broad lines of spontaneous conduction block around the circumference of the preparation (Figure 7, top 8 frames), while in another we saw concentric-circumferential activity propagating in a restricted region of intestine (Figure 7, bottom 8 frames). This latter wave of activity bears some resemblance to elliptical propagation initiated at discrete sites observed in [25].

We estimated velocities for spike burst propagation to be 6.8–8 cm/s for longitudinal activity and 18.7 cm/s for circumferential activity, values which are in the range reported by previous studies. Spike burst activity was observed to propagate at 1.0 cm/s in mongrel cat in vitro [25]. Using a videography technique, Hennig et al saw peristaltic contractions propagating at 3.0 cm/s in guinea pig in vitro [15]; multiple action potentials occurring in quick succession have previously been observed to coincide with such contractile activity [3, 13], which would suggest that spike bursts also propagated at 3.0 cm/s. In an in vivo canine model, Lammers et al observed individual spike activity propagating anisotropically at about 10 cm/s longitudinally and 20 cm/s circumferentially [24], values which correspond reasonably well with those we observed for spike bursts. Noted differences could possibly be attributed to species-specific variations, experimental preparations (including in vitro vs. in vivo models), fundamental changes in spike burst conduction due to ischemic conditions, or a combination thereof.

Whether and how spike burst propagation patterns are altered due to ischemia remains to be fully investigated. Additionally, further study is needed to resolve the relationship of spike burst and SW propagation patterns in disease states. The spike burst detection algorithm significantly accelerates data analysis for invasive, high-resolution mapping studies, which may help elucidate the fundamental patho-physiology and electrical hallmarks of disease states. Insights gained from such experiments could inform efforts to develop non-invasive SQUID magnetometer [41] and cutaneous electrode [48] techniques for clinical diagnosis of mesenteric ischemia, which continues to have high rates of misdiagnosis and mortality [38].

In our recordings from ischemic pig intestine analyzed thus far, spike bursts constituted a principal type of electrical event, hence the motivation to detect them in their entirety. Since the intraburst number and timing (rate) of spikes may be associated with the further physiologically relevant information, such as contractile force [17, 44], it would be desirable to augment the method presented herein to detect individual intraburst spike times. Such an extension should be directly feasible and will be the subject of future work.

In conclusion, we have presented a substantially improved fully automated GI spike burst detection algorithm. Its performance has been quantified to achieve highly satisfactory accuracy for application to investigate fundamental research questions, and we demonstrated its utility in a study of the ischemic intestine. To make this spike detection tool available to other investigators, the algorithm has also been integrated into the Gastrointestinal Electrical Mapping Suite (GEMS) software package [47] , and is distributed freely for academic use upon request.

Supplementary Material

Suppl Material 1

Supplemental Figure 1: SVM overall accuracy metric A_roc across all 31 possible parameter combinations. The mean ± s.d. is shown for 10-fold leave-one-out validation. The text annotating line segments at bottom denotes the number of features used for SVM training, also grouped by color. For 5 features, 2 results are reported; one for a radial-basis function kernel and the other for a linear kernel. All other results shown are for an SVM implemented with radial basis functions. A substantial increase in performance is noted, in general, going from 1 to 2 features. Additional gains are relatively incremental. Best performance is achieved using all 5 input features with a radial-basis kernel. The asterisk denotes a statistically significant difference between the optimal outcome for SVM training with 1 feature versus all 5 features with radial basis function (Student's t-test; p < 0.0001).

Supplemental Figure 2. High resolution spatial mapping of spike activity. Following induction of full ischemia, a retrograde-longitudinal wave of activity propagates in the retrograde direction. The electrode array was 32 × 128 mm. Scale bar at upper left indicates 15 mm. Labels P and D atop first frame indicate proximal and distal directions, respectively. During the experiment, the electrode array, shown in planar projection here, was wrapped around the circumference of the small intestine such that the top and bottom borders of each frame were nearly adjacent, and positioned on either side of the mesenteric blood supply arcade. Relative times of each snapshot in units of ms are noted at top-right in each successive frame. The “on” time of a spike burst at a single electrode is indicated by a bright red pixel. Pixels are set to progressively fade to white in 250 ms, in order to help visualize the propagation pattern.

Supplemental Figure 3: Isochrone activation map of circumferential spike propagation, with contours drawn at 50 ms intervals; formatting otherwise is the same as described in Figure 6. The circumferential propagation illustrated here provides an alternate and complementary means of visualizing the same activity shown in Figure 7, bottom 8 frames. The circumferential activity originating toward top-left (adjacent to mesenteric vasculature) spread in a somewhat concentric manner with a velocity of about 21 cm/s. The propagation patch width is self-limiting to a intestinal segment about 40 mm in length.