How Boxers Decide to Punch a Target: Emergent Behaviour in Nonlinear Dynamical Movement Systems

Abstract

Previous research has shown how dynamical systems theory provides a relevant framework for investigating decision-making behavior in sport. The aim of this study was to adopt concepts and tools from nonlinear dynamics in examining effects of boxer-target distance and perceived punching efficiency on emergent decision-making during a typical practice task in boxing. Results revealed the existence of critical values of scaled distances between boxers and targets for first time appearance and disappearance of a diverse range of boxing actions including jabs, hooks and uppercuts. Reasons for the diversity of actions were twofold: i) abrupt (qualitative) changes in the number of the possible punches, i.e. motor solutions to the hitting task; and ii), fine modification of the probabilities of selecting specific striking patterns. Boxers were able to exploit the emerging perception of strikeability, leading to a changing diversity of selected actions and a cascade of abrupt changes in the perceptual-motor work space of the task. Perceived efficiency of a punching action by the participants also changed as a function of the scaled distance to a target and was correlated with the probability of occurrence of specific boxing actions. Accordingly, scaled distance-dependent perceived efficiency seems an important perceptual constraint in the training task of punching a heavy bag in boxers.

Key Points.

• During the practicing with static (i.e. non moving) heavy bags novice boxers' perceptual-action system is sensitive to the scaled distance and efficiency informational constraints. These interdependent constraints shape the action behaviour of the novice boxers;

• During heavy bag practice novice boxers are subject to a kind of discovery learning by exploring the efficiency of their motor repertoire when changing the performer - target distances;

• The region close to D = 0.6 maximizes the flexibility of switching among different types of punching actions and is optimal for practicing the temporal couplings between all types of boxing actions;

• Strategic positioning among boxers spontaneously emerges under the pressure of the key constraints revealed in these research. Applying practice strategy that emphasizes learning in which trainees would themselves explore, discover and thus adapt to the information - movement demands of diverse sparring situations is thus of great importance.

Introduction

How do boxers choose their actions? What are the perceptual information sources used for coordinating punches at opponents? In combat sports such as boxing, studying decision- making behavior could inform sport scientists and coaches how to structure practice sessions so that athletes learn to perceive information and select appropriate actions as performance contexts change. Studying decision-making processes in motor behavior permits insights into the coordination of actions with respect to the environment i.e. investigating how perceptual information from the environment (e.g., information on target location and movement) constrains actions. Research from the theoretical perspective of dynamical systems theory is revealing that sports are providing rich movement models for the study of the dynamics of adaptive human movement behaviour, characterized as performer-performer and performer-environment interactions (Davids et al., 2005; McGarry et al., 2002).

The main characteristic of nonlinear dynamical systems theory is that it emphasizes the study of biological movement systems under the constraints of their natural environments, focusing on the parametric control of such systems. In nonlinear dynamical systems modeling, control parameters are defined as informational variables that can guide a system between different states of organization and order parameters are defined as collective variables that describe the organization of such systems. Control parameters are mathematical representations of the constraints that act on biological movement systems. These can be nonspecific (i.e. constraints that have a distinct informational nature from movement characteristics) and specific (i.e. constraints which have the same informational nature as movement characteristics). For example, perceptual information is a nonspecific source of information which can be harnessed to regulate the directional or timing characteristics of a movement because it does not specifically inform the dynamical characteristics of movement systems. On the other hand, intentions are specific constraints that can impose particular (intended) directional or timing information on a desired movement pattern. An important example of specific constraints on a biological movement is task constraints.

In nonlinear dynamical systems, unlike anything in the linear characterization of the movement systems, a minute change in the value of a control parameter can bring about a drastic (qualitative) change in a movement system's dynamics. For example, such an apparently small change in a control parameter can lead to the emergence of a new type of system organization such as a new type of punch in boxing or a new phasing mode among the limbs during walking which was not present before (see Kelso, 1995). This event is called a bifurcation or a phase transition in the systems' dynamics and is related to the spontaneous (i.e. not prescribed by some agent or system controller) self-organization of the motor system degrees of freedom. This spontaneous change is a result of the loss of the stability of a previous state of organization (e.g. an original action) and is not a consequence of some specific agent prescribing the change. Therefore, it is of particular interest in the movement and sport sciences to uncover the influential constraints (i.e. the key control parameters of the movement system), especially those with high ecological validity, which play an essential role in bringing about such spontaneous changes and determining the context in which athletes assemble goal directed movements. Perceptual constraints (i.e. key perceptual control parameters of the movement system) with the highest ecological validity are the directly perceivable affordances (see Vicente, 2003). These variables refer to the objective properties of the environment in which an organism (for example a boxer) acts in relation to his or her personal capabilities. They directly (not inferentially) specify to the organism what the environment affords him or her to do. Due to their dispositional nature the affordances take such names as reachability, climbability, pass - through - ability etc. For these reasons, specific boxing strikeability of the target (i.e. the heavy bag or an opponent) is a possible affordance candidate).

So, control parameters are key variables which act as information sources to harness the movement system dynamics. Of equal importance is the discovery of so called 'order parameters' which are collective variables which capture the macroscopic order of a movement system manifested as a characteristic action pattern (e.g., the relative phasing of two limbs). Such a dynamical systems modeling of boxer-opponent interactions requires that control parameters and order parameters are identified.

In an analysis of boxing movements inspired by dynamical systems theory, punching movements can be taken to represent classes of short lived, interceptive action patterns formed amongst upper limb motor system degrees of freedom. These actions are assembled or annihilated depending on emerging performance constraints on individual boxers considered as nonlinear dynamic movement systems (Davids et al., 2002). In boxing, the temporarily stable (meta-stable) actions represent time-varying intra- and inter- limb coordination states in movement systems with respect to more or less dynamic targets such as opponents, speed bags, hand pads and heavy bags (Turvey, 1990).

In this paper, we present data showing how the selection of punching actions in combat sports such as boxing can be considered as phenomenon which emerges as the critical environmental constraints gradually change. Theoretical modeling from the perspective of nonlinear dynamics has already disclosed the emergent characteristic of decision-making in performer-performer interactions (i.e. 1 v 1 sub-phases) in a range of different sports including sailing, basketball and rugby (Araújo et al., 2004; 2005; Passos et al., 2006). The study described in this article extends such analyses to the task constraints of combat sports. In many sports, a rule- governed system formed by a performer-performer dyad may be conceptualized as a dynamical system exemplifying interpersonal coordination and linked by visual (and other) informational fields (e.g. , Araújo et al., 2004). Araújo et al. (2004) have argued that, as with any other dynamical system, the emergent behaviour of performer-performer dyads (e.g., attackers and defenders) can be characterized by control parameter and order parameter relations.

This conceptual model of human interpersonal activity implies that a boxer and opponent may form a temporarily stable interactive dynamic system, since any striking movement of the boxer may be counterbalanced by defensive movements of an opponent. Anecdotal evidence from observing performer- performer interactions in boxing matches reveals that boxers do not activate striking patterns in all situations with equal probability. As in the 1 v 1 sub-phases of team ball sports, it seems likely, therefore, that diverse striking patterns are emergent, being conceptualized as a dynamic 'perceptual-motor landscape' assembled by boxers as they attempt to satisfy a range of interacting constraints arising from a specific performer-target system. In the perceptual-motor landscape formed by each boxer, actions differ in probability of emergence and stability, depending on the constraints acting on each specific performer-target system (Davids et al., 2003). For example, in boxing, observations suggest that jabs usually emerge at specific locations and distances from targets which differ from uppercuts and hooks. More formal dynamical systems modeling is needed to verify this observation. Analysis of the coaching literature in boxing (e.g., Walker, 2003) reveals that a candidate control parameter for an attacker-target system could be the intrinsic metric of the interpersonal distance between the attacker and a target such as an opponent or punch bag. This system metric is 'action-scaled' (Konczak, 1990; Konczak et al., 1992), because the dimensions formed by each individual performer-target dyad will differ. The use of an intrinsic metric signifies that the value of the control parameter might change depending on the action- scaled features (e.g., limb sizes) of specific performer-target systems. Furthermore, because of the configuration of motor system degrees of freedom into different boxing actions during performance, it is tempting to assume that each punching action has its own reachability domain, dependent on unique physical constraints of each individual, e.g., effective arm length, and the objective distance to a target. Thus, by intentionally changing the relative distance to a target, performers can influence the emergence of certain types of punches and consequently the diversity of their action space. Hence, it might be useful to examine whether adaptive behaviour of boxers might emerge as a consequence of the context, potentially defined by a finite set of task, environmental and personal constraints, varying on different time scales.

Informational Constraints in Boxing: What sources of information do boxers use to coordinate their actions towards a target?

In combat sports learners need to become attuned to relevant properties of the environment that produce unique patterns of information flows (e.g., optical information from a punch bag or opponent's body). Such flow patterns can act as invariant information sources to constrain decision-making on the type of attack to be made (e.g., upper cut or jab). During training boxers learn to couple their movements to these critical information sources when selecting appropriate punches. Because of the time constraints on action, boxers need to narrow down the minimal information needed to select a stroke and to regulate their movements from the enormous amount available in the performance environment. In the sports sciences' literature there have been no previous attempts to study the perceptual variables that might act as informational constraints as boxers punch targets during practice. However, previous motor development and motor control research on interceptive actions point to some possible candidate variables. One candidate variable that contains relevant information for generating specific boxing actions could be based on information used to perceive a target's 'reachability'. Reachability has been shown to be perceived very early in infant development (Rochat, 1995; Rochat and Goubet, 1995), acting as a constraint on the tendency to reach in 4-5-month-old infants. Reachability depends on the distance to a target and on the relative propensity of an individual to lean forward (Yonas and Hartman, 1993). Theoretically, the capacity to perceive reachability from the information provided by a target is developed during infancy and could underpin decision-making in boxing since opponents cannot be contacted with a fist if he/she is not reachable. In other words, the decision to punch or not to punch could depend strongly on a 'perception of reachability' affordance (see Ulrich et al., 1990).

From this theoretical perspective, there were two main aims of the present study. First, we sought to identify some of the key informational constraints from the whole set that boxers might use to generate punching actions in a tactical manner. During training sessions, boxers explore and discover the most adaptive relations between the informational sources and their actions. Coaching literature from the martial arts in general suggests that one of the most important constraints regulating the punches of fighters is the perception of scaled distance to the opponent (e.g., Walker, 2003). From this text it is clear that expert pedagogists advise that most, but not all, punches should be completed from a distance that affords full extension of the hitting arm. In boxing, for example, optimizing the punching efficiency of jabs requires full arm extension, whereas hooks and uppercuts depend on coordinated phasing of elbow flexion and extension. Overextension of the arm should be avoided because it decreases the power of the punch and could cause over-balancing, providing an opportunity for an opponent's counter-attack (Walker, 2003). This reasoning led us to surmise that distance-to-target is a significant informational constraint on the decision making of fighters, and to clarify this issue we examined whether there was a relationship between specific distances and the type of punches selected by boxers.

Second, we believed that this type of informational constraint might interact with other constraints used by boxers to shape a kind of 'perceptual-motor landscape' of emergent actions based on their perceived efficiency of punches. We expected that the relations between intentionality and distance to target information would mould this perceptual-motor landscape in boxers as they selected the most efficient punches at specific locations. In this study we manipulated performer-target distances to understand effects of perceived striking efficiency in boxing, allowing us to plot the dynamic probability landscape of striking patterns that might emerge in boxers. During the task of punching a heavy bag, six classical types of boxing action patterns were under consideration: right jab, left jab, right hook, left hook, right uppercut and left uppercut. Our hypothesis was that the initial activation of a punching action, its probability of occurrence and its disappearance would all exhibit dependence on the distance to the target and on perceived striking efficiency by boxers.

Methods

To achieve these empirical aims, 8 novice boxers, who had just completed a two-semester course of elementary boxing techniques, aged 21-23 years, were required to select appropriate punches to a black leather hanging heavy bag fixed to the wall with its bottom 95 cm from the floor. Two boxers reported weak left handedness and all other participants reported being right handed. Participants were not given prescriptive instructions on punches to be selected but were required to maximize the efficiency and the diversity of their punching actions. Figure 1A shows how a distance of one meter from the target was calibrated in 10 equal segments of 10 cms so that each performer could perform 60 punches at each distance to ensure efficient collision magnitude.

Figure 1 A-C. A).

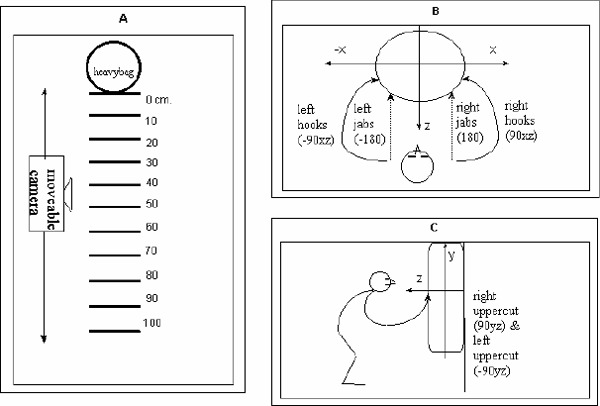
The apparatus for the study of adaptive movements of boxers viewed from above. Distance from the target (heavy bag) was divided into 10 segments of 10cm each. Boxers started at the largest distance which afforded them to apply a punch under the task constraints outlined in the text; B) A schematic representation of boxers'punching coordination patterns seen from above. The boxing movements are defined with respect to their dominant projections on the axes. Jabs move predominantly along the z (sagital) axis, i.e. the central visual line, in the opposite direction (±180 deg). Hooks predominantly move along the horizontal (x) and sagital (z) axes and their projections on these axes create a relative angle of ±90_xz deg.; C) Uppercuts predominantly move along the vertical (y) and sagittal (z) axes and their projections on these axes create a relative angle of ±90_yz deg.

The boxers also complied with a number of other instructional constraints including the requirement to perform sequences of strikes in a parallel stance with their toes aligned with different distance markers from the target. Before starting the activity, performers were stringently reminded not to overbalance which is a prerequisite for a successful punch (Walker, 2003). The choice of distance between the lower limbs in the parallel stance was left to the boxers. Also, there were no specific instructions on the movements of performers' feet except to maintain a constant distance from the target. At distance D = 0 (see Figure 1A), participants had to lean into the target (heavy bag) making the distance between their body and the target equal to 0. Participants were free to apply uppercut punches to any location on the target, including the bottom, middle or upper part of the heavy bag, depending on their perception of strike efficiency. Before starting the activity boxers were told to pay particular attention to the efficiency of the strikes produced and each boxer was questioned about their perceptions of punching efficiency for each shot selected after they had finished each sequence of activity. Perceived efficiency was scaled by participants on a 6-point (0-5) continuous scale with 0 reflecting absence of a stroke and 5 signifying a maximally efficient stroke. Modes of boxer-target co-ordination patterns were operationally defined as directions of upper limb movements with respect to the central visual line connecting the participant and the target facing him. This procedure allowed a notational strategy to be used in classifying shot frequency as a measure of decision-making. For example, right jabs have a dominant projection parallel to the central visual axis (z axis) and were numerically classified as 180 degrees. Left jabs, providing a mirror image of right jabs, were classified as -180 deg (see Figure 1B). Notation of hooks was considered to have projections along the sagittal (z) and horizontal (x) axes, with right hooks being classified as 90_xz deg. and their mirror image left hooks as -90_xz deg. (see also Figure 1C). Furthermore, upper cuts were recorded as projections on the sagittal (z) axis, with right and left uppercuts varying along the vertical (y) axis at 90_yz deg. and -90_yz deg. respectively (see Figure 1C).

In our analysis the following measures were recorded:

(i) scaled boxer - target distances D determined as a ratio between the physical distance of the participants from the target (X) and performers' arm length (L) i.e. D = X/L. Actually, the reachability condition can be formally expressed as R = X/( L_eff + L_lean) ≤ 1, or as a scaled distance (ratio) between the objective physical target - participant distance X and the sum of the effective length of the arm (L_eff) and the lean length (L_lean). The effective length of the arm depends on the degree of flexion in the elbow joint. The larger the angle of flexion (as in hooks and uppercuts with respect to the jab strokes) the smaller is effective arm length. L_lean = X - X₁, where X₁ is the distance measured from the target to the projection of the participant's active arm acromion process on the floor. If the forward lean leads the projection of the acromion to pass over the X position, which is a usual consequence of a forward lean, then a positive value of effective arm length will result. During participants' activity, due to the non-rigid instructional constraints L_eff, L_lean, and consequently reachability, R values were strongly fluctuating quantities and thus less suitable as stable distance measures.

(ii) the absolute probabilities of occurrence of action patterns i.e. relative frequencies p(k(D)) = k(D)/n, where k(D) is the number of occurrences of a certain type of punch at each scaled boxer - target distance (D) and n is the constant length of the sequence (n = 60); (iii) the mean group probabilities P_i of each of the three types of punches (jabs, hooks and uppercuts) at each scaled boxer - target distance (D): P_i(D) = 1 - P_j (D) + P_k(D), where P_i(D), P_j (D) and P_k (D) are the mean group probabilities of the three types of punches; (iv) mean group perceived punching efficiencies for each type of boxing shot (jab, hook and upper cut), at each scaled boxer - target distance: (E₁,…,E₃ (D)); (v) unpredictability of punching activity by the participants was assessed by the Shannon entropy measure: H(p(D)) = -Σ_i P_i(D)ln P_i(D); for (i =1,…,j; in our case j = 6, equal to the number of punching actions), i.e. as average information over all outcomes in the sequence; (vi) diversity was assessed by the symmetry measure S(p(D)) = 1 - (1/N) Σ_i |∆p(D)|_i, for (i = 1,…,N), where N is the number of combinations of class 2 for a set of 6 elements (6 types of strokes), and | ∆p(D)|_i is the absolute value of the differences between the probabilities of occurrence of each action pattern. In this study, for 6 possible types of strokes, there were N = 15 probability differences to calculate for each sequence per participant. (vii) efficiency ratio was calculated as E = Σ_i E_i (D) /Σ_i |∆E|_i (D), for (i = 1…N), where N is the number of general types of actions (jabs, hooks and uppercuts) and the number of differences between the perceived punching efficiencies, making N=3; E_i (D) are the scaled distance (D) dependent mean group perceived punching efficiencies and |∆E|_i(D) are the absolute values of the D dependent mean group perceived punching efficiency differences ( |∆E|₁ = |E_jabs - E_hooks|; |∆E|₂ = | E_jabs - E_uppercuts|; |∆E|₃ = | E_hooks - E_uppercuts |). E measure increases if the sum of the perceived efficiencies increases and the sum of the perceived efficiency differences decreases. The group mean probability differences for the action modes were calculated as:

∆P₁(D) = P_jabs(D) - P_hooks(D); ∆P₂(D) = P_jabs(D) - P_uppercuts(D); ∆P₃(D) = P_hooks(D) - P_uppercuts(D).

Results and Discussion

Distance affordances

From the data several characteristics concerning decision-making behaviour in boxing are readily apparent. In particular, it was noted that specific boxing action patterns emerged as affordances of the individually-scaled distance to the target. We observed significant differences between the bounded regions of scaled distances for first time appearances and disappearances of specific boxing action patterns in the boxers. A one-way repeated measures analysis of variance revealed a significant distance main effect for the initial emergence scaled distances of the boxing action modes F(5,35) = 44.58; p < 0.00001. Kolmogorov-Smirnov D statistics of the critical scaled distance distributions for the first time activation of the whole set of the boxing action modes were not significant (p > 0.20). In similar vein Lilliefors probabilities (p > 0.20) as well as Shapiro -Wilk W statistics (all larger than p < 0.62) showed no significant departure from normal distribution.

In almost all comparisons of distances we obtained significant differences (see Table 1) except for comparisons between the initial emergence of the right and left jabs (180, -180), right and left hooks (90_xz, -90_xz) and left hooks and right uppercuts (-90_xz, 90_yz).

Table 1.

Results of the post - hoc Tukey comparison tests for the critical scaled boxer - target distances (D_C) effects on the first time activations of the punching patterns. In the grid rows are the critical mean values of the first time use of each of the punching patterns.

	180	-180	90xz	-90xz	90 yz	-90 yz
DC Means	1.15	1.15	.91	.89	.80	.65
180	.000	.000	-.24	-.26	-.35	-.50
-180	1.000	.000	-.24	-.26	-.35	-.50
90xz	.0000	.0000	.000	-.018	-.12	-.26
-90xz	.0002	.0002	.3506	.000	-.10	-.24
90 yz	.0000	.0000	.0491	.0948	.000	-.15
-90 yz	.0000	.0000	.0021	.0035	.0338	.000

Under the main diagonal are given the p-levels. On and above the main diagonal are given the differences between the scaled distances of the first time use of each of the punching patterns. Significant p-levels and differences are underlined.

Even the more stringent criteria such as Bonferroni corrections for alpha levels preserved these distance effects. In similar vein, boxer - target distance dependency was revealed by a repeated - measures analysis of variance on the distances at which disappearance of previously formed action patterns occurred F(3,21) = 2467.93; p < 0.00001). Post - hoc tests yielded significant scaled distance differences between the annihilation of the jab (180, -180) and uppercut (90_yz, -90_yz) punching activity (see Table 2). Kolmogorov-Smirnov D statistics of the critical scaled distance distributions for the annihilation of the jab action modes were not significant (p > 0.20). In similar vein Lilliefors probabilities (p > 0.20) as well as the Shapiro - Wilk W statistics (p < 0.72) showed no significant departure from normal distribution. The critical scaled distances of the disappearance of uppercut punches possessed delta distributions. However, this violation of normality assumption did not affect the conclusions since the differences between the jab annihilation critical distance means (D_C = 0.45) and the uppercut annihilation critical distances (D_C = 0) are much larger than their internal distribution variability. See Figure 2A for illustration.

Table 2.

Results of the post - hoc Tukey comparison tests for the critical scaled boxer - target distances (D_C) effects on the annihilation of punching patterns. In the grid row are the critical mean values of the annihilations of the punching patterns.

	180	-180	90 yz	-90 yz
DC Means	0.45	0.45	0.0001	0.0001
180	.00	.00	-.45	-.45
-180	1.0000	.00	-.45	-.45
90 yz	.00001	.00001	.00	--
-90yz	.00001	.00001	1.0000	.00

Under the main diagonal are the p-levels. On and above the main diagonal are given the differences between the boxer - target relative distances of annihilation of punching patterns. Significant p-levels and differences are underlined.

Figure 2A-D. A).

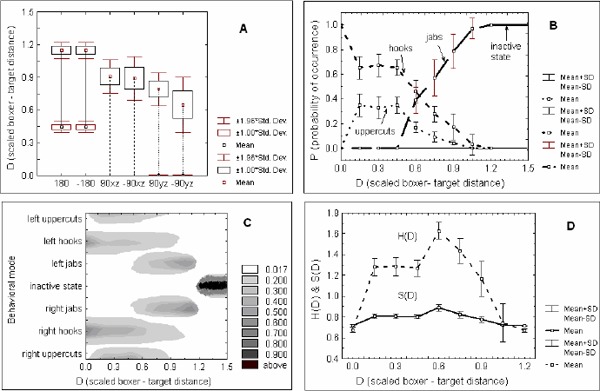
Bounded regions of the scaled boxer - target distances (D) of the first time activations and annihilations of the boxing action patterns are given by box and whisker plots. The vertical solid lines correspond to the activity region of the right jabs (180) and left jabs (-180); dashed lines to the activity region of the right hooks (90_xz) and left hooks (-90_xz) and the longer dashed lines to the activity region of the right uppercuts (90_yz) and left uppercuts (-90_yz). It can be observed that the first time activations (given by the upper group of box and whisker plots) and the dissolutions of the action modes (given by the lower group of box and whisker plots) arise for different values of the scaled boxer - target distances; B) Probabilities of occurrence of the boxing action patterns as a function of the scaled boxer - target distance. The polarized structure of the probability of occurrence of the punching modes is readily observable; C) Branching (bifurcations) of the movement solutions to the punching training task. Legend on the right corresponds to the probability of occurrence of the behavioral modes. D) The change of the entropy H and symmetry S measures as a function of the scaled boxer - target distance D. For both measures the maximum is around D = 0.6 pointing to the region of maximal selection meta - stability (i.e flexibility of switching) between the boxing action modes.

Even the more stringent criteria such as Bonferroni corrections for alpha levels preserved these distance effects. In similar vein, boxer - target distance dependency was revealed by a repeated -measures analysis of variance on the distances at which disappearance of previously formed action patterns occurred F(3,21) = 2467.93; p < 0.00001). Post - hoc tests yielded significant scaled distance differences between the annihilation of the jab (180, -180) and uppercut (90_yz, -90_yz) punching activity (see Table 2). Kolmogorov-Smirnov D statistics of the critical scaled distance distributions for the annihilation of the jab action modes were not significant (p > 0.20). In similar vein Lilliefors probabilities (p > 0.20) as well as the Shapiro - Wilk W statistics (p < 0.72) showed no significant departure from normal distribution. The critical scaled distances of the disappearance of uppercut punches possessed delta distributions. However, this violation of normality assumption did not affect the conclusions since the differences between the jab annihilation critical distance means (D_C = 0.45) and the uppercut annihilation critical distances (D_C = 0) are much larger than their internal distribution variability. See Figure 2A for illustration.

These results corroborated our expectations that different action patterns would disappear at different scaled boxer - target distance bounded areas.

Overall, boxers revealed the following behavior: At scaled distances D > 1.2 the only observed state for the performers was the guard (i.e. the quiescent) state (0 deg.). At scaled distances of D around 1.2 the previously quiescent jab modes of action (180 deg. and -180 deg.) emerged. We observed that, in all performers, right and left jab action modes emerged for the same individual values of D (see Figure 2A and C).

The obtained Pearson product - moment correlation coefficient r = 1.00 between the right and left jab initial action emergence corroborated this finding. For values around D = 0.9 the hooks (90_xz deg. and -90_xz deg.) action modes emerged. In only one out of eight performers the hook patterns emerged at different values of the scaled distance D. All of the other performers activated the hook patterns at the same individual D values. This finding was verified by the significant Pearson product - moment correlation coefficient between the right and left hook action modes r = 0.86; p = 0.006. Interestingly, uppercut action patterns did not show this kind of relationship. Right uppercut action modes emerged around greater D values (D = 0.8) than the left uppercuts (D = 0.65). The Pearson product - moment correlation coefficient between the right and left uppercut first time emergence D values was r = - 0.09; p = 0.826. This result signified that the initial emergence of uppercuts was the least coupled of events to scaled distance information. Taking into account that left and right jabs as well as left and right hooks emerged for the first time at the same individual scaled distances D, which was not the case for the left and right uppercuts, it can be assumed that scaled distances at which left and right uppercuts emerged for the first time might reveal the specific boxing handedness of the performers.

Generally, the full set of boxing actions was active in the region 0.65 < D <0. 45.

At the scaled distance D = 0.45 a spontaneous disappearance of the jab action patterns occurred. The Pearson product - moment correlation coefficient between the right and left jabs r = 1.00 confirmed that this disappearance occurred for the same individual D values (see Figure 2 A and C). Another abrupt disappearance, this time for uppercuts, arose at D = 0. At this scaled distance only the hooks remained active. Overall, these results showed that the initial emergence of the jab and hook punching modes of action showed a strong tendency to be related to scaled distance from the target, whereas uppercuts were much more variable in this respect.

These data suggested that decisions emerged as boxers picked up and exploited information about specific types of actions afforded at specific distances scaled for each individual. Significant differences between the mean group relative distances of the initial activation of different action patterns depended on the interaction between environmental constraints (absolute distance from the target) and the structural anatomical constraints of each individual boxer (effective length of upper limbs). The initiation of jab punches enabled the use of full arm length, making the effective limb length equal to its real length in extension, whereas hooks and uppercuts, depending on the degree of flexion in the elbow joint, always had a shorter effective length at the moment of collision with the target. Consequently different critical relative distances for the emergence of different action patterns were identified in the experiment. In other words, changes to the perceived context led the motor system of each boxer into and out of different functional coordination states. This feature of performance is depicted in Figure 2B where a clear polarized structure of bounded regions in the perceptual-motor landscape of the boxers is visible as a function of the scaled distance to target. At greater distances jabs were much more frequent, and hooks and upper cuts at shorter distances. Thus, participants activated specific punches at distances that fitted the effective length of their arms, signifying that they exploited a kind of body-scaled distance information in constraining this action, as reported elsewhere in the motor behaviour literature (Konczak, 1990; Konczak et al., 1992).

The results support the expressed view that, in picking up affordances of target strikeability, information on perceived reachability to a target plays a crucial role. Hence, it could be tentatively assumed that the perceived strikeability by participants is merely a special case of this early acquired affordance reported in the motor development literature. However, our data revealed that reachability is not solely responsible for the observed decision-making behaviour of the boxers. First, at the point of jab annihilation the target was reachable, although at that very point jabs ceased to be active. Second, at the point of disengagement of uppercuts the target was also reachable, although uppercut actions were being annihilated at this point. These data imply that besides reachability, other performer and task constraints, perhaps specifically related to the intended intensity of collision between the fists and target, are considered by boxers for the target to be perceived as strikeable. From a constraints-led perspective, these data confirm that handstrike selection is an emergent phenomenon dependent on the continuing interaction of intentionality, perceptual information and body-scaled affordances for each individual boxer (see Newell, 1986; Davids et al., 2003).

Movement-information coupling

As reported in Table 3, the values of the partial correlation coefficients revealed strong positive relationships between the perceived efficiency of each type of punch (taken as an independent variable) and the associated probability of occurrence of a punch, treated as dependent variable. Also, strong inverse relationships between the perceived efficiency of hooks and the probability of occurrence of jabs and between the perceived efficiency of jabs and uppercuts and the probability of occurrence of hook punches were obtained.

Table 3.

Partial correlations between group mean scaled distance dependent perceived punching efficiencies E_i (D) and scaled distance dependent group mean probabilities of occurrence of the punching action patterns P_i(D); (i =|180| = jabs; i = |90|_xz = hooks ; i = |90|_yz = uppercuts.

	P|180|(D)	P|90|xz(D)	P|90|yz(D)
E|180| (D)	.97;p = .0004	-.96; p = .0007	-.34; p = .4559
E|90|xz (D)	-.96; p = .0007	.95; p = .0011	.13; p = .7808
E|90|yz (D)	.69; p = .0848	-.90; p = .0054	.97; p = .0005

Similarly, Table 4 shows the relations between the differences of the perceived efficiency of punches (taken as independent variables) and differences in the probability of occurrence of each type of action mode, treated as dependent variables. High positive relationships were obtained. These data showed that, as long as boxers perceived some type of actions as more efficient, they tended to use them more often than other modes of action.

Table 4.

Partial correlations between scaled distance dependent group mean efficiency differences ∆E_i (D) and the scaled distance dependent group mean probability differences ∆P_i(D) for the punching action patterns.

Efficiency Differences	Partial Correlation	Probability differences
∆E1(D)	.98; p = .0000	∆P1(D)
∆E2(D)	.99; p = .0000	∆P2(D)
∆E3(D)	.92; p = .0011	∆P3(D)

Significant partial correlations between the probabilities of occurrence of action patterns and perceptual judgments of their efficiency suggest that the dynamic perceptual-motor landscape formed by boxers during performance is particularly sensitive to the perception of punching efficiency. The positive and negative influences of perceived efficiencies exemplify how the distance-dependent reciprocal enhancements and suppressions of action patterns were shaping the perceptual-motor landscape of individual boxers (see Table 3 and 4). In other words, boxers were simultaneously exploring and modifying their distance-dependent perceptual-motor landscapes by increasing the probability of the most successful types of punches, i.e. those which afforded punching efficiencies of greater magnitude, while suppressing those with efficiencies perceived as less functional. This interpretation suggests that boxers do not perceive targets solely as strikeable or not, but these perceptions interact with intentions and cognitions to continuously regulate decisions about how a target can be most efficiently punched (which action pattern to activate more frequently at specific locations). These findings demonstrated how decision-making is an emergent phenomenon which can be considered context- and individual-dependent, as the interaction of cognitions, intentions and perceptions of individual boxers modifies the functional coupling between perceived efficiencies and actions. In this way, combat sports like boxing can be characterized as a continuous search for the essential relationship between performer, task and environmental constraints, leading to the discovery of the most efficient action patterns, manifest in distance-dependent changes of the action probability landscape.

Punching unpredictability, diversity and efficiency ratio dependencies

Pearson product - moment correlation coefficients between the scaled distance dependent unpredictability as measured by entropy (H), diversity as measured by symmetry (S) and efficiency ratio (E) are presented in Table 5.

Table 5.

Pearson product - moment correlation coefficients between the unpredictability (H), diversity (S) and efficiency ratio (E) of the boxing punching action patterns. A nonlinear regression (stretched exponential) fit between the entropy (unpredictability) and symmetry (diversity) measures with the efficiency ratio (E) reveals much higher relationships.

	H	S	E
H	1.000
S	.991 (p = .000)	1.000
E	.77 (p = .016)	.83 (p = .006)	1.000

These three measures showed significant positive relationships. Change of group mean punching unpredictability and diversity as a function of the performer - target scaled distance is presented in Figure 2D. In similar vein, the change of the group mean punching unpredictability and efficiency ratio is presented in Figure 3. It is readily visible that these three measures reached their maximal values for performer - target scaled distances around D = 0.6. In other words, for the distance region where the punching efficiency ratio becomes maximal, the unpredictability and the diversity of punching action modes become maximal as well. This relationship is probably connected to the following causes: The efficiency ratio measure E increases when the sum of perceived efficiencies of selected punches increases and their difference decreases. The obtained efficiency ratio scaled distance dependence shows that around D = 0.6 this ratio is maximal.

Figure 3.

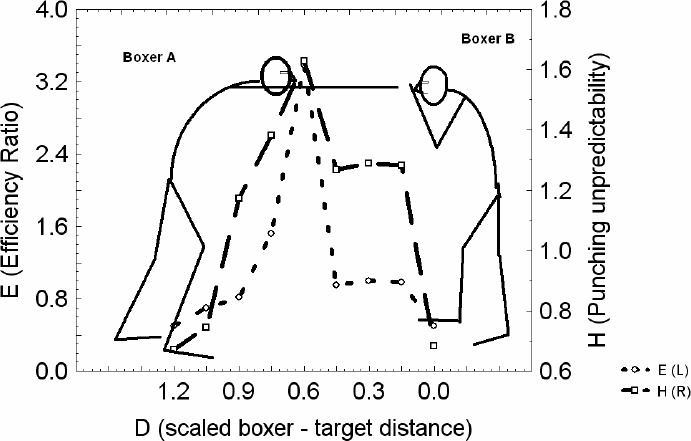
Boxer - boxer coordination (i.e. sparring) spontaneously emerges. The punching unpredictability (H) (dashed line) and efficiency ratio (E) (dotted line) minima, located around D =1.2 and D = 0 are the attractive states, and their maxima located around D = 0.6 are the repellent states of the coordination. The global minimum is located around D =1.2 and represents the optimal strategic position area in which boxers continually spend the most of time since it minimizes the unpredictability, efficiency ratio and consequently the efficiency of the opponents punching actions.

The maximum of perceived efficiency ratio does not imply that all of the action patterns attained maximal perceived efficiency values. For example hooks and uppercuts possessed larger perceived efficiency values for smaller scaled boxer - target distances than D = 0.6. Jabs attained maximal perceived efficiency values for somewhat larger scaled distance values. The maximum of the perceived efficiency ratio signified that there is an optimal proportion between the perceived efficiencies of the actions and their differences. The maximum of this function is attained when there are relatively high perceived efficiencies of the whole set of actions and small inter-efficiency differences.

In other words, in this region the sum of the perceived punching efficiencies is relatively high and the perceived punching efficiency differences are minimal. This proportion maximizes the efficiency ratio function. On the other hand the unpredictability and diversity measures increase when the probabilities of all action patterns attain closer values. From the previously discussed results it was clear that in this specific region all types of punching action patterns were active and the probabilities of their occurrence possessed relatively similar values. This characteristic maximizes the unpredictability and diversity measures as well.

Now starting from D = 0.6 and moving toward the larger or lower D values (see Figures 2 D and 3), these criteria are satisfied to a lesser extent due to the paucity of the action repertoire of the performers available at these distances and the larger differences between the perceived efficiencies, which leads to the overall decrement of these three functions.

Overall, the relations between handstriking unpredictability (H), diversity (S) and efficiency ratio (E) show that the performers were able to discover and exploit the scaled distances D where the perceived efficiency differences of their action patterns were minimal and yet their absolute values were relatively high making the efficiency ratio (E) maximal. The observed relationships between the perceived efficiency ratio and the action unpredictability and diversity is yet another corroboration of the sensitivity of human movement systems (represented here by the novice boxers) to the interacting environmental and individual information flows which constrain their actions toward a target.

Movement selection meta-stability and diversity

The meta-stability (dynamics at the edge of instability) evident in the boxers' punching data is portrayed in Figure 2C. The probabilistic nature of the activation and temporal coupling of particular punching modes suggests this fundamentall meta - stable nature of the dynamics.

For fixed values of scaled distance to the target there are coexisting (simultaneously available) states of actions implying that the dynamics of boxers' movement systems over time is dominated by transitions between different regions of the perceptual- motor landscape. To enable the flexible switching between the punching modes the boxers' movement system has to be poised at the edge of instability from where each punching mode can be spontaneously activated under the task and the perceived environmental constraints.

It is important to note first that through a systematic gradual change of the scaled boxer - target distance, the number of available movement solutions changed abruptly. The probability of these abrupt changes (i.e. bifurcations) of specific punching action modes increased in well defined D regions, i.e. when the perceptual - motor system of the boxers became maximally susceptible to the small changes of the scaled distances, which together showed that these changes were most probably due to nonlinear dynamical causes. As presented on Figure 2C, at scaled boxer - target distance D = 1.2 the inactivity state splits (i.e bifurcates) into two punching solutions (right and left jabs). Around D = 1.05 two more motor solutions to the punching task emerged (hook punches) and eventually at D = 0.9 another two motor solutions emerged, this time the uppercut punches. In the interval 0.9 > D > 0.45 the whole set of punching modes was simultaneously available. Around D = 0.45 jab punching modes ceased to be used and at D = 0 the uppercuts ceased to exist as well. Also, as shown above (Figure 2 B), with each abrupt change in the motor solution to the task, the whole probability landscape changed making some of the already active striking patterns less or more probable than before. This finding signified that with each newly formed or annihilated movement solution, not only local, but a global restructuring of the action landscape arose allowing a greater degree of flexibility in the decision - making space of boxers. The newly formed movement solutions reduced the probability of occurrence of the other previously active punching modes and effectively created a more equilibrated medium in the decision-making space of the boxers increasing the competition between the different action modes.

The meta-stability (weak instability) of punch selection is a key characteristic of the action flexibility of boxers because it avoids maladaptive mode-locked (more rigid) forms of behaviour that are too stable (and thus predictable) in the dynamic context of the martial arts. This adaptive behavior enables boxers to increase the uncertainty of their actions with a maximum occurring in the region around D = 0.6 that corresponds to the maximum values of the unpredictability diversity and efficiency ratio measures (see Figure 2D and 3). These data highlighted that one of the most important constraints on the dynamics of the movement-information couplings of boxers is the scaled relative distance to a target. This constraint shapes decision-making from moment to moment by altering the dynamic range of available action solutions via the distance-dependent perception of punching efficiency in individual boxers.

Emergence of performer - performer coordinative states

Strategic positions of boxers may be observed as performer - performer coordination dynamical states similar to those observed during sub-phases of sports such as dribbling in basketball and sailing regattas (see Araújo et al., 2005; Davids et al., 2005). These states are formed spontaneously which means that there is no specific rule imposed from an external source to which boxers should adhere in forming the strategic positions. In other words, 1 v 1 coordination states in boxing emerge (i.e. they are not imposed by external influences) in a self - organized fashion from the interactions between the perceptual, cognitive, intentional and motor subsystems of the boxers. Anecdotal observations from boxing matches suggest that boxers spend a lot of time in well-defined relative distances from each other, which are the regions around the edge of jab reachability D = 1.2. In Figure 3 it can be noted that these regions are actually regions of minimum unpredictability (H), diversity (not presented on Figure 3, but see Figure 2D) and perceived efficiency ratio (E) of an opponent's actions.

Under the task constraints of boxing, on the one hand opponents are attracted towards one another due to the main goal of the task (to strike each other), whereas on the other, the region of striking unpredictability, peaking at D = 0.6, acts as a repeller, driving opponents towards its minima D = 1.2 and D = 0. Through competition and cooperation of these contrary tendencies relatively stable regions are formed around the unpredictability and efficiency ratio minima. Data from this study supported anecdotal evidence that those minima are located at the edge of jab reachability and fluctuate so that the jabs could emerge. The incursions of the attacker (boxer A in Figure 3) on shorter scaled distances especially those around D = 0.6 enables him to increase and maximize the unpredictability, diversity and the efficiency ratio of his actions, however simultaneously he is also being exposed to increased action possibilities by the defending opponent (boxer B in Figure 3). So after the incursions of the attacker, typically, previously stable coordination states are quickly re-established either by withdrawal of the attacker or by the evasion of the defender or both. Actually, the culmination of sudden incursions of the attacker is usually twofold: either the previous “at the edge of jab reachability” (the first unpredictability and efficiency ratio minimum) dynamics are spontaneously re-established around D = 1.2, or the boxer - boxer coordination dynamics transits to the D = 0 zone where boxers stick together and lean on each other, so that only sporadic hooks could emerge (clench position). These system dynamics are characterized by the second unpredictability and efficiency ratio minimum, at D = 0, which was also observed in this investigation. One should note, however, that this minimum possesses larger values of unpredictability and efficiency ratio measures than the one at D = 1.2, meaning that it is only a local minimum. On the other hand the global minimum is the one located around D =1.2. This means that the area around the global minimum is more stable (i.e. more often visited) strategic position than the one located at D = 0. The reason why boxers do not constantly spend much time at distances close to D = 0.6, is that those distances represent repellent areas of coordination dynamics landscape (i.e. from this position it is easy for boxers to move to other specific parts of the perceptual-motor landscape). Certainly, other constraints like the defensive position of the arms of the opponent may regulate the attacker's intentions in specific ways which requires further investigation.

Conclusions

The data from this study have shown how a constraints-led framework on movement behaviour emphasizes the importance of the environmental, task and individual constraints on human movement systems. The results of this investigation on decision-making in boxers permit a number of practical conclusions to be drawn, as outlined below:

1. In training tasks involving punching static (i.e. non - moving) heavy bags, novice boxers are sensitive to two types of interacting constraints of high ecological validity: (i) The scaled performer - target distance; and (ii), the perceived efficiency of punching actions. The first constraint is instrumental in creating new and annihilating previously active striking patterns. The second influential constraint is used to fine tune the action landscape of individual boxers by suppressing less efficient, and facilitating use of more efficient boxing action patterns.

2. The typical training task constraints studied in this investigation showed that novice boxers are subject to a kind of discovery learning by exploring the efficiency of their motor repertoire when changing the performer - target distances as evident by the strong efficiency - action probability relationships observed in the data. With regard to these findings it is important that the attention of the novice boxers should be directed by coaches to the major informational constraints identified in this paper (i.e. the reachability specific to each kind of punching actions and the associated perceived punching efficiencies) so that stable movement-information couplings are formed during practice. Particularly important is the relationship, between 3 parameters in the reachability condition (see the Methods section) i.e. the physical performer - target distance (X), the forward body lean length (L_lean) and the effective arm length (L_eff), which itself depends on the elbow joint angle at the moment of hand - target collision. By allowing novice boxers during the basic training sessions, when the heavy bag practice is mostly used, to explore the whole spectrum of constraints enabled by each combination of parameters, they would learn how to adjust emergent motor solutions to the hitting task which are specific to their individual organismic constraints. Once these efficient coordination patterns have been established with the heavy bag, learners could move to the task of hitting moving opponents during light sparring;

3. Novice boxers are able to discover and exploit the scaled performer - target distance region that affords maximization of the unpredictability (H), diversity (S) and the efficiency ratio (E) of their punching actions. It is located around D = 0.6; The regions around this distance are those which maximize the meta-stability (i.e. dynamics at the edge of instability) of movement selection and consequently the flexibility of creating punching actions in novices. This region is an optimal area for practicing all possible temporal couplings of boxing action patterns which is not the case for other regions where some of the action patterns are decoupled or are much less likely to occur;

4. Spontaneous emergence of boxer - boxer coordinative states and strategic positioning as a consequence of boxers' perception of essential interacting constraints points to the possibility that practice should be less loaded with verbal instructions from the coach to impose decisions. Rather, practice could be directed towards creating a variety of learning situations (by manipulating the dynamics' constraints) in which trainees would themselves explore, discover and thus adapt to the information - movement demands of diverse 1 v 1 interpersonal coordinations (i.e.sparring situations).

The results obtained in this study demonstrated that dynamical systems theory could provide a useful and relevant theoretical framework for investigating decision making behaviour in sports such as boxing, as exemplified by the task of punching a heavybag. Interesting questions are raised over the differences and similarities of dynamical properties amongst a range of combat sports such as boxing, karate and kickboxing. One should expect that a variety of dynamical differences exist due to the differences in the number of limbs involved, the inter- and intra-limb coordination states that are enabled by rules and permissible actions and differences in limb lengths of participants. It is expected that differences in all of the measures and their interdependencies used in this investigation exist which would also change the properties of performer - performer coordination. These issues should be addressed in further investigations of combat sports motivated by dynamical systems theory.

Biographies

Robert HRISTOVSKI

Employment

Associate Professor at the Faculty of Physical Culture in the University of St. Cyril and Methodius in the city of Skopje, Republic of Macedonia.

Degrees

PhD

Research interests

Nonlinear dynamical systems theory applied to human movements and adaptation to the training process

E-mail: robert_hristovski@yahoo.com

Keith DAVIDS

Employment

Professor and Dean of the School of Physical Education at the University of Otago, NZ.

Degrees

PhD

Research interests

The theoretical frameworks of ecological psychology and dynamical systems theory applied to the study of movement coordination and control in sports. The role of constraints in motor learning and the implications for the development of a nonlinear pedagogy.

E-mail: k.davids@qut.edu.au

Duarte ARAÚJO

Employment

Assistant Professor at the Faculty of Human Kinetics at Technical University of Lisbon in Portugal.

Degrees

PhD.

Research interests

Decision-making in sport.

E-mail: Daraujo@fmh.utl.pt

Chris BUTTON

Employment

Director of the Human Performance Centre in the School of Physical Education at the University of Otago in NZ.

Degrees

PhD.

Research interests

Movement coordination and interception skills, skill learning, and coaching.

E-mail: cbutton@pooka.otago.ac.nz