Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 Oct 8;9(11):5176–5189. doi: 10.1021/ct4005933

Energetics of Multi-Ion Conduction Pathways in Potassium Ion Channels

Philip W Fowler †, Enrique Abad †, Oliver Beckstein †, Mark S P Sansom †,*
PMCID: PMC3864263  PMID: 24353479

Abstract

graphic file with name ct-2013-005933_0009.jpg

Potassium ion channels form pores in cell membranes, allowing potassium ions through while preventing the passage of sodium ions. Despite numerous high-resolution structures, it is not yet possible to relate their structure to their single molecule function other than at a qualitative level. Over the past decade, there has been a concerted effort using molecular dynamics to capture the thermodynamics and kinetics of conduction by calculating potentials of mean force (PMF). These can be used, in conjunction with the electro-diffusion theory, to predict the conductance of a specific ion channel. Here, we calculate seven independent PMFs, thereby studying the differences between two potassium ion channels, the effect of the CHARMM CMAP forcefield correction, and the sensitivity and reproducibility of the method. Thermodynamically stable ion–water configurations of the selectivity filter can be identified from all the free energy landscapes, but the heights of the kinetic barriers for potassium ions to move through the selectivity filter are, in nearly all cases, too high to predict conductances in line with experiment. This implies it is not currently feasible to predict the conductance of potassium ion channels, but other simpler channels may be more tractable.

Introduction

Ion channels are the canonical example of a protein nanomachine; they perform vital physiological functions, are exquisitely sensitive, and can make solid-state electronic devices look crude by comparison.1 They have been studied extensively for over 50 years, and a wealth of electrophysiological, structural, and biophysical data have been accumulated.2 We cannot yet calculate the conduction properties of an ion channel from an experimental (static) structure. Instead, once a structure of a particular ion channel becomes available, its conduction properties are explained intuitively, perhaps by comparison to other channels. This indirect linking of structure and function is somewhat unsatisfactory. Calculating functional properties of ion channels from their structures, directly linking structure and function, not only is desirable in itself but also is an excellent test of our ability to accurately model the behavior of membrane proteins in general.

We shall focus on potassium ion channels, as the first structure of an ion channel belongs to this family and it remains the family with the most experimental structures. All potassium ion channels have a tetrameric central pore domain through which potassium ions and waters pass. For example compare KcsA,3 a bacterial pH-gated K channel, and Kvchim,4 a chimeric mammalian voltage-gated K channel (Figure 1). Their central pore domains are remarkably similar despite the two channels being gated by different stimuli and both having additional large domains, namely, voltage sensors and an intracellular tetramerization domain for Kvchim versus a C-terminal intracellular domain for KcsA. The primary difference between the high-resolution structures of the pore domains of KcsA and Kvchim is that the intracellular gate is closed in the former but open in the latter.5

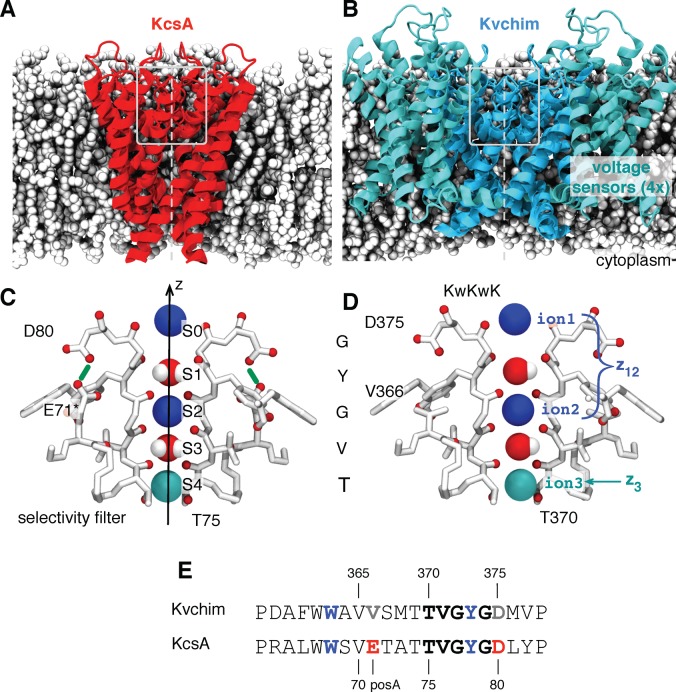
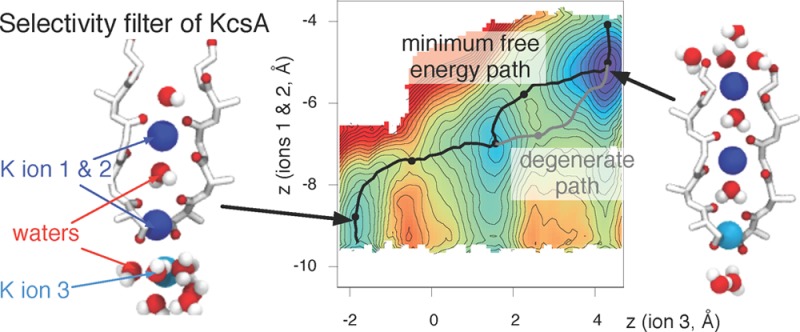
Figure 1.

Figure 1

Open in a new tab

Potassium ion channels (A) KcsA3 (in red), a pH-gated bacterial channel, and (B) Kvchim4 (in blue), a voltage-gated chimeric mammalian channel, share a similar central pore domain. Lipids are drawn in gray for illustration. Ions pass through the channel along the 4-fold symmetric pore axis, z, shown as a dotted gray line. The C-terminal domain of KcsA and tetramerization domain of Kvchim are not shown. The narrowest part of the pore, the selectivity filter, is found above the central cavity toward the extracellular side of the bilayer; this region is enclosed in a gray box. The selectivity filters of (C) KcsA and (D) Kvchim have the same TVGYG amino acid sequence and are structurally very similar. The backbone oxygens, along with the side chain hydroxyl of the threonine residue, form octahedral cages of oxygen within which an ion or a water are stabilized. These are conventionally labeled S0–S4 as shown. We follow the nomenclature of Bernèche and Roux6 and label the three potassium ions as shown. Ion 1 and ion 2 are blue, whereas ion 3 is cyan. The position of the center of mass of the top two ions along the pore axis, z, is therefore denoted by z12, while the position of the lower ion is denoted by z3 (see Methods). We shall describe the configuration of the selectivity filter as a string of letters denoting the species present in each binding site, from S0 to S4, reading from left to right with the cavity species, where appropriate, given in parentheses. The configuration shown is KwKwK. (E) KcsA has a glutamate at position A. This is protonated, leading to a hydrogen bond between GluH71 and Asp807 (drawn in green). In Kvchim, the equivalent residues are Val366 and Asp375, and therefore, no such hydrogen bond is possible. For clarity, only two of the four monomers are drawn, and the coordinating oxygens are red.

Potassium ions can flow through in either direction; for convenience, we shall consider a potassium ion approaching either channel from the cytoplasm. It first moves past the intracellular gate, if open, and enters the central cavity. The ion then passes through the narrowest part of the pore, the selectivity filter, before exiting the cell. The selectivity filter is formed by four loops, one from each monomer, each having the conserved sequence TVGYG. The loops are arranged such that their backbone carbonyls point toward the pore axis creating a series of octahedral cages of oxygens in which potassium ions and waters are stabilized; these are conventionally labeled S0–S4 (Figure 1). Before passing through the selectivity filter, a potassium ion must shed its solvating waters. The dominant view is that waters and ions are thought to enter the filter alternately and move through in single file, with at least two ions bound at all times.8 We shall call this the ion–water–ion (KwK) mechanism (Figure 1). As a potassium ion approaches the filter from the central cavity, a “knock-on” event occurs leading to a potassium ion being ejected from the top of filter. As the name suggests, the selectivity filter is thought to discriminate between potassium and sodium ions.9

Although the selectivity filters of KcsA and Kvchim have the same TVGYG sequence (Figure 1C and D), KcsA has a very low open probability due to C-type inactivation. Replacing the glutamate at position 71 of KcsA with alanine dramatically reduces the degree of C-type inactivation.10 In KcsA, this glutamate is protonated and forms a hydrogen bond with Asp80.7 Kv channels typically have a valine or isoleucine at the equivalent position to Glu71 and so lack this hydrogen bond.11 The E71A KcsA mutant therefore behaves more like a Kv channel, such as Kvchim.

Over half a billion potassium ions pass through a single KcsA channel each second at physiological voltages.12 This is near the diffusive limit for potassium ions, which is remarkable considering the high selectivity this channel has for potassium over sodium ions. According to Nernst–Planck theory estimates,13 this implies that the potassium ions must not encounter any barriers greater than ∼5 kT (3 kcal/mol at 300 K), otherwise the conductance would be markedly reduced.

Since the first structure of KcsA was published,14 theoretical methods have been applied to investigate or calculate the conductance of a range of potassium ion channels.15 We shall consider here hierarchical approaches that use a potential of mean force (PMF).16 The first step in the calculation of a PMF is to identify which species to follow, and their corresponding reaction coordinates, zi, are understood as a set of relevant collective variables that emerge naturally from the underlying transport dynamics. In ion channels, this is straightforward; one wants to follow the motion of the n ions along the pore axis, z. 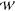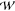Each point on the n-dimensional PMF landscape, Inline graphic(z1, z2, ..zn), defines a unique configuration of ions within the selectivity filter, and the gradient yields the average force experienced by each of the conducting species. 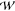It has been shown that the total PMF, Inline graphictotal(z1, z2, ..zn), can be written as the following:13,17

graphic file with name ct-2013-005933_m003.jpg 1

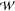where Inline graphicequilibrium(z1, z2, ..zn) is the potential of mean force measured at equilibrium, i.e., with a transmembrane potential of zero, q is the elementary charge and ϕmembrane(zi) describes how the transmembrane potential changes along the pore axis. The effect of the channel on the permeating species is collapsed down to a single, multi-dimensional PMF, Inline graphicequilibrium(z1, z2, ..zn), which, along with the variation in transmembrane potential along the pore axis, ϕmembrane(zi), may be used as inputs into a higher-level model18,19 that predicts the conductance of the channel.

The first equilibrium PMF was calculated over 10 years ago by Bernèche and Roux6 using the first low-resolution structure of KcsA.14 This seminal study firmly established the technique, and the authors suggested a plausible conduction mechanism. Because the barriers were 2–3 kcal/mol high (≤5 kT) they were able to use this PMF to calculate, with some success, the current–voltage relationship of KcsA using Brownian dynamics.13 Subsequent studies by other groups calculated PMFs for different potassium channels20−25 suggested there might be conduction mechanisms involving vacancies,20 examined the selectivity,26 and even applied the methodology to bacterial outer membrane pores.27 Following an early pioneering study28 and the relentless increase in computational power, it is now possible to directly simulate multiple conduction events at different magnitudes of the electric field thereby permitting the direct in silico measurement of the conductance.29−31 A direct approach is intuitive but inevitably requires far more computational resource than the equivalent PMF-based method, and there remain difficulties applying an electric field in a simulation. Calculating an appropriate PMF also allows other important questions to be answered; for example, one can study the stability of multi-ion configurations and devise kinetic models to compute the escape rate of an ion over an energetic barrier.

In this paper, we shall calculate seven independent 2D PMFs that encapsulate the conduction of potassium through two different channels, KcsA and Kvchim. We shall (1) introduce the E71A mutation into KcsA to facilitate comparison with Kvchim, (2) determine the effect on both channels of removing the CHARMM CMAP forcefield correction, and (3) examine the reproducibility of these types of calculation. This will permit us to discuss the current feasibility of calculating the conductance of potassium ion channels from experimental structures.

Results

We shall first focus on examining the sensitivity and reproducibility of equilibrium PMFs, 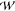Inline graphicequilibrium(z1, z2, ..zn), before later examining how the transmembrane potential varies along the pore axis, ϕmembrane(zi). Following the method of Bernèche and Roux,6 we used a two-coordinate system (z12, z3) to follow the motion of potassium ions 1 ,2, and 3 in the selectivity filter (Figure 1 and Methods). Like the majority of studies, we assumed that the sites of the selectivity filter are alternately filled by water molecules and potassium ions (KwK mechanism). We produced a series of carefully equilibrated structures of the pore domain of wild-type KcsA3 embedded in lipid bilayers as described in Methods. Each structure had a different configuration of ions and waters in the selectivity filter, all of which conformed to the KwK mechanism. These were then used to seed 577 simulations, each of which was 0.2 ns long and sampled a different region of (z12, z3) space by applying biasing forces to the potassium ions. This is the stratified umbrella sampling method.32

The KwK Mechanism Is Not Always Maintained

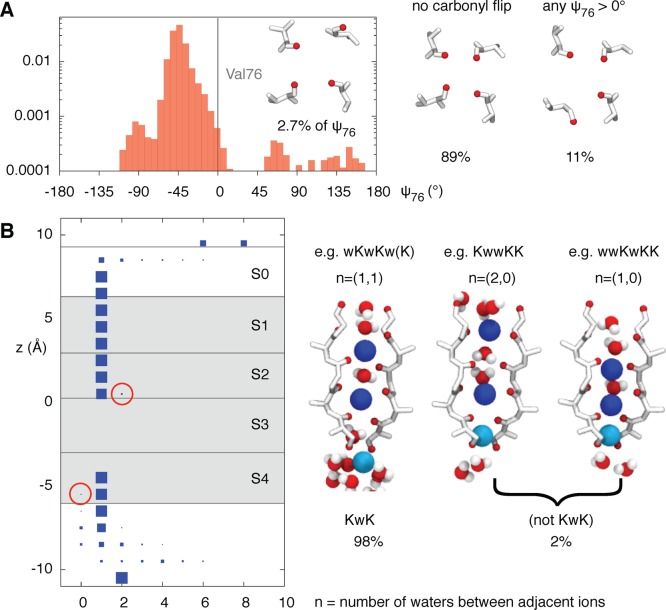
Close inspection of individual umbrella simulations revealed two complications concerning the assumption of a simple KwK mechanism. First, one or more Val76 carbonyls on occasion flipped by ∼180°, reducing the oxygen coordination number within sites S2 and S3 (Figure 2A) and breaking the 4-fold symmetry of the selectivity filter. The flipping of carbonyls, especially those of the valine, has been observed several times before34−36 and has been suggested to lead to C-type inactivation.33

Figure 2.

Figure 2

Open in a new tab

Checking the assumptions that (1) the selectivity filter remains conductive and (2) that the ions and water proceed through the selectivity filter in an alternating single file. (A) Log histogram of the backbone ψ dihedral angle of Val76 shows that the first assumption does not always hold; 2.7% of valines have a ψ > 0° that corresponds to a flipping of the backbone carbonyl oxygen and, as suggested by Bernèche,33 leads to a selectivity filter with altered conduction properties. Because KcsA is a tetramer and only a single flip is required, 11% of frames are affected in this way. We remove these frames and those where the KwK mechanism is not followed from all subsequent analyses. (B) To check the second assumption, we have plotted the number of waters between adjacent ions as a function of the z coordinate of the ion furthest from the center of the selectivity filter. The area of each blue square is proportional to its percentage occurrence at that value of z. We further define an ion to be within the selectivity filter if it is within sites S1–S4 (gray area); for a detailed definition, see Methods. There is only a single water between any two ions in the selectivity filter for most (98%), but not all, of the time (circled in red). Waters occasionally squeeze past the potassium ions in the filter leading to unexpected configurations, two examples of which are shown.

Second, the KwK ordering was not always maintained. In common with previous studies,6,13,20,25,26,33 we have implicitly assumed that applying biasing forces to the potassium ions would trap the water between the cations, as long as the cations remain within the confines of the filter. This has the advantage of reducing the number of collective variables and, therefore, the dimensionality of the PMF from five to two. However, our simulations show that this assumption does not always hold (Figure 2B). First, a water trapped between two potassium ions in the filter can occasionally escape by squeezing past one of the ions leaving a vacancy (e.g., KwwKK configuration in Figure 2B). Second, as ion 3 approaches the bottom of the selectivity filter, more than one water may become trapped between it and ion 2 inside the filter. Reversing this process leads to a similar behavior, i.e., moving ion 3 from inside the filter into the central cavity because the trapped water above ion 3 can escape as before. We cannot therefore assume that applying biasing forces to only the potassium ions will strictly maintain the alternating sequence of ions and waters necessary for the KwK conduction mechanism. This is an important result, and we shall discuss it later.

To resolve these two problems, we only kept data where there was exactly one water between any two adjacent ions (as long as both ions are “inside” the filter, see Methods), and there were no carbonyl flips. As a result, 12% of the data were discarded (Table S1, Supporting Information). The resulting PMF (and all others in this paper) hence assumes (1) the KwK conduction mechanism and (2) the filter is in a conducting state. We are therefore implicitly testing the classical KwK conduction mechanism, because if it is true, we would expect the heights of the barriers to be <5 kT.

Three Stable Configurations of the KcsA Selectivity Filter Are Identified

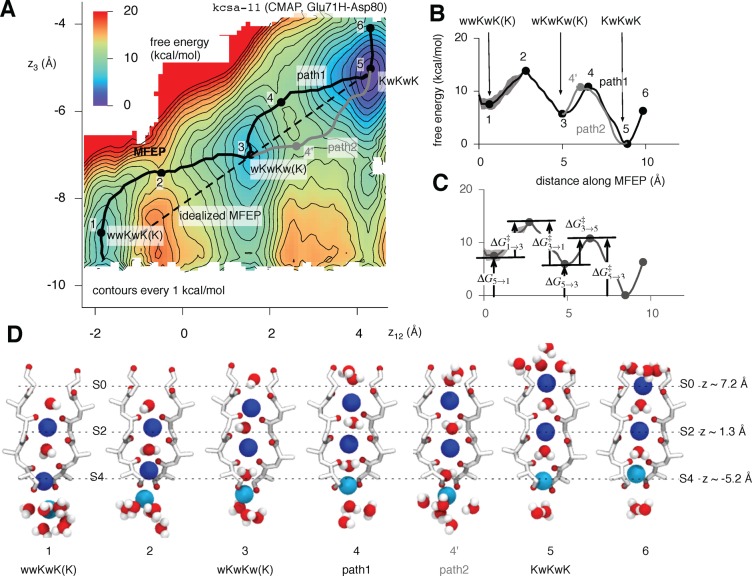
Following this filtering, each of the 577 umbrella simulations was divided into 100 bins, each 2 ps wide. A 2D PMF was calculated for each using the weighted histogram analysis method37 and the minimum free energy path (MFEP) found as described in Methods. The height of the first barrier was measured and plotted as a function of time. Calculating the statistical inefficiency38 suggested that we should discard the first 100 ps of the data to ensure equilibration and that a conservative estimate of the correlation time for the remaining 100 ps is 20 ps (Figure S1, Supporting Information). Because each umbrella simulation is 200 ps long, five independent 2D PMFs were calculated and averaged, with errors estimated in the usual way (Figure S2, Supporting Information). The resulting averaged 2D PMF for wild-type KcsA is shown in Figure 3A.

Figure 3.

Figure 3

Open in a new tab

There are three stable configurations of the selectivity filter of KcsA and three potassium ions. (A) The 2D PMF of wild-type KcsA with the CMAP correction has three minima. The axes correspond to the center of mass of the two potassium ions closest to the periplasm (ion 1 and ion 2, z12) and the position of the third potassium ion (z3). Both are measured along the axis defined by the selectivity filter. Contours are drawn every 1 kcal/mol, and the minimum free energy path (MFEP) as calculated by the nudged elastic band method is drawn as a black line. A second, degenerate path between points 3 and 5 is drawn as a gray line. A dashed straight line between the wKwKw(K) and KwKwK configurations is drawn; this is the MFEP in the idealized case where the permeating species are represented as hard spheres. The smallest value of the free energy is defined as zero by the WHAM procedure. Six points along this line are labeled; these correspond to stationary points. (B) The free energy along the MFEP more clearly shows the heights of the barriers between the identified stable states. The second pathway and the estimated error are also shown. (C) The relative free energies of the three stable configurations and the heights of the forward and reverse barriers between them is defined as shown (Table 2). (D) Six illustrative images of the positions of the ions and waters and the structure of the selectivity filter. These correspond to the points labeled in A and B. Ion 1 and ion 2 are blue, whereas ion 3 is cyan. For clarity, only two of the four monomers are drawn, and the coordinating oxygens are red.

The 2D PMF has three minima corresponding to the following configurations: wwKwK(K), wKwKw(K), and KwKwK (see the legend of Figure 1 for the definition of this nomenclature). The MFEP between the wwKwK(K) and KwKwK configurations was calculated using the nudged elastic band method (see Methods) and, as expected, it visits the wKwKw(K) configuration.

There Are Two Paths between the wKwKw(K) and KwKwK Configurations

It appeared possible, by inspection, that there are alternative pathways between the wKwKw(K) (point 3) and KwKwK (point 5) configurations. Calculating the MFEP using a slightly different initial condition bore out our suspicion and shows that there are two main pathways, labeled path 1 and path 2. The latter is similar, but not identical, to the secondary pathway previously seen by Bernèche and Roux.6 The height of the barrier encountered is similar along both paths (Figure 3B, Table 2), and hence, they are degenerate. Consider for a moment the shape of the MFEP if the conducting species were hard spheres and the selectivity filter a cylinder—because the ions and waters would smoothly move through the filter, the MFEP would be a straight line between the two bound configurations. Both paths are instead curved in an approximately symmetrical fashion about the idealized MFEP. From path 1, we infer that the ions and waters are “compressible” because ion 3 has to nearly enter S4 before the knock-on occurs, and from path 2, we infer that, as expected, the cations can interact at a distance. There is therefore an equal probability of the two ions in the filter “knocking-on” either spontaneously once ion 3 is immediately below S4 (path 2), or after ion 3 has begun to enter S4 (path 1).

Table 2. Heights (kcal/mol) of the forward and reverse barriers between the filter configurationsa.

      ΔG3→5‡ ΔG5→3‡ ΔG3→5‡ ΔG5→3‡    
name ΔG1→3‡ ΔG3→1‡ path 1 path 2 ΔG5→1 ΔG5→3
kcsa-11 6.4 ± 1.2 7.9 ± 0.4 5.1 ± 0.2 10.8 ± 0.1 5.1 ± 0.2 10.7 ± 0.1 7.5 ± 1.1 6.0 ± 0.1
kcsa-10 n.d. 6.0 ± 0.2 3.2 ± 0.3 12.3 ± 0.2 3.4 ± 0.3 12.5 ± 0.3 n.d. 9.5 ± 0.2
kcsa-00 2.1 ± 0.4 11.7 ± 0.4 6.2 ± 0.5 5.9 ± 0.5 6.7 ± 0.4 6.5 ± 0.4 9.2 ± 0.1 –0.3 ± 0.2
kvchim-10 n.d. 7.2 ± 1.5 5.5 ± 0.2 11.1 ± 0.2 5.4 ± 0.2 10.9 ± 0.1 n.d. 4.9 ± 0.1
kvchim-11 2.9 ± 1.2 8.7 ± 0.8 n.d. n.d. n.d. n.d. n.d. n.d.
Open in a new tab
a

For comparison 5 kT = 3 kcal/mol at 300 K. For a definition of the barrier heights, e.g., ΔG1→3‡, see Figure 3C.

Following the MFEP allows us to suggest how potassium moves through the selectivity filter of KcsA (Figure 3D). As ion 3 approaches the filter from the central cavity, ion 1 moves from site S2 to S1, ion 2 moves from site S4 to S3, and a water simultaneously enters the filter to occupy site S4. This is the first “knock-on” event. As ion 3 approaches Thr70, a second “knock-on” event occurs. This either occurs spontaneously with ion 3 still some distance from entering S4 (path 1), thereby creating a “partial vacancy”, or it happens when ion 3 has begun to enter S4. After the second “knock-on”, during which all the species within the filter move one site closer to the extracellular side of the channel, ion 3 enters S4. The net effect of these motions is the displacement of a potassium ion from the central cavity, where it is entirely coordinated by water, to site S0, where it is only partly coordinated by water. This PMF therefore captures almost an entire single conduction event and suggests a plausible conduction mechanism that is consistent with the original proposals of Hodgkin and Keynes.39 The quasi-1D PMF suggests that the KwKwK configuration, which is the only one with three ions inside the filter, is more stable than the other two by 6–10 kcal/mol, although this could be because the intracellular gate is closed, destabilizing the wwKwK(K) configuration.40,41 The heights of the kinetic barriers between the configurations are 5–11 kcal/mol (Table 2), which is significantly larger than the estimate of ∼3 kcal/mol (5kT) required by the electro-diffusion model of Bernèche to reproduce conduction at the rates observed for this channel.12 Our PMF would appear to incorrectly predict that KcsA has a negligible conductance. We shall discuss this later.

Sensitivity of the 2D PMFs

We shall now examine how sensitive this 2D PMF is to a number of factors. An additional four sets of umbrella simulations were run, kcsa-10, kcsa-00, kvchim-10, and kvchim-00 (Table 1). The data from these 1194 × 0.2 ns simulations were filtered as before (Table S1, Figures S3 and S4, Supporting Information) to remove instances where either one or more carbonyl oxygens had flipped or the ions and waters did not stay in an alternate single file. We assumed that, as shown for kcsa-11, discarding the first 100 ps of each umbrella simulation would ensure equilibration, and 20 ps is a reasonable estimate of the correlation time for the remaining 100 ps. This permitted us to calculate five independent 2D PMFs from each set of umbrella simulations (Figure S5, Supporting Information) and estimate errors in the usual way (Figure S6, Supporting Information). In most cases, the error is ≤1.0 kcal/mol along the MFEP, although it reaches 1.5 kcal/mol in places. The additional four filtered converged 2D PMFs, along with that of wild-type KcsA (kcsa-11), are plotted in Figure 4, and illustrative snapshots of the configurations of the selectivity filters can be found in Figure S7 of the Supporting Information.

Table 1. Details of the Seven independent 2D Potentials of Mean Force Shown in Figures 4 and 5a.

name channel PDB CMAP h-bond? posA #sims k12 k3
kcsa-11 KcsA 1K4C(3) yes yes GluH 577 40 or 80 20
kcsa-10 KcsA 1K4C(3) yes no Ala 248 20 20
kcsa-00 KcsA 1K4C(3) no no Ala 233 30 20
kvchim-10 Kvchim 2R9R(4) yes no Val 480 80 or 20 20
kvchim-00 Kvchim 2R9R(4) no no Val 233 80 or 30 20
kcsa-11a KcsA 1K4C(3) yes yes GluH 196 40 20
kcsa-11b KcsA 1K4C(3) yes yes GluH 381 80 20
kvchim-10a Kvchim 2R9R(4) yes no Val 242 20 20
kvchim-10b Kvchim 2R9R(4) yes no Val 237 80 or 20 20
Open in a new tab
a

The kcsa-11 and kvchim-10 umbrella simulations can be further decomposed into two independent sets of simulations as shown, and hence, two 2D PMFs can be calculated from each (Figure 5). The h-bond column details whether a hydrogen bond can be formed at posA (Figure 1E) in the channel. The two digits in the name of the simulation indicate whether the CMAP correction was used (1) or not (0) and whether the h-bond is present (1) or not (0), respectively. The units of the spring constants are kcal mol–1 Å2.

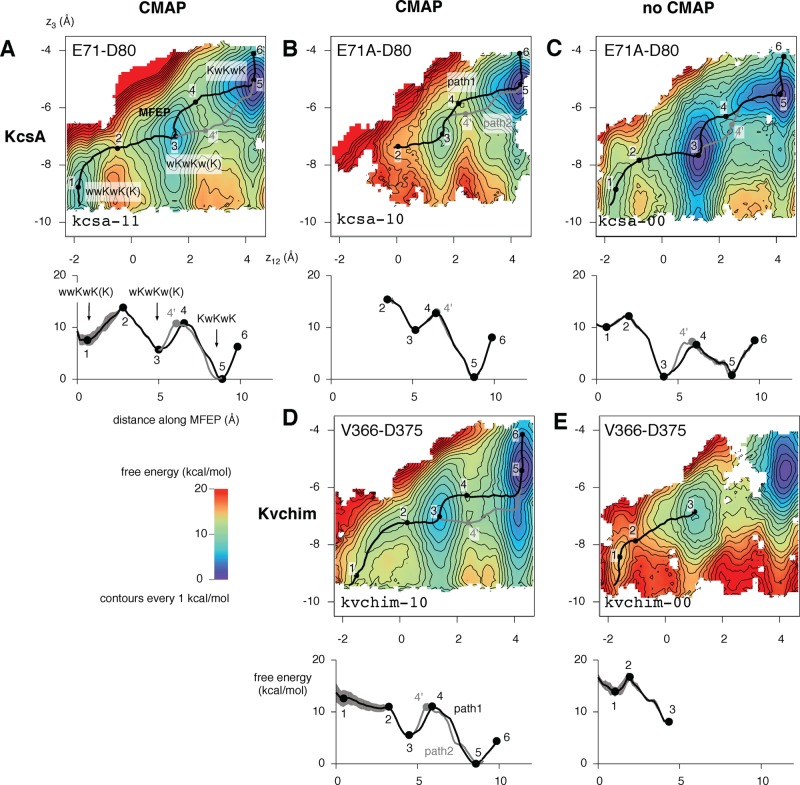
Figure 4.

Figure 4

Open in a new tab

Positions of the stable ion–water selectivity filter configurations are insensitive to the use of CMAP or the presence of the GluH71–Asp80 hydrogen bond. The configurations are also similar in both KcsA and Kvchim. The relative stability of these states and the heights of the barriers between the states, however, changes markedly. (A) The result from Figure 3 is shown in the top left; this is for wild-type KcsA (i.e., possessing the hydrogen bond behind the selectivity filter) with the CMAP correction to the CHARMM forcefield. (B) Removing this hydrogen bond using the E71A mutant appears to increase the relative stability of the KwKwK configuration. (C) When the CMAP correction is not used, the KwKwK and wKwKw(K) configurations have the same energy. (D) The 2D PMF for the pore domain of the paddle chimera, which naturally does not have the hydrogen bond behind the filter, is similar to the equivalent PMF of KcsA (B). (E) Not using CMAP, however, leads to quite a different 2D PMF. In all cases, the same color scheme and labeling is used as in Figure 3, and contours are drawn every 1 kcal/mol. Regions colored white are where data were removed due to the KwK mechanism not being followed in the simulations. These gaps occasionally prevented the full MFEP being calculated, as in B and E. Where possible, an alternate MFEP between points 3 and 5 (path 2) is drawn in gray.

How does the 2D PMF change when the Kvchim channel is used in place of KcsA? Because the selectivity filter of Kvchim is similar to the E71A mutant of KcsA, let us first consider the effect of the E71A mutation on KcsA (kcsa-11 vs kcsa-10). Almost a third of the data from the kcsa-10 KcsA E71A umbrella simulations were removed, primarily due to carbonyl flips of Val76 (Table S1, Supporting Information). The 2D PMF does not, as a result, sample the wwKwK(K) configuration; the start of the MFEP was instead placed close to the wKwKw(K) configuration. Both this and the KwKwK configurations are identified, and the heights of the barriers are also similar to the wild-type (Table 2), although the difference in free energy between the two configurations is slightly larger for the mutant. Again, two paths between the wKwKw(K) and KwKwK configurations can be identified, although they are more similar to one another, and so do not represent significantly different conduction mechanisms.

We can now compare the 2D PMFs of E71A KcsA and Kvchim (Figure 4B and D). Although the selectivity filters of KcsA and Kvchim have the same sequence, one should not expect identical 2D PMFs because, as has been suggested before, the energetics of conduction may be altered by the remainder of the channel.24,31 Even if this effect is small, one would still expect the energetics of the wwKwK(K) configurations to be different because the intracellular gate that is directly below the central cavity is closed in KcsA but open in Kvchim.40,41 The Kvchim 2D PMF (kvchim-10) clearly identifies the KwKwK and wKwKw(K) configurations, and again, there are degenerate MFEPs that connect the two. However, no stable wwKwK(K) state is identified. Unfortunately, we cannot determine if this state exists for KcsA because, as mentioned above, most of the data from this region of the 2D PMF were removed by the filtering. In the Kvchim PMF, the wKwKw(K) configuration has a slight shoulder at lower values of z12, and the shape of the well defining the KwKwK configuration is more elongated in the z3 direction, indicating that the free energy is less sensitive to the position of ion 3 than in E71A KcsA, perhaps because the intracellular gate is closed in the latter structure.

Like the majority of previous studies, we have used the CHARMM forcefield because its potassium–carbonyl oxygen nonbonded parameters have been altered to better reproduce the interaction energies between potassium and both water and N-methylacetamide.42 The CHARMM forcefield has undergone further improvements in recent years, the most notable being the CMAP correction.43 This enhances the protein (ϕ,ψ) angular dependence of the potential energy and has been shown to improve the simulated dynamics of soluble proteins.44 The study by Bernèche and Roux6 predated the development of the CMAP correction, but it has subsequently been shown to be required to simulate the cation selectivity of the Kv1.2 channel.45 Let us therefore examine the effect of not using this forcefield modification for both the E71A KcsA mutant (Figure 4B, C) and wild-type Kvchim (Figure 4D, E). In both cases, we identify all three expected stable configurations of the selectivity filter, but not using CMAP alters the heights of the kinetic barriers between the configurations.

The wKwKw(K) and KwKwK configurations of the CMAP E71A KcsA mutant (kcsa-00) have similar energies and a similar level of degeneracy in the MFEP compared to when the CMAP correction is used (kcsa-10), with the barrier between these configurations being reduced to ∼6 kcal/mol (Table 2). The wwKwK(K) configuration has a free energy of 9 kcal/mol more than the KwKwK configuration, similar to what was seen in the 2D PMF of wild-type KcsA with the CMAP correction (kcsa-11).

All three stable configurations of the filter are picked out by the 2D PMF of Kvchim when the CMAP correction is not used (kvchim-00), although the wwKwK(K) configuration is only marginally stable. Part of the 2D PMF between the wKwKw(K) and KwKwK configurations is not defined, making it difficult to determine the MFEP and accurately determine the height of the barrier. This is despite that the filtering only removing 7.5% of the data (Table S1, Supporting Information). Compared to kvchim-10, the KwKwK configuration is more stable than the other configurations. This is the opposite to what we observe when not using the CMAP correction factor for E71A KcsA.

One of the PMFs Is Reproducible

Two of the five 2D PMFs (kcsa-11 and kvchim-10) were calculated by combining two independent data sets of umbrella simulations. We will now look at these data sets separately (kcsa-11a and kcsa-11b and kvchim-10a and kvchim-10b, Table 1) to test the reproducibility of the 2D PMF maps. The kcsa-11a data set was produced using structures of KcsA embedded in a 7:3 POPE/POPG lipid bilayer, whereas a simple POPC lipid bilayer was used in the simulation used to seed the kcsa-11b data set and all other simulations. Although anionic lipids have been shown to modulate the opening probability of KcsA,46 they do not change the conductance, and therefore, we do not expect to observe any differences between kcsa-11a and kcsa-11b. The umbrella spring constant k12 in the kcsa-11b set was twice as large as the kcsa-11a set, which in turn necessitated tighter spacing between umbrella simulations along the z12 coordinate, and hence, 381 umbrella simulations contribute to the kcsa-11b PMF, whereas only 196 were required for the kcsa-11a PMF. Only 6% of frames were removed from the kcsa-11a simulations to ensure an KwK conduction mechanism with no carbonyl flips, whereas 15% were removed from the kcsa-11b data set (Table S1, Supporting Information). Despite these differences, the kcsa-11a and kcsa-11b PMFs and their minimum free energy paths, including the degenerate path 2, are remarkably similar (Figure 5A). This suggests the 2D PMFs are reproducible.

Figure 5.

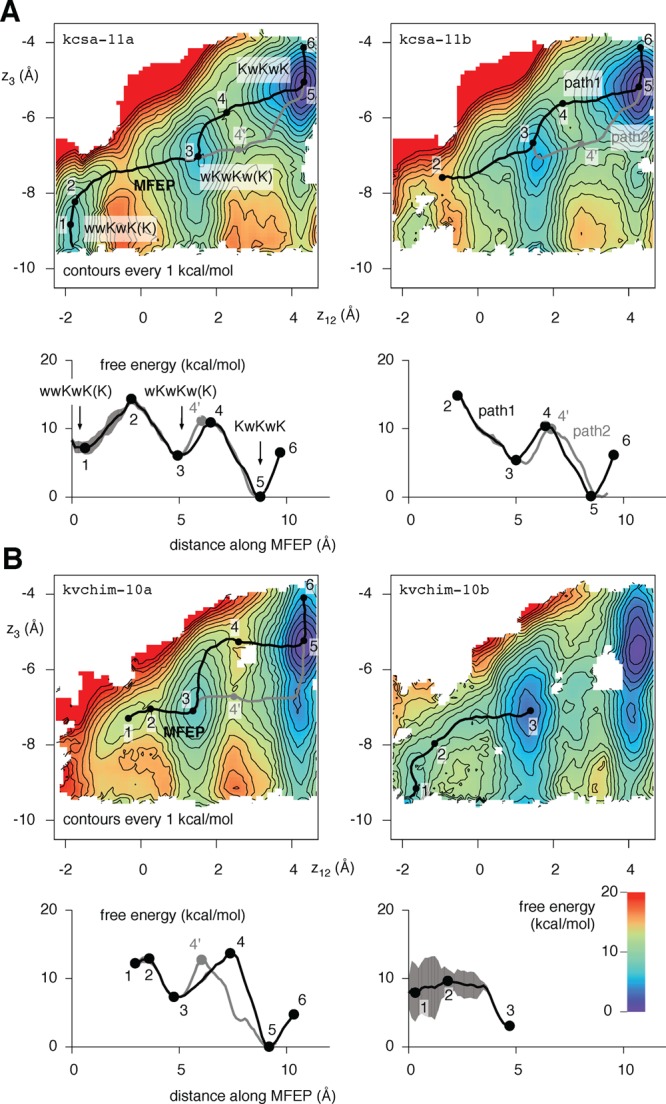
Figure 5

Open in a new tab

(A) The kcsa-11 2D PMF in Figure 3 can be decomposed into two independent 2D PMFs; these are shown here. The 2D PMFs are similar but not identical and yield similar MFEPs. Note that kcsa-11a and kcsa-11b were seeded from different structures, and different amounts of data were discarded in ensure a KwK conduction mechanism (Table S1, Figures S3 and S4, Supporting Information.) (B) The kvchim-10 2D PMF in Figure 4 can also be decomposed into two independent 2D PMFs. Both PMFs identify the same bound configurations of the selectivity filter but differ significantly in their estimate of the free energy change between the states. kvchim-10a and kvchim-10b were seeded using the same equilibrated structure of the pore of the paddle chimera, and similar proportions of data were removed to ensure that the KwK mechanism is maintained. The difference in the 2D PMFs is therefore surprising.

The kvchim-10a and kvchim-10b sets both used the same initial structures. The only difference was the spacing of the umbrella simulations, and a few additional umbrella simulations with a higher value of k12 were required for kvchim-10b. Both PMFs identify the wKwKw(K) and KwKwK configurations and suggest that the KwKwK configuration is the most stable (Figure 5B). Unfortunately, removing the data necessary to ensure the KwK mechanism is maintained created an unsampled region in the kvchim-10b 2D PMF that one would expect to lie on the MFEP between the wKwKw(K) and KwKwK configurations. The error is also estimated to be very high, especially in the region around where the wwKwK(K) configuration would be (Figure S8, Supporting Information). These difficulties prevent us from drawing any conclusions about the reproducibility of the kvchim-10 2D PMF.

Not All of the Voltage Drop Occurs Across the Selectivity Filter

So far we have focused on the feasibility of calculating 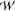Inline graphicequilibrium(z1, z2, ..zn) from eq 1. Now, let us briefly examine how the transmembrane potential changes along the pore axis; this is the ϕmembrane(zi) term in eq 1. The transmembrane potential is usually assumed to drop linearly across the selectivity filter.13 Solving the Poisson–Boltzmann equation numerically for both the (closed) KcsA and (open) Kvchim structures shows that only ∼45% and ∼60%, respectively, of the voltage drop occurs across the selectivity filter (Figure 6).16 The value for KcsA is likely to be an underestimate because the intracellular gate is closed, and we note that it agrees with a previous calculation of how much the potential drops across the low resolution closed structure of KcsA.13 Of more concern is that not all the voltage drop is predicted to take place across the selectivity filer of Kvchim. The Poisson–Boltzmann method assumes the lipid bilayer can be represented by a dielectric slab and is therefore less accurate than, for example, simulating the electric field more directly using a double-bilayer arrangement.47 This is complex and beyond the scope of this work but deserves further investigation.

Figure 6.

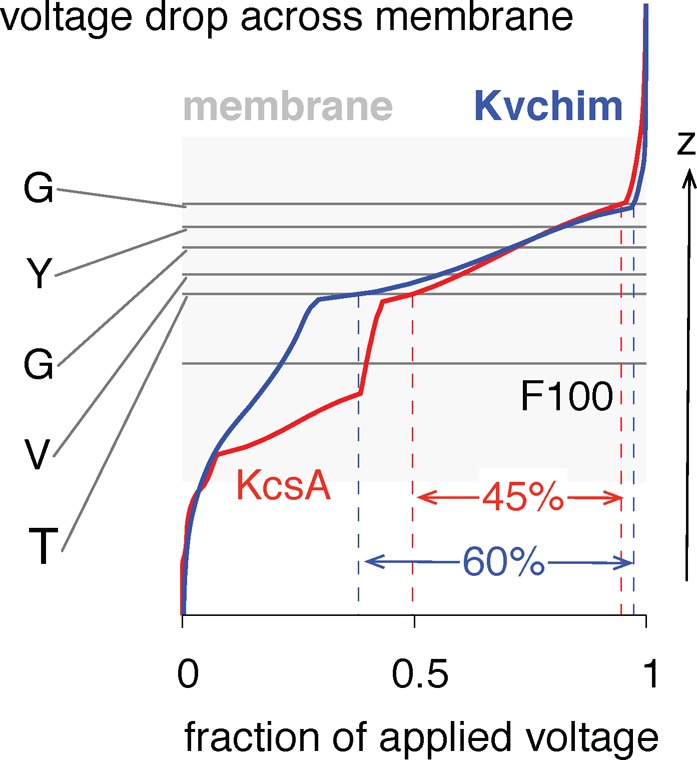
Figure 6

Open in a new tab

Poisson–Boltzmann calculations on the crystal structure suggest that around 60% of the voltage drop occurs across the selectivity filter for the open structure of Kvchim, and this is approximately linear. As described in Methods, these calculations were adjusted to take account of the presence of the membrane.

Discussion

We have investigated the conduction of potassium ions through two potassium ion channels, focusing mainly on a bacterial channel (KcsA3) but also examining a mammalian chimeric (Kvchim4) channel. This was done by calculating 2D potential of mean force (PMF) maps that capture the energetics of almost an entire conduction event. The minima in all seven 2D PMF maps corresponded to the arrangements of ions and waters bound in the selectivity filter required for a single-file “knock-on” mechanism (Table S2, Supporting Information). These are the wwKwK(K), wKwKw(K), and KwKwK configurations (for a definition of the nomenclature, see the legend of Figure 1). Because we have enforced the KwK conduction mechanism, this might at first glance appear unsurprising; however, this does not guarantee that these configurations would be identified as the most stable. Our simulations predict a qualitative similarity in the conduction of potassium ions by KcsA and Kvchim, which is not unexpected given the sequence and structural similarity of both selectivity filters and the surrounding pore domains (Figure 1). The functional similarity has been demonstrated by the sensitivity of KcsA to toxins that have evolved to block mammalian voltage-gated K channels.48

The most stable configuration of the filter (KwKwK) was obtained when three potassiums were bound (at sites S0, S2, and S4) with waters at the intervening positions (S1 and S3) in six of the seven PMF maps. With one exception, this configuration was 5–9 kcal/mol more stable than the wKwKw(K) configuration (ΔG5→3, Table 2) and 7–14 kcal/mol more stable than the wwKwK(K) configuration (ΔG5→1). This is consistent with other published computational studies; this three-ion configuration is estimated to be more stable than the other two-ion states from 0.5 kcal/mol29 to 5.5 kcal/mol25 for Kv1.2 and from 1 kcal/mol6 to 2.5 kcal/mol25 or 4 kcal/mol26 for KcsA.

Our simulations indicate that the heights of all the forward and reverse energetic barriers between the stable configurations are 5–13 kcal/mol (Table 2), with three exceptions where the barrier height was only 2–3 kcal/mol. Barriers of this magnitude are too large to reproduce using a standard electro-diffusion model; the high conductances (97 pS for KcsA at 0 V12) were measured by single-channel electrophysiology. Of the published PMF studies, only two determined the heights of all the barriers to be less than 3 kcal/mol.6,29 For the remainder, the heights of the barriers were in the range of 3–8 kcal/mol, with only a few barriers <3 kcal/mol.25,26 Relatively few of these studies estimated error, which is an important consideration given the sensitivity of the conductance to the barrier heights.

We examined the reproducibility of two of the PMFs. One was reproducible despite large differences in the setup of the simulations, and the results of the second set were inconclusive (Figure 5). Finally, not using the CMAP correction to the CHARMM forcefield resulted in substantial changes to the 2D PMFs of both channels, with the relative stabilities of the filter configurations and the heights of the energetic barriers both changing. This is important, as it suggests that such 2D PMFs are more sensitive to initial conditions and methods than might be anticipated.

We are forced to conclude that it is currently too challenging to accurately calculate the conductance of a potassium ion channel from an experimental structure using classical forcefields, as the heights of the barriers derived from the PMFs are consistently too high and the PMFs themselves are too sensitive to the method employed. The last point is important because, as pointed out by Bernèche and Roux,13 the predicted ion flux is very sensitive to small changes in the predicted heights of any energetic barriers.

One way to avoid the conflation of errors involved in a hierarchical modeling approach13 is to simply measure the current through a pore domain by “brute force” computer simulation for a range of applied electric fields. Worryingly, the extensive simulations of the pore domain Kv1.2 carried out by Jensen et al.29 dramatically underestimated the conductance for positive membrane potentials, and no conduction events at all were observed for negative values of the membrane potential. The membrane potentials were underestimated,29 a fact corrected in their more recent papers,30,31 further exacerbating the lack of agreement with experiment. This further hints that classical forcefields may not yet be able to accurately model the conduction of ions through a potassium channel selectivity filter.

There are five mutually compatible main reasons that could account for the failure to accurately capture the kinetics of the conductance of a potassium ion channel: (1) The description of the atomic interactions is inaccurate. (2) There is insufficient sampling. (3) The standard electro-diffusion theory is unable to predict current–voltage relationships from equilibrium PMFs. (4) The simulations fail to take into account some important factor present in the electrophysiological experiments. (5) There are other mechanisms in addition to KwK that contribute to conduction. Of course, any combination of these five reasons could also account for the failure to accurately capture the kinetics of the conductance of a potassium ion channel.

We shall now give examples of these five reasons. First, as mentioned above, it is likely that the current classical forcefields do not describe well enough the high-field environment within the selectivity filter. Simulating conduction through potassium channels will always be a very hard problem because the ions completely dehydrate upon entering the narrow selectivity filter, and therefore, it is likely that polarization, at the very least, and maybe quantum mechanical effects also, will need to be incorporated into any forcefield before we can accurately model the key interactions between the conducting species and the carbonyl oxygens of the selectivity filter.49 Second, despite the reproducibility of the kcsa-11 2D PMF, it remains possible that our simulations have insufficiently sampled conformational space. Longer simulations and running repeats will also reduce the statistical errors inherent in these calculations. Third, an applied external electrical field is a nonequilibrium perturbation and could result in structural changes within the pore domain, thereby making eq 1 invalid. Such changes could either make the channel more conductive or alter how the electrical potential changes across the selectivity filter, affecting the heights of the barriers between configurations in complex ways. Alternatively, it is usually assumed that all of the entire transmembrane voltage drops across the selectivity filter; our Poisson–Boltzmann calculations suggest this is not the case. Standard electro-diffusion theory also ignores defects arising from the discrete nature of ions. More sophisticated methods that take this account may be required.18 Fourth, it has been shown that the conduction properties of Kvchim are sensitive to changes in the pressure across a patch of cell membrane;50 therefore, the conditions we have simulated may not match those of the published electrophysiological data. Finally, let us now reflect on how likely it is that there are other mechanisms in addition to KwK that contribute to the conductance.

Consider an oversimplified model of the selectivity filter where it is represented as a hollow cylinder, and the ions and waters are modeled as hard spheres with no long-range interactions. Ions and waters would smoothly progress through the filter, resulting in a straight MFEP (Figures 3 and 7A). Because we observe stable configurations, there must be regions in the filter that can stabilize ions and water, which is obvious from the structures. The MFEPs are curved, from which we infer that the distances between the species in the filter, i.e., ions and waters do not remain constant during conduction, and hence, the conducting species can be described as “compressible” (Figure 7A).

Figure 7.

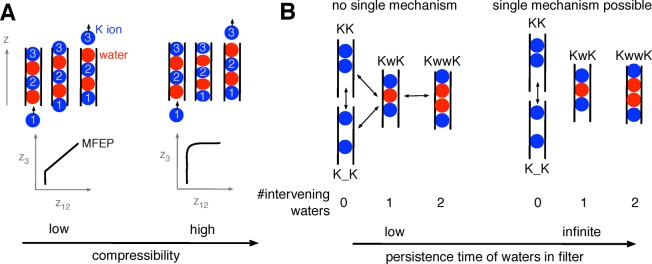
Figure 7

Open in a new tab

(A) We can infer how “compressible” the permeating species are from the shape of the MFEP. A single file of ions and waters would smoothly move through the selectivity filter if they were hard spheres, leading to a straight line on the MFEP. If the ions and waters are “softer”, then one would expect the MFEP to be curved as the approach of ion 3 causes the species in the selectivity filter to be squeezed together. (B) If the waters between potassium ions remain trapped when in the selectivity filter, i.e., their persistence time is infinite, then each conduction event is governed by a single conduction mechanism. If, as we have observed, the persistence time is long but finite, then the situation is more complex because the water in a KwK configuration may leave the filter, leading to other configurations (KK and K_K). In both panels, ions and waters are drawn schematically as filled red and blue circles, respectively.

One usually assumes that a water between two potassium ions in the selectivity filter would remain trapped and therefore have an infinite persistence time (of course, in practice the water would eventually escape as the ions move through the filter). If true, then each conduction event can be completely described by the order of the conducting species (e.g., KwK). We made two key observations about the behavior of water. First, “trapped” waters can occasionally squeeze past a potassium ion and thereby escape the selectivity filter, suggesting that the water persistence time is long (nanoseconds perhaps) but not infinite. Second, a variable number of waters can enter the filter ahead of ion 3, as has been in seen in direct simulations of potassium conductance.29 We infer that not only is it possible for the selectivity filter to start in configurations with variable numbers of waters between ions but also the order of the conducting species itself can change during a conduction event (Figure 7B). Clearly this complicates matters because a filter that starts in a KwK configuration could end up with a vacancy (KK, K_K) or two intervening waters (KwwK) (Figure 7B). The implications of this are as follow: (1) There is no unique simple conduction mechanism. (2) While it is likely “KwK-like” conduction mechanisms dominate, other mechanisms will contribute toward conductance. (3) It is incorrect to assume, as done in previous studies, that the intervening waters remain trapped and so only the positions of the potassium ions along the pore axis have to be treated as collective variables. One must either filter the data, as we have done, or also make the positions of waters along the pore axis collective variables and thereby explicitly control their dynamics. The second option would substantially increase the complexity and cost of any PMF calculation and will almost certainly require the use of more efficient adaptive free energy methods.51 Finally, the apparent stability of the three-ion configuration KwKwK suggests that four-ion knock-on mechanisms may exist, as has been suggested for KirBac1.1.21

What is the evidence that potassium ions and waters alternate in the selectivity filter and move through it in a single file (the KwK mechanism)? Hodgkin and Keynes39 deduced that ions were conducted through channels in a single file; however, the evidence that they must alternate with water molecules is less convincing. In the subsequent structures of a range of potassium ion channels,3,4,14 electron density is observed at well-defined positions along the pore axis, but it is not possible to uniquely infer what mixture of filter configurations leads to the observed electron density because this is an under-determined problem. For example Zhou and MacKinnon52 successfully fitted a simple model to electron density observed along the pore axis, but because the model assumed that either an ion or a water must be present in each site, it cannot prove that other mechanisms do not exist. The KwK mechanism is usually justified through an appeal to electrostatics8 (i.e., it is intuitive that two adjacent potassium ions should be higher in energy than having two potassiums separated by a water molecule), but this does not constitute strong evidence given the presence of surrounding oxygen atoms from the filter. Hodgkin and Keynes39 also suggested that vacancies (empty sites) may arise during conduction, and this was subsequently investigated by Furini and Domene.29 Vacancies were also occasionally observed in extensive simulations of Kv1.2.29

With hindsight, the calculation of a conduction PMF over 10 years ago was a tour de force,6 given the scaling of molecular dynamics codes and speed and availability of high performance computers at the time. There have been significant improvements on both fronts. Codes are more optimized and scale better, and high performance computers are more powerful and numerous. It has become feasible to repeat the calculation of a PMF map several times (or try to reproduce a published result53), and our results show that this is instructive. Despite this, most published studies do not repeat the simulations that underlie the PMF, although there are some notable exceptions.54 Neither do most published studies explicitly test the convergence of the resulting PMF nor calculate the statistical error. This state of affairs is somewhat unsatisfactory, especially where only additional analysis is required. As we have shown, examining the sensitivity of a PMF to the method employed, such as the precise forcefield used, is a useful test of the universality of a result. Adopting these, and no doubt other, best practices55,56 will help improve the accuracy, utility, and hence adoption of computational free energy methods in molecular biology.

The historical focus on calculating PMFs of ions conducting through potassium channels and thereby predicting the conductance was primarily due to the determination of high resolution crystal structures of potassium ion channels. Now that structures of other ion channels are being solved, it is likely that sodium channels in particular57,58 will be more amenable to this approach. Unlike potassium channels, not only do the ions pass through hydrated but also the conduction mechanism appears to be simpler with fewer ions involved. A classical forcefield is therefore more likely to be more accurate. Indeed, reasonable barriers to conduction have already been calculated for Na channels,41,59,60 and even good estimates of the single-channel conductance have been measured by “brute-force” approaches.61,62

In conclusion, assuming the KwK mechanism dominates, we have successfully predicted the expected stable configurations of the selectivity filter but have been unable to recover energy barriers sufficient low to predict the conductance of either KcsA or the pore domain of Kvchim. In future work, we will examine the detailed structural changes that occur during a conduction event.

Methods

Producing Equilibrated Structures for Umbrella Sampling

Crystallographic structures of KcsA3 (PDB:1K4C) and Kvchim4 (PDB: 2R9R) were obtained. The voltage sensors of Kvchim were removed, leaving the pore domain (residues 321–417), and missing atoms were added as described in Fowler and Sansom.5 The psfgen package of VMD63 was used to add the missing atoms to Arg117 of KcsA and to protonate Glu71 or mutate it to alanine, where necessary. Potassium ions were then placed at the S0, S2, and S4 positions with waters at S1 and S3. The cavity of the pore was solvated using the voidoo and flood programs.64 The resulting pore domains were embedded in simple lipid bilayers by conversion into a coarse-grained representation and subsequent self-assembly of a lipid bilayer around the protein as described elsewhere.5,65 All simulations used a simple POPC bilayer, with the exception of kcsa-11a, which used a mixed POPE/POPG bilayer in the ratio 7:3. Simulations of KcsA had 234 lipids (66 POPG and 168 POPE for kcsa-11a) and simulations of the pore domain of Kvchim had 227 POPC lipids. The small patch of lipid bilayer was solvated with explicit water using the solvate plugin to VMD63 and neutralizing sodium and chloride ions added making a total of 70 268–70 889 atoms for KcsA and 72 354 atoms for Kvchim. The CHARMM forcefield with CMAP correction was used,43 and therefore, all hydrogens are explicitly modeled. The energy of the resulting simulation unit cells was minimized for 1000 steps using NAMD2.7,66 and then the temperature was gradually increased from 100 to 300 K in steps of 20 K, running for 40 ps at a time. During this procedure, the positions of the heavy atoms of the lipid headgroups (atom names N C11 C15 O2 P1 O3 C1) were constrained in the direction of the membrane normal with a spring constant of 10 kcal/mol/Å2. The constraints on the lipids were then reduced 10 fold, and a further 60 ps of MD was run at 310 K. This and all subsequent simulations were run in the NpT ensemble. The temperature was held at 310 K using a Langevin thermostat with a damping coefficient of 1.0 ps–1. The pressure was maintained at 1 atm using either a Berendsen barostat67 (applied anisotropically with a compressibility of 4.46 × 10–5 bar–1 and a relaxation time of 0.2 ps) or a Langevin Piston barostat68 (with an oscillation period of 200 fs and a damping time constant of 100 fs). Electrostatic forces were calculated between charged atoms using the particle mesh Ewald method69 with a grid spacing of 1 Å and a real space cutoff of 13.5 Å. van der Waals forces were truncated at 12 Å with a switching function applied from 10 Å. SETTLE,70 and SHAKE71 used to constrain the length of all bonds involving a hydrogen atom, permitting an integration time step of 2 fs. The dynamics of the system were then simulated until the pore domain had equilibrated, as measured by RMSD. This was typically for 10–20 ns.

Defining the Coordinates z12 and z3

We follow the method of Bernèche and Roux6 and define the pore axis as follows. The origin of the axis is the center of mass of the heavy backbone atoms (atom names C CA N) of the residues TVGY in the selectivity filter. The direction of the axis is defined by a unit vector pointing from the center of mass of the residues TV to the center of mass of the residues GY. The positions of ion 1, ion 2, and ion 3 along this axis (z1, z2, z3) were then calculated using linear algebra. As per Bernèche and Roux,13 we simplified the calculation by only following the center of mass of ion 1 and ion 2, ion 12 (z12), in addition to ion 3 (z3). We assumed then that the configuration of the selectivity filter can be described by a point in (z12, z3) space. During the equilibration process described above, harmonic potentials with spring constants 10 kcal/mol/Å2 were applied to ion 12 and ion 3 to prevent the selectivity filter changing configuration. The coordinates of the ions were calculated, and the harmonic forces updated every time step using the TclForces module in NAMD. This was also used to write out every 200 fs the coordinates of the heavy atoms of the selectivity filter and the three bound potassium ions and intervening waters. The positions of the ions was written to disc every 20 fs and coordinates of the entire system every 10–20 ps.

Running the Umbrella Simulations

Each umbrella simulation sampled a region of (z12, z3) space. They were either arranged on a rectangular or trigonal grid (we found the latter to be more efficient). During the umbrella simulations, harmonic potentials with spring constants k12 and k3 were applied to ion 12 and ion 3, and their coordinates recorded as described above. The spacing between the coordinates of neighboring constraints was 0.5 Å. The spring constant k3 was set to 20 kcal/mol/Å2, whereas a range of magnitudes for k12 was used in the range 20–40 kcal/mol/Å2. Occasionally, additional simulations were run with k12 set to 80 kcal/mol/Å2 to improve the sampling of the umbrella simulations in some regions of (z12, z3) space (Table 1). The exception was kcsa-11b, where k12 was set to 80 kcal/mol/Å2 for all simulations; this necessitated reducing the spacing of the simulations in the z12 direction to 0.25 Å. A set of initial structures with the selectivity filter in a range of configurations was generated from the equilibrated structure of the channel by permuting the positions of the ions and water molecules. To prevent distortion of the filter, the magnitude of the umbrella force was capped at 5.0 kcal/mol/Å2 for the first 20–50 ps of each simulation. In total, 1 771 umbrella simulations were run, each for 200 ps, making a total of 0.354 μs of simulations.

All the umbrella simulations were then analyzed, and the number of waters between each potassium ion was counted (Figure S3, Supporting Information) using VMD.63 A potassium ion was defined as being inside the filter if its pore axis coordinate was within the bounds set by the centers of mass of the hydroxyl oxygen of Thr75 (KcsA or Thr371 - Kvchim) and the backbone carbonyl oxygens of Tyr78 (Kcsa or Tyr374, Kvchim). Any frame where there was not a single water between both potassium ions and were themselves inside the filter was discarded. To be conservative, all subsequent frames from a single umbrella simulation were also discarded because the escape of an intervening water is a slow process. If either potassium ion was deemed to be outside the filter by the above definition, any number of intervening waters was permitted. The number of frames removed is given in Table S1 of the Supporting Information. The ψ backbone dihedral angle of Val-76 (KcsA) or Val-371 (Kvchim) was also calculated (Figure S4, Supporting Information) using MDAnalysis72 for all 1 771 umbrella simulations. Any frame where ψ was >0 was also discarded.

Unbiasing the Data, Determining Convergence, and Estimating a Correlation Time

The resulting seven data sets (Table 1) were first divided into 100 bins, each 2 ps wide. The bias was removed, and a 2D potential of mean force for each bin was calculated using an implementation73 of the weighted histogram analysis method (WHAM).37 The minimum free energy path was found using an implementation of the nudged elastic band method.74 The height of the barrier between the first two configurations was measured, as shown for kcsa-11 in Figure S1B of the Supporting Information. Plotting this against time gives a qualitative check of when the calculation has converged (Figure S1C, Supporting Information). The statistical inefficiency75 was then calculated for this data set. The statistical inefficiency, s(n), is defined as

graphic file with name ct-2013-005933_m008.jpg

where x is the 100 (presumably) correlated values of the barrier height, which are then binned with width n to produce a second data set of xn values. If the data set is converged then the ratio of the variances multiplied by the bin width, n, should tend toward a limit as n tends to ∞. We followed the method of Yang et al.76, and by penetrating the reversed data set x to different degrees and calculating s(n), one can estimate both the convergence and subsequent correlation times. This is shown in Figure S1D and E of the Supporting Information. From this, we estimate that the first 100 ps should be discarded, and 20 ps is a conservative estimate of the correlation time for the remaining data. We assumed that the other data sets (kvchim-10, etc.) would behave similarly. Five independent 2D PMFs can therefore be produced for each data set (Figure S6, Supporting Information) and combined in the usual way to estimate errors (Figure S7, Supporting Information). All graphs were produced using gnuplot, and all images were rendered using VMD63

Calculating the Minimum Free Energy Path

We implemented the nudged elastic band method in python,5 including several of enhancements suggested by the authors, such as gradually turning on the perpendicular component of the spring force when the path is kinky.74 The initial path was formed by connecting 64 beads in a straight line between two points: one just below the wKwKw(K) configuration (−1.9,9.4), and the other just above the KwKwK configuration (4.3,–4.1). We investigated whether a second degenerate pathway existing by connecting 48 beads between points 3 and 5 taken from the first MFEP. The initial path taken was not a simple straight line but ran via a waypoint to the right of point 3. This was usually sufficient for the algorithm to find the second path, path2.

Calculating the Voltage Drop along the Pore Axis

The potential drop across the channel pore was calculated via Poisson–Boltzmann electrostatics calculations with the PBEQ module77 in CHARMM 35b1.78 The Poisson–Boltzmann (PB) equation was solved without and with applied voltage at an ionic strength of 150 mM. The difference of values Δϕ(z) = ϕ(V) – ϕ(0 V) of the potential along the pore axis represents the contribution from the external potential to the total potential. Calculations were performed on a grid of dimensions 100 × 100 × 110 grid points and a spacing of 1 Å. The position of the transmembrane domain inside the lipid bilayer was extracted from simulations and a dielectric slab of thickness 45 Å with dielectric coefficient ε = 2 was set up to mimic the low-dielectric environment of the protein. The protein itself was set to ε = 4 and the aqueous environment to 80. The channel pore was also modeled as aqueous solution. The linear Poisson–Boltzmann was solved, and the solution used as a starting point for solving the nonlinear PB equation with under-relaxation and λ = 0.6.

Acknowledgments

This work was funded by the Wellcome Trust through Programme Grants 083547/Z/07/Z and 092970/Z/10/Z. We are grateful to the UK National Grid Service, Oxford Supercomputing Centre, and EPSRC Complementary Capability Computing Initiative through Grant EP/G042659/1 for providing access to the HPCx supercomputer. E.A. gratefully acknowledges additional financial support by the Wiener Anspach Foundation at the early stages of this work, as well as support by the Ministerio de Ciencia y Tecnologia (Spain) through Grant No. FIS2010-16587 (partially financed by FEDER funds) and Junta de Extremadura through Grant No. GRU10158.

Supporting Information Available

Supplementary tables and figures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

‡ Departamento de Física Aplicada, Centro Universitario de Mérida, Universidad de Extremadura, Mérida, Spain.

Author Present Address

Department of Physics, Arizona State University, Phoenix, Arizona 85004, United States.

The authors declare no competing financial interest.

Supplementary Material

ct4005933_si_001.pdf (5.3MB, pdf)

References

  1. Eisenberg B. Biophys. Chem. 2003, 100, 507–517. [DOI] [PubMed] [Google Scholar]
  2. Hille B.Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates, Inc: Sunderland, MA, 2001. [Google Scholar]
  3. Zhou Y.; Morais-Cabral J. H.; Kaufman A.; MacKinnon R. Nature 2001, 414, 43–48. [DOI] [PubMed] [Google Scholar]
  4. Long S. B.; Tao X.; Campbell E. B.; MacKinnon R. Nature 2007, 450, 376–382. [DOI] [PubMed] [Google Scholar]
  5. Fowler P. W.; Sansom M. S. P. Nature Commun. 2013, 4, 1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bernèche S.; Roux B. Nature 2001, 414, 73–77. [DOI] [PubMed] [Google Scholar]
  7. Ranatunga K. M.; Shrivastava I. H.; Smith G. R.; Sansom M. S. Biophys. J. 2001, 80, 1210–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Morais-Cabral J. H.; Zhou Y.; MacKinnon R. Nature 2001, 414, 37–42. [DOI] [PubMed] [Google Scholar]
  9. Fowler P. W.; Tai K.; Sansom M. S. P. Biophys. J. 2008, 95, 5062–5072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cordero-Morales J. F.; Jogini V.; Lewis A.; Vásquez V.; Cortes D. M.; Roux B.; Perozo E. Nat. Struct. Mol. Biol. 2007, 14, 1062–1069. [DOI] [PubMed] [Google Scholar]
  11. Lee S.-Y.; Banerjee A.; MacKinnon R. PLoS Biol. 2009, 7, e1000047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. LeMasurier M.; Heginbotham L.; Miller C. J. Gen. Physiol. 2001, 118, 303–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Bernèche S.; Roux B. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 8644–8648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Doyle D.; Cabral J.; Pfuetzner R.; Kuo A.; Gulbis J. M.; Cohen S. L.; Chait B. T.; MacKinnon R. Science 1998, 280, 69–77. [DOI] [PubMed] [Google Scholar]
  15. Chung S.-H.; Corry B. Soft Matter 2005, 1, 417–427. [DOI] [PubMed] [Google Scholar]
  16. Tai K.; Fowler P. W.; Mokrab Y.; Stansfeld P.; Sansom M. S. P. In Methods in Cell Nano Biology, 1st ed.; Jena B. P., Ed.; Elsevier: B.V., 2008; Vol. 90, Chapter 12, pp 233.–. [DOI] [PubMed] [Google Scholar]
  17. Roux B. Biophys. J. 1999, 77, 139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Abad E.; Reingruber J.; Fowler P.; Sansom M. S. P.; Wei D.-Q.; Wang X.-J. AIP Conf. Proc. 2009, 1102, 236–243. [Google Scholar]
  19. Abad E.; Reingruber J.; Sansom M. S. P. J. Chem. Phys. 2009, 130, 085101. [DOI] [PubMed] [Google Scholar]
  20. Furini S.; Domene C. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 16074–16077. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Furini S.; Domene C. J. Mol. Biol. 2011, 409, 867–878. [DOI] [PubMed] [Google Scholar]
  22. Furini S.; Domene C. Biophys. J. 2011, 101, 1623–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Domene C.; Klein M. L.; Branduardi D.; Gervasio F. L.; Parrinello M. J. Am. Chem. Soc. 2008, 130, 9474–9480. [DOI] [PubMed] [Google Scholar]
  24. Treptow W.; Tarek M. Biophys. J. 2006, 91, L81–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bastug T.; Kuyucak S. Biophys. J. 2011, 100, 629–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Egwolf B.; Roux B. J. Mol. Biol. 2010, 401, 831–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Pongprayoon P.; Beckstein O.; Wee C. L.; Sansom M. S. P. Proc. Natl. Acad. Sci. U.S.A. 2009, 106, 21614–21618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Khalili-Araghi F.; Tajkhorshid E.; Schulten K. Biophys. J. 2006, 91, L72–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Jensen M. O.; Borhani D. W.; Lindorff-Larsen K.; Maragakis P.; Jogini V.; Eastwood M. P.; Dror R. O.; Shaw D. E. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 5833–5838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jensen M. O.; Jogini V.; Borhani D. W.; Leffler A. E.; Dror R. O.; Shaw D. E. Science 2012, 336, 229–233. [DOI] [PubMed] [Google Scholar]
  31. Jensen M. O.; Jogini V.; Eastwood M. P.; Shaw D. E. J. Gen. Physiol. 2013, 141, 619–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Roux B. Comput. Phys. Commun. 1995, 91, 275–282. [Google Scholar]
  33. Bernèche S.; Roux B. Structure 2005, 13, 591–600. [DOI] [PubMed] [Google Scholar]
  34. Bernèche S.; Roux B. Biophys. J. 2000, 78, 2900–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Capener C. E.; Proks P.; Ashcroft F. M.; Sansom M. S. P. Biophys. J. 2003, 84, 2345–2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Domene C.; Sansom M. S. P. Biophys. J. 2003, 85, 2787–2800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Kumar S.; Rosenberg J. M.; Bouzida D.; Swendsen R. H.; Kollman P. A. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
  38. Friedberg R. J. Chem. Phys. 1970, 52, 6049–6058. [Google Scholar]
  39. Hodgkin A. L.; Keynes R. D. J. Physiol. 1955, 128, 61–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Zhou Y.; MacKinnon R. Biochemistry 2004, 43, 4978–4982. [DOI] [PubMed] [Google Scholar]
  41. Furini S.; Domene C. PLos Comput. Biol. 2012, 8, e1002476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Roux B.; Bernèche S. Biophys. J. 2002, 82, 1681–1684. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Mackerell A. D. J. Comput. Chem. 2004, 25, 1584–1604. [DOI] [PubMed] [Google Scholar]
  44. Buck M.; Bouguet-Bonnet S.; Pastor R. W.; MacKerell A. D. Biophys. J. 2006, 90, L36–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Bastug T.; Kuyucak S. Biophys. J. 2009, 96, 4006–4012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Marius P.; Zagnoni M.; Sandison M. E.; East J. M.; Morgan H.; Lee A. G. Biophys. J. 2008, 94, 1689–1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Denning E. J.; Woolf T. B. Biophys. J. 2008, 95, 3161–3173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. MacKinnon R. Science 1998, 280, 106–109. [DOI] [PubMed] [Google Scholar]
  49. Bucher D.; Raugei S.; Guidoni L.; Dal Peraro M.; Rothlisberger U.; Carloni P.; Klein M. L. Biophys. Chem. 2006, 124, 292–301. [DOI] [PubMed] [Google Scholar]
  50. Schmidt D.; Del Mármol J.; Mackinnon R. Proc. Natl. Acad. Sci. U.S.A 2012, 109, 10352–10357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Chipot C.; Pohorille A.. Free Energy Calculations: Theory and Applications in Chemistry and Biology; Springer: Berlin, 2007. [Google Scholar]
  52. Zhou Y.; MacKinnon R. J. Mol. Biol. 2003, 333, 965–975. [DOI] [PubMed] [Google Scholar]
  53. Peng R. D. Science 2011, 334, 1226–1227. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Faraldo-Gómez J. D.; Roux B. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 13643–13648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Allen T. W.; Andersen O. S.; Roux B. Biophys. Chem. 2006, 124, 251–267. [DOI] [PubMed] [Google Scholar]
  56. Pohorille A.; Jarzynski C.; Chipot C. J. Phys. Chem. B 2010, 114, 10235–10253. [DOI] [PubMed] [Google Scholar]
  57. Payandeh J.; Scheuer T.; Zheng N.; Catterall W. A. Nature 2011, 475, 353–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. McCusker E. C.; Bagnéris C.; Naylor C. E.; Cole A. R.; D’Avanzo N.; Nichols C. G.; Wallace B. A. Nature Comms. 2012, 3, 1102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Corry B.; Thomas M. J. Am. Chem. Soc. 2012, 134, 1840–1846. [DOI] [PubMed] [Google Scholar]
  60. Stock L.; Delemotte L.; Carnevale V.; Treptow W.; Klein M. L. J. Phys. Chem. B 2013, 117, 3782–3789. [DOI] [PubMed] [Google Scholar]
  61. Ulmschneider M. B.; Bagneris C.; McCusker E. C.; DeCaen P. G.; Delling M.; Clapham D. E.; Ulmschneider J. P.; Wallace B. A. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 6364–6369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Chakrabarti N.; Ing C.; Payandeh J.; Zheng N.; Catterall W. A.; Pomès R. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 11331–11336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Humphrey W.; Dalke A.; Schulten K. J. Mol. Graph 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]
  64. Kleywegt G. J.; Jones T. A. Acta. Cryst. D 1994, 50, 178–185. [DOI] [PubMed] [Google Scholar]
  65. Scott K. A.; Bond P. J.; Ivetac A.; Chetwynd A. P.; Khalid S.; Sansom M. S. P. Structure 2008, 16, 621–630. [DOI] [PubMed] [Google Scholar]
  66. Phillips J. C.; Braun R.; Wang W.; Gumbart J.; Tajkhorshid E.; Villa E.; Chipot C.; Skeel R. D.; Kalé L.; Schulten K. J. Comput. Chem. 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar]
  68. Feller S. E.; Zhang Y.; Pastor R. W.; Brooks B. R. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar]
  69. Darden T.; York D.; Pedersen L. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar]
  70. Miyamoto S.; Kollman P. A. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar]
  71. Ryckart J.; Ciccotti G.; Berendsen H. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar]
  72. Michaud-Agrawal N.; Denning E. J.; Woolf T. B.; Beckstein O. J. Comput. Chem. 2011, 32, 2319–2327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Grossfield A. WHAM: The Weighted Histogram Analysis Method. Version 2. http://membrane.urmc.rochester.edu/content/wham/ (accessed September 19, 2013).
  74. Jónsson H.; Mills G.; Jacobsen K. W.. Classical and Quantum Dynamics in Condensed Phase Simulations - Proceedings of the International School of Physics; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1998; Chapter 16, pp 385–404. [Google Scholar]
  75. Chodera J. D.; Swope W. C.; Pitera J. W.; Seok C.; Dill K. A. J. Chem. Theory Comput. 2007, 3, 26–41. [DOI] [PubMed] [Google Scholar]
  76. Yang W.; Bitetti-Putzer R.; Karplus M. J. Chem. Phys. 2004, 120, 2618–2628. [DOI] [PubMed] [Google Scholar]
  77. Nina M.; Beglov D.; Roux B. J. Phys. Chem. B 1997, 101, 5239–5248. [Google Scholar]
  78. Brooks B. R.; et al. J. Comput. Chem. 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct4005933_si_001.pdf (5.3MB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES