Atmospheric deposition of methanol over the Atlantic Ocean

Significance

Transport of gases between the ocean and the atmosphere has profound implications for our environment and the Earth’s climate. An example of this transport is the oceanic uptake of carbon dioxide, which has buffered us from a higher concentration of this greenhouse gas in the atmosphere while also causing ocean acidification. Here we describe the first direct measurements of air–sea methanol transfer. Atmospheric methanol, a ubiquitous and abundant organic gas of primarily terrestrial origin, is observed to be transported over thousands of kilometers and deposited over the ocean, where it is likely consumed by marine microbes. We quantify the rate of methanol deposition and examine the governing processes near the air–sea interface.

Abstract

In the troposphere, methanol (CH₃OH) is present ubiquitously and second in abundance among organic gases after methane. In the surface ocean, methanol represents a supply of energy and carbon for marine microbes. Here we report direct measurements of air–sea methanol transfer along a ∼10,000-km north–south transect of the Atlantic. The flux of methanol was consistently from the atmosphere to the ocean. Constrained by the aerodynamic limit and measured rate of air–sea sensible heat exchange, methanol transfer resembles a one-way depositional process, which suggests dissolved methanol concentrations near the water surface that are lower than what were measured at ∼5 m depth, for reasons currently unknown. We estimate the global oceanic uptake of methanol and examine the lifetimes of this compound in the lower atmosphere and upper ocean with respect to gas exchange. We also constrain the molecular diffusional resistance above the ocean surface—an important term for improving air–sea gas exchange models.

Background

Atmospheric methanol affects tropospheric oxidative capacity and air pollution by participating in the cycling of ozone and the hydroxyl radical (OH). Methanol is primarily released to air from terrestrial plants (during growth and decay); other identified sources include industrial emissions, biomass and biofuel burning, and atmospheric production (1–5). Methanol reacts with OH in the troposphere with a photochemical lifetime of ∼10 d, leading to formaldehyde (6) and carbon monoxide (7), among other products. Observations suggest that methanol can be further removed from air via deposition to land (8) and to the sea surface (9, 10). In the upper ocean, methanol supports the growth of methylotrophic bacteria (11) and has recently been found to be consumed by SAR11 alphaprotoeobacteria, the most abundant marine heterotrophs (12). The turnover time of seawater methanol is thus quite short, on the order of a few days (13, 14). However, significant oceanic concentrations of methanol have been detected in the range of 50∼400 nM (9, 15–17), leading to questions about its source.

To understand the global cycling of methanol, it is imperative to quantify its transport between the ocean and the atmosphere. Heikes et al. (3) modeled a gross air-to-sea depositional loss of −80 Tg⋅y⁻¹ and also argued for an oceanic source of 30 Tg⋅y⁻¹ to sustain an observed concentration of 0.9 ppb in the marine atmospheric boundary layer (MABL) of the Pacific and Atlantic. Based on aircraft measurements over the Pacific, Singh et al. (18) estimated a loss of −8 Tg⋅y⁻¹ to the surface ocean with no appreciable oceanic source, which was later modified to −10 Tg⋅y⁻¹ by Jacob et al. (4). Millet et al. (5) modeled a gross deposition of −101 Tg⋅y⁻¹ to the ocean—a sink largely offset by an oceanic production of 85 Tg⋅y⁻¹. From in situ seawater concentration measurement and modeled atmospheric distribution over the Atlantic, Beale et al. (17) recently calculated a net oceanic emission of 12 Tg⋅y⁻¹, but saw evidence for both oceanic production and uptake. Amid these large discrepancies is the fact that the air–sea methanol flux has never been measured directly (e.g., with eddy covariance)—a void we address with this report.

Due to challenges in direct quantification, the flux of a gas across the air–sea interface is often approximated as the product of the gas transfer velocity and the air–sea concentration difference using the two-layer model (19):

Here, C_w and C_a are the bulk concentrations of the gas in water and atmosphere. H is the dimensionless Henry’s solubility expressed as the ratio of liquid-to-gas concentrations at equilibrium. C_w/H denotes the concentration on the airside of the interface that would be equilibrated with the waterside. When C_w/H is less than C_a, surface water is undersaturated relative to the atmosphere and the flux is from air to sea. K_a is the total gas transfer velocity from the perspective of atmospheric concentrations. Governed by molecular and turbulent transfer in both phases, K_a encompasses the kinetic forcing in gas exchange.

Molecular sublayers exist on both sides of the air–sea interface, where turbulent transport diminishes and molecular diffusion dominates. Conceptualizing the system as two resistors in series, K_a can be partitioned to individual transfer velocities in air and water (k_a and k_w, respectively):

For sparingly soluble gases (low H), transport through the aqueous molecular sublayer is the rate-limiting step (i.e., K_a ∼ Hk_w). Such waterside controlled gases, including carbon dioxide (CO₂) and sulfur hexafluoride (SF₆), have been the subjects of decades of research (20). In contrast, transfer of very soluble (high H) and/or surface reactive gases is limited on the airside (i.e., K_a ∼ k_a). For the highly soluble methanol with H of ∼5,000 at 25 °C (21), the second term in Eq. 2 contributes at most a few percent to K_a.

The airside transfer velocity is dictated by resistances from aerodynamic transport in the turbulent atmosphere (R_t) and diffusion in the airside molecular sublayer (R_m):

Our knowledge of k_a stems mostly from studies of latent heat (water vapor) and sensible heat (conduction due to the air–sea temperature difference). Resistance-based models (22, 23) and, more recently, the Center for Coupled Ocean-Atmosphere Response Experiment (COARE) gas transfer model (24) suggest that at a height well above the sea surface (e.g., 10 m), R_t substantially exceeds R_m. The predominance of turbulent transport might be one reason why rates of water vapor transfer measured over the ocean are significantly lower than those observed in laboratories (25, 26), where dynamics are different.

To relate k_a of water vapor or sensible heat to other gases, R_m is assumed to be proportional to Sc_a^1/2∼2/3, where Sc_a is the airside Schmidt number (ratio of kinematic viscosity to molecular diffusivity in air). However, limited open-ocean observations of airside-controlled trace gases have demonstrated diverging behaviors from water vapor, which are so far unexplained. Eddy covariance measurements of the very soluble acetone resulted in air–sea flux at times opposite in direction to the prediction from the two-layer model (27). In the case of the surface reactive sulfur dioxide, aircraft flux measurements yielded k_a values ∼30% lower than expected (28). Thus, flux observation of another gas with predominantly airside control, such as methanol, has the potential to reduce the uncertainty in k_a and ultimately improve flux estimations based on Eq. 1.

Results

On the 22nd Atlantic Meridional Transect (AMT-22) cruise on the Royal Research Ship James Cook (October∼November 2012) from Southampton, United Kingdom, to Punta Arenas, Chile, we measured the air–sea flux of methanol directly with the eddy covariance method. Quantified by a proton transfer reaction mass spectrometer (PTR-MS) with an isotopically labeled standard, atmospheric methanol concentration (C_a) was correlated with motion-corrected vertical wind velocity (w) to yield its net vertical transport. We also measured the dissolved concentration of methanol (C_w) at ∼5 m depth from hydrocasts with the same PTR-MS coupled to a membrane inlet (16).

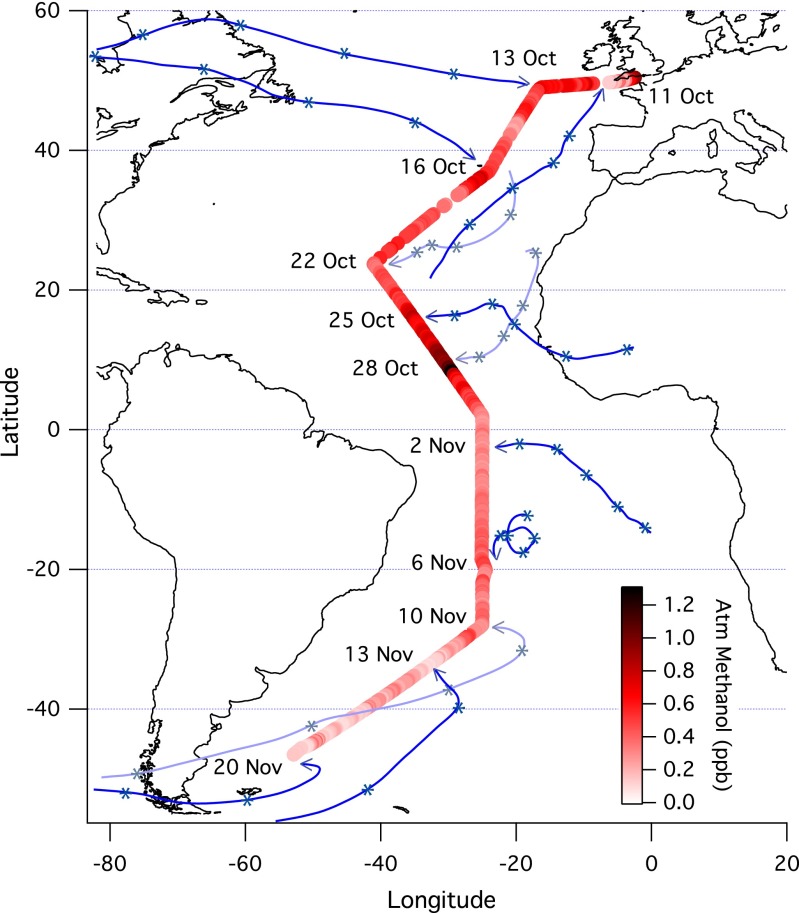
Fig. 1 shows the cruise track of AMT-22, color-coded by the atmospheric methanol concentration. To illustrate where sampled air masses resided previously, we overlay 5-d back-trajectories from the Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) model (29). C_a was higher in the Northern Hemisphere, as expected from the greater landmass and anthropogenic activity. At the same latitudes, our C_a values are comparable to previous maritime measurements at Cape Verde (30) and near the tropics (9). From north to south across the Intertropical Convergence Zone at ∼3°N, C_a decreased rapidly from ∼0.6 to ∼0.3 ppb. Plumes of higher C_a can be seen in continental outflow regions (e.g., off Northern Africa and North America), whereas lower values are observed in air masses that had not been in contact with land for several days. Sudden depletion in C_a often coincided with precipitation (e.g., October 11, October 14, November 13), likely in part due to removal by wet deposition and heterogeneous chemistry (3).

Fig. 1.

Cruise track of AMT-22 color-coded by the hourly atmospheric methanol concentration (n = 734) and overlaid with 5-d back-trajectories (initiated from the MABL and marked on daily intervals) for selected days. Methanol concentration was higher in the Northern Hemisphere than in the Southern, and particularly elevated in continental outflow regions (e.g., Northern Africa and North America). In contrast, depleted concentrations were observed for air masses that had not been in recent contact with land and during precipitation. Given its atmospheric lifetime of several days, methanol may be considered a tracer for terrestrial emissions, but is unlikely to undergo interhemispheric transport, which has a timescale of ∼1 y.

Latitudinal distributions of atmospheric and seawater methanol concentrations are shown in Fig. 2A. Compared with previous measurements (9, 15–17), C_w was considerably lower during AMT-22, with a mean (range) of 29 (15∼62) nM. C_w correlated weakly with C_a (r² = 0.11, P = 0.003, two-tailed) and demonstrated no clear hemispheric trend. Surface water was undersaturated in methanol with respect to the atmosphere (Fig. 2B), consistent with rapid oceanic destruction. Saturation level was lower on average in the Northern Hemisphere (24%) than in the Southern (34%), correlating weakly with wind speed (r² = 0.10, P = 0.007, two-tailed). Measured air–sea methanol flux (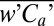) averaged to latitude bins is shown in Fig. 2C. Greater air-to-sea flux occurred in regions of high C_a and strong winds, with the largest oceanic uptake found in the subtropical and tropical North Atlantic.

Fig. 2.

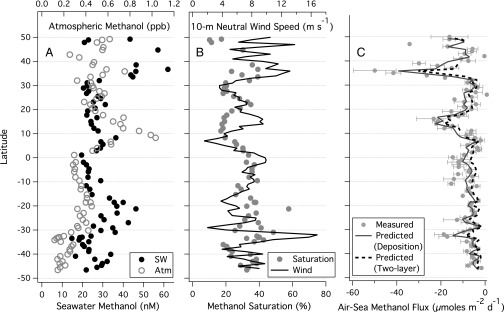
(A) Latitudinal distributions of atmospheric and seawater methanol concentrations; (B) saturation level of methanol and wind speed; (C) air–sea methanol flux measured by eddy covariance and predicted by a two-layer model and a purely deposition model based on observed concentrations (n = 73). Error bars on flux represent SE. Seawater concentration did not demonstrate any hemispheric trend, and was significantly undersaturated with respect to the atmosphere, implying rapid oceanic degradation. Methanol flux was consistently from air to sea, peaking in regions of high atmospheric concentration and strong wind. Flux averaged −14 μmol⋅m⁻²⋅d⁻¹ in the subtropical and tropical Atlantic, and was as much as −50 μmol⋅m⁻²⋅d⁻¹. In the South Atlantic, flux was lower in magnitude, with a mean of −8 μmol⋅m⁻²⋅d⁻¹.

Two approaches of predicting bulk air–sea methanol flux based on observed concentrations are shown in Fig. 2C: the first from the two-layer model (Eq. 1) with k_a from Mackay and Yeun (25) and k_w from the COARE (24), and the second as purely deposition (−k_a C_a) with k_a from ref. 24. Though both approaches yield reasonable fits to measured flux, the agreement is somewhat fortuitous. Based on volatilization experiments in a wind-wave tank, k_a from ref. 25 overestimates water transfer relative to observed rate over the ocean, which is better represented by ref. 24. However, the formulation, k_a C_a, specifies a unidirectional transfer of methanol from air to sea and no return flux. Using k_a from ref. 24 in the two-layer model or k_a from ref. 25 in the purely deposition model results in significant underestimation and overestimation, respectively.

Discussion

We first examine the influence of air–sea exchange on the atmospheric and oceanic methanol budgets. The vertical gradient in C_a within the atmospheric surface layer (the lowest ∼10% of the MABL) can be approximated from similarity theory as −Flux/(κ u_* z), with κ being the von Karmon constant and z the sampling height. In this case, C_a is estimated to increase with height at an average rate of ∼0.002 ppb⋅m⁻¹. For a 1-km-high MABL with a mean mixing ratio of 1 ppb, deposition to the ocean removes methanol from air with a timescale of ∼4 d. Crudely assuming the global ocean to have the same methanol and wind speed distributions as during our cruise, an average methanol flux of −10 μmol⋅ m⁻²⋅ d⁻¹ extrapolates to a net air–sea transport of −42 Tg⋅y⁻¹. Substituting this flux into previous global budgets (3–5), it is evident that air–sea exchange accounts for 18∼23% of the total removal of atmospheric methanol.

The atmosphere does not appear to be the sole source of seawater methanol, however. Assuming a 50-m-deep oceanic mixed layer with a dissolved methanol concentration of 29 nM, at a mean flux of −10 μmol⋅m⁻²⋅d⁻¹, the replacement time for seawater methanol is 140 d with respect to gas exchange, approximately two orders of magnitude longer than the typical turnover time due to biological consumption (13, 14). Thus, a suggested “missing” source of seawater methanol (3, 5, 13) seems justified for mass balance. Furthermore, we found methanol concentration at ∼500 m depth to be 60∼80% of the 5-m value, proportionally similar to depth profiles observed previously (9, 17). Given the measurable biological consumption of methanol at depth (14), the presence of significant concentration there suggests that its production is not limited to the near surface. A recent work shows that methanol may be produced by the marine proteobacteria Alteromonadales (31).

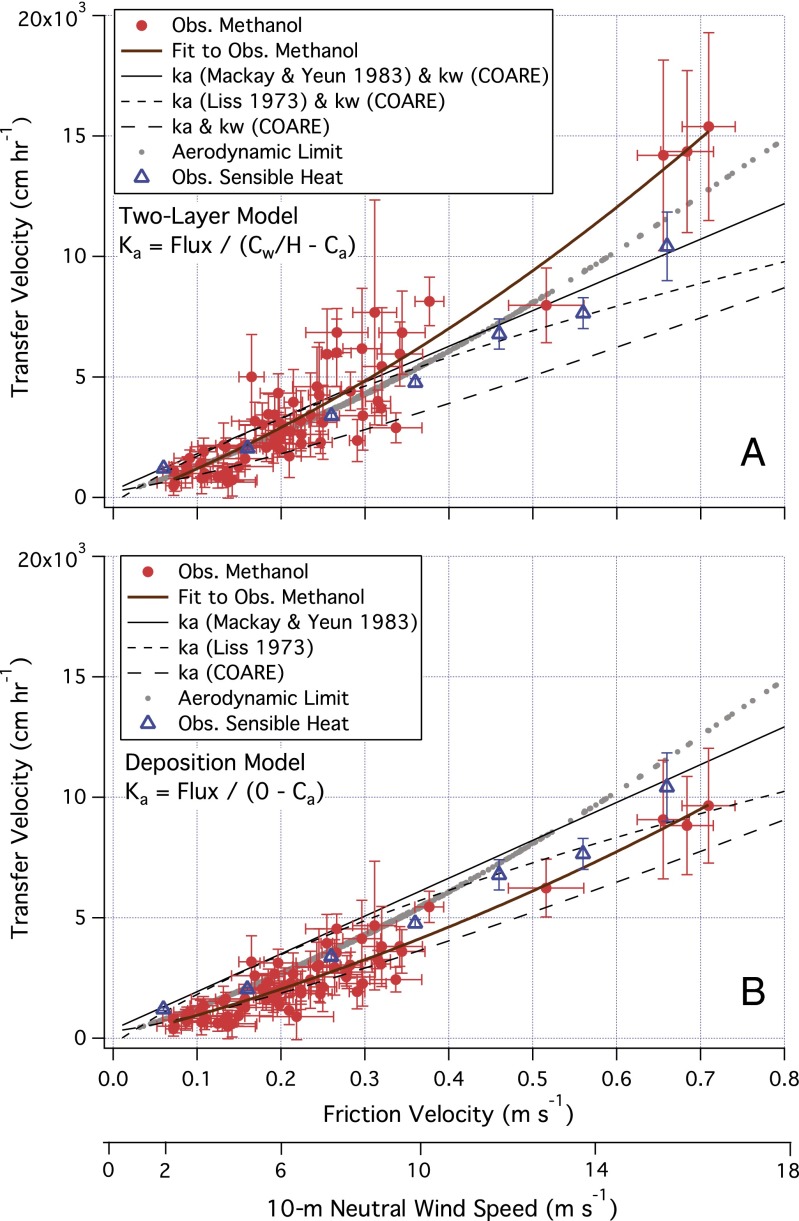
Now we turn our attention to the process of air–sea methanol transfer. We calculate K_a from measured flux using observed C_w (Fig. 3A) and by setting C_w to zero (Fig. 3B). To account for buoyancy effects, K_a is adjusted to neutral atmospheric stability based on similarity theory (32) and plotted against the measured friction velocity (u_*, related to wind stress) as well as the approximate 10-m neutral wind speed. Also shown are parameterizations from Mackay and Yeun (25), Liss (26) adjusted for molecular weight (19), and COARE (24). The aerodynamic limit from COARE (1/R_t) defines the theoretical rate of atmospheric turbulent transfer. In addition, we show the in situ transfer velocity of sensible heat 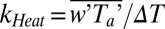, where T_a is the air temperature from the sonic anemometer corrected for humidity, and ∆T the air–sea temperature difference.

Fig. 3.

(A) Methanol transfer velocity calculated using measured C_w; (B) calculated using C_w = 0 (n = 73). Measured friction velocity and the approximate wind speed are shown on the abscissae. Using measured C_w, calculated methanol transfer velocity sometimes exceeds the aerodynamic limit, particularly in high winds. In contrast, using C_w = 0 leads to more reasonable K_a, implying low dissolved methanol concentrations close to the air–water interface. K_Heat adjusted to neutral stability is shown as averages in u_* bins. Error bars on K_a, K_Heat, and u_* correspond to the respective SEs.

With the two-layer approach using observed C_w (Fig. 3A), the polynomial fit 11,766 u_* + 13,804 u_*² (R² = 0.87) describes the nonlinear relationship between K_a and u_*. K_a is similar to k_Heat and the aerodynamic limit at low to moderate winds (u_* < 0.4 m⋅s⁻¹), which confirms the expectation that methanol is airside controlled and has minimal waterside resistance. At u_* > 0.4 m⋅s⁻¹, K_a trends ∼15% higher than the aerodynamic limit, and significantly exceeds k_Heat by ∼20% (χ² test at 95% confidence), which is inconsistent with physical theory. Uncertainties in K_a amplify in high winds due to the small sample size as well as greater measurement errors (Methods). Nevertheless, based on Eq. 3, K_a for methanol should be ∼10% lower than k_Heat because of the higher Sc_a for methanol (1.09) (33) relative to heat (Sc_a = 0.64), which is not reflected in Fig. 3A.

Transfer velocity calculated with C_w = 0 equates to a one-way deposition velocity (Fig. 3B). By specifying the maximum air–sea concentration difference, the deposition velocity represents the lower limit of k_a. The mean deposition velocity of 2,444 cm⋅h⁻¹ converts to 0.68 cm⋅s⁻¹, which is several times higher than previous estimates based on temporal trends in the atmospheric methanol concentration (10) and vertical profiles from the MABL to the free troposphere (18). We note that our measurements by eddy covariance are the most direct and do not require assumptions about the seawater saturation or atmospheric chemistry of methanol.

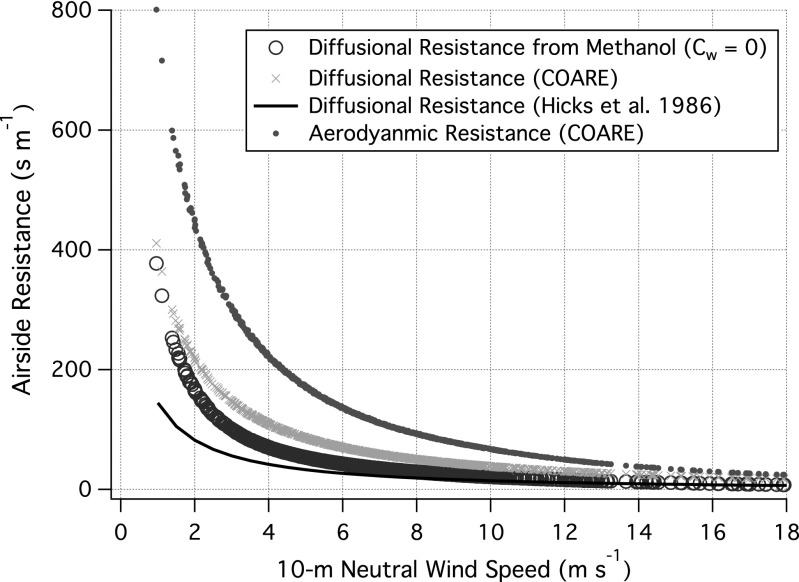
With C_w = 0, K_a demonstrates a near linear relationship with u_*, and may be fitted by 8,814 u_* + 6,810 u_*² (R² = 0.89), which is lower than the aerodynamic limit as well as measured k_Heat, and lies between laboratory results (25, 26) and the resistance-based parameterization (24). Compared with Fig. 3A, as expected, the periods with the highest saturation values had the largest reductions in K_a. We further solve for resistance in the airside molecular diffusion sublayer above the ocean surface by taking the difference between R_t and 1/K_a, which is illustrated in Fig. 4. The derived R_m is between the parameterization of 5 Sc_a^2/3/ u_* from Hicks et al. (22) and 13.3 Sc_a^1/2/ u_* from COARE (24). Because using C_w = 0 yields the minimum K_a and so maximum airside resistance, our results suggest that R_m may be overestimated in the COARE model.

Fig. 4.

Resistance in the molecular diffusion sublayer above the ocean surface (R_m), calculated as the difference between aerodynamic resistance (R_t) and 1/K_a of methanol (with C_w = 0). R_m estimated from methanol transfer lies between the parameterizations from Hicks et al. (22) and COARE (24). In all cases, R_t at a height of 18 m is several times greater than R_m.

It is surprising that using C_w = 0 yields a more physically consistent K_a than using the measured C_w. For K_a in Fig. 3A to be ∼15% lower (i.e., to approach the aerodynamic limit), C_w needs to be reduced by ∼50%. We examine the possibility of a near surface gradient in C_w. Microorganisms and dissolved organic matter tend to be enriched in the ∼0.1-mm-thick aqueous molecular sublayer (34, 35). This microlayer covers both the productive regions and the oligotrophic waters and at wind speeds of up to ∼10 m⋅s⁻¹ (36). Breaking waves temporally disrupt the surface, but a coherent microlayer appears to reform within seconds, in part due to efficient scavenging of surface active organic materials from bulk water by rising bubbles (37). Considering the methanol budget in the microlayer, the air-to-sea transport in our study adds 10 μmol⋅m⁻²⋅d⁻¹. If the concentration in the microlayer were maintained at 50% lower than in the bulk water, 26 μmol⋅m⁻²⋅d⁻¹ of methanol would be diffusing into the microlayer from below at steady state (with k_w = 11 cm⋅h⁻¹ from COARE). The total methanol input into the microlayer (36 μmol⋅m⁻²⋅d⁻¹) divided over a thickness of 0.1 mm would yield a concentration increase of 4 nM⋅s⁻¹. A methanol depletion of the same rate is required for mass balance (without any in situ production), which would be at least three orders of magnitude faster than any observed biological consumption (13, 14).

The mixing time between the sea surface and 5 m depth, dependent on the turbulent diffusivity, is typically on the order of a few minutes (38). Thus, enhanced consumption in the top meters of the ocean with a timescale of a few nM per minute could result in a vertical gradient in bulk C_w. Photochemically mediated destruction of methanol by OH radical in water is fast, with a rate constant of 1 × 10⁹ M⁻¹⋅s⁻¹ (39). However, the OH concentration in the surface ocean is only 1∼10 × 10⁻¹⁸ M (40) and therefore too low to be a significant sink for dissolved methanol. A pronounced photochemical effect would also imply a greater K_a during the day than at night, which was not observed during this cruise. In sum, known methanol sinks do not appear to be rapid enough to cause a substantially lower dissolved concentration at the interface relative to the bulk seawater. Interestingly, in an earlier measurement of acetone flux (8), a lower dissolved concentration at the surface would also to help reconcile the difference between observed uptake and predicted emission in the tropical Pacific. Along with previously measured SO₂ deposition velocities that are lower than expected (28), these results allude to potential processes not well understood in the transfer of airside controlled trace gases.

Conclusion

In this study, we report direct measurements of air–sea methanol transfer by eddy covariance. The surface ocean consistently took up methanol from the atmosphere, with enhanced influx in continental outflow regions and during high winds. The low saturation of methanol in the surface seawater implies rapid oceanic destruction of this compound. Methanol transfer resembles a one-way depositional process, suggesting that methanol concentrations at the water surface may be even lower than what were measured at ∼5 m depth due to processes currently unknown. Further field measurements along with other airside-controlled compounds (e.g., water vapor, ethanol), as well as laboratory experiments of methanol uptake with and without biology would help to determine whether the deposition model always holds for highly soluble gases.

Methods

Atmospheric Measurements.

During AMT-22, atmospheric and seawater methanol concentrations were alternately quantified by a high-resolution PTR-MS (Ionicon), which was housed in the meteorological laboratory near the foredeck of the ship. Acetone and acetaldehyde were also measured and will be described elsewhere. For ∼19 h of a day, the PTR-MS operated under atmospheric mode and continuously measured at ∼2.1 Hz. Air was drawn in from an intake on the starboard side of the ship’s foremast (∼18 m above mean sea level) via ∼25 m of 6.4 mm (inner diameter) perfluoroalkoxy tubing by a vacuum pump at a flow rate of ∼23 standard liters per minute, as monitored by a digital thermal mass flow meter. A triply deuterated methanol gas standard (2.0 ± 0.1 ppm of methanol-d3; Scientific and Technical Gases Ltd.) was injected continuously into the inlet line at 30(±0.3) standard cubic centimeter per minute, as regulated by a digital thermal mass flow controller; this allows C_a to be calculated from the ratio between the ambient and deuterated signals. The use of the isotopic standard minimizes uncertainties due to instrumental drift and variable efficiencies. Background values were taken by directing ambient air through a platinum catalytic converter (350 °C) for 2 min every hour. The detection limit for mean atmospheric concentration (minutely averaged) and the noise level at ∼2.1 Hz were 0.048 and 0.21 ppb, respectively. The standard injection system was initially designed and the instrument performance characterized in detail at a coastal site (41).

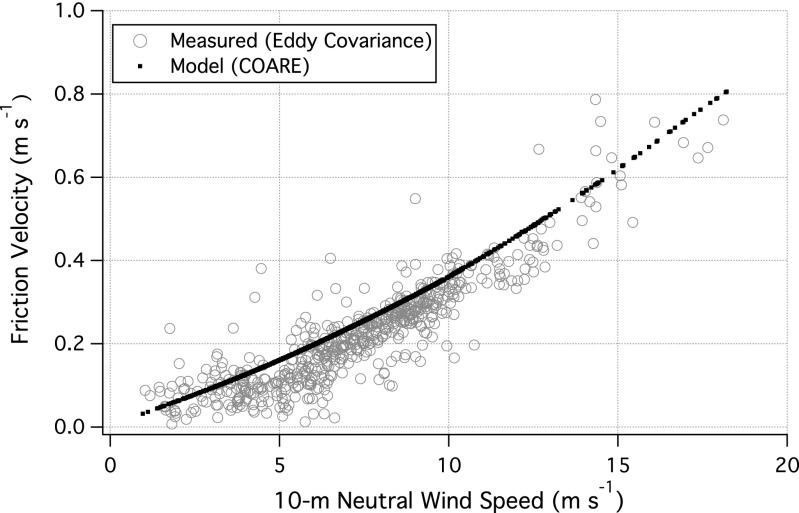
In eddy covariance (EC), C_a is correlated with concurrent vertical wind velocity (w) and averaged over time to yield the vertical flux (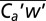, where primes denote deviations from the respective means and the overbar signals averaging over nominally ∼1 h). Wind measurements on a ship are influenced by the ship’s movement, necessitating a motion correction. Mounted ∼40 cm from the gas intake, a sonic anemometer (WindMaster; Gill Instruments) and a motion sensor (Motionpak II; Systron Donner) measured 3D wind velocities, linear accelerations, and rotational rates at 10 Hz. Observed winds were corrected for ship’s motion (42), and further sequentially decorrelated with ship velocities and accelerations to yield true winds (24). The EC friction velocity (derived from 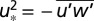, where u is the wind velocity along the mean wind direction) closely agrees with modeled u_* (24) as a function of wind speed, validating the motion correction (Fig. 5).

Fig. 5.

Friction velocity (u_*) as a function of 10-m neutral wind speed. Measured u_* by eddy covariance (n = 584) agrees well with prediction from the COARE model (24), validating the motion correction on observed winds.

Methanol flux is computed as the integral of the C_a:w cospectrum from 0.002∼1 Hz, omitting low-frequency contributions possibly related to horizontal heterogeneity. Only the wind sector from −50 to 110 degrees is considered for flux, excluding periods of contamination from the ship’s exhaust and distortion of ambient wind fields due to the ship’s superstructure. A total of 484 h of valid methanol flux observations were made, of which 29 h were during high wind conditions (u_* > 0.4 m⋅s⁻¹). As expected, correlating the methanol-d3 signal with w resulted in “null” fluxes scattered around zero. After dividing by u_*, methanol flux also does not correlate with measured sensible heat flux or computed latent heat flux, implying minimal sensitivity in the instrument response to ambient fluctuations in temperature and humidity. However, in heavy swells, C_a exhibited some spurious correlations with the vertical platform acceleration and displacement at the frequency of ship’s motion (∼0.1 Hz). The former artifact was likely due to motion-induced variability in the water vapor source flow of the PTR-MS, and the latter from heaving of the ship vertically across the C_a gradient. Applying a similar decorrelation algorithm as described above to C_a removes the erroneous spike at ∼0.1 Hz and also reduces the magnitude of methanol flux by an average of 24%.

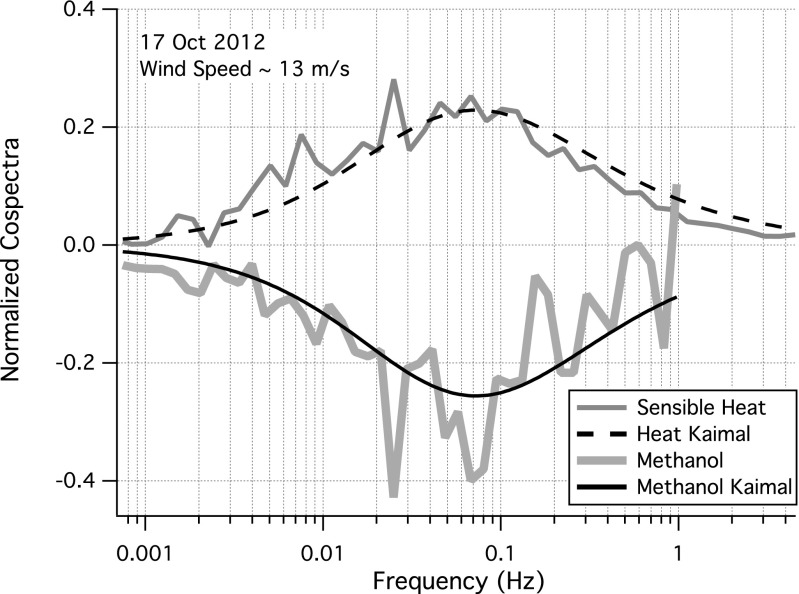
Mean methanol and sensible heat cospectra over 10 h on October 17 are shown in Fig. 6, which are well described by the expected spectral shape for atmospheric turbulent transport (43). Based on an empirical filter function (44) with a response time of 0.5 s and the shape of the theoretical spectrum at frequencies above the Nyquist (∼1 Hz), a correction for high-frequency attenuation is applied to the measured methanol flux, which is on average 17% and increases with wind speed, consistent with estimates from an ogive approach (41). Fluxes are processed hourly and averaged to 1° latitude bins. At a nominal ship velocity of 18 km⋅h⁻¹, each latitude bin corresponds to ∼6 h. Random uncertainty in methanol flux is ∼20% for the bin average given a sampling error of ∼50% for hourly measurements (45).

Fig. 6.

Normalized cospectra of sensible heat and methanol over 10 h on October 17, a day with high winds and large methanol flux. Both cospectra are well described by the theoretical spectral shape characteristic of atmospheric turbulent transport (43). Attenuated flux at high frequency is corrected following a filter-function approach (44).

Seawater Measurements and Computation of K_a.

Discrete seawater samples (triplicates) were taken primarily from predawn and noontime conductivity, temperature, salinity (CTD) hydrocasts daily. Unfiltered water was transported from the 5-m Niskin bottle via a short piece of Tygon tubing into opaque glass bottles (∼300 mL). Contact with air was avoided by sampling first from the Niskin and overfilling the glass bottles before capping. An additional sample from the deepest Niskin (nominally at 500 m depth) was collected at noon. Several water samples were also obtained from the ship’s nontoxic underway water supply on November 13, when no CTD was commenced during a storm, and on November 20, after the completion of CTD work. An intercomparison earlier during the cruise yielded no significant difference in C_w between the 5-m CTD and the water collected underway.

To minimize any loss due to bacterial consumption, water samples were kept at ambient water temperature and analyzed within 3 h of sampling. Methanol was extracted from seawater across a semipermeable silicon membrane thermostated at 50 °C into a supply of clean nitrogen flowing directly into the PTR-MS, as described in ref. 16. The first of the triplicate samples was used to condition the membrane; reported C_w values represent the average of the latter two samples. The system was calibrated every 2 wk using water standards prepared by serial dilution of reagent-grade methanol. Calibration constants were stable over the entire cruise, varying less than 10%. Estimated as three times the noise of the nitrogen blanks, the detection limit for seawater methanol concentration was ∼6 nM.

For the computation of K_a, latitudinally bin-averaged flux and C_a were linearly interpolated to the times of water collection. Given the transect format of the cruise, uncertainties due to horizontal gradients were random and should not contribute to any bias in K_a. Any proportional error in C_a should also be reflected in the flux and so not affect K_a. Judging from a recent survey (46), uncertainties in H for methanol should be within 10%.