Using Mixture Models with Known Class Membership to Address Incomplete Covariance Structures in Multiple-Group Growth Models

Abstract

Multi-group latent growth modeling in the structural equation modeling framework has been widely utilized for examining differences in growth trajectories across multiple manifest groups. Despite its usefulness, the traditional maximum likelihood estimation for multi-group latent growth modeling is not feasible when one of the groups has no response at any given data collection point, or when all participants within a group have the same response at one of the time points. In other words, multi-group latent growth modeling requires a complete covariance structure for each observed group. The primary purpose of the present study is to show how to circumvent these data problems by developing a simple but creative approach using an existing estimation procedure for growth mixture modeling. AMonte Carlo simulation study was carried out to see whether the modified estimation approach provided tangible results and to see how these results were comparable to the standard multi-group results. The proposed approach produced the results that were valid and reliable under the mentioned problematic data conditions. We also presented a real data example and demonstrated that the proposed estimation approach can be used for the chi-square difference test to check various types of measurement invariance as conducted in a standard multi-group analysis.

There are many situations where we want to know if a measurement or structural equation model for one group has the same parameter values as in other groups (Bollen, 1989). This question can be addressed using a multi-group approach in which various forms of invariance are tested across groups, with or without latent variables, in the structural equation modeling (SEM) framework (Jöreskog, 1971; Sörbom, 1974). There has been a plethora of multi-group SEM research on various methodological and substantive topics (e.g., see Byrne, Shavelson, & Muthén, 1989; Cheung & Rensvold, 2000; Cole, Martin, & Steiger, 2005; LaGrange et al., 2011; Mun, Fitzgerald, von Eye, Putter, & Zucker, 2001; Muthén, 1989; Rivera & Satorra, 2002; Vandenberg & Lance, 2000). In recent years, multi-group SEM has been extended to latent growth modeling (LGM; McArdle, 1986; Meredith & Tisak, 1984, 1990) to examine differences in growth trajectories across multiple manifest (observed) groups. For substantive, as well as methodological, examples, see Little, Schnabel, and Baumert (2000), McArdle (1989), Muthén and Asparouhov (2002), Palardy (2008), and Wang, Siegal, Falck, Carlson, and Rahman (1999).

Despite the usefulness of a multi-group LGM approach, a couple of data problems may arise especially when one of the known, manifest groups is small. For example, Figure 1 shows a hypothetical situation in which heterogeneity in depression trajectories is examined using LGM across several race groups, with Native American and Asian groups having small sample sizes. If any one of these small groups has completely missing responses at a single time point, either due to study design (no planned follow-up) or empirical missingness, then the subsequent estimation fails because the traditional ML estimation for multi-group analysis in the SEM framework initiates its estimation procedures with complete covariance structures for all groups. That is, the estimation fails because a covariance structure for one group cannot be fully specified (i.e., an indicator variable has neither variance nor covariance within the group). Similarly, if all participants within a group have the same response or if only one participant within a group has a response on an indicator, the traditional estimation method also fails because of the same reason--neither variance nor covariance can be determined.

Figure 1.

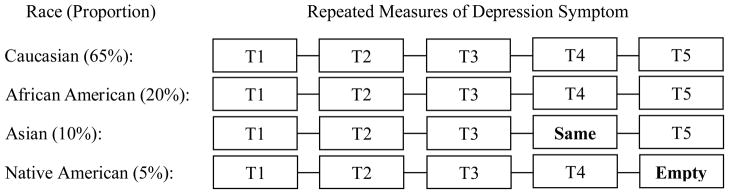
A longitudinal, multi-group data example. Depression symptom measures over five time points are collected across four race groups. ‘Empty’ represents a completely missing data cell, indicating all Native American participants provide no response at T5. ‘Same’ represents a same response data cell, indicating all Asian participants provide the same response at T4.

These problematic data situations in multi-group analysis are a serious barrier for anyone who wants to implement a multi-group growth model in the SEM framework. The simplest option is to exclude the indicator variable that has no variance from the data. However, such an action has several unattractive implications. First, this approach will result in not fully utilizing existing data for all other groups. Second, depending on the model, removing a critical indicator variable may result in less optimal estimation of the entire model. For example, removing a final follow-up time point could lead to biased growth factor estimates for all groups. Third, in a more complex model, such as piecewise LGM (Bollen & Curran, 2006; Muthén & Muthén, 2010; Raudenbush & Bryk, 2002), reducing the number of indicator variables may not be a viable option (in terms of identification) especially when there exists a minimal number of time points within a single phase or when higher order polynomials, such as quadratic growth models, have to be specified with a few available time points.

This estimation problem can be skirted, however, using a simple but creative adjustment approach that takes advantage of an existing estimation procedure for finite mixture modeling with known classes (Muthén & Muthén, 2010). In this adjustment approach, a mixture estimation procedure is employed with a single latent class that encompasses multiple manifest groups. Since there is only one latent class with multiple manifest groups, the model specification is essentially the same as the standard multi-group analysis that has multiple manifest groups. However, unlike the standard multi-group SEM estimation procedure that begins with the premise that a covariance structure per each manifest group must be complete, the mixture estimation approach does not have that requirement. Mixture modeling with known classes in Mplus (Muthén & Muthén, 2010) technically treats manifest groups as a special case of latent classes in the sense that the membership of latent classes is known beforehand (i.e., known classes).¹ This alternative to multi-group SEM, the mixture approach with known classes, does not check whether all a priori known classes (i.e., manifest groups) have complete covariance structures. Theoretically, it is unreasonable to check the individual covariance structure per each known class prior to estimating model parameters, because the known classes in a mixture model, as opposed to manifest groups in a standard multi-group LGM, are technically ‘latent’classes. Latent class membership is determined based on posterior probabilities that are assigned during the estimation process. By regarding the manifest groups as latent classes whose membership is known in this mixture estimation approach, the procedure checks the covariance structure of entire data as a whole, not group-specific covariance structures. The differing approaches to data between these two estimation procedures (the standard multi-group LGM and the mixture multi-group LGM) makes a critical difference when estimating a model using data with incomplete covariance structures for some groups. It is not estimable in the former but estimable in the latter.

Mixture multi-group LGM has been utilized as an alternative to multi-group LGM when analyzing data with some of these challenging characteristics in recent applied research. For example, supplemental figures available in the online version of the recent article by White, Lee, Mun, and Loeber (2012) were drawn with the estimates produced by using this mixture multi-group LGM approach. While these two approaches are considered as equivalent by many for practical reasons, a couple of differences exist conceptually and procedurally. Most important, there is a need to examine these two procedures methodologically and systematically, and to empirically examine whether the mixture estimation approach with known classes produces valid estimates under these problematic data conditions.

The present study describes the estimation procedures of these two approaches in depth, and reports findings from both a simulation study and a real data example. We conducted a Monte Carlo (MC) simulation study to examine whether the mixture multi-group estimation provides tangible results, as opposed to the standard multi-group estimation, when a group has no variability on an indicator variable. In addition, we examined how comparable the known class mixture estimation results are to the standard estimation results when there are no data problems. To show these, the present study applied the two estimation procedures to simulated data sets with or without the data problems across several select conditions. Details for the simulations are provided in the MC simulation section. A real data example from a smoking cessation clinical trial (Bolt, Piper, Theobald, & Baker, 2011; Piper et al., 2009, 2011) is also provided to show the feasibility of the mixture estimation with known classes in the presence of one of the specified data problems, and to show how to test invariance of growth factors using likelihood ratio tests in the context of multi-group LGM analysis.

Data Problems

A couple of data characteristics for which standard SEM estimation cannot give results for a multi-group analysis are presented in this section. To begin, consider a simple, typical type of multi-group data structure in the context of a longitudinal study design. Suppose a researcher is interested in the efficacy of a depression medication for individuals who have a history of alcohol dependence. Depression symptom levels after the pharmacological intervention are collected through hand-held PCs or Palm Pilots daily for 5 days using a 7-point Likert scale. Let the group variable be race: Caucasian (65%), African American (20%), Asian (10%), and Native American (5%). These kinds of real-time ecological momentary assessment (EMA; Stone & Shiffman, 1994) data tend to have a substantial portion of missing responses. Thus, we suppose that the depression symptom levels are available from 400 individuals with 30% of all possible responses missing. A brief illustration is provided in Figure 1.

By fitting a multi-group latent growth model (Bollen & Curran, 2006; McArdle, 1989; Muthén & Muthén, 2010), we would like not only to see the change in depression after the intervention but also to see whether there are significant differences in those changes across the four different race groups. Suppose, unfortunately, a small group has only one response or even no response at one time point. For example, only one participant in the Native American group responds at T5, or responses by the Native American group are completely missing at T5 as shown in Figure 1. In this case, the standard multi-group SEM procedure fails because a covariance matrix involving T5 data is incomplete for that group, which means an incomplete covariance structure exists for the Native American group. Another situation in which every subject in a group has the same response at least for one time point also results in an estimation problem because of the same reason as before, namely no variance. For example, suppose that all subjects in the Asian group rate their depression symptom levels as two on a scale of seven at T4 as shown in Figure 1. In this case, covariances or correlations involving the 4^th indicator cannot be calculated for the Asian group, resulting in an incomplete covariance structure.

As discussed previously, one possible solution to this estimation failure due to the completely missing data cell or the same response data cell in Figure 1 would be to eliminate these data at T4 or T5 for all groups from analysis. However, valuable post-intervention outcome data for the majority of the sample will not be utilized, and any resulting growth trajectories may not be very trustworthy because the growth trajectories are based on only three or four time points in this particular hypothetical example. The validity of a latent growth curve model is directly related to the number of indicator variables, i.e., the number of time points in growth models (Kim, 2012). Data from four time points are normally acceptable for a linear growth model, but they are not enough, for example, when the sample size is small or when a quadratic slope needs to be estimated. Moreover, when both the missing data problem and the same response data problem simultaneously happen at different time points or when there are a limited number of time points, it may not be feasible to exclude multiple time points in analysis. For example, with four assessment time points, we cannot eliminate data from two waves because it will prevent us from fitting a latent growth curve model.

These situations are not uncommon, especially for cohort sequential longitudinal data. A cohort sequential, longitudinal design is often recommended as an economical way to assess a behavior of interest over a long period of time (Duncan, Duncan, & Hops, 1996). Assuming there is sufficient overlap in assessment time periods across cohorts, we can draw valid inference about developmental trajectories from multiple cohorts. For example, White et al. (2012) conducted a multi-group, four-piecewise linear growth curve model and examined alcohol use trajectories during the transition from adolescence to adulthood for the following five violence groups: nonviolent (n = 580; 65%), late-onsetters (n = 51; 6%), desisters (n = 76; 9%), persisters (n = 103; 12%), and one-time offenders (n = 84; 9%). The sample was comprised of two different cohorts: youngest and oldest cohorts who were followed up from the 1^st and 7^th grade, respectively (Loeber, Farrington, Stouthamer-Loeber, & White, 2008). Thus, this cohort-sequential longitudinal design made it possible to examine alcohol trajectories from ages 12 through 24/25 years, a much larger developmental window than using data from either cohort alone. However, this also created a situation where data were sparse at both ends of the age range and even sparser or completely missing when examined separately for each cohort. More specifically, the covariance (data) coverage between some of the time points was low, and there were either zero valid observations or only one valid observation (no variance in either case) for some of the violence groups at a couple of time points. We also provide a real data example of the same response data problem (Bolt et al., 2011; Piper et al., 2009, 2011) to further examine the mixture multi-group procedure with known classes for the tricky data problems, in the section of Real Data Analysis.

Growth Mixture Model with Known Classes

Mixture modeling with known classes (Muthén & Muthén, 2010) can be used when one wants to perform a mixture analysis while taking manifest group membership, such as gender, into consideration. In the mixture model with known classes, there are two types of categorical latent variables: one is a latent class variable, whose values are unknown and estimated by the model, and the other is a known class variable that corresponds to manifest group membership, such as boys and girls or intervention and control groups. Therefore, this model is a combination of latent class analysis (i.e., mixture models) and multi-group analysis. For example, if two latent classes are specified along with four known classes (i.e., four manifest groups), a total of eight (4×2) class patterns are formed in the model: from ‘1 and 1’(1^st known class and 1^st latent class), ‘1 and 2’(1^st known class and 2^nd latent class), and so on up to ‘4 and 2’(4^th known class and 2^nd latent class).

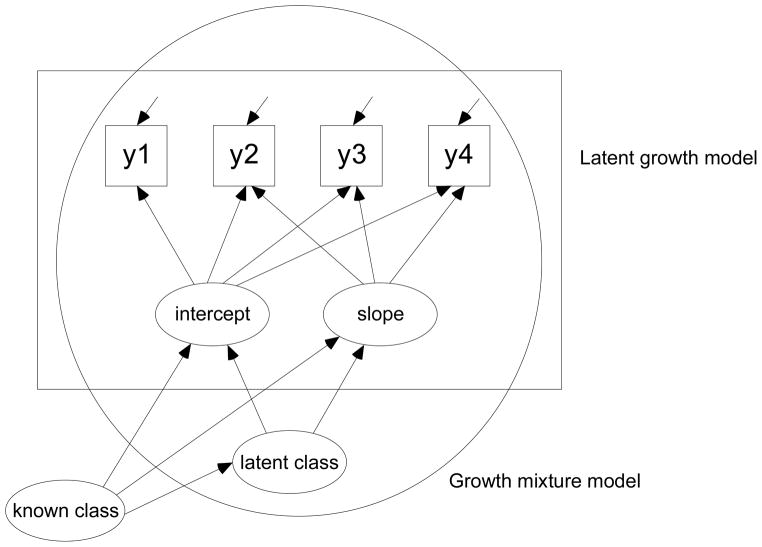
For the purpose of the present study, the mixture modeling with known classes is applied to a latent growth model in this section, resulting in growth mixture modeling with known classes (Muthén & Muthén, 2010). A path diagram is provided in Figure 2 for a graphical illustration of the model. Thorough model specification is omitted here because growth mixture modeling (GMM; Muthén, 2001a, 2001b; Muthén, 2004; Muthén & Shedden, 1999) and multiple group analysis (e.g., Jöreskog, 1971; Sörbom, 1974; Vandenberg & Lance, 2000) are well documented elsewhere, and because the specifications of these models for the purpose of the estimation are explained in the next section. From the path diagram, notice that this path diagram is the same as that of GMM with the difference being the introduction of a known class variable (manifest group variable in the form of a categorical latent variable). Both latent class and known class variables are technically categorical latent variables. However, while latent classes are really latent, known classes, in fact, correspond to manifest groups.

Figure 2.

A path diagram of growth mixture model with known classes. A LGM in the rectangular framework extends to a GMM with the introduction of a latent class variable, which is in the circular framework. In turn, a GMM extends to a GMM with known classes with the introduction of a known class variable (i.e., manifest group variable).

The present study utilizes this special extension of GMM that includes one latent class variable and one a priori known class variable. We identified some critical data problems in a multi-group longitudinal data analysis mentioned previously and applied one special case of the GMM with a known class variable to data to circumvent these problems. This approach involves specifying one latent class variable with a single category and the other latent class variable (i.e., known class variable) to indicate multiple manifest groups.² As a result, the GMM with one latent class and multiple known classes is equivalent to the standard multi-group LGM because the known classes of this mixture approach are fundamentally the manifest groups. The two approaches, the GMM with one latent class and multiple known classes and the standard multi-group LGM, can be used interchangeably when data across all manifest groups have complete covariance structures.

Model Specification and Estimation

In this section, the estimation procedures for a standard multi-group SEM and for a mixture multi-group SEM with known classes are compared to show that they have the same model specifications for estimation. Then, one important difference in the procedures between the two methods is discussed. There have been articles and books that showed estimation procedures for a general structural equation model and a mixture model (Bollen, 1989; Jöreskog, 1973; McLachlan & Peel, 2000). However, the following section is presented to draw attention to the commonality and difference between the two approaches targeted in this present study: a standard multi-group SEM and a mixture multi-group SEM estimation procedures.

A Standard Multi-group SEM

Jöreskog (1973) discussed ML estimation for general structural equation models. Slightly different or modified versions also appear in Bollen (1989) and Kaplan (2009). To begin, let the observed responses x (exogeneous variables) and y (endogeneous variables) be denoted as a vector z, and let the observed responses be based on a sample of n. Central to the development of the ML estimation is the assumption that observations are derived from a population that follows a multivariate normal distribution (Kaplan, 2009). The multivariate normal density function of z can be written as:

$$\phi (z_i;\mu ,\mathrm{\sum })=\frac{1}{{(2\pi )}^{\frac{p+q}{2}}{\mid \mathrm{\sum }\mid }^{\frac{1}{2}}}{exp}^{-\frac{{(z_i-\mu )}^{\prime }(z_i-\mu )}{2\mathrm{\sum }}},$$ (1)

where μ is a mean vector, Σ is a covariance matrix, p is the number of y variables, and q is the number of x variables. The μ and Σ can be further structured by imposing a structural equation model (Tueller & Lubke, 2010) as follows:

$$\mu =\nu +\mathrm{\Lambda }{(I-\text{B})}^{-1}\alpha \text{and}$$ (2)

$$\mathrm{\sum }=\mathrm{\Lambda }{(I-\text{B})}^{-1}\mathrm{\Psi }{\left[{(I-\text{B})}^{-1}\right]}^{\prime }{\mathrm{\Lambda }}^{\prime }+\mathrm{\Theta },$$ (3)

where ν is a vector of equation intercepts, Λ is a matrix of factor loadings, I is an identity matrix, B is a matrix of regression coefficients between factors, α is a vector of factor means, 1 is a covariance matrix for the factors, and Θ is a covariance matrix of the measurement error terms with error variances on the diagonal.

Under the assumption that the observations are independent of one another, the joint density function (i.e., the likelihood function) for a typical structural equation model can be derived (Bollen, 1989). After making some adjustments to make the calculation easier,³ we need to maximize Equation (4), the log likelihood function without the constant term, with respect to the parameters of the model:

$$\begin{array}{l}logL(\theta )=\sum _{i=1}^{n}log\phi (z_i;\mu ,\mathrm{\sum })=-\left(\frac{n}{2}\right)log\mid \mathrm{\sum }(\theta )\mid -\left(\frac{1}{2}\right)\sum _{i=1}^n{z}_i^{\prime }{\mathrm{\sum }}^{-1}(\theta )z_i\\ =-\left(\frac{n}{2}\right)log\mid \mathrm{\sum }(\theta )\mid -\left(\frac{n}{2}\right)\text{tr}\left[S{\mathrm{\sum }}^{-1}(\theta )\right],\end{array}$$ (4)

where θ is a vector of parameters, and S is an unbiased sample covariance matrix corresponding to z.

For the estimation of a multi-group structural equation model, each group’s (denoted by using a subscript g) observed covariance matrix (S_g) is the object of the analysis. The hypothesized structure implies a covariance matrix Σ_g (θ_g) for each group. The total log likelihood for the multi-group SEM is a weighted sum of the group-specific log likelihoods by the group sample size:

$$logL{(\theta )}_{\mathit{multiple}\mathit{group}}=\sum _{g=1}^G\left\{-\left(\frac{n_g}{2}\right)log\left|{\mathrm{\sum }}_g\left({\theta }_g\right)\right|-\left(\frac{n_g}{2}\right)\text{tr}\left[S_g{\mathrm{\sum }}_g^{-1}\left({\theta }_g\right)\right]\right\},$$ (5)

where G is the total number of groups. When the observed covariance matrices, S_g, are closer to the model-implied covariance matrices, Σ_g (θ_g), for all groups, the multi-group model fits better.

A Mixture SEM with Known Classes

The multivariate normal density function of a finite mixture extension of a structural equation model (Kaplan, 2009; McLachlan & Peel, 2000; Muthén, 2002; Tueller & Lubke, 2010; Vermunt & Magidson, 2005) is given by

$$f(z)=\sum _{k=1}^K{\pi }_k{\phi }_k(z_i;{\mu }_k,{\mathrm{\sum }}_k),$$ (6)

where z is a vector of observed variables, K is the number of latent classes, π_k is the class proportions such that ${\sum }_{k=1}^K{\pi }_k=1,{\phi }_k(z_i;{\mu }_k,{\mathrm{\sum }}_k)$ are multivariate normal density functions with class specific mean vectors μ_k and class-specific covariance matrices Σ_k. The μ_k and Σ_k can be further structured by imposing a structural equation model, and those are the same equations as Equations (2) and (3) with the latent class subscript k. The observed log likelihood function of a mixture SEM model is:

$$logL(\theta )=\sum _{i=1}^{n}logf(z_i)=\sum _{i=1}^{n}log\left(\sum _{k=1}^K{\pi }_k{\phi }_k(z_i;{\mu }_k,{\mathrm{\sum }}_k)\right).$$ (7)

For the estimation of a single-class mixture SEM model, we apply K =1 to the finite mixture extension of an SEM model in Equations (5) and (6). When K =1, the last term of Equation (7) becomes the right-hand side of Equation (8),

$$\sum _{i=1}^{n}log\left(\sum _{k=1}^K{\pi }_k{\phi }_k(z_i;{\mu }_k,{\mathrm{\sum }}_k)\right)=\sum _{i=1}^{n}log\phi (z_i;\mu ,\mathrm{\sum })$$ (8)

because the multivariate normal density function in Equation (7), φ_k (z_i; μ_k, Σ_k) without the subscript k (i.e., the multivariate normal density with a single latent class), is equivalent to the multivariate normal density function shown in Equation (1), φ(z_i; μ, Σ). The right-hand side of Equation (8) is equivalent to Equation (4), i.e., the log likelihood of the SEM is equal to the log likelihood of the single-class mixture SEM. Therefore, the standard SEM model is equivalent to the single-class mixture SEM model from the point of the log likelihood equations. Thus, the same multi-group adjustment as in the standard SEM in Equation (5) can be applied to the single-class mixture SEM. Consequently, for the purpose of estimation, the model specifications for the standard multi-group SEM and the single-class mixture SEM with multiple known classes are basically equivalent. Now the only difference between the two approaches lies in how each estimation procedure handles multiple groups: a group variable is manifest in the standard multi-group analysis, whereas it is latent (known class variable) in the mixture multi-group analysis.

In a multi-group analysis, the mean vector and the covariance matrix for each group can be modeled and estimated separately without taking into account the other groups or the entire sample because the mean vector and covariance matrices are not correlated across groups (Arminger & Stein, 1997). That is, a multi-group model is nothing but the sum of group-specific models. In contrast, in the case of mixture analysis, k posterior probabilities are assigned to each individual. For example, one individual case has a probability of 0.7 that it belongs to the first latent class and, at the same time, has a probability of 0.3 that it belongs to the second latent class. All individuals within the entire sample are linked to one another through posterior probabilities within and across the latent classes. Therefore, a mixture model is not the sum of class-specific models as in a multi-group model; class-specific models are rather regarded as the derivatives from a complete mixture model. Thus, when manifest groups are specified as known classes in a mixture analysis, these known classes are treated as derived subgroups from the entire sample, even if the posterior probabilities of the individuals belonging to these known classes are pre-determined (either 1 or 0).

In sum, the completeness of each covariance structure per each manifest group is required in the estimation procedure for the standard multi-group analysis, whereas only the completeness of the whole covariance structure across all known classes is required for the mixture multi-group analysis. Consequently, the mixture multi-group procedure can provide results under the problematic data structures for which the standard multi-group procedure fails to begin the estimation process. Needless to say, if data are missing on an indicator variable for all groups, even the mixture multi-group procedure cannot give any results involving that indicator variable.

Monte Carlo Simulation

In the present study, we performed a Monte Carlo simulation study to see whether the mixture method with known classes provides tangible results and to see how those results are comparable to the standard multi-group results under two situations: (1) when data did not have any problems, and (2) when data had problems (e.g., either missing or the same). The simulations were carried out under several limited conditions, since the purpose of the present study was to demonstrate the general idea of how to utilize two different analytic approaches for a given data characteristic, rather than to thoroughly evaluate the performance of the estimation methods under various simulation conditions.

Design and Data Analysis

In a Monte Carlo study, a model or models to be studied should be chosen first; the multi-group latent growth model was examined in this study. For the choice of design (or manipulated) factors and Monte Carlo variables, a normative condition of latent growth models was decided: 5 indicator variables, linear slope, 20% of missing proportion, no covariate, a sample size of 500, and 100 replications. Four groups with the following proportions, 65% (N_G1 = 325), 20% (N_G2 =100), 10% (N_G3 = 50), and 5% (N_G4 = 25), were specified for N = 500. Once data sets at the normative condition were generated across the four groups, the standard multi-group procedure and the mixture multi-group procedure were applied to the generated data sets to see whether the results from the two estimation procedures were comparable. Then, all responses on the 5^th indicator variable in the 4^th group of the generated data sets were (1) totally removed to emulate the completely missing data condition, and (2) replaced with a single constant⁴ to emulate the same response data condition. The mixture multi-group procedure was applied to the manipulated, problematic data sets, and the results were compared to the results from the previous step that had no data problems.

Next, each of the design factors was varied while the other factors were held constant at their normative values. The following four design factors were examined: (1) an added quadratic growth slope, (2) an added continuous covariate, (3) an increased missing proportion up to 50%, and (4) a decreased sample size of 300. For the generated data sets with each varying factor, both the standard and the mixture multi-group procedures were used for estimation to see whether the results were comparable. Then, the data manipulation procedures described above were applied to the generated data sets to simulate the completely missing data condition as well as the same response data condition in one group. Only the mixture multi-group procedure was applied to the problematic data sets.

Finally, the effect of the multiple missing data problem and the effect of both missing and same response data problems were investigated. For the multiple missing data modification from the generated data sets at the normative values, two cases were considered: completely missing data in two different groups and completely missing data at two different time points in one group. For the missing and same response modification, two cases were also considered: two different problems in two different groups versus in one group. The mixture multi-group procedure was applied to the manipulated data sets, and the results were compared as before. In the interest of space, only the parameters related to growth factors (i.e., means and variances of growth factors) are presented for the simulation results in Tables 1 – 4.

Table 1.

Monte Carlo Estimates (Mean and Variance) of a Multigroup LGM at the Normative Condition

				Standard estimation	Mixture estimation
Group	Growth factor		Parameter	Generated	Generated	Missing	Same
G1	Intercept	Mean	5.0	5.000 (.074)	5.000 (.074)	5.000 (.074)	5.000 (.074)
		Variance	1.0	1.019 (.121)	1.019 (.121)	1.019 (.121)	1.019 (.123)
	Linear slope	Mean	0.1	0.098 (.024)	0.098 (.024)	0.098 (.024)	0.098 (.024)
		Variance	0.05	0.050 (.014)	0.050 (.014)	0.050 (.015)	0.048 (.014)
G2	Intercept	Mean	3.0	2.988 (.131)	2.988 (.131)	2.988 (.131)	2.988 (.132)
		Variance	1.0	1.019 (.121)	1.019 (.121)	1.019 (.121)	1.019 (.123)
	Linear slope	Mean	0.5	0.501 (.043)	0.501 (.043)	0.501 (.043)	0.500 (.043)
		Variance	0.05	0.050 (.014)	0.050 (.014)	0.050 (.015)	0.048 (.014)
G3	Intercept	Mean	7.0	6.990 (.188)	6.990 (.188)	6.990 (.188)	6.990 (.188)
		Variance	1.0	1.019 (.121)	1.019 (.121)	1.019 (.121)	1.019 (.123)
	Linear slope	Mean	−0.1	−0.098 (.061)	−0.098 (.061)	−0.098 (.061)	−0.098 (.061)
		Variance	0.05	0.050 (.014)	0.050 (.014)	0.050 (.015)	0.048 (.014)
G4	Intercept	Mean	6.0	5.980 (.253)	5.980 (.253)	5.980 (.260)	5.964 (.283)
		Variance	1.0	1.019 (.121)	1.019 (.121)	1.019 (.122)	1.019 (.123)
	Linear slope	Mean	−0.6	−0.615 (.083)	−0.615 (.083)	−0.615 (.107)	−0.600 (.064)
		Variance	0.05	0.050 (.014)	0.050 (.014)	0.050 (.015)	0.048 (.014)

Note. Under the ‘Generated’ columns, estimates were from the data sets generated at the normative values: 5 indicators, linear slope, 20% of missing proportion, no covariate, a sample size of 500, and 100 replications. Four groups with proportions, 65% (N_G1= 325), 20% (N_G2 = 100), 10% (N_G3 = 50), and 5% (N_G4 = 25), were specified for N = 500. Under the ‘Missing’ and ‘Same’ columns, all the responses on the 5^th time point in Group 4 were completely missing and had the same response, respectively.

Table 4.

Monte Carlo Estimates When Both a Missing Data Cell and a Same Response Data Cell are Present

			Mixture estimation
Group	Growth factor	Parameter	Generated	Missing and same cells in different groups	Missing and same cells in one group
G1	Intercept	5.0	5.000 (.074)	5.000 (.074)	5.000 (.074)
	Linear slope	0.1	0.098 (.024)	0.098 (.024)	0.098 (.024)
G2	Intercept	3.0	2.988 (.131)	2.988 (.132)	2.988 (.132)
	Linear slope	0.5	0.501 (.043)	0.500 (.043)	0.500 (.043)
G3	Intercept	7.0	6.990 (.188)	6.991 (.188)	6.990 (.188)
	Linear slope	−0.1	−0.098 (.061)	−0.097 (.066)	−0.098 (.061)
G4	Intercept	6.0	5.980 (.253)	5.964 (.283)	5.975 (.282)
	Linear slope	−0.6	−0.615 (.083)	−0.600 (.064)	−0.601 (.065)

Note. The multigroup latent growth model was based on five indicator variables. Under the ‘Generated’ column, estimates were from the data sets generated at the normative values. Under the ‘Missing and same cells in different groups,’ all the responses on the 5^th time point in Group 4 were completely missing and all the responses on the 4^th time point in Group 3 were the same. Under the ‘Missing and same cells in one group,’ all the responses on the 5^th time point were the same and all the responses on the 3^rd time point were completely missing in Group 4.

Simulation Results

Relative parameter recovery at the normative condition was compared between the results from the two approaches under generated (unproblematic) and manipulated (problematic) data sets. Averaged point estimates across 100 replications and their averaged standard errors (in parentheses) for growth factors are provided in Table 1.⁵ The results from the mixture multi-group analysis were exactly the same as those from the standard multi-group analysis across all estimates. This is not surprising because the model specifications for the two models are statistically equivalent. Results from the condition of completely missing data at one time point in one group are shown under the ‘Missing’ column in Table 1. The point estimates under the ‘Missing’ column were the same as the results of the standard multi-group procedure and also the results of the mixture multi-group procedure with the generated data sets. Standard errors of the simulations, however, were somewhat changed for Group 4; the standard errors of the mean and variance of the intercept were slightly inflated. Results from the same response data condition are shown under the ‘Same’ column in Table 1. Overall, point estimates and standard errors were also similar to the results of the standard and the mixture multi-group procedures under the ‘Generated’ column in Table 1. The point estimates and the standard errors of the intercept and linear slope in Group 4 changed a bit, though the differences were small in magnitude.

Table 2 provides the Monte Carlo estimates when each design factor varied, while holding the other factors at their normative values. The patterns of the results were very similar to those in Table 1 across the following four different conditions: (1) when a quadratic slope was added, (2) when a continuous covariate was added, (3) when the missing proportion was increased up to 50%, and (4) when the sample size was decreased to 300. First, the results of the mixture multi-group procedure were the same as those of the standard multi-group procedure with generated data sets. Second, the results were still very comparable when the missing data and same response data conditions were manipulated. The results of Groups 1, 2, and 3 were the same or nearly the same regardless of the conditions. The results of Group 4 that had the missing data or the same response data conditions had somewhat different growth factor estimates, though the differences were minimal.

Table 2.

Monte Carlo Estimates (Mean Only) at Some Specific Conditions

			Standard estimation	Mixture estimation
Group	Growth factor	Parameter	Generated	Generated	Missing	Same
Condition 1: Quadratic slope added
G1	Intercept	5.0	5.001 (.081)	5.001 (.081)	5.004 (.081)	5.005 (.081)
	Linear slope	0.1	0.089 (.072)	0.089 (.072)	0.089 (.072)	0.089 (.072)
	Quad slope	0.02	0.022 (.019)	0.022 (.019)	0.022 (.019)	0.022 (.019)
G2	Intercept	3.0	2.974 (.144)	2.974 (.144)	2.974 (.144)	2.974 (.144)
	Linear slope	0.5	0.530 (.130)	0.530 (.130)	0.530 (.130)	0.530 (.130)
	Quad slope	0.03	0.022 (.033)	0.022 (.033)	0.022 (.033)	0.022 (.033)
G3	Intercept	7.0	6.997 (.204)	6.997 (.204)	6.997 (.204)	7.000 (.204)
	Linear slope	−0.1	−0.115 (.183)	−0.115 (.183)	−0.116 (.183)	−0.115 (.183)
	Quad slope	0.04	0.045 (.047)	0.045 (.047)	0.045 (.047)	0.045 (.047)
G4	Intercept	6.0	5.987 (.278)	5.987 (.278)	5.989 (.284)	6.000 (.268)
	Linear slope	−0.6	−0.624 (.257)	−0.624 (.257)	−0.620 (.347)	−0.674 (.286)
	Quad slope	0.02	0.020 (.067)	0.020 (.067)	0.017 (.114)	0.020 (.069)
Condition 2: Continuous covariate added
G1	Intercept	5.0	4.986 (.073)	4.986 (.073)	4.986 (.073)	4.986 (.073)
	Linear lope	0.1	0.100 (.024)	0.100 (.024)	0.100 (.024)	0.100 (.025)
G2	Intercept	3.0	2.997 (.131)	2.997 (.131)	2.997 (.131)	2.997 (.131)
	Linear lope	0.5	0.496 (.043)	0.496 (.043)	0.496 (.043)	0.496 (.043)
G3	Intercept	7.0	7.000 (.185)	7.000 (.185)	7.000 (.185)	6.999 (.186)
	Linear lope	−0.1	−0.101 (.060)	−0.101 (.060)	−0.101 (.060)	−0.102 (.061)
G4	Intercept	6.0	5.995 (.259)	5.995 (.259)	6.010 (.265)	5.991 (.300)
	Linear lope	−0.6	−0.592 (.086)	−0.592 (.086)	−0.607 (.109)	−0.590 (.131)
Condition 3: Increased missing proportion (50%)
G1	Intercept	5.0	5.003 (.085)	5.003 (.085)	5.003 (.085)	5.003 (.085)
	Linear lope	0.1	0.097 (.031)	0.097 (.031)	0.097 (.031)	0.097 (.031)
G2	Intercept	3.0	3.000 (.151)	3.000 (.151)	3.000 (.151)	3.000 (.151)
	Linear lope	0.5	0.500 (.054)	0.500 (.054)	0.500 (.055)	0.500 (.055)
G3	Intercept	7.0	6.981 (.212)	6.981 (.212)	6.981 (.213)	6.981 (.213)
	Linear lope	−0.1	−0.104 (.078)	−0.104 (.078)	−0.104 (.078)	−0.104 (.079)
G4	Intercept	6.0	5.979 (.290)	5.979 (.290)	5.989 (.308)	5.963 (.319)
	Linear lope	−0.6	−0.609 (.104)	−0.609 (.104)	−0.620 (.141)	−0.595 (.077)
Condition 4: Decreased sample size (N = 300)
G1	Intercept	5.0	4.991 (.098)	4.991 (.098)	4.991 (.098)	4.991 (.098)
	Linear lope	0.1	0.095 (.032)	0.095 (.032)	0.095 (.032)	0.095 (.032)
G2	Intercept	3.0	3.010 (.167)	3.010 (.167)	3.010 (.169)	3.010 (.169)
	Linear lope	0.5	0.503 (.055)	0.503 (.055)	0.503 (.055)	0.503 (.055)
G3	Intercept	7.0	6.980 (.196)	6.980 (.196)	6.980 (.197)	6.980 (.157)
	Linear lope	−0.1	−0.095 (.063)	−0.095 (.063)	−0.095 (.063)	−0.095 (.018)
G4	Intercept	6.0	5.959 (.331)	5.959 (.331)	5.947 (.341)	5.940 (.372)
	Linear lope	−0.6	−0.607 (.105)	−0.607 (.105)	−0.595 (.137)	−0.588 (.085)

Note. The multi-group latent growth model was based on five indicator variables. Under the ‘Generated’ columns, estimates were from the data sets generated at the normative values. Under the ‘Missing’ and ‘Same’ columns, all the responses on the 5^th time point in Group 4 were completely missing and had the same responses, respectively.

The Monte Carlo estimates for the condition of completely missing data at two time points in one group or two groups are provided in Table 3. Regardless of whether this condition was limited to one group or two groups, the mean estimates of intercepts and slopes, as well as standard errors, were very similar to the results from the generated data sets without missing data. The standard errors in parentheses were slightly different, though the differences were very small. The Monte Carlo estimates for the condition of both the completely missing data and the same response data are provided in Table 4. The results were still very comparable to the findings from the generated data sets, whether the two kinds of data problems occurred in one group or two groups.

Table 3.

Monte Carlo Estimates through Mixture Estimation When Two Missing Data Cells are Present

			Mixture estimation
Group	Growth factor	Parameter	Generated	Two missing cells in different groups	Two missing cells in one group
G1	Intercept	5.0	5.000 (.074)	5.000 (.074)	5.000 (.074)
	Linear slope	0.1	0.098 (.024)	0.098 (.024)	0.098 (.024)
G2	Intercept	3.0	2.988 (.131)	2.987 (.132)	2.988 (.132)
	Linear slope	0.5	0.501 (.043)	0.501 (.043)	0.501 (.043)
G3	Intercept	7.0	6.990 (.188)	6.991 (.188)	6.990 (.188)
	Linear slope	−0.1	−0.098 (.061)	−0.097 (.066)	−0.098 (.061)
G4	Intercept	6.0	5.980 (.253)	5.986 (.260)	5.988 (.263)
	Linear slope	−0.6	−0.615 (.083)	−0.622 (.107)	−0.620 (.112)

Note. The multigroup latent growth model was based on five indicator variables. Under the ‘Generated’ column, estimates were from the data sets generated at the normative values. Under the ‘Two missing cells in different groups,’ all the responses on the 5^th time point in Group 4 and on the 4^th time point in Group 3 were completely missing. Under the ‘Two missing cells in one group,’ all the responses on the 3^rd and 5^th time point in Group 4 were completely missing.

Real Data Analysis

In this section, the mixture multi-group approach is applied to a real data set with one of the identified data problems as an alternative to the standard multi-group approach. We show a case of the same response problem in this example, because an example of the missing data problem was briefly described in the previous section (White et al., 2012). We present this analysis example to show the feasibility of the mixture multi-group procedure under these problematic data situations and to show that we can calculate a χ² difference test statistic for invariance tests that are typically implemented in a standard multi-group analysis using provided log likelihood values in the results. It should be noted that the example provided is for the purpose of demonstration and thus no serious substantive conclusions should be construed from the findings. The Mplus code is provided in the Appendix.

The data used in this analysis are from a large placebo-controlled, comparative effectiveness smoking cessation clinical trial conducted at the University of Wisconsin Center for Tobacco Research and Intervention (Bolt et al., 2011; Piper et al., 2009, 2011). This study was designed to test the efficacy of five cessation pharmacotherapy treatments (nicotine lozenge, nicotine patch, sustained-release bupropion, nicotine patch plus nicotine lozenge, and bupropion plus nicotine lozenge) versus placebo (see Piper et al., 2009 for more details about study methods and main results). As part of the study assessment, intensive longitudinal data (ILD) were collected via EMA. Study participants completed four daily EMA reports (just after waking, prior to going to bed, and two additional reports timed to occur randomly during the day) for one week prior to making a quit attempt and for two weeks after the quit day. Participants made ratings of nicotine withdrawal symptoms, self-efficacy, motivation, cessation fatigue, smoking, alcohol use, stress, and context (situational factors that may increase risk of smoking). The EMA methodology is described in more detail in Bolt et al. (2011) and Piper et al. (2011).

For a growth model, we utilized seven waves of daily negative affect (NA) ratings in the cessation clinical trial, from quit day to one week postquit. The main outcome measure, NA, was an average score of two 5-point (1 to 5) Likert-type scale items: one item was “upset” and the other was “distressed.” Therefore, NA ranged from 1 to 5, in increment of 0.5. The group variable of interest was marital status that was assessed using six categories (Married: n = 565,46.3%; Divorced: n = 263,21.5%; Widowed: n = 34,2.8%; Separated: n = 29,2.4%; Never married: n = 222,18.2%; Domestic partner: n =108,8.8%). Descriptive statistics for the indicator variables and frequencies of responses are presented in Table 5.

Table 5.

Descriptive Statistics of Negative Affect by Martial Groups

Marital status		Time
		T1	T2	T3	T4	T5	T6	T7
Married	M	1.313	1.320	1.321	1.254	1.327	1.276	1.264
	SD	0.620	0.675	0.686	0.554	0.700	0.622	0.615
	n	534	493	479	475	451	449	453
Divorced	M	1.406	1.464	1.424	1.429	1.367	1.448	1.403
	SD	0.638	0.766	0.731	0.868	0.721	0.790	0.752
	n	245	235	230	219	210	201	206
Widowed	M	1.288	1.300	1.350	1.161	1.148	1.250	1.286
	SD	0.468	0.726	0.559	0.351	0.477	0.553	0.615
	n	33	30	30	31	27	28	28
Separated	M	1.173	1.273	1.250	1.068	1.023	1.048	1.000
	SD	0.468	0.650	0.511	0.234	0.107	0.218	0.000
	n	26	22	24	22	22	21	19
Never married	M	1.552	1.500	1.398	1.377	1.387	1.389	1.457
	SD	0.864	0.780	0.687	0.749	0.738	0.675	0.771
	n	212	185	182	175	173	166	163
Not married, but living with Domestic partner	M	1.500	1.355	1.340	1.272	1.356	1.283	1.328
	SD	0.883	0.719	0.657	0.572	0.654	0.566	0.655
	n	103	100	97	101	94	90	87

Note. M = Mean; SD = Standard deviation. Married: n = 565; Divorced: n = 263; Widowed: n = 34; Separated: n = 29; Never married: n = 222; Domestic partner: n = 108. The subjects in the Separated group on T7 (n = 19) gave all the same responses, which were 1’s.

The objective of this multi-group analysis was to examine whether or not the six growth trajectories corresponding to the six groups were comparable to one another. One problem in this typical multi-group latent growth model was that all subjects in the Separated group had the same response at Wave 7 (i.e., all 1s; see Table 5). Substantively or conceptually, the fact that all participants had the same response is not a problem. However, with this sameness in a data set, SEM programs, including Mplus, will not initiate the estimation process. For example, Mplus outputs an error message, “One or more variables have a variance of zero. Check your data and format statement.” Thus, we implemented the mixture multi-group procedure with one latent class and six known classes, which then estimated all different growth factor means and variances across the six marital groups. The results are provided in Table 6a, and the growth trajectories are shown in Figure 3a. One of the important purposes of estimating a typical multi-group latent growth model is to test whether some of the growth factors are invariant across groups. Thus, we also ran the same multi-group model with the constraint of the same slope means across the six groups using the mixture procedure.⁶ The results of the restricted model are presented in Table 6b, and the growth trajectories are shown in Figure 3b.

Table 6.

The Results of Mixture Multigroup Analysis with Seven Waves of Negative Affect Real-Time Data

a. Without any constraint
Marital status	Frequency	Proportion	Intercept	Slope	Parameters	Log likelihood
Married	565	46.3%	1.323	−0.008	27	−8111.019
Divorced	263	21.5%	1.446	−0.004
Widowed	34	2.8%	1.277	−0.004
Separated	29	2.4%	1.284	−0.032*
Never married	222	18.2%	1.513	−0.017*
Domestic partner	108	8.8%	1.451	−0.026*

b. With a constraint of the same slope estimates
Marital status	Frequency	Proportion	Intercept	Slope	Parameters	Log likelihood
Married	565	46.3%	1.331	−0.011*	22	−8113.509
Divorced	263	21.5%	1.466	−0.011*
Widowed	34	2.8%	1.296	−0.011*
Separated	29	2.4%	1.224	−0.011*
Never married	222	18.2%	1.494	−0.011*
Domestic partner	108	8.8%	1.404	−0.011*

Note.

^*p <.05

Figure 3.

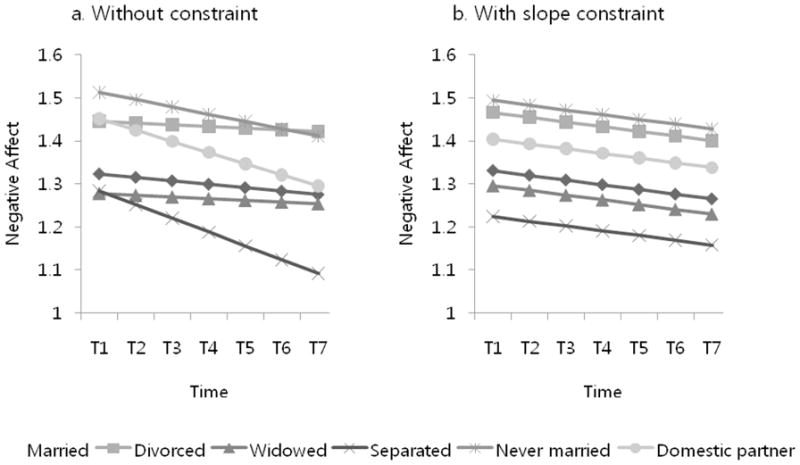
Growth trajectories of negative affect across the six marital groups without and with constraint.

A likelihood ratio test was then performed to test the invariance of the slopes (H₀ : The six marital groups have the same slopes vs. H₁ : At least one slope is different from the others). Since maximum likelihood estimation with robust standard errors (MLR; Muthén & Muthén, 2010) was used in Mplus 6, scaling correction factors were adjusted to calculate the χ² difference statistic (see Satorra, 2000; Satorra & Bentler, 2001). Given the simpler model’s log likelihood (ll_s), scaling correction factor (scf_s), and number of parameters (p_s), and given the more complex model’s log likelihood (ll_c), scaling correction factor (scf_c), and number of parameters (p_c), the χ² difference statistic is calculated as:

$${\chi }_{\mathit{diff}}^2=\frac{-2({ll}_s-{ll}_c)}{\frac{p_s\times {\mathit{scf}}_s-p_c\times {\mathit{scf}}_c}{p_s-p_c}},$$ (9)

and the ${\chi }_{\mathit{diff}}^2$ follows the χ² distribution with p_c − p_s degrees of freedom. In our particular example,

$${\chi }_{\mathit{diff}}^2=\frac{-2(-8113.509+8111.019)}{\frac{22\times 2.590-27\times 2.267}{22-27}}=5.8879$$ (10)

and this statistic was compared to the χ² distribution with 5 degrees of freedom (i.e., 2 7– 22 = 5). The p -value was 0.3173, suggesting that growth slopes were not different across the six groups. Likewise, when the standard multi-group procedure was not feasible because of problematic data situations, the mixture multi-group procedure provided not only the trajectory estimates across the groups but also the χ² difference statistic for invariance tests, just like a standard multi-group analysis without any problematic data conditions.

Discussion and Conclusion

The purpose of the present study was to show how to circumvent an estimation problem for a multi-group latent growth model when an indicator variable or variables had no variance in any of the groups examined. Since a multi-group analysis in the SEM framework initiates its estimation process with the complete check of covariance structures for all groups, the parameters for a multi-group model are not estimable when a group has completely missing data (or just one response) or same response data on an indicator variable or variables. This situation can be quite common in cohort sequential longitudinal studies (or accelerated longitudinal studies) or in a complex longitudinal model with multiple distinct phases, because data are likely to be sparser as the time moves farther from a baseline or an intervention point. If a target group of interest is small in size, these data problems can occur more often than in other groups with a larger number of observations because participants in a small, homogeneous group are more likely to have a similar experience at a given time point. The mixture multi-group approach provided tangible results with problematic data sets by applying a creative, straightforward adjustment to an existing mixture modeling approach.

Theoretically and empirically, the mixture multi-group procedure can provide valid and reliable results when used as an alternative to the standard multi-group procedure under the problematic data situations. However, without a Monte Carlo simulation study, it is hard to know how closely those estimates from the mixture approach match the results from the standard multi-group LGM. When there was no data problem, the mixture multi-group estimation procedure showed exactly the same results, in terms of means and variances of growth factors, as the standard multi-group estimation procedure. When the generated data sets were manipulated to simulate the problematic data examples, the mixture multi-group approach provided quite reliable results. Although the Monte Carlo study showed very reassuring results of the mixture estimation procedure, one should also note that this was a simulation study and the scope and thoroughness of the conditions simulated were limited.

Upon verifying that the mixture multi-group procedure showed valid and reliable results in the Monte Carlo study, we then checked whether this mixture approach could be used as an alternative to the standard multi-group approach in the aspect of a real data analysis. In other words, we demonstrated that the mixture approach could be used for the χ² difference test to check various types of measurement invariance as conducted in a standard multi-group analysis. Through the results of the real data example utilizing negative affect data collected over one week postquit in a real smoking cessation clinical trial, we demonstrated that the provided log likelihood values from the two models, one of which was the more restricted model (i.e., the model with the same slopes), could be used to test the slope invariance across the six marital groups.

The mixture estimation procedure appears to be useful in the presence of the data problems described. Of the two data problems, however, one needs to differentiate the completely missing data problem from the same response data problem. The fact that a group has the same response on an indicator variable by chance is not a substantive or design problem but an estimation problem. By comparison, the completely missing data can be a substantive problem because actual responses for an indicator variable in a group have never been observed. If this missingness occurred by a research design as in cohort, sequential longitudinal studies, it is reasonable to assume that the missing-at-random (MAR) assumption is satisfied (Graham, Hofer, & MacKinnon, 1996). Thus, in this mixture multi-group analysis, it is assumed that the potential responses in a completely missing data cell could lie on an extension of the growth trajectory based on the other valid indicators. If data are missing-not-at-random (MNAR; e.g., non-ignorable dropouts of patients from a treatment program), then, needless to say, the mixture multi-group approach will not provide valid results over unobserved data points. Although, in the simulation study, the results showed quite good growth parameter recovery with completely missing data, one should carefully check the growth estimates with the completely missing data problem for interpretation.

In line with this cautionary note, researchers ought to carefully use the mixture estimation approach for a factor analytic model. A latent growth model is fundamentally a factor analytic model, and therefore, this mixture approach can also be used for a factor model under the same kinds of data problems. However, in a latent growth model, one characteristic (e.g., depression) is measured multiple times across time, whereas in a factor analytic model, multiple characteristics (e.g., depression, craving, and negative affect) are measured only once. It may or may not be relevant to assume that the potential responses of completely missing depression scores are comparable realizations of the other indicators, e.g., craving and negative affect,⁷ and that this missing pattern meets MAR. Thus, one should be careful when using the mixture multi-group approach with the completely missing data problem, especially in a common factor model.

The present study introduced and demonstrated a modified estimation procedure to circumvent some problematic data situations which hinder estimation in a multi-group longitudinal data analysis. More specifically, the mixture multi-group procedure was shown to reliably estimate a multi-group latent growth model with completely missing data or the same response data on an indicator variable(s). Furthermore, the validity of invariance tests using likelihood ratios from the mixture analysis output was demonstrated. In the current research environment where limited resources are maximized to produce valid inference using efficient study designs (e.g., accelerated longitudinal or cohort sequential longitudinal designs [Duncan et al., 1996] or planned missing follow-ups [Brown, Indurkhya, & Kellam, 2000]), the mixture approach maximizes the use of the existing data to answer often critical questions in the literature. Thus, this modified mixture approach to a multi-group analysis can have important implications for applied research.

Appendix

Mplue code for a growth mixture model with known classes - A smoking cessation data example with six known classes and one true latent class (no slope constraint across six marital groups)

Title: A mixture model with known classes-no slope constraint
Data: File is TTURC2_EDData.dat;
     Format is 14f8.2;
Variable: Names are id y1-y7 gender marital educatio
              wages income race;
        Usevar are y1-y7 marital;
        Classes = cg(6) c(1);
        Knownclass is cg (marital=1 marital=2 marital=3
                       marital=4 marital=5 marital=6
);
        Missing are all(999);
Analysis: Model = nomeanstructure;
        Type = mixture; estimator = mlr;
Model: %Overall%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
    %cg#1.c#1%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
    %cg#2.c#1%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
    %cg#3.c#1%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
    %cg#4.c#1%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
    %cg#5.c#1%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
    %cg#6.c#1%
    i s | y1@0 y2@1 y3@2 y4@3 y5@4 y6@5 y7@6;
Plot: Type = plot2;
    Series = y1(0) y2(1) y3(2) y4(3) y5(4) y6(5) y7(6);
Output: Tech9;