High throughput film dosimetry in homogeneous and heterogeneous media for a small animal irradiator

Abstract

Purpose

We have established a high-throughput Gafchromic film dosimetry protocol for narrow kilo-voltage beams in homogeneous and heterogeneous media for small-animal radiotherapy applications. The kV beam characterization is based on extensive Gafchromic film dosimetry data acquired in homogeneous and heterogeneous media. An empirical model is used for parameterization of depth and off-axis dependence of measured data.

Methods

We have modified previously published methods of film dosimetry to suit the specific tasks of the study. Unlike film protocols used in previous studies, our protocol employs simultaneous multichannel scanning and analysis of up to nine Gafchromic films per scan. A scanner and background correction were implemented to improve accuracy of the measurements. Measurements were taken in homogeneous and inhomogeneous phantoms at 220 kVp and a field size of 5 × 5 mm². The results were compared against Monte Carlo simulations.

Results

Dose differences caused by variations in background signal were effectively removed by the corrections applied. Measurements in homogeneous phantoms were used to empirically characterize beam data in homogeneous and heterogeneous media. Film measurements in inhomogeneous phantoms and their empirical parameterization differed by about 2%–3%. The model differed from MC by about 1% (water, lung) to 7% (bone). Good agreement was found for measured and modelled off-axis ratios.

Conclusions

EBT2 films are a valuable tool for characterization of narrow kV beams, though care must be taken to eliminate disturbances caused by varying background signals. The usefulness of the empirical beam model in interpretation and parameterization of film data was demonstrated.

Introduction

The last decade has seen considerable advances in pre-clinical radiotherapy research. Several devices for small animal radiation research have been developed, allowing the delivery of conformal doses in a precise and reproducible fashion [1]. Until recently, small animal radiotherapy research relied on relatively crude methods such as broad-field and whole-body irradiations of test subjects. However, with new small animal radiation therapy platforms, it has become possible to better mimic modern treatment modalities commonly found in the human clinic, such as image guidance, 3D-conformal, and arc deliveries. This is an important step forward in bringing pre-clinical research closer to clinical application.

Modern pre-clinical systems often employ X-rays in the kV energy range for therapy [1]. While this is necessary to minimize penumbrae and build-up effects, which can extend several millimetres for photons in the MV range, it comes with a practical advantage, as X-ray tubes are much cheaper and treatment rooms require less shielding. However, precise dose calculation becomes much harder, as determining water-equivalent thickness for the different tissue types at this energy range is more complex than for MV beams due to a stronger dependence of absorption on tissue composition. Hence, established pre-clinical dose calculation systems capable of providing accurate tissue-dependent dose calculations for small animal radiotherapy treatment using kV beams have yet to be established [1].

Accurate dose calculations for small animal treatment planning and experimental verification measured doses can be performed using Monte Carlo simulations. Unlike most conventional dose calculation engines, Monte Carlo directly includes cross sections for tissue heterogeneities, thereby considerably improving the accuracy of the final dose distribution [2]. Monte Carlo approaches have been chosen by research groups, at John Hopkins [1,3], Maastricht [4], Toronto [5], and Stanford [6,7]. The last group managed to achieve a statistical uncertainty of 1%, but a computation time of up to 100 h was needed [6]. Much larger uncertainties would be acceptable for animal radiotherapy treatment. Nevertheless, considerable computation times render Monte Carlo an inconvenient tool for dose calculation, especially in a small-animal laboratory setting. Currently, Monte Carlo in this setting has only involved fairly simple treatment planning, as of now falling short of its potential as a powerful dose calculation tool [1]. Therefore, for practical applications, many groups rely on analytical methods based on the standard beam model to calculate point dose and dose distributions [3,8], but none of these approaches consider tissue or phantom inhomogeneities. Recently, preliminary results for a convolution-superposition dose calculation system have been reported [9,10], but they do not contain sufficient experimental verification in heterogeneous media, which is not an easy task.

Verifying a new treatment planning dose calculation model experimentally is especially challenging for small animal radiotherapy, since field beam diameters usually range from 0.5 to 15 mm, making it impossible to rely on more common dosimeters such as ion chambers. Therefore, EBT and EBT2 Gafchromic films have become generally accepted as a means to measure 2D dose distributions under these conditions [3,11], as they provide the high resolution required for this task. Their high acceptance was increased as they have previously been shown in some studies to be energy-independent for energies ranging from 75 kVp–6 MV [12], which includes the energy ranges used for small animal radiotherapy, though more recent data suggest otherwise [13–15]. However, Gafchromic film dosimetry for narrow beams (1 mm–100 mm size) is typically associated with relatively large pixel-to-pixel noise, film-to-film variability and poor dynamic range (in measurement of in- vs. out-of-field, shallow vs. deep depths). For this reason, film data analysis requires a beam model-based approach to guide interpretation of the data, especially for heterogeneous media. Until now, empirical beam data in heterogeneous media for extremely narrow kV beams is scarce [3] and there are no empirical models that would help with its characterization.

In view of the above, the aims of this study are: (1) to modify the existing film dosimetry protocol and make it more accurate and efficient in simultaneous processing of many films, and (2) parameterize the obtained data using an empirical beam model for simultaneous homogeneous and inhomogeneous media. For the first goal, we modified the current EBT2 film dosimetry approach for the SARRP [3] to include the new dosimetry approach introduced in Micke et al. [16], which was further studied by other groups [13,17], with additional modifications of our own, and to increase the number of processed films while removing uncertainties due to scanner non-uniformity and film inhomogeneities. This protocol was then used to generate an extensive film dose database employed for the derivation of beam model parameters. Relative and absolute dose measurements were taken in inhomogeneous media of various settings and were compared against an empirical beam model for a 5 × 5 mm² field. The model was then determined by experimentally determining the attenuation and scatter of different materials and determining the radiological pathlength through water-equivalent thicknesses.

Material and methods

Phantom material and setup

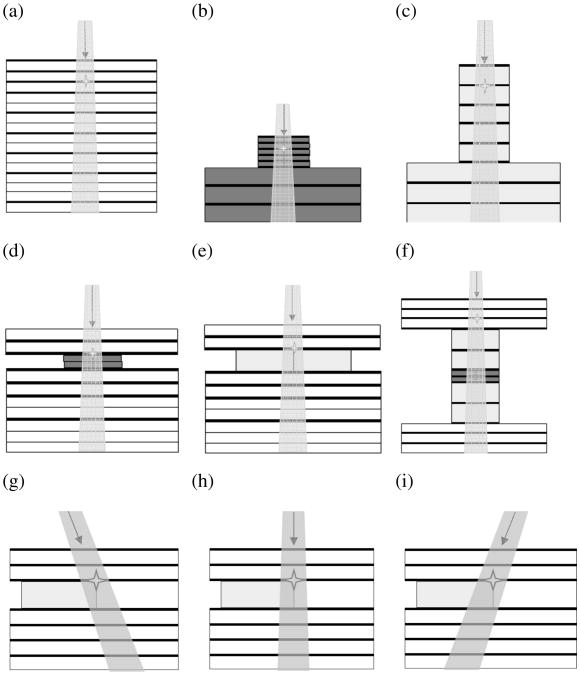
An overview of the phantoms used in this study can be seen in Fig. 1. Solid water slabs measured 60 × 60 × 5 mm³ and were water-equivalent for kV beams according to the manufacturer (CIRS, Norfolk, VA). Bone-equivalent material (Gammex Inc., Middleton, WI) was cut to measure 50 × 10 × 2 mm³; inflated lung-equivalent material (Gammex Inc., Middleton, WI) had the dimensions 50 × 20 × 10 mm³. The material densities were 1.85 g/cm³ for bone-equivalent material and 0.26 g/cm³ for the inflated lung-equivalent material. EBT2 Gafchromic films for PDD measurements were placed between the slabs as indicated in Fig. 1. For phantoms (a), (d), (e), and (f), a commissioning jig similar to that described previously [3] was employed, for the other set-ups, a custom-made phantom jig was used. To minimize setup errors, phantoms were marked and aligned to lasers corresponding to the beam axis.

Figure 1.

Phantom setups for the experiments. The respective materials are colour-coded: solid water (white), bone-equivalent material (dark gray) and lung-equivalent material (light gray). Phantoms (a) through (c) are homogeneous consisting of solid water (a), bone-equivalent material (b) and lung-equivalent material (c). Phantoms (d) through (e) were inhomogeneous phantoms used for PDD measurements. Phantoms (g) through (i) consist of solid water, with a lung inhomogeneity inserted between d₁ = 11 mm and d₂ = 21 mm. The isocenter is marked with an asterix.

Irradiations were performed using a Small Animal Radiation Research Platform (SARRP™) from Xtrahl, Ltd. (Surrey, UK) with a collimator that resulted in a field size of 5 × 5 mm² at the isocenter. Photon energy was set to 220 kV with a tube current of 13 mA and a total irradiation time of 1.5 min. Unless stated otherwise, the phantoms were setup at a source-to-surface distance (SSD) of 340 mm. The gantry angle was set to θ = 0° for all phantom setups, except for phantoms (g) and (i), where it was set to θ = −15° and θ = 15°, respectively.

EBT2 film dosimetry

Our film dosimetry protocol largely followed the one described previously in Tryggestad et al. [3] which had since been adjusted to apply multi-channel dosimetry [16]. In addition, we included an improved scanner correction that allowed for faster processing of multiple films and a film background correction to reduce the impact of off-sets found between different deliveries of films of the same LOT number.

EBT2 films (LOT A08161005A) were cut into 60 × 60 mm² pieces using a cutting template, and scanned in landscape orientation as 48-bit RGB image in transmission mode using an Epson Perfection V700 Photo scanner. All colour corrections provided by the scanner software were disabled. The resolution of the scanned images was 400 dpi, and the images were saved as TIFF files. To ensure the scanner lamp was sufficiently warmed up, the warm-up routine was run and two preview scans were performed. Nine films were scanned in a scanning frame that allowed reproducible setup, which could hold nine films of 60 × 60 mm² simultaneously. Films were scanned prior and approximately 12 h after irradiation, with values defined as the average over three consecutive scans to reduce random scanner noise. Each time, it was ensured that the scanning direction for each film was consistent in regard to the orientation of the uncut film.

To correct for non-uniformity in scanner response, lateral scanner correction based on the approaches described in previous publications was performed [18,19]. For this, films were exposed to five different dose levels (0, 100, 200, 300, 400 cGy at 6 MV in solid water) to achieve increasing levels of darkness and scanned in the different positions of the frame. The separate scans were patched together in Matlab (MathWorks, Inc., Natick, MA, USA). In contrast to previous publications, this scanner correction can only be applied to certain regions of interest, which correspond to the locations the films on the scanning frame. This was done to ensure that lack of scatter due to the missing plastic frame would not affect the scanner response. Each film location was divided into smaller areas for which an average pixel value for each dose level was determined. These were then normalized to the average of all pixels in the regions of interest at each dose level to determine a correction factor for this area.

As the previous publications and our own preliminary analysis have shown, lateral scanner response perpendicular to the scanning direction (y) can vary considerably while longitudinal scanner response along the scanning direction (x) remains rather uniform. Therefore, averages were taken over correction factors along x for each exposure level, resulting in a correction factor k_l for each lateral location y and dose level:

$$k_l(y)=\frac{\frac{1}{N}\cdot {\sum }_{i=1}^N\mathit{\text{PV}}(x_i,y)}{{\mathit{\text{PV}}}_{\text{mean}}}$$ (1)

where PV (x_i,y) is the pixel value of a given pixel located at (x,y), PV_mean is the average pixel value of all pixels in a given scan, and N is the number of lateral locations.

The results were stored in a lookup-table [20] according to the average pixel value corresponding to each dose level, lateral location on the scanner and colour channel. This look-up table was then applied to the scanned images. Correction factors for pixel values that were not part of the look-up table were determined by linear interpolation.

After this, we applied a background correction to account for film-intrinsic differences in pixel value that were not caused by radiation exposure. The exact reason for these differences are unclear, but were found to occur frequently between films delivered in different boxes, even if they were of the same LOT number. To correct for this and prevent us from having to establish a new calibration curve for every film delivery, the average pixel value of a large number of pre-scanned unexposed films was determined as a reference and a correction factor k_b was determined by dividing this average to the average intensity of each individual unexposed film.

$$k_b=\frac{{\mathit{\text{PV}}}_{\text{mean}}}{{\mathit{\text{PV}}}_{\text{unexposed}}}$$ (2)

where PV_mean is the average pixel value of a given colour channel of an entire given film before exposure, and PV_unexposed is the expected pixel intensity before exposure for a given colour channel based on an average over a large number of pre-scanned films. This correction factor was then applied to the scanned images of the irradiated films after the lateral scanner correction. This was done for all three colour channels, as all of them would be needed for triple-channel dosimetry.

For determination of a calibration curve, output of the SARRP was determined using an ion chamber largely following guidelines given in TG-61 [21]. A few adjustments were required for our setup: a reduction of field size, for which a small correction factor was extrapolated from Fig. 4 of TG-61, a reduction of SSD to 33 cm, and the use of CIRS solid water instead of a water tank. Films were placed between CIRS solid water slabs at a depth of 2 cm, and exposed 12 different dose levels ranging from 0 to 900 cGy. To improve accuracy, each exposure time was measured twice, which means that total of 24 films were used. Scanner correction and background correction were applied as described above and the pixel values were correlated to their corresponding dose levels. Data points for each channel were fitted to a rational function, similar to the description in Micke et al. [16], but fitted to the corrected pixel value (PV_corr) rather than optical density:

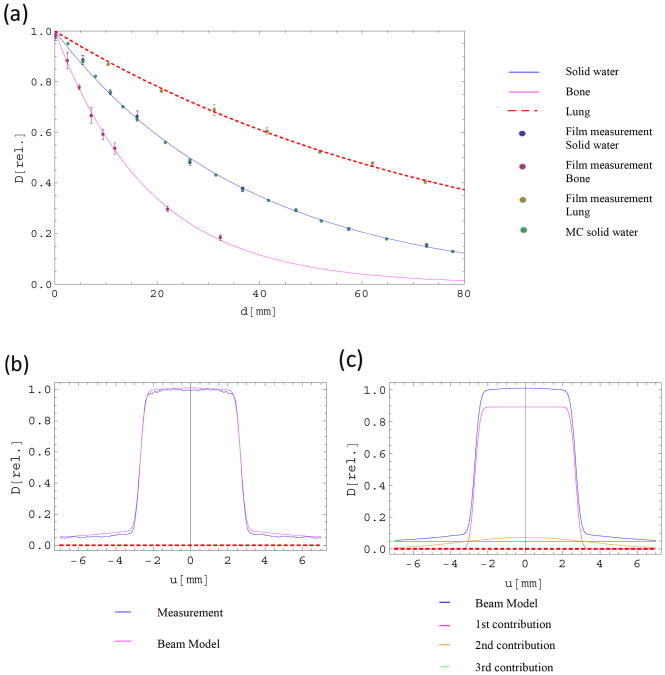
Figure 4.

Film measurements in homogeneous phantoms: (a) Plots of the average relative measurements and their corresponding standard error of the mean for all three homogeneous materials and the corresponding fitted curves using Equations (A.1) and (B.2). The parameters are: solid water (μ = 0.0265 mm⁻¹; η = 0.0001 mm⁻¹), bone (μ = 0.052 mm⁻¹; η = 0.0001 mm⁻¹; k = 2.054), lung (μ = 0.0126 mm⁻¹; η = 0.0006 mm⁻¹; k = 0.467). (b) Beam model and the corresponding fitted measured data at a depth of 26.42 mm. (c) The beam model in (b) split up into its individual contributions. The dashed line indicates the x-axis.

$$D(x,y)=\frac{a-c\cdot {\mathit{\text{PV}}}_{\text{corr}}}{{\mathit{\text{PV}}}_{\text{corr}}-b}$$ (3)

Using a rational function rather than a polynomial fit is recommended by the manufacturer as they are simple to invert and have a rational behaviour with respect to the physical reality whereas polynomial functions usually show no correspondence to physical reality outside the data range over which they are fitted [22].

To evaluate measured dose, we applied triple-channel dosimetry with non-uniformity correction to correct for a dose disturbance Δd. This method is described in further detail in Micke et al. [16].

$${\mathit{\text{PV}}}_{\Delta d}={10}^{(lg(\mathit{\text{PV}})/\Delta d)}$$ (4)

Here, Δd is chosen such that the following condition is fulfilled:

$$\Omega (\Delta d)=\sum _{i\ne j}{(D_{{\mathit{\text{PV}}}_{{\Delta d}_i}}-D_{{\mathit{\text{PV}}}_{{\Delta d}_j}})}^2\to min$$ (5)

All image processing steps were implemented in Matlab. Results were tabulated and written in excel files that could be read into Mathematica (Wolfram Inc, Champaign, IL, USA) for further analysis.

Monte Carlo simulations

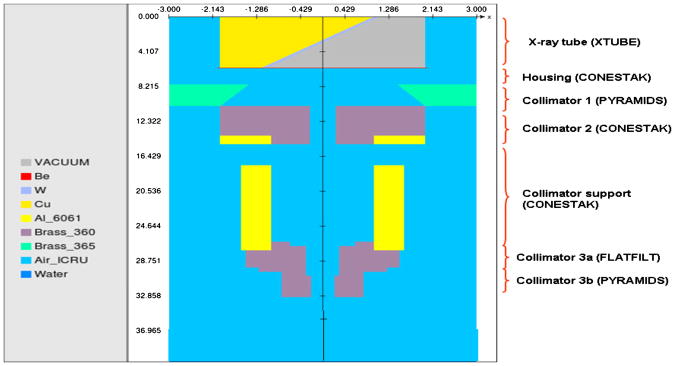
Monte Carlo simulations for the small animal irradiator were done by using EGSnrc code. BEAMnrc code was used for the head simulation while for the phantom simulation DOSXYZnrc code was used. The geometry and materials of SARRP were based on the blueprints and previous publications with certain necessary modifications [3,23]. All components of the head structure were included in the simulation (X-ray-tube, filter and collimation components of the head). Figure 2 shows a cut-off view of the head geometry assembly.

Figure 2.

The head geometry of the SARRP used for the Monte Carlo simulations with the 5 × 5 cm square collimator insert.

Physics input parameters were implemented to reduce simulation time and simulate lower energy physics accurately. All EGSnrc default parameters were used, except for options “Bound Compton scattering”, “Rayleigh scattering” and “electron impact ionization” which were turned on. For Bremsstrahlung angular sampling, Koch-Motz (KM) distribution was chosen while “Pair angular sampling” was set to Off. Bremsstrahlung yields were taken from the NIST library and XCOM photon cross sections were used.

Directional Bremsstrahlung splitting (DBS) variance reduction technique was selected for Bremsstrahlung photons with splitting of 50,000 and field radius of 1 cm and the SSD set at 34 cm. Simulations were run with 400 million histories and one output phasespace was scored at SSD = 34 cm in a Linux parallel computer cluster with 32 CPUs.

Source 13 as provided as part of the EGSnrc code was used for the modelling of the electron target. Kinetic energy of the electrons was 220 kV, while the half width of the beam was set to 0.2 cm and 0.5 cm for the Y and Z axis respectively. The phantom used for scoring dose was made of water and had a size of 60 × 60 × 80 mm³. For heterogeneity experiments, the simulated phantoms mimicked the descriptions in Fig. 1. New lung and bone materials were created for the simulation by using a special tool provided in the EGSnrc code. The exact composition and density of these materials were provided by the manufacturer (Gammex Inc., Middleton, WI). In order to keep MC statistical uncertainty below 1.5%, 1.5 billion histories were simulated for all phantoms. Voxel size for the simulated phantoms varied by case.

Parameterization of beam data

The SARRP utilizes narrow cones from 0.5 mm to 15.0 mm to deliver radiation with static beams or with arcs. For each given cone kV beam properties are determined from Gafchromic film dosimetry (depth and off-axis dose profiles) in homogeneous phantoms comprised of different material types. To facilitate analysis and organization of the film data, beam model parameters were determined for three materials: water, bone and lung. Empirical formulas for percent depth dose (PDD) and off-axis dose ratio (OAR) for homogeneous media are summarized in the Appendix A. The film data was fitted to these formulas to determine the model parameters and provide a consistency check for the film data, which is especially important due to film-to-film variability and noise/artifacts occurring within the same film. As part of the analysis we examined how the aforementioned beam quantities apply to heterogeneous media. The empirical beam data formulas for heterogeneous media are meant to help with interpretation and management of dose data, not as a stand-alone dose calculation model. Though potentially interesting, any applications of such a simplistic empirical model for dose calculation in treatment planning in heterogeneous media are therefore not the focus of this paper.

Film dosimetry is performed either in homogeneous media or in heterogeneous media with infinite-slab or half-slab geometry. For this reason, we refer to the axis perpendicular to the beam alignment as u, and omit dependence on the other perpendicular axis. However, this one-dimensional description is sufficient to determine the parameters of the model (weights and variances of the dose deposition kernels), which are applicable to 2D cases as well. The beam parameterization we applied is an extension of the standard beam parameterization, where percent depth dose (PDD) and off-axis ratio (OAR) model functions are used to determine parameters through fitting of measurements in several inhomogeneous media. PDD is modelled as an exponential function, whereas the OAR model is described as a sum of error functions (Appendix A).

Extending the model to heterogeneous media is performed by the introduction of water-equivalent thickness (wet) as the measure of the effective pathlength. The presence of inhomogeneities in the medium changes the attenuation along the beam path in a material-dependent fashion. This can be accounted for by rescaling material properties using radiological pathlength instead of physical depth in the medium. For this, the relative attenuation coefficient k, a ratio of μ for a given material and μ for water, was determined for each phantom material (Appendix B).

The conversion factor C(u.d) is based on MC-simulated spectra (Appendix B, Fig. S1) and converts dose to water to dose in any given medium, where u refers to the distance from the central axis and d the depth in material. This dose conversion factor was also used to determine absolute dose to a medium for film measurements taken in materials other than water, since absolute dose for film measurements was calibrated as dose to water.

The cumulative dose at any given point (u,d) is a sum of dose contributions from a number of n micro pencil beams, which was shown useful in previous studies [24]. Dose profile associated with a given micro-pencil beam can expressed in terms of wet, making wet dependent on both u and d (Appendix C).

All the calculations and their corresponding plots were done using Mathematica.

Results

Film dosimetry

Analysis of unexposed films for three different boxes clearly showed that the background signal can vary significantly between separate deliveries even if the films are of the same LOT number and the temperature indicator shows no heat exposure. The results are shown in Table 1.

Table 1.

Average raw scanner values on a 48-bit scale for unexposed films of three different boxes. Values are based on averages of at least 36 films of 60 × 60 mm².

Channel	Box 1	Box 2	Box 3
Red	(5.0854 ± 0.64) × 10−4	(5.1341 ± 0.66) × 10−4	(5.2358 ± 1.17) × 10−4
Green	(4.7084 ± 0.49) × 10−4	(4.7528 ± 0.49) × 10−4	(5.0008 ± 1.05) × 10−4
Blue	(2.6082 ± 0.39) × 10−4	(2.6299 ± 0.40) × 10−4	(2.9075 ± 0.64) × 10−4

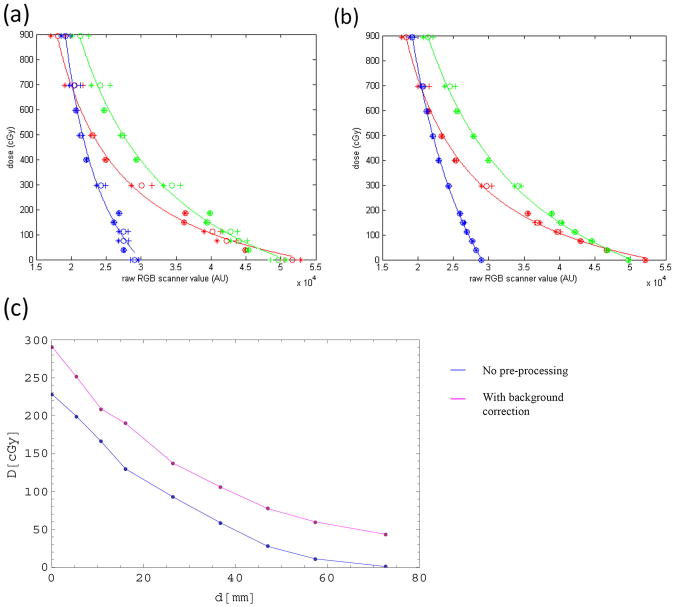
Figure 3 shows the impact of the correction steps on the calibration curve. Applying the fit to uncorrected data shows that while the curve matches the measured points in the high dose regions with acceptable accuracy, pixel values of films exposed to low amounts of radiation often deviate quite considerably from the curve, as seen in Fig. 3(a). Applying lateral scanner correction and film background correction makes the calibration considerably smoother, as seen in Fig. 3(b). The plot shows results for two measurements and their average. The improvement of the calibration was considerable: For the red channel, the average difference between the calibration curves and their resulting fits decreased from 20.0 cGy to 11.5 cGy for the red channel, from 20.2 cGy to 9.1 cGy for the green channel and from 30.1 cGy to 7.2 cGy. The fitting parameters changed slightly when the background correction was applied to the calibration films, which lead to about 2–3% higher doses for doses above 100 cGy and up to 25% lower doses in the low dose regions up to 30 cGy.

Figure 3.

Calibration curves (a) using raw data and (b) after applying scanning and background correction. Channels are colour-coded. The plots show results for two measurements and their average. Fitting was done to the average of both measurements. Figure 3 (c) shows the dosimetric impact of the background correction on a depth dose curve measured at an SSD of 340 mm and a 5 × 5 mm² field size.

Applying the background correction to film measurement was essential to reduce off-sets introduced by strong variations in the background signal. Figure 3(c) shows the same depth dose measurement taken at an SSD of 34 cm and a 5 × 5 mm² field size, analysed once with the background correction and once without any corrections. Such offsets ranged from 0 to 70 cGy in either direction depending on the original background signal. We found they could be reliably removed by applying the background correction, leading to consistent results regardless of the original signal.

Homogeneous media

Figure 4 shows the film measurements of the depth dose for the three homogeneous materials used in this study, which are shown in Fig. 1(a)–(c). Data points shown are the average over two (solid water) and three sets of measurements (lung and bone-equivalent material) and were normalized to their extrapolated surface dose. Reported dose rates are the averages within a square region of 2.5 mm². Error bars indicate the standard error of the mean.

While the measured average data for bone- and lung-equivalent materials tended to be considerably noisier than the data for solid water, the standard error for all measured data was found to be smaller than 5%. An average was taken over all sets of normalized measurements for each material and the resulting data points were fitted to a PDD fitting function (A.1) to determine attenuation coefficient μ and beam hardening parameter η for each material. Relative attenuation k of each material was determined, using μ = 0.0265 mm⁻¹ and η = 0.0001 mm⁻¹ as determined for solid water. For simplicity's sake, we assumed k to be homogeneous through the path of each ray in homogeneous media, which is likely not the case due to insertion of films for measurements and pores inside lung material. Values for k ranged from k_L = 0.47 for lung-equivalent material to k_b = 2.05 for bone-equivalent material, with k_w = 1 by definition. The fitted curve for solid water was compared to Monte Carlo simulations, which were benchmarked against film data in solid water (Fig. S2) and used as another means of comparison for this experiment. Agreement was very good, with an average deviation of 1.0% from the model (maximum difference 2.4%).

Data for OAR was determined by normalizing measured profiles to their respective dose averages. Measured data over all depths was used to derive parameters for OAR (A.2), with n = 3 contributions. Figure 4(b) shows the measured profile data in homogeneous solid water at a depth of 26.4 mm with its corresponding fit. The three contributions making up the final fit are shown in Fig. 4(c).

Heterogeneous media: infinite slab

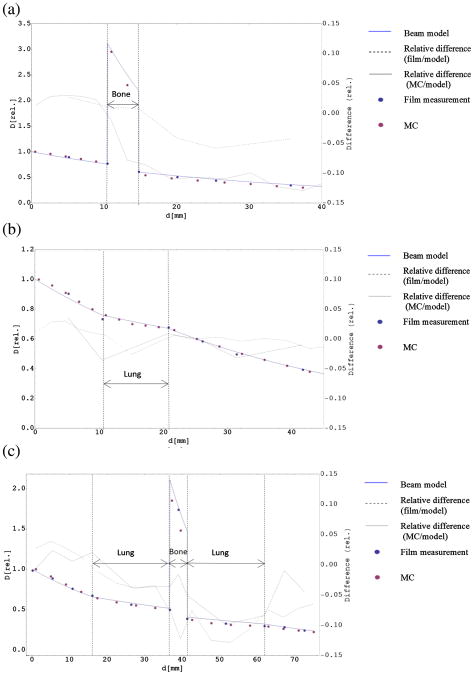
Figure 5(a) and (b) shows relative dose rate averages obtained in the heterogeneous phantoms shown in Fig. 1(d) and (e). Measurements were done twice for phantom d and three times for phantom e, and average dose rate for each measurement was obtained by forming the average within a square region of 2.5 mm². The material-dependent conversion factor for bone (B.3) was 4.1 above the inhomogeneity and 3.62 below the inhomogeneity due to beam hardening in the spectrum (Fig. S1). Values in between were determined through linear interpolation. The line indicates the expected dose according to the beam model (B.2). The k values derived from Fig. 4(a) were used as input to determine wet-function and differences between measurement data and calculation were determined. Overall, the agreement between film data and model is quite good. Except for one measurement point with a difference of 5.8%, the differences between film measurement and model were found to be well below 5%, with a mean difference of 3.1% for phantom (d) and 2.1% for phantom (e). Monte Carlo simulations were in reasonable agreement with the model, though considerably better for phantom (e), with the average difference of 1.5%, compared to an average difference of 7.1% for phantom (d). These discrepancies could arise from different composition of bone from NIST tables compared to our phantom material.

Figure 5.

Measurements in inhomogeneous slab phantoms: Average measurements for two inhomogeneous setups, one containing an inhomogeneity of 4 mm bone starting at depth of 11 mm (a), the other containing an inflated lung inhomogeneity of 10 mm starting at the same depth (b), and their corresponding PDD calculated using wet. Error bars for standard error of the mean are smaller than the size of the symbols. Relative differences compared to the model are shown for films and MC, the scale is given on the right. (c) Average measurements of PDD in the phantom shown in Fig. 1(f) and the PDD that was calculated using wet-function. Lung inhomogeneities were inserted between 16.2 mm and 36.5 mm and between 41.2 mm and 61.5 mm. A bone inhomogeneity was located between 36.8 mm and 41 mm. Error bars for standard error of the mean are smaller than the size of the symbols. Relative differences compared to the model are shown for films and MC, the scale is given on the right.

Measurement data obtained in the more complex phantom setup shown in Fig. 1(f) and the calculation based on the beam model (B.2) are shown in Fig. 5(b). In addition to the film measurements, Monte Carlo simulations were performed as an additional verification and compared to both film dosimetry and the model. Again, overall agreement is good. The highest difference between measurement and calculation was found to be 6.3% in lung, with an average difference of 2.9%. The MC results compared to the empirical calculation with an average difference of 6.6%. It has to be noted that lung phantom material was very heterogeneous (foam structure), which was not possible to simulate in Monte Carlo. For all depth dose measurements, discrepancies were found to increase with depth.

Heterogeneous media: half-slab

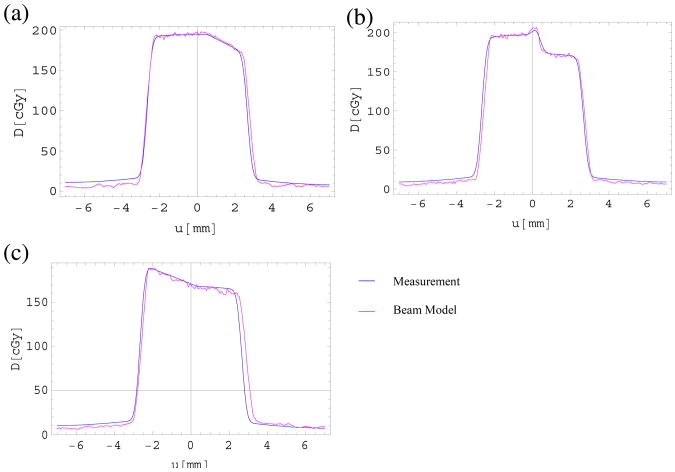
Using the phantom shown in Fig. 1(g)–(i), irradiations were performed with three different gantry angles (θ₁ = −15°; θ₂ = 0°; θ₃ = 15°) and compared to calculations using a sum of 23 micro pencil beams (C.1). Measurements were performed in seven depths ranging from 0.1 to 37.1 mm, with an inhomogeneity of lung-equivalent material located between 11 and 21 mm. Four of the measurements were done below the inhomogeneity. Figure 6 shows absolute dose measurements for each gantry angle at a depth of 21.1 mm below the inhomogeneity in comparison to the calculated dose distributions based on the parameters derived from the measurements in homogeneous media, with a number of n = 23 beamlets. Local 2D Gamma indices were determined for the plots shown in Fig. 6 (Fig. S3) and the passing rates were found to be 90.3% at θ = −15°, 97.4% at θ = 0°, and 96.6% at θ = 15°, with a passing threshold of 3%/0.3 mm.

Figure 6.

Beam model and measurement results at a depth of 21.1 mm for setups shown in Fig. 1(g)–(i), irradiating a phantom with half-slab geometry coming from gantry angles (a) θ = −15°, (b) θ = 0°, and (c) θ = 15°. The shown depth is representative for all other depths measurements were performed for.

Discussion

Film dosimetry

As Fig. 3 indicates, scanner correction and background correction contributed considerably towards improving the accuracy of the results, leading to better fits in the low dose regions for all three channels. While several publications have shown that it is sufficient for EBT2 dosimetry to rely on multichannel non-uniformity correction alone [13,16], we found that using the background correction was necessary to remove background signal variations that occurred between different boxes of the same lot that would have introduced off-sets to the dosimetry results if multi-channel non-uniformity correction alone had been used. It thus removed the need for tedious recalibration of the separate boxes while giving reliable and reproducible results. Unlike the background correction, which applied a fixed factor to all pixels of the same film, the multichannel optimization is pixel-specific, reducing the impact of variations within the same film, while the background correction only removes an off-set that affects the entire film homogeneously.

For good results, it is critical to select the right exposure time. Film dosimetry works reliably only in a relatively small dose range. If total doses are selected too low (<100 cGy), signals become increasingly noisy, making the results less reliable. If doses are selected too high, noise amplification occurs, as previously described [3]. In their study, the authors claim that noise amplification becomes important for doses larger than 3 Gy, with a noise amplification factor of more than five for doses of 10 Gy, and is caused by the relationship between dose and detected transmission, since high doses lead to saturation of the films, making response of the films very sensitive to small deviations in RGB values. While the triple channel dosimetry is likely to reduce this issue somewhat by taking another two channels into account, exposure time must be chosen carefully. For measurement of a wider range of dose levels, certain measures can be taken to reduce noise levels [25].

Parameterization of beam data

Throughout the study, we found that the empirical formulas were essential in interpretation and parameterization of film data and in comparison of Monte Carlo simulations to experimental data. Extension of the empirical formulas to dose calculation would require further study and goes beyond the scope of this paper. In the assessment of film dosimetry it has to be kept in mind that film dosimetry with its inherent limitations provides the experimental ground truth and that Monte Carlo is the secondary method, as its fine-tuning is reliant on empirical data. In this regard the empirical beam model is convenient.

Overall, relative measurements and the dose distribution calculated by the micro pencil beam model agree quite well, with more than 90% of measured data points passing a local 2D gamma analysis of 3%/0.3 mm (Fig. S3). Discrepancies are found in regions with large dose gradients, where the OAR model showed a larger dose gradient than the measured data, which was likely due to the inability of the model to account for field size changes in the horizontal plane when the gantry is rotated. Further dose deviations were found in low dose regions outside the beam for which calibration of film data is difficult (small changes in film opacity result in large changes in calculated doses). For the measurement at θ = 0°, an air gap of 0.6 mm was modelled to account for a small gap between the solid water slabs and the lung-equivalent material, with k_air set to 0.01. In addition, a setup error of 0.5 mm was introduced when aligning the phantom to the beam, which has been accounted for in the dose calculations. Here, the model proved capable of modelling the nature and magnitude of setup errors. This can be of considerable benefit for explaining discrepancies between film measurements and expected results and proved the model's worth as an interpretation and parameterization tool for experimental data.

Applying the relative densities k determined empirically for each of the materials to model PDD in inhomogeneous setups gives results which agree with the measurement usually within 5%, regardless of the inhomogeneity inserted. Considering the inherent limits of film dosimetry, this confirms that approximating radiological pathlength by water-equivalent thickness (wet) is a valid method to describe the depth dose in inhomogeneous material. The model even holds true for more complex setups that contain several inhomogeneities of varying materials with varying thickness, showing that the parameterization of film data using a simple empirical model is possible even in complex phantom setups.

For depth dose data in solid water, film measurements agreed well with MC predictions, showing the validity of our dosimetry approach. This was also true for inhomogeneous media containing lung-equivalent material, and to a lesser degree, for media containing bone.

According to our model, we expected an increase in bone dose due to the photoelectric effect, a dominant interaction at the photon energies used in this experiment. This would be in agreement with our Monte Carlo simulations as well as previously published studies [26], which reported a significant bone dose enhancement in a mouse model of up to three times higher when simulating irradiation with 225 kV X-rays, with no significant changes in lung dose compared to homogeneous tissue.

Attenuation of photons inside higher-Z materials such as bone is accounted for in our model by explicitly taking measurements for bone material and experimentally determining k and μ for bone. It has to be noted that wet-function defined as a path integral does not model dose enhancements due to the photoelectric effect inside bone explicitly, which is a common shortcoming of approaches based on water-equivalent pathlengths. However, using mass energy absorption coefficients provided in the NIST database and the spectral information gained from our MC studies and knowing the locations of bone materials (which are in principle obtainable from cone-beam CT), we were able to derive a material-dependent conversion factor (B.3) that allowed us to convert dose to water to dose to bone and lung. Hybrid approaches were adopted in two studies, [27,28] which used Monte Carlo-based corrections for dose in lung and bone. Our correction was included in the model and also applied to measurements inside media other than water, as films had been calibrated to dose to water. We found that this correction was crucial for dose determination inside bone-equivalent material, where the dose to the material was almost four times as high as dose to water (3.86 on average), while it was negligible for lung-equivalent material, with a factor of 1.01. Therefore, by using a correction of dose for bone, it is possible to obtain a reasonably accurate representation of dose distribution not only in soft tissues, but also in bony tissues.

Another important point is that even though this conversion factor allowed for dose corrections, the main focus of our study was to develop a sound empirical approach to describe and explain the experimental data obtained using EBT2 film. As such our empirical model proved very robust for film analysis and characterization of the beam data.

When modelling OAR for micro size beams of the kV irradiator, the differences between parallel and divergent geometry are extremely small. This is due to the fact that since the SDD is much larger than the beam width, increase in depth due to beam divergence is negligible. For the 5 × 5 mm² cone that was used in the study, it was found to be smaller than 0.1%. Therefore, we assumed parallel beam geometry for our model.

In inhomogeneous media, particularly in Fig. 5, and penumbra regions (Fig. 6), dose deviations of several percent compared to the model can be observed. As the energy independence of EBT2 film has been called into question [13–15], a change of the beam spectra caused by the passage through various media (Fig. S1) could have contributed to these errors.

In a few films, a shift of a few percent of the whole dose distribution was observed for the absolute dose measurements. The reasons for this remain unclear, but as each measurement was performed at least twice and amount and direction of the shift appeared random, we suspect this to be caused by an intrinsic error of the film rather than a systematic error in the method. This is supported by the observation that these films often showed a strong deviation in their signal in the preexposed scans.

Conclusions

We could demonstrate that despite its intrinsic limitations, film dosimetry is a sound approach for 2D dose measurement in the low energy range for small field sizes where a high resolution is required. The modifications introduced to the film dosimetry protocol allow us to evaluate up to nine films in one scan while keeping a high level of accuracy, making it easier to process large numbers of film for experiments and commissioning, about 800 films in the case of this study.

We have shown that the empirical beam model is a useful tool in the analysis of experimental results in various homogeneous and heterogeneous media and essential for determining reason and magnitude of setup errors. The method has been validated in a variety of phantoms and can be used to predict film measurements percentage depth dose and profiles with sufficient accuracy, making it an interesting tool for interpreting film data and as a comparison to Monte Carlo simulations.

Appendix A

We will use the following convention: d is depth in water, or another homogeneous material; u is the off-axis distance and wet is the water-equivalent thickness of material along the central axis.

Percent depth dose function (PDD) in homogeneous materials is described with respect to its normalization to the dose rate at the surface:

$$\text{PDD}(d)=\frac{D(d)}{D(d=0)}=e^{-\mu d(1-\eta d)}$$ (A. 1)

where beam model parameters (μ, η) depend on the cone size and kVp, with μ being the linear attenuation coefficient and η being a nonlinear parameter that accounts for beam hardening. The nonlinear parameter η is included to account for beam hardening.

OAR is defined as the relative dose distribution in the plane perpendicular to the beam axis and is modelled as a sum of three contributions related to the primary, secondary and tertiary scatter doses:

$$\text{OAR}(u,d,c)={\sum }_{i=1}^n{w}_i(1+w_{0,i}d)\cdot \text{OAR}(u,-\frac{c}{2},\frac{c}{2},{\sigma }_i(1+{\sigma }_{0,i}d))$$ (A. 2)

where w_i is a weighting factor determining the amplitude of the contribution and w_o,i is a weighting factor that accounts for changes of OAR amplitude with increasing depth. The OAR function on the right is the error function defined as

$$\text{OAR}(u,u_1,u_2,\sigma )=\frac{1}{2}\left[\mathit{\text{erf}}\right(\frac{2\cdot (u_2-u)}{\sigma })+\mathit{\text{erf}}(\frac{2\cdot (u_1-u)}{\sigma }\left)\right]$$ (A.3)

The boundaries of the OAR, u₁ and u₂, are user specific and can also be selected to model asymmetric fields.sis the Gaussian scatter kernel size. In our case, we chose u₁ = −c/2 and u₂ = c/2, with c accounting for beam divergence with increasing depth, which is dependent on SSD and defined as follows:

$$c=c_0\frac{\text{SSD}+d}{d_0+\text{SSD}}$$ (A. 4)

where d₀ is the reference depth, and c₀ the width of OAR at a depth of d = 0 at an SSD of 34 cm.

Appendix B

One approach of doing this is to integrate over all relative densities along the path of one micro beamlet. We will refer to this integral as water-equivalent thickness (wet):

$$\text{wet}(u,d)=cos(\phi )\underset{\text{path}}{\int }k(t)\text{d}t$$ (B. 1)

where k(t) is relative attenuation coefficient of medium compared to water and integration is carried along a ray from the source to the point inside the medium at (u,d), with cos(φ) accounting for beam divergence and φ being the angle between the path of integration and the central axis.

Using this definition of wet, attenuation of a ray in heterogeneous media can be defined as follows:

$${\text{PDD}}_{\text{het}}(u,d)=C(u,d)\cdot e^{-\mu \cdot \text{wet}(u,d)\cdot (1-\eta \cdot \text{wet}(u,d))}$$ (B. 2)

In which μ and η are the parameters determined for water and wet(u,d) accounts for spatially dependent dose deposition in water-equivalent heterogeneous medium.

The conversion factor C(u,d) is determined from the mass energy absorption coefficients μ_en as listed in the NIST database and MC-generated spectra (Fig. S1) using the following formula:

$$C(u,d)=\frac{\underset{0}{\overset{E\text{max}}{\int }}E\cdot \Phi (E,d)\cdot {\mu }_{\text{en}}(E,u,d)\cdot \text{d}E}{\underset{0}{\overset{E\text{max}}{\int }}E\cdot \Phi (E,d)\cdot {\mu }_{\text{en},\text{water}}(E)\cdot \text{d}E}$$ (B. 3)

where E is the energy in keV, and Φ(E,d) is the photon flux for a specific energy at a specific depths. μ_en(E,u,d) is the linear mass energy absorption coefficient for the material located at (u,d) for a specific photon energy E, while μ_{en, water}(E) is the mass energy absorption coefficient of water for energy E.

Appendix C

Dose profile associated with a given micro-pencil beam is expressed in terms of wet calculated as in the above equation. If micro pencil beams are rectangular, then the dose profile can be described as follows:

$$D_{\text{het}}(u,d)=D_0\cdot {\sum }_{i=1}^n\text{OAR}(u+\frac{c}{n}(i-1)-\frac{c}{2}+\frac{c}{2n},d,\frac{c}{n})\cdot {\text{PDD}}_{\text{het}}(\frac{c}{n}(i-1)-\frac{c}{2}+\frac{c}{2n},d)$$ (C. 1)

where D₀ equals the dose measured in homogeneous solid water at (u,d) = (0,0).