Multi-Atlas Segmentation with Joint Label Fusion

Abstract

Multi-atlas segmentation is an effective approach for automatically labeling objects of interest in biomedical images. In this approach, multiple expert-segmented example images, called atlases, are registered to a target image, and deformed atlas segmentations are combined using label fusion. Among the proposed label fusion strategies, weighted voting with spatially varying weight distributions derived from atlas-target intensity similarity have been particularly successful. However, one limitation of these strategies is that the weights are computed independently for each atlas, without taking into account the fact that different atlases may produce similar label errors. To address this limitation, we propose a new solution for the label fusion problem, in which weighted voting is formulated in terms of minimizing the total expectation of labeling error, and in which pairwise dependency between atlases is explicitly modeled as the joint probability of two atlases making a segmentation error at a voxel. This probability is approximated using intensity similarity between a pair of atlases and the target image in the neighborhood of each voxel. We validate our method in two medical image segmentation problems: hippocampus segmentation and hippocampus subfield segmentation in magnetic resonance (MR) images. For both problems, we show consistent and significant improvement over label fusion strategies that assign atlas weights independently.

I. Introduction

Atlas-based segmentation is motivated by the observation that segmentation strongly correlates with image appearance. A target image can be segmented by referring to atlases, i.e. expert-labeled sample images. After warping the atlas to the target image via deformable registration, one can directly transfer labels from the atlas to the target image. As an extension, multi-atlas based segmentation makes use of more than one atlas to compensate for potential bias associated with using a single atlas and applies label fusion to produce the final segmentation. This method requires higher computational costs but, as extensive empirical studies have verified in the recent literature, e.g. [16], [3], [22], it is more accurate than single atlas based segmentation. Enabled by availability and low cost of multi-core processors, multi-atlas label fusion (MALF) is becoming more accessible to the medical image analysis community. Recently, the concept has also been applied in computer vision for segmenting natural images [37], [21].

Errors produced by atlas-based segmentation can be attributed to dissimilarity in the structure (e.g., anatomy) and appearance between the atlas and the target image. Recent research has been focusing on addressing this problem. For instance, such errors can be reduced by optimally constructing a single atlas that is the most representative of the population using training data [12], [11], [18]. Constructing multiple representative atlases from training data has been considered as well and usually works better than single-atlas based approaches. Multi-atlas construction is done either by constructing one representative atlas for each mode obtained from clustering training images [5], [2], [32] or by simply selecting the most relevant atlases for the unknown image on-the-fly [30], [1], [41]. Either way, one needs to combine the segmentation results obtained by referring to different atlases to produce the final solution.

Most existing label fusion methods are based on weighted voting, [30], [16], [3], [17], [33], where each atlas contributes to the final solution according to a non-negative weight, with atlases more similar to the target image receiving larger weights. Among weighted voting methods, those that derive weights from local similarity between the atlas and target, and thus allow the weights to vary spatially, have been most successful in practice [3], [17], [33]. One common property of these spatially variable weighted voting MALF methods is that the weights for each atlas are computed independently, only taking into consideration the similarity between the warped atlas and the target image. As such, these methods are less effective when the label errors produced by the atlases are not independent, e.g. most atlases produce similar errors. As a simple example, suppose that a single atlas is duplicated multiple times in the atlas set. If weights are derived only from atlas-target similarity, the total contribution of the repeated atlas to the consensus segmentation will increase in proportion to the number of times the atlas is repeated, making it more difficult to correct the label error produced by the duplicated atlas. Likewise, if the atlas set is dominated by a certain kind of anatomical feature or configuration, there will be an inherent bias towards that feature, even when segmenting target images which do not share that feature. As the result, the quality of the segmentation for the less frequent anatomical features/configurations may be reduced.

Another class of label fusion methods perform majority voting among a small subset of atlases that globally or locally best match the target image, discarding the information from poor matching atlases [3], [7]. These methods are less susceptible to the problem described, since the atlas appearing multiple times would only be included in the voting if it is similar to the target image. However, by completely discarding information from poorer matches, these methods lose the attractive property of voting arising from the central limit theorem. In particular, when all atlases are roughly equally similar to the target image, performing voting only among the few best atlases will have greater expected error than voting between all atlases.

This paper derives a novel label fusion strategy that aims to reduce the bias due to the fact that atlases may produce correlated segmentation errors, without sacrificing the attractive properties of voting. The strategy is derived from formulating the weighted voting problem as an optimization problem over unknown voting weights, with the expected total error of the consensus segmentation relative to the unknown true segmentation being minimized. This formulation requires the joint distribution of label errors produced by any pair of atlases in the neighborhood of each voxel to be known. In practice, this distribution is unknown, and we estimate it using image intensity similarity. However, unlike previous methods, similarity with the target image is not measured independently at each atlas. Instead, intensity similarity between the target and each pair of images is considered, which leads to an ability to explicitly estimate the probability that a pair of atlases produce the same segmentation error. We hypothesize that this strategy will improve segmentation accuracy over existing techniques that consider atlas-target similarity independently [3], [33]. To test this hypothesis, we perform cross-validation segmentation experiments in manually labeled MRI datasets, and report significant improvements over earlier methods.

Preliminary versions of this work appeared in [39], [38].

II. Multi-Atlas Based Segmentation

We start with a brief overview of MALF. Let F_T be a target image to be segmented and A₁ = (F₁, S₁),…,A_n = (F_n, S_n) be n atlases. F_i and S_i denote the i_th warped atlas image and the corresponding warped manual segmentation of this atlas, obtained by performing deformable image registration to the target image. Each atlas produces one candidate segmentation for the target image. Each of the candidate segmentations may contain some segmentation errors. Label fusion is the process of integrating the candidate segmentations produced by all atlases to improve the segmentation accuracy in the final solution.

Errors produced in atlas-based segmentation are mainly due to registration errors, i.e. registration associates wrong regions from an atlas to the target image. Under the assumption that the errors produced by using different atlases are not identical, employing multiple atlases can effectively reduce label errors. For example, the majority voting method [13], [19] simply counts the votes for each label from each warped atlas and chooses the label receiving the most votes to produce the final segmentation Ŝ_T:

$${\widehat{S}}_T(x)={\text{argmax}}_{l\in \{1\dots L\}}\sum _{i=1}^n{S}_i^l(x)$$ (1)

where l indexes through labels and L is the number of all possible labels, x indexes through image pixels. $S_i^l(x)$ is the vote for label l produced by the i_th atlas, defined by:

$$S_i^l(x)=\{\begin{array}{cc}1\hfill & \text{if}{S}_i(x)=l;\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (2)

The power of voting in removing independent noise has been long recognized. For instance, for a simple binary (yes/no) voting problem, in a group of 23 voters, if three voters always give the same vote and the remaining voters vote randomly, the chance that the final voting result is consistent with what the three resolute voters choose is ~75% [28]. For multi-way voting problems, majority voting is even more powerful in removing independent noise. In our problem, suppose that atlas A_i produces correct labels for the target image with probability p_i. The probability that the atlas will produce any particular wrong label can be roughly estimated by (1−p_i)/(L−1). When p_i > (1−p_i)/(L−1), the atlas works better than random guess. When segmentation errors produced by different atlases are independent, the probability that multiple atlases agree on the same wrong label is exponentially suppressed compared to the probability that they agree on the same correct label. Hence, the combined results are expected to produce significantly fewer errors than those produced by any single atlas.

Since majority voting assigns equal weights to different atlases, it makes a strong assumption that different atlases produce equally accurate segmentations for the target image. However, as a complex optimization problem, the performance of deformable registration is sensitive to the input images. Hence, it is common that different atlases may produce different registration qualities, therefore segmentations with different qualities, for the same target image.

To improve label fusion accuracy, recent work focuses on developing segmentation quality estimations based on local appearance similarity and assigning greater weights to more accurate segmentations. For instance, the votes received by label l can be estimated by:

$${\widehat{S}}_T^l(x)=\sum _{i=1}^n{w}_i(x)S_i^l(x)$$ (3)

w_i(x) is a local weight assigned to the i_th atlas, with ${\sum }_{i=1}^n{w}_i(x)=1$. One way to estimate the weight is based on local image similarity under the assumption that images with similar appearance are more likely to have similar segmentations. When the summed squared distance (SSD) and a Gaussian weighting model are used [33]¹, the weights can be estimated by:

$$w_i(x)=\frac{1}{Z(x)}{e}^{-{\mathrm{\Sigma }}_{y\in 𝒩(x)}{[F_T(y)-F_i(y)]}^2/\sigma }$$ (4)

where 𝒩(x) defines a neighborhood around x and Z(x) is a normalization constant. In our experiment, we use a (2r +1)×(2r +1)×(2r +1) cube-shaped neighborhood specified by the radius r. Since segmentation quality usually is nonuniform over the entire image, the estimation is applied based on local appearance dissimilarity. The inverse distance weighting has been applied as well [3], [17]²:

$$w_i(x)=\frac{1}{Z(x)}{\left[\sum _{y\in 𝒩(x)}{(F_T(y)-F_i(y))}^2\right]}^{-\beta }$$ (5)

where σ and β are model parameters controlling the weight distribution.

Despite the highly competitive performance produced by these image similarity based local weighted voting approaches [16], [3], [22], the key limitation of these methods is that they assign voting weights to each atlas independently, and thus cannot account for the fact label errors produced by different atlases may be correlated, as pointed out in the Introduction. Next, we introduce a method to address this limitation.

III. Joint Label Fusion

For simplicity, in the theoretical exposition that follows, we consider binary segmentation, i.e. segmentation into foreground and background labels. We assume that each voxel in the target image is labeled 0 or 1, and that each atlas segmentation also assigns 0 or 1 to each voxel. Probabilistic segmentation (where each voxel is assigned a probability of having a given label) can also be achieved in practice by using the same weighting scheme as we develop below. Likewise, a segmentation problem with more than two labels can be decomposed into multiple binary segmentation problems, i.e. segmenting each label from the remaining labels. Our method can be applied to multi-label segmentation problems by producing weight maps as described below, using weighted voting to compute a consensus segmentation for each label, and selecting at each voxel the label with the highest value of the consensus segmentation.

In binary segmentation, we can model segmentation errors produced in atlas-based segmentation as follows:

$$S_T(x)=S_i(x)+{\delta }^i(x)$$ (6)

where δⁱ(x) is the label difference between the i_th atlas and the target image at x. δⁱ(x) ∈ {−1, 0} when S_i(x) = 1 and δⁱ(x) ∈ {0, 1} when S_i(x) = 0. We model the label difference as a discrete random variable, characterized by the following distribution:

$$q^i(x)=p(|{\delta }^i(x)|=1|F_T,F_1,\dots ,F_n)$$ (7)

We adopt the weighted voting framework, where at each x, a consensus segmentation S̅(x) is generated as the weighted sum

$$\overline{S}(x)=\sum _{i=1}^n{w}_i(x)S_i(x)$$ (8)

where w_i(x) are spatially varying weight maps that add up to 1 at each x. Note that whereas the candidate and target segmentations are taken to be binary, the consensus segmentation S̅(x) is not. Our aim is to find the set of voting weights that minimize the total expected error between S̅(x) and the true segmentation S_T (x), given by

$$E_{{\delta }^1(x),\dots ,{\delta }^n(x)}[{(S_T(x)-\overline{S}(x))}^2|F_T,F_1,\dots ,F_n]=$$ (9)

$$=E_{{\delta }^1(x),\dots ,{\delta }^n(x)}[{(\sum _{i=1}^n{w}_i(x){\delta }^i(x))}^2|F_T,F_1,\dots ,F_n]=\sum _{i=1}^n\sum _{j=1}^n{w}_i(x)w_j(x)E_{{\delta }^i(x),{\delta }^j(x)}[{\delta }^i(x){\delta }^j(x)|F_T,F_1,\dots ,F_n]={\mathbf{w}}_x^t{M}_x{\mathbf{w}}_x,$$ (10)

where w_x = [w₁(x);…;w_n(x)], and t stands for transpose. M_x is a pairwise dependency matrix with:

$$M_x(i,j)=E_{{\delta }^i(x){\delta }^j(x)}[{\delta }^i(x){\delta }^j(x)|F_T,F_1,\dots ,F_n]$$ (11)

$$=p({\delta }^i(x){\delta }^j(x)=1|F_T,F_1,\dots ,F_n).$$ (12)

M_x(i, j) estimates how likely atlases i and j are to both produce wrong segmentations for the target image, given the observed feature images. Note that the product δⁱ(x)δ^j(x) can only take values 0 or 1, with δⁱ(x)δ^j(x) = 1 if and only if both atlases produce a label different from the target segmentation.

Under this formulation, to achieve optimal label fusion, the voting weights should be selected such that the expectation of the combined label difference is minimized, i.e.,

$${\mathbf{w}}_x^{*}=\underset{{\mathbf{w}}_x}{\text{argmin}}{\mathbf{w}}_x^t{M}_x{\mathbf{w}}_x\text{subject to}\sum _{i=1}^n{\mathbf{w}}_x(i)=1$$ (13)

Using Lagrange multipliers, we can derive a closed-form solution to this minimization problem, given by

$${\mathbf{w}}_x=\frac{M_x^{-1}1n}{1_n^t{M}_x^{-1}{1}_n}$$ (14)

where 1_n = [1; 1;…; 1] is a vector of size n. When M_x is not full rank, the weights can be estimated using quadratic programming optimization [27]. However, the weights that minimize (13) are not unique. We take an alternative solution by always adding an identity matrix weighted by a small positive number α to M_x. With the conditioning matrix, we minimize the following objective function instead:

$${\mathbf{w}}_x^t(M_x+\alpha I){\mathbf{w}}_x={\mathbf{w}}_x^t{M}_x{\mathbf{w}}_x+\alpha {\Vert {\mathbf{w}}_x\Vert }_2\text{subject to}\sum _{i=1}^n{\mathbf{w}}_x(i)=1$$ (15)

Hence, adding a small conditioning identity matrix can be interpreted as enforcing a regularization term that prefers more similar voting weights assigned to different atlases.

To make sure that the added conditioning matrix is sufficient to avoid inverting an ill-conditioned matrix and the resulting voting weights also give a solution close to the global minimum of the original objective function, ${\mathbf{w}}_x^t{M}_x{\mathbf{w}}_x$, α should be chosen with respect to the scale of the estimated dependency matrix M_x. We found that setting α ≃ 1–2% of the maximal scale of estimated M_x works well. In our experiments, we estimate M_x using normalized intensity patches and the estimated M_x is in the range of [0, 4] (see below). We apply conditioning identity matrices with a fixed weight α=0.1 in all of our experiments.

A. Toy example

Suppose that a pair of atlases A₁ and A₂ produce statistically independent label errors for a given target image. If A₁ produces a wrong label 50% of the time and A₂ produces a wrong label 20% of the time, we have

$$M_x=\left[\begin{array}{cc}0.5\hfill & 0.1\hfill \\ 0.1\hfill & 0.2\hfill \end{array}\right].$$

The optimal voting weights computed by (14) are w = [0.2, 0.8]^t. Using (14) with a conditioning matrix with α = 0.01 produces a solution w = [0.2115, 0.7885]^t. By contrast, if we compute weights independently for each atlas, e.g., w_i ∝ p(|δ_i| = 1)⁻¹, we obtain w = [2/7, 5/7]^t. The expected total segmentation errors (9) for these three weight vectors are 0.18, 0.1801, and 0.1837, respectively.

Now suppose that another atlas A₃, which is identical to A₁, is added to the atlas library. A₁ and A₃ produce identical label errors for the target image, i.e., p(δ₁(x)δ₃(x) = 1) = p(|δ₁(x)| = 1) = p(|δ₃(x)| = 1). Then

$$M_x=\left[\begin{array}{ccc}0.5\hfill & 0.1\hfill & 0.5\hfill \\ 0.1\hfill & 0.2\hfill & 0.1\hfill \\ 0.5\hfill & 0.1\hfill & 0.5\hfill \end{array}\right],$$

and the optimal voting weights are not unique any more, but obey the following constraint: w₁ + w₃ = 0.2 and w₂ = 0.8. The total weight assigned to the duplicated atlas remains the same. Using (14) with a conditioning matrix with α = 0.01 produces a solution w = [0.1068, 0.7864, 0.1068]^t. By contrast, if we compute weights independently for each atlas, e.g., w_i ∝ p(|δ_i| = 1)⁻¹, we obtain the weight vector [2/9, 5/9, 2/9]^t, with the weight for A₂ substantially reduced and the weight for the repeated atlas A₁/A₃ boosted. The total expected errors for the three weighting strategies are 0.18, 0.1801 and 0.2099, respectively. Thus, unlike the scheme that assigns weights to atlases independently, the accuracy of the proposed scheme does not suffer from adding an atlas with redundant information. The same holds true even if atlases A₁ and A₃ are not identical, but strongly correlated.

B. Estimating M_x from intensity similarity

Our approach relies on knowing M_x, the matrix of expected pairwise joint label differences between the atlases and the target image. Note that these terms are conditioned on the target image and all atlas images. Assuming that given the target image and the atlas images in consideration, the pairwise joint label difference term is conditionally independent from the remaining atlas images, we simplify the term as follows:

$$M_x(i,j)=p({\delta }^i(x){\delta }^j(x)=1|F_T,F_1,\dots ,F_n)=p({\delta }^i(x){\delta }^j(x)=1|F_T,F_i,F_j)$$ (16)

Furthermore, by assuming that given the image patches centered around the location in consideration, the pairwise joint label difference term is conditionally independent from distant voxels, we have:

$$p({\delta }^i(x){\delta }^j(x)=1|F_T,F_i,F_j)=p({\delta }^i(x){\delta }^j(x)=1|\{F_T(y),F_i(y),F_j(y)|y\in 𝒩(x)\}),$$ (17)

In the image registration and segmentation literature, it is a common practice to use local image information between two images to predict their label difference. To make our method more comparable to previous label fusion methods, we propose to adapt the inverse distance function (5) to estimate the probability of pairwise joint label difference as follows:

$$M_x(i,j)=p({\delta }^i(x){\delta }^j(x)=1|\{F_T(y),F_i(y),F_j(y)|y\in 𝒩(x)\})\propto {[\sum _{y\in 𝒩(x)}|F_T(y)-F_i(y)||F_T(y)-F_j(y)|]}^{\beta }.$$ (18)

The constant of proportionality in (18) is irrelevant, since multiplying M_x by a positive constant does not change the solution w. Note that when i = j,

$$M_x(i,i)=p({\delta }^i{(x)}^2=1|\{F_T(y),F_i(y),|y\in 𝒩(x)\})\propto {\left[\sum _{y\in 𝒩(x)}{(F_T(y)-F_i(y))}^2\right]}^{\beta }.$$

i.e., M_x(i, i) is the inverse of the voting weight defined by inverse distance weighting function (5). Intuitively, our approximation is based on the assumption that the expectation of the label difference produced by one atlas is large when the image intensity difference between the warped atlas and the target image is large. Similarly, the expectation of any two atlases both producing a label difference is large only when both atlases have large intensity differences from the target image and the error patterns are strongly correlated.

C. Refining label fusion by local patch search

Registration errors (i.e., failure by the registration algorithm to correctly recover correspondences between objects in images) are the principal source of error in MALF. Because of the regularization constraints involved in registration, and for other reasons, such as failure to reach a global optimum of the registration objective function, the correspondences computed by registration may not always give maximum local similarity between image patches. That is, given a patch F_T [𝒩(x)] in the target image and the patch F_i[𝒩(x)] in the i-th registered atlas image, it is often possible to find a nearby point x′ such that F_T [𝒩(x)] is more similar to the patch F_i[𝒩(x′)] than to the patch F_i[𝒩(x)]. As shown recently in [8], [39], MALF performance can be moderately improved by using the displaced patch F_i[𝒩(x′)] for computing the consensus segmentation of the target image. This local patch search technique can be viewed as refining the point-to-point correspondences computed by registration, while relaxing the regularization constraints that registration imposes on deformation fields.

Motivated by this observation, we determine the local search correspondence map between the atlas i and the target image as follows:

$${\xi }_i(x)=\underset{x\prime \in 𝒩\prime (x)}{\text{arg min}}{\Vert F_i(𝒩(x\prime ))-F_T(𝒩(x))\Vert }^2.$$ (19)

Note that the domain of the minimization above is restricted to a neighborhood 𝒩′(x). Again, we use a cubic neighborhood definition, specified by a radius r_s. Note that 𝒩′ and 𝒩 may represent different neighborhoods. Given the set of local search correspondence maps {ξ_i}, we refine the definition of the consensus segmentation (8) as

$${\overline{S}}_T(x)=\sum _{i=1}^n{w}_i({\xi }_i(x))S_i({\xi }_i(x))$$ (20)

To search for the most similar image patches, larger search windows 𝒩′ are more desirable. However, using larger searching windows more severely compromises the regularization constraint on the deformation fields, which makes the task of predicting label differences from local appearance similarities more ambiguous. As a result, the approximation (18) may become less effective. It is reasonable to expect an optimal search range that balances these two factors.

IV. Experiments

In this section, we apply our method to two segmentation problems using two types of magnetic resonance (MR) images. The first problem is whole hippocampal segmentation using T1-weighted MRI. We choose this problem because hippocampus segmentation is one of the most studied problems in brain image analysis. The hippocampus plays an important role in memory function [36]. Macroscopic changes in brain anatomy, detected and quantified by magnetic resonance imaging (MRI), consistently have been shown to be predictive of AD pathology and sensitive to AD progression [34], [9]. Accordingly, automatic hippocampus segmentation from MR images has been widely studied e.g. [6], [24], [29]. On the other hand, the hippocampus is not a homogeneous structure. It contains several distinct subfields with different roles and susceptibilities to pathology. A number of recent studies (see overview of the literature in [23]), have proposed imaging techniques and manual segmentation protocols aimed at accurately measuring hippocampal subfield volumes. Clinical utility of hippocampal subfield volumetry was recently demonstrated in dementia (e.g. [25], [26]) and other brain diseases. Hence, automatic hippocampal subfield segmentation is attracting more attention. In the second experiment, we apply our label fusion method to hippocampal subfield segmentation using focal T2-weighted MRI.

Since recent empirical studies, e.g. [3], [33], have shown that image similarity based local weighted voting is the most effective label fusion approach compared with other benchmark segmentation tools such as STAPLE [40] and FreeSurfer [11], in our experiments we focus on comparing our joint label fusion method (LWJoint) with similarity-based local weighted label fusion. For local weighted label fusion, we apply Gaussian weighting (4) (LWGaussian) and inverse distance weighting (5) (LWInverse). We also use majority voting (MV) and STAPLE [40] to define the baseline performance.

Our method has three free parameters: r, the radius of the local appearance window 𝒩 used in similarity-based M_x estimation; r_s, the radius of the local searching window 𝒩′ used in remedying registration errors; and β, the parameter used to transfer image similarities in the pairwise joint label difference term (18). For each segmentation experiment, the parameters are optimized by exhaustive search among a range of values in each parameter (r ∈ {1, 2, 3} for whole hippocampus segmentation and r ∈ {3, 4, 5} for subfield segmentation; r_s ∈ {0, 1, 2, 3}; β ∈ {0.5, 1,…, 10}) using the atlases in a leave-one-out cross-validation strategy. We measure the average overlap between the automatic segmentation of each atlas obtained via the remaining atlases and the reference segmentation of that atlas, and find the optimal parameters that maximize this average overlap.

The optimal local appearance window and optimal local searching window are determined for LWGaussian and LWInverse methods using cross-validation as well. In addition, the optimal parameters for the weight assignment models are also determined for LWGaussian and LWInverse, with the searching range σ ∈ [0.05, 0.1,…, 1] and β ∈ [0.5, 1,…,10], respectively.

In our experiment, we normalize the intensity vector obtained from each local image intensity patch, such that the normalized vector has zero mean and a constant norm, for each label fusion method. Note that the normalization is applied independently at each image location, which may make the resulting voting weights for nearby voxels in an atlas less consistent with each other. To enhance the spatial consistencies of voting weights for nearby voxels, we apply mean filter smoothing with the smoothing window 𝒩, the same neighborhood used for local appearance patches, to spatially smooth the voting weights for each atlas.

A. Segmentation of the hippocampus

We use the data in the Alzheimer’s Disease Neuroimaging Initiative (ADNI)³. ADNI MRI data include 1.5 T structural MRI from all 800 subjects and 3 T structural MRI from 200 subjects. Our study is conducted using only 3 T MRI and only includes data from mild cognitive impairment (MCI) patients and controls. Overall, the data set contains 139 images (57 controls and 82 MCI patients). The images were acquired sagittally, with 1 mm × 1 mm in-plane resolution and 1.2 mm slice thickness. To obtain manual segmentation for these data, we first apply a landmark based semi-automatic hippocampal segmentation method [29] to produce the initial segmentation for each image. Each fully-labeled hippocampus was then manually edited using the paintbrush and polygon manual segmentation tools in ITK-SNAP [42] by one of the authors (MA) following a previously validated protocol [15].

Segmentation performance is evaluated using cross-validation. Note that cross-validation is performed twice, once to separate the dataset into an atlas subset and a test subset, and the second time, to search for the optimal value of the label fusion parameters among the atlas subset. For outer cross-validation, we randomly select 20 images to be the atlases and another 20 images for testing. Image-guided registration is performed between all pairs of atlases, and between all atlases and the target image. Global registration was performed using the FSL FLIRT tool [35] with six degrees of freedom and using the default parameters (normalized mutual information similarity metric; search range from −5 to 5 in x, y and z). Deformable registration was performed using the ANTS Symmetric Normalization (SyN) algorithm [4], with the cross-correlation similarity metric (with radius 2) and a Gaussian regularizer with σ = 3. After registration, reference segmentations from each of the atlases were warped into the target image space.

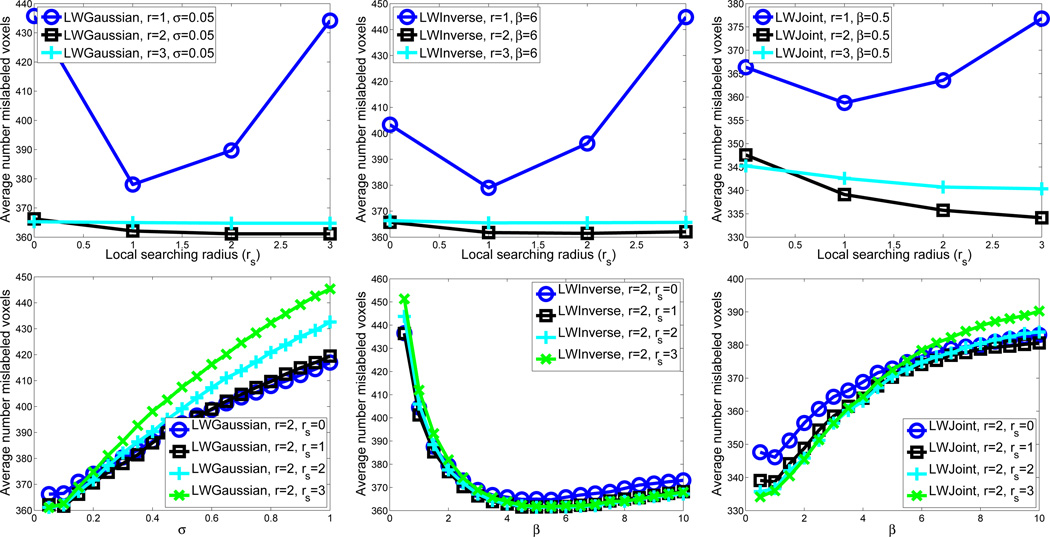
Fig. 1 illustrates optimal label fusion parameter selection for the three methods in the first cross-validation experiment. The figure plots the number of voxels mislabeled by the automatic segmentation, averaged over 20 inner cross-validation experiments, against the value of each parameter. Note that although the figure plots each parameter separately, the actual search for optimal parameters considers all possible combinations of parameter values. Note that using the appearance window with r = 1, all methods performed significantly worse than using larger appearance windows. This indicates that estimation of joint atlas error probabilities in (18) is inaccurate for very small appearance windows. For this cross-validation experiment, the optimal parameters for LWGaussian, LWInverse and LWJoint are (σ= 0.05, r=2, r_s = 2), (β= 6, r=2, r_s = 2) and (β= 0.5, r=2, r_s = 3), respectively.

Fig. 1.

Optimal label fusion parameter selection for LWGaussian (left), LWInverse (middle) and LWJoint (right) using leave-one-out cross-validation. The upper figures plot the average number of mislabeled voxels against the local searching radius r_s and the appearance window radius r. The weighting function parameters σ, β are held fixed in these figures at its optimal value for the three methods, respectively. The lower figures plot the average number of mislabeled voxels against the local searching radius r_s and the weighting function parameter, σ and β, respectively. The appearance window radius r is held fixed in this figure at its optimal value.

In all 10 cross-validations, for all three methods the optimal appearance window has radius r = 2. Most frequently selected local search windows have radius r_s = 2 or r_s =3. For LWGaussian, the most frequently selected weighting model parameters (σ) are 0.05 or 0.1. For LWInverse, the most frequently selected model parameters (β) are located in the range [4,6], while for LWJoint, the most frequently selected β are located in the range [0.5,1.5].

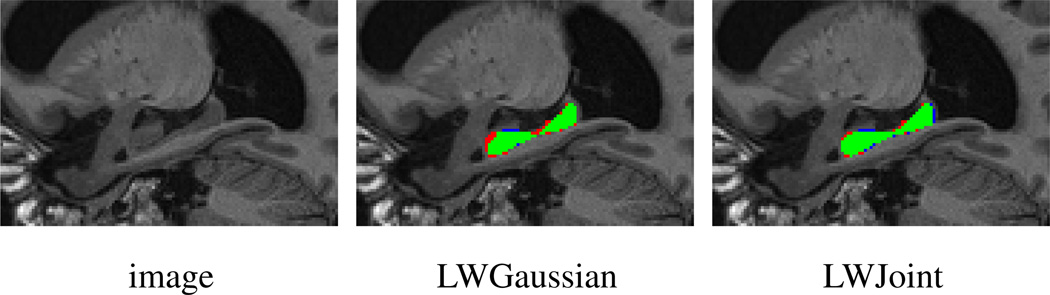
Table I shows the segmentation performance of each method in terms of Dice similarity coefficient between MALF results and reference segmentations. The Dice similarity coefficient is the ratio of the volume of overlap between two segmentations and their average volume [10]. Average overlap (and standard deviation) is reported, with averaging over all 10 outer cross-validation experiments and over the 20 test images in each experiment. In each outer cross-validation experiment, optimal parameters are computed for each method using inner cross-validation. In addition to the local weighted voting methods, we also show the performance by the STAPLE algorithm [40] and majority voting. Overall, STAPLE slightly outperformed majority voting. LWGaussian and LWInverse produced similar results, both significantly outperforming majority voting and STAPLE. LWJoint outperformed LWGaussian and LWInverse over 1% Dice overlap. This improvement is statistically significant, with p < 0.00001 on the paired Student’s t-test for each cross-validation experiment. Table I also gives the results produced by each local weighted voting method without using local search. Our method produced significant improvement over the competing methods without local search as well. See Fig. 2 for a segmentation example produced by our method and LWGaussian.

TABLE I.

whole hippocampus segmentation performance for each label fusion method, in terms of Dice similarity between MALF results and reference segmentations. Average dice similarity ( ± standard deviation) are computed across 10 outer cross-validation experiments, each having 20 test images. The results produced by each local weighted voting methods without applying local search are shown in parenthesis. Greatest similarity is obtained using the proposed LWJoint method.

Label Fusion Strategy	Dice Similarity (Left Hippocampus)	Dice Similarity (Right Hippocampus)
Majority Voting	0.836 ± 0.084	0.829 ± 0.069
STAPLE [40]	0.846 ± 0.086	0.841 ± 0.086
LWGaussian	(0.885 ± 0.025) 0.886 ± 0.027	(0.873 ± 0.030) 0.875 ± 0.030
LWInverse	(0.884 ± 0.026) 0.885 ± 0.027	(0.872 ± 0.030) 0.873 ± 0.030
LWJoint	(0.893 ± 0.025) 0.897 ± 0.024	(0.884 ± 0.027) 0.888 ± 0.026

Fig. 2.

Sagittal views of a segmentation produced by LWGaussian and our method. Red: reference segmentation; Blue: automatic segmentation; Green: overlap between manual and automatic segmentation.

Table II presents the average hippocampal volume in control and MCI cohort obtained using different label fusion techniques. The corresponding Cohen’s d effect size [14] is also shown (computed as the difference of the sample means of the two cohort, divided by the pooled sample standard deviation). To account for differences in head size, the effect size is computed after normalizing the hippocampal volumes by the subject’s intracranial volume. Larger values of Cohen’s d indicate greater effect, i.e., greater ability to tell cohorts apart based on hippocampal volume. Our method produced more accurate volume measurements than LWGaussian and LWInverse, compared to the reference segmentations. Since volume differences produced by different automatic segmentation methods are all proportional to that of manual segmentation, the hippocampus volume measured using different methods show similar separability between the two population groups. LWJoint yields a slightly better effect size than other MALF methods, indicating the volume measurements produced by LWJoint find a slightly more significant difference between the two populations. All MALF algorithms yield greater effect sizes than manual segmentation, likely due to reduced variance in volume estimation.

TABLE II.

Hippocampal volume (mm³) (left/right) measured by different label fusion methods for control and MCI cohorts. The results are averaged over 10 cross-validation experiments, which together include test images from 94 control subjects and 106 MCI subjects. The last column shows the corresponding Cohen’s d effect size, whose magnitude indicates the difference between the two populations. The Hippocampus volume is normalized by intracranial volume for computing the Cohen’s effect size.

	Left Hippocampus			Right Hippocampus
Label Fusion Method	Volume (CTL)	Volume (MCI)	Cohen’s d	Volume (CTL)	Volume (MCI)	Cohen’s d
LWGaussian	2026 ± 277	1642 ± 334	1.7260	1947 ± 311	1553 ± 346	1.5576
LWInverse	2014 ± 274	1635 ± 326	1.7266	1930 ± 309	1544 ± 338	1.5504
LWJoint	2156 ± 285	1755 ± 353	1.7468	2083 ± 322	1668 ± 373	1.5700
Reference Seg.	2258 ± 325	1841 ± 368	1.5747	2201 ± 378	1785 ± 408	1.3643

B. Hippocampal subfield segmentation

To illustrate the performance of LWJoint on a segmentation problem with multiple labels, we apply it to the problem of automatic segmentation of the subfields of the hippocampal formation from oblique coronal T2-weighted MRI. Our experiments use different similarity weighted voting strategies to improve upon the segmentation results presented in our earlier work [43]. This earlier work also used MALF with spatially varying similarity-weighted label fusion, but the strategy employed there did not consider optimality, and as we show below, performed worse than any of the local weighted voting methods considered here.

1) Imaging Data, Manual Segmentation and Experimental Setup

The experiments use in vivo MRI from 32 subjects from an aging and dementia study [26]. The data were acquired on a Bruker Med-Spec 4T system controlled by a Siemens Trio™ console and equipped with a USA instruments eight channel array coil that consisted of a separate transmit coil enclosing the eight receiver coils. The following sequences, which were part of a larger research imaging and spectroscopy protocol, were acquired: 1. 3D T1-weighted gradient echo MRI (MPRAGE) TR/TE/TI = 2300/3/950 ms, 7° flip angle, 1.0×1.0×1.0 mm³ resolution, FOV 256×256×176, acquisition time 5.17 min; 2. high resolution T2 weighted fast spin echo sequence (TR/TE: 3990/21 ms, echo train length 15, 18.6 ms echo spacing, 149° flip angle, 100% oversampling in ky direction, 0.4×0.5 mm² in plane resolution, 2 mm slice thickness, 24 interleaved slices without gap, acquisition time 3:23 min, oblique coronal slice orientation, angulated perpendicular to the long axis of the hippocampal formation.

The T1-weighted and T2-weighted MR images have complimentary characteristics. The T2- weighted MRIs depict details of the internal structure of the hippocampus with high in-slice resolution and good contrast between subfields, but these images also have a limited field of view and large slice spacing. On the other hand, the T1-weighted images have nearly isotropic voxels and cover the entire brain, but lack contrast between subfields. Manual segmentation protocols that can reliably subdivide the hippocampus into subregions corresponding to its anatomical subfields have been developed for focal T2-weighted data [44], [26]. Our manual segmentation protocol is derived from [26]; it has been expanded to include more slices and additional subfields. Each hippocampus formation is partitioned into anterior (head), posterior (tail), mid-region (body), subiculum (SUB), entorhinal cortex (ERC) and parahippocampal gyrus (PHG). The hippocampal body is further divided into cornu Ammonis fields 1–3 (CA1-3), dentate gyrus (DG), and a miscellaneous label, which contains cysts, arteries, etc. Manual segmentation of hippocampal subfields is unreliable in the head and tail. The boundaries between head, tail and the body regions are defined by a pair of slices in the MRI image. Overall, there are nine subfields defined. See [43] for more detail about the manual subfield segmentation.

As in whole-hippocampus segmentation, we perform a series of 10 cross-validation experiments. In each, 22 subjects are randomly selected as atlases, and the remaining 10 are selected for testing. Registration between all pairs of subjects is performed using SyN using a multi-modality similarity term that assigns equal weight to the T1-weighted image similarity and T2-weighted image similarity (see [43] for details). However, as in [43], similarity-weighted label fusion is applied only using T2-weighted image intensities. The motivation for this is that the T1-weighted MR images mainly serve to align the hippocampal region, while the T2-weighted MR image provide details used for subfield alignment.

Since the in-plane resolution of the T2-weighted images is much higher than slice thickness, instead of the cubic neighborhood definition used in the whole hippocampus segmentation experiment, we use an anisotropic neighborhood definition 2r × 2r × 3 for the local appearance window and 2r_s × 2r_s × 3 for the local searching window in this experiment, with r and r_s specifying the in-plane neighborhood radius. For instance, r = 3 and r_s = 3 both define a neighborhood of size 7 × 7 × 3.

2) Results

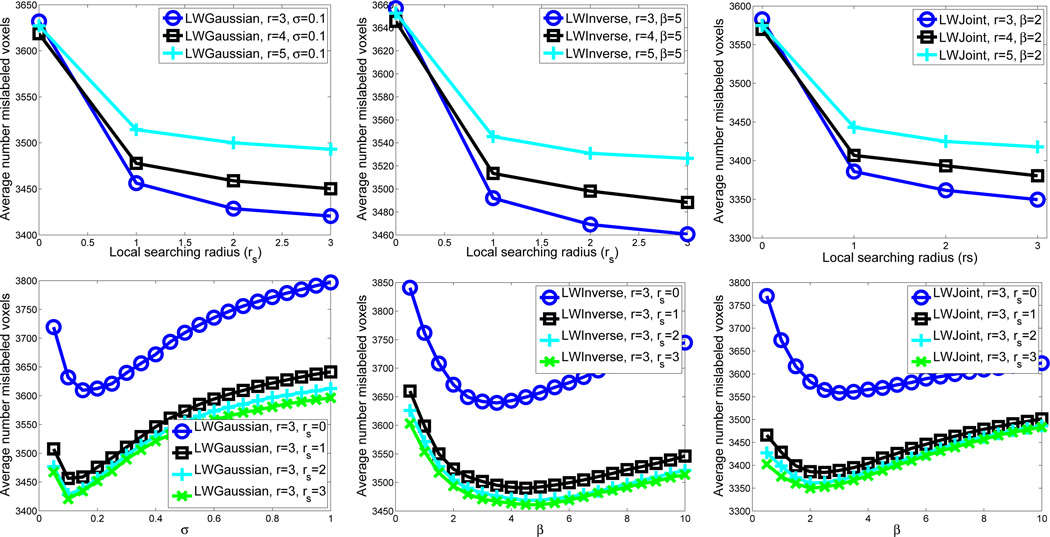
Fig. 3 illustrates some of the parameter selection experiments for the three methods using the atlases in the first outer cross-validation experiment. For this cross-validation experiment, the optimal parameters for LWGaussian, LWInverse and LWJoint are (σ= 0.1, r=3, r_s = 3), (β= 5, r=3, r_s = 3) and (β= 2, r=3, r_s = 3), respectively.

Fig. 3.

Optimal label fusion parameter selection for LWGaussian (left), LWInverse (middle) and LWJoint (right) using leave-one-out cross-validation. The upper figures plot the average number of mislabeled voxels against the local searching radius r_s and the appearance window radius r. The weighting function parameters σ, β are held fixed in these figures at its optimal value for the three methods, respectively. The lower figures plot the average number of mislabeled voxels against the local searching radius r_s and the weighting function parameter, σ and β, respectively. The appearance window radius r is held fixed in this figure at its optimal value.

In all 10 cross-validations, all three label fusion methods select the same optimal appearance window and optimal local searching window, which are r = 3 and r_s = 3, respectively. For LWGaussian, the most frequently selected weighting model parameters (σ) are 0.1 or 0.15. For LWInverse, the most frequently selected model parameters (β) are located in the range [4,6], while for LWJoint, the most frequently selected β are in the range [1.5,2.5].

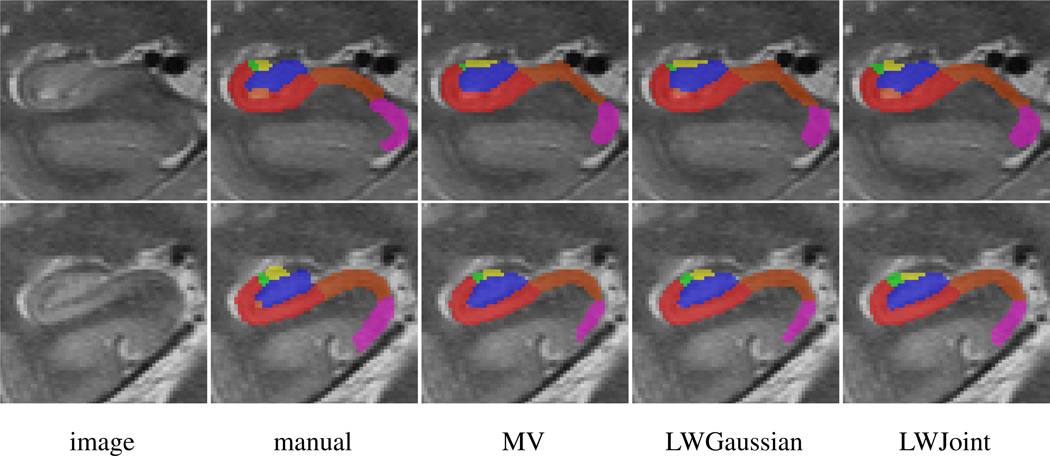
Table III reports the average segmentation accuracy, relative to manual segmentation, obtained by majority voting, STAPLE⁴, our earlier work [43], LWInverse, LWGaussian, and LWJoint. For this application, STAPLE performed comparably to majority voting. Again, LWGaussian and LWInverse produced similar performance, which is significantly better than majority voting and STAPLE. Our method produced the best average Dice similarity for all subfields. On average, we outperformed similarity-based label fusion methods by ~1% Dice similarity. Improvements made by LWJoint for most subfields are statistically significant. Table III also reports the optimal results produced by each local weighted voting methods without applying local search, our joint method outperformed the competing methods in most subfields as well. Fig. 4 shows some segmentation results produced by different methods.

TABLE III.

Average performance of different label fusion strategies in hippocampal subfield segmentation experiments. Average Dice similarity (± standard deviation) are shown between the MALF result and corresponding manual segmentation for each subfield, also averaging over left and right hemispheres and over 10 cross-validation experiments. the results produced by each local weighted voting methods without applying local search are shown in parenthesis. Asterisks in the last column indicate results where the improvement of LWJoint over LWGaussian and LWInverse was statistically significant, as per paired student’s t-test.

Subfield	Maj. Voting	STAPLE [31]	[43] (Table 6)	LWInverse	LWGaussian	LWJoint
CA1	0.731±0.070	0.719±0.102	0.770±0.065	(0.766±0.064) 0.782±0.061	(0.769±0.063) 0.786±0.060	(0.773±0.059) 0.789±0.057**
CA2	0.322±0.180	0.357±0.191	0.422±0.175	(0.427±0.173) 0.427±0.177	(0.431±0.174) 0.431±0.178	(0.442±0.170) 0.455±0.176***
CA3	0.497±0.142	0.523±0.141	0.532±0.137	(0.537±0.124) 0.559±0.124	(0.541±0.125) 0.560±0.125	(0.549±0.121) 0.572±0.123***
DG	0.741±0.090	0.738±0.100	0.773±0.067	(0.768±0.070) 0.785±0.068	(0.767±0.070) 0.786±0.069	(0.767±0.070) 0.789±0.068*
head	0.864±0.028	0.860±0.033	0.874±0.025	(0.874±0.023) 0.882±0.024	(0.875±0.023) 0.883±0.024	(0.876±0.022) 0.885±0.023***
tail	0.739±0.123	0.720±0.144	0.744±0.119	(0.743±0.124) 0.752±0.128	(0.746±0.123) 0.755±0.129	(0.748±0.121) 0.759±0.125**
SUB	0.706±0.062	0.705±0.083	0.727±0.061	(0.726±0.067) 0.733±0.064	(0.729±0.066) 0.736±0.062	(0.734±0.061) 0.745±0.060***
ERC	0.606±0.138	0.603±0.131	0.627±0.123	(0.630±0.124) 0.647±0.128	(0.632±0.125) 0.648±0.129	(0.634±0.120) 0.652±0.126*
PHG	0.604±0.076	0.626±0.080	0.625±0.076	(0.629±0.075) 0.632±0.078	(0.629±0.076) 0.632±0.078	(0.630±0.074) 0.640±0.076***

^*p < 0.05

^**p < 0.01

^***p < 0.0001

Fig. 4.

Coronal views of some subfield segmentation results produced by MV, LWGaussian and our method. All results are produced with local searching using the optimal parameter for each method. Label description: red - CA1; green - CA2; yellow - CA3; blue - DG; light brown - miscellaneous label; brown - SUB; cyan - ERC; pink - PHG.

Note that since the same set of cross-validation experiments (with the same atlas/test partitions in each) were conducted in [43], the segmentation accuracy reported there can be directly compared with our results. In [43], a different local weighting algorithm was implemented. Instead of using Gaussian or inverse distance weighting, weights used in [43] were normalized by the image similarity rank. Unlike our implementation of image similarity based local weighted label fusion, the implementation in [43] did not apply the local searching technique. Furthermore, [43] did not select the optimal parameters for each cross-validation experiment. As a result, the Dice scores produced by LWInverse and LWGaussian similarity-based weighted voting without local search are slightly better than those reported in [43], and the results with local search are on average about 1% higher for all subfields. Our method outperformed [43] by about ~2% on average.

The manual segmentation protocol in [43] always uses slice boundaries to delimit the hippocampal body from the head and tail. This is an artificial boundary, necessitated by the anisotropy of the T2 images, for which there is no real anatomical counterpart. In fact, head, body and tail do not truly constitute different anatomical regions, but rather separate regions of the hippocampus where partitioning into subfields is deemed reliable or unreliable, due to the bending and folding of the hippocampus. Thus, to make the comparisons between automatic and manual segmentation more fair, [43] allows the automatic algorithm to make use of the manual partitioning of slices into head, body, and tail. This is accomplished by a heuristic “fix-up” algorithm. For example, if MALF labels a voxel as HEAD, but the slice is considered a body slice by the manual rater, the MALF result is changed by choosing the body subfield (i.e., CA1-4, DG, or SUB) with the highest label probability. Table IV presents the results of LWGaussian, LWInverse and LWJoint label fusion strategies with/without local search, after applying the fix-up algorithm. Again, LWJoint is the top performer, with accuracy for all subfields except TAIL within 1.5% of the inter-rater precision.

TABLE IV.

Average performance of different label fusion strategies in hippocampal subfield segmentation experiments, when using manual head/body/tail slice partitioning (see text). average dice similarity (± standard deviation) are shown between the MALF result and corresponding manual segmentation for each subfield, also averaging over left and right hemispheres and over 10 cross-validation experiments. The results produced by each local weighted voting methods without applying local search are shown in parenthesis. Asterisks in the LWJoint column indicate results where the improvement of LWJoint over LWGaussian and LWInverse was statistically significant, as per paired student’s t-test. the last column gives average dice overlap between manual segmentations produced by two trained human raters.

Subfield	Maj. Voting	[43] (Table 1)	LWInverse	LWGaussian	LWJoint	Inter-Rater
CA1	0.804±0.059	0.851±0.040	(0.853±0.040) 0.869±0.038	(0.855±0.038) 0.870±0.037	(0.858±0.037) 0.874±0.035***	0.883±0.032
CA2	0.357±0.194	0.470±0.179	(0.474±0.183) 0.486±0.180	(0.477±0.182) 0.489±0.180	(0.487±0.177) 0.510±0.176***	0.522±0.160
CA3	0.530±0.145	0.583±0.133	(0.591±0.124) 0.619±0.123	(0.595±0.125) 0.620±0.123	(0.605±0.121) 0.634±0.123***	0.668±0.087
DG	0.813±0.087	0.859±0.045	(0.855±0.047) 0.870±0.046	(0.857±0.045) 0.871±0.045	(0.858±0.045) 0.875±0.044***	0.885±0.034
head	0.878±0.021	0.893±0.018	(0.892±0.016) 0.900±0.017	(0.893±0.015) 0.900±0.016	(0.894±0.016) 0.903±0.016***	0.900±0.016
tail	0.793±0.112	0.828±0.105	(0.804±0.105) 0.812±0.108	(0.806±0.104) 0.814±0.109	(0.809±0.103) 0.819±0.105***	0.901±0.059
SUB	0.715±0.062	0.742±0.063	(0.741±0.067) 0.747±0.065	(0.743±0.066) 0.749±0.064	(0.748±0.062) 0.758±0.062***	0.768±0.079
ERC	0.606±0.138	0.738±0.093	(0.745±0.096) 0.759±0.095	(0.745±0.096) 0.759±0.095	(0.750±0.094) 0.768±0.090***	0.786±0.123
PHG	0.627±0.074	0.658±0.073	(0.662±0.071) 0.666±0.075	(0.662±0.072) 0.666±0.075	(0.664±0.071) 0.675±0.072***	0.706±0.106

^*p < 0.05

^**p < 0.01

^***p < 0.0001

V. Conclusions and Discussion

We presented a novel formulation to solve the weighted-voting based label fusion problem. Unlike previous label fusion techniques that independently assign voting weights to each atlas, our method takes the dependencies among the atlases into consideration and attempts to directly reduces the expected label error in the combined solution. Provided estimated pairwise dependencies among the atlases, the voting weights can be efficiently solved in a closed form. In our experiments, we estimated the pairwise dependency terms from local image intensities and compared our method with previous label fusion methods in whole hippocampus segmentation and hippocampus subfield segmentation using MR images. For both problems, our method outperformed competing methods.

a) Comparing to the state of the art in hippocampus segmentation

Since the hippocampus segmentation problem has been widely studied, putting our results in the context helps to reveal the significance of our results. Before making a formal comparison, we note that, as pointed out in [7], direct comparisons of quantitative segmentation results across publications are difficult and not always fair due to the inconsistency in the underlying segmentation protocol, the imaging protocol, and the patient population. However, the comparisons carried out below indicate the highly competitive performance achieved by our label fusion technique.

In the recent hippocampus segmentation literature, some of the best reported accuracy results have been obtained using MALF [7], [8], [20]. All three of these best-performing methods are based on independent label fusion with similarity-based local weighting. Collins et al. [7] and Coupe et al. [8] conduct leave-one-out experiments in a data set containing 80 control subjects, i.e. 79 atlases are used in their experiment. They report average Dice overlaps of 0.887 and 0.884, respectively. In contrast, we report average Dice overlap of 0.900±0.020 for control subjects, more than 1% Dice overlap improvement. For patients with MCI, we report Dice overlap of 0.885±0.028. Leung et al. [20] use a template library of 55 images. However, for each image in the library, both the original and its flipped mirror image are used as atlases. Hence, [20] effectively uses 110 atlases for label fusion. Leung et al. [20] report results in terms of the Jaccard index ($JI(A,B)=\frac{|A\cap B|}{|A\cup B|}$), reporting an average of 0.80±0.03 for the left side hippocampus in 10 control subjects and 0.81±0.04 in 10 MCI patients. Our results for the left side hippocampus, in terms of JI, are 0.826±0.031 for controls and 0.803±0.041 for MCI patients. Overall, we produced results that compare favorably to the state-of-the-art, using significantly fewer atlases.

b) Computational complexity

Comparing to independently assigning voting weights to each atlas, our method requires an additional step of solving the inverse of the pairwise dependence matrix. Since the number of atlases applied in practice is often small, solving the matrix inverse does not substantially increase the computational burden for label fusion. In fact, the most time consuming step is the local searching algorithm. Without the local searching algorithm, for our hippocampus segmentation experiment on ADNI data, our algorithm segments one hippocampus in a few seconds on a single core 2G HZ CPU using our current Matlab implementation. Regardless, the vast majority of the computational time is spent performing deformable registration between the atlases and the target image, and the cost of label fusion is negligible in comparison.

c) Relation to the STAPLE algorithm

Comparing to the popular expectation-maximization based STAPLE algorithms [40], [31], there are two key differences in our work. First, like other label fusion methods, the STAPLE algorithms also assume that the segmentation errors from different candidate segmentations are independent. Hence, they can not reduce consistent bias in the candidate segmentations. Second, the classic STAPLE algorithms ignore the appearance information in the target image and the atlas images after the registration. This limitation may affect the reliability of the estimated accuracy in each candidate segmentation.

d) Estimation of the pairwise dependency matrix

The label fusion accuracy of our method depends on the accuracy of the estimated pairwise dependencies between atlases. Hence, one natural way to extend our work is to improve the pairwise dependence estimation. Following the common practice, our current method uses the image intensity to estimate the segmentation label relations. Since local image appearance similarity may be unreliable in predicting registration errors, to further improve the performance, one can incorporate prior knowledge that is empirically learned from the atlases to compliment the similarity-based estimation. For example, to estimate the optimal parameters for label fusion method, we applied a leave-one-out strategy on the set of atlases that segments each atlas using the remaining atlases. These leave-one-out experiments also provide the error redundancy produced by each pair of the remaining atlases in the native space of each segmented atlas. By registering and warping each atlas to a common reference space, one can estimate the empirical average error redundancy between any pair of the atlases. The empirical estimation complements the local appearance based estimation and can be combined with the appearance based estimation for segmenting new images. This is a natural direction for future research.

Biographies

Hongzhi Wang received his Bachelor, Master degrees in computer science from University of Science and Technology Beijing in 2000 and 2003, respectively. In 2008, he received his PhD degree in computer science from Stevens Institute of Technology. His PhD research focused on perceptual organization and its application in shape-based object recognition. Since then he has been a postdoctoral researcher at Penn Image Computing and Science Lab, University of Pennsylvania, working on applications in medical image analysis. His research interests include developing techniques that allow effective information fusion for accurate quantitative measurements from medical images. Dr. Wang is a member of the IEEE.

Jung W. Suh received B.S. and M.S. degrees in electronics and computer engineering from Hanyang University, Korea, in 1996, 1998 and a Ph.D. degree in electrical and computer engineering from the Virginia Tech, Blacksburg, in 2007. From 1998 through 2003, he was with the Samsung Electronics Company, Korea, where he was involved in the development of MPEG-4 and Digital Mobile Broadcasting (DMB) systems. He is currently a senior medical imaging scientist at HeartFlow, Inc. His research interests are in the fields of biomedical image processing, computer vision and pattern recognition, image enhancement and compression.

Sandhitsu Das received his B.Tech. M.Tech. degrees in Electrical Engineering from the Indian Institute of Technology, Kanpur in 1997 and 1999, respectively. He obtained his Ph.D. in Bioengineering, studying computational models of human visual system, from the School of Engineering and Applied Sciences at the University of Pennsylvania in 2006. Since then, he has been at the Penn Image Computing and Science Laboratory at the Department of Radiology, where he currently holds the position of Senior Research Investigator. His research interests include developing novel techniques for analyzing structural and functional brain imaging data, and their applications to clinical and basic neuroscience. His current work includes development of imaging-based biomarkers for various brain disorders like epilepsy, Alzheimer’s disease, and other forms of dementia, as well as measurements for studying mechanisms of human episodic memory using functional MRI.

John B. Pluta was born in Chester, Pennsylvania, in 1982. He attended Drexel University in Philadelphia, Pennsylvania, from 2000–2005 and graduated with a B.S. in psychology. He is currently a graduate student at the University of Pennsylvania, studying biostatistics.

He began his career in 2004, as a research assistant at Moss Rehabilitation Institute. After graduating, he took a position as a Research Specialist at the University of Pennsylvania. His main areas of interest are hippocampal anatomy, segmentation methods, and image registration.

Caryne Craige was born in Philadelphia, PA on June 20, 1984. Ms. Craige achieved a Bachelor of Science degree in biology in 2006 from the University of Richmond in Richmond, VA, U.S.A. She worked as a Research Technician at the Children’s Hospital of Philadelphia from March 2007-June 2009, working within the Stress Neurobiology group, in the laboratory of Dr. Sheryl Beck. With this position, Ms. Craige studied dorsal raphe and hippocampal neurocircuitry in the context of stress disorders, with the use of transgenic and behavioral animal models. In January of 2008, Ms. Craige began work as a Research Assistant in the laboratory of Dr. Paul Yushkevich at the University of Pennsylvania. Her work in this laboratory is ongoing and her main contributions entail hippocampal subregion manual segmentation of T2- and T4-weighted magnetic resonance images using ITK-SNAP software. Ms. Craige is currently affiliated with Temple University School of Medicine in Philadelphia, PA, U.S.A., where she is a third-year graduate student in the Pharmacology Ph.D. program. Ms. Craige is a member of the Society for Neuroscience.

Paul A. Yushkevich (M06) became a Member (M) of IEEE in 2006. He was born in Moscow, Russia. He holds the degrees of B.S. in Computer Science and Mathematics (1996) from the University of North Carolina at Charlotte; M.S. in Computer Science (2000) and Ph.D. in Computer Science (2003) from the University of North Carolina at Chapel Hill.

He is an Assistant Professor of Radiology at the University of Pennsylvania, Philadelphia, PA, USA since 2009. Previously, he was a Research Assistant Professor (2006–2009) and a Postdoctoral Fellow (2003–2008) at the University of Pennsylvania. He has authored 30 journal publications and 34 peer-reviewed conference papers, spanning many areas of the biomedical image analysis field, including geometrical object representation, shape analysis, image segmentation, and image registration. His applied research primarily focuses on the problem of developing imaging biomarkers in aging and dementia, but also includes other neuroimaging applications and cardiac imaging analysis. He maintains and develops ITK-SNAP software for interactive image segmentation (itksnap.org), which is among the most widely used open-source image analysis tools. Prof. Yushkevich is a Member of the IEEE BISP.