Comparison of Generated Parallel Capillary Arrays to Three-Dimensional Reconstructed Capillary Networks in Modeling Oxygen Transport in Discrete Microvascular Volumes

Abstract

Objective

We compare Reconstructed Microvascular Networks (RMN) to Parallel Capillary Arrays (PCA) under several simulated physiological conditions to determine how the use of different vascular geometry affects oxygen transport solutions.

Methods

Three discrete networks were reconstructed from intravital video microscopy of rat skeletal muscle (84×168×342 μm, 70×157×268 μm and 65×240×571 μm) and hemodynamic measurements were made in individual capillaries. PCAs were created based on statistical measurements from RMNs. Blood flow and O₂ transport models were applied and the resulting solutions for RMN and PCA models were compared under 4 conditions (rest, exercise, ischemia and hypoxia).

Results

Predicted tissue PO₂ was consistently lower in all RMN simulations compared to the paired PCA. PO₂ for 3D reconstructions at rest were 28.2±4.8, 28.1±3.5, and 33.0±4.5 mmHg for networks I, II, and III compared to the PCA mean values of 31.2±4.5, 30.6±3.4, and 33.8±4.6 mmHg. Simulated exercise yielded mean tissue PO₂ in the RMN of 10.1±5.4, 12.6±5.7, and 19.7±5.7 mmHg compared to 15.3±7.3, 18.8±5.3, and 21.7±6.0 in PCA.

Conclusions

These findings suggest that volume matched PCA yield different results compared to reconstructed microvascular geometries when applied to O₂ transport modeling; the predominant characteristic of this difference being an over estimate of mean tissue PO₂. Despite this limitation, PCA models remain important for theoretical studies as they produce PO₂ distributions with similar shape and parameter dependence as RMN.

INTRODUCTION

Effectively delivering oxygen in the form of saturated red blood cells is a primary function of the microvasculature. Within skeletal muscle capillaries provide the largest surface area compared to arterioles and venules, for oxygen to diffuse out of the blood and into surrounding tissues. In combination with increased surface area, capillary networks allow for multiple transit paths for erythrocytes to deliver oxygen in a more spatially homogenous fashion. Modeling both normal and impaired oxygen transport in capillary networks can aid in the understanding of the consequences of different disease states as well as the normal functioning of living tissue (7, 13, 14). Precise models utilizing accurate reconstructions of capillary networks and direct measurements made in vivo are critical when examining perturbations to a complex system such as the microvasculature (1, 9, 15, 28). It is unclear whether or not simplified capillary network geometries such as parallel oriented vascular arrays are sufficient to represent the complex morphology observed in vivo.

Several characteristics of blood flow and network morphology have previously been identified as critical to the adequate delivery of oxygen to living tissue. August Krogh’s seminal work on tissue oxygenation identified capillary density and distance between adjacent capillaries as a limiting factor to oxygen delivery in resting and working muscle (23). Red blood cell supply rate and oxy-hemoglobin saturation directly affect tissue oxygenation and limit the amount of oxygen available for consumption by surrounding tissue (6, 8).

Capillary density, oxygen consumption, SO₂, and RBC SR can be easily manipulated as variables in a computer model and values for these parameters can be readily obtained through mean measurements from histological, in vitro and in vivo means (9, 17, 25, 26). Previous efforts have been made to represent microvascular geometry using parallel networks that approximate what is seen in vivo (9, 15, 16). The resulting computer models of oxygen transport in the microvasculature have provided important insight into both the convective and diffusive delivery of oxygen to tissue. This use of parallel networks is an attractive approach given the difficulty, expense and time required to characterize capillary networks in vivo. The specific challenge of obtaining a data set that includes vascular geometry, hemodynamics and oxygen saturations has been addressed in part (11, 21); however, considerable investment in manpower and specialized equipment is still required to analyze and collect the experimental data.

The goal of this work is to compare the efficacy of using simplified, equivalent parallel capillary arrays compared to three-dimensional network reconstructions mapped using in vivo measurements. Furthermore we apply hemodynamic measurements to produce a flow model for the reconstructed networks that closely represents the flow profile observed experimentally. Using this approach, we hope to illustrate how the result of oxygen transport simulations may differ depending on the characteristics of the capillary geometry.

Materials and Methods

Intravital Video Microscopy

Capillary networks from rat EDL muscle, captured using intravital video microscopy for a previous works were used in this study. The experimental protocol used to observe and record flow conditions in the microvasculature has been described previously (12). Briefly, male Sprague-Dawley (Networks I and II) and Zucker Diabetic Fatty lean rats (Network III) were randomly selected on the day of experiment and weighed to verify a suitable mass between 140 – 180g. Animals were given an interperitoneal injection of sodium pentobarbital solution for anesthetic. Mechanical ventilation was used to maintain a mean breathing rate of 74 breaths per minute. Cannulas were inserted into the carotid artery, to monitor heart rate and blood pressure, and the jugular vein, to deliver supplementary saline and anesthetic as needed. EDL muscle was dissected as described by Tyml and Budreau (30), the muscle was isolated, secured with silk ligature, and reflected on the microscope stage such that the lateral side of the muscle faced the objectives. The ligature tied to the muscle was secured with surgical tape leaving the muscle in an orientation approximate to rest in situ. The muscle was kept moist with warm saline then covered with plastic film (Saran Wrap; Dow Chemical, Midland, MI, USA) and a glass cover slip to isolate it from the air. Animals were euthanized with Euthanyl Forte (Bimeda MTC, Cambridge, ON, Canada) at the completion of experimental protocols.

A Nikon Diaphot 300 inverted microscope (Nikon, Tokyo, Japan) fitted with a white light, 100W Xenon lamp for transillumination was used to visualize the EDL muscle. The intravital image was reproduced via a parfocal beam splitter fitted with 421 nm and 430 nm band pass filters. Simultaneous frame-by-frame video was captured at each wavelength using two identical computer systems, each connected to a charged-coupled device camera through real-time analog to digital capture cards. A live video output was displayed locally on closed-circuit monitors to allow the user to select regions of interest and maintain focus during capture.

Mapping Network Morphology

Intravital video sequences were used to create detailed maps of microvascular networks. Discrete networks were mapped from video sequences using custom MATLAB (Mathworks, Natick, MA, USA) software using techniques described elsewhere (12). Briefly, a series of overlapping video sequences were recorded throughout the volume of interest, allowing for the observation of a discrete capillary network with inlet and outlet vessels intersecting with the X-Z plane of the target volume. Variance images were generated for each video sequence (19) and characteristic features in functional images were used as fiducial markers allowing for registration between overlapping fields and between different focal planes. Vessel segments within variance images were outlined using a series of automated and manual methods. Connections between vessels were identified by the user allowing for complex interconnected networks to be mapped. During network reconstruction several tools were available to aid in accurate reproduction of the experimental network including dynamic 3D generation of mapped vessels, overlaid transparent composite maps of functional images and review of intravital video to determine appropriate network connections. The resulting reconstructed networks (Figure 1) provide a detailed map of the functional morphology of contiguous networks observed in vivo.

Figure 1.

Vascular maps for reconstructed capillary networks I (top left), II (middle left) and III, shown beside equivalent parallel capillary arrays I (top right), II (middle right) and III, generated to have the same vascular volume as the reconstructions. The foreground of each network image is the arteriolar end.

Capillary Hemodynamic and Oxygen Saturation Measurements

Hemodynamic and saturation measurements were made offline from video sequences using custom software similar to that described previously (5, 6, 12, 20). Briefly, individual in focus capillary segments from each field of view were selected from variance images. Space time images were generated and used to measure velocity, hematocrit and lineal density within individual capillaries (6). Oxygen saturations at inlet capillaries were measured using a spectrophotometric method utilizing a dual camera system recording oxygen sensitive and oxygen insensitive wavelengths (5, 12). Measurements were made on a frame-by-frame basis and averaged over a 60 second collection period. Mean hemodynamic and oxygen saturation measurements were indexed to the corresponding vessels in the network reconstructions.

Equivalent Parallel Arrays

The morphology and hemodynamics of each reconstructed 3D network were quantified using simple software that provided volumetric capillary density, bounding Euclidian X, Y and Z dimensions, mean and standard deviation of capillary diameters, mean red blood cell velocity and mean tube hematocrit. These measured parameters were used as the input for a computer program that randomly generated equivalent parallel capillary arrays that matched the source 3D reconstructions in dimensions, volumetric capillary density, mean velocity and hematocrit. This method of generating parallel arrays is similar to that described by Goldman and Popel (15) to create straight unbranched vessels populated around hexagonally packed muscle fibers. A summary of the geometric measurements for each parallel capillary array is shown in Table 1. An additional, surface area matched, parallel array (PCA II_SA) was created with the same vessel configuration as PCA II to compare with the volume matched model.

Table 1. Summary of network geometry parameters.

Statistical summary of vascular geometry data and capillary density.

	Volume Dimensions (μm × μm × μm)	Total Vessel Volume (μm3)	Total Vessel Surface Area (μm2)	Volumetric Capillary Density (%)	Capillary Length Density (mm × mm3)	Mean Krogh Radius (μm)	Mean Capillary Diameter (μm)
Network I	84 × 168 × 342	61.2 E3	45.4 E3	1.27	554.2	25.6 ± 3.9	5.4 ± 0.31
Parallel Network I	84 × 168 × 342	61.0 E3	45.7 E3	1.26	565.2	23.6 ± 0.0	5.3 ± 0.37
Network II	70 × 157 × 268	43.3 E3	33.1 E3	1.47	684.8	23.3 ± 3.9	5.2 ± 0.27
Parallel Network II	70 × 157 × 268	43.1 E3	34.0 E3	1.46	727.5	20.8 ± 0.0	5.1 ± 0.34
Network III	65 × 240 × 571	158.1 E3	114.5 E3	1.77	745.3	21.3 ± 2.1	5.5 ± 0.35
Parallel Network III	65 × 240 × 571	158.0 E3	116.3 E3	1.77	769.9	20.2 ± 0.0	5.4 ± 0.40

Modeling Flow in 3D Capillary Networks

Measurements from the 3D reconstructions made in vivo were used as the basis for modeling flow in the corresponding network geometries using a method that has been described previously (10). Blood flow and hematocrit values were estimated for vessel segments for which no data was recorded by using mass balance from connected downstream capillaries. Where needed mass balance was applied incrementally from downstream bifurcations until hematocrit and velocity had been estimated for all inlet vessels.

The total network red blood cell supply rate was calculated from in vivo measurements of vessels that lay within a cross section of the network that intersected a majority of vessels for which direct hemodynamic measurements had been made. Vessels in the cross section for which no measurement was recorded experimentally were assigned a mean supply rate calculated from the measurements made in other vessels in the cross section. The resulting SR_N is the total supply of red blood cells to the network volume as measured experimentally. We have previously demonstrated that (SR_N) is a major factor in determining oxygen delivery to a given tissue volume and changes to SR_N result in a proportional change to mean tissue PO₂ (10).

Hematocrit and velocity values for inlet vessels were calculated by recursively applying a mass balance to upstream vessels until the inlet values were determined. Resulting inlet hematocrits were set for the reconstructed networks and an existing flow model (16) was applied to calculate hemodynamic conditions throughout the network vessels. Boundary pressures were adjusted iteratively at the inlets and outlets of the network to roughly match the velocities observed in vivo. SR_N was matched to the experimental measurements by linearly increasing inlet boundary pressures until the target SR_N was reached. Flow solutions for 3D reconstructions matched in vivo measurements of total SR_N to within < 0.1%. Similarly for the parallel array networks cell velocity was linearly scaled such that the SR_N was identical to the supply rate determined by the flow solution for each corresponding 3D reconstruction. The mean pressure drop across the networks for the resting flow solution were 3.00, 1.98, and 4.23 mmHg for reconstructed networks I, II and III respectively.

In order to test how perturbations to the initial parameters of consumption and oxygen delivery may alter the outcome of oxygen transport simulations between RMN and PCA networks, three conditions in addition to rest were created. As described above, the resting condition utilized the flow solution based on the total SR_N for each network and a baseline consumption estimated from matching in vivo measurements of capillary SO₂. Ischemic cases were created for each reconstructed geometry with specific flow solutions for each network volume where the SR_N was decreased by 40%. Hypoxia utilized the same flow profile and SR_N as rest but used a decreased inlet SO₂ of 37.8%. Exercise cases used a higher maximum consumption rate of 6X rest and specific flow solutions for each network with a SR_N 5X above the resting case. A summary of the network statistics and the other parameters used in each simulation can be found in Tables 1 and 2.

Table 2. Summary of parameters used in oxygen transport models.

Summary of network geometry and hemodynamic parameters used in oxygen transport simulations.

	RBC SR/Volume (mL RBC × mL tissue−1 × s−1)	Entrance Saturation (%)	Consumption Rate (mL O2 × mL tissue−1 × s−1)
Network I	8.3 E-4 (Exercise: 41.3 E-4) (Ischemia: 5.0 E-4)	63 (Hypoxia: 37.8)	1.5 E-4 (Exercise: 9.0 E-4)
Parallel Network I	8.3 E-4 (Exercise: 41.3 E-4) (Ischemia: 5.1 E-4)	63 (Hypoxia: 37.8)	1.5 E-4 (Exercise: 9.0 E-4)
Network II	8.5 E-4 (Exercise: 42.2 E-4) (Ischemia: 5.0 E-4)	63 (Hypoxia: 37.8)	1.5 E-4 (Exercise: 9.0 E-4)
Parallel Network II	8.5 E-4 (Exercise: 42.2 E-4) (Ischemia: 5.1 E-4)	63 (Hypoxia: 37.8)	1.5 E-4 (Exercise: 9.0 E-4)
Network III	9.4 E-4 (Exercise: 46.9 E-4) (Ischemia: 5.6 E-4)	63 (Hypoxia: 37.8)	1.5 E-4 (Exercise: 9.0 E-4)
Parallel Network III	9.4 E-4 (Exercise: 46.9 E-4) (Ischemia: 5.6 E-4)	63 (Hypoxia: 37.8)	1.5 E-4 (Exercise: 9.0 E-4)

Oxygen Transport Model

A finite difference model of oxygen transport developed by Goldman and Popel was used to calculate PO₂ in the tissue surrounding the networks (10, 16). The flow conditions generated for each case were used as the input to the oxygen transport model to yield oxygen transport solutions describing the PO₂ within the tissue volume. The volume was discretized into a series of grid points each representing 8 μm³ volume. At each time step PO₂ for each volume element, P(x,y,z,t), was determined by calculating the diffusion between individual volume elements as follows: (10, 16).

$$\frac{\partial P}{\partial t}={\left[1+\frac{c_{Mb}}{\alpha }\frac{{dS}_{Mb}}{dP}\right]}^{-1}\left\{D{\nabla }^{2}P-\frac{1}{\alpha }M(P)+\frac{1}{\alpha }{D}_{Mb}{c}_{Mb}\nabla ·\left(\frac{{dS}_{Mb}}{dP}\nabla P\right)\right\}$$ (1)

where D, α, and M(P) are the diffusion coefficient, solubility and consumption rate of O₂ respectively of the tissue. Myoglobin concentration (c_Mb), diffusivity (D_Mb), and saturation (S_Mb) are also addressed through Equation 1 where S_Mb is determined by S_Mb(P) = P/(P + P_50,Mb) where S_Mb(P) is the myoglobin saturation at a given partial pressure and P_50,Mb is the partial pressure at which myoglobin is 50% saturated. Oxygen levels in the blood were determined within each vessel at each axial location (ξ) using a convective mass balance equation that describes blood oxygen saturation S(ξ,t):

$$\frac{\partial S}{\partial t}=-u\frac{\partial S}{\partial \xi }-\frac{1}{\pi R}{\left[C+{\alpha }_b\frac{{dP}_b}{dS}\right]}^{-1}\oint j·d\theta$$ (2)

where u is the mean blood velocity, R is capillary radius, j is the oxygen flux out of the capillary at the axial location (ξ,θ), C is the O₂-binding capacity of blood, P_b is the intracapillary PO₂ and α_b is the solubility of O₂ in plasma.

The flux of O₂ between capillaries and tissue is was defined as:

$$j=\kappa \left(P_b-P_w\right)$$ (3)

where κ is the mass transfer coefficient and P_w is the tissue PO₂ at the capillary surface. κ is a function of the capillary hematocrit in a given vessel and reflects the effect of red blood cell spacing on diffusional exchange between capillary and tissue (4). The boundary condition at the capillary-tissue interface was specified as:

$$-D\alpha \frac{\partial P_w}{\partial n}=j$$ (4)

where n is the unit vector normal to the capillary surface and j is defined by Eq. 3. In the current work, the boundary condition at the tissue boundaries was specified as a zero flux boundary condition.

As described previously by Goldman et al. (15) the above O₂ transport equations 1 – 4 were combined with Michaelis-Menten consumption kinetics, M = M₀ P/(P + P_cr) and the Hill equation for oxyhemoglobin saturation, S(P) = Pⁿ/( Pⁿ + P₅₀ⁿ) to define O₂ transport within the 3D volume. The baseline oxygen consumption rate M₀ (Table 2) was selected such that the resulting capillary SO₂ throughout the network fit approximately with experimental observations. Values for the above constants can be found in Table 3. Distinct oxygen transport models were run for each of the 6 network geometries under each of the 4 test conditions. Simulations were run to convergence on an Apple Mac Pro workstation with approximate runtimes of 18 – 36 hours needed to approximate steady state conditions determined by a 0 slope in PO₂ values over time within the corners of the simulation volume and a zero change in oxygen consumption.

Table 3.

List of constants and values used in oxygen transport simulations.

Constant	Value
α	3.89 E-5 ml O2 ml−1 mmHg−1
αb	2.82 E-5 ml O2 ml−1 mmHg−1
C	0.52 ml O2 ml−1
D	2.41 E-5 cm2 s−1
Pcr	0.5 mmHg
cMb	1.02 E-2 ml O2 ml−1
DMb	3 E-7 cm2 s−1
P50	37 mmHg
P50,Mb	5.3 mmHg

Results

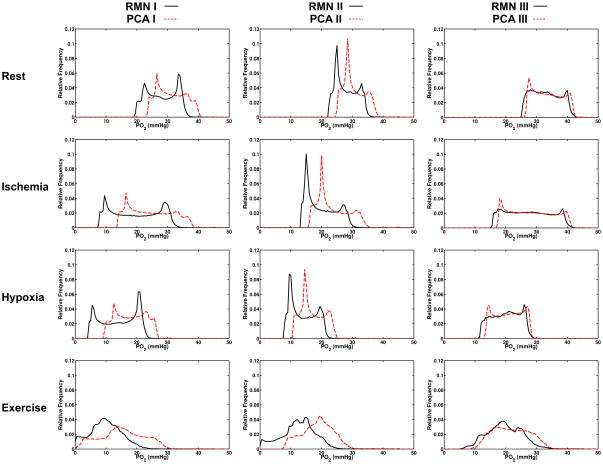
Figures 2 illustrates tissue PO₂ distributions in each of the three reconstructed networks and corresponding parallel arrays for the 4 simulation cases (rest, hypoxic challenge, ischemia and exercise). In each set of simulations the tissue PO₂ in the 3D capillary network reconstructions were left shifted compared to the solutions for the corresponding equivalent parallel capillary array.

Figure 2.

Tissue oxygen distribution for each set of oxygen transport simulations. Relative frequency of PO₂ within the volume for reconstructed (solid black line) and parallel array (broken red line) are shown for networks I (left column), II (middle column), and III (right column) under rest (top row), ischemia (second row), hypoxia (third row), and exercise (bottom row). Ischemia was simulated by imposing a 40% decrease in RBC SR compared to rest. Inlet SO₂ for hypoxia simulations was 37.8% compared to 63% at rest (a 40% relative decrease). Exercise simulations utilized a 6X increase in consumption and a 5X increase in RBC SR. Note that the parallel array for Network II has a higher minimum tissue PO₂ due to a counter current vessel that spans the volume.

Mean tissue PO₂ in the resting simulation for the 3D reconstructions were 28.15±4.78, 28.07±3.53 and 33.03±4.49 mmHg for networks I, II, and III respectively compared to the equivalent parallel arrays means values of 31.24±4.54, 30.57±3.44, and 33.76±4.55 mmHg (top row of Figure 2). The PO₂ distributions in the ischemia cases spanned a wider range compared to rest with minimum PO₂ values 3.1 – 6.51 mmHg lower in the 3D reconstructions (second row of Figure 2). The 40% flow reduction resulted in decreased mean tissue PO₂ of 19.81±7.63, 19.90±4.92, and 27.48±7.06 in the reconstructions versus 24.64±6.89, 23.62±5.07, and 28.41±703 mmHg in the associated parallel arrays.

Tissue PO₂ distributions in the hypoxia simulations were comparable to the ischemic case with wide ranges of PO₂ values (third row of Figure 2). Again, reconstructed networks a had lower mean PO₂ values of 14.22±5.84, 14.06±4.11, and 20.10±4.45 mmHg, compared to mean values determined for the parallel capillary arrays of 18.07±4.79, 17.08±3.78, and 20.95±4.35 mmHg. Exercise simulations resulted in the widest PO₂ distributions (bottom row of Figure 2) with minimum PO₂ values approaching 0 in reconstructed networks I and II, and parallel array I. The relatively high minimum PO₂ (7.5 mmHg) in parallel array II is caused by a counter current flow vessel which was set to mimic a shorter counter current vessel segment present in reconstructed network II. Under simulated exercise conditions mean tissue PO₂ in the reconstructed capillary networks was 10.07±5.37, 12.61±5.70, and 19.67±5.70 mmHg compared to 15.32±7.26, 18.76±5.25, and 21.73±5.96 in the equivalent parallel networks.

In order to illustrate the localized difference in PO₂ between reconstructed networks and equivalent parallel arrays the PO₂ within each volume element from RMN simulations was plotted against the corresponding value in PCA volumes for each set of networks and condition (Figure 3). Discrete points in Figure 3 have been color coded to correspond to the difference between each RMN and PCA element. Under baseline conditions the relative dispersion of matched PO₂ values was small with outliers primarily being composed of volume elements in or near vessels. The spread of matched PO₂ elements was higher in ischemia and hypoxia simulations with matched elements in both cases being distinctly lower in the RMN network volumes. Under the exercise conditions there was the largest discrepancy of tissue PO₂ between the two types of network geometry with large portions of the volume having higher PO₂ in the RMN/PCA I simulations. A relatively tighter distribution of values was seen under exercise in RMN/PCA II and III with the majority of the points showing higher tissue PO₂ in the PCA simulations.

Figure 3.

Scatter plots showing the localized PO₂ difference between RMN and PCA simulations. PO₂ for RMN simulations is plotted against the PO₂ values for the PCA simulations for each network and condition. The colormap shows the calculated difference between the two values and corresponds to the spatial depiction shown in figure 4.

To further show how the tissue PO₂ differs between reconstructed and parallel networks three-dimensional difference maps were created (Figure 4). Difference maps were generated by subtracting the tissue PO₂ values from the RMN oxygen transport simulations from the corresponding PCA simulations on an element-by-element basis. The resulting voxelated maps show the spatial distribution of differences in PO₂ in each set of simulations. The underlying geometry from both network types are visible in the three dimensional difference maps since the largest difference in PO2 is in volume elements that are in or near capillaries. In all of the rest, ischemia and hypoxia cases tissue PO₂ was uniformly lower in RMN simulations compared to PCA. The exercise cases showed some heterogeneity with RMN and PCA I having substantial regions of both higher and lower PO2 in the RMN simulation compared to the PCA.

Figure 4.

Volumetric tissue PO₂ difference map for each set of oxygen transport simulations. The PO₂ difference values were calculated by subtracting the transport simulation results for the PCA from the RMN simulations on an element-by-element basis. The resulting map shows how the oxygen transport simulations vary spatially where negative values represent ares where tissue PO₂ was higher in the PCA simulations and positive values where PO₂ was higher in RMN simulations. Each voxel element is semi-transparent allowing PO₂ deep within the tissue volume to be visible. The volume elements with the largest differences are located in and around individual vessels from each of the RMN and PCA geometries. The PO₂ range of colormaps was selected such that differences were easiest to view and do not encompass the entire range of values.

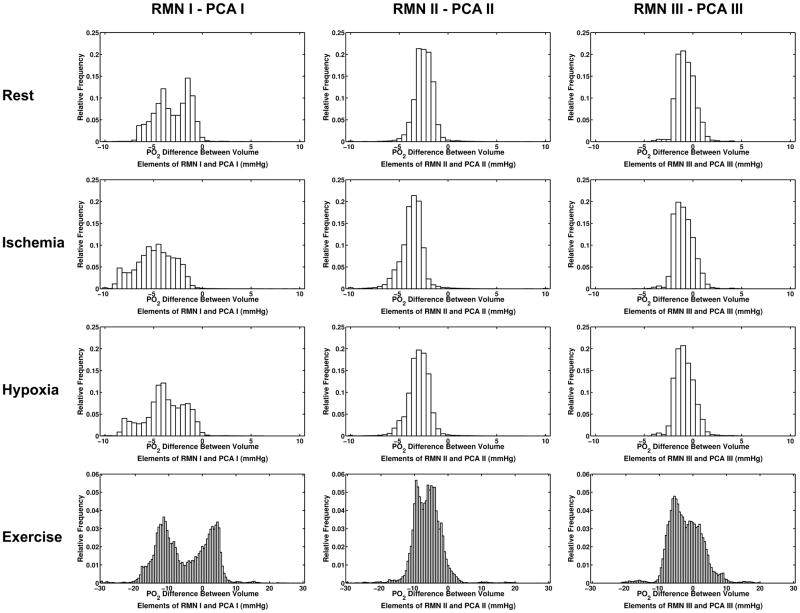
Relative difference between volume elements in each simulation was quantified by generating histograms showing the relative frequency of PO₂ differences between RMN and PCA simulations (Figure 5). Bins for rest, ischemia and hypoxia ranged from −10 to 10 mmHg with a bin size of 0.5 mmHg. The larger spread of PO2 differences in exercise required bins to range from −30 to 30 with a bin size of 0.5 mmHg. Histograms show the relative frequency of the PO₂ differences represented spatially in Figure 4.

Figure 5.

Histograms showing the relative frequency of the difference values calculated by subtracting PCA simulation tissue PO₂ from RMN values on an element-by-element basis. The vast majority of tissue elements in rest, ischemia and hypoxia simulations have a higher PO₂ in PCA simulations resulting in a high proportion of negative values in the difference histograms.

Capillary point density in reconstructed networks varied longitudinally through the volume. The arteriolar end of the vascular bed had lower capillary density increasing towards the venular end in all three reconstructed geometries. Figure 6 shows the relative capillary density in 10 μm sections taken longitudinally along each network. Reconstructed networks I and II had lower than half the capillary density at the arteriolar end than the corresponding equivalent parallel arrays. The capillary density at the arteriolar end of RMN III was closer to that of the PCA; however the number of vessels in the cross section was lower with 8 vessels in the RMN compared to 12 in the PCA cross section. Mean tissue PO₂ in longitudinal X-Z planes was higher in all parallel networks due to higher capillary density at the arteriolar end, a more homogeneous distribution of vessels within the cross section, and uniform capillary density from arteriolar to venular end. Krogh radius was calculated for each 10 μm section longitudinally along each network

Figure 6.

Longitudinal capillary density for reconstructed networks and associated parallel arrays along the long axis of the network volumes. Normalized capillary density (number of vessels/mm²) was calculated for slices every 10 μm. The longitudinal position of arteriolar (A) and venular (V) ends of the network have also been indicated.

( $\mathit{Krogh}\mathit{radius}=\sqrt{(\mathit{tissue}\mathit{area})/(\pi \times \mathit{number}of\mathit{capillaries})}$) and mean values are shown in Table 1. Mean Krogh radius was lower in RMN compared to the volume matched PCA in each of the three pairs of networks. Figure 7 illustrates the longitudinal difference in mean tissue PO₂ for each X-Z slice between reconstructed networks and parallel arrays for the resting case.

Figure 7.

Mean tissue PO₂ in each longitudinal X-Z slice for reconstructed networks (solid black line) and parallel arrays (broken red line) for resting case in networks I (top), II (middle), and III (bottom). Tissue PO₂ in the parallel networks is higher due to greater capillary density at the arteriolar end and uniform spacing throughout the network volume. The lower difference in density between RMN and PCA III results in a smaller difference in mean tissue PO2 across the volume.

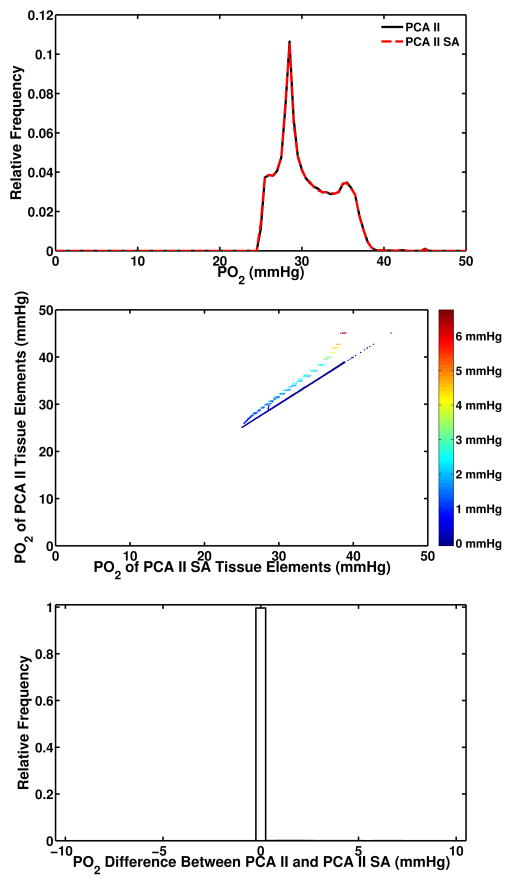
Total vascular volume and surface area for each geometry is shown in Table 1. Although vascular volume was used as a matching metric for the construction of equivalent parallel arrays the surface areas for each equivalent network also matched closely. The largest difference in total vessel surface area was 2.7% between RMN and PCA II. To test the effect of this difference in surface area an additional parallel array was constructed with surface area equal to the RMN II and the results are shown in Figure 8. The resulting oxygen transport simulation showed 0.1% difference in mean tissue PO₂ and small, localized, PO₂ differences in volume elements associated with vessels.

Figure 8.

An additional simulation was conducted to compare the result of using a surface area parallel array compared to a volume matched parallel array. The relative distribution of PO₂ values (top) for both the volume matched (PCA II) and surface area matched (PCA II SA) overlap almost exactly. A scatter plot of PO₂ values in the same voxel within each network (middle) shows that the tissue elements have the same PO₂ in nearly every element. A histogram of the differences between PO₂ values in matched voxels within each volume shows that nearly 100% of tissue elements have a zero difference in PO₂ between the PCA II and PCA II SA simulations.

Discussion

We have presented a comparison of tissue oxygen distribution within reconstructed 3D capillary network volumes and equivalent parallel capillary arrays. Utilizing resting conditions based on in vivo measurement our model has shown that volume matched parallel capillary arrays result in a higher overall tissue PO₂ in the volume of interest when compared to the 3D reconstructions. Capillary density at the upstream end of the tissue volumes was higher in the parallel capillary arrays resulting in higher tissue PO₂ in tissue surrounding inlet vessels (Figure 9). The higher tissue PO₂ is likely due to reduced diffusion distance between vessels resulting in higher PO₂ in tissue at the inlet end of the volume. Similarly, since the outlet end of parallel array volumes have the same spatial distribution of vessels and uniform diffusion distances, we observed higher tissue PO₂ levels at the venous end of parallel networks compared to the reconstructions. The more homogeneous distribution of vessels in the cross section of parallel arrays results in higher tissue PO₂ within the volume due to the uniform spacing between vessels along their length. This effect can also be observed in RMN III in that the relative higher density both throughout the network and at the arteriolar end yielded results closer to the PCA III simulations. However the higher capillary density at the arteriolar end of PCA III and the uniform distribution throughout the network volume caused higher PO₂ values longitudinally across the volume (Figure 7). Mean PO₂ levels under resting conditions for parallel arrays (31.2, 30.6, and 33.8 mmHg) are consistent with modeling results reported by Ellsworth et al. (27 – 30 mmHg) using experimentally measured input parameters applied to parallel vessel models (9). In addition, the mean tissue PO₂ in the reconstructed networks under rest conditions (28.2, 28.1, and 33.0 mmHg) is similar to average PO₂ measured in spinotrapezius muscle (27.8 mmHg) using Whalen-type oxygen microelectrodes (24). The localized PO₂ difference between the rest simulations (Figures 3 – 5) show higher PO₂ throughout each PCA volume. In networks I and II the vast majority of volume element had a lower PO₂ in RMN simulations compared to the matched PCA tissue volumes.

Figure 9.

Tissue PO₂ at arteriolar end of network volumes for RMN I (top) and PCA I (bottom) illustrating volumetric regions with PO₂ values above 35 mmHg for resting conditions. PO₂ values below 35 mmHg are transparent to show the range of interest.

Under simulated ischemia, hypoxia and exercise conditions we also observed higher mean tissue PO₂ in each of the three parallel array models compared to the corresponding 3D reconstructed networks. Lower flow in the ischemic simulations yielded an increased difference in mean tissue PO₂ between reconstructed and parallel networks compared to rest. Larger differences in mean tissue PO₂ between reconstructions and parallel arrays compared to rest were also seen in simulated hypoxia models. Ischemia and hypoxia caused a higher variation in element-by-element PO₂ differences between the two types of network, however again the vast majority of volume elements had lower PO₂ values throughout the volume in RMN simulation compared to PCAs.

Of the four input conditions exercise was the only perturbation to create regions of anoxia in a test volume. Mean tissue PO₂ for reconstructed networks (10.1 and 12.6 mmHg) was lower than previous calculated values for mild exercise (17 mmHg) but consistent with heavy exercise conditions (12 mmHg) (9). Similarly Goldman et al. reported mean tissue PO₂ of 23.2 mmHg for simulated working conditions in fiber-structured vessels (analogous to parallel networks in this study) which is somewhat higher than what was found under exercise conditions in the equivalent parallel arrays (15.3 and 18.8 mmHg). There are however some differences in the blood flow and oxygen consumption values used in this study compared to previous reports. For comparison, the 10 fold increase in consumption applied by Goldman and Ellsworth (9, 15) results in an oxygen consumption of 15.7E-4 (mL O₂ × mL tissue⁻¹ × s⁻¹); 70% higher than that used in the present study. Furthermore the 5 fold blood flow increase described previously (15) yields a RBC SR of 62E-4 (mL RBC × mL tissue⁻¹ × s⁻¹), which is 50% higher than the RBC SR per unit volume used for exercise conditions in this study. With these differences in mind the relative scaling of blood flow and oxygen consumption is comparable between this and previous studies. Increasing consumption and blood flow caused greater heterogeneity in PO₂ distribution spatially throughout the network (Figure 5). Localized differences in vessel position due to the different underlying geometries created large variations in the tissue PO₂ surrounding individual vessels. Even given these localized differences the majority of tissue elements in each set of exercise simulations had lower PO₂ values in the RMN simulations compared to PCA.

An additional consideration for interpretation of these results is the presence of a single counter current vessel in Network II which was mimicked in the equivalent parallel array. The imposed counter current vessel spans the full length of the parallel volume, compared to a short counter current segment in the corresponding reconstructed network. This likely prevented oxygen levels from falling to 0 in the parallel array II exercise simulation. Counter current exchange between this vessel and other vessels increased the mean tissue PO₂ substantially compared to the 3D reconstruction. It has been noted previously that the presence of counter current flow significantly affects the distribution of oxygen within a volume (15). It is important to note that while the difference in mean tissue PO₂ between parallel and reconstructed networks increased in each of the three perturbed cases compared to rest, the overall magnitude of the shift was relatively similar between parallel and reconstructed networks as was the underlying shape of the paired distributions in each case.

A previous study compared several variations of computer generated capillary networks to study the effect of anastomoses and tortuosity on oxygen delivery (15). Goldman et al. applied oxygen transport simulations using straight unbranched capillary networks, similar to those used in the current study, and showed that networks with anastomotic vessels yielded mean tissue PO₂ values 1 mmHg higher than the comparable simulations with straight unbranched vessels. Similarly networks with tortuous vessels resulted in a mean tissue PO₂ 1 mmHg higher than straight unbranched networks. This effect did not appear to be additive, in that network cases combining tortuosity and anastomoses did not further increase mean tissue PO₂ beyond 1 mmHg above the straight and unbranched case. Goldman et al. concluded that the presence of tortuous and anastomotic vessels increased mean tissue PO₂. In the present study we found that parallel arrays (equivalent to straight unbranched networks) delivered more oxygen when compared to the reconstructed networks. From this it is reasonable to conclude that adding tortuosity and anastomoses to our parallel arrays would further increase the difference compared to real networks reconstructed from in vivo data. Ellsworth et al. also noted that the homogeneity of vessel SO₂ increased longitudinally in a parallel vessel model of oxygen transport (9). The cause of this uniformity was attributed to a high degree of diffusional exchange amongst adjacent capillaries causing a convergence of SO₂ levels towards the venular end of the network. This effect is likely to similarly impact tissue PO₂ longitudinally causing more uniform gradients of oxygen perpendicular to the direction of flow resulting in higher tissue PO₂ throughout the tissue volume.

Morphological differences between reconstructed networks and parallel arrays, specifically varying capillary density longitudinally along the network in RMN versus a more uniform distribution of vessels throughout the volume in PCA, have a marked impact on oxygen delivery. Mean capillary point density is higher in PCA networks and does not vary longitudinally (Figure 6); this effectively reduces the diffusion distance from vessels to tissue particularly at the arteriolar end of the PCA networks which results in higher PO₂ within the tissue volume. In addition to the effect of higher point density, the tessellation of vessels within the parallel arrays creates a more uniform vessel spacing which further serves to reduce diffusion distance within these volumes. This difference in diffusion distance is also illustrated by the mean Krogh radius which was smaller in each PCA compared to the paired RMN (Table 1). Due to these factors, parallel networks that utilize a homogeneous and ordered distribution of vessels throughout the network volume will have a shorter mean diffusion distance to tissue resulting in higher tissue PO₂ when compared to simulations based on reconstructed vascular geometries.

The method used to generate parallel networks was based on the absolute capillary volume in the corresponding reconstructed network. Alternative metrics could be used to create parallel arrays that could be considered equivalent. We consider producing networks with equal vascular volume to be a realistic approach though we acknowledge it does not directly compare to the approach of using the number of vessels per cross sectional area. Furthermore since mean capillary diameter was also used as an input to create the volume matched PCAs the total vessel surface area was within 2.7% of the reconstructed networks in each case. An additional simulation using a surface area matched PCA showed almost no difference between the volume matched equivalent (Figure 8) illustrating how the location of vessels has an impact on oxygen delivery with the volume. An additional benefit of using volume matched network geometries is that the total consuming tissue volume is maintained between the parallel array and the network reconstruction; use of a metric such as point density would cause a mismatch in the consuming volume for parallel arrays based on the reconstructed networks used in this study.

The equivalent parallel arrays in the present work were generated by randomly assigning vessel locations within a hexagonally tessellated grid. Given the size of the tissue volume and the resulting tessellation, each of the equivalent parallel arrays used in this study is one of numerous possible configurations. For example, there are 3003 different possible vessel configurations for PCA I given a tessellation grid of 14 different vessel positions for 8 discrete vessels. Although it is impossible to know a priori which configuration would best match oxygen transport simulation results from the corresponding reconstructed vasculature, it is worth examining a subset of random configurations to determine whether or not varying vessel orientation in parallel arrays will have an impact on oxygen delivery. To interrogate this problem, ten additional random configurations were generated for the network I volume and resting oxygen transport simulations were run for each. The resulting PO₂ distributions for each random configuration (Figure 10) showed some variability, with mean tissue PO₂ ranging between 31.0 and 31.6 mmHg. The small differences in PO₂ between the random configurations tested demonstrate that within a given random array, vessel position itself will have some minor effect on oxygen delivery and mean tissue PO₂. Regardless of the methods employed to generate a parallel array it is important to realize that the collection and characterization of a given network with respect to specific geometry and hemodynamic parameters was first accomplished experimentally in order to identify representative values to apply to the resulting generated arrays. We would assert that models are made more realistic when they employ a representative range of network morphologies and input parameters; ideally reconstructed 3D geometries and flow conditions calculated using direct in vivo measurements would be used. The limited number of reconstructed networks used in this study certainly does not encompass all of the diversity that may be seen in living muscle. However, we believe the ability to utilize specific cases and accurately represent a degree of variation is a step forward from the application of mean values to represent what is certainly a widely variable system that exhibits a distinct heterogeneity of vascular density and relative flow distribution.

Figure 10.

To demonstrate the variability in PO₂ distributions due to alternate random vessel configurations ten additional resting simulations were conducted based on the PCA I volume. Each random configuration (R1 – R10) shown above represents a unique solution and illustrates the variability in oxygen transport simulations that are due to changing vessel placement within the tessellation grid.

Considerations

The approach used in this study to create parallel capillary arrays addresses a common type of synthetic vessel network used in oxygen transport modeling. Generated networks of this type have been used to simulate vessels found in skeletal muscle and as such, the conclusions of this study should be considered with the understanding that the results presented here may not apply to more complex vascular structures such as those found in kidney, liver, heart and brain (3, 18, 22, 27, 29). These results do however point to the importance of obtaining detailed experimental data and, in particular, capillary geometry. Future studies should consider the impact of synthetic networks particularly when simulating complex geometries with non-parallel vascular orientations.

Several studies have used synthetic networks to simulate skeletal muscle vascular that include tortuosity and branching segments (2, 15). This study does not address the effect of these characteristics when applied to synthetic networks, though there is some evidence to suggest that simply adding tortuosity and branches to a continuous density array does not substantially affect oxygen delivery (15). Additional work will need to be done in order to examine this question in more detail and to compare synthetic geometries that include these features with equivalent reconstructed networks. Furthermore, the inclusion of longitudinal capillary density variations in synthetic geometries that utilize branching and tortuous segments may serve to minimize the different results in oxygen transport simulation shown between reconstructed and synthetic networks in this study. Provided that data describing variations in longitudinal capillary density was available, synthetic networks could be generated to incorporate such variations while maintaining vascular volume either measured experimentally or estimated from stereological measurements.

Conclusion

Using a computational oxygen transport model we have demonstrated that the source and structure of the underlying vascular geometry will produce distinctly different results. We have shown this effect in discrete network volumes ranging from 268 to 571 μm in length. The application of 3D reconstructed capillary networks and matching blood flow profiles created using in vivo data, yielded lower mean tissue PO₂, and lower mean cross sectional PO₂ throughout the tissue volume, compared to parallel arrays generated using equivalent volumetric and hemodynamic parameters. When examined on an element-by-element basis rest, ischemia, and hypoxia conditions RMN had lower PO₂ values spread uniformly throughout the sample volumes compared to PCA. These perturbations to oxygen delivery and consumption increased the observed difference in tissue PO₂ between reconstructed and parallel source geometries resulting in larger differences in PO₂ between tissue elements. Simulated exercise caused significant localized heterogeneity in element-by-element tissue PO₂ differences suggesting that the underlying geometry between RMN and PCA has a more profound affect under this condition. The results of this study illustrate the value of using precise representations of vascular structures when modeling oxygen transport. In every case tested, PCAs had a higher mean tissue PO₂ that was caused by higher PO₂ values spread uniformly throughout the tissue volumes. The range of differences in mean tissue PO₂ between RMN and PCA simulations varied from 2.2% in the network III rest simulations to 52% between the network I exercise simulations. These results clearly suggest that at this length scale, volume matched equivalent parallel arrays yield different oxygen transport solutions than reconstructed networks collected from in vivo experiments. These finding are tempered somewhat by the observation that tissue PO₂ distributions from parallel arrays and the paired reconstructions were very similar both in shape and in the relative changes resulting from the three test perturbations. Continued efforts to directly measure larger and more complex microvascular networks will provide a broader scope of input data allowing existing models to reflect the structural and functional variability seen in vivo.

Perspective

The use of reconstructed 3D capillary networks can provide a more precise spatial picture of oxygen delivery within the microvasculature under a variety of normal and pathological conditions. Heterogeneities in oxygen tension within a given geometry could be used to explore angiogenesis and other physiological responses to hypoxic challenges. The future possibility of combining several distinct network geometries with models of larger vessels could aid in producing more integrated models of blood flow and O₂ delivery in whole tissue as well as providing a framework for exploring control mechanisms that involve oxygen sensing in the microvasculature. Existing parallel array models continue to have great utility when simulating large vascular beds although modelers should attempt to incorporate observed diversity in morphology and blood flow. The availability of reconstructed network geometries and associated in vivo data sets, will improve the predictive power of existing models and facilitate the validation of the resulting solutions.

ABBREVIATIONS USED

3D

three-dimensional

EDL

extensor digitorum longus

PO₂

partial pressure of oxygen

RBC

red blood cell

SO₂

oxygen saturation

SR

supply rate

SR_N

network supply rate