Adjusting for Population Stratification in a Fine Scale with Principal Components and Sequencing Data

Abstract

Population stratification is of primary interest in genetic studies to infer human evolution history and to avoid spurious findings in association testing. Although it is well studied with high-density single nucleotide polymorphisms (SNPs) in genome-wide association studies (GWASs), next-generation sequencing brings both new opportunities and challenges to uncovering population structures in finer scales. Several recent studies have noticed different confounding effects from variants of different minor allele frequencies (MAFs). In this paper, using a low-coverage sequencing dataset from the 1000 Genomes Project, we compared a popular method, principal component analysis (PCA), with a recently proposed spectral clustering technique, called spectral dimensional reduction (SDR), in detecting and adjusting for population stratification at the level of ethnic subgroups. We investigated the varying performance of adjusting for population stratification with different types and sets of variants when testing on different types of variants. One main conclusion is that principal components based on all variants or common variants were generally most effective in controlling inflations caused by population stratification; in particular, contrary to many speculations on the effectiveness of rare variants, we did not find much added value with the use of only rare variants. In addition, SDR was confirmed to be more robust than PCA, especially when applied to rare variants.

Introduction

Inference of population structure is critical to controlling false positives in association testing with many applications, such as to understanding different drug responses (Sirugo et al., 2008; Bryc et al., 2010). Although population stratification has been well studied with high-density single nucleotide polymorphism (SNP) data in genome-wide association studies (GWASs), next-generation sequencing has posed both hopes and challenges to identifying population structure in a finer scale. Populations in a fine-scale, including subgroups within a continent, as compared to different continental groups, share more recent ancestors, and may only be genetically distinct in a subtle way (Henn et al., 2010). Nevertheless, genetic differences among subpopulations are expected to cause population stratification at a fine scale, which in turn may lead to spurious findings in association testing if not properly adjusted.

Many approaches have appeared to account for population stratification in GWASs. Genomic control (Devlin and Roeder, 2004) aims to estimate an inflation factor from many test statistics and then correct each test statistic with a common inflation factor estimate. This method is impaired in unrealistically assuming that all tests across the genome share one common inflation factor. Principal component analysis (PCA) extracts a few top principal components (PCs) related to ancestries and then includes them in a regression model to adjust for population stratification (Patterson et al., 2006). Individual SNPs can also be used to cluster the samples before carrying out a stratified analysis (Pritchard et al., 2009). This approach is computationally demanding and perhaps more suitable for discrete populations. Another approach is to use a genetic similarity score to match cases and controls before applying conditional logistic regression (Epstein et al. 2007; Guan et al. 2009). More recently, linear mixed models have emerged (Kang et al., 2008). Due to the simplicity and good performance of PCA in GWAS (Wu et al., 2011), and its possible extensions (Lin and Zeng, 2011), we consider PCA and a related method.

Rare variants (RVs, with minor allele frequencies, MAFs < 1%) have been shown to play important roles in several diseases (Bodmer and Bonilla, 2008; Hindorff et al., 2009) and are expected to account for some disease risk beyond common variants (CVs, with MAFs ≥ 5%). More relevantly here, as pointed out by Henn et al. (2010), “Rare variants are likely to have recently arisen and segregate between populations and are informative markers of ancestry”. Accordingly, there is great interest in examining how RVs would perform in detecting population structure (e.g. Baye et al 2011; Siu et al 2012). In particular, Zhang et al. (2013) showed that population stratification could be a serious issue when testing on low frequency variants (LFVs, MAFs between 1% and 5%) and on RVs. Including a few top PCs of a set of 10000 CVs or LFVs in a logistic regression model could effectively control the confounding effects of two continental groups. However, the issue of population stratification at the level of ethnic subgroups and the role of RVs in uncovering population structure were not fully investigated. Naturally, the following questions arise: can PCA, or other more robust dimension reduction methods like spectral dimension reduction (SDR), satisfactorily address population stratification at the level of subgroups? In doing so, which types of variants should be used, CVs, LFVs, RVs, or a mixture of all, and pruned or non-pruned ones? The main goal of this paper is to address these questions using sequencing data.

Several studies have touched on some of these issues, but with different types of data. Heath et al. (2008) used autosomal SNPs selected from the Illumina HumanHap 300 chip to show that PCs based on CVs, LFVs or RVs had similar patterns for 13 subpopulations in Europe. The authors also observed that the top two PCs had strong correlations with geographic coordinates. However, Babron et al. (2012) used the SNPs on the Affymetrix 500K chip to show some non-negligibly different influences by different types of variants on population stratification in 12 UK regions. It was suggested that the effect of population stratification was stronger when testing RVs. But in a simulated case-control study, they did not observe any major difference with the use of a few top PCs constructed from different types of variants when testing on variants with MAF ≥ 0.005. Both papers agreed that the top PCs of CVs performed considerably well in controlling population stratification, and the number of variants used to construct PCs mattered in extracting ancestry information. Furthermore, the two papers showed that clustering analyses with either STRUCTURE (Pritchard et al., 2000) or Admixture (Alexander et al., 2009) did not satisfactorily uncover the population subgroups. Using simulated sequencing data, Mathieson and McVean (2012) clearly showed that none of the several commonly used adjustment methods worked well when testing on RVs in the presence of a local non-genetic risk; in contrast, all the methods performed well for testing on CVs. Due to the possible limitation with the use of the above genotyping or simulated data, it is not clear whether the above conclusions hold with real sequencing data.

Our study differs from the previous ones in the following aspects. First, instead of focusing only on one continent or one country, we used multiple subgroups of European and African ancestries, imposing a challenge to differentiating both dramatic and subtle genetic variations across the subgroups. Secondly, we compared PCA with another dimensional reduction method, spectral dimension reduction (SDR), in several scenarios with different types or sets of variants. We also simulated both binary traits and quantitative traits with varying population structures. Finally, we used a low-coverage whole genome sequencing dataset released in August 2010 by the 1000 Genomes Project (1000 Genomes Project Consortium 2010), not genotyping array data or simulated sequencing data. In particular, compared to genotyping array data, our data included much more variants of each type, facilitating a more realistic assessment on various approaches.

We tackled the problems by first visualizing the subpopulation structure using scatter plots of the top PCs. We also inspected how well we could uncover the subgroups by model-based clustering on a few top PCs, shedding light on which subgroups were genetically separable. The clustering result was evaluated mainly by the (adjusted) Rand Index ((a)RI) (Rand, 1971; Hubert and Arabie, 1985). Then we used three configurations of the subgroups to generate a binary trait with population stratification, and tested on pruned CVs, RVs and LFVs on chromosomes 1 and 2, with or without adjustment by a few top PCs constructed with various methods and types or sets of genome-wide variants. Lastly, a quantitative trait in the presence of a local non-genetic risk (i.e. spatially structured population) was simulated and studied. The estimated Type I error rates and inflation factors (Devlin and Roeder, 2004) were both used to evaluate to what extent population stratification could be controlled.

Methods

Data

We focused on the 283 European and 174 African samples (Table 1). Across the 22 autosomes, after excluding 19,938 monomorphic single nucleotide variants (SNVs), there were 8,932,149 polymorphic variants, including 6,227,535 CVs, 1,849,693 LFVs, and 854,921 RVs. Following the suggestion of using nearly uncorrelated SNVs to construct PCs in PCA (Patterson et al., 2006), we pruned all variants by PLINK (Purcell et al., 2007) using a sliding window of size 50, shifted by 5 and with r² ≤ 0.05; after pruning, 880,426 variants remained. The same pruning procedure was applied to all CVs, all LFVs and all RVs respectively, leading to 149,324 CVs, 384,751 LFVs and 328,813 RVs remaining. We also randomly selected a set of 10000 pruned variants of each type to construct PCs. There were 27 individuals identified to be admixed Americans (AMRs), offering opportunities to explore the performance of PCA or SDR in the presence of outliers.

Table 1.

Subgroups with European (EUR) or African (AFR) ancestries in the 1000 Genomes Project data. The MXL, PUR and PUR2 samples are also classified as admixed Americans (AMRs).

Populations	EUR						AFR
Subgroups	CEU Utah residents	TSI Italian	GBR British	FIN Finnish	MXL Mexican in LA	PUR Puerto Rican	PUR2 Puerto Rican	YRI Nigerian	LWK Kenyan	ASW African in SW US
#Samples	90	92	43	36	17	5	5	78	67	24

PCA and SDR

Suppose X̃ is an n by p matrix, with n subjects and p SNVs, and X̃_im denotes the genotype score of the m^th SNVs for the i^th subject. X̃_im is coded 0, 1 or 2 as the minor allele count. Before we apply any method to construct PCs, each SNV is standardized as $({\stackrel{\sim }{X}}_{\mathit{im}}-2p_m)/\sqrt{p_m(1-p_m)}$ for all i and m, where p_m is the MAF for SNV m. We denote the standardized SNV matrix as X.

To contrast PCA and SDR, we will review PCA and SDR briefly. Both methods can be regarded as an eigen-analysis on a similarity matrix. Suppose we measure the genetic similarity between any two subjects by the correlation between their genotype scores, we use a similarity matrix

$$A=X{X}^T.$$

The eigenvalues of A are ordered from the largest to smallest as δ_q with corresponding eigenvectors as w_q, for q = 1, …, n − 1. Then the lth PC (or more precisely, a vector of PC scores) is

$$P{C}_l=\sqrt{{\delta }_l}{w}_l.$$

Typically we only need to use a few top PCs, e.g. with l ≤ 30.

PCA is known to be sensitive to outliers, or unsuccessful in separating closely related sub-populations (Luca et al., 2008). Lee et al. (2009) proposed a spectral clustering method, called SDR here. It is based on a normalized graph Laplacian matrix,

$$L=I-D^{-1/2}W{D}^{-1/2},$$

where W is a matrix measuring the similarities among subjects with elements

$$W_{\mathit{ij}}=\{\begin{array}{ll}\sqrt{X_{i.}^{\prime }{X}_{j.}}& \mathrm{if}{X}_{i.}^{\prime }{X}_{j.}\ge 0,\\ 0& \mathrm{if}{X}_{i.}^{\prime }{X}_{j.}<0,\end{array}$$

where X_i. is the i^th row of X containing the standardized genotype scores of subject i, and D = diag(D₁₁, …, D_nn) with $D_{\mathit{ii}}={\sum }_{r=1}^n{W}_{\mathit{ir}}$. We sort the eigenvalues θ_q of D^−1/2W D^−1/2 with the corresponding eigenvectors υ_q for q = 1, … n − 1. As D^−1/2W D^−1/2 may not be positive semi-definite, we define λ_q = max{0, θ_q}. Hence, similar to PCA, slightly abusing the notation, we call the following scaled eigenvector the lth PC of SDR

$$P{C}_l=\sqrt{{\lambda }_l}{\upsilon }_l.$$

Regarding how many PCs of PCA or SDR to use, we applied the Tracy-Widom (TW) test (Patterson et al., 2006) or the eigengap heuristic method (Lee et al., 2009) respectively. Depending on the type of the variants used, it yielded varying numbers of the significant PCs (p-value<0.05 for TW test) (Table 2). Note that using pruned RVs, the heuristic method identified a large number (453) of “significant” eigenvalues (or PCs) based on a calculated cut-off at 0.00575; if the cut-off was slightly increased to 0.00576, then only 48 eigenvalues were to be “significant”. We also checked the top eigenvalues of the similarity matrices calculated based on different sets of SNVs: they appeared to be similar, but not exactly the same. In summary, in most cases, 25 PCs appeared to suffice. We also tried adding more than 25 PCs in some simulations, but the performance was not improved.

Table 2.

Numbers of significant eigenvalues from PCA by the Tracy-Widom test or those from SDR by a heuristic method.

Methods	w/o pruning				with pruning				10000 pruned
	all	CVs	LFVs	RVs	all	CVs	LFVs	RVs	all	CVs	LFVs	RVs
PCA	19	22	11	28	27	26	19	14	20	18	15	12
SDR	11	3	11	31	13	9	14	453	13	9	14	9

Clustering analysis

After dimension reduction with PCA or SDA, we can apply clustering analysis, aiming to discover the clusters corresponding to the subgroups. Here we choose to use Gaussian model-based cluster analysis (Banfield and Raftery, 1993). Specifically, denote the vector of the top 25 PCs from sample i as Q_i; for a specified K, it is assumed that Q_i’s come from a finite mixture of Gaussian distributions with a density function

$$f(Q_i)=\sum _{j=1}^K{\pi }_{j}N({\mu }_j;V_j),$$

where N(μ_j; V_j), corresponding to cluster j, is the density function for a multivariate Gaussian with mean μ_j and covariance matrix V_j, and the unknown parameters Θ = {(π_j, μ_j, V_j) : j = 1, …, K} are to be estimated by maximum likelihood. The Bayesian information criterion (BIC) is commonly applied to select K. We used its implementation in R package mclust.

The Rand Index (RI) is applied to measure how well clustering assignments agree with the subjects’ true subgroup labels (Rand, 1971). RI is a measure of similarity between two sets of clusters. Suppose the true cluster or group membership is C = {C₁, …, C_s} for n subjects, where C_e is the set of subjects that are in cluster e. The clustering result is M = {M₁, …, M_z}, where M_f is the set of subjects that are assigned to cluster f. Then RI is calculated as $\mathit{RI}=(a+b)/\left(\begin{array}{l}n\\ 2\end{array}\right)$, where a is the number of pairs of subjects that are in the same set in both C and M, and b is the number of pairs of subjects that are in different sets in both C and M. However, RI will increase to 1, the upper bound, as the number of clusters increases. Furthermore, RI does not correct for the effects of random chance; that is, we will have an RI > 0 even for randomly assigned clusters. As an alternative, we also use another statistic, an Adjusted Rand Index (aRI) (Hubert and Arabie, 1985).

Association Testing

For the purpose of association testing, all 10,848 pruned CVs with MAF>0.2, all 61,279 pruned LFVs and 50,476 pruned RVs were extracted from chromosomes 1 and 2 to be tested. We conducted a single SNP analysis by the score test on each CV. We scanned the RVs with 10092 overlapping sliding windows (with window size 20 and moving step 5) by the T1 and Fp tests implemented in software SCORE-Seq developed by Lin and Tang (2011). Both the T1 and Fp tests belong to the class of the burden tests, assessing the aggregated effects of a group of RVs (i.e. multiple RVs inside a sliding window here). Specifically, the T1 test only includes the RVs with MAF < 0.01 to be tested, while the T5 test only includes those with MAF < 0.05; the Fp test gives each RV j a weight $1/\sqrt{f_j(1-f_j)}$, where f_j is a stabilized estimate of the MAF for RV j. The phenotypes were simulated independent of any SNVs, but solely related to ethnic subgroups to create population stratification.

Since the resampling method is computationally intensive, and as far as we observed, asymptotic p-values and resampling-based p-values were close in a few examples in this study, we only used asymptotic p-values. At the nominal significance level 0.05, the Type I error rate was estimated as the proportion of the test with a p-value less than 0.05 with single run over the set of the SNVs to be tested, as the simulated phenotypes were not associated with any SNVs to be tested. The inflation factor, λ, was defined as the ratio of the median of the χ² statistics corresponding to the observed p-values and that of the expected ones under the null hypothesis of no association, as proposed in genomic control (Devlin and Roeder, 2004); we used R package gap for its calculation.

Simulation of binary traits

To assess the performance of PCs constructed by SDR or PCA in association testing, we first designed three case-control studies with population structures as the following: we assigned different subgroups as “cases” and the rest as “controls”, as summarized in Table 3. The presence of population stratification was expected given that the MAFs of some SNVs varied among the subgroups. At the same time, due to the arbitrary assignments of the “disease” status, there should be no association between any SNV and the “disease” after a proper adjustment for population stratification. Hence, the above simulation set-ups were used to investigate how well various PCs could control Type I error rates and λ’s in association testing.

Table 3.

Simulation set-ups with binary traits.

Set-up	Cases	Controls	all samples #Cases/#Controls	w/o AMRs #Cases/#Controls
1	CEU, FIN, MXL, PUR, LWK, ASW	GBR, TSI, PUR2, YRI	239/218	217/213
2	CEU, TSI, FIN, PUR, ASW	GBR, MXL, YRI, LWK, PUR2	247/210	242/188
3	CEU, TSI, ASW	GBR, FIN, MXL, YRI, LWK, PUR/2	206/251	206/224

Simulation of quantitative traits with a local non-genetic risk

As in Mathieson and McVean (2012), we were also interested in investigating how PCs could control inflations caused by spatially structured populations induced by a local non-genetic risk. Specifically, we looked into the scenarios where only a neighborhood area endured a high environmental risk factor. To mimic the well-known correspondence between top PCs and geographical locations, we used the top two PCs constructed by PCA based on 10000 pruned CVs as the location coordinates and chose a medium or small region to have a high non-genetic risk. Two such local regions were selected: one with 65 out of 78 YRI samples to form the risk region R1, and the other with 10 out of 24 ASW samples to form R2 (Figure 1).

Figure 1.

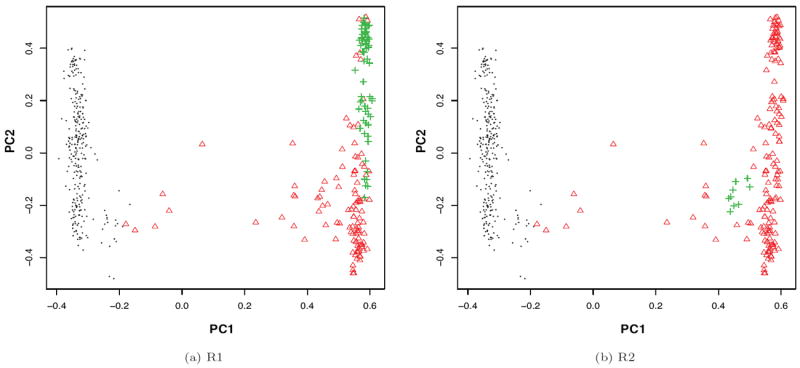
Two local risk regions R1 and R2 (in (green) crosses) represented by the top two PCs of PCA. EURs are in (black) dots and AFRs are in (red) triangles.

The trait y_i for subject i was simulated as y_i = μ_i + ε_i, where ε_i ~ N (0, 1) and μ_i was the non-genetic risk. We used a so-called “square risk” such that only the samples in the risk region suffered from the elevated environmental risk: μ_i = 10 for any sample i in the risk region, and μ_i = 0 otherwise. We used a large μ_i = 10 with a strong confounding effect to better demonstrate possible performance differences among different methods. We obtained similar results with a smaller μ_i = 5 for both R1 and R2, and with μ_i = 2 for R1; with μ_i = 2, there were no noticeable confounding effects and no inflations for R2 due to the small effect size on the small region.

Results

Population structure

We first looked at Wright’s Fst statistic (Wright, 1984) calculated in software EIGENSTRAT (Price et al., 2006; Patterson et al., 2006) to assess the genetic differences among the subgroups. The software was downloadable at http://www.hsph.harvard.edu/faculty/alkes-price/software/.

Since Mathieson and McVean (2012) showed by simulations that Fst statistics varied dramatically when calculated with SNVs of different MAFs, we calculated Fst statistics based on all pruned variants, all pruned CVs and all pruned RVs (Supplementary Tables 1-3). We noticed that Fst statistics based on all pruned variants were very similar to those based on all pruned CVs, but quite different from those based on the pruned RVs. The Fst statistics from the latter were much smaller than those of the former two, perhaps suggesting the less informativeness of the RVs. Due to the small sample size, the Fst statistic between PUR and PUR2 was negative.

Given the small genetic difference between CEU and GBR subgroups with their Fst statistic as small as 0.004 (based on all pruned variants), one might wonder whether they could be treated as a homogeneous population without causing any problem. We tested all the pruned CVs on chromosomes 1 and 2 between the two subgroups by the score test (Figure 2). If indeed there was no genetic difference between the two subgroups, we would expect to have a rejection rate of 0.05 and an inflation factor around 1. In contrast, we had an inflated rejection rate of 0.074 and an estimated inflation factor of 1.427, indicating the presence of population stratification for these two genetically similar subgroups. Furthermore, an adjustment with the top 5 PCs of SDR based on all CVs reduced the inflation factor to 1.041. These results suggested that CEU and GBR samples were still genetically different enough to warrant a careful controlling for population stratification, and importantly the population stratification could be largely controlled by using a few top PCs.

Figure 2.

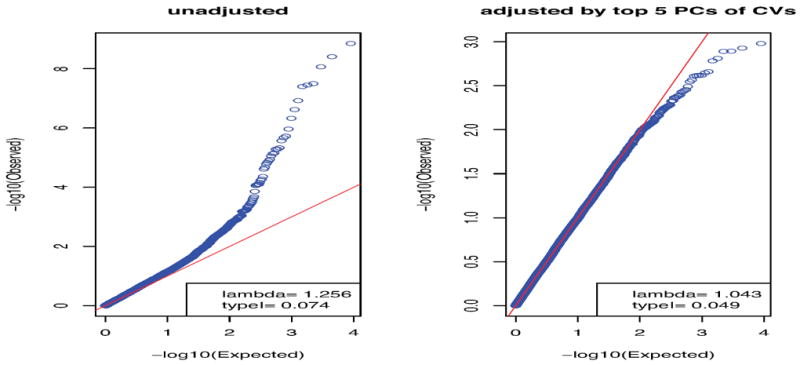
Q-Q plots of the p-values for the score test in the simulated case-control study where CEUs are “cases” and GBRs are “controls”.

Pairwise PC-plots for PCA and SDR

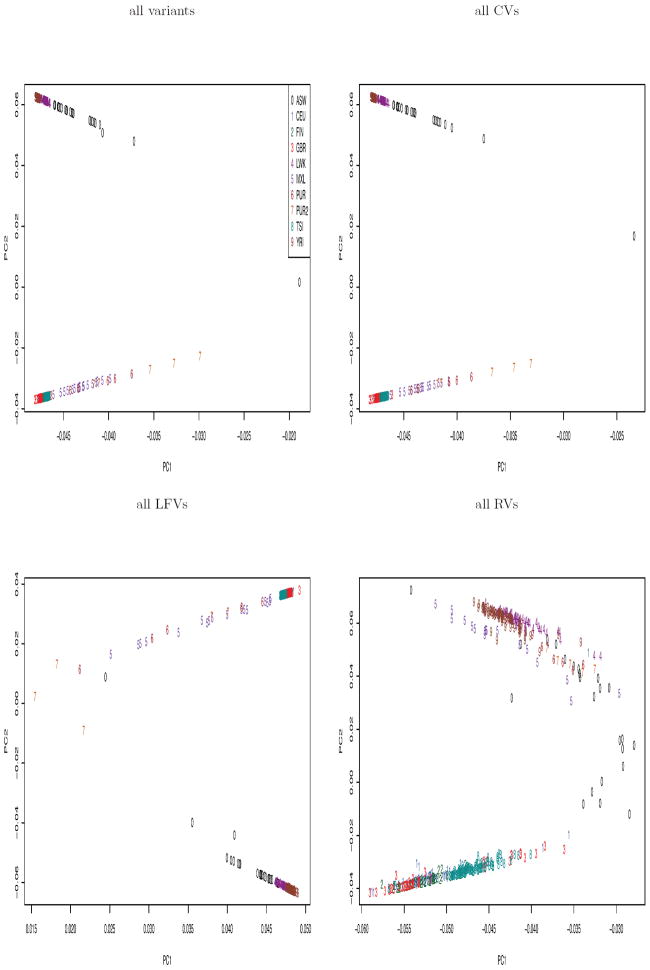
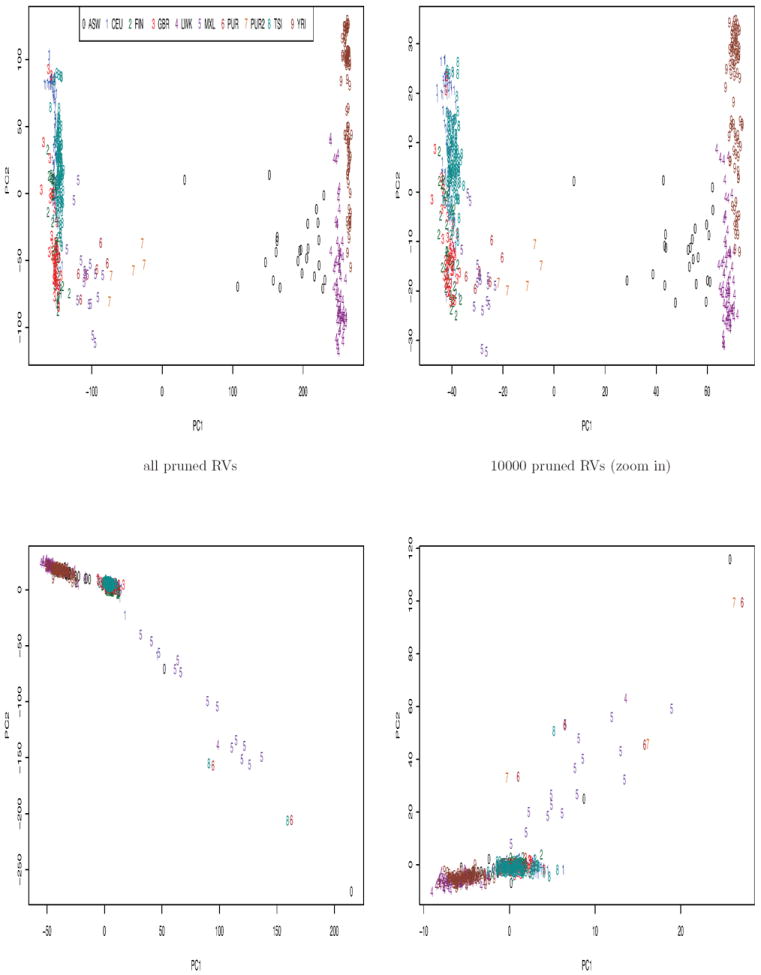
To visualize the population structure, we examined the scatter plots of a few top PCs of PCA and SDR. First we look at SDR. The top two PCs based on any type of variants could successfully separate the two continental groups, EURs and AFRs (Figure 3). It is also not difficult to notice the similarity between the plots using all variants and using all CVs. This was probably due to that the number of CVs was 3~4 times as large as that of LFVs or of RVs. Based on all variants and all CVs, the subgroups of AFRs were also generally distinguishable.

Figure 3.

The top 2 PCs of SDR.

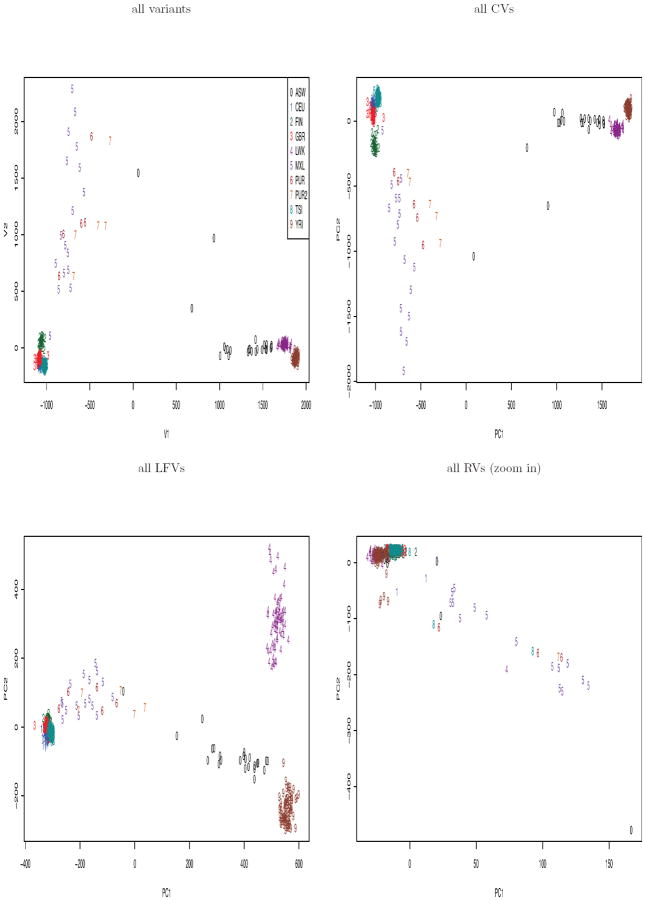
The scatter plots of PCs of PCA (Figure 4) appear to show different patterns from those of SDR. While the second PC of SDR separated continental groups, the 1st PC of PCA separated them. The top 2 PCs based on all variants were again very similar to those of all CVs. The subgroups of AFRs were separable by the PCs of all variants, all CVs or all LFVs. However, based on the PCs of all RVs we were not able to differentiate any subgroups; the top 2 PCs separated out two outliers (PURs) from the main body of other samples (Suppl Figure 6). This confirms that PCA may be heavily influenced by outliers. The pairwise plots of the 3rd and 4th PCs (i.e. PC3 and PC4) constructed by SDR or PCA are included in the supplementary material (Suppl Figures 1 and 2).

Figure 4.

The top 2 PCs of PCA.

We were interested in seeing whether excluding the AMRs would improve the performance of PCs since the AMRs appeared different from other EUR and AFR subgroups. The plots without AMRs are shown in Suppl Figures 3 and 4. Excluding the AMRs barely changed the pairwise plots of the top 2 PCs of either SDR or PCA as it did not help differentiate the EUR subgroups. This might not be surprising according to Patterson et al. (2006); they discussed that adding an admixed population will not change the significant number of PCs. In our case, considering AMRs as admixed American samples founded by Europeans, native Americans and some other ancestry groups, these samples had coordinates joining the centers of the EURs and other founding populations. In other words, with or without the AMRs, the significant number of axes of variation stayed the same. This situation differed from that in Lee et al. (2009), in which it was shown that in a dataset of 580 Europeans, all self-identified as Italians and British, adding 1 African American, 1 East Asian, 1 Indian and 1 Mexican sample had a great impact on the top 4 PCs of PCA.

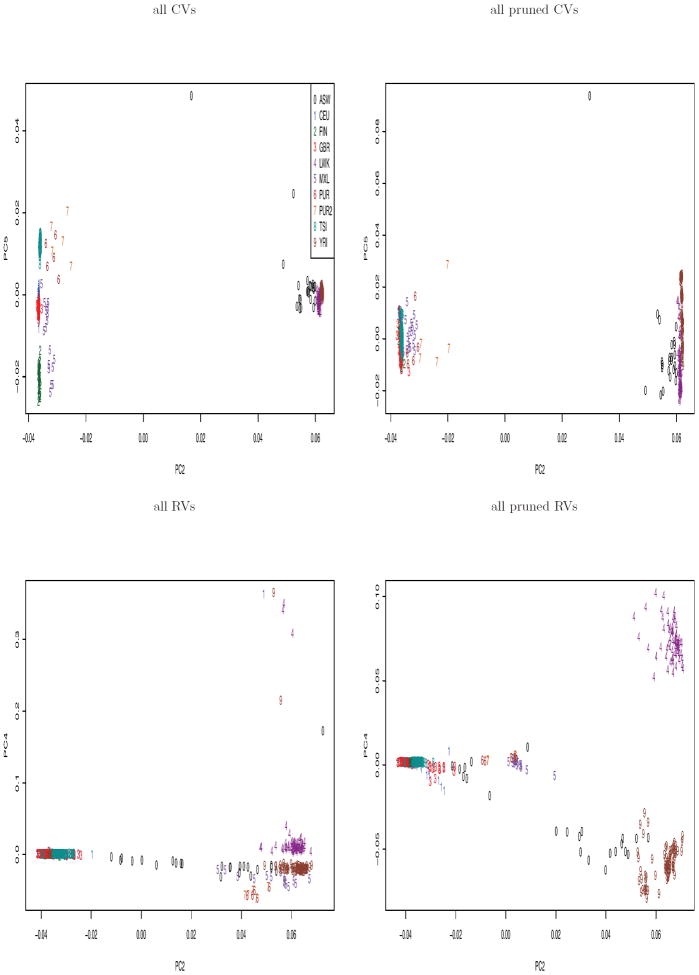
As the 2nd PC of SDR accounted for the variation between continental groups, we projected the data onto the panel of the 2nd and other PCs in order to find the best visualization of the subgroups by a pairwise PC plot. Figure 5 shows that with the 2nd and 5th PCs of SDR based on all CVs, we could almost separate all the subgroups except CEUs and GBRs. But based on all pruned CVs, all RVs or all pruned RVs, EUR subgroups were still mixed together.

Figure 5.

The subgroups represented by two PCs of SDR based on all CVs, all pruned CVs, all RVs and all pruned RVs.

It is suggested that instead of using all variants, we should prune variants to infer the ancestry information, as it was claimed that linkage disequilibrium (LD) “will seriously distort the eigenvector/eigenvalue structure” and thus result in misleading PCs (Patterson et al., 2006), though we could not find any theoretical justification for such a claim. It is also common to randomly select a large number of, e.g. 10000, pruned variants to construct PCs for its computational convenience. We show a comparison among the top 2 PCs of PCA based on all pruned CVs, 10000 pruned CVs, all pruned RVs or 10000 pruned RVs (Figure 6); a comparison of PCs of SDR is shown in Suppl Figure 5. We notice that the plot of the top 2 PCs based on all pruned CVs (or RVs) resembled that of 10000 pruned CVs (or RVs); however, there might be differences in other top PCs.

Figure 6.

Comparison of the top 2 PCs of PCA based on all (or 1000) pruned CVs (or RVs).

In summary, the continental groups were generally differentiable by a few top PCs of either SDR or PCA. With a few top PCs of PCA or SDR based on all variants, all CVs or all LFVs, the subgroups of AFRs were scattered apart. Even better, most samples represented by the top PCs of SDR based on all CVs could be divided into separate subgroups. However, the top PCs based on RVs were weaker in separating the subgroups.

Clustering analysis

Since it is difficult to visualize high-dimensional scatter plots, we applied Gaussian model-based cluster analysis (Banfield and Raftery, 1993) to the top 25 PCs to see whether we could reach the same conclusions as before.

Due to the importance of a specified number of clusters in clustering analysis, we first studied how the RI and aRI changed with the number of clusters (Suppl Figure 7). This allowed us to choose the cluster number to achieve the best separation of the samples. Suppl Figure 7 shows that based on all variants, all LFVs and all RVs, the maximum (a)RI values of clustering based on the top 25 PCs of SDR outperformed those of PCA. But based on all CVs, PCs of SDR and PCA performed equally well. Overall, the (a)RI based on all variants and all CVs were higher than those based on all LFVs and all RVs.

Table 4 shows the results with the optimal number of clusters (giving the largest RI), and with 10 clusters, which was the number of the true subgroups. The highest RI (0.957) and aRI (0.830) with all samples included were obtained using the PCs of SDR based on all variants at 8 clusters. It was followed by clustering using the PCs of SDR based on all CVs (RI=0.953 and aRI=0.805) at 10 clusters. The PCs of PCA based on all CVs also did a good job. The PCs of SDR based on the pruned RVs achieved the 4th highest (a)RI (RI=0.941 and aRI=0.777). After excluding the AMRs (Suppl Table 4), the best clustering results were still obtained when using the top PCs of SDR with all variants (RI=0.963 and aRI=0.865) or all CVs (RI=0.959 and aRI=0.842).

Table 4.

Clustering results with the top 25 PCs for all samples.

		w/o pruning				with pruning				10000 pruned
		all	CVs	LFVs	RVs	all	CVs	LFVs	RVs	all	CVs	LFVs	RVs
SDR	best cluster #	8	10	9	10	13	17	14.	7	10	26	28	15
	best RI	0.957	0.953	0.928	0.889	0.907	0.876	0.901	0.941	0.891	0.880	0.889	0.897
	best aRI	0.830	0.805	0.719	0.532	0.554	0.383	0.510	0.777	0.526	0.348	0.421	0.562
	RI at 10 clusters	0.947	0.953	0.917	0.889	0.888	0.863	0.882	0.892	0.891	0.849	0.836	0.836
	aRI at 10 clusters	0.776	0.805	0.662	0.532	0.535	0.438	0.480	0.578	0.526	0.382	0.442	0.511
PCA	best cluster #	13	8	22	6	15	12	15	23	8	9	16	13
	best RI	0.929	0.947	0.900	0.755	0.888	0.890	0.897	0.850	0.904	0.917	0.888	0.828
	best aRI	0.675	0.803	0.508	0.404	0.435	0.474	0.479	0.394	0.629	0.643	0.467	0.375
	RI at 10 clusters	0.925	0.931	0.884	0.730	0.879	0.869	0.881	0.832	0.881	0.914	0.868	0.822
	aRI at 10 clusters	0.682	0.698	0.558	0.312	0.478	0.432	0.471	0.376	0.502	0.620	0.464	0.435

In conclusion, in agreement with the earlier visual inspection of the PC plots, the best clustering results were obtained by using the top PCs of SDR with all variants or with all CVs. These two types of variants were anticipated to be able to adjust for population stratification. The results also confirmed that we could not perfectly estimate every sample’s subgroup identity based on the top 25 PCs of the whole-genome data.

Association Testing

Binary traits and CVs

We started with controlling population stratification in testing CVs. In general λ ≤ 1.05 was the recommended criterion to determine that there was no population stratification (Price et al., 2010). However, due to the relatively small sample size and possibly correlated variants (and thus correlated p-values), here we would use a less restrictive criterion of λ ≤ 1.15. Across all three simulation set-ups with all samples included (Table 5, Suppl Tables 7-11), the best adjustments were obtained by using the top 15 PCs of SDR based on all variants, all CVs and all pruned CVs. For example, in simulation set-up 2 (Table 5), without adjustment, the Type I error rate was far beyond the nominal level 0.05 while the inflation factor λ was as high as 23.755. After adjusted with a few top PCs, the Type I error rates and λ were much reduced. With the top 10 PCs of SDR based on all variants, we obtained Type I error 0.066 and λ 1.126; with the top 15 PCs of SDR based on all CVs, we reduced Type I error further to 0.064 and λ to 1.098; with the PCs based on the pruned CVs, of either SDR or PCA, the Type I error was about 0.06 and λ was about 1.166. However, adjusting with 25 PCs might give worse results, which was probably related to the small sample size issue to be discussed later. With the AMR samples excluded (Supple Table 7), the results were similar. Overall, the three types of PCs named above – the PCs of SDR based on all variants, all CVs or all pruned CVs were the best performers.

Table 5.

Results of association testing on CVs with a binary trait in simulation set-up 2.

		#PCs	w/o pruning				with pruning				10000 pruned
			all	CVs	LFVs	RVs	all	CVs	LFVs	RVs	all	CVs	LFVs	RVs
Type I	SDR	0	0.677	0.677	0.677	0.677	0.677	0.677	0.677	0.677	0.677	0.677	0.677	0.677
		10	0.066	0.069	0.092	0.094	0.077	0.077	0.093	0.093	0.083	0.099	0.089	0.102
		15	0.069	0.064	0.091	0.097	0.086	0.066	0.097	0.097	0.092	0.092	0.092	0.102
		20	0.068	0.064	0.086	0.101	0.090	0.079	0.084	0.084	0.091	0.078	0.097	0.102
		25	0.086	0.066	0.088	0.103	0.083	0.100	0.125	0.125	0.093	0.092	0.098	0.105
	PCA	10	0.083	0.084	0.085	0.088	0.083	0.087	0.081	0.081	0.088	0.084	0.080	0.091
		15	0.090	0.070	0.090	0.096	0.094	0.070	0.090	0.090	0.085	0.074	0.083	0.092
		20	0.092	0.070	0.093	0.103	0.098	0.062	0.089	0.089	0.088	0.073	0.089	0.093
		25	0.094	0.077	0.095	0.102	0.101	0.081	0.101	0.101	0.087	0.080	0.090	0.097
λ	SDR	0	23.755	23.755	23.755	23.755	23.755	23.755	23.755	23.755	23.755	23.755	23.755	23.755
		10	1.126	1.136	1.302	1.349	1.225	1.205	1.331	1.331	1.307	1.410	1.304	1.414
		15	1.164	1.098	1.319	1.391	1.280	1.168	1.376	1.376	1.383	1.355	1.360	1.426
		20	1.174	1.150	1.312	1.434	1.315	1.255	1.310	1.310	1.290	1.233	1.440	1.427
		25	1.295	1.118	1.320	1.463	1.324	1.419	1.663	1.663	1.361	1.350	1.453	1.447
	PCA	10	1.318	1.340	1.325	1.273	1.309	1.362	1.310	1.310	1.361	1.350	1.283	1.323
		15	1.308	1.167	1.317	1.347	1.372	1.216	1.374	1.374	1.297	1.276	1.327	1.324
		20	1.360	1.210	1.368	1.443	1.402	1.166	1.363	1.363	1.340	1.241	1.375	1.357
		25	1.382	1.225	1.380	1.466	1.424	1.309	1.452	1.452	1.325	1.244	1.403	1.370

Suppl Figure 8 shows the Q-Q plots of the p-values of the tests with or without adjustment by the top PCs of SDR in all three simulation set-ups. We could see that without adjustment, the p-values were far above the 45 degree identity line, while after adjustment with SDR, the p-values were almost uniformly distributed along the identity line. The top PCs of SDR based on all variants, all CVs or all pruned CVs consistently well controlled inflations due to population stratification across all three simulation set-ups.

One interesting observation was that, while the PCs of SDR based on the pruned RVs achieved higher (a)RI than those based on the pruned CVs in clustering analysis, the former ones could not, but the latter could, effectively control Type I errors in association testing. To explore the reasons for this discrepancy, we first compared the clustering results by using the top PCs of SDR based on the pruned CVs or the pruned RVs (Suppl Tables 4-5). However, both mis-classified several subgroups such that we could not determine which type of variants yielded a higher accuracy. Next we fitted a logistic regression model on the simulated disease status (in simulation set-up 2) against the top 25 PCs of SDR and plotted the predicted probability of each sample’s having disease versus his/her subgroup membership (Figure 7). When we used the PCs based on the pruned RVs, the predicted probabilities of having disease for both CEU and GBR samples were close to 1, while in fact all the GBRs were assigned to be controls. But when we used the PCs based on the CVs or the pruned CVs, in agreement to the truth, the predicted probabilities of CEUs were close to 1 and those of GBRs were close to 0. Furthermore, with the PCs of all CVs or the pruned CVs, we could even separate the 5 PUR samples and 5 PUR2 samples. These results indicated that with the PCs of SDR based on the pruned RVs, we could not differentiate GBRs from CEUs, but by PCs of all CVs or the pruned CVs we could largely distinguish the two genetically similar subgroups.

Figure 7.

Distributions of the estimated probabilities of having disease for subjects in each subgroup based on the top 25 PCs of SDR in simulation set-up 2. The subgroups marked in red are cases.

Binary traits and RVs/LFVs

To investigate controlling population stratification when testing variants with lower MAFs, we scanned all the pruned RVs (or all the pruned LFVs) on chromosomes 1 and 2 with sliding windows using the T1 (or T5) and Fp tests (Table 6 and Suppl Tables 12-16).

Table 6.

Results of association testing on RVs with a binary trait in simulation set-up 2.

		#PCs	Test	w/o pruning				with pruning				10000 pruned
				all	CV	LFVs	RVs	all	CVs	LFVs	RVs	all	CVs	LFVs	RVs
Type I	SDR	0	T1	0.417	0.417	0.417	0.417	0.417	0.417	0.417	0.417	0.417	0.417	0.417	0.417
			Fp	0.392	0.392	0.392	0.392	0.392	0.392	0.392	0.392	0.392	0.392	0.392	0.392
		10	T1	0.040	0.044	0.058	0.071	0.065	0.047	0.076	0.092	0.066	0.060	0.076	0.112
			Fp	0.041	0.045	0.058	0.072	0.063	0.048	0.074	0.094	0.066	0.059	0.074	0.111
		25	T1	0.087	0.064	0.071	0.090	0.074	0.081	0.146	0.123	0.071	0.066	0.075	0.113
			Fp	0.087	0.066	0.071	0.088	0.073	0.082	0.145	0.120	0.074	0.069	0.075	0.116
	PCA	10	T1	0.114	0.114	0.124	0.099	0.101	0.112	0.077	0.068	0.138	0.111	0.079	0.091
			Fp	0.116	0.114	0.126	0.103	0.101	0.113	0.078	0.065	0.141	0.115	0.078	0.091
		25	T1	0.066	0.098	0.072	0.063	0.074	0.120	0.098	0.066	0.085	0.125	0.084	0.074
			Fp	0.065	0.097	0.071	0.063	0.075	0.124	0.099	0.063	0.085	0.131	0.085	0.071
λ	SDR	0	T1	6.114	6.114	6.114	6.114	6.114	6.114	6.114	6.114	6.114	6.114	6.114	6.114
			Fp	5.665	5.665	5.665	5.665	5.665	5.665	5.665	5.665	5.665	5.665	5.665	5.665
		10	T1	1.009	1.025	1.122	1.246	1.161	0.988	1.297	1.470	1.237	1.098	1.309	1.669
			Fp	1.004	1.006	1.137	1.253	1.187	0.986	1.289	1.472	1.222	1.107	1.308	1.705
		25	T1	1.463	1.206	1.214	1.431	1.293	1.336	1.841	1.707	1.257	1.147	1.228	1.693
			Fp	1.459	1.198	1.202	1.440	1.284	1.334	1.844	1.731	1.212	1.170	1.238	1.701
	PCA	10	T1	1.699	1.708	1.854	1.530	1.491	1.656	1.314	1.205	2.002	1.610	1.311	1.454
			Fp	1.774	1.763	1.892	1.556	1.525	1.687	1.347	1.192	2.027	1.690	1.339	1.479
		25	T1	1.191	1.482	1.342	1.199	1.230	1.624	1.456	1.213	1.350	1.781	1.308	1.254
			Fp	1.218	1.487	1.368	1.199	1.241	1.623	1.465	1.191	1.343	1.786	1.305	1.276

Across all three simulation set-ups, the top PCs of SDR based on all variants, all CVs or all pruned CVs could generally control the Type I error rates around 0.06 and λ’s below 1.15 as in testing CVs. For example, in Table 6, with the top 10 PCs of all variants the Type I error of the T1 test was 0.040 and λ=1.009; with the top 10 PCs of all CVs the Type I error of the T1 test was 0.044 and λ = 1.025, while with the top 10 PCs of the pruned CVs the Type I error was 0.047 and λ=0.988. However, different from testing CVs, none of the top PCs of PCA could effectively control the inflation factor below 1.15 when testing RVs.

In conclusion, our simulation results demonstrated that a few top PCs based on all variants, all CVs or all pruned CVs constructed by SDR could generally control population stratification in testing multiple RVs or multiple LFVs.

Testing RVs in the presence of a local non-genetic risks

Population stratification can be a more severe issue in association testing for RVs when the samples collected were exposed to some localized environmental risks, as discussed in Mathieson and McVean (2011). One of their main observations was that, when the non-genetic risk region was small, the inflation of Type I error could be controlled for testing CVs, but not for RVs, after adjusting with a few top PCs of PCA. Since they used simulated sequencing data while acknowledging the need to use real sequencing data, we addressed the problem with real sequencing data. As shown in Suppl Tables 17-21, the same phenomena were confirmed. In summary, in the presence of a local non-genetic risk, although a few top PCs of any type of variants without pruning could control the inflation effectively when testing CVs, it was not the case when testing RVs. Both SDR and PCA, regardless of the sets and types of the variants used, could largely, but not satisfactorily, control the inflation; nevertheless, we found that a few top PCs of SDR based on all variants or all CVs were among the best candidates, while the top PCs of SDR based on all RVs sometimes performed well or even slightly better, though none of them controlled the inflation satisfactorily.

Why not only RVs

Based on our association testing results, in most situations, a few top PCs based on CVs performed better than those based on RVs in SDR for controlling population stratification. This might be surprising given that RVs are expected to be more recent and population-specific. Babron et al. (2012) and Moore et al. (2012) both pointed out that RVs were more likely to cluster in a few subpopulations than to be distributed uniformly across all subpopulations.

As there were 457 samples in total, we could observe at most 9 copies of the minor allele for any RV, meaning that the minor allele of the RV could appear in at most 9 subgroups across all the samples. 705 RVs were singletons, which were population-specific but could also have resulted from sequencing errors. Table 7 shows the distribution of the minor alleles of all RVs across the subgroups from all the 457 samples. The proportion of the RVs whose minor alleles were present in varying numbers of the subgroups are reported. We see only a small proportion of the RVs with their minor alleles appearing in 1 or 2 subgroups. For example, for the RVs with 6 copies of the minor allele, only 7.8% of them appeared in only 1 or 2 subgroups while the rest appeared in 3-6 subgroups. Albeit inconclusive, these results might suggest that most of the RVs were not population-specific. Next, we applied Fisher’s exact test (as implemented in R function fisher.test) to test whether the minor allele of each RV was randomly distributed across (or independent of) the subgroups at the significance level 0.05. The results are given in Table 7; in total, only 25.62% of 68,434 RVs were significant with their minor alleles distributed subgroup-specifically.

Table 7.

Distribution of the RVs with minor alleles present in a given number of the subgroups. In the first 9 rows, the number in cell (i, j) is the proportion of the RVs each with j copies of its minor allele and present in i subgroups; the last two rows give the total number of RVs and the proportion of significant ones by Fisher’s exact test.

# of subgroups	# of the minor allele across the 457 samples
	1	2	3	4	5	6	7	8	9
1	1.0000	0.0225	0.0116	0.0056	0.0026	0.0021	0.0010	0.0043	0.0004
2		0.9775	0.4442	0.2426	0.1399	0.0764	0.0539	0.0368	0.0276
3			0.5441	0.5197	0.4478	0.3801	0.2962	0.2527	0.2161
4				0.2321	0.3430	0.3972	0.4343	0.4031	0.3938
5					0.0667	0.1293	0.1751	0.2290	0.2435
6						0.0149	0.0362	0.0635	0.0942
7							0.0033	0.0103	0.0230
8								0.0003	0.0013
9									0.0000
# of RVs	705	9653	9972	9234	8785	8258	7792	7197	6838
prop. of sig. RVs	0.000	0.111	0.163	0.222	0.230	0.290	0.314	0.379	0.442

As a comparison, we also tested the random distribution across the 10 subgroups of the minor alleles of CVs or of LFVs in chromosome 1 (with R function prop.test). In total, there were 82.53% of 478,208 CVs shown to be significant (p-value<0.05) while 74.28% of 146,350 LFVs significant. After pruning CVs and LFVs respectively, there were 79.25% out of 12,269 pruned CVs significant and 72.40% out of 32,080 LFVs significant. Although Fisher’s exact test could be conservative, these results lent some support for our observation that PCs of CVs were more capable of adjusting for population stratification than those of RVs. In summary, we found that more CVs and LFVs were subgroup-specific, which, in combination with a RV’s less informativeness due to its extremely low MAF, offers a preliminary explanation to better performance of CVs when used to construct PCs to adjust for population stratification than that of RVs.

Conclusions and Discussions

As a continuation of our previous study on adjusting for population stratification at the continental group level (Zhang et al., 2013), we used the same whole-genome sequencing dataset from the 1000 Genomes Project to study the issue in a finer scale. We were interested in investigating what types or sets of variants and what dimension reduction method, SDR or PCA, could best find the axes of genetic variations among multiple continental subgroups. We first used the Fst statistic and a few top PCs to study population structure. We also confirmed that even the genetically similar subgroups, like CEU and GBR samples, could still induce population stratification in association testing. We have also observed that, with or without the AMR samples from admixed populations, the top PCs barely changed. Our observations in these exploratory analyses were later confirmed in clustering analysis and association testing. The main conclusions are the following. First, in association testing of CVs, RVs or LFVs, we found that a few top PCs based on all variants, all CVs or all pruned CVs constructed by SDR could consistently control the Type I error around the nominal 0.05 level, and reduce the inflation factor, λ, to around 1, in most situations. The difficulty in perfectly uncovering ethnic subgroups did not appear to notably impair the effectiveness of a few top PCs in adjusting for population stratification. Second, in the presence of a local non-genetic risk (i.e. spatially structured populations), while it was rather easy to control inflations when testing CVs, it was much harder when testing RVs. For RVs, using a few top PCs of SDR based all variants or all CVs could be largely, but not satisfactorily, effective; a few top PCs of SDR, but not of PCA, based on all RVs also showed good performance in controlling inflations. Third, our study confirmed that SDR was more robust to outliers and noises, producing PCs more informative for subgroups than PCA. This led to better performance in both association testing and clustering. The difference was the largest and thus most clearly seen when RVs were used to construct PCs. In particular, it is noted that when testing RVs or LFVs, none of the top PCs of PCA were sufficient to control inflated false positives. Lastly, we observed that there was a larger proportion of CVs or of LFVs significantly distributed non-randomly across the subgroups than that of RVs, offering an explanation of why we witnessed better adjustment performance of the PCs based on CVs than that on RVs. A similar conclusion was reached in a recent study with a real sequencing dataset (Zhang and Pan, in press).

There are some limitations in our study. First, we used a low-coverage sequencing dataset, hence the conclusions drawn here may or may not be applicable to high-coverage sequencing data. For example, high-coverage sequencing is expected to yield data of higher quality, especially with RVs, so that there may be more subgroup-specific RVs, which may lead to different conclusions. Second, although the dataset we used is one of the largest sequencing datasets available nowadays with multiple population subgroups, the sample size is still relatively small, especially at the subgroup level. As a consequence, we only considered some more extreme simulation set-ups with each whole subgroup belonging to one of the case and control groups. In fact, we could not randomly assign any subgroup to be cases or controls because there might be a complete separation between cases and controls. For example, in the simplest case, if we had all the EUR subgroups as the cases and all AFRs as the controls, then the second PC of SDR could perfectly separate the cases from the controls, leading to non-existence of the MLE and a convergence problem when fitting the logistic regression model. One remedy was, as we did here, to assign inseparable subgroups as cases and controls respectively. We also considered some less extreme set-ups, in which each subgroup was assigned a different probability for its subjects’ being in the case group (results not shown), from which we reached the same conclusions, though the performance difference between SDR and PCA appeared smaller. Another consequence of the small sample size was possibly inflated Type I error rates (and inflation factor) when an increasing number of PCs were included in a logistic regression model (see Table 5). This phenomenon was also shown in Bouaziz et al., 2011: when the authors included 20 PCs in the logistic regression to adjust for population stratification, the Type I error was around the 5% level; however, when 5 more PCs were added, the estimated Type I error increased to the upper bound of the 95% confidence interval. Note that this problem also appeared in linear regression with quantitative traits, albeit in a less severe way. More generally, this important question is related to that of how to determine the number of the top PCs to use for adjusting for population stratification. Third, in this study we considered association testing on only single CVs or only multiple RVs (or LFVs). It would be of interest to check how population stratification could be controlled when testing both multiple CVs and multiple RVs at the same time. Finally, it is also most important to assess statistical power when adjusting for population stratification. As shown by Zhang et al. (2013) and others, there could be power loss with an adjustment by a few top PCs of PCA. One would wonder to what extent this could happen when using a few top PCs of SDR with all variants, all CVs or all RVs.