Abstract
Background and Aims
The growth of crops in a mixture is more variable and difficult to predict than that in pure stands. Light partitioning and crop leaf area expansion play prominent roles in explaining this variability. However, in many crops commonly grown in mixtures, including the forage species alfalfa, the sensitivity and relative importance of the physiological responses involved in the light modulation of leaf area expansion are still to be established. This study was designed to assess the relative sensitivity of primary shoot development, branching and individual leaf expansion in alfalfa in response to light availability.
Methods
Two experiments were carried out. The first studied isolated plants to assess the potential development of different shoot types and growth periods. The second consisted of manipulating the intensity of competition for light using a range of canopies in pure and mixed stands at two densities so as to evaluate the relative effects on shoot development, leaf growth, and plant and shoot demography.
Key Results
Shoot development in the absence of light competition was deterministic (constant phyllochrons of 32·5 °Cd and 48·2 °Cd for primary axes and branches, branching probability of 1, constant delay of 1·75 phyllochron before axillary bud burst) and identical irrespective of shoot type and growth/regrowth periods. During light competition experiments, changes in plant development explained most of the plant leaf area variations, with average leaf size contributing to a lesser extent. Branch development and the number of shoots per plant were the leaf area components most affected by light availability. Primary axis development and plant demography were only affected in situations of severe light competition.
Conclusions
Plant leaf area components differed with regard to their sensitivity to light competition. The potential shoot development model presented in this study could serve as a framework to integrate light responses in alfalfa crop models.
Keywords: Medicago sativa, leaf area, light competition, branching, shoot, development, leaf growth, morphogenesis, model
INTRODUCTION
Leaf area largely determines light interception and transpiration in plants (Monteith, 1977). An increase in crop leaf area over time depends on variables at different levels of organization: plant density at the population level; the number of shoots per plant and shoot development at the organism level; and ultimately individual leaf expansion at the organ level (Monteith and Elston, 1983; Ong and Baker, 1985; Varlet-Grancher and Gautier, 1995; Lafarge, 1998). However, all these variables are seldom considered in crop models. Plant density (crops) and shoot/tiller density (perennial forages such as grasses or alfalfa) are often taken as fixed input parameters in the most detailed representations based on an average plant/shoot leaf area expansion (e.g. CERES, Jones et al., 1984; APSIM, Robertson et al., 2002). In many cases, the potential leaf area index (LAI) of a crop is even described directly as a function of time, encompassing the effects of all these variables in the parameters of a growth function (Gosse et al., 1984; Goudriaan and Monteith, 1990; Brisson et al., 2003). Combined with plant responses that modulate leaf area expansion as a function of drought, temperature or nitrogen (Jones et al., 1984; Brisson et al. 2008), these approaches have yielded good estimates of light interception and biomass production in many crops (Boote et al., 1996; Hammer et al., 2002).
In crop mixtures, on the other hand, success has been more limited and much work is still required to predict the LAI dynamics of different species when they interact (Malezieux et al., 2009). Indeed, crop leaf area expansion may differ markedly, at both the plant and canopy levels, between pure and mixed crops (Sinoquet and Cruz, 1993; Nassiri, 1998). One critical point is usually to explain the effects of competition on the population dynamics of plants or shoots (Kiniry and Williams, 1995; Brisson et al., 2004; Soussana and Oliveira Machado, 2000). In particular, account needs to be taken of the effects of light, as this factor is often ignored with respect to leaf area expansion in pure crops (Jones et al., 1984; Brisson et al., 2008).
Light can affect morphogenesis and leaf area expansion, through trophic effects related to the photosynthetic photon flux density (PPFD), and light quality effects (Lötscher and Nösberger, 1997; Tardieu et al., 1999; Gautier et al., 2000; Cookson et al., 2006). At the population level, competition for light commonly induces a size structure of plant populations at high densities (Obeid et al., 1967; Weiner and Thomas, 1986; Gosse et al., 1988) or in populations of subordinate species in mixtures (Weiner, 1985; Louarn et al., 2012a). Self-thinning may occur under severe light competition and modify plant density (Kays and Harper, 1974; Westoby and Howell, 1982), preferentially affecting smaller plants in the population, in which the carbon balance may become negative (Dewar, 1993; Louarn et al., 2012b). At the plant level, total plant leaf area is the consequence of the organogenesis process, controlled by the functioning of meristems and individual leaf growth. The effects of light competition on plant development, and on a reduction of branching in particular, are well established (Deregibus et al., 1985; Kasperbauer and Karlen, 1986; Gautier et al., 1999). However, they are difficult to predict and intimately related to the distribution of light into the canopy and to the location of plant meristems (Holmes and Smith, 1977; Ballaré et al., 1997; Gautier et al., 2000; Evers et al., 2006; Stamm and Kumar, 2010). At the organ level, a reduction in PPFD causes no effect on leaf expansion during the rapid growth period, while the leaf is autotrophic, but considerably reduces the relative expansion rate during early leaf development (Tardieu et al., 1999). On the other hand, modifications to light quality can result in increased leaf size (Varlet-Grancher and Gautier, 1995). In many crops commonly grown in mixtures, including the forage species alfalfa (Medicago sativa L.), the relative sensitivity of these plant responses to light availability, as well as their relative importance to LAI modulation, still need to be established.
Alfalfa–grass mixtures are among the most widespread forage crops in many temperate areas (Fick et al., 1988; Basigalup, 2007). In such communities, alfalfa leaf area expansion has been shown to be the main attribute that explains light interception by the legume component and its biomass production at both the canopy and plant scales (Barillot et al., 2011; Louarn et al., 2012a, b). Alfalfa leaf area components display systematic variations across regrowth cycles in response to temperature and photoperiod (Brown et al., 2005). Light responses are mostly inferred from density experiments in pure stands, where a trade-off between plant density and the number of shoots per plant is usually reported (Cowett and Sprague, 1962, 1963; Mattera et al., 2013), leading to relatively steady shoot density. In mixtures, however, the persistence of the legume is an issue, and such substitutive relationships are not ensured (Jones and Carter, 1989). Density-dependent mortality can lead to a permanent decline of the legume proportion in favour of the companion species. In alfalfa, density-dependent mortality may be related to the plant's ability to maintain shoots with a consistent leaf area (Louarn et al., 2012b). The aspects of plant leaf area (PLA) regulation most affected by light competition may therefore be important traits that could be improved to promote legume persistence in mixtures.
The main objective of this study was therefore to assess the relative sensitivity of the morphogenetic processes of alfalfa involved in PLA expansion (namely primary shoot development, branching and leaf expansion) in response to light availability. The intensity of competition for light was manipulated using a range of canopies in pure stands and in a mixture with tall fescue (Festuca arundinacea Schreb.) at two densities. Growth and regrowth phases were studied during the vegetative period of development. Shoot development in the various situations was analysed with respect to a potential shoot development model established for plants in the absence of competition (isolated plants under non-limiting supplies of water and nutrients).
MATERIALS AND METHODS
Plant materials and growing conditions
The experiments were performed outdoors between April and August in 2009, 2010 and 2012 at the INRA Lusignan research station in France. Alfalfa (Medicago sativa L.) cultivar ‘Orca’ (large stems, erect cultivar) was used for all the studies. The seeds were pre-germinated in the dark at 25 °C for 48 h before being transplanted into pots. All the plants were then grown in individual 1 L pots (5 × 52 cm cylindrical pots at high density; 8 × 21 cm cylindrical pots at low density) filled with a medium that comprised sterile potting mix, sand and brown soil (1:1:1, v/v/v). The pots were ferti-irrigated three times a day with a complete nutrient solution. The nitrogen concentration of the solution (8 mm) was non-limiting and prevented the nodulation of alfalfa roots.
Experiment 1
In 2009 and 2012, a total of 20 isolated plants (i.e. 0·25 m distance between the pots in all directions) were grown to assess the potential development of alfalfa shoots in the absence of light competition. The plants were followed during the initial growth phase from seeds, and during the first regrowth phase (cut back at the mid-bloom stage, to 5 cm above soil level).
Experiment 2
In 2009 and 2010, plants were grown in stands to assess the impact of light competition on shoot and whole-plant growth and development. The plants were cultivated at two densities: low density (LD; 15 cm between plants, 50 plants m−2, about 2 m2 stand) and high density (HD; 5 cm between plants, 460 plants m−2–, about 1 m2 stand). In 2009, the plots consisted of pure alfalfa stands whereas in 2010 they consisted of 50/50 mixtures of alfalfa (M. sativa ‘Orca’) and tall fescue (Festuca arundinacea Schreb. ‘Noria’). Grass plants were also grown in individual pots and ferti-irrigated, so that were competing with alfalfa for light only. In all the stands, the pots were arranged according to a hexagonal lattice, making all plants equidistant within the stand (Harper, 1961; Boffey and Veevers, 1977). In addition, each individual in the mixed stands was surrounded by three of its own species and three of the other species. The plants in each stand were followed during the initial growth phase from seeds, and during the first two regrowth phases (cut at the mid-bloom stage, to 5 cm above soil level).
Meteorological measurements and thermal time calculations
Air temperature (Tm), PPFD and air humidity (RH) data were collected every 30 s, and mean values were calculated and stored every 3600 s in a Datalogger (CR10 Wiring Panel; Campbell Scientific Ltd, Shepshed, Leics., UK). Supplementary Data Table S1 presents the daily average, mean and maximum values for temperature, PPFD and vapour pressure deficit (VPD) observed during the different regrowth periods in expts 1 and 2.
Thermal time was calculated from the daily integration of air temperatures minus the base temperature (Tb):
| (1) |
where TT is thermal time expressed in cumulative degree-days (°Cd; Bonhomme, 2000).
TT is expressed in degree-days, calculated as the sum of the mean daily temperature minus the base temperature (Tb). During this study, the Tb value used depended on the daily average temperature and changed according to the relationships proposed by Brown et al. (2005). Above 15 °C, Tb equalled 5 °C. In between 1 and 15 °C, Tb increased linearly so that Tb was 1 °C at 1 °C and 5 °C at 15 °C.
Nine PPFD sensors were distributed at ground level in each of the studied stands. The ratio of the PPFD between their averaged value and incoming light value enabled calculation of the canopy light interception efficiency (LIE).
Plant measurements
Plant and shoot development
The number of shoots per plant was counted at 5–7 d intervals on 20 plants in expt 1 and on 50 and 30 plants at HD and LD, respectively, in expt 2. Several types of shoots can be distinguished in alfalfa. During the initial growth phase, a primary axis (PA) develops from the seed, and secondary shoots subsequently develop from the axillary buds of cotyledons and PA leaves (Fick et al., 1988). After cutting, two types of shoots can be distinguished as a function of their origin; namely type 2 shoots (T2 for primary axes emerging from buds on the taproot crown) and type 1 shoots (T1 from axillary buds on the stem bases remaining after the previous harvest) during regrowth periods (Leach, 1968; Gosse et al., 1988). The PA, T1 and T2 may present differences in their potential ontogeny (Gosse et al., 1988). A distinction was therefore made between them for our shoot measurements. In expt 1, the numbers of visible leaves per shoot were recorded at 5–7 d intervals for 20 plants on the PA during the initial growth phase, and on two shoots per plant (one T1 and one T2) during regrowth (Supplementary Data Fig. S1). Unfolded leaves were included and counted according to the scoring scale proposed by Maitre et al. (1985). The number of leaves was determined on the main axis (primary leaves) and on each branch (distinction between secondary and tertiary axes) from the second node onwards (corresponding to the first trifoliate leaf on the PA). Branches were referred to as a function of their position on the primary axis, branch B1 corresponding to the axil of the first trifoliate leaf. In expt 2, the same measurements were performed on all the shoots of 20 plants at HD and on 10 plants at LD, the two stages of development corresponding to the dates of magnetic digitization of the plants (see the following section). The rate of leaf appearance was calculated for each axis by linear regression between the time in °Cd and the number of visible leaves. The phyllochron was calculated as the reciprocal of the rate of leaf appearance (RLA−1). The thermal time of budburst of a secondary branch was calculated as the intercept of the line y = 0 with the linear regression between branch leaf number and thermal time accumulated since emergence. A probability Pi of axillary bud burst was calculated for each of the ith node positions on the primary axis by dividing the number of branches actually observed at this position throughout the shoot population studied by the total number of shoots.
Leaf size and plant leaf area
In expt 2, the topological relationships between phytomers and the length of the central leaflet of each phytomer were recorded by 3D magnetic digitization (3Space Fastrak, Polhemus Inc., Colchester, VT, USA) on samples of 20 plants at HD and 10 plants at LD. The pots were moved indoors just before digitization and plants were measured using 3A software (Adam et al., 1999). Two measurement periods were fixed every year, one in the course of the first growth phase (PSG and MSG for the pure stand and mixed stand, respectively), and one at the end of the second regrowth (PSR and MSR for pure stand and mixed stand, respectively). Lateral leaflets sizes (length and width) and central leaflet width were recorded on a sub-sample of phytomers corresponding to the primary leaves of the most developed shoot on each plant. Allometric relationships were built specifically for each plant using these data, considering (1) central leaflet length as a predictor of lateral leaflet length and (2) leaflet length and phytomer position along the stem as predictors of leaflet width. This enabled an estimate of the length and width of the remaining leaflets on each leaf. The precision of leaflet length and width estimated by digitization were checked against manual measurements with a ruler, and proved accurate with no bias [y = 0·98x – 0·01; r2 = 0·94; n = 204; root mean square error (RMSE) = 0·23 cm].
The sub-sample of leaflets used for simultaneous length and width determinations was scanned (Konica Minolta C352/C300, Konica Minolta Sensing, Osaka, Japan) and their surface measured was by image analysis (ImageJ software, http://rsbweb.nih.gov/ij/). An allometric relationship common to all leaflets was found between the leaflet surface and the product of its length and width (surface = 0·732 × length × width, r2 = 0·99; n = 62; RMSE = 0·14 cm2). This relationship was applied to all the leaflets of the digitized plants. The total surface of each plant (PLA) was then calculated as the sum of the surfaces of all its leaflets.
Plant mass distributions and size structure of the study populations
At each harvest during expt 1 (30 plants in 2012) and expt 2 (100 plants at HD and 60 plants at LD), individual above-ground parts of alfalfa plants were collected, dried (48 h at 60 °C) and weighed. The dry mass distribution of plants in each situation was used to assess the degree of inequality of resource partitioning among individuals in the population. In addition, 100 seeds were weighed to estimate an initial value of size inequality. We used the Gini coefficient (G), which is a measure of the relative mean difference (i.e. the arithmetic average of differences between all pairs of individuals; Sen, 1973; Weiner and Solbrig, 1984), to perform this estimate:
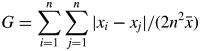 |
(2) |
The G values thus calculated were then multiplied by n/(n – 1) to give unbiased values (G′). These G′ values ranged from 0 (all individuals sharing resources equally) to 1 (all resources captured by a single individual). As light was the only contested resource in these experiments, G′ was used as an indicator of competition intensity among plants in the different populations studied.
Statistical analyses
Statistical analyses were performed using R software (R Development Core Team, 2012). Analyses of variance (ANOVA, aov procedure) were used to test for significant differences between means. Analyses of covariance (ANCOVA, lm procedure) were used to test for the effects of continuous and categorical variables simultaneously and to compare the slopes and intercepts of linear relationships. Data transformation (root square transformation) was applied prior to ANCOVA analyses for variables related through a quadratic relationship (e.g. total number of leaves on branches as a function of time or primary axis development). Two-sample Kolmogorov–Smirnov (KS) tests (ks.test procedure) were used to compare the distributions of shoot size between the density treatments. The null hypothesis of identical distributions was rejected for P-values <0·05.
RESULTS
Potential development of an alfalfa shoot
Primary axis development
Primary axis development reached up to 19·6 ± 0·82 leaves in expt 1–2009 and 25·2 ± 2·06 in expt 1–2012 during the initial growth phase. During the regrowth phase, the number of expanded leaves at the time of the cut was 14·5 ± 0·92 in T2 and 12·3 ± 0·57 in T1. The appearance of leaves on the different shoots during the growth and regrowth phases was linear as a function of TT (Fig. 1). The ANCOVA analyses did not demonstrate any significant differences in the rate of development regarding the different shoot types and growth periods (P > 0·1053, PA in expt 1 and expt 2 for the growth phase; T2 and T1 in expt 1 for the regrowth phase). The phyllochron was 32·54 ± 0·40 °Cd and did not change shortly after the beginning of flowering.
Fig. 1.
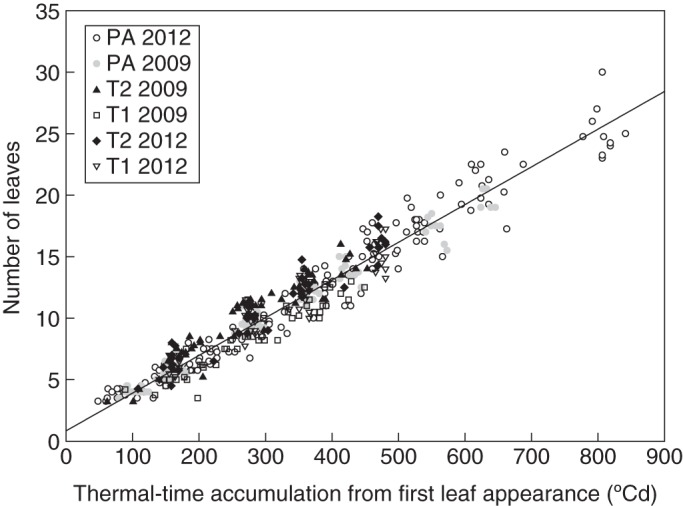
Number of visible primary leaves as a function of thermal time expressed in cumulative degree-days from first leaf appearance during the growth and regrowth phases of expt 1. The regression was estimated for all data on the plot (y = 0·0301x + 1·09, n = 433, r2 = 0·94). PA, primary axis; T1, type 1 axis; T2, type 2 axis.
Probability of branching, delay of budburst and development on secondary axes
Figure 2 shows the increase in the total number of secondary leaves in relation to TT, demonstrating that branch development had a marked effect on the total number of leaves accumulating on a shoot. For instance, the number of secondary leaves was more than five times higher than that of primary leaves at the bloom stage in both years on the shoots of isolated plants. This total number of secondary leaves resulted from the sum of all secondary axes developing at the axil of primary leaves. To determine the number of secondary axes at a given time, we examined the probability and time delay of branching at each position on the primary axis (Fig. 3). At all positions, branching was systematic after a delay (branching probability reached 1), in both the growth and regrowth cycles. The ANCOVAs revealed that the rate of appearance of new branches was the same as that of primary leaf appearance (P < 0·0001) and that there was a constant delay of 1·75 ± 0·15 phyllochrons between primary leaf appearance and its axillary bud burst, irrespective of the position on the shoot (Fig. 3B). The results were the same during both the growth and regrowth cycles (not shown).
Fig. 2.
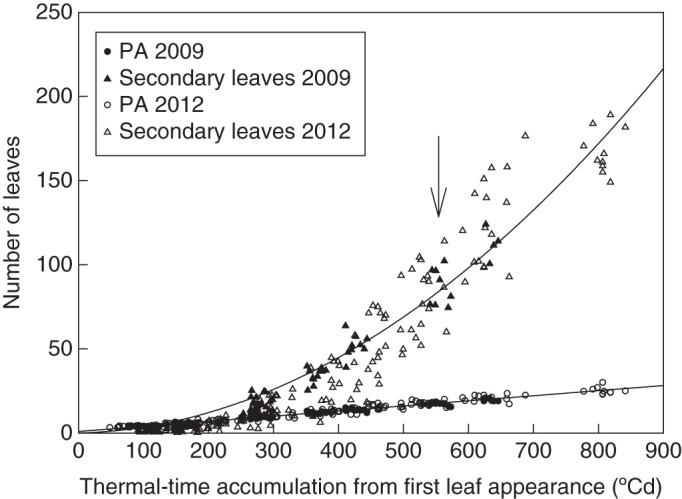
Numbers of primary and total number of secondary leaves as a function of thermal time expressed in cumulative degree-days from first leaf appearance during the growth phases of expt 1. The regressions were estimated for all data on the plot (y = 0·0003x2 – 0·0275x, n = 207, r2 = 0·91 for secondary leaves; same fit as Fig. 1 for primary leaves). The arrow indicates the early bloom stage. PA, primary axis.
Fig. 3.
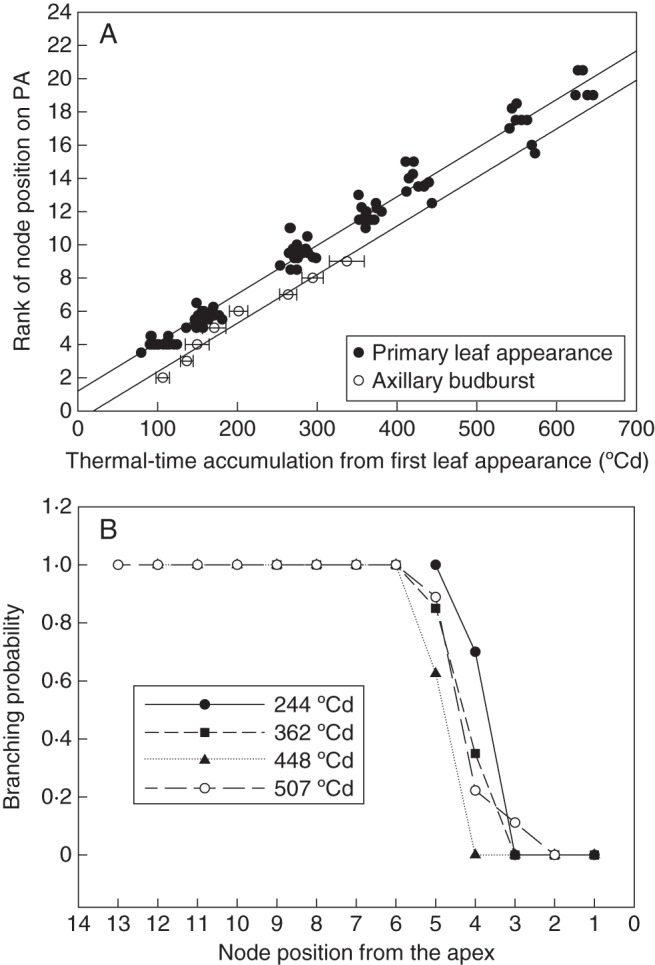
(A) Thermal time of primary leaf appearance and axillary budburst according to node position on the primary axis (PA) and (B) branching probability with respect to nodal position from the apex at four developmental stages for shoots during the growth phase of expt 1. The regressions were estimated for all data on the plot (y = 0·029x – 0·5682, n = 8, r2 = 0·96 for branch budburst; same fit as Fig. 1 for primary leaves).
Secondary axes thus appeared sequentially on the shoots, from B1, located in the node of the first trifoliate leaf, to Bn, on the nth primary leaf. The appearance of leaves on secondary axes was also linear as a function of TT (r2 ranging from 0·85 to 0·90). The rate of development was compared between branches at different positions during expt 1 in 2009 and 2012 (Supplementary Data Fig. S2). The rates of development of branches were always lower than those of the PA (51·68 ± 4·57 °Cd, ANCOVA, P < 0·0001). No significant differences between the phyllochron of the different branches were found (ANCOVA, P > 0·06; on average 48·2 ± 3·38 °Cd), except for B1, which developed more rapidly than all the other branches (P < 0·02). No significant effects of years were found (ANCOVA, P ≥ 0·17).
Modelling of potential shoot development
The results presented above suggest that the potential development of an alfalfa shoot subjected to low competition for light is fairly deterministic (constant phyllochrons, branching probability of 1) and identical irrespective of the origin of its apical meristem (from the seed, T2 taproot bud or T1 axillary bud) and of the year (expt 1 in 2009 and 2012). For the two first branching orders, potential development could be deduced from the phyllochron of the primary axis, a time delay for secondary axis budburst and a single phyllochron for secondary axes. These variables could be used to summarize spatial and temporal variations in leaf appearance on a shoot under non-limiting growing conditions. A simple model of primary and secondary axis development is thus proposed:
| (3) |
| (4) |
| (5) |
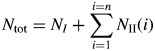 |
(6) |
where a1 represents the phyllochron of the primary axis, a2 the phyllochron of secondary axes, b1 accounts for pre-formed leaves at shoot emergence, db represents the delay of budburst of branches (expressed in number of new leaves which appeared on the primary axis since bearing node appearance), TTbud(i) represents the time of budburst in °Cd of the ith secondary branch, and NI and NII stand for the numbers of primary and secondary leaves, respectively. Such a model can predict over (thermal) time the maximum number of primary and secondary leaves, and their topological distribution. Figure 4 shows the changes to the secondary leaf profile as a function of TT as predicted by this model, taking a1 = 32 °Cd, a2 = 48 °Cd and db = 1·75.
Fig. 4.
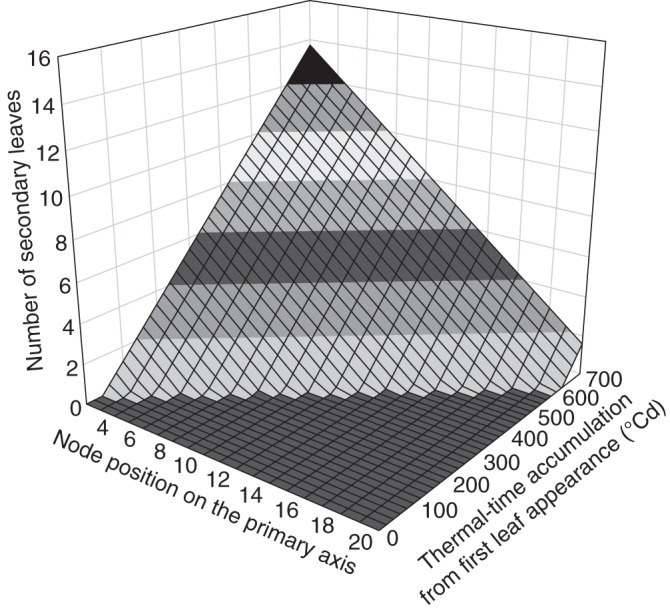
Number of secondary leaves as a function of branch position and thermal time as predicted by the potential shoot development model [eqns (3–6)].
In the following, we used this potential shoot development model, derived from independent experiments with limited light competition, as a neutral benchmark to assess the developmental effects induced by light competition in a series of competition experiments.
Impact of light competition on development and plant leaf area expansion
Size structure and competition intensity in the different alfalfa populations studied
The competition intensity was characterized through estimates of light interception efficiencies at the whole-stand scale (Supplementary Data Fig. S3) and with unbiased Gini coefficients (G′) at the plant population scale (Table 1). Irrespective of the treatment, canopy closure (LIE >0·95) was faster during the regrowth than during the initial growth phase. Canopy closure was also systematically faster at HD than at LD, and for pure stands with respect to mixtures. In mixtures, however, LIE cannot indicate the share of light intercepted by each plant population. G′ was thus used to account for the degree of inequality in resource capture within the different populations studied. Isolated plants had a relatively low G′ value (e.g. G′ = 0·10 in expt 1–2012) which was close to that of the initial seed population (G′ = 0·12). This confirmed that competition for light in these populations resulted in a weak impact of larger plants on the growth of smaller plants. The range of G′ values observed for alfalfa in the competition studies (Table 1) covered competition intensities from situations close to those characterized for isolated plants (e.g. G′ = 0·17 for LD–PSG, no mortality) to populations with severe competition experiencing self-thinning (e.g. G′ = 0·52 for HD–PSR, 13 % of plant mortality during the last regrowth). As for LIE, the G′ coefficient increased in line with both density and time (growth and regrowth differences), indicating that these two factors tended to increase competition intensity. The G′ coefficient also increased more markedly in pure stands than in mixed stands (0·52 > 0·31 at HD). Overall, contrasted situations relative to competition for light were thus actually generated by the study treatments in alfalfa populations. An approximate ranking observed for the two densities was PSG < MSG < MSR < PSR.
Table 1.
Gini coefficient values for plants in pure stands and mixed stands at high density (HD) and low density (LD) in expt 2
| Seeds | PSG | MSG | MSR | PSR | |
|---|---|---|---|---|---|
| LD | 0·12 | 0·17 | 0·21 | 0·25 | 0·26 |
| HD | 0·12 | 0·21 | 0·23 | 0·34 | 0·52 |
PSG, primary stand growth; MSG, mixed stand growth; PSR, primary stand regrowth; MSR, mixed stand regrowth.
Relative impacts on plant development and leaf growth
The impact of light competition on the developmental and growth processes controlling PLA was assessed (Fig. 5). Four situations were distinguished for which all the plants experienced the same environment (sowing date, cutting date, air temperature, VPD, etc.) except for their light interception (modulated by overall density and neighbouring plants). In each situation, marked variations in individual PLA values were shown (variations ranging from 4- to 10-fold between individual PLAs in the sample of digitized plants). The part of PLA variations explained by plant development (as reflected by the total number of leaves) and leaf growth (as reflected by the average leaflet area of fully expanded leaves in the zone of maximum primary leaf size, between nodes ranking 8–10) was examined by means of ANCOVA and regression analysiss in each situation. The ANCOVA revealed that the total number of leaves did indeed explain a significant part of PLA variations in all the situations studied. Plants displaying a larger number of leaves also had a higher PLA. A single relationship between PLA and leaf number was found in three out of four cases (MSG, MSR and PSR) which explained individual PLA variations both within and between the density treatments. The part of variance explained by plant development was high (r2 > 0·44) and increased over time (r2 > 0·85 in the regrowth cycles). In contrast, PLA variations were usually loosely associated with maximum leaf size. No significant relationship was found between PLA and maximum leaf size in the MSG, MSR and PSR situations, either within or between density treatments (ANCOVA, P > 0·08), indicating that plants with larger leaves were not necessarily those with the largest total leaf area, and vice versa. For PSG, ANCOVA revealed an interaction between density and maximum leaf size, the relationship between PLA and leaf size only being significant at LD.
Fig. 5.
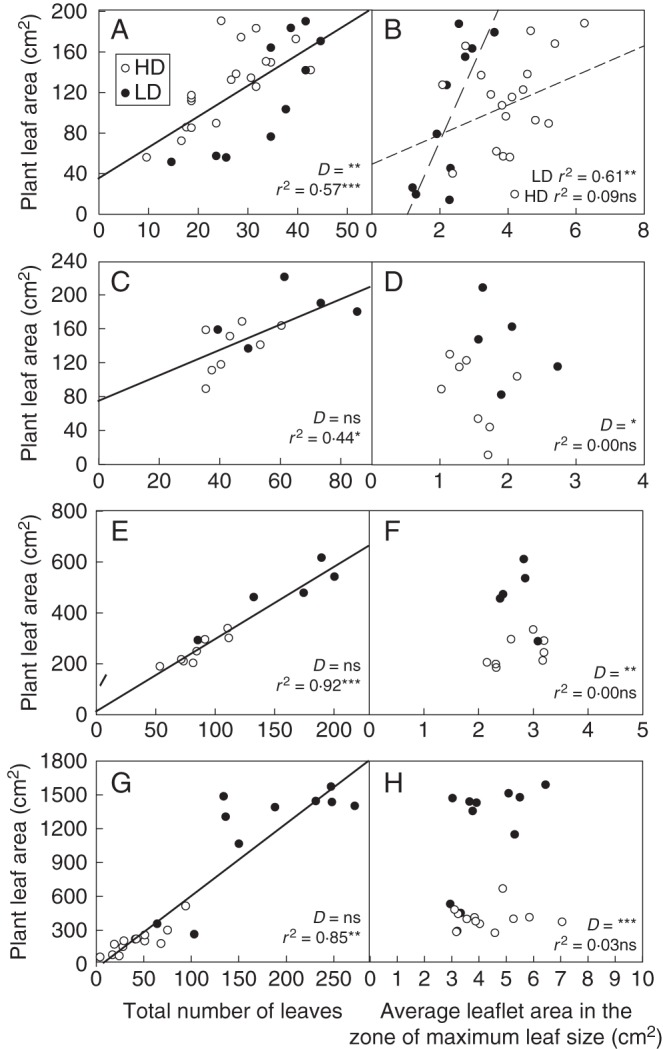
Relationships between plant leaf area and leaf number (left), and plant leaf area and maximum leaf size (right) in the four situations studied during exp 2: (A, B) PSG, pure stand growth; (C, D) MSG, mixed stand growth; (E, F) MSR, mixed stand regrowth; and (G, H) PSR, pure stand regrowth. High (HD) and low density (LD) are as indicated in the key in (A). ANCOVA results are presented in each panel: two lines in the case of an interaction between the categorical independent variable (i.e. density) and the continuous variable, no line in the case of a non-significant effect of the continuous variable, and a single line in the case of a significant effect of the continuous variable without any interaction. In the absence of interaction, D indicates the level of significance of the categorical independent variable (*P < 0·05; **P < 0·01; ***P < 0·001; ns, not significant). r2 indicates the coefficient of determination of the regression in the case of a significant effect of the continuous variable.
Important plant to plant variations in maximum leaf size were observed in all the situations and densities. A significant interaction effect on maximum leaf size was found between density treatments and the overall growing conditions that prevailed during the period of study (ANOVA, P < 0·001; Table 2). Once again, the density effect was significant for PSG only.
Table 2.
Average leaflet area in the zone of maximum primary leaf size (node rankings 8–10) in the different populations and growth phases of expt 2
| Stands | Density | Growth | Regrowth |
|---|---|---|---|
| Pure stand | HD | 4·07a | 4·31a |
| LD | 2·28bc | 4·33a | |
| Mixed stand | HD | 1·60c | 2·75b |
| LD | 1·99bc | 2·73b |
Means with the same letter are not significantly different according to the Duncan test (P > 0·05).
HD, high density; LD, low density.
PLA variations as explained by shoot number and shoot development
We further broke development down into shoot production and shoot development (as reflected by the average number of leaves per shoot) to understand how each component was affected by light competition (Fig. 6). Irrespective of density, PLA was tightly related to the shoot number in regrowth cycles (ANCOVA, P < 0·001 in MSR and PSR). Over 75 % of PLA variance could be explained by shoot number during these periods. In the initial growth phase, on the other hand, most plants had very similar shoot numbers (2–4) and PLA was either not significantly (PSG) or weakly (MSG) related to shoot numbers. Furthermore, shoot development was significantly related to PLA in all the situations studied. As compared with shoot numbers, shoot development explained larger parts of PLA variance during the initial growth phase, but contributed to a lesser extent during later regrowth phases (except for HD–MSR).
Fig. 6.
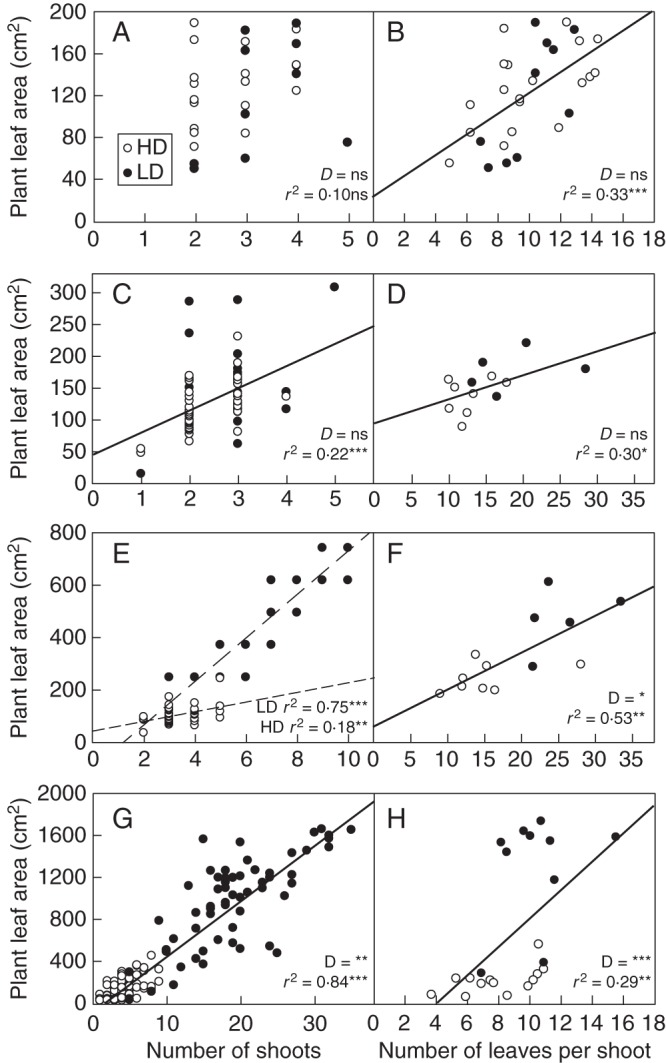
Relationships between plant leaf area and the shoot number (left), and plant leaf area and the number of leaves per shoot (right) in the four situations studied during exp. 2: (A, B) PSG, pure stand growth; (C, D) MRG, mixed stand growth; (E, F) MSR, mixed stand regrowth; and (G, H) PSR, pure stand regrowth. High (HD) and low density (LD) are as indicated in the key in (A). ANCOVA results are presented in each panel: two lines in the case of an interaction between the categorical independent variable (i.e. density) and the continuous variable, no line in the case of a non-significant effect of the continuous variable, and a single line in the case of a significant effect of the continuous variable without any interaction. In the absence of interaction, D indicates the level of significance of the categorical independent variable (*P < 0·05; **P < 0·01; ***P < 0·001; ns, not significant). r2 indicates the coefficient of determination of the regression in the case of a significant effect of the continuous variable.
Shoot developmental responses to light competition
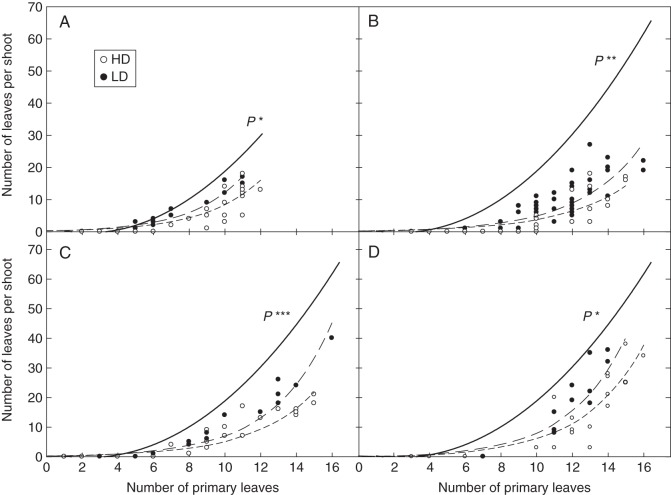
At the shoot level, potential shoot development and branching are strongly dependent on primary axis development. Figure 7 presents the relationships between primary axis development and the number of leaves on secondary branches. As predicted by the potential shoot development model, the total number of secondary leaves increased with primary axis development according to a power law superior to 1 (more than linearly) in all the situations studied and under all density treatments. However, a reduction in the total number of secondary leaves for a given number of primary leaves was seen on all shoots subjected to light competition when compared with potential shoot development. A significant reduction in branch development was also observed between the LD and HD treatments, in all situations (ANCOVA, P < 0·04). The profiles of secondary axis development are presented in Fig. 8 at HD and LD for shoots having reached a similar primary axis development. Except for LD–PSG, significant departures from the potential shoot development pattern were observed in all the situations studied. The reductions in branch development as compared with the potential pattern were usually small at the top of the canopy for the youngest branches (up to three leaves) and were maximum for the oldest branches. Branches in the various canopies studied apparently ceased their development after a time which varied in line with both the competition intensities (regrowth < growth cycles; pure < mixed stands).
Fig. 7.
Number of secondary leaves per shoot as a function of primary axis development in the four situations studied during expt. 2: (A) PSG, pure stand growth; (B) PSR, pure stand regrowth; (C) MSG, mixed stand growth; and (D) MSR, mixed stand regrowth. High (HD) and low density (LD) are as indicated in the key in (A). The solid line represents the relationship predicted by the potential shoot development model [eqns (3–6)]. ANCOVA results comparing HD and LD relationships are presented in each panel: two dashed lines are plotted in the case of an interaction between the categorical independent variable (i.e. density) and the continuous variable. P-values indicate the level of significance of the interactions (*P < 0·05; **P < 0·01; ***P < 0·001; ns, not significant).
Fig. 8.
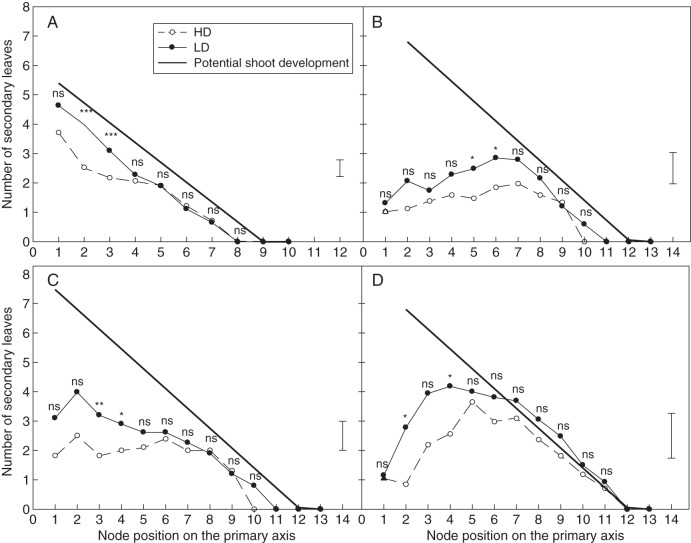
Number of secondary leaves at each node position on high (HD) and low density (LD) plants in the four situations studied during expt 2: (A) PSG, pure stand growth; (B) PSR, pure stand regrowth; (C) MSG, mixed stand growth; and (D) MSR, mixed stand regrowth. Shoots were selected at a given stage of development in each situation (shoots with 12–14 primary leaves). The dotted line represents the number of secondary leaves predicted by the potential shoot development model [eqns (3–6)]. P-values indicate the results of the t-test for a comparison between LD and HD at each node position (*P < 0·05; **P < 0·01; ***P < 0·001; ns, not significant).
Distribution of shoot size and organogenesis of primary axes
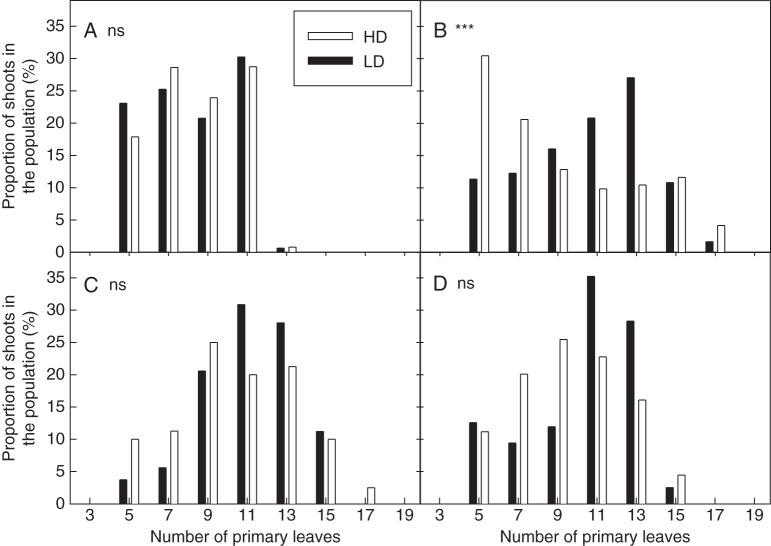
Not all shoots within a plant or within a density treatment displayed synchronous development. The final number of primary leaves could thus vary, which in turn could affect some of the average shoot characteristics mentioned above. Figure 9 presents the distribution of final shoot size (as reflected by the number of emerged primary leaves) in the different situations and densities studied. Final shoot size did vary in all the situations. However, remarkably, shoot size distributions were not affected by density in three of the four situations (PSG, MSG and MSR; KS tests P-values >0·24), suggesting that factors other than light competition might have caused these developmental variations. In PSR, however, significant differences were observed between the primary development of shoots in the HD and LD populations (KS tests, P-values <0·001). At LD, the mode of the distribution showed that the highest proportion of shoots were of a large size (12–14 primary leaves). At HD, only a small proportion of the shoots growing during the same period were able to reach this stage of development, suggesting that many primary axes had ceased or reduced their development as compared with LD.
Fig. 9.
Comparison between primary shoot size distributions at high (HD) and low density (LD) in the four situations studied during expt 2: (A) PSG, pure stand growth; (B) PSR, pure stand regrowth; (C) MSG, mixed stand growth; and (D) MSR, mixed stand regrowth. P-values indicate the level of significance of the Kolmogorov–Smirnov test (*P < 0·05; **P < 0·01; ***P < 0·001; ns, not significant).
DISCUSSION
Potential shoot development was a deterministic function of thermal time in the range of temperature and photoperiod tested
Our results suggest that the potential development of an alfalfa shoot is deterministic when expressed as a function of thermal time and identical irrespective of its apical meristem origin (from the seed, from T2 taproot buds or T1 axillary buds) and of the year (expt 1 and expt 2 on isolated plants). Our study covered the whole vegetative period and extended to mid-bloom. We showed that four characteristics could summarize the potential organogenesis of a whole shoot: primary axis phyllochron; systematic branching of all axillary buds; delayed bud burst; and a constant phyllochron for secondary branches. Similar patterns of whole-shoot development and branching have previously been reported in several species with indeterminate growth (Belaygue et al., 1996; Seleznyova et al., 2002; Lebon et al., 2004; Louarn et al., 2007; Moreau et al., 2007). The stability of primary axis development (constant rate of leaf appearance) was also characteristic in these studies. In alfalfa, however, it has remained a matter of debate. Various studies have reported a linear relationship between NI and TT during the vegetative growth period (although there have been controversies regarding the Tb value used to calculate TT; Wolf and Blaser, 1971; Sharratt et al., 1989; Brown and Moot, 2004; Brown et al., 2005; Teixeira et al., 2011). However, unlike our results, which showed similar phyllochron values in the growth and regrowth phases [32 °Cd, close to the phyllochrons reported by Brown et al. (2005) or Teixeira et al. (2011) in the field and Allirand (1998) or Pearson and Hunt (1972) under controlled environments for isolated plants], several studies have supported the idea of a primary axis phyllochron that is significantly higher during the initial growth phase (Robertson et al., 2002; Teixeira et al., 2011). Our results demonstrated that no ontogeny-related difference could explain the slower rate of leaf appearance in the field. In contrast to field experiments, we controlled nitrogen nutrition using an N-rich nutrient solution. We can thus hypothesize that a part of the differences previously reported might be related to a degree of nitrogen limitation during the initial growth phase when nodules hosting rhizobia, and allowing atmospheric nitrogen fixation, were forming (Voisin et al., 2003). Differences in phyllochron related to the photoperiod have also been reported, in particular between growth periods during increasing and decreasing photoperiods (Brown et al., 2005, 2006). Our experiments were all performed close to the summer solstice (the photoperiod between 14 h and 16 h), with both growth and regrowth phases starting when photoperiods were still increasing. No significant photoperiodic effect is expected under such conditions, in contrast to field conditions with autumn sowing (Brown et al., 2005). This could also explain some discrepancies with the literature.
The development of branches had a great importance in controlling the potential number of leaves of alfalfa shoots subjected to a low level of light competition. Under these conditions, every leaf axil produced a branch after a constant delay. Such a systematic branching had previously been reported on Medicago truncatula (Moreau et al., 2007) or grapevine (Lebon et al., 2004; Louarn et al., 2007) and assisted greatly in simplifying the formalism to model potential shoot development using a simple deterministic approach. The rate of development of branches was also constant over time, but the phyllochron was lower than for the primary axis, with a reduction of around 30 % for B1 and 50 % for other branches. Allirand (1998) and Moreau et al. (2007) also reported a reduced rate of development of branches when compared with the primary axis. These authors also demonstrated changes in the phyllochron of branches as a function of their position on the main stem. However, their study mainly covered the reproductive growth period of M. truncatula. The development of flowers along the primary axis is likely to be a factor that reduces the phyllochron of branches in alfalfa as well (Brown et al., 2005).
Plant development tunes leaf area expansion in alfalfa competing for light
Competition for light tends to be the principal factor leading to size inequalities and size structure in even-aged plant populations of productive habitats (Weiner, 1985; Weiner and Thomas, 1986; Schwinning and Weiner, 1998). Louarn et al. (2012a, b) showed that PLA was the most important variable in alfalfa to explain light partitioning and individual plant productivity in pure and mixed stands. However, little was known about the relative importance of physiological processes governing PLA to cope with changes in light competition intensity.
Tissue expansion and final individual leaf size have been shown to play key roles in the light response of many crops (Dosio et al., 2003; Chenu et al., 2005). Lower levels of PPFDs tend to decrease the leaf expansion rate but to increase the duration of leaf expansion (Corré et al., 1983; Tardieu et al., 1999; Chenu et al., 2005; Cookson and Granier, 2006). In this study, differences between HD and LD populations in the final size of leaves were observed only at the lowest levels of competition intensity studied (PSG, with G′ <0·21). More shaded plants had larger leaves. In all other situations, no density effect could be demonstrated. Marked variations in maximum leaf size were observed between plants within a treatment, irrespective of density, dates or total PLA (2- to 3-fold variations). The same range of variation was also found in isolated plants (not shown). This variability could be related to the fact that alfalfa cultivars are a population of genetically distinct plants, thus containing significant genetic and phenotypic variability (Julier et al., 2000). Leaf size variability did not generally reflect variations in total plant area. A significant relationship was only found for LD–PSG, a situation where competition intensity was very low and where most plants were close to their potential development (i.e. did not differ in their total number of leaves).
Organogenesis, resulting from meristem activities, is the other physiological process that plays a key role in regulating PLA. It has been shown to control PLA expansion in many indeterminate woody plants and herbaceous species (Pagès et al., 1993; Belaygue et al., 1996; Turc and Lecoeur, 1997; Seleznyova et al., 2002) and to affect PLA regulation in response to environmental constraints (Christophe et al., 2006; Lebon et al., 2006; Pallas et al., 2011). Our results definitely confirmed a strong role for plant development in regulation of the PLA of alfalfa in response to light availability, which was far stronger than any effect on tissue expansion. The total number of leaves accounted for variations in PLA both within and between density treatments. It explained >85 % of PLA variance in all situations after the first regrowth.
Developmental processes differ in their response to competition intensity
The total number of leaves on a plant can be described as resulting from several intertwined developmental processes: the initiation of new shoots at the level of the crown; primary development; and finally the degree of secondary branching for each shoot. Our findings suggest that these developmental processes were not affected to the same extent or could display differences in the timing of their response when subjected to different light competition intensities. The development of secondary axes appeared as the only variable that was affected in all the stands studied. Significant reductions were systematically observed as compared with isolated plants. The higher the intensity of competition, the more marked was the reduction in branch development. Only the branches at the base of the shoots were affected. Because alfalfa cv. Orca presents an upward canopy development, the zones where secondary development ceased corresponded to canopy heights with reduced light transmission (Louarn et al., 2012a) and correlatively modified light quality (Escobar-Gutiérrez et al., 2009). The greater reduction observed at HD, vs. LD, probably resulted from more rapid canopy closure and earlier effects of local light quantity/quality on the organogenesis of branches. Differences in the shape of secondary branch profiles between the pure and mixed stands for a given growth period may also have been induced by different light distributions in these two situations. Similar light quantity and quality effects on the branching of vegetative shoots have been reported on various species (Ballaré et al., 1997; Smith and Whitelam, 1997; Ballaré and Casal, 2000; Christophe et al., 2006). In alfalfa, Brown et al. (2005) showed that shorter branches at the bottom of the shoot resulted from an earlier cessation of their development and not from a delay in the outgrowth of axillary buds.
The regulation of branch organogenesis is critical with regard to the PLA response to stress in species where the number of branching shoots is fixed (e.g. determined by pruning rules: Lebon et al., 2006; Pallas et al., 2008). In our study, however, the part of PLA variance explained by average shoot development remained limited (r2 ranging from 0·29 to 0·55, Fig. 7). This may have been due (1) to the fact that an important variation of primary shoot development was observed within each treatment and the effect of which was only imperfectly captured by an average shoot (the relationship between primary and secondary development not being linear), and (2) to the variation in shoot numbers per plant that might explain a significant proportion of PLA variance. Changes in the shoot number did explain a significant part of PLA variance in three out of four situations (except for PSG, the lowest level of competition intensity), its importance relative to shoot development increasing with time. As previously reported (Fick et al., 1988; Kephart et al., 1992), increased densities resulted in a reduced number of shoots per plant. However, the relationship between competition intensity and average shoot number was not straightforward (e.g. very similar G′ values between HD–MSG, LD–MSR and LD–PSR produced markedly different average shoot numbers: 2·5, 6·1 and 20·3, respectively). The branching of the initial primary axis (and thus the number of buds initiated at the crown level) is likely to limit the possibility of achieving a large number of shoots per plant during the early stages. Conversely, important plant to plant variations in shoot numbers reported at a later stage may have derived from the cumulative effects of branching on the number of buds, as well as from the effects of the light environment on the dynamics of shoot population (Teixeira et al., 2007).
Finally, primary axis development was also involved in the plant response to light competition, but only at the highest competition intensities recorded. At HD–PSR, most of the shoots had a very limited final size (4–6 leaves), suggesting that many primary axes ceased to develop during regrowth. Possibly the smaller primary axes might stop developing in the shade of taller ones, in line with phenomena already discussed in the case of branches. The delayed response of primary axes to competition intensity could in part be explained by differences in the growth behaviour of primary and secondary axes (primary axes grow vertically, at a higher elongation rate than branches) and local light conditions at the apex (Louarn et al., 2012b). Similarly, the difference in the fate of primary axes of T1 and T2 reported in dense stands (Gosse et al., 1988) could simply result from shorter nodes and reduced growth of T1 stems (not shown), even if they present the same potential of development under favourable light conditions.
To sum up, developmental processes controlled plant and crop leaf area expansion in alfalfa and differed in their response to light competition intensity. These findings should help in defining relevant traits (such as rapid plant/shoot branching) that could be favoured in the definition of mixtures to prevent legume density-dependent mortality and mixture failure. Moreover, as a result of light competition, alfalfa leaf area dynamics and light interception efficiencies varied greatly among the treatments studied. The deterministic pattern of shoot development identified should aid in the development of more versatile models of leaf area expansion. In particular, it may be possible to overcome the limitations of fixed patterns of crop leaf area dynamics (Gosse et al., 1984; Goudriaan and Monteith, 1990) to deal with the question of light partitioning in heterogeneous intercropping systems by introducing formalisms that account specifically for the light effects on the key developmental variables involved in the response to light availability.
SUPPLEMENTARY DATA
ACKNOWLEDGEMENTS
This study was supported by the Conseil Régional Poitou-Charentes (http://www.poitou-charentes.fr) and the CAPES/Cofecub exchange programme from Brazil [project 684/10]. We would like to thank S. Carre, A. Eprinchard, A. Philiponneau and V. Dunoyer for their assistance with the experiments, and A. Escobar-Gutiérrez for fruitful discussions.
LITERATURE CITED
- Adam B, Sinoquet H, Godin C, Donès N. France: UMR PIAF INRA-UBP: Clermont-Ferrand; 1999. 3A-software for the acquisition of plant architecture Version 2.0. [Google Scholar]
- Allirand JM. Modelisation morphologique de la croissance de la Luzerne (Medicago sativa L.) en fonction de la temperature. France: Institute Nationale de Recherche Agronomique; 1998. PhD Thesis. [Google Scholar]
- Ballaré CL, Casal JJ. Light signals perceived by crop and weed plants. Field Crops Research. 2000;67:149–160. [Google Scholar]
- Ballaré CL, Scopel AL, Sanchez RC. Foraging for light: photosensory ecology and agricultural implications. Plant, Cell and Environment. 1997;20:820–825. [Google Scholar]
- Barillot R, Louarn G, Escobar-Gutiérrez AJ, Huynh P, Combes D. How good is the turbid medium-based approach for accounting for light partitioning in contrasted grass–legume intercropping systems? Annals of Botany. 2011;108:1013–24. doi: 10.1093/aob/mcr199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basigalup DH. El cultivo de la alfalfa en la Argentina. Buenos Aires: INTA; 2007. [Google Scholar]
- Belaygue C, Wery J, Cowan AA, Tardieu F. Contribution of leaf expansion, rate of leaf appearance and stolon branching to growth of plant leaf area under water-deficit in white clover. Crop Science. 1996;36:1240–1246. [Google Scholar]
- Boffey TB, Veevers A. Balanced designs for two-component competition experiments. Euphytica. 1977;26:481–484. [Google Scholar]
- Bonhomme R. Bases and limits to using ‘degree.day’ units. European Journal of Agronomy. 2000;13:1–10. [Google Scholar]
- Boote KJ, Jones JW, Pickering NB. Potential uses and limitations of crop models. Agronomy Journal. 1996;88:704–716. [Google Scholar]
- Brisson N, Gary C, Justes E, et al. An overview of the crop model STICS. European Journal of Agronomy. 2003;18:309–332. [Google Scholar]
- Brisson N, Bussière F, Ozier-Lafontaine H, Tournebize R, Sinoquet H. Adaptation of the crop model STICS to intercropping. Theoretical basis and parameterisation. Agronomie. 2004;24:409–421. [Google Scholar]
- Brisson N, Launay M, Mary B, Beaudoin N. Conceptual basis, formalisations and parameterization of the STICS crop model. Versailles: Quae; 2008. [Google Scholar]
- Brown HE, Moot DJ. Proceedings of the 4th International Crop Science Congress. Brisbane, Australia: 2004. Main-stem node appearance of Lucerne regrowth in a temperate climate. [Google Scholar]
- Brown HE, Moot DJ, Teixeira EI. The components of lucerne (Medicago sativa) leaf area index respond to temperature and photoperiod in a temperate environment. European Journal of Agronomy. 2005;23:348–358. [Google Scholar]
- Brown HE, Moot DJ, Teixeira EI. Radiation use efficiency and biomass partitioning of lucerne (Medicago sativa) in a temperate climate. European Journal of Agronomy. 2006;25:319–327. [Google Scholar]
- Chenu K, Franck N, Dauzat J, Barczi J, Rey H, Lecoeur J. Integrated responses of rosette organogenesis, morphogenesis and architecture to reduced incident light in Arabidopsis thaliana results in higher efficiency of light interception. Functional Plant Biology. 2005;32:1123–1134. doi: 10.1071/FP05091. [DOI] [PubMed] [Google Scholar]
- Christophe A, Moulia B, Varlet-Grancher C. Quantitative contributions of blue light and PAR to the photocontrol of plant morphogenesis in Trifolium repens (L.) Journal of Experimental Botany. 2006;57:2379–2390. doi: 10.1093/jxb/erj210. [DOI] [PubMed] [Google Scholar]
- Cookson SJ, Granier C. A dynamic analysis of the shade-induced plasticity in Arabidopsis thaliana rosette leaf development reveals new components of the shade-adaptative response. Annals of Botany. 2006;97:443–452. doi: 10.1093/aob/mcj047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corré WJ. Growth and morphogenesis of sun and shade plants II. the influence of light quality. Acta Botanica Neerlandica. 1983;32:185–202. [Google Scholar]
- Cowett ER, Sprague MA. Factors affecting tillering in alfalfa. Agronomy Journal. 1962;54:294–297. [Google Scholar]
- Cowett ER, Sprague MA. Effect of stand density and light intensity on the microenvironment and stem production of alfalfa. Agronomy Journal. 1963;55:432–434. [Google Scholar]
- Deregibus VA, Sanchez RA, Casal JJ, Trlica MJ. Tillering responses to enrichment of red light beneath the canopy in a humid natural grassland. Journal of Applied Ecology. 1985;22:199–206. [Google Scholar]
- Dewar RC. A mechanistic analysis of self-thinning in terms of the carbon balance of trees. Annals of Botany. 1993;71:147–159. [Google Scholar]
- Dosio GAA, Rey H, Lecoeur J, et al. A whole-plant analysis of the dynamics of expansion of individual leaves of two sunflower hybrids. Journal of Experimental Botany. 2003;54:2541–2552. doi: 10.1093/jxb/erg279. [DOI] [PubMed] [Google Scholar]
- Escobar-Gutiérrez AJ, Combes D, Rakocevic M, et al. Functional relationships to estimate morphogenetically active radiation (MAR) from PAR and solar broadband irradiance measurements: the case of a sorghum crop. Agricultural and Forest Meteorology. 2009;149:1244–1253. [Google Scholar]
- Evers JB, Vos J, Andrieu B, Struik PC. Cessation of tillering in spring wheat in relation to light interception and red:far-red ratio. Annals of Botany. 2006;97:649–658. doi: 10.1093/aob/mcl020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fick GW, Holt DA, Lugg DG. Environmental physiology and crop growth. In: Hanson AA, Barnes DK, Hill RR, editors. Alfalfa and alfalfa improvement. Madison, WI: ASA/CSSA/SSSA; 1988. pp. 163–194. [Google Scholar]
- Gautier H, Varlet-Grancher C, Hazard L. Tillering responses to the light environment and to defoliation in populations of perennial ryegrass (Lolium perenne L.) selected for contrasting leaf length. Annals of Botany. 1999;83:423–429. [Google Scholar]
- Gautier H., Mech R, Prusinkiewicz P, Varlet-Grancher C. 3D architectural modelling of aerial photomorphogenesis in white clover (Trifolium repens L.) using L-systems. Annals of Botany. 2000;85:359–370. [Google Scholar]
- Gosse G, Chartier M, Lemaire G. Mise au point d'un modèle de prevision de production pour une culture de Luzerne. Comptes Rendus de l'Academie des Sciences. 1984;298:541–544. [Google Scholar]
- Gosse G, Lemaire G, Chartier M, Balfourier F. Structure of a Lucerne population (Medicago sativa L.) and dynamics of stem competition for light during regrowth. Journal of Applied Ecology. 1988;25:609–617. [Google Scholar]
- Goudriaan J, Monteith JL. A mathematical function for crop growth based on light interception and leaf area expansion. Annals of Botany. 1990;66:695–701. [Google Scholar]
- Hammer GL, Kropff MJ, Sinclair TR, Porter JR. Future contributions of crop modelling – from heuristics and supporting decision making to understanding genetic regulation and aiding crop improvement. European Journal of Agronomy. 2002;18:15–31. [Google Scholar]
- Harper JL. Approaches to the study of plant competition. In: Milthorpe FL, editor. Mechanisms in biological competition. Cambridge: Symposia of the Society for Experimental Biology; 1961. pp. 1–39. [Google Scholar]
- Holmes MG, Smith H. The function of phytochrome in the natural environment. I. Characterization of daylight for studies in photomorphogenesis and photoperiodism. Photochemistry and Photobiology. 1977;25:533–538. [Google Scholar]
- Jones CA, Ritchie JT, Kiniry JR, Godwin DC, Otter-Nacke SI. Proceedings International Symposium on Minimum Datasets for Agrotechnology Transfer. Pantancheru, India: ICRASET; 1984. The CERES wheat and maize model. [Google Scholar]
- Jones RM, Carter ED. Demography of pasture legumes. In: Marten GC, Matches AG, Barnes RF, Brougham RW, Clements RJ, Sheath GW, editors. Persistence of forage legumes. Madison, WI: ASA, CSSA, SSSA; 1989. pp. 139–158. [Google Scholar]
- Julier B, Huyghe C, Ecalle C. The within-cultivar part of genetic variance is higher for morphological traits and yield than for digestibility and fiber content in alfalfa. Crop Science. 2000;40:365–369. [Google Scholar]
- Kasperbauer MJ, Karlen DL. Light-mediated bioregulation of tillering and photosynthate partitioning in wheat. Physiologia Plantarum. 1986;66:159–163. [Google Scholar]
- Kays S, Harper JL. The regulation of plant and tiller density in a grass sward. Journal of Ecology. 1974;62:97–105. [Google Scholar]
- Kephart KD, Twidwell EK, Bortnem R, Boe A. Alfalfa yield component responses to seeding rate several years after establishment. Agronomy Journal. 1992;84:827–831. [Google Scholar]
- Kiniry JR, Williams JR. Simulating intercropping with the ALMANAC model. In: Sinoquet H, Cruz P, editors. Ecophysiology of tropical intercropping. Paris: INRA; 1995. pp. 387–396. [Google Scholar]
- Lafarge T. Analyse de la mise en place de la surface foliaire du sorgho-grain (Sorghum bicolor L. Moench) au champ. Etablissement d'un modèle de développement valable en conditions sahéliennes et nord méditerranéennes. Paris: Orsay Paris-Sud University; 1998. PhD Thesis. [Google Scholar]
- Leach G. The growth of the lucerne plant after cutting: I. The effects of cutting at different stages of maturity and at different intensities. Australian Journal of Agricultural Research. 1968;19:517–530. [Google Scholar]
- Lebon E, Pellegrino A, Tardieu F, Lecoeur J. Shoot development in grapevine (Vitis vinifera) is affected by the modular branching pattern of the stem and intra- and inter-shoot trophic competition. Annals of Botany. 2004;93:263–274. doi: 10.1093/aob/mch038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lebon E, Pellegrino A, Louarn G, Lecoeur J. Branch development controls leaf area dynamics in grapevine (Vitis vinifera) growing in drying soil. Annals of Botany. 2006;98:175–185. doi: 10.1093/aob/mcl085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louarn G, Guedon Y, Lecoeur J, Lebon E. Quantitative analysis of the phenotypic variability of shoot architecture in two grapevine (Vitis vinifera) cultivars. Annals of Botany. 2007;99:425–437. doi: 10.1093/aob/mcl276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louarn G, Da Silva D, Godin C, Combes D. Simple envelope-based reconstruction methods can infer light partitioning among individual plants in sparse and dense herbaceous canopies. Agricultural and Forest Meteorology. 2012a;166–167:98–112. [Google Scholar]
- Louarn G, Frak E, Combes D, Escobar-Gutiérrez AS. Modelling variations in individual plant productivity within a stand: comparison of top-down and bottom-up approaches in an alfalfa crop. In: Kang MZ, Dumont Y, Guo Y, editors. Plant growth modeling, simulation, visualization and their applications (PMA12) IEEE Press; 2012b. pp. 254–261. [Google Scholar]
- Lötscher M, Nösberger J. Branch and root formation in Trifolium repens is influenced by the light environment of unfolded leaves. Oecologia. 1997;111:499–504. doi: 10.1007/s004420050263. [DOI] [PubMed] [Google Scholar]
- Maitre JP, Assemat L, Jacquard P. Croissance du trèfle violet (Trifolium pratense L.) en association avec du ray-grass d'Italie (Lolium multiflorum Lam. ssp. italicum). I. – Description de l'organisation morphologique du trèfle. Agronomie. 1985;5:251–260. [Google Scholar]
- Malézieux E, Crozat Y, Dupraz C, Laurans M, Makowski D, Valantin-Morison M. Mixing plant species in cropping systems: concepts, tools and models. A review. Agronomy for Sustainable Development. 2009;29:43–62. [Google Scholar]
- Mattera J, Romero LA, Cuatrín AL, Cornaglia PS, Grimoldi AA. Yield components, light interception and radiation use efficiency of lucerne (Medicago sativa L.) in response to row spacing. European Journal of Agronomy. 2013;45:87–95. [Google Scholar]
- Monteith JL. Climate and the efficiency of crop production in Britain. Philosophical Transactions of the Royal Society B: Biological Sciences. 1977;281:277–294. [Google Scholar]
- Monteith JL, Elston JF. Performance and productivity of foliage in field. In: Dale JE, Milthorpe FL, editors. The growth and functioning of leaves. London: Cambridge University Press; 1983. pp. 499–518. [Google Scholar]
- Moreau D, Salon C, Munier-Jolain N. A model-based framework for the phenotypic characterization of the flowering of Medicago truncatula. Plant, Cell and Environment. 2007;30:213–224. doi: 10.1111/j.1365-3040.2006.01620.x. [DOI] [PubMed] [Google Scholar]
- Nassiri MM. Modeling interaction in grass–clover mixtures. The Netherlands: Wageningen Agricultural University; 1998. PhD Thesis. [Google Scholar]
- Obeid M, Machin D, Harper JL. Influency of density on plant to plant variation in Fiber Flax, Linum usitatissimum L. Crop Science. 1967;7:471–473. [Google Scholar]
- Ong CK, Baker NR. Temperature and leaf growth. In: Baker NR, Davies WJ, Ong CK, editors. Control of leaf growth. Seminar Series, Society for Experimental Biology, No. 27. Cambridge: Cambridge University Press; 1985. pp. 175–200. [Google Scholar]
- Pallas B, Louarn G, Christophe A, Lebon E, Lecoeur J. Influence of intra-shoot trophic competition on shoot development of two grapevine cultivars (Vitis vinifera L.) Physiologia Plantarum. 2008;134:49–63. doi: 10.1111/j.1399-3054.2008.01100.x. [DOI] [PubMed] [Google Scholar]
- Pallas B, Loi C, Christophe A, Cournède PH, Lecoeur J. Comparison of three approaches to model grapevine organogenesis in conditions of fluctuating temperature, solar radiation and soil water content. Annals of Botany. 2011;107:729–745. doi: 10.1093/aob/mcq173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagès L, Génard M, Kervella J. Analyse quantitative du développement végétatif du système aérien de jeunes pêchers (Prunus persica L. Batsch) Agronomie. 1993;13:135–144. [Google Scholar]
- Pearson C, Hunt LA. Effects of temperature on primary growth and regrowth of alfalfa. Canadian Journal of Plant Science. 1972;52:1017–1027. [Google Scholar]
- R Development Core Team. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2012. [Google Scholar]
- Robertson M, Carberry PS, Huth NI, Turpin JE, Probert ME, Poulton PL, Bell M, Wright GC, Yeates SJ, Brinsmead RB. Simulation of growth and development of diverse legume species in APSIM. Australian Journal of Agricultural Research. 2002;53:429–446. [Google Scholar]
- Schwinning S, Weiner J. Mechanisms determining the degree of size asymmetry in competition among plants. Oecologia. 1998;113:447–455. doi: 10.1007/s004420050397. [DOI] [PubMed] [Google Scholar]
- Seleznyova AN, Thorp TG, Barnett AM, Costes E. Quantitative analysis of shoot development and branching patterns in Actinidia. Annals of Botany. 2002;89:471–482. doi: 10.1093/aob/mcf069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen AK. On ecnonomic inequality. Oxford: Clarendon Press; 1973. [Google Scholar]
- Sharratt BS, Sheaffer CC, Baker D. Base temperature for the application of the growing-degree-day model to field-grown alfalfa. Field Crops Research. 1989;21:95–102. [Google Scholar]
- Sinoquet H, Cruz P. Analysis of light interception and use in pure and mixed stands of Digitaria decumbens and Arachis pintoi. Acta Oecologica. 1993;14:327–39. [Google Scholar]
- Smith H, Whitelam GC. The shade avoidance syndrome: multiple responses mediated by multiple phytochromes. Plant, Cell and Environment. 1997;20:840–844. [Google Scholar]
- Soussana JF, Oliveira Machado A. Modelling the dynamics of temperate grasses and legumes in cut mixtures. In: Lemaire G, Hodgson J, de Moraes C, Cavalho P, Nabinger C, editors. Grassland ecophysiology and grazing ecology. Wallingford, UK: CABI International; 2000. pp. 169–190. [Google Scholar]
- Stamm P, Kumar PP. The phytohormone signal network regulating elongation growth during shade avoidance. Journal of Experimental Botany. 2010;61:2889–2903. doi: 10.1093/jxb/erq147. [DOI] [PubMed] [Google Scholar]
- Tardieu T, Granier C, Muller B. Modelling leaf expansion in a fluctuating environment: are changes in specific leaf area a consequence of changes in expansion rate? New Phytologist. 1999;143:33–43. [Google Scholar]
- Teixeira EI, Moot DJ, Brown HE, Fletcher AL. The dynamics of lucerne (Medicago sativa L.) yield components in response to defoliation frequency. European Journal of Agronomy. 2007;26:394–400. [Google Scholar]
- Teixeira EI, Brown HE, Meenken ED, Moot DJ. Growth and phenological development patterns differ between seedling and regrowth lucerne crops (Medicago sativa L.) European Journal of Agronomy. 2011;35:47–55. [Google Scholar]
- Turc O, Lecoeur J. Leaf primordium initiation and expanded leaf production are co-ordinated through similar response to air temperature in pea (Pisum sativum L.) Annals of Botany. 1997;80:265–273. [Google Scholar]
- Varlet-Grancher C, Gautier H. Plant morphogenetic responses to light quality and consequences for intercropping. In: Sinoquet H, Cruz P, editors. Ecophysiology of tropical intercropping. Paris: INRA Editions; 1995. pp. 231–256. [Google Scholar]
- Voisin AS, Salon C, Jeudy C, Warembourg FR. Symbiotic N2 fixation activity in relation to C economy of Pisum sativum L. as a function of plant phenology. Journal of Experimental Botany. 2003;54:2733–2744. doi: 10.1093/jxb/erg290. [DOI] [PubMed] [Google Scholar]
- Weiner J. Size hierarchies in experimental populations of annual plants. Ecology. 1985;66:743–752. [Google Scholar]
- Weiner J, Solbrig OT. The meaning and measurement of size hierarchies in plant populations. Oecologia. 1984;61:334–336. doi: 10.1007/BF00379630. [DOI] [PubMed] [Google Scholar]
- Weiner J, Thomas SC. Size variability and competition in plant monocultures. Oikos. 1986;47:211–222. [Google Scholar]
- Westoby M, Howell J. Self-thinning in Trifolium subterraneum populations transferred between full daylight and shade. Journal of Ecology. 1982;70:615–621. [Google Scholar]
- Wolf DD, Blaser RE. Leaf development of alfalfa at several temperatures. Crop Science. 1971;11:479–482. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.