Abstract
Background and Aims
Natural selection and genetic drift are important evolutionary forces in determining genetic and phenotypic differentiation in plant populations. The extent to which these two distinct evolutionary forces affect locally adaptive quantitative traits has been well studied in common plant and animal species. However, we know less about how quantitative traits respond to selection pressures and drift in endangered species that have small population sizes and fragmented distributions. To address this question, this study assessed the relative strengths of selection and genetic drift in shaping population differentiation of phenotypic traits in Psilopeganum sinense, a naturally rare and recently endangered plant species.
Methods
Population differentiation at five quantitative traits (QST) obtained from a common garden experiment was compared with differentiation at putatively neutral microsatellite markers (FST) in seven populations of P. sinense. QST estimates were derived using a Bayesian hierarchical variance component method.
Key Results
Trait-specific QST values were equal to or lower than FST. Neutral genetic diversity was not correlated with quantitative genetic variation within the populations of P. sinense.
Conclusions
Despite the prevalent empirical evidence for QST > FST, the results instead suggest a definitive role of stabilizing selection and drift leading to phenotypic differentiation among small populations. Three traits exhibited a significantly lower QST relative to FST, suggesting that populations of P. sinense might have experienced stabilizing selection for the same optimal phenotypes despite large geographical distances between populations and habitat fragmentation. For the other two traits, QST estimates were of the same magnitude as FST, indicating that divergence in these traits could have been achieved by genetic drift alone. The lack of correlation between molecular marker and quantitative genetic variation suggests that sophisticated considerations are required for the inference of conservation measures of P. sinense from neutral genetic markers.
Keywords: Psilopeganum sinense; Chinese privet; stabilizing selection; genetic drift; quantitative traits; QST; neutral microsatellite markers; FST; local adaptation, habitat fragmentation
INTRODUCTION
Understanding how natural populations respond to selection, gene flow and genetic drift is important for conservation and evolutionary biology (Merilä and Crnokrak, 2001; Leinonen et al., 2013), particularly in the light of increasing habitat fragmentation. Habitat fragmentation imposes negative effects on the persistence of populations and species (McGarigal and Cushman, 2002; Fahrig, 2003) by reducing gene flow, elevating random genetic drift and lessening the effectiveness of selection (e.g. Young et al., 1996; Sork et al., 1999; Aguilar et al., 2008; Charlesworth, 2009), which likely restrain the evolutionary response of populations to future changes (Caro and Laurenson, 1994; Young et al., 1996; Lande, 1998; Booy et al., 2000). Despite the awareness of the negative fitness consequences of population fragmentation, we know little about the relative strength of different evolutionary forces in shaping genetic and phenotypic differentiation in small and isolated natural populations (Frankham, 1999; Rogell et al., 2010).
One approach for evaluating the relative importance of natural selection and genetic drift in determining the levels of adaptive trait divergence is to compare population differentiation at neutrally evolving genetic markers, as measured by FST (Wright, 1951), with differentiation for quantitative genetic traits, as measured by QST (e.g. Lande, 1992; Merilä and Crnokrak, 2001; McKay and Latta, 2002; Leinonen et al., 2008; Lamy et al., 2012). The difference between QST and FST is compared against the null expectation of QST = FST for neutral additive traits differentiating via genetic drift. As FST represents neutral divergence that depends on gene flow–drift equilibrium, significant QST > FST comparisons suggest the presence of local adaptation, whereas QST < FST comparisons imply that stabilizing selection has prevented populations from diverging by drift (Leinonen et al., 2008). Because of the logistic difficulty of performing reciprocal transplantation among multiple populations, comparing QST and FST is a particularly useful approach for studying local adaptation.
Meta-analyses of empirical QST–FST contrast studies have shown that QST typically exceeds FST (Merilä and Crnokrak, 2001; Leinonen et al., 2008), suggesting that quantitative genetic variation is often under the influence of divergent selection. However, it is not clear whether the general tendency of QST > FST applies to small, fragmented and usually genetically impoverished populations in which genetic drift is presumably the primary evolutionary force (Johansson et al., 2007). Empirical evidence of strong impacts of genetic drift on quantitative trait differentiation among isolated populations was found in amphibian species (Rana temporaria, Johansson et al., 2007; Bufo calamita, Rogell et al., 2010). In the common frog R. temporaria, the differences between QST and FST approached zero in populations that inhabited fragmented environments, but higher QST relative to FST was observed in continuous habitats (Johansson et al., 2007). In the offshore island-dwelling natterjack toad Bufo calamita, no significant QST–FST contrasts were detected (Rogell et al., 2010). However, not only genetic drift but also divergent selection could be enhanced in small and isolated populations. Willi et al. (2007) found that QST and FST increased when population sizes decreased in the clonal creeping spearwort Ranunculus reptans; significant positive QST–FST differences were maintained in small populations. Relative to the well-documented theoretical and empirical evidence of increased differentiation at neutral genetic markers in small populations (Thompson, 1999), the responses of quantitative genetic differentiation to decreased population size and increased fragmentation remain poorly understood. Increased efforts are required to study the interactions and relative importance of selection, gene flow and drift in explaining quantitative genetic divergence among small plant populations.
Psilopeganum sinense (Rutaceae) is an endangered herbaceous species, and the genus Psilopeganum is monotypic. This species is endemic to the Yangtze River valley, a biodiversity hot spot in south-central China. As P. sinense is primarily distributed on hillsides at an elevation of 800 m in the Three Gorges Reservoir Area, the completion of the Three Gorges Dam has inundated at least three wild populations of P. sinense. In addition to habitat loss, over-harvesting of this species for traditional Chinese medicine has resulted in a rapid decline in population sizes and local extinction. A recent extensive field survey (2001–2009, Q. G. Ye, F. Y. Tang and Y. Zhang, unpubl. res.) retrieved only ten small, isolated populations. Previous studies using random amplification of polymorphic DNA (RAPD) markers and amplified fragment length polymorphisms (AFLP) showed low within-population genetic diversity and strong genetic differentiation in P. sinense (Song et al., 2004; Yang et al., 2007). Limited gene flow and the naturally small population sizes of this endangered species provide a suitable study system for examining the relative roles of natural selection and genetic drift in determining genetic and phenotypic differentiation among small plant populations.
This study aimed to assess the mechanisms of differentiation at quantitative genetic traits among seven small populations of P. sinense. We compared FST, measured as variation in polymorphic simple sequence repeat (SSR) loci, with QST estimates derived using a Bayesian hierarchical variance component approach. The correlation between variation at neutral genetic markers and that at quantitative genetic traits was examined to evaluate the utility of data on neutral molecular differentiation in aiding conservation efforts in rare and endangered plants.
MATERIALS AND METHODS
Study species and sites
Psilopeganum sinense is a diploid perennial hermaphroditic plant. It flowers from late March to early December. The primary pollinators are hoverflies and bees (Zhang and Ye, 2011). Seeds are discharged explosively from mature capsules and secondarily dispersed by gravity. Reproductive plants have 4–20 stems that are green, brown or red in autumn and winter. Psilopeganum sinense is often found in disturbed habitats (e.g. roadsides and farmland surroundings), co-occurring with Lophatherum gracile, Vitex negundo var. heterophylla, Rhus chinensis, Artemisia lactiflora, Hypericum perforatum and Sinopteris albofusca.
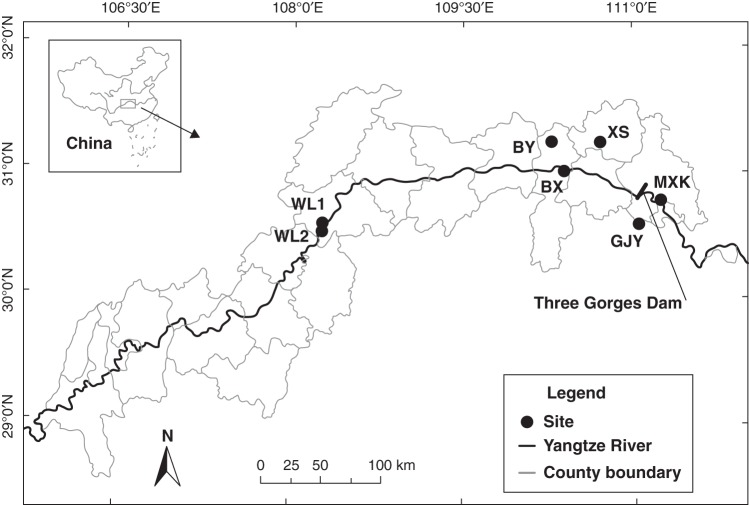
Field sampling was conducted in seven populations of P. sinense distributed along the Yangtze River (Fig. 1) in 2006. In 2006, we performed an extensive census of adult plants of P. sinense (Np, Table 1) in the seven populations, coded as WL1, WL2, BY, BX, XS, GJY and MXK. Pairwise population distances averaged 148 km (range 1·9–287 km). Environmental variables of the seven locations were acquired at 1-km resolution from the WorldClim database (http://www.worldclim.org). The mean annual temperature ranged from 11·5 °C in BY to 18·5 °C in WL2; the mean temperature of the coldest quarter was between 1·4 °C (BY) and 8·2 °C (WL2). Annual precipitation averaged between 938 mm (XS) and 1257 mm (WL1); precipitation in the driest quarter ranged from 59 mm (WL2) to 84 mm (GJY).
Fig. 1.
Geographic locations of the seven sampled populations of Psilopeganum sinense.
Table 1.
Study populations, sample size and summary of genetic variability measures for Psilopeganum sinense
| Population | Latitude/longitude | Np | NFST | NQST | A | HE | FIS | tm |
|---|---|---|---|---|---|---|---|---|
| WL1 | 30 °32′ N/108 °16′ E | 281 | 25 | 27 | 1·250 | 0·020 | −0·021 | – |
| WL2 | 30 °31′ N/108 °16′ E | 55 | 15 | 19 | 1·000 | 0 | – | – |
| BY | 31 °15′ N/110 °17′ E | 139 | 30 | 17 | 2·215 | 0·273 | 0·470 | 0·324 |
| BX | 31 °01′ N/110 °24′ E | 107 | 31 | 15 | 4·250 | 0·424 | 0·346 | 0·416 |
| XS | 31 °15′ N/110 °43′ E | 100 | 22 | 17 | 1·625 | 0·196 | 0·426 | – |
| GJY | 30 °36′ N/111 °03′ E | 50 | 17 | 17 | 2·375 | 0·472 | 0·676 | – |
| MXK | 30 °47′ N/111 °15′ E | 512 | 24 | 24 | 3·875 | 0·568 | 0·294 | 0·461 |
| Average | – | 178 | 23 | 19 | 2·370 | 0·279 | 0·365 | 0·400 |
Breeding system
The breeding system affects QST estimation, particularly in the presence of varying degrees of outcrossing and inbreeding. To estimate the outcrossing rate (tm) in self-compatible P. sinense, we collected 15 open-pollinated seeds from 30 individual female plants (n = 450). These 30 female plants were randomly chosen from three populations (BY, BX and MXK) with ten female plants per population. Genomic DNA was then isolated from these seeds and the silica-dried leaves of their maternal plants using the modified CTAB method (Doyle and Doyle, 1987). DNA was checked for quality and quantity on 0·8 % agarose gels. Four microsatellite loci (Psh2, Psh4, Psh5, Psh9; Tang et al., 2008) of varying allelic richness were selected for genotyping. The PCR reaction system and conditions followed the protocol described previously (Tang et al., 2008). Amplified products were visualized and scored using 6 % denatured polyacrylamide gels and silver staining.
Population differentiation at neutral genetic markers
To estimate neutral genetic differentiation (FST), we collected leaf tissues from 15–31 adult plants in each of the seven populations (NFST, Table 1), contingent on census population sizes (Np, Table 1). In total, we obtained 164 adult individuals of P. sinense. DNA extraction from silica dried leaves and microsatellite genotyping were performed as described above, except that 11 microsatellite loci (Psh1–Psh11; Tang et al., 2008) were used here for assessing population genetic structure.
Common garden experiment
Genetic differentiation of quantitative traits was estimated using seeds from 136 maternal families collected in the seven populations. The number of maternal families per population (NQST) varied between 15 and 27 (Table 1). Seeds from targeted maternal plants were harvested for subsequent experiments.
All seeds were stored at 4 °C before sowing. In February 2007, seeds of individual maternal families were sown into sandy loam. Thirty days after germination, seedlings (n = 1632; 12 seedlings per family) were transferred to individual pots and were allowed to grow in a common garden in Wuhan Botanical Garden. To minimize the potential effects of microenvironment variation in a common garden on seedling growth, we randomized the locations of individual seedling pots irrespective of their maternal and population provenance.
Seedling mortality occurred before they reached maturity for measuring quantitative traits in our common garden experiment. As a result, six to ten individuals from each maternal family (n = 1016) were retrieved for quantifying the following five traits: (1) area of the largest leaf (LA); (2) shape of the largest leaf (LS; ratio of length/width); (3) total number of flowers per plant (SF; fruits produced and flower buds were both included); (4) stem colour (SC; green, brown or red) in autumn and winter; and (5) height of the tallest stem in each individual (HS). The leaf traits were measured using a digital leaf area meter (LI-3000A, LI-COR, USA) in August 2009 and the other traits were measured in December 2009. Stem colour was coded numerically.
Data analyses
Genetic variation and outcrossing rate. Population genetic variation, including mean allelic richness per locus (A), expected heterozygosity (HE) and the inbreeding coefficient (FIS), was estimated using GENEPOP (Raymond and Rousset, 1995). Null alleles were checked in MICRO-CHECKER 2·2 (Van Oosterhout et al., 2004). Multilocus outcrossing rate (tm) was estimated using a maximum likelihood-based mixed mating model implemented in MLTR (Ritland, 2002).
FST estimate. The QST–FST comparisons demand genetic differentiation measured at neutral molecular markers. We tested the neutrality of the 11 microsatellite markers using FDIST2 (Beaumont and Nichols, 1996). An FST outlier was detected if it exceeded the expected 95 % confidence intervals that were simulated under the assumptions of stepwise mutations, infinite alleles and finite demes. Three 50 000-iteration simulations were carried out assuming 10, 50 and 100 demes respectively. FST outliers were excluded from the following analysis of neutral genetic differentiation.
Genetic differentiation at neutral microsatellite markers was estimated using BAPS (Corander et al., 2003). First, the posterior distribution of genetically district populations was obtained based on the marginal likelihood of a particular population structure relative to the sum of marginal likelihoods of all likely population configurations. In P. sinense, the estimated genetic clusters (n = 7) corresponded to their geographical populations. Second, given the posterior probabilities of allele frequencies and population configurations, FST and its uncertainty could be derived accordingly (Corander et al., 2003). Here the Bayesian estimate of FST was acquired using 50 000 Markov chain Monte Carlo (MCMC) iterations after a burn-in of 10 0000.
Isolation by distance. Mantel tests (Mantel, 1967) implemented in the program IBD (Bohonak, 2002) were used to evaluate the pattern of isolation by distance, by comparing FST/(1 – FST) against geographical distances. Confidence intervals of isolation by distance were inferred from 10 000 bootstrap samples. We calculated population pairwise geographical distances (km), using GEODETIC II (http://www.infoairports.com/freeservices/worlddistance.html). Gene flow (Nm) among populations was indirectly estimated from FST values: Nm = (1 – FST)/4FST (Slatkin and Barton, 1989).
QST estimation. The estimated multilocus outcrossing rate described above was 0·4, indicating that P. sinense mates predominantly by selfing. We therefore calculated QST in the same way as for predominantly selfing species:
| (1) |
where σ2B is the component of additive genetic variance between populations and σ2W the component within populations (Bonnin et al., 1996). Due to unequal family sizes and family numbers, among- and within-population additive genetic variances were derived using Bayesian hierarchical modelling in WINBUGS 1·4 (Spiegelhalter et al., 2003), as described by Waldmann et al. (2005). Specifically, linear regression with nested random effects was fitted for each trait as follows:
| (2) |
where Yijk is the observed quantitative trait of the kth individual from the jth family in the ith population; trait-specific mean μ is fixed; popi and famij are random effects with variance of σ2p and σ2f respectively. The quantitative traits except height (HS) and stem colour (CS) were log-transformed.
Among-population additive genetic variance σ2B is equivalent to σ2p; whereas within-population additive genetic variance σ2W equals σ2f in predominantly selfing systems. QST therefore equals σ2p/(σ2p + σ2f). To ensure MCMC convergence, two parallel chains were allowed to run 250 000 iterations after a burn-in of 25 000 in WINBUGS. Two types of uninformative priors [gamma (0·001, 0·001) and uniform (0, 10 000)] of inversed variances (1/σ2p, 1/σ2f, 1/σ2e) were analysed separately. As these two priors produced similar results, only the results based on gamma priors are presented. QST was considered statistically different from FST when the 95 % credibility intervals of the two estimates did not overlap (Yang et al., 1996). We also examined the isolation-by-distance pattern in quantitative traits using Mantel tests, compared with that in neutral genetic differentiation. Population pairwise distances of quantitative traits were calculated using NTSYSpc (Rohlf, 1998).
In addition to QST, broad-sense heritability [h2 = σ2f/(σ2f + σ2e)] and coefficients of genetic variation (CV = σf /μ in predominantly selfing systems; Houle, 1992) were calculated to quantify the ability of a population to respond to selection. The relationship of these two quantitative genetic variation variables (CV and h2) with neutral genetic variation (HE) was assessed at an individual trait level.
RESULTS
Microsatellite DNA variation
Three of the 11 microsatellite loci (Psh6, Psh8 and Psh11) deviated significantly from the neutral expectation. As these three loci may have been affected by selection, they were excluded from the following genetic analyses. The eight remaining microsatellite loci collectively generated 53 alleles. Several alleles were found to be unique to their specific populations: one unique allele in each of WL2, BY and XS, two in WL1 and CY, four in BX and six in MXK. The intra-population microsatellite variation averaged across alleles was A = 2·37 (range 1·00–4·25) and HE = 0·279 (range 0–0·568) (Table 1). Null alleles were not detected at any locus. Multilocus estimates of outcrossing rate (tm) ranged from 0·324 to 0·461, with a mean of 0·400.
The overall FST among populations was 0·467 (95 % CI 0·441–0·494). Pairwise estimates of FST between populations varied from 0·210 to 0·920. A significant correlation was detected between genetic differentiation (FST) and geographical distance (Mantel tests: r = 0·463, P = 0·049). Gene flow among populations (Nm) was low, with a mean value of 0·21.
Quantitative variation and QST/FST comparison
Posterior distributions of QST are presented in Fig. 2. Trait-specific QST estimates ranged from 0·067 (for height of the tallest stem) to 0·564 (for stem colour). For two morphological traits (stem colour and shape of the largest leaf), QST values were relatively high (0·381–0·564) (Table 2). Despite high QST in these two traits, QST was not significantly different from FST as FST fell within the 95 % confidence intervals of QST. By contrast, we found that QST was significantly lower than FST in three functional traits, including height of the tallest stem, area of the largest leaf and total number of flowers (Table 2, Fig. 2).
Fig. 2.
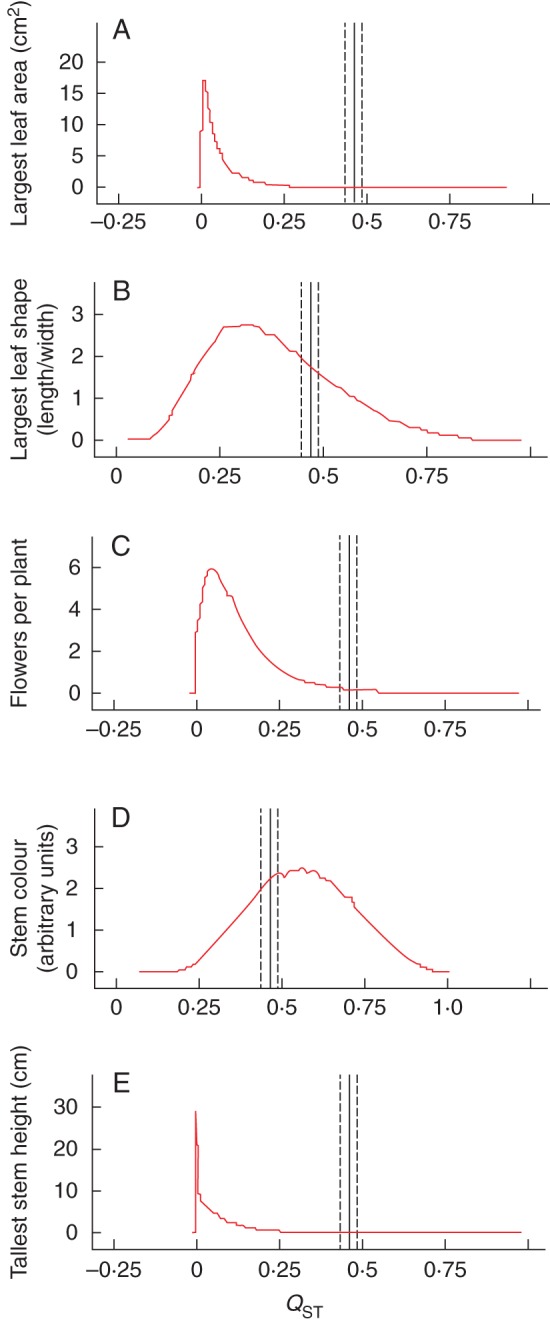
Bayesian posterior probability distributions of trait-specific QST for (A) area of the largest leaf, (B) shape of the largest leaf, (C) total number of flowers per plant, (D) stem colour and (E) height of the tallest stem; the y-axes indicate Bayesian posterior probability (%). The vertical solid lines represent FST; dashed lines are 95 % confidence intervals of FST estimated in BAPS.
Table 2.
Trait-specific QST estimates (± 95 % CI) in Psilopeganum sinense and correlation coefficients (R2) (P values in parentheses) between genetic variation at quantitative traits (genetic variance and heritability) and neutral genetic variation (HE)
| Traits | QST | HE vs genetic variance | HE vs heritability |
|---|---|---|---|
| Area of the largest leaf | 0·069 (0·005–0·316) | 0·262 (0·531) | −0·119 (0·779) |
| Shape of the largest leaf | 0·381 (0·149–0·720) | 0·167 (0·693) | 0·262 (0·531) |
| Total number of flowers per plant | 0·130 (0·008–0·433) | −0·619 (0·102) | −0·286 (0·493) |
| Stem colour | 0·564 (0·290–0·854) | 0·000 (1·000) | 0·252 (0·548) |
| Height of the tallest stem | 0·067 (4·982 × 10−5 to 0·314) | −0·617 (0·071) | −0·707 (0·050) |
No significant correlation was detected between Euclidean distances of quantitative traits and geographical distance (Mantel tests, r = 0·124, P =0·112). Likewise, molecular variation (HE) demonstrated poor correlations with the coefficient of genetic variation and heritability (h2) (Table 2). Broad-sense heritability varied from 0·068 for height of the tallest stem to 0·402 for shape of the largest leaf. The coefficient of genetic variation was less variable than heritability values, ranging from 0·047 to 0·152 (Table 3).
Table 3.
Coefficient of genetic variation (CV) and broad-sense heritability (h2, in parentheses) for five traits in seven populations of Psilopeganum sinense distributed along the Yangtze River
| Population | LA | LS | SF | SC | HS |
|---|---|---|---|---|---|
| WL1 | 0·237 (0·638) | 0·087 (0·514) | 0·113 (0·135) | 0·254 (0·325) | 0·018 (0·017) |
| WL2 | 0·055 (0·118) | 0·109 (0·263) | 0·140 (0·128) | 0·101 (0·051) | 0·137 (0·226) |
| BY | 0·037 (0·046) | 0·086 (0·386) | 0·026 (0·012) | 0·043 (0·025) | 0·021 (0·016) |
| BX | 0·073 (0·188) | 0·066 (0·303) | 0·108 (0·147) | 0·155 (0·331) | 0·026 (0·023) |
| XS | 0·079 (0·140) | 0·088 (0·470) | 0·067 (0·051) | 0·036 (0·029) | 0·094 (0·163) |
| GJY | 0·085 (0·156) | 0·522 (0·722) | 0·063 (0·078) | 0·031 (0·025) | 0·015 (0·016) |
| MXK | 0·047 (0·069) | 0·108 (0·461) | 0·042 (0·042) | 0·194 (0·466) | 0·016 (0·014) |
| Average | 0·088 (0·194) | 0·152 (0·402) | 0·080 (0·085) | 0·116 (0·179) | 0·047 (0·068) |
DISCUSSION
Population differentiation in neutral genetic markers and quantitative traits
Psilopeganum sinense exhibited strong neutral genetic differentiation among populations, which is consistent with what is expected for species with small population size and isolated populations. The FST estimates based on microsatellite data agreed with those reported in previous studies (Song et al., 2004; Yang et al., 2007). In contrast to high differentiation at neutral genetic markers, we found little differentiation in quantitative traits. Trait-specific QST was either equal to or lower than FST.
Our results contrast with most previous studies, where QST typically exceeded FST, thereby implying a predominant role for divergent or directional selection in shaping genetically based trait divergence (Merilä and Crnokrak, 2001; Leinonen et al., 2008). The predominant pattern of QST > FST may be partly due to publication bias (Leinonen et al., 2008; Whitlock, 2008; Lamy et al., 2012). The lower magnitude of QST relative to FST detected here was likely the consequence of small population size and high levels of population isolation. Corroborative evidence of the effects of habitat isolation on QST–FST contrasts has been found in other rare plant species, where stabilizing selection and/or genetic drift were the key drivers for divergence in quantitative traits in small isolated populations (Waldmann and Andersson, 1998; Petit et al., 2001; Gravuer et al., 2005). For instance, QST values in the rare plants Scabiosa canescens and Silene diclinis were similar to or slightly lower than FST, while higher QST relative to FST was found in the common and widespread Scabiosa columbaria (Waldmann and Andersson, 1998). Similarly, Petit et al. (2001) found that QST of two rare plants, Centaurea corymbosa and Brassica insularis, was significantly smaller than FST for juvenile traits.
Psilopeganum sinense is a naturally rare endemic species and it has recently become endangered because of anthropogenic disturbance, including habitat loss and fragmentation due to construction of the Three Gorges Dam (Tang, 2008; Zhang and Ye, 2011). The significant correlation between genetic differentiation and geographical distance and the low level of gene flow (Nm = 0·21) among populations suggest that geographical isolation generates barriers to gene movement and leads to population differentiation. But P. sinense has a narrow spectrum of habitat suitability and thus grows in similar environments (e.g. roadside or farmland surroundings; Tang, 2008). Limited habitat heterogeneity imposes more or less homogeneous selective pressures, and thus stabilizing selection may determine population divergence in quantitative traits, as manifested by smaller QST than FST in three functional traits (height of the tallest stem, area of the largest leaf and total number of flowers). In addition, we found that QST estimates were of the same magnitude as FST for two morphological traits (stem colour and shape of the largest leaf), which stood in contrast with the general findings of pronounced positive QST–FST differences for morphological characters (Merilä and Crnokrak, 2001; Leinonen et al., 2013). Due to the lack of divergent selective regimes under relatively homogeneous environmental conditions, genetic drift may hold the key for differentiation in these two morphological traits (Yang et al., 1996).
Theoretical and empirical investigations indicate a positive correlation between heritability and QST of quantitative traits (Lynch et al., 1999; Merilä and Crnokrak, 2001; Whitlock, 2008). Consistent with previous findings, two morphological traits (stem colour and shape of the largest leaf) in this study that had high heritability also exhibited high QST. Likewise, the relatively low heritability of three functional traits (height of the tallest stem, area of the largest leaf and total number of flowers) was associated with low QST.
Relation between molecular and quantitative genetic variation within populations
In principle, genetic variation in quantitative traits is positively correlated with molecular genetic diversity (Falconer and Mackay, 1996; Lynch et al., 1999; Merilä and Crnokrak, 2001), which enables molecular genetic diversity to serve as a convenient predictor of the ability of a population to respond to environment change. However, this prediction is only partially confirmed by empirical studies (Merilä and Crnokrak, 2001; Reed and Frankham, 2001; McKay and Latta, 2002; Evanno et al., 2006). In the present study, a correlation between molecular and quantitative genetic variation was not evident, in line with the results of other studies performed on wild plant species (e.g. Waldmann and Andersson, 1998; Podolsky, 2001; Volis et al., 2005).
Limitations of QST/FST comparisons
Although QST–FST contrast is a conventional method of testing for evidence of natural selection driving population divergence, the interpretation of results from such comparisons is potentially complicated by many factors, such as the number of populations studied, the presence of environmental maternal effects and non-additive genetic variance due to dominance and epistatic effects (Whitlock, 1999; Hendry, 2002; López-Fanjul et al., 2003; Miller et al., 2008; Pujol et al., 2008; Whitlock, 2008; Edelaar and Björklund, 2011).
Theoretical studies have shown that bias and variance in the estimation of QST are especially large when few populations are studied; however, most QST/FST comparisons were made in a small number of populations (O'Hara and Merilä, 2005). Due to the rare status of P. sinense, sampling enough natural populations to meet the theoretical need to reduce such biases was not feasible. One advantage of Bayesian models when dealing with the problem of small sample size is that model uncertainties are correctly summarized, which allows accurate estimation of confidence intervals of parameters (Waldmann et al., 2005; O'Hara and Merilä, 2005; Rogell et al., 2010). A second point to consider is the potential upward bias in σ2W estimation, which could result in a downwardly biased QST due to maternal effects, which may apply to our study as the quantitative traits were measured from seeds collected from wild populations. Maternal effects have a stronger impact on precocious traits like early growth and survival (Evanno et al., 2006). In our study, all quantitative traits used for QST inference were measured at a relatively late phase of their development, but we cannot exclude the potential confounding role of maternal effects. Additionally, the generally small variance among and within populations found in this study suggests that maternal effects were weaker than additive genetic effects. In addition, although dominance and epistatic effects may deflate QST estimates (Goudet and Buchi, 2006), these non-additive genetic effects are generally rather small and unlikely to bias QST considerably (e.g. Goudet and Büchi, 2006; Hill et al., 2008; Rogell et al., 2010). Consequently, although we cannot exclude the possibility of downward bias in QST, it seems likely that the QST estimates reflect true genetic differentiation among the study populations of P. sinense.
Conclusions
The present study did not detect any evidence of local adaptation in well-differentiated populations at a relatively large spatial scale. As none of the QST values of the quantitative traits we measured exceeded FST, genetic drift and stabilizing selection may explain the pattern of differentiation in P. sinense. However, the fact that QST = FST does not necessarily imply absence of directional selection, but it pinpoints the inability to reject the null hypothesis that the observed genetic structure has been driven by genetic drift. Moreover, our study found no positive relationship between neutral and quantitative genetic variation. Thus, genetic variation at molecular marker loci has its limitations for use as a predictor of the ecological divergence of natural populations of P. sinense.
ACKNOWLEDGEMENTS
We are grateful to Jordan Bemmels, John Guittar, Ming Kang, Hua Tian and Yongmei Ruan for their assistance and advice. We thank Patrick Waldmann for providing the codes for Bayesian estimates and further assistance on its application. We also thank Sophie Karrenberg and three anonymous reviewers for their constructive comments on the manuscript. This work was supported in part by the Natural Scientific Foundation of China (Grant No. 31270384, 30870241) and the Director fund of Wuhan Botanical Garden, the Chinese Academy of Sciences (KSCXZ-EW-J-20).
LITERATURE CITED
- Aguilar R, Quesada M, Ashworth L, Herrerias-Diego Y, Lobo J. Genetic consequences of habitat fragmentation in plant populations: susceptible signals in plant traits and methodological approaches. Molecular Ecology. 2008;14:1811–1820. doi: 10.1111/j.1365-294X.2008.03971.x. [DOI] [PubMed] [Google Scholar]
- Beaumont MA, Nichols RA. Evaluating loci for use in the genetic analysis of population structure. Proceeding of The Royal Society B: Biological Sciences. 1996;263:1619–1626. [Google Scholar]
- Bohonak AJ. IBD (Isolation by Distance): a program for analyses of isolation by distance. Journal of Heredity. 2002;93:153–154. doi: 10.1093/jhered/93.2.153. [DOI] [PubMed] [Google Scholar]
- Bonnin I, Prosperi JM, Olivieri I. Genetic markers and quantitative genetic variation in Medicago truncatula (Leguminosae): a comparative analysis of population structure. Genetics. 1996;143:1795–1805. doi: 10.1093/genetics/143.4.1795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booy G, Hendriks RJJ, Smulders MJM, Van Groenendael JM, Vosman B. Genetic diversity and the survival of populations. Plant Biology. 2000;2:379–395. [Google Scholar]
- Caro TM, Laurenson KM. Ecological and genetic factors in conservation: a cautionary tale. Science. 1994;263:485–486. doi: 10.1126/science.8290956. [DOI] [PubMed] [Google Scholar]
- Charlesworth B. Effective population size and patterns of molecular evolution and variation. Nature Reviews Genetics. 2009;10:195–205. doi: 10.1038/nrg2526. [DOI] [PubMed] [Google Scholar]
- Corander J, Waldmann P, Sillanpää M. Bayesian analysis of genetic differentiation between populations. Genetics. 2003;163:367–374. doi: 10.1093/genetics/163.1.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle JJ, Doyle JL. A rapid DNA isolation procedure for small quantities of fresh leaf tissue. Phytochemical Bulletin. 1987;19:11–15. [Google Scholar]
- Evanno G, Castella E, Goudet J. Evolutionary aspects of population structure for molecular and quantitative traits in the freshwater snail Radix balthica. Journal of Evolutionary Biology. 2006;19:1071–1082. doi: 10.1111/j.1420-9101.2006.01098.x. [DOI] [PubMed] [Google Scholar]
- Edelaar P, Björklund M. If FST does not measure neutral genetic differentiation, then comparing it with QST is misleading. Or is it? Molecular Ecology. 2011;20:1805–1812. doi: 10.1111/j.1365-294X.2011.05051.x. [DOI] [PubMed] [Google Scholar]
- Fahrig L. Effects of habitat fragmentation on biodiversity. Annual Review of Ecology, Evolution and Systematics. 2003;34:487–515. [Google Scholar]
- Falconer DS, Mackay TFC. Introduction to quantitative genetics. 4th edn. London: Longman; 1996. [Google Scholar]
- Frankham R. Quantitative genetics in conservation biology. Genetics Research. 1999;74:237–244. doi: 10.1017/s001667239900405x. [DOI] [PubMed] [Google Scholar]
- Goudet J, Büchi L. The effects of dominance, regular inbreeding and sampling design on QST, an estimator of population differentiation for quantitative traits. Genetics. 2006;172:1337–1347. doi: 10.1534/genetics.105.050583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gravuer K, von Wettberg E, Schmitt J. Population differentiation and genetic variation inform translocation decisions for Liatris scariosa var. novae-angliae, a rare New England grassland perennial. Biological Conservation. 2005;124:155–167. [Google Scholar]
- Hendry AP. QST>= ≠<FST? Trends in Ecology & Evolution. 2002;17:502. [Google Scholar]
- Hill WG, Goddard ME, Visscher PM. Data and theory point to mainly additive genetic variance for complex traits. PloS Genetics. 2008;4 doi: 10.1371/journal.pgen.1000008. pe1000008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle D. Comparing evolvability and variability of quantitative traits. Genetics. 1992;130:195–204. doi: 10.1093/genetics/130.1.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson M, Primmer CR, Merilä J. Does habitat fragmentation reduce fitness and adaptability? A case study of the common frog (Rana temporaria) Molecular Ecology. 2007;16:2693–2700. doi: 10.1111/j.1365-294X.2007.03357.x. [DOI] [PubMed] [Google Scholar]
- Lamy J, Plomion C, Kremer A, Delzon S. QST < FST as a signature of canalization. Molecular Ecology. 2012;21:5646–5655. doi: 10.1111/mec.12017. [DOI] [PubMed] [Google Scholar]
- Lande R. Genetics and demography in biological conservation. Science. 1988;241:1455–1460. doi: 10.1126/science.3420403. [DOI] [PubMed] [Google Scholar]
- Lande R. Neutral theory of quantitative genetic variance in an island model with local extinction and colonization. Evolution. 1992;46:381–389. doi: 10.1111/j.1558-5646.1992.tb02046.x. [DOI] [PubMed] [Google Scholar]
- Leinonen T, O'Hara RB, Cano JM, Merilä J. Comparative studies of quantitative trait and neutral marker divergence: a meta-analysis. Journal of Evolutionary Biology. 2008;21:1–17. doi: 10.1111/j.1420-9101.2007.01445.x. [DOI] [PubMed] [Google Scholar]
- Leinonen T, McCairns RJ, O'Hara RB, Merilä J. QST – FST comparisons: evolutionary and ecological insights from genomic heterogeneity. Nature Reviews Genetics. 2013;14:179–190. doi: 10.1038/nrg3395. [DOI] [PubMed] [Google Scholar]
- López-Fanjul C, Fernández A, Toro MA. The effect of neutral nonadditive gene action on the quantitative index of population divergence. Genetics. 2003;164:1627–1633. doi: 10.1093/genetics/164.4.1627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Pfrender M, Spitze K, et al. The quantitative and molecular genetic architecture of a subdivided species. Evolution. 1999;53:100–110. doi: 10.1111/j.1558-5646.1999.tb05336.x. [DOI] [PubMed] [Google Scholar]
- Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Research. 1967;27:209–220. [PubMed] [Google Scholar]
- McGarigal K, Cushman SA. Comparative evaluation of experimental approaches to the study of habitat fragmentation effects. Ecological Applications. 2002;12:335–345. [Google Scholar]
- McKay JK, Latta RG. Adaptive population divergence: markers, QTL and traits. Trends in Ecology & Evolution. 2002;17:285–291. [Google Scholar]
- Merilä J, Crnokrak P. Comparison of genetic differentiation at marker loci and quantitative traits. Journal of Evolutionary Biology. 2001;14:892–903. [Google Scholar]
- Miller JR, Wood BP, Hamilton MB. FST and QST under neutrality. Genetics. 2008;180:1023–1037. doi: 10.1534/genetics.108.092031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Hara RB, Merilä J. Bias and precision in QST estimates: problems and some solutions. Genetics. 2005;171:1331–1339. doi: 10.1534/genetics.105.044545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petit C, Frėville H, Mignot A, et al. Gene flow and local adaptation in two endemic plant species. Biological Conservation. 2001;100:21–34. [Google Scholar]
- Podolsky RH. Genetic variation for morphological and allozyme variation in relation to population size in Clarkia dudleyana, an endemic annual. Conservation Biology. 2001;15:412–423. [Google Scholar]
- Pujol B, Wilson AJ, Ross RIC, Pannell JR. Are QST–FST comparisons for natural populations meaningful? Molecular Ecology. 2008;17:4782–4785. doi: 10.1111/j.1365-294X.2008.03958.x. [DOI] [PubMed] [Google Scholar]
- Raymond M, Rousset F. Genepop, version 1·2: population genetics software for exact tests and ecumenicism. Journal of Heredity. 1995;86:248–249. [Google Scholar]
- Reed DH, Frankham R. How closely correlated are molecular and quantitative measures of genetic variation? A meta-analysis. Evolution. 2001;55:1095–1103. doi: 10.1111/j.0014-3820.2001.tb00629.x. [DOI] [PubMed] [Google Scholar]
- Ritland K. Extensions of models for the estimation of mating systems using n independent loci. Heredity. 2002;88:221–228. doi: 10.1038/sj.hdy.6800029. [DOI] [PubMed] [Google Scholar]
- Rogell B, Eklund M, Thörngren H, Laurila A, Höglund J. The effect of selection, drift and genetic variation on life-history trait divergence among insular populations of natterjack toad, Bufo calamita. Molecular Ecology. 2010;19:2229–2240. doi: 10.1111/j.1365-294X.2010.04642.x. [DOI] [PubMed] [Google Scholar]
- Rohlf FJ. Setauket, NY: Exeter Software; 1998. NTSYSpc Numerical Taxonomy and Multivariate Analysis System, version 2·0. [Google Scholar]
- Slatkin M, Barton NH. A comparison of three indirect methods for estimating average levels of gene flow. Evolution. 1989;43:1349–1368. doi: 10.1111/j.1558-5646.1989.tb02587.x. [DOI] [PubMed] [Google Scholar]
- Song WH, Li XD, Li XW, Huang HW, Li JQ. Genetic diversity and conservation strategy of Psilopeganum sinense, a rare species in the Three-Gorges reservoir area. Biodiversity Science. 2004;12:227–236. [Google Scholar]
- Sork VL, Nason J, Campbell DR, Fernandez JF. Landscape approaches to historical and contemporary gene flow in plants. Trends in Ecology & Evolution. 1999;14:219–224. doi: 10.1016/s0169-5347(98)01585-7. [DOI] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Thomas A, Best N, Lunn D. Cambridge, UK: MRC Biostatistics Unit; 2003. WinBUGS. Ver. 1·4 user manual. Available at http://www.mrc-bsu.cam.ac.uk/bugs . [Google Scholar]
- Tang FY. Population genetic structure and gene flow of Psilopeganum sinensis, a rare and endangered plant in the Three Gorges reservoir area. 2008 Doctoral dissertation: Graduate University of Chinese Academy of Sciences, Beijing, China. [Google Scholar]
- Tang FY, Ye QG, Yao XH, Huang H. Isolation and characterization of microsatellite loci in Psilopeganum sinense Hemsl (Rutaceae), an endangered herb endemic to Yangtze River valley. Molecular Ecology Resources. 2008;8:227–229. doi: 10.1111/j.1471-8286.2007.01933.x. [DOI] [PubMed] [Google Scholar]
- Thompson JD. Population differentiation in Mediterranean plants: insights into colonization history and the evolution and conservation of endemic species. Heredity. 1999;82:229–236. doi: 10.1038/sj.hdy.6885040. [DOI] [PubMed] [Google Scholar]
- Van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P. MICRO-CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Molecular Ecology Notes. 2004;4:535–538. [Google Scholar]
- Volis S, Yakubov B, Shulgina I, Ward D, Mendlinger S. Distinguishing adaptive from nonadaptive genetic differentiation: comparison of QST and FST at two spatial scales. Heredity. 2005;95:466–475. doi: 10.1038/sj.hdy.6800745. [DOI] [PubMed] [Google Scholar]
- Waldmann P, Andersson S. Comparison of quantitative genetic variation and allozyme diversity within and between populations of Scabiosa canescens and S. columbaria. Heredity. 1998;81:79–86. [Google Scholar]
- Waldmann P, García-Gil MR, Sillanpää MJ. Comparing Bayesian estimates of genetic differentiation of molecular markers and quantitative traits: an application to Pinus sylvestris. Heredity. 2005;94:623–629. doi: 10.1038/sj.hdy.6800672. [DOI] [PubMed] [Google Scholar]
- Whitlock MC. Neutral additive variance in a metapopulation. Genetics Research. 1999;74:215–221. doi: 10.1017/s0016672399004127. [DOI] [PubMed] [Google Scholar]
- Whitlock MC. Evolutionary inference from QST. Molecular Ecology. 2008;17:1885–1896. doi: 10.1111/j.1365-294X.2008.03712.x. [DOI] [PubMed] [Google Scholar]
- Willi Y, Van Buskirk J, Schmid B, Fischer M. Genetic isolation of fragmented populations is exacerbated by drift and selection. Journal of Evolutionary Biology. 2007;20:534–542. doi: 10.1111/j.1420-9101.2006.01263.x. [DOI] [PubMed] [Google Scholar]
- Wright S. The genetical structure of populations. Annals of Eugenics. 1951;15:323–354. doi: 10.1111/j.1469-1809.1949.tb02451.x. [DOI] [PubMed] [Google Scholar]
- Yang J, Li XD, Li XW, Shi QF, Li JQ. Analysis of AFLP variation of the endemic and rare species Psilopeganum sinense in Central China. Journal of Wuhan Botanical Research. 2007;25:226–234. [Google Scholar]
- Yang RC, Yeh FC, Yanchuk AD. A comparison of isozyme and quantitative genetic variation in Pinus contorta ssp. latifolia by FST. Genetic. 1996;142:1045–1052. doi: 10.1093/genetics/142.3.1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young AG, Boyle T, Brown T. The population genetic consequences of habitat fragmentation for plants. Trends in Ecology & Evolution. 1996;11:413–418. doi: 10.1016/0169-5347(96)10045-8. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Ye QG. Breeding system of the endangered species Psilopeganum sinense and its pollination process in a botanical garden. Plant Science Journal. 2011;29:599–606. [Google Scholar]