Reduced hierarchical models with application to estimating health effects of simultaneous exposure to multiple pollutants

Summary

Hierarchical models (HM) have been used extensively in multisite time series studies of air pollution and health to estimate health effects of a single pollutant adjusted for other pollutants and other time-varying factors. Recently, Environmental Protection Agency (EPA) has called for research quantifying health effects of simultaneous exposure to many air pollutants. However, straightforward application of HM in this context is challenged by the need to specify a random-effect distribution on a high-dimensional vector of nuisance parameters. Here we introduce reduced HM as a general statistical approach for analyzing correlated data with many nuisance parameters. For reduced HM we first calculate the integrated likelihood of the parameter of interest (e.g. excess number of deaths attributed to simultaneous exposure to high levels of many pollutants), and we then specify a flexible random-effect distribution directly on this parameter. Simulation studies show that the reduced HM performs comparably to the full HM in many scenarios, and even performs better in some cases, particularly when the multivariate random-effect distribution of the full HM is misspecified. Methods are applied to estimate relative risks of cardiovascular hospital admissions associated with simultaneous exposure to elevated levels of particulate matter and ozone in 51 US counties during 1999–2005.

1 Introduction

The US Environmental Protection Agency (EPA) estimated that thousands of premature deaths and hundred of thousands cases of illness may be avoided by reducing pollution (EPA, 2011). Most epidemiological studies of air pollution and health have estimated the health effects associated with ambient exposure to individual pollutants adjusted for exposure to other pollutants and confounders. However, National Research Council (NRC) has recently questioned whether the current approach of setting separate National Ambient Air Quality Standards (NAAQS) for each of the six criteria pollutants adequately protects population health, as this approach may greatly under-estimate risk (NRC, 2004). To meet the challenges of the NRC recommendations, new statistical methods are needed to account for multiple exposures and their interactions.

Previous multisite time series studies of the health effects of air pollution have estimated risks associated with exposure to a single pollutant. Dominici et al. (2000) developed a two-stage hierarchical model to combine information across locations on the association between daily changes of a given pollutant and daily changes in the health outcome, adjusted for other pollutants and confounders. This approach has been applied to several national US studies for estimating independent associations of various pollutants of epidemiologic interest with different health outcomes, including mortality and cardiovascular and respiratory emergency hospital admissions (Dominici et al., 2006; Bell et al., 2004; Peng et al., 2008, 2009). Two-level random-effect models have also been used to estimate health effects of exposure to individual pollutants and to identify factors that explain heterogeneity in the health risks across European cities (Katsouyanni et al., 2001). Addressing the potential for biased estimates due to measurement error of correlated exposures in multipollutant models, Zeka and Schwartz (2004) applied methodology developed by Schwartz and Coull (2003) to estimate independent effects of individual pollutants that minimizes the impact of measurement error.

To estimate the health effects of simultaneous exposure to multiple pollutants, we specify a hierarchical model (HM) that, at the first stage, flexibly specifies the air pollution-health outcome risk surface by incorporating interactions among pollutants and allowing for smooth nonlinear functions of pollutant concentrations. In the full HM, we define β_i to be the random effects describing the association between the health outcome and the multiple exposure variables included in the regression model (e.g. nonlinear functions of main effects and interactions of pollution variables and potential confounders) for the ith location. The parameter of primary scientific interest (θ_i) is the increased health risk when daily ambient levels of the pollutants considered are simultaneously above their national standards compared to when daily levels are below their national standards. Our goals are to obtain more precise estimates of θ_i by borrowing strength across locations, to estimate overall regional or national risks θ*, and to identify site-specific factors (e.g. population demographics, traffic patterns, long-term averages of other pollutants) that modify the association between simultaneous exposure to multiple pollutants and adverse health outcomes.

More generally, the hierarchical modeling approaches we consider apply to problems where the parameter of interest θ_i can be defined as a known function of β_i where dim(β_i) ≫ dim(θ_i). Many difficulties may arise upon implementation of standard Generalized Linear Mixed Models (GLMM) or full HM in the presence of a high-dimensional vector of random effects (β_i). First, one must specify a multivariate random-effect distribution on the full vector β_i, which might not be of primary scientific interest. There is an extensive literature on the consequences of misspecification of random-effect distributions in GLMM (Verbeke and Lesaffre, 1997; Heagerty and Kurland, 2001; Litière et al., 2008; Agresti et al., 2004). Though small to moderate misspecification of the random-effect distribution may not have a large impact in the estimation of fixed effects, there are situations for which misspecification can result in efficiency loss and biased estimates of the random effects (Neuhaus et al., 1992; Heagerty and Kurland, 2001; Agresti et al., 2004; Litière et al., 2010; McCulloch and Neuhaus, 2011). Several approaches have been proposed for specifying flexible semi- or non-parametric distributions for the random effects (Laird, 1978; Magder and Zeger, 1996; Komárek and Lesaffre, 2008; Gallant and Nychka, 1987; Chen et al., 2002). However, most of these approaches cannot be implemented in the context of a high-dimensional vector of random effects, and the validity of the assumption on the random-effect distribution is sometimes difficult to verify (Agresti et al., 2004; Litière et al., 2008). Second, if one is interested in estimating effect modification, at the second stage the full HM presents the additional challenge of specifying a high-dimensional multivariate regression model. Third, implementing diagnostic methods for misspecification of a multivariate random-effect distribution can be very challenging. Fourth, it may be computationally intensive and/or challenging to implement an MCMC sampler that mixes well and converges quickly to the stationary distribution as the number of random effects increases.

In this paper, we introduce reduced hierarchical models as a general statistical approach for eliminating nuisance parameters in hierarchical models with a large number of random effects. The reduced HM combines information across clusters (e.g. locations) directly on the parameter of interest θ_i. At the first stage, we calculate an integrated likelihood for θ_i, and at the second stage, we specify a flexible random-effect distribution directly on the θ_i. Reduced HM overcome many of the practical challenges in the specification and implementation of full HM in the context of a high-dimensional vector of nuisance parameters. Though developed to study health effects of simultaneous exposure to multiple pollutants, reduced HM are widely applicable for other studies of multiple exposures, and in general to clustered datasets with a large number of nuisance parameters. Accordingly, much of the methods section is presented in a general context while maintaining a close connection to the scientific motivation for this work.

Previous studies have used likelihoods of the parameter of interest at the first stage of a hierarchical model for conducting a meta analysis of randomized trials of a treatment for stomach ulcers (Efron, 1996; Liao, 1999). Specifically, Efron (1996) used a conditional likelihood for the clinical trial-specific log odds ratio (θ_i) and developed empirical Bayes methods for combining the likelihoods in order to conduct inference (interval estimation) on the θ_i. Liao (1999) also eliminated nuisance parameters at the first stage using conditional likelihoods, but he modeled the θ_i using a Bayesian approach, assuming a normal random-effect distribution for the θ_i. In these two studies, the vector of cluster-specific parameters β_i is just two-dimensional, and a conditional likelihood for θ_i is available in closed form. While not explicitly defining a likelihood function to eliminate nuisance parameters at the first stage of the HM, Warn et al. (2002), building upon the work by Smith et al. (1995), reparameterized the cluster-specific parameters β_i as (λ_i, θ_i), where θ_i is the parameter of interest, and then proposed to use noninformative priors for the nuisance parameter λ_i, which were assumed to be independent across clusters. However, it may not always be possible to define such a reparametrization (e.g., if θ_i is a complex function of β_i), and this approach still requires sampling the nuisance parameter λ_i at each iteration of the MCMC, which can become computationally expensive when the dimension of λ_i is large. In this paper we generalize parameter reduction for HM to very general situations where (1) no conditional or marginal likelihood is available; (2) an integrated likelihood is not available in closed form; (3) there does not exist a reparametrization (λ_i; θ_i) of the within-cluster parameter space; (4) the second-level model includes cluster-specific covariates; and (5) flexible specifications of the random-effect distribution are desired. This generalization is referred to as reduced HM. Additionally, while there are several practical advantages of the reduced HM arising from the elimination of nuisance parameters at the first stage, even in the specific context where this approach has been applied previously (2-dimensional setting with conditional likelihood available in closed form), there is a lack of evidence supporting the reduced HM as performing competitively with the full HM across a range of scenarios. To address this gap, we will provide a critical evaluation of the reduced HM as an alternative to fitting the full HM in a series of simulation studies.

In Section 2, we describe the multisite time series data used to estimate the health risks associated with simultaneous exposure to multiple pollutants. In Section 3, we describe the level-one model of an HM aimed at estimating the association between joint exposure to ozone and fine particulate matter and hospital admissions. In Section 4, we introduce the reduced HM in a general setting where an integrated likelihood is estimated for each cluster and a flexible random-effect distribution is specified directly on the cluster-specific parameter of interest. Section 5 describes our simulation study. In Section 6, we present our results from the data analysis. We provide discussion and concluding remarks in Section 7.

2 Data

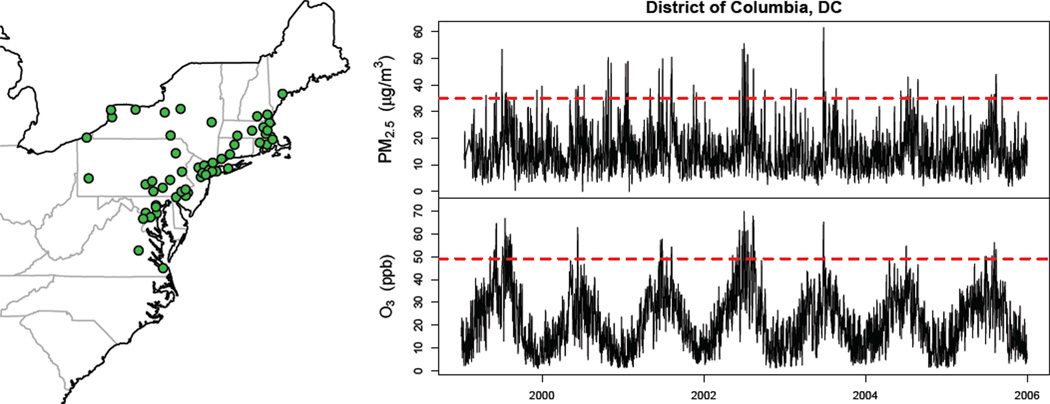
We used data from a national database consisting of parallel time series from 60 counties in the northeastern United States during the period 1999–2005. Daily counts of emergency hospital admissions for cardiovascular diseases (CVD), which comprise heart failure (ICD-9 code 428), heart rhythm disturbances (426–427), cerebrovascular events (430–438), ischemic heart disease (410–414, 429), and peripheral vascular disease (440–448) were obtained from billing claims of US Medicare enrollees. CVD admissions were stratified by two age categories, 65–74 and ≥ 75. Concentrations of fine particulate matter (PM_2.5; units µg/m³) and ozone (O₃; units parts per billion), which for many counties are measured on either a 1-in-3 or 1-in-6 day schedule, were obtained from the US EPA’s Air Quality System. Daily temperature and dewpoint temperature were obtained from the National Climatic Data Center. Among the 60 northeastern US counties with available data, we considered the 51 counties having at least 100 days where PM_2.5 and O₃ were measured concurrently, as well as at least one day when both pollutants were above their national standard (defined below). Figure 1 shows a map of the locations, as well as example time series of PM_2.5 and O₃ for Washington, DC.

Figure 1.

Left panel shows a map of the 51 northeastern US counties used for a multi-site time series study of the association between joint exposure to PM_2.5 and O₃ and hospitalization for cardiovascular diseases. Right panel shows daily times series of PM_2.5 (in µg/m³) and O₃ (in parts per billion; ppb) for the District of Columbia for the period 1999–2005. Horizontal lines correspond to the daily national standards for each pollutant.

3 Poisson regression model for multiple pollutants

In this section we describe the first level of an hierarchical model for estimating health effects associated with simultaneous exposure to fine particulate matter (PM_2.5) and ozone (O₃). We assume for county i on day j for age group k, the number of CVD admissions y_ijk has a Poisson distribution with mean model

$$\text{log}𝔼[y_{\mathit{\text{ijk}}}]=\text{log}(n_{\mathit{\text{ijk}}})+{\gamma }_{i0}+ns({\text{PM}}_{2.5ij};3\mathit{\text{df}},{\mathbf{b}}_{i1})\cdot \mathit{\text{ns}}({\mathrm{O}}_{3ij};3\mathit{\text{df}},{\mathbf{b}}_{i2})+{\gamma }_{i1}{\text{age}}_k+{\gamma }_{i2}^{\prime }{\text{dow}}_{ij}+ns({\text{temp}}_{ij};6\mathit{\text{df}},{\gamma }_{i3})+ns({\text{dptp}}_{ij};3\mathit{\text{df}},{\gamma }_{i4})+ns({\overline{\text{temp}}}_{ij}^{(3)};6\mathit{\text{df}},{\gamma }_{i5})+ns({\overline{\text{dptp}}}_{ij}^{(3)};3\mathit{\text{df}},{\gamma }_{i6})+ns(j;7\mathit{\text{df}}/\text{year},{\gamma }_{i7}),$$ (1)

where n_ijk is the number of individuals of the kth age group at risk, and ns(·) denotes natural cubic splines with the specified degrees of freedom (df) and b_ij (j = 1, 2) and γ_ij (j = 3,…, 7) representing the spline coefficients. The product of the cubic spline bases for PM_2.5 and O₃, which includes both main effects and interaction terms, provides a flexible specification of the unknown joint pollutant-hospital admissions exposure-response surface. Here age denotes an indicator for being in the ≥ 75 age category (versus 65–74); dow is a vector of indicator variables for day of week; ${\text{temp}}_{ij}({\overline{\text{temp}}}_{ij}^{(3)})$ is the current day’s (average of the previous three days’) average temperature; and ${\text{dptp}}_{ij}({\overline{\text{dptp}}}_{ij}^{(3)})$ is the current day’s (average of the previous three days’) average dew point temperature. The smooth function of calendar time ns(j; 7 df/year, γ_i7) accounts for seasonality and longer-term, time-varying trends in hospital admissions.

This within-county model extends those developed to study PM_2.5 and O₃ individually (Dominici et al., 2006; Bell et al., 2004) by allowing for nonlinear associations of each of the pollutants and their interaction. In particular, the choice of covariates and df in the smooth functions are based on those used by Dominici et al. (2006). Previous studies have assessed the sensitivity of health effect estimates from single-pollutant models to adjustment for temperature and the smooth function of calendar time, finding that results were robust across specifications of the confounder model (Peng et al., 2006; Welty and Zeger, 2005).

To place model (1) within the more general context of HM for two-level clustered data, we introduce some notation. Let b_i = (b_i1, b_i2) be the vector of random effects for the exposure-response surface characterizing the relation between joint exposure to ozone and fine particulate matter and the health outcome. Let γ_i = (γ_i0, γ_i1,…, γ_i7) be the vector of random effects describing the association between the confounders and the health outcome, and define β_i = (b_i, γ_i). Note that these random effects are introduced in order to model variation across counties, not as a random-effects parameterization of penalized splines (the number of df in the spline terms is fixed). Let x_ij denote the full vector of covariate data for day j in county (cluster) i, and let ${\mathbf{x}}_{ij}^{\mathbf{b}}$ denote the 15-dimensional subvector of x_ij that is the concatenation of the basis terms for the main effects and interactions of the spline bases for ozone and fine particulate matter, ns(PM_2.5ij; 3 df, b_i1) · ns(O_3ij; 3 df, b_i2).

We next define a variable that identifies whether the daily levels of either PM_2.5 and/or O₃ are above or below their corresponding 24-hour National Ambient Air Quality Standards (NAAQS),

$${\text{NAAQS}}_{ij}=\{\begin{array}{c}A\text{\hspace{1em}if}{\text{PM}}_{2.5}>35\mu g/m^3\text{ and }{\mathrm{O}}_3>0.049\text{ ppm }\\ B\text{\hspace{1em}if}{\text{PM}}_{2.5}>35\mu g/m^3\text{ and }{\mathrm{O}}_3\le 0.049\text{ ppm }\\ C\text{\hspace{1em}if}{\text{PM}}_{2.5}\le 35\mu g/m^3\text{ and }{\mathrm{O}}_3>0.049\text{ ppm }\\ D\text{\hspace{1em}if}{\text{PM}}_{2.5}\le 35\mu g/m^3\text{ and }{\mathrm{O}}_3\le 0.049\text{ ppm }.\end{array}$$

The values 35 µg/m³ and 0.049 ppm were derived from the NAAQS, which are defined in Appendix A of the Supplementary Materials.

We define θ_i to be the log of the expected number of CVD admissions on days when both PM_2.5 and O₃ are above their respective national standards divided by the expected number of CVD admissions on days when both pollutants are lower than their national standards, adjusted for the potential confounding variables:

$${\theta }_i:=h({\beta }_i;{\mathbf{x}}_i)=\text{log}\frac{\frac{1}{N_{\mathit{\text{iA}}}}{\displaystyle {\sum }_{j:{\text{NAAQS}}_{\mathit{\text{ij}}=A}}\text{exp}({\mathbf{b}}_i^{\prime }{\mathbf{X}}_{ij}^{\mathbf{b}})}}{\frac{1}{N_{\mathit{\text{iD}}}}{\displaystyle {\sum }_{j:{\text{NAAQS}}_{\mathit{\text{ij}}=D}}\text{exp}({\mathbf{b}}_i^{\prime }{\mathbf{X}}_{ij}^{\mathbf{b}})}}.$$ (2)

Here N_iA (N_iD) are the number of days when both pollutants are above (below) their respective national standards in county i during the study period 1999–2005. Derivation of the formulation for the parameter of interest is in Appendix B of the Supplementary Materials. Other definitions of θ_i that may be of interest, such as the log of the expected number of CVD admissions on days when only PM_2.5 (or when only O₃) is above its national standard divided by the expected number of CVD admissions on days when both pollutants are lower than their national standards could be defined similarly and the same methods (described below) could be straightforwardly applied.

4 Reduced hierarchical model

Rather than specify a full HM on the large number of random effects β_i, we define a reduced HM directly on the parameter of interest θ_i:

$${\mathbf{y}}_i|{\theta }_i~L_i({\theta }_i);\text{\hspace{1em}independent},i=1,\dots ,I$$ (3)

$${\theta }_i|\mathbf{\alpha }~\text{RE}({\theta }_i|\mathbf{\alpha });\text{\hspace{1em}independent},i=1,\dots ,I.$$

Here L_i(θ_i) denotes a likelihood function (detailed below) and RE(θ_i|α) denotes an arbitrary random-effect distribution. Note that the likelihood function in general depends on the vector of outcome data from the ith cluster y_i and on the set of covariate data x_i, though we suppress this dependency in our notation. To conduct inference in the Bayesian framework, a prior distribution is placed on α.

The reduced HM may be further generalized by allowing the random-effect distribution RE(θ_i|α) to depend on cluster-level covariates z_i, in order to study potential effect modification. In particular, for the second-stage model we assume ${\theta }_i={\alpha }_{0i}+{\mathbf{\alpha }}_1^{\prime }{\mathbf{z}}_i$ and place the random-effect distribution on the α_0i. The second level model may also be extended to allow the θ_i to be spatially correlated across clusters.

4.1 Integrated Likelihood

In the general setting where the parameter of interest θ_i is a complicated function of the level 1 parameters β_i as in (2), we propose to use an integrated likelihood for L_i(θ_i). For notational simplicity the cluster-specific subscript i is suppressed in what follows. An integrated likelihood for the ith cluster may be expressed as

$$f_{\mathbf{y}|\theta }(\mathbf{y}|\theta )\propto f_{\theta |\mathbf{Y}}(\theta |\mathbf{y})/{\pi }_{\theta }(\theta ),$$ (4)

where π_θ(θ) is the prior distribution for θ and f_θ|Y is the corresponding posterior distribution of θ based on the data from only that cluster. Note that in the special case where the cluster-specific parameters β can be reparametrized as (θ,λ), this expression can be rewritten as f_y|θ(y|θ) = ∫ f_y|θ,λ (y|θ, λ) π_λ|θ(λ|θ)dλ, where f_y|θ,λ is the joint likelihood, and π_λ|θ is the prior density of λ given θ (Berger et al., 1999).

When such a reparametrization of β is not available or when f_y|θ(y |θ) is not available in closed form, we propose a simulation approach to approximate (4) as follows:

1. Assign a prior distribution to the vector β of level-1 parameters, such that the induced prior distribution π_θ(θ) on θ = h(β; x) is diffusely spread out over the range of plausible values for θ. Simulate R prior samples from π_θ(θ).

2. Fit a within-cluster model to generate R samples β^(r) from the posterior f_β|y(β|y).

3. Obtain the posterior samples θ^(r) = h(β^(r); x).

4. Select a grid of points {θ_k} covering the range of θ and apply a Gaussian kernel smoother to estimate both f_θ|y (θ|y) and π_θ(θ) on this grid.

We repeat this process for each cluster i to obtain approximations f̂_yi|θ_i (y_i | θ_i), i = 1,…, I. Note that the choice of prior distribution for β in Step 1 will depend on the form of the function h. Also note that while this procedure requires drawing from the posterior f_βi|yi (β_i | y_i), since this is done within each cluster independently, the sampling is greatly simplified as compared to fitting the full HM where the β_i are correlated across clusters (i.e. sampling from f_{β1,…,βI |y1,…,yI} (β₁,…, β_I |y₁,…, y_I)). In addition, since this step is performed a single time prior to fitting the reduced HM, estimating the parameters of the reduced HM remains fast. Further details of our implementation are in Appendix C of the Supplementary Materials.

4.2 Dirichlet process mixture model for RE(θ_i|α)

To allow for flexible specification of the random-effect distribution we propose to use a Dirichlet process mixture model for RE(θ_i|α). The Dirichlet process mixture model (Ferguson, 1973; Neal, 2000) can be expressed as the limit as the number of components K goes to infinity of the mixture model

$${\theta }_i|c_i,\varphi ~F({\theta }_i|{\varphi }_{ci});\text{\hspace{1em}independent},i=1\dots ,I$$

$$c_i|\mathbf{p}~\text{Discrete}(c_i|p_1,\dots ,p_K);\text{\hspace{1em}independent},i=1,\dots ,I$$

$${\varphi }_c~G_0\text{ for any }c$$

$$\mathbf{p}~\text{Dirichlet}(\delta /K,\dots ,\delta /K),$$

where Discrete(c_i | p₁,…, p_K) corresponds to the p.m.f. ℙ(c_i = k) = p_k (k = 1, …, K) and δ/K is the concentration parameter written so that it approaches 0 as K goes to infinity. Here we consider a normal mixture so that F(· | ϕ_c) = N(· | µ_c, τ_c), and we select the conjugate prior so that G₀ = NormalGamma(λ, γ, a, b), i.e. τ_c ~ Gamma(τ | a, b) and µ_c | τ_c ~ N(λ, γτ_c).

4.3 Computational details

The reduced HM (3) may be fit using Markov Chain Monte Carlo (MCMC) methods (Metropolis et al., 1953; Gilks et al., 1995) to generate samples from the posterior distribution of the unknown parameters

$$\mathbb{P}({\theta }_1,\dots ,{\theta }_I,\mathbf{\alpha }|{\mathbf{y}}_1,\dots ,{\mathbf{y}}_I)\propto \pi (\mathbf{\alpha }){\displaystyle \prod _{i=1}^I\{\text{RE}({\theta }_i}|\mathbf{\alpha })L_i({\theta }_i)\},$$

where π(α) denotes the prior distribution on the vector of parameters of the random-effect distribution. At each iteration of the MCMC algorithm, a sample is drawn from the full conditional

$$f_c({\theta }_i)\propto \text{RE}({\theta }_i|\mathbf{\alpha })L_i({\theta }_i)$$ (5)

for each cluster i. When the integrated likelihood has been estimated using the approach from Section 4.1, we replace L_i(θ_i) in equation (5) by f̂ _yi|θi (y_i | θ_i). Since f_c(θ_i) is not a known distribution, we sample from it by applying a Metropolis-Hastings step. In the Metropolis-Hastings step, we need to evaluate the likelihood f̂_yi|θi at an arbitrary point θ. We do this by selecting the grid point θ_k that is closest to θ and evaluating the likelihood at that grid point.

For generating posterior samples of α when RE(θ_i | α) is the Dirichlet process mixture model defined in Section 4.2, we adapt an MCMC sampling algorithm described by Neal (2000). Details are in Appendix C of the Supplementary Materials.

5 Simulation study

There are instances for which the reduced HM may be preferred to the full HM due to practical considerations such as its simplified implementation and the ease with which prior information may be incorporated directly on the parameter of interest. However, a more thorough understanding of situations when the reduced HM works well is needed. In this section we conduct simulation studies to compare performance of the reduced HM to the full HM across a range of scenarios.

We base our studies on data from a meta-analysis of 41 randomized trials of a treatment for stomach ulcers, provided by Efron (1996). Rather than use the multipollutant case study as a basis for simulation studies, a meta-analysis example is used to highlight the broad utility of the reduced HM methodology across diverse applications. In addition, even in the simpler context of this application (two-dimensional vector of random effects β_i) for which a full HM may be straightforwardly implemented, the relative performance of the reduced HM to the full HM is not well understood and, as we shall see, the full HM may not always be the optimal choice even in the low-dimensional case.

The data from the ith trial is {y_i = (y_i0, y_i1), x_i = (n_i0, n_i1)}, where y_i0, y_i1 are the number of occurrences of ulcers for the control and treatment groups, and n_i0, n_i1 are the number of subjects in the control and treatment groups, respectively. Let p_i = (p_i0, p_i1) be the vector of probabilities of the occurrence of ulcers in the control and treatment groups. The distribution of the data from experiment (cluster) i is assumed to be ${\mathbb{P}}_i({\mathbf{y}}_i|{\mathbf{x}}_i;{\mathbf{p}}_i)=\left(\begin{array}{c}{n}_{i1}\\ y_{i1}\end{array}\right)p_{i1}^{y_{i1}}{(1-p_{i1})}^{n_{i1}-y_{i1}}\left(\begin{array}{c}{n}_{i0}\\ y_{i0}\end{array}\right)p_{i0}^{y_{i0}}{(1-p_{i0})}^{n_{i0}-y_{i0}}$, and the parameter of interest is the log odds ratio

$${\theta }_i=h({\mathbf{p}}_i)=\text{log}\frac{p_{i1}/(1-p_{i1})}{p_{i0}/(1-p_{i0})}.$$ (6)

In this example, a full HM would require the specification of a random-effect distribution for p_i = (p_i1, p_i0). Alternatively, a commonly used specification first defines a one-to-one transformation of the p_i into ℝ² through the logit link and assumes a bivariate normal distribution for the random effects:

$$y_{ki}|p_{ik}~\text{Binom}(n_{ik},p_{ik})\text{\hspace{1em}for}k=0,1$$ (7)

$$\text{logit}(p_{ik})={\beta }_{i0}+{\beta }_{i1}\mathbf{I}(k=1)$$

$$({\beta }_{i0},{\beta }_{i1})\prime ~\mathrm{N}(({\beta }_0^{*},{\beta }_1^{*})\prime ,\mathrm{\Sigma }).$$

For a reduced HM, we first summarize the information contained in experiment i about the log odds ratio θ_i through a likelihood function, and we then specify a random-effect distribution directly on the θ_i. For this problem, a conditional likelihood for θ_i is available in closed form. By conditioning on the margins of the two-by-two table for each experiment, the conditional likelihood may be expressed as

$$L_i^C({\theta }_i)=\frac{\left(\begin{array}{c}{n}_{i0}\\ y_{i0}\end{array}\right)\left(\begin{array}{c}{n}_{i1}\\ y_{i1}\end{array}\right)\text{exp}({\theta }_i{y}_{i1})}{{\sum }_{u=0}^{\text{min}(n_{i1},y_{i0}+y_{i1})}\left(\begin{array}{c}{n}_{i0}\\ u\end{array}\right)\left(\begin{array}{c}{n}_{i1}\\ y_{i1}+y_{i0}-u\end{array}\right)\text{exp}({\theta }_{i}u)}.$$ (8)

We may then use $L_i^c({\theta }_i)$ for the likelihood function in the reduced HM (3). Computing integrated likelihoods for each of the randomized trials in the ulcer data set (Efron, 1996), we found them to be generally quite similar to the corresponding conditional likelihoods, and so only the conditional likelihoods were considered in the simulation study.

We simulated data under four data generating mechanisms, and we estimated model parameters under four HM formulations. We next describe each of the hierarchical modeling approaches used to fit the data, after which we detail the four data generating models.

5.1 Hierarchical models

We fit each simulated data set using four approaches: a full HM assuming the logistic model (7) with a normal random-effect distribution on the β_i (FHM); a reduced HM using the conditional likelihood $L_i^c({\theta }_i)$ from equation (8) with a normal random-effect distribution on the θ_i (RHM-L-N); a reduced HM using the conditional likelihood $L_i^c({\theta }_i)$ from (8) with a flexible random-effect distribution on the θ_i (RHM-L-DP); and a reduced HM using a normal approximation to the likelihood with a normal random-effect distribution on the θ_i (RHM-N-N). For the flexible random-effect distribution, we considered the Dirichlet Process normal mixture model described in Section 4.2. For each approach, we estimated the cluster-specific log odds ratios θ_i as well as the overall log odds ratio θ* = 𝔼(θ_i), where the expectation is taken over all of the clinical trials included in the analysis. Additionally, we obtained 95% posterior intervals for the overall (θ*) and cluster-specific (θ_i) parameters. Details of estimation for each of the four models are in Appendix D of the Supplementary Materials.

5.2 Data generating models

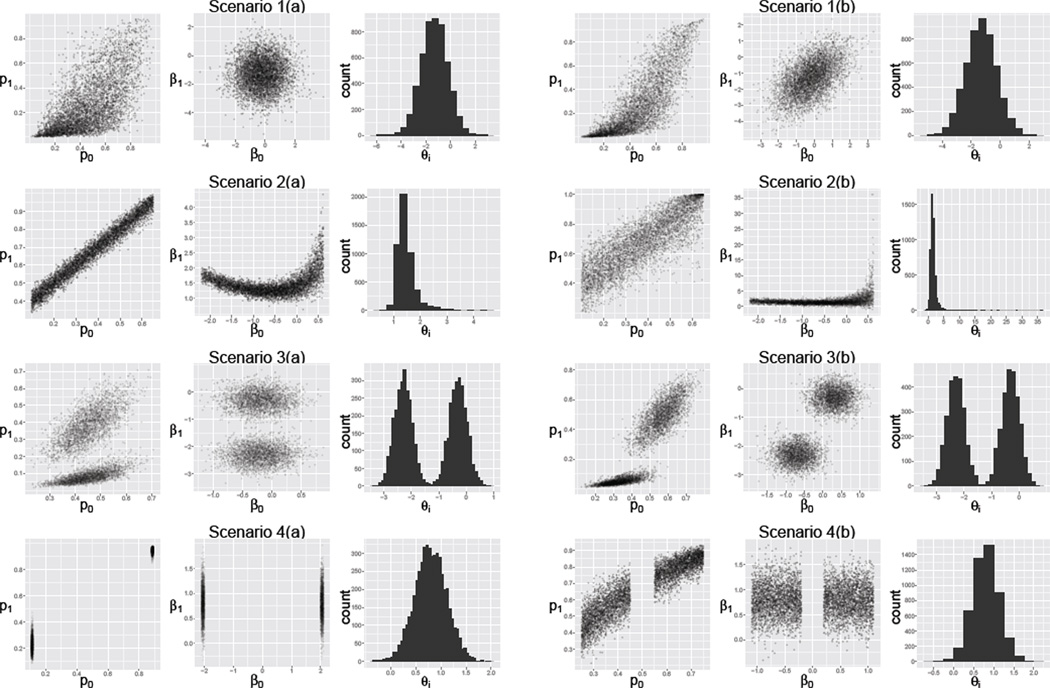
We considered four data generating models. We always assumed y_i0 ~ Binom(n_i0, p_i0) and y_i1 ~ Binom(n_i1, p_i1), and we selected different models for generating p_i0 and p_i1 (i = 1,…, I). Note that each model for generating p_i0 and p_i1 induces a distribution on the log odds ratio θ_i through (6). Thus, each time we generated a dataset, we obtained I values of the cluster-specific, true log odds ratios θ_i (one for each cluster i). The models were selected in order to distinguish among scenarios where the full HM is expected to outperform the reduced HM and vice versa. Figure 2 shows, for each of the four data generating models, the distribution of the (p_i0, p_i1), along with the corresponding distributions of the $({\beta }_{0i},{\beta }_{1i})=\left(\text{log}\frac{p_{i0}}{1-p_{i0}},{\theta }_i\right)$ and the log odds ratios θ_i.

Figure 2.

Plots of simulated data under each scenario from four data-generating models. First row displays data from model 1, scenarios (a)–(b); second row shows data from model 2, scenarios (a)–(b); third row corresponds to model 3, scenarios (a)–(b); and fourth row to model 4, scenarios (a)–(b). For each scenario 5000 data points (p_i0, p_i1) are plotted, as well as the corresponding points (β_i0, β_i1) under the transformation logit(p_ik) = β_i0 + β_i1 I(k = 1), and histograms of the corresponding log odds ratios θ_i.

In each case, we set n_i0 = n_i1 = n, and we considered n = 100 for I = 100, 50, and 25. These parameter values were selected to correspond to a large within-cluster sample size for either a large, moderate, or small number of clusters.

Model 1 - Bivariate Normal

We generated data from

$$({\beta }_{0i},{\beta }_{1i})\prime ~\mathrm{N}(({\beta }_0^{*},{\beta }_1^{*})\prime ,\mathrm{\Sigma })$$

$$\text{logit}(p_{ki})={\beta }_{0i}+{\beta }_{1i}\mathbf{I}(k=1),$$

where $({\beta }_0^{*},{\beta }_1^{*})=(-0.2,-1.3)$, and we considered two different values for Σ,

$${\mathrm{\Sigma }}_a=\left[\begin{array}{cc}0.9& 0\\ 0& 1.1\end{array}\right]\text{\hspace{1em}and\hspace{1em}}{\mathrm{\Sigma }}_b=\left[\begin{array}{cc}0.9& 0.5\\ 0.5& 1.1\end{array}\right]$$

(see scenarios 1(a) and 1(b) in Figure 2). These parameter values were selected to be the same order of magnitude of those from the ulcer data set. Since this model fully specifies a normal random-effect distribution on the β_i, particularly in scenario 1(b) where a moderate correlation between the random effects is assumed, we expected it to favor the full HM (7).

Model 2 - Uniform/Beta

We generated p_i0 ~ Uniform(0.1, 0.6) and p_i1 | p_i0 ~ Beta(m = p_i0 + 0.3, ϕ), where the beta distribution is parametrized by its mean m and variance ϕ. We considered two values for ϕ, namely ϕ_a = 0.001 and ϕ_b = 0.01. Since this model is not based on either the full or reduced HM a priori we didn’t expect it to favor either of these two approaches (see scenarios 2(a) and 2(b) in Figure 2).

Model 3 - Normal Mixture

We generated (p_i0, p_i1) by

$$({\beta }_{0i},{\beta }_{1i})\prime ~\alpha \mathrm{N}({\beta }^{*}-\mathit{\nu },\mathrm{\Sigma })+(1-\alpha )\mathrm{N}({\beta }^{*}+\mathit{\nu },\mathrm{\Sigma })$$

$$\text{logit}(p_{ki})={\beta }_{0i}+{\beta }_{1i}\mathbf{I}(k=1),$$

where we fixed β* = (−0.2; 1.3), α = 0.5, and Σ = diag{(0.1, 0.1)}. We considered two values for ν, namely ${\mathit{\nu }}_a^{\prime }=(0,1)\text{ and }{\mathit{\nu }}_b^{\prime }=(0.5,1)$. This data generating model was selected because the random-effect distribution will be misspecified for both the full and the reduced HM (since θ_i = β_i1), when a normal random-effect distribution is assumed; thus, we expected neither approach to perform particularly well (see scenarios 3(a) and 3(b) in Figure 2).

Model 4 - Normal-θ_i

Finally, we generated data by first simulating values for the log odds ratios θ_i and for the log odds ${\lambda }_i=\text{log}\left(\frac{p_{0i}}{1-p_{0i}}\right)$, which induces a distribution on the $(p_{0i},p_{1i})=\left(\frac{\text{exp}({\lambda }_i)}{1+\text{exp}({\lambda }_i)},\frac{\text{exp}({\lambda }_i+{\theta }_i)}{1+\text{exp}({\lambda }_i+{\theta }_i)}\right)$. In particular, we simulated θ_i ~ N(µ, σ²) and λ_i ~ 0.5U(−u₂, −u₁) + 0.5U(u₁, u₂), where we fixed µ = 0.8, σ² = 10. We considered two scenarios for u₁ and u₂, namely (u_1a, u_2a) = (2, 2.1) and (u_1b, u_2b) = (0.2, 1.1). This model was chosen because it was expected to favor the reduced HM over the full HM, since the normal random-effect distribution on the (β_i0, β_i1)′ for the full HM will be misspecified, while the random-effect distribution for θ_i in the reduced HM will be correctly specified (see scenarios 4(a) and 4(b) in Figure 2).

5.3 Results

We evaluated the relative performance of the four modeling approaches (FHM, RHM-L-N, RHML-DP, and RHM-N-N) in estimating both the cluster-specific (θ_i) and overall (θ*) log odds ratios. Because disparity in performance across methods was attenuated for the smaller values for the numbers of clusters, in this section we focus our discussion on results for I = 100 (Table 1). Results for cases I = 25 and I = 50 are in Tables S1 and S2 of the Supplementary Materials.

Table 1.

Simulation results for the cluster-specific log odds ratios θ_i: squared error loss ${\displaystyle {\sum }_{i=1}^I{({\tilde{\theta }}_i-{\theta }_i)}^2}$ for the posterior mean estimates θ̃_i (sq. error), and coverage of 95% posterior intervals. Results for the mean log odds ratio θ*: bias, standard deviation, and rMSE of the posterior mean estimates θ̃* and coverage of 95% posterior intervals. Methods compared are the full hierarchical model (FHM), reduced HM with conditional likelihood and normal random-effect distribution (RHM-L-N), reduced HM with normal approximation to the likelihood and normal random-effect distribution (RHM-N-N), and reduced HM with conditional likelihood and Dirichlet-Process normal mixture for the random-effect distribution (RHM-L-DP).

	Simulation	Cluster θi		Overall θ*
		Sq. Error	Coverage	Bias	SD	rMSE	Coverage
Model 1: Bivariate Normal	1(a)*				θ*=−1.3
	(i) FHM	14.4	0.95	0.00	0.11	0.11	0.94
	(ii) RHM-L-N	14.8	0.95	0.02	0.11	0.11	0.95
	(iii) RHM-L-DP	14.8	0.95	0.03	0.11	0.11	0.94
	(iv) RHM-N-N	18.0	0.94	0.09	0.10	0.14	0.89
	1(b)*				θ*=−1.3
	(i) FHM	14.9	0.95	−0.01	0.12	0.12	0.94
	(ii) RHM-L-N	18.9	0.94	0.04	0.11	0.12	0.93
	(iii) RHM-L-DP	18.9	0.94	0.06	0.11	0.12	0.92
	(iv) RHM-N-N	27.5	0.92	0.14	0.10	0.17	0.74
Model 2: Uniform/ Beta	2(a)				θ* = 1.46
	(i) FHM	7.5	0.88	−0.03	0.04	0.05	0.87
	(ii) RHM-L-N	8.0	0.91	−0.03	0.04	0.05	0.90
	(iii) RHM-L-DP	7.5	0.95	−0.04	0.04	0.06	0.90
	(iv) RHM-N-N	9.6	0.89	−0.07	0.04	0.08	0.66
	2(b)				θ*= 1.67
	(i) FHM	99.5	0.90	−0.14	0.08	0.16	0.55
	(ii) RHM-L-N	104.2	0.91	−0.13	0.08	0.16	0.56
	(iii) RHM-L-DP	96.2	0.92	−0.14	0.09	0.17	0.57
	(iv) RHM-N-N	137.6	0.89	−0.23	0.07	0.24	0.11
Model 3: Normal Mixture	3(a)				θ*= −1.3
	(i) FHM	10.6	0.95	−0.01	0.11	0.11	0.97
	(ii) RHM-L-N	11.6	0.95	0.00	0.11	0.11	0.97
	(iii) RHM-L-DP	9.8	0.96	0.02	0.10	0.11	1.00
	(iv) RHM-N-N	11.6	0.95	0.06	0.10	0.12	0.94
	3(b)				θ* = −1.3
	(i) FHM	10.1	0.95	−0.02	0.12	0.13	0.93
	(ii) RHM-L-N	13.5	0.95	0.02	0.12	0.12	0.94
	(iii) RHM-L-DP	12.1	0.96	0.03	0.12	0.12	0.99
	(iv) RHM-N-N	15.0	0.94	0.12	0.11	0.17	0.80
Model 4: Normal-θi	4(a)				θ*= 0.8
	(i) FHM	7.9	0.84	0.00	0.06	0.06	0.85
	(ii) RHM-L-N	7.2	0.93	0.01	0.06	0.06	0.94
	(iii) RHM-L-DP	7.3	0.97	−0.01	0.06	0.06	0.96
	(iv) RHM-N-N	7.5	0.90	−0.05	0.05	0.07	0.86
	4(b)				θ*= 0.8
	(i) FHM	5.1	0.93	0.00	0.05	0.05	0.93
	(ii) RHM-L-N	5.2	0.94	0.00	0.05	0.05	0.94
	(iii) RHM-L-DP	5.2	0.96	−0.01	0.04	0.05	0.94
	(iv) RHM-N-N	5.2	0.94	−0.02	0.04	0.05	0.93

^*For scenarios 1(a) and 1(b), the summary statistics for RHM-L-DP are based on 999 and 998 simulation repetitions, respectively. The other repetitions were excluded because the MCMC didn’t converge within the maximum number of iterations.

The main disparity in performance across the reduced HM (RHM-L-N and RHM-L-DP) and full HM approaches occurred for estimation of the cluster-specific parameters θ_i; methods (except RHM-N-N) performed comparably for estimating the overall θ*. The two situations where FHM yielded similar or slightly better cluster-specific estimates than the reduced HM were those for which the data generating model implied considerable correlation between β_0i and β_1i, which could be captured to varying degrees by the bivariate normal random-effect distribution on the β_i. This occurred for data generating models 1(b) and 3(b), which had correlation of ≈ 0.5 and 0.8, respectively (see Figure 2). Because nuisance parameters are eliminated before pooling, the reduced HM do not take advantage of this correlation structure. For the other scenarios, the reduced HM generally performed comparably to or better than the FHM. Comparing the reduced HM with different random-effect distributions, we found that RHM-L-DP performed just as well or only slightly worse than RHM-L-N when the true distribution was normal (models 1(a)–(b) and 4(a)–(b)), but performed moderately better when the true random-effect distribution was non-normal (models 2(a)–(b) and 3(a)–(b)).

Across simulation scenarios we generally found that the model using the normal approximation to the likelihood (RHM-N-N), although most efficient computationally, was not competitive with the other approaches. For estimating θ_i, the RHM-N-N either performed comparably (scenarios 2(a), 3(a) and 4(a)–(b)), or moderately worse (scenarios 1(a)–(b), 2(b), and 3(b)) than the other approaches. For estimating the overall θ*, the RHM-N-N generally had larger rMSE and coverage markedly lower than the nominal rate (exceptions are scenarios 3(a) and 4(c)). One reason for the poor performance of RHM-N-N is that the normal approximation to the likelihood does not provide a good approximation in this application, particularly when y_i1 or y_i0 is equal to zero or n (which occurs most frequently under models 1(a)–(b) and 3(a), scenarios where RHM-N-N performs worst). In addition, we note that under scenario 2(b), none of the approaches performed particularly well for estimating the mean (θ*) of the highly skewed random-effect distribution for θ_i.

5.4 Conclusions

Our simulation studies were designed to assess the relative performance of the reduced HM to the full HM across different scenarios of misspecification of the random-effect distribution. We found that large correlation in the random effects β_i generally led to slightly improved estimation of the cluster-specific θ_i by the full HM as compared to the reduced HM. However, in other scenarios, namely those for which the random-effect distribution for the full HM was misspecified, the reduced HM achieved superior performance. In addition, for estimating the overall θ* we found performance to be very similar across methods. Overall, in our simulation studies the reduced HM performed nearly as well as the full HM, and even performed better in some cases.

6 Application

We applied the reduced HM to our multisite time series study of 51 urban counties in the north-eastern US for the period 1999–2005. Our goal was to estimate the county-specific and overall log relative risks of emergency cardiovascular hospital admissions associated with levels of PM_2.5 and O₃ above their national standards.

We considered three types of reduced HM. The first uses a normal approximation to the likelihood at the first stage and a normal random-effect distribution at the second stage (RHM-N-N). The second uses an integrated likelihood at the first stage and a normal random-effect distribution at the second stage (RHM-L-N). The third uses an integrated likelihood at the first stage and a Dirichlet process normal mixture for the random-effect distribution (RHM-L-DP). The parameter of interest θ_i, defined in (2), is the log relative risk of cardiovascular admissions when PM_2.5 and O₃ are both above their national standards compared to when both are below their standards. For each reduced HM we assumed little prior information, by incorporating diffuse priors on the overall θ* We first fit each reduced HM without including any second-level covariates. We subsequently considered inclusion, at the second stage, of a county-specific measure of the average level of NO₂ during the study period to demonstrate how reduced HM may be used to identify effect modification. Long-term average NO₂ may be an important effect modifier because it a proxy for traffic exposure. This was done by assuming, at the second level that θ_i = α_0i + α₁z_i, where z_i is the long-term average NO₂ for the ith county, and placing each of the normal $({\alpha }_{0i}~\mathrm{N}({\alpha }_0^{*},{\tau }^2))$ and flexible (Section 4.2) random-effect distributions on the α_0i. Details of the implementations for each reduced HM are in Appendix C of the Supplementary Materials.

Prior to fitting the reduced HM using the integrated likelihood (RHM-L-N and RHM-L-DP), we evaluated the performance of the integrated likelihood in the air pollution context through simulation study (detailed in Appendix E). Brifley, we considered a model based on our air pollution and health outcome data for which the integrated likelihood may be written in closed form. We simulated data under this model, applied our approach to estimate the integrated likelihood (described in Section 4.1), and compared our estimated integrated likelihood to the true integrated likelihood, finding that the estimate closely matched the truth.

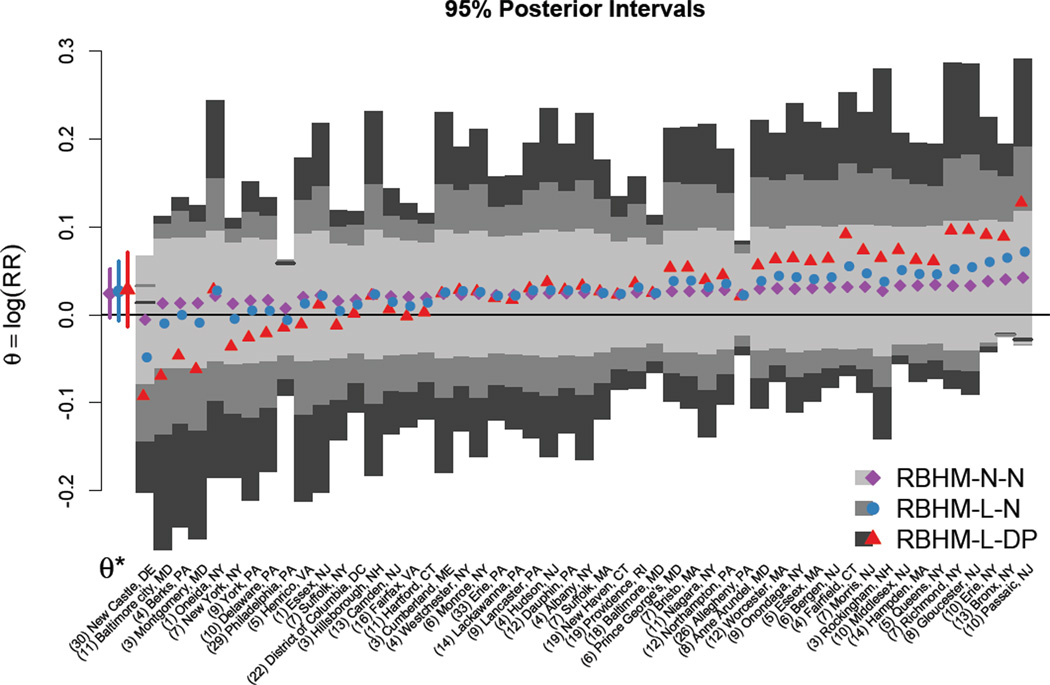
Figure 3 shows the posterior mean estimates and 95% posterior intervals for the overall θ* and for the cluster-specific θ_i obtained under each reduced HM. We found that on average, across all counties, there was an increase in CVD admissions on days when both ozone and fine particulate matter were above their national standards compared to days when both pollutants were below their national standards. In particular, we estimated that the overall log relative risk of CVD admissions associated with levels of O₃ and PM_2.5 both above their national standards (θ*) was 0.024 (95% posterior interval −0.004 to 0.053) for RHM-N-N, 0.027 (−0.007 to 0.061) for RHM-L-N, and 0.029 (−0.014 to 0.071) for RHM-L-DP. A log relative risk of 0.024 corresponds (approximately) to a 2.4% increase in cardiovascular hospital admissions on days when both O₃ and PM_2.5 are above their standards compared to days when both pollutants are below their standards. We also found variability across counties in the estimate of the cluster-specific effects θ_i. For most counties, θ_i was estimated to be positive, though for each county the posterior interval covered zero. The random-effect estimates exhibited the largest shrinkage for RHM-N-N, followed by RHM-L-N, with the RHM-L-DP estimates remaining furthest from the overall regional estimate.

Figure 3.

Results of a multisite time series study of 51 northeastern US counties, 1999–2005. County-specific (θ_i) and overall (θ*) estimates, with 95% posterior intervals, of the log relative risk of cardiovascular admissions on days when both O₃ and PM_2.5 exceed their national standard compared to days when both pollutants are below their standards, across three reduced HMs: normal approximation to the likelihood with normal random-effect distribution (RHM-N-N) and integrated likelihood with normal (RHM-L-N) and flexible (RHM-L-DP) random-effect distributions. Counties are ordered from left to right by increasing values of ${\widehat{\theta }}_i/\widehat{{\text{SE}}_i}$ where θ̂_i is the MLE and $\widehat{{\text{SE}}_i}$ is the estimated standard error. The number of days with both O₃ and PM_2.5 greater than their national standards is listed beside each city.

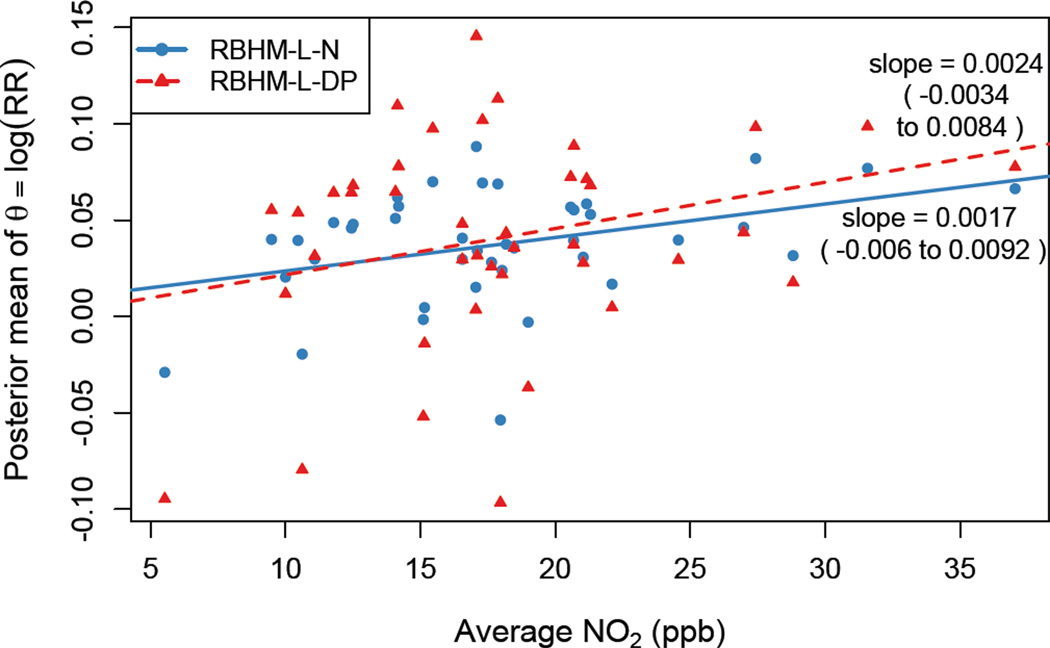
Figure 4 shows the posterior mean estimates of the location-specific θ_i from the reduced HM including average NO₂ as a covariate at the second stage, plotted against the location’s long-term average NO₂. The positive slopes (α₁) suggest that the risk of cardiovascular admissions associated with daily levels of O₃ and PM_2.5 greater than their national standards is higher in locations with greater NO₂ levels and lower in locations with lower NO₂ levels, though the estimates were not statistically significant. More precisely, we estimated that an interquartile range increase in long-term average NO₂ is associated with a percentage increase in the relative risk of cardiovascular hospital admissions associated with O₃ and PM_2.5 both above their national standards of 1.2% (−3.8% to 6.2%) under RHM-L-N, and 1.6% (−2.2% to 5.7%) under RHM-L-DP.

Figure 4.

For the 41 northeastern US counties with NO₂ measurements, estimates of θ_i from the reduced HM incorporating long-term average NO₂ as a covariate in the second stage model. Estimates of slopes α₁ (95% posterior intervals) are shown beside the corresponding trend line. The parameter of interest θ_i is the log relative risk of cardiovascular admissions on days when both O₃ and PM_2.5 exceed their national standard compared to days when both are below their standards.

We performed several diagnostic assessments and sensitivity analyses to evaluate our model fit and demonstrate the robustness of our results to model specification (see Appendix F of the Supplementary Materials for details). Though the within-county model (1) does not account for the potential for autocorrelation in the hospitalization time series, exploratory data analysis revealed little evidence of residual autocorrelation in our data. In particular, when we fit model (1) separately for each county and inspected the autocorrelation function (ACF) of the deviance residuals, we did not find a consistent pattern in the ACF. We further investigated whether there was spatial correlation across counties by plotting a variogram of the estimated county-specific θ_i, as well as whether there was residual spatial correlation in the county-specific estimates after accounting for long-term average NO₂ (Appendix F). We did not find evidence of spatial dependence across counties in the risk of cardiovascular admissions associated with O₃ and PM_2.5 both above their national standards. To assess the sensitivity of our results to the specification of the exposure-response surface, we refit the reduced HM where the joint association of ozone and PM_2.5 with the health outcome in equation (1) was instead modeled as the product of cubic spline bases with just 2 df. We found that the resulting cluster-specific estimates θ_i were very similar and that the overall estimates θ* were nearly identical.

7 Discussion

While previous studies have estimated health effects of single pollutants, understanding how complex mixtures of pollutants affect health remains a challenging goal. Quantifying health risks resulting from exposure to a single pollutant is a useful analytical construct, but it is not representative of true exposure. It is therefore critical to develop models for estimating health effects of simultaneous exposure to multiple pollutants.

In this paper we developed methodology for estimating both county-specific and regional average risks of multipollutant exposure. This approach extends previous single pollutant models by allowing for nonlinear smooth functions of multiple pollutants and their interactions at the first stage and for effect modification at the second stage. Because flexible associations of several exposures are modeled concurrently, the inclusion of interactions of spline terms leads to a high-dimensional vector of random effects. As a result, several challenges to the application of the usual full HM framework are introduced. To address these challenges, we have proposed the reduced HM as a general statistical approach for combining information across locations directly on the parameter of interest, in the context of many nuisance parameters. In this approach, information about the parameter of interest is summarized through a likelihood function (e.g. integrated likelihood) in the first stage. At the second stage, a flexible random-effect distribution (e.g. Dirichlet process normal mixture) is specified directly on the parameter of interest. We conducted simulation studies to compare performance of the reduced HM to the full HM, and we applied the reduced HM to a multisite time series study of 51 northeastern US counties during the period 1999–2005.

In comparison with the reduced HM, on first inspection the full HM is the seemingly optimal approach, as it uses all of the available data in a single model to combine information across clusters. However, many practical difficulties may arise upon implementation. First, for the full HM one must specify a random-effect distribution on the vector β_i parametrizing the within-cluster model. This may be difficult when the β_i are high-dimensional or when they do not have meaningful interpretations (e.g. regression spline coefficients as in equation (1)). Additionally, for conducting Bayesian inference, prior distributions must be selected for the parameters of the random-effect distribution (e.g. mean vector β* and variance-covariance matrix Σ), which may also be complicated if these parameters do not have meaningful interpretations. If there does not exist a reparametrization of β_i such that β_i = (θ_i, λ_i) for λ_i a (q−1)-dimensional nuisance parameter, then prior information about the quantity of interest θ_i = h(β_i; x_i) cannot be easily translated into prior information about the model parameters β_i. Moreover, if one is interested in effect modification of cluster-specific covariates z_i at the second level, then a potentially high-dimensional multivariate regression model for β_i | β*, z_i must be specified. Finally, fitting the model (e.g. implementing the MCMC sampler) will become increasingly challenging and computationally intensive as the dimension of β_i (number of random effects) increases.

For the reduced HM, on the other hand, rather than specify a high-dimensional random-effect distribution on parameters that are not of primary scientific interest, one only needs to specify a random-effect distribution for a one-dimensional parameter that has a meaningful interpretation. Additionally, it is frequently much easier to incorporate prior information about the parameter of interest θ_i than about a large vector of nuisance parameters β_i that may be hard to interpret (e.g. spline coefficients). Furthermore, reducing a hierarchical model on a high-dimensional vector of parameters to a hierarchical model on a much lower dimensional space yields simpler implementation and greater computational efficiency, and makes model diagnostics and sensitivity analyses more wieldy.

Although the reduced HM overcomes many difficulties in the specification and implementation of the full HM, it also introduces new challenges. At the first stage, one must eliminate nuisance parameters to obtain the likelihood function L_i(θ_i). While the literature on likelihood-based methods for eliminating nuisance parameters is vast (Pawitan, 2001; Edwards, 1992), in this paper we restricted our attention to those likelihoods that correspond to true probability distributions, including the integrated and conditional likelihood. In the case of large within-cluster sample sizes, the choice of which likelihood function to use should make little difference compared with the impact of the selection of the random-effect distribution. For smaller sample sizes, an integrated likelihood, though more computationally intensive than a normal approximation, allows greater flexibility for capturing the true form of the likelihood. Second, while the reduced HM avoids the need to specify a high-dimensional random-effect distribution on the complex β_i, use of the integrated likelihood for θ_i still necessitates specifying priors for β_i (Section 4.1). However, because we seek an objective likelihood function in the sense that it should summarize the information contained in the data about the parameter of interest such that the prior has as little influence as possible, any prior distribution for β_i that induces a vague prior for θ_i will suffice. For the applications we have considered, assuming diffuse normal priors for each component of β_i leads to a prior for θ_i that is at over a large range of reasonable values for θ_i, and we have found this approach to work well. Alternative approaches for approximating the likelihood function one could also be considered, such as the data cloning method of Lele et al. (2007). Third, while one gains simplicity by eliminating nuisance parameters at the outset, it is possible that some information may be lost before combining information across clusters.

We conducted a series of simulation studies to evaluate the relative performance of the reduced HM as compared to the full HM across a range of potential scenarios (Section 5). For the full HM, because one must specify random-effect distributions for a larger number of parameters, which may also be hard to interpret, there is more potential for model misspecification than for the reduced HM where a random-effect distribution is placed on the lower-dimensional parameter of interest. On the other hand, if the parameter of interest θ_i is correlated with nuisance parameters within a cluster, then information may be lost by reducing the parameter space to a single parameter and pooling the θ_i. We based the simulation study on an application for which a conditional likelihood for θ_i was available in closed form so as to focus on the impact on inference of misspecifying the random-effect distribution, rather than of misspecifying the likelihood function. In addition, though prior studies have considered the special case of reduced HM where a conditional likelihood is available (Efron, 1996; Liao, 1999), the relative performance of this approach as compared to the full HM had not been previously studied. When we refit the reduced HM using an integrated likelihood for a subset of the simulations (I = 100 and n = 100), we found that the performance for estimating the cluster-specific and overall parameters were either identical or just slightly worse than using the conditional likelihood. Across simulation scenarios, we found that the reduced HM generally achieved comparable performance to the full HM, and even had superior performance in some cases. We also performed a separate simulation study to evaluate the performance of our approach for estimating the integrated likelihood (Section 4.1) in a scenario based on our multipollutant application, finding that the estimated integrated likelihood closely matched the true integrated likelihood (Appendix E of the Supplementary Materials). Taken together, our findings from these simulation studies highlight the utility of the reduced HM both specifically to the multipollutant application and more generally to the context of two-level clustered data.

Development of reduced HM was motivated by methodological needs for estimating health risks of joint exposure to multiple pollutants. We applied the reduced HM methodology to estimate the risk of emergency cardiovascular admissions associated with simultaneous exposure to fine particulate matter and ozone. For the overall effect θ*, we found marginal evidence of increased risk on days when both pollutants exceeded their national standards compared to when both were below their national standards. The reduced HM with normal random-effect distribution on the parameter of interest θ_i (RHM-L-N) led to more shrinkage of the county-specific random effects than the reduced HM with flexible random-effect distribution (RHM-L-DP). Further, the RHM-L-N had narrower credible intervals for the county-specific parameters θ_i than RHM-L-DP. If the normal random-effect distribution is misspecified (e.g. if the analysis is missing an important county-level effect modifier) then the RHM-L-N may understate statistical uncertainty in the θ_i. We illustrated how diagnostics on the reduced parameter space could be performed to assess modeling assumptions, by investigating spatial autocorrelation in the risk of simultaneous exposure to PM_2.5 and O₃. Though we did not find evidence of spatial autocorrelation in the θ_i in this application, it would be straightforward to model spatial dependence in the second stage of the reduced HM by specifying a spatial model for cov(θ_i, θ_j). We also demonstrated that the reduced HM can easily accommodate effect modifiers. Specifically, we examined the inclusion of long-term county-level NO₂, a surrogate for traffic exposure. We found a larger relative risk of cardiovascular admissions associated with levels of PM_2.5 and O₃ higher than their national standards in locations with high average NO₂ compared to locations with low average NO₂, although the effect modification was not statistically significant. For our within-county model (1) and parameter of interest θ_i (defined in (2)) we only considered the association of current day’s exposure to PM_2.5 and O₃ with hospitalization on the same day, though previous days’ exposure (e.g., at different lags from the present day) may also be predictive of health outcome. This choice of lag was motivated by previous single pollutant studies, which have found that the strongest effects for PM_2.5 and O₃ occur at short (current or 1 day prior) lags (Dominici et al., 2006; Bell et al., 2004). Furthermore, to demonstrate our methodology, we considered just a single example of a policy-relevant parameter of interest. The US EPA is considering introducing joint national standards to better protect human health from the risks of exposure to complex mixtures, and so studies providing a scientific basis for joint standards are needed (Dominici et al., 2010). Depending on the scientific question, alternative parameters of interest may be specified and the same methodology applied. We could consider, for example, the gradient of the air pollution-hospitalization exposure-response surface at the national standards, or the relative risk of adverse health events when both PM_2.5 and O₃ exceed their national standard at different temporal lags compared to when just one of the pollutants exceeds its standard. In the future we will apply this approach to systematically conduct a national investigation of the health effects associated with simultaneous exposure to multiple pollutants. Methods can be extended to an arbitrarily large number of pollution variables and locations, and to consider joint pollutant exposure at different lags as well as multiple parameters of interest that summarize different salient features of the multivariate exposure-response surface.

There are several extensions to the reduced HM methodology we have proposed. First, we assumed a within-location model that had the same form across locations. However, this assumption could be relaxed. One could specify different within-cluster models for each cluster, as long as the interpretation of the parameter of interest remains constant across models. For example, for the within-cluster model (1) in the multipollutant application, the full HM would require a common spline basis (e.g. common knot locations) for the joint O₃ and PM_2.5 association across locations, while the reduced HM can allow for locally optimized spline bases. Thus the reduced HM approach can readily accommodate heterogeneity in the appropriate model to use across locations. In this manuscript we focused on two-level clustered datasets and a scalar parameter of interest. However, the reduced HM could be generalized to three- or higher-level models, and to situations where the parameter of interest θ_i = h(β_i) is a multivariate parameter with dim(θ_i) < dim(β_i).

We have described the reduced HM within the context of estimating health risks of exposure to many pollutants. However, this hierarchical modeling strategy is broadly applicable to clustered data in which the parameter of interest is a known function of the vector of parameters β_i of the within-cluster model. The meta-analysis of stomach ulcer treatment that served as the basis for our simulation study is one example. Another example is the estimation of heat wave mortality risk in multisite time series studies (Bobb et al., 2011). One can build a location-specific model similar to (1) where the exposure-response function of interest is the temperature-mortality relation, adjusted for time-varying covariates. One can then define a heat wave day indicator variable as a function of temperature on current and previous days. The parameter of interest θ_i, defined as the log relative risk of mortality on heat wave days compared to non-heat wave days (see for example Peng et al. (2011)), can then be written as a known function of the temperature-mortality exposure-response function (parameterized by β_i), and the reduced HM framework may be applied.

The reduced HM is especially useful in situations where β_i is high-dimensional, where the components of β_i are not easily interpretable, or where one wishes to incorporate prior information directly on the parameter of interest. For such applications, the reduced HM allows one to specify a random-effect distribution directly on the parameter of interest θ_i and to study effect modification by specifying an across-cluster regression model for θ_i. Further, the reduced parameter space leads to simpler implementation, which facilitates the specification of flexible random-effect distributions that do not require strong assumptions on the random effects. For problems that are very high-dimensional in the number of clusters, the number of observations within a cluster, and the number of parameters in the within-cluster model, it may not be computationally feasible to fit a full HM. In such cases, the reduced HM is a practical alternative.