The Importance of k-Space Trajectory on Off-Resonance Artifact in Segmented Echo-Planar Imaging

Abstract

Segmented interleaved echo planar imaging (EPI) is a highly efficient data acquisition technique; however, EPI is sensitive to artifacts from off-resonance spins. The choice of k-space trajectories is important in determining how off-resonance spins contribute to image artifacts. Top-down and center-out trajectories are theoretically analyzed, simulated, implemented, and tested in phantom and volunteer experiments. Theoretical results show off-resonance artifact manifests as a simple positional shift for the top-down trajectory, while for the center-out trajectory off-resonance artifact manifests as a splitting of the object, which entails both shift and blurring. These results were validated using simulation and phantom scan data where a frequency-offset was introduced ranging from –300 Hz to +300 Hz. As predicted by the theoretical results, inferior image quality was observed for the center-out trajectory in a single volunteer. Off-resonance produces more severe and complex artifacts with the center-out trajectory than the top-down trajectory.

INTRODUCTION

Echo planar imaging (EPI) introduced in 1977 by Mansfield (1) is one of the most efficient acquisition methods. However, EPI sequences are prone to artifacts due to T2* decay, eddy currents, flow, and off-resonance spins. Segmented EPI, also known as multi-shot EPI, reduces these artifacts by shortening the echo train length. Interleaving the k-space trajectories in multi-shot EPI further reduces the artifact by increasing bandwidth in the phase encode direction.

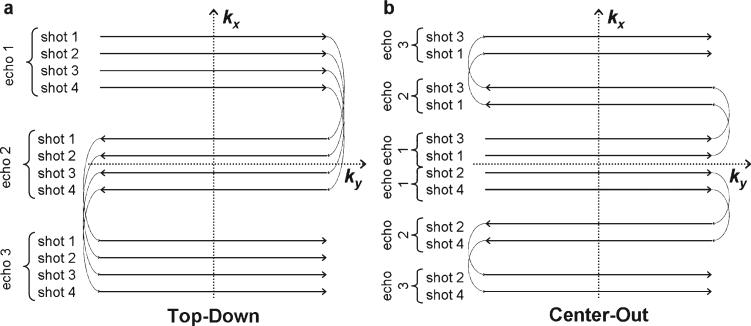
Two interleaved multi-shot EPI k-space trajectories are commonly used: top-down (1–3) and center-out (2–12). In a top-down trajectory, the first echo in the echo train is used to acquire an outer line at the positive (or negative) edge of k-space. Subsequent echoes traverse the entire k-space such that the last echo in the train captures an outer line on the opposite edge of k-space [Fig. 1(a)]. The center-out trajectory acquires a central line of k-space on the first echo with subsequent echoes traversing one half of k-space such that the last echo in the train captures an outer line on either the positive or the negative side of k-space [Fig. 1(b)].

Figure 1.

k-space trajectories for top-down (a) and center-out (b) trajectories. Four shots with three echoes are shown for both, although this could be generalized to any segmented interleaved or single shot acquisition. Note in the center-out trajectory (b) that each echo train traverses only half of k-space.

The effective echo time of an EPI sequence is defined as the time from the excitation pulse to the echo encoding the central line of k-space. Thus, effective echo time is minimized with a center-out trajectory, providing advantages of reduced signal decay due to T2*, and minimizing flow and motion induced dephasing (2, 4). This holds true for flow and motion in both the frequency and phase encode directions (2). The center-out trajectory has therefore been recommended for applications such as functional imaging of the brain (5–8), myocardial perfusion (3, 9), coronary artery imaging (10), and velocity mapping and imaging in the presence of physiological motion (6, 10, 11). It has been suggested that the center-out trajectory be used instead of gradient moment nulling (GMN) to reduce motion and flow artifacts (11). However, the source and severity of off-resonance artifacts should also be considered when choosing an EPI echo train trajectory. Special consideration must be given to off-resonance artifact in areas of high field inhomogeneity such as the heart, where it has been shown magnetic field inhomogeneities can lead to off-resonance of 100 Hz at 1.5T (13), and can be even larger at higher field strengths.

Off-resonance artifacts arise from both magnetic field inhomogeneity and “chemical shift”. With the top-down trajectory, off-resonance introduces the relatively simple and well-understood shift artifact (14, 15), which arises from a linear accumulation of phase across k-space. The center-out trajectory, however, introduces a nonlinear phase modulation of the acquired signal (2, 4–6, 10) causing off-resonance artifacts to become significantly more complicated. Although the different manifestation of off-resonance artifact with the center-out trajectory has been previously described (16), to our knowledge an analytical and in-depth description is lacking. Previous work by Hetzer et al. (5) has noted the splitting but failed to mention blurring and did not demonstrate the artifact in simulation, a phantom, or in vivo. Work by Luk-Pat et al. (2) simulated splitting and blurring effects but failed to demonstrate the artifact in a phantom or volunteer. Neither work described the relative magnitude of the positional shift or the point spread function (PSF).

This work extends these initial understandings of the center-out off-resonance artifacts and provides a direct comparison to the competing top-down k-space trajectory. The novel analysis provided here leads to a formal description of the impact on the PSF and recognition that the center-out trajectory has twice the positional shift of top-down. Additionally, for the first time the center-out off-resonance artifact is demonstrated in a phantom and a volunteer.

THEORY

Phase due to off-resonance accrues over the duration of the echo train in an EPI sequence. This phase linearly modulates the k-space data in the frequency and phase encoding directions. For this analysis the focus is on the phase encoding direction only; the phase variation in the frequency encode direction is ignored due to its relatively small magnitude.

In the image domain, the magnitude of the spatial shift (Δy_off) along the phase encoding direction is given by

$$\Delta y_{\text{off}}=\frac{\Delta f_{\text{off}}}{\Delta v_{\text{phase}}}\Delta y$$ [1]

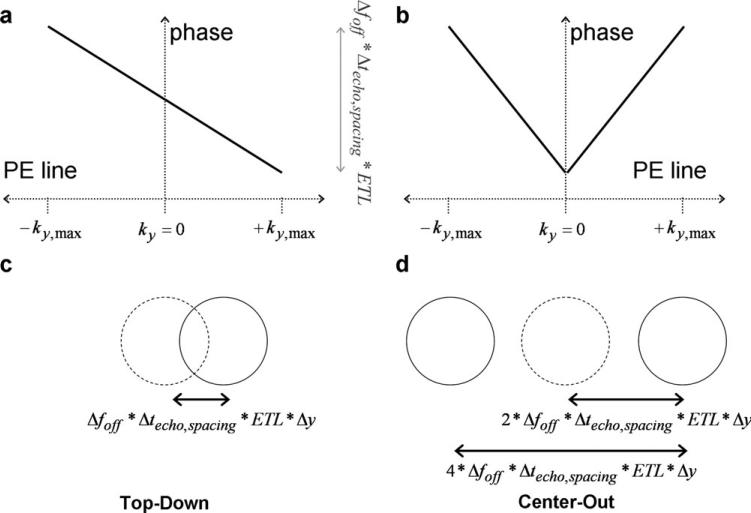
where Δy is the voxel size in the phase encoding direction, Δf_off is the frequency offset, and Δv_phase is the bandwidth per pixel in the phase encoding direction (14). Δv_phase is analogous to bandwidth as typically described for the frequency encoding direction, but much lower (on the order of 10 Hz/pixel) due to the long time intervals between phase encode sample points. For a linear phase variation, the magnitude of the position shift in the image domain is completely determined by the slope of the phase variation in the k-space domain (Fig. 2).

Figure 2.

Simulation results are shown for top-down (a, c) and center-out (b, d) trajectories of equivalent echo spacing and echo train length. k-space effects are shown in (a) and (b), and image domain effects in (c) and (d). Note the doubling of the slope in phase offset as a function of k-space caused by the center-out trajectory (b), leading to the increase in image domain shift and bi-directional split along the phase encode direction seen in (d). The lower, monotonic slope in phase across k-space of the top-down trajectory leads to a unidirectional shift of lower magnitude.

For a top-down trajectory, the bandwidth can be calculated by (14):

$$\Delta v_{\text{phase},\text{top}-\text{down}}=\frac{N_{\text{shot}}}{\Delta t_{\text{esp}}\ast N_y}=\frac{1}{\Delta t_{\text{esp}}\ast ETL},$$ [2]

where N_shot is the number of shots in a multishot top-down EPI acquisition, N_y is the total number of samples along the phase encoding direction, ETL is the echo train length, and Δt_esp is the temporal echo spacing, i.e., the time between two adjacent echoes in a given echo train. From Eqs. [1] and [2], the positional shift caused by off-resonance can be calculated as

$$\Delta y_{\text{off},\text{top}-\text{down}}=\Delta f_{\text{off}}\ast \Delta t_{\text{esp}}\ast \mathrm{ETL}\ast \Delta y.$$ [3]

In comparison to the top-down trajectory, the step-size (along the phase encoding direction in k-space) from one echo to the next is half for the center-out trajectory. This reduction is step-size is achieved by reducing the phase encoding gradient pulse area to half. Since the bandwidth is directly proportional to gradient pulse area (14), the bandwidth for the center-out trajectory is reduced by a factor of two and is given by,

$$\Delta v_{\text{phase},\text{center}-\text{out}}=\frac{1}{2\ast \Delta t_{\text{esp}}\ast \mathrm{ETL}},$$ [4]

From Eqs. [1] and [4], Δy_off for the center-out trajectory can be written as

$$\Delta y_{\text{off},\text{center}-\text{out}}=2\ast \Delta f_{\text{off}}\ast \Delta t_{\text{esp}}\ast \mathrm{ETL}\ast \Delta y.$$ [5]

A comparison of Eqs. [3] and [5] reveals that for a given value of ETL the spatial shift in the image domain or, equivalently, the phase slope along the phase encoding direction of k-space is double for the center-out trajectory as opposed to the top-down trajectory. Since the center-out trajectory is collected separately for two halves of the k-space, a k-space weighting function (Ŵ) is defined:

$$\widehat{W}\left(k_y\right)=e^{i2\pi \ast \Delta y_{\text{off}}\ast \mid k_y\mid }.$$ [6]

To analytically solve, k-space is split into positive and negative halves. This is mathematically accomplished using two unit step functions, u(-k_y) and u(k_y). Each side of k-space can be separated in the weighting function,

$$\widehat{W}\left(k_y\right)=u(-k_y)\ast e^{i2\pi \ast \Delta y_{\text{off}}\ast (-k_y)}+u\left(k_y\right)\ast e^{i2\pi \ast \Delta y_{\text{off}}\ast k_y},$$ [7]

by the multiplication of a unit step component and a linear phase component. The phase component slopes are equal and opposite directions for the positive and negative halves of k-space. Intuitively, the linear phase across the positive half of k-space shifts the object in one direction, and the linear phase of opposite slope across the negative half of k-space shifts the object in the other direction. This leads to the generation of two replicas of objects that are off-resonance, separated in the image by a distance of 2*Δy.

The phase nonlinearity at the center of k-space leads to more complex image artifacts, including both shifting and blurring. Taking the Fourier transform of the weighting function in Eq. [7], it can be seen that the weighting function in image space

$$W\left(y\right)=\left[\frac{1}{2}\delta (\Delta y_{\text{off}}+y)+\frac{1}{2\pi \ast i\ast (\Delta y_{\text{off}}+y)}\right]+\left[\frac{1}{2}\delta (\Delta y_{\text{off}}-y)+\frac{1}{2\pi \ast i\ast (\Delta y_{\text{off}}-y)}\right],$$ [8]

entails both shifting and blurring. Note that from Eq. [5], Dy_off is a function of frequency offset Δf_off, and thus the extents of both shifting and blurring are dependent on the magnitude of frequency offset.

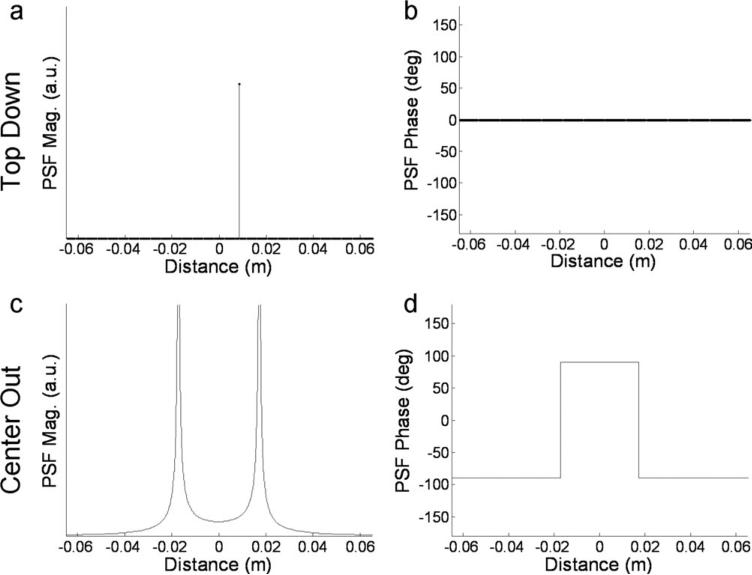
Equation [8] represents the PSF for the center-out artifact. The PSF magnitude and phase for both trajectories was plotted in Fig. 3. This only accounts for off-resonance and not the effects of T2* or motion. Also note for both the trajectories it is assumed that echo time shifting (17, 18) is employed; appropriate time shifts are introduced at the beginning of each echo-train so the phase ramps linearly across k-space when multiple echo-trains are interleaved.

Figure 3.

Theoretical PSF magnitude (a, c) and phase (b, d) for top-down (a, b) and center-out trajectory (c, d) for Δf_off = 300 Hz, Δt_esp = 0.53 ms, ETL = 15, Δy = 3.61 mm. Off-resonance results only in a unidirectional position shift with the top-down trajectory as indicated in (a) by the shift of the delta function away from the origin. The center-out trajectory magnitude results shown in (d) demonstrate a bi-directional split of the signal as evidenced by two separate peaks in the PSF, as well as blurring shown by the spatial spread of each peak.

METHODS

Computer Simulation

The effect of off-resonance with the center-out trajectory was simulated using a 1D rectangular (rect) function in the image domain. The rect function is the profile of a line in the phase encode direction cutting through the center of a circle such as the circular cross section of uniform cylindrical phantom such as that used in the following experiment. The width of the rect was matched to the 1” (25.4 mm) diameter of the phantom and imaging parameters of Δf_off = 300Hz, Δt_esp = 0.53 ms, ETL = 15, Δy = 3.61 mm were matched to the phantom acquisition.

Phantom

A gradient-echo echo-planar imaging (GRE-EPI) sequence was implemented on a 3.0T MR system (Tim Trio, Siemens Healthcare, Malvern, PA). Both center-out and top-down k-space trajectories were programmed for comparison. For each echo train, the top-down trajectory traversed all of k-space and the center-out trajectory traversed one-half of k-space. A frequency encoding bandwidth of 3,256 Hz/px was used with an echo train length of 15 resulting in an effective echo time of 2.2 ms for center-out and 6.3 ms for the top-down trajectory. Additional common parameters across all acquisitions were TR = 13.5 ms, 90 × 128 image matrix, 10 mm slice, 300 mm × 400 mm rectangular field-of-view. Maxwell correction was used to account for the effect of concomitant gradients on the phase maps (19). 3D volume-selective shimming was used to improve field homogeneity. Off-resonance was intentionally introduced by measuring the resonance frequency of water and then adding an offset to the RF transmitter frequency.

A 4’ (1.22 m) long by 1” (25.4 mm) diameter tube containing 618 ml of water doped with 2.5 ml Magnevist Gadolinium contrast agent (2.02 mmol/L). No parallel acceleration was used and six echo trains per image were acquired. Thirty-two images were acquired and averaged to maximize SNR. A birdcage head coil and a standard truncated sinc RF excitation pulse with a flip angle of 30° were used. Frequency offsets from –300 Hz to +300 Hz were added in increments of 100 Hz for both trajectories.

Volunteers

Volunteer imaging was performed using the same imaging parameters as the phantom unless otherwise noted. Parallel imaging technique TGRAPPA (20) with acceleration rate 3 was used allowing a complete cine to be acquired each heartbeat. A 32-channel cardiac array (16-channel anterior + 16-channel posterior) coil was used. A 1-1 water excitation binomial pulse with composite flip angle of 30° was used to avoid signal from fat (21). Prospective ECG triggering and breath holding were used to minimize motion artifact. Images were acquired using both trajectories with frequency offsets of 0 and 100 Hz.

RESULTS

Computer Simulation

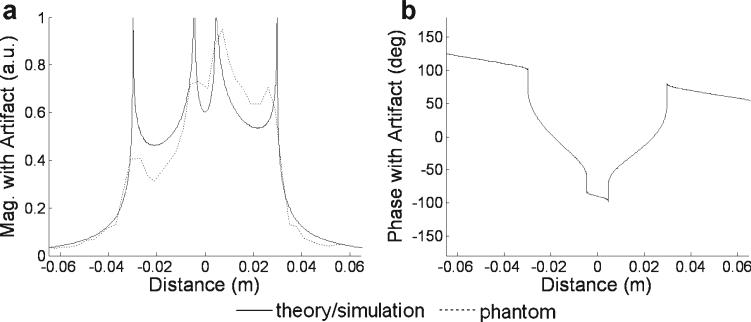
A simulated off-resonance frequency of 300 Hz resulted in a simple position shift with the top-down trajectory, but caused a spatial split and blur with the center-out trajectory. As shown in Fig. 4, the relatively simple rect shape was significantly distorted by the center-out trajectory in the simulated presence of off-resonance. The original rect shape was blurred and demonstrated regions of signal cancellation and enhancement.

Figure 4.

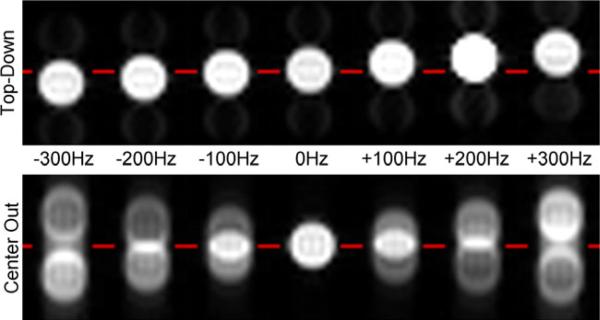
Computer simulation of the same conditions as in Fig. 3 shows the magnitude (a) and phase (b) of the rect function blurred by center-out PSF. The splitting and blurring predicted by the simulation matched reasonably the results obtained in a phantom (dashed line overlay in (a)) imaged under similar conditions.

Phantom

For center-out trajectory, the magnitude of a line of pixels running in the phase encode direction through the center of the phantom was overlaid with the computer simulation in Fig. 4(a) to show the similarity of results. Signal was normalized to the simulation by equalizing the total signal across the phase encode direction.

The phantom image results shown in Fig. 5 over a range of frequency offsets also confirmed the PSF analysis. For a frequency offset of +300Hz, theoretical calculations predicted a positional offset of 8.6mm for top-down trajectory (Eq. [3]) and 17.2 mm for center-out trajectory (Eq. [5]). Measured offsets were 9.3 mm and 17.8 mm for top-down and center-out trajectories respectively.

Figure 5.

Phantom scans for top-down (top) and center-out trajectory (bottom) for off-resonance frequencies ranging from 300 Hz to +300 Hz (left to right). As predicted by theory and simulation, the top-down trajectory causes only a unidirectional shift in position in the presence of off-resonance, while the center-out trajectory causes bi-directional splitting of the signal as well as blurring. Note that the shift of each of the split signals (ghost images) with center-out is twice as large as the unidirectional shift observed with the top-down trajectory.

Volunteers

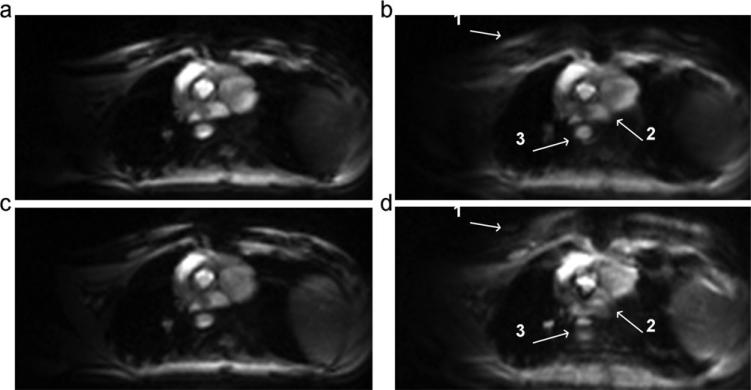
A systolic frame of the cardiac cycle for each of the tested conditions is shown in Fig. 6. Images acquired using either trajectory were similar for a zero offset frequency [Figs. 6(a,c)]. Significantly, splitting and blurring artifacts were observed in the images acquired using the center-out trajectory when the 100 Hz off-resonance frequency was introduced. Finer structures such as the boundary of the right and left atrium [Fig. 6(b.2)] are lost along with larger structures such as the descending aorta [Fig. 6(b.3)].

Figure 6.

Images for top-down (a, b) and center-out trajectory (c, d) for an off-resonance frequency of 0 Hz (a, c) and 100 Hz (b, d). White arrows in image acquired with center-out trajectory (d) point to artifacts caused by splitting and blurring at the (1) chest wall, (2) boundary between the right and left atrium, and (3) the descending aorta not seen in images acquired with top-down trajectory (b). While this 100 Hz off-resonance frequency was artificially introduced for demonstration purposes, frequency offsets of this magnitude can be expected in the myocardium at 1.5T (13).

DISCUSSION

In addition to factors that motivate minimization of echo time, the complexity and severity of off-resonance artifacts must be considered in selecting the k-space trajectory in EPI. The results showed that the top-down trajectory, while lengthening TE, is less sensitive to off-resonance artifacts than the center-out trajectory.

Theoretical analysis showed that the center-out trajectory caused a “v” shaped phase modulation in the k-space domain. The center-out PSF showed a complex artifact which consisted of three distinct components: a shift in position, a split in the object, and blurring. For the center-out trajectory, each of the two split objects is shifted from the true position by two times the position shift seen with a top-down trajectory. The PSF also demonstrated that the artifact affects both the magnitude and phase of the signal for the center-out trajectory. The blurring component of the complex artifact was shown by Equation 8 to be a function of offset frequency, and this effect could be observed to some degree in the phantom results shown in Fig. 5.

Phantom scans showed agreement with the splitting and positional shift predicted by the simulation. One of the two shifted and split images of the phantom appeared brighter than the other (Fig. 5). The brighter object (shifted up for positive frequency offset and down for negative offset) corresponded to the side of k-space that included the central line.

In the volunteer images, introduction of a 100 Hz off-resonance produced notably worse artifacts and blurring with the center-out trajectory. A binomial water excitation pulse was used to suppress fat signal. Shifting the transmitter center frequency to create a controllable off-resonance altered the effectiveness of fat suppression; however, the 100Hz offset frequency was small enough that the water excitation pulse remained effective, yet large enough to demonstrate the difference between center-out and top-down trajectories. While this off-resonance frequency was artificially introduced for demonstration purposes, frequency offsets of up to 100 Hz can be expected in the myocardium at 1.5T (13), and could be even worse at higher field strengths.

For the top-down trajectory, the positional offset can lead to artifact when tissues with different resonance frequencies, i.e., fat and water, are located adjacent to one another. On the other hand, when an inhomogeneous field causes smooth variations in resonant frequency, the positional offset will only lead to geometric distortion and blurring of the image but not distinct artifacts. For the center-out trajectory, blurring occurs whether the resonance frequency is slowly spatially varying or not due to the splitting of the object. The shift from the original position is twice that of a top-down trajectory.

The results of this work can also be applied to an alternative center-out trajectory, sometimes called “centric” or “alternating center-out”, which acquires echoes from both the right and left side of k-space in a single echo train in alternating fashion; odd echoes are used to collect one side of k-space, and even echoes the other (4). The alternating center-out trajectory covers the entire k-space in a single echo train. Imaging splitting would still occur, but because the effective bandwidth is doubled relative to the center-out trajectory, the positional shift would be equivalent to that of the top-down trajectory. Inherent to the alternating trajectory is a higher sensitivity to eddy currents due to the large, rapidly switching phase encode blips needed to travel from one half of k-space to the other, especially for echoes later in the echo train (4). The alternating center-out trajectory can also cause worse ghosting artifact due to discontinuous flow and motion-induced phase error in k-space domain compared to the nonalternating center-out trajectory (4). Likewise, artifacts similar to what was demonstrated for center-out would apply to an “outside-in” trajectory where the first echo starts at the outer line of k-space and the last echo ends at the center of k-space; this trajectory has been suggested for imaging of stationary objects like the head (11) to improve T2 contrast.

CONCLUSIONS

Segmented EPI offers very high scan efficiency that can be especially useful in cardiac imaging, but a number of factors must be considered when choosing an appropriate k-space trajectory. This work points out the important difference in sensitivity to off-resonance of two commonly used trajectories, top-down and center-out. Given the trend towards imaging at higher field strengths, and the significant level of susceptibility-induced inhomogeneities that may be encountered around the heart and nasal sinuses, this trade-off warrants consideration.

Biography

Jacob A. Bender studied Electrical and Biomedical Engineering at Duke University and obtained a Bachelor's of Science in 2008. He earned his Master's degree from The Ohio State University in 2011 under the supervision of Prof. Orlando Simonetti, and specialized in high speed MRI using echo planar imaging and parallel acquisition techniques.

Rizwan Ahmad received the B.S. degree with honors in electrical engineering from The University of Engineering and Technology, Lahore, Pakistan in 2000, and the M.S. and Ph.D. degrees in electrical and computer engineering from The Ohio State University in 2004 and 2007, respectively. In his Ph.D., he worked as a research assistant on fast data collection and recon struction methods for EPR imaging. Since 2007, he has been with the Davis Heart & Lung Research Institute at The Ohio State University, where he is currently appointed as a Research Scientist. His research interests include biomedical signal processing, tomographic reconstruction, in vivo oximetry, electron paramagnetic resonance imaging, and cardiac magnetic resonance imaging.

Orlando P. Simonetti is Professor of Internal Medicine and Radiology and Research Director of Cardiovascular MR and CT at The Ohio State University. After earning his B.S. (’83) and M.S. (’85) degrees at OSU, and his Ph.D. in biomedical engineering at Case Western Reserve University (’92), he went to work for Siemens where he served as Director of Cardiovascular MR Research and Development. While at Siemens he led the development of several cardiac MRI techniques currently in widespread clinical use. He joined the OSU faculty in 2005 where his research continues to focus on developing magnetic resonance technology for diagnostic cardiovascular imaging.