Coherent fiber supercontinuum for biophotonics

Abstract

Biophotonics and nonlinear fiber optics have traditionally been two independent fields. Since the discovery of fiber-based supercontinuum generation in 1999, biophotonics applications employing incoherent light have experienced a large impact from nonlinear fiber optics, primarily because of the access to a wide range of wavelengths and a uniform spatial profile afforded by fiber supercontinuum. However, biophotonics applications employing coherent light have not benefited from the most well-known techniques of supercontinuum generation for reasons such as poor coherence (or high noise), insufficient controllability, and inadequate portability. Fortunately, a few key techniques involving nonlinear fiber optics and femtosecond laser development have emerged to overcome these critical limitations. Despite their relative independence, these techniques are the focus of this review, because they can be integrated into a low-cost portable biophotonics source platform. This platform can be shared across many different areas of research in biophotonics, enabling new applications such as point-of-care coherent optical biomedical imaging.

1. Introduction

It has been a longstanding goal in biophotonics to realize a versatile optical source that is applicable to a wide variety of applications in possibly challenging environments. In this sense, fiber-based broadband supercontinuum generation has become an attractive solution since its discovery. After a decade of research along this path, a practical way to approach this goal is now available (Sect. 1.3).

1.1. Supercontinuum generation linking biophotonics and nonlinear fiber optics

Biophotonics studies employ light-matter interaction in a biological setting, and has therefore benefited human health in the form of optical imaging (or diagnosis), light-activated therapy, and laser surgery [1]. Because it is often preferable that biological matter remain in its natural environment and state with little to no perturbations other than the incident light, it is desirable to vary this interaction by manipulating the incident light only (i. e., no manipulation or perturbation of the biological matter). As an example, label-free optical imaging is often preferred over dye- or probe-based fluorescence imaging where the introduced exogenous dye(s) may modify the function of the biological matter. This restriction often demands light sources with unique properties, including wavelength (restricted to 350–2450 nm in this review), bandwidth, and coherence. Historically, the invention of lasers in the 1960s triggered a profound advancement of biophotonics, driven by the monochromatic wavelength, high energy and power, and uniform spatial profile (spatial coherence) of the laser light [2]. The widespread use of ultrafast lasers since the early 1990s has allowed the temporal coherence of the incident light and light-matter interaction to impact various biophotonics applications. The emergence of the corresponding coherent techniques reflects a new trend of biophotonics in the 21st century (Sect. 1.2).

Nonlinear fiber optics investigates the spectrotemporal transformation of an optical pulse propagating in an optical fiber [3]. This field emerged in the 1970s when the low-loss optical fiber [4] and mode-locked ultrafast laser [5] became available. The invention of nonlinear pure-silica photonic crystal fibers (PCF) [6, 7] in the 1990s stimulated a dramatic development in 1999 [8], termed as the “supercontinuum revolution” [9]. The phenomenon of supercontinuum generation, manifested as the extreme spectral broadening of an optical pulse due to light-medium interaction, was first discovered in bulk materials [10]. However, the phenomenon occurring in optical fibers allows wide and cost-effective access to the supercontinuum [11], resulting in a pulsed laser-like source spanning a broad bandwidth. Thus, many biophotonics applications were greatly enhanced by the use of fiber supercontinuum generation in the past decade (Table 1). With advances and novel applications, the field of biophotonics has increasingly demanded improved performance characteristics of fiber supercontinuum, and in turn, these have motivated the most recent developments in nonlinear fiber optics.

Table 1.

Comparison of biophotonics applications employing incoherent and coherent optical techniques.

	Biophotonics employing incoherent optical techniques	Biophotonics employing coherent optical techniques
Typical light-matter interactions	fluorescence, phosphorescence, spontaneous Raman, linear absorption, elastic scattering of incoherent light	harmonic generation, four-wave mixing, stimulated Raman, transient absorption, stimulated emission, nonlinear absorption, elastic scattering of coherent light
Complementary beneficial features	alignment-insensitive optics, widespread portable setup, low cost and low maintenance, ability to interact with large samples	high molecular specificity, high spatial resolution, intrinsic optical sectioning, capability for in vivo label-free molecular imaging without fluorescent labeling
Traditional light sources	lamp, light emitting diode, superluminescent diode, diode laser, gas laser, dye laser	mode-locked laser, pulsed laser amplifier, optical parametric amplifier or oscillator, broadband coherent source
Representative applications using fiber supercontinuum	optical sensing [12], diffuse optical tomography [13], fluorescence (lifetime) spectroscopy/imaging [14], confocal microscopy [15], optical tweezers [16], stimulated emission depletion microscopy [17]	optical coherence tomography [18], pump-probe spectroscopy and imaging [19], nonlinear optical spectroscopy and imaging [20], coherently controlled nonlinear micro-spectroscopy [21] and flow cytometry [22]

A fiber supercontinuum has several noticeable advantages over traditional light sources (Table 1). First, the supercontinuum permits simultaneous access to multiple wavelengths in a uniform spatial profile. It has the bandwidth of sunlight but is 10⁴ times brighter [7], and has the directionality of a single-wavelength laser to allow diffraction-limited focusing. These properties are useful in spectroscopic and microscopic applications of biophotonics where intense lamp-based sources or arrays of diode lasers are needed. Second, the pulsed nature of the supercontinuum permits time-resolved spectroscopy or imaging such as fluorescence lifetime and pump-probe techniques (Table 1). At a lower cost and with a simpler setup, the supercontinuum can replace the synchronized ultrafast solid-state lasers (pump-probe) or the arrays of pulsed diode lasers (fluorescence lifetime). Third, fiber supercontinuum generation is compatible with fiber-based components such as mode-locked fiber lasers, fiber-coupled handheld probes, and endoscopes/catheters, so that all-fiber alignment-free optical configurations may be realized for portable applications in biophotonics. Fourth, the supercontinuum can potentially be versatile to accommodate multiple biophotonics applications, which employ temporally incoherent and coherent techniques (Table 1).

1.2. Emergence of biophotonics employing coherent optical techniques

By using optical coherence as an additional control of light-matter interaction, coherent biophotonics imaging has gained popularity over its incoherent counterpart since the early 1990s because of its label-free capability and molecular specificity [23–25] (Table 2). The coherence may present as the content in the signal, the extraction of which can be used to deduce the structural reflectance of the biological tissues or the vibrational (Raman) spectra of biomolecules. The coherence may be employed to control the incident field for two-photon absorption, and in turn, to selectively excite a targeted molecule among background molecules. In other scenarios, the coherence plays an indirect but indispensable role, including dispersion compensation of incident ultrashort pulses to attain maximum incident peak intensity and coherent synchronization (or synchronized delay) of two ultrashort pulses in two-beam imaging (Table 2).

Table 2.

Summary of label-free coherent optical imaging in biology.

Modality	Contrast	Excitation beam(s)	Role of coherence
Optical coherence tomography [26]	structural reflectance	1	content in signal
Two-photon excited autofluorescence [27], two-photon absorption [28]	two-photon absorption	1	maximum incident peak intensity
Second harmonic generation [29], third harmonic generation [30]	nonlinear susceptibility	1	maximum incident peak intensity
Four-wave mixing [31, 32]	electronic response	2	maximum incident peak intensity, synchronization
Coherent anti-Stokes Raman scattering [31, 32], stimulated Raman scattering [33, 34]	molecular vibrations	2	maximum incident peak intensity, synchronization
Transient absorption [35], stimulated emission [36]	excited-state transition	2	synchronized delay of two ultrashort pulses
Single-beam multiplex coherent anti-Stokes Raman scattering [37]	vibrational spectrum	1	Fully-controlled incident field, content in signal
Selective two-photon excited autofluorescence or two-photon absorption [38]	two-photon absorption	1	Fully-controlled incident field

It should be noted that coherent optical techniques are not limited to optical imaging (or corresponding spectroscopy). There are no fundamental factors that prohibit the use of the coherence to control photophysical and photochemical processes [39, 40], particularly those associated with photosynthesis [41] and vision [42]. With its unique beneficial features (Table 1), biophotonics employing coherent optical techniques will continue to evolve, and may produce novel applications in two-photon photodynamic therapy, femtosecond laser surgery, and nano-biophotonics, etc. Unfortunately, except for optical coherence tomography, the complexity, cost and inadequate portability of traditional solid-state ultrafast laser sources (Table 1) have limited the widespread (clinical) applications of coherent optical techniques. Numerous studies have thus attempted to overcome this limitation by generating coherent fiber supercontinuum from a mode-locked femtosecond laser (Table 1).

1.3. Portable coherent supercontinuum platform for multiple biophotonics applications

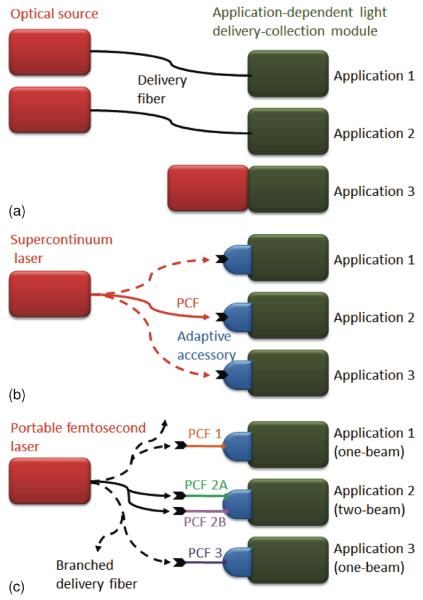
Because of the broad bandwidth, uniform spatial profile, and potentially high coherence and spectral power density, fiber supercontinuum has the potential to become a “universal source” for biophotonics and replace the conventional “one-source-one-application” configuration that is often present today [Fig. 1a]. An engineered portable source generating fiber supercontinuum, along with various plug-and-play adaptive accessories (for wavelength filtering, beam conditioning, and pulse shaping) integrated into application-dependent light delivery (and optional signal collection) modules [Fig. 1b], could be more cost-effective and reliable than an assembly of dedicated sources [Fig. 1a]. This is especially useful in hospitals or advanced research laboratories that utilize and investigate an increasing number of coherent biophotonics applications. Also, the portability of the supercontinuum platform enables comprehensive point-of-care or in-the-field studies, which have largely been restricted to biophotonics employing incoherent optical techniques. Thus, the search for the optimal supercontinuum platform for biophotonics has attracted academic and commercial interests since the start of the supercontinuum revolution.

Figure 1.

(online color at: www.lpr-journal.org) Optical sources for biophotonics applications. (a) Conventional one-source-one-application configuration; (b) Supercontinuum laser for multiple applications; (c) Coherent supercontinuum platform for multiple applications.

After a decade of research, however, only two supercontinuum platforms have found moderate success. One is based on coupling the picosecond (~ 5 ps) pulses of a mode-locked (80 MHz repetition rate, typically) ytterbium fiber laser into a long (> 1 m) engineered PCF with a zero-dispersion wavelength around 1050 nm [43]. The commercialization of this platform (e. g., by NKT Photonics, Inc. or Fianium, Ltd.) has produced a supercontinuum with a broad bandwidth (390–2450 nm) and a large spectral power density (~ 2 mW/nm). This source can therefore directly replace the gas and solid-state lasers in many standard biophotonics instruments employing incoherent optical techniques, such as fluorometers, cytometers, microscopes, and multiwell plate readers, offering full spectral coverage at reduced cost, size and complexity [44]. However, the intrinsically poor coherence of supercontinuum generation by picosecond pulses [11] has largely prohibited the coherent applications of this platform in biophotonics. The other supercontinuum platform [45] is based on coupling the femtosecond (~ 100 fs) fiber ~ 80 MHz pulses of an erbium master-oscillator-power-amplifier [46] into a short (< 10 cm) dispersion-engineered circular fiber [47]. Along with some key techniques of coherence-preserving nonlinear wavelength conversion [48–52], this platform has been commercialized (by Toptica Photonics AG) to cover a spectral range of 488–2200 nm, except for a gap of 640–830 nm. The overall good coherence allows the application of this platform to both incoherent and coherent biophotonics imaging [53–56]. Unfortunately, the desired tuning of the supercontinuum requires free-space light coupling between the fiber amplifier and the circular fiber, which forbids the simple plug-and-play fiber connection between the source and the adaptive accessories [Fig. 1b]. Moreover, the spectral power density (~0.1 mW/nm) is frequently too low for many biophotonics applications.

Due to the restrictions of nonlinear fiber optics, it is difficult (if not impossible) for one “magic” combination of ultrafast source laser and nonlinear fiber to generate a supercontinuum with high coherence, broad bandwidth, and large spectral power density (i. e., the three have intrinsic trade-offs) [Fig. 1b]. It is easier and more flexible to select different nonlinear fibers for different applications. In this platform [Fig. 1c], the fiber-delivered femtosecond pulses from a portable mode-locked source laser are coupled to a dispersion-engineered PCF optimized for a particular biophotonics application. The fiber is integrated into the adaptive accessory and the corresponding application-dependent light delivery-collection module. Switching among different applications is facilitated by a simple plug-and-play fiber connection between the pulse delivery fiber and the PCF. To accommodate the two-beam coherent biophotonics applications (Table 2), the source laser has a branched output delivering two synchronized pulse series, which are separately coupled to two different PCFs [Fig. 1c]. This platform capitalizes on the powerful dispersion engineering of the PCFs [6, 7] to produce tailored supercontinuum or isolated spectral bands for individual applications, with potentially high coherence and large spectral power density. In this sense, it is advantageous over the above two supercontinuum platforms, each of which relies on a single dispersion-engineered fiber [Fig. 1b].

In the following sections, we review several key techniques that enable this novel supercontinuum platform [Fig. 1c], including coherent supercontinuum generation around the central wavelength of the source laser (Sect. 2), coherence-preserving optical frequency down- or up-conversion of the source laser by self-frequency shifted soliton or fiber-optic Cherenkov radiation (Sect. 3), plug-and-play fiber connection between one source laser and multiple PCFs (Sect. 4), and post-supercontinuum-generation pulse shaping by programmable phase control (Sect. 5). Finally, we discuss how these techniques can be integrated for biophotonics applications and provide some perspectives along this line of research (Sect. 6). It should be noted that this paper is not an up-front review of the biophotonics applications that have employed fiber supercontinuum generation (for this type of review, we refer to ref. 44). Rather, for these relevant biophotonics applications, we specify the requirements of their optical sources.

2. Uniform coherent fiber supercontinuum generation from nonlinear PCFs

Supercontinuum generation, or white-light generation, was first conducted in bulk materials [10]. However, fiber media makes this process significantly easier and more controllable [3]. For detailed reviews of fiber supercontinuum generation, we refer to Ref. 11 and the references therein. Here we focus on the coherence aspect of the fiber supercontinuum generation.

2.1. A short history

The history of coherent fiber supercontinuum generation is intertwined with that of pulse compression of supercontinuum pulses, because the generation of a supercontinuum that is coherent is equivalent to the generation of one that is compressible [11, 57]. Before the supercontinuum revolution, supercontinuum was typically generated in a conventional fiber with its full bandwidth falling into a normal dispersion regime of the fiber, so that the fiber behaved like an all-normal dispersion (ANDi) fiber. This was a natural condition dictated by the available laser sources and nonlinear fibers. Although pulse compression down to 6 fs (i. e., broad coherent bandwidth) was attained [58], the complicated source laser (low repetition-rate amplifier) limited the widespread application of this supercontinuum.

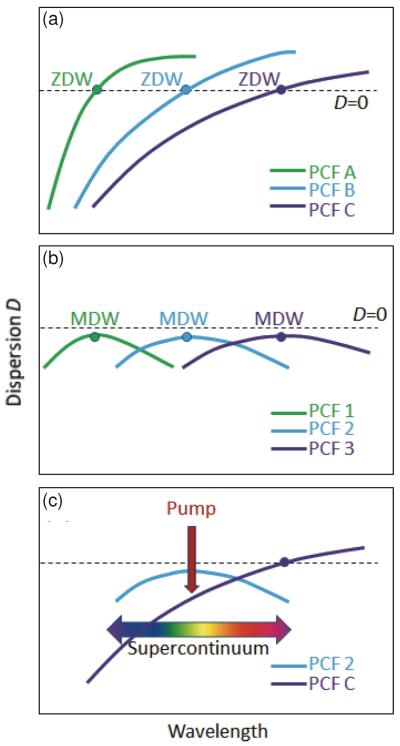
After the supercontinuum revolution, supercontinuum was commonly generated in a zero-dispersion wavelength (ZDW) PCF with its bandwidth falling into both normal and anomalous regimes of the fiber (i. e., the ZDW lies within the spectrum of the supercontinuum). The powerful dispersion engineering of PCFs shifts the ZDW of the fiber close to the wavelength of a standard mode-locked (femtosecond or picosecond) source laser, leading to this widely accessible supercontinuum dominated by soliton dynamics. Unfortunately, the pulse compressibility (or coherence) of the supercontinuum is generally poor due to the intrinsic noise of the soliton dynamics [11]. Although the compressibility can be improved [59–62] by using short fiber lengths (< 10 mm), short source laser pulses (< 50 fs), or low input pulse energies (< 4 nJ), these conditions are practically undesirable due to difficulty in fiber-handling, laser complexity, and low power throughput. After a decade of intense research, it is becoming increasingly clear that the ZDW PCFs and the associated dispersion engineering [Fig. 2a], which have promoted soliton generation to initiate the supercontinuum revolution, and continue to play important roles in broadband (incoherent) supercontinuum generation, must be abandoned for practical coherent supercontinuum generation.

Figure 2.

(online color at: www.lpr-journal.org) (a) Dispersion engineering of ZDW PCFs; (b) Dispersion engineering of DFDD-ANDi PCFs; (c) The relationship between pump wavelength and the dispersion property of a DFDD-ANDi PCF and a ZDW PCF in supercontinuum generation.

A recent concept of dispersion engineering of PCFs [Fig. 2b] [63–66], which was suggested by earlier studies on conventional circular fibers [67, 68] and the PCFs with two closely spaced ZDWs [69, 70], is raised as a method to generate soliton-free supercontinuum. This trend reflects a shift of focus for dispersion engineering from pursuing the broadest supercontinuum generation to preserving the coherence of supercontinuum generation. The engineered PCF has a flattened convex profile of normal dispersion with a distinct maximum-dispersion wavelength (MDW) but no ZDW, and is thus termed as a dispersion-flattened dispersion-decreased all-normal dispersion (DFDD-ANDi) fiber. Just as with the well-documented dispersion engineering that shifts the ZDW of a typical PCF anywhere between 550 and 1250 nm [Fig. 2a], the new dispersion engineering can place the MDW of a DFDD-ANDi fiber anywhere inside the same spectral range [Fig. 2b] [65, 66]. The DFDD-ANDi PCFs have dominated the recent studies on coherent supercontinuum generation and pulse compression [71–77], marking a dramatic post-supercontinuum-revolution resurgence of ANDi fibers.

2.2. Uniform coherent supercontinuum generation from DFDD-ANDi PCFs

A well-known procedure for broadband supercontinuum generation is to match the ZDW of the PCF with the central wavelength of the source laser. Similarly, the procedure for uniform coherent supercontinuum (UCSC) generation is to match the MDW of the PCF with the central wavelength of the source laser. The mismatch between the two leads to the increased dispersion of the input laser pulses, which is unfavorable for nonlinear spectral broadening [73]. Because only the supercontinuum generated in a normal dispersion region of the fiber is guaranteed to be coherent [11], it is fair to compare the DFDD-ANDi PCF with the ZDW PCF that behaves effectively as an ANDi fiber [Fig. 2c]. In this ZDW PCF, the supercontinuum generation occurs only in the short wavelength end of the ZDW, i. e., in a normal dispersion of the fiber [78–80]. Due to the sloped dispersion profile, the ZDW of this fiber must be placed at a longer wavelength than the red edge of the intended supercontinuum. Thus, an undesirably large dispersion of the input laser pulses occurs and adversely influences the spectral broadening [Fig. 2c]. This clearly illustrates the advantage of the DFDD-ANDi PCF over the ZDW PCF in broadband coherent supercontinuum generation.

DFDD-ANDi PCFs have been fabricated in-house with a MDW around 625 nm [74], 800 nm [81], 1050 nm [70, 72], and 1550 nm [82]. Also, a DFDD-ANDi PCF with a MDW of 1050 nm has been commercially available and extensively studied [65, 71, 73, 75–77, 83]. Representative results of UCSC from this fiber (~ 9 cm in length) by the use of an ytterbium mode-locked femtosecond solid-state laser are summarized in Fig. 3 [65, 77]. The known spectrotemporal property of the input laser pulses and the dispersion of the fiber allow the spectra of the UCSC at different coupling powers to be quantitatively predicted by the scalar generalized nonlinear Schrödinger equation of nonlinear fiber optics [Fig. 3a] [65]. More importantly, the measured spectrum and spectral phase (i. e., the spectrotemporal field) of the supercontinuum pulses can be simultaneously predicted [Fig. 3b]. A phase mask can thus compensate the phase distortion of the pulses to generate the corresponding transform-limited pulses of 9.6-fs (FWHM) [Fig. 3c], and the full coherence of the supercontinuum is confirmed [77]. In addition to a relatively high and uniform spectral power density (~ 1 mW/nm), large pulse energy (4.7 nJ), fast pulse repetition rate (76 MHz), and broad bandwidth (~ 300 nm), the supercontinuum has excellent long-term stability (over 200 hrs and counting) [77]. These results definitively demonstrate the predictability and reliability of UCSC generation. The same level of controllability has not been possible in conventional (incoherent) supercontinuum generation from ZDW PCFs because of the intrinsic soliton-induced noise, which directly degrades the coherence of the supercontinuum [11].

Figure 3.

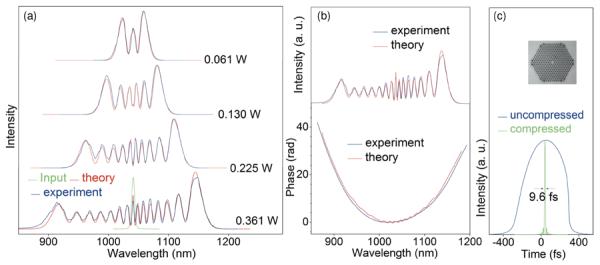
(online color at: www.lpr-journal.org) (a) Comparison of observed and calculated UCSC spectra of a 9-cm DFDD-ANDi PCF (NL-1050-NEG-1, NKT Photonics) at fiber output powers of 0.061 W, 0.130 W, 0.225 W, and 0.361 W. The narrowband (green curve) input pulses were from a Yb:KYW source laser (1041 nm, 229-fs FWHM, 76 MHz); (b) Comparison of measured spectrum and spectral phase of UCSC pulses at 0.361 W with calculated spectrum and spectral phase; (c) Temporal intensity profiles of uncompressed and compressed UCSC pulses at 0.361 W. Inset: cross-section image of the PCF. Adapted from [65, 77, 83], with permission.

Although shorter (~ 4 fs) supercontinuum pulses with a broader bandwidth have been produced from this fiber [75, 76], very short (< 15 fs) input pulses from high-maintenance ultra-broadband mode-locked lasers [84, 85] must be employed, resulting in a relatively small compression-ratio (4× or less). In contrast, the use of a standard narrowband (~ 229 fs FWHM) low-maintenance mode-locked laser takes full advantage of the spectral broadening by the supercontinuum generation [Fig. 3a], and attains a large compression-ratio of 24×. The large-compression-ratio supercontinuum generation shifts the load of the spectral broadening from the active (environmentally unstable) broadband mode-locking in the source laser to the passive (environmentally stable) nonlinear fiber optics of supercontinuum generation, and is thus more reliable. The compression-ratio (or the bandwidth of the UCSC) is currently limited by the nonlinear depolarization of the DFDD-ANDi PCF, which can be overcome by a polarization-maintaining fiber design [83]. The beneficial features of broader bandwidth (730–1350 nm) and flatter spectrum foreseen by simulations [64, 83] may be realized in longer fiber lengths (> 9 cm) once such polarization-maintaining fiber is fabricated. Also, a maintenance-free ytterbium fiber laser can directly replace the solid-state source laser, making this coherent supercontinuum source portable and environmentally stable.

3. Non-uniform coherent supercontinuum generation from nonlinear PCFs

3.1. Optical frequency down- and up-conversion under unique conditions

For a narrowband mode-locked femtosecond source laser emitting at a fixed wavelength, the MDW-matched DFDD-ANDi PCF can only produce moderately broadened UCSC centering on this wavelength (Sect. 2). To generate coherent (narrow) bands outside this bandwidth, other fiber-based techniques that can frequency up- or down-convert the source laser are needed. Popular processes of nonlinear frequency conversion (second-harmonic generation, third-harmonic generation, four-wave mixing, etc.) have been inefficient in optical fibers due to the rapid walk-off between the incident pulse (pump) and the frequency-converted pulse(s) (signal), and perhaps more importantly, the strict requirement of the phase-matching condition [3]. Rather than to seek the exotic fiber dispersion in order to satisfy the phase-matching condition, it is easier to search alternative nonlinear techniques with the existing dispersion engineering of ZDW PCFs, providing the coherence is preserved during the frequency conversion.

Although only the supercontinuum generated from an ANDi fiber is guaranteed to be coherent (Sect. 2), a specific operational condition of a ZDW PCF, termed as low-soliton-order (LSO) condition, can produce highly coherent supercontinuum [11]. The soliton order N is determined by both (input) pulse and fiber parameters through N² = L_D/L_NL, where $L_D=T_0^2∕{\beta }_2$ (T₀ is pulse width, β₂ is fiber anomalous dispersion) and L_NL =1/γP₀ (γ is fiber nonlinear coefficient, P₀ is peak pulse intensity) are the characteristic dispersive and nonlinear length scales, respectively [3, 11]. For given input pulses with constant T₀ and central wavelength, N² is thus proportional to γP₀/β₂. We also define the condition of a large β₂as a short-anomalous-interaction (SAI) condition, which characterizes the fast anomalous dispersion of the input pulse in a relatively short fiber length, so that the nonlinear interaction length is short. The typical way to invalidate (or satisfy) the SAI condition is to place the wavelength of the source laser slightly longer (or far longer, >100 nm) than the ZDW of a PCF, as shown in Fig. 4a [or Fig. 4b].

Figure 4.

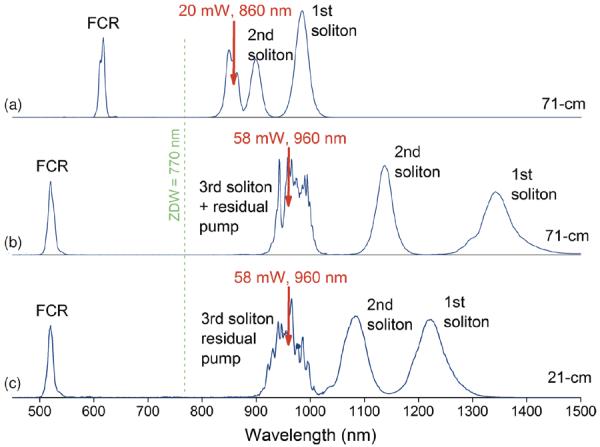
(online color at: www.lpr-journal.org) (a,b) Spectra of non-uniform supercontinuum from a 71-cm long PCF (NL-1.7-770, NKT Photonics) for varying output-power/input-wavelength (red labels); (b,c) Spectra of non-uniform super-continuum from the PCF at fixed output-power/input-wavelength (red labels) but different fiber lengths (71-cm and 21-cm). The input pulses (170-fs FWHM, 80 MHz) were produced by a widely tunable Ti:sapphire laser. Adapted from [86], with permission.

Under the combined LSO and SAI condition, the input pulses transfer their energy into a few isolated bands that span a broad bandwidth of 500–1500 nm [Fig. 4b] [86]. The two bell-shaped bands in an anomalous dispersion region of the ZDW PCF undergo redshifts along the fiber [Fig. 4b,c], and can thus be assigned to two self-frequency shifted solitons (SFSS). The most blue-shifted band resides in an adjacent normal dispersion regime with no wavelength shifts along the fiber [Fig. 4b,c], and can thus be assigned to fiber-optic Cherenkov radiation (FCR) [86]. The soliton order N (N ≈3 in this case) can be estimated from the number of the observable spectrally-resolved SFSSs exiting a long fiber [3]. While the LSO condition results in the high coherence of this non-uniform supercontinuum, the SAI condition ensures the broad spectral separation between the most red-shifted SFSS (1st SFSS) and the FCR. The invalidation of the SAI condition under the LSO condition would lead to a significantly diminished SFSS-FCR spectral separation [Fig. 4a]. These observations indicate that SFSS and FCR are the two most fundamental processes for fiber supercontinuum generation, and more importantly, broad frequency down-conversion and up-conversion of the source laser can be realized by the 1st SFSS and the FCR, respectively.

It should be noted that this LSO-SAI condition is incompatible with typical fiber supercontinuum generation in which uniform spectral broadening is pursued. The key strategy for uniform supercontinuum generation is to match the ZDW of the fiber with the source laser wavelength (i. e., to attain a very small β₂). Thus, the input pulse sustains high peak intensity over a long fiber length to enhance nonlinear interaction, while a large number (>30) of spectrally overlapping SFSSs are generated to produce a rather uniform but incoherent spectrum [11]. In other words, the non-uniform coherent supercontinuum generation is mutually exclusive with the uniform incoherent supercontinuum generation. The promotion of one necessitates the suppression of the other. It might be the very purpose of the uniform spectral broadening that had long obscured the observation of this SFSS-FCR-dominated non-uniform supercontinuum under the rather unusual LSO-SAI condition.

3.2. Intense self-frequency shifted solitons at controlled fiber lengths

Optical solitons are particulate-like wave packets that maintain their temporal profiles with propagation and under mutual collisions [3]. The phenomenon of soliton self-frequency shift in an optical fiber was discovered in 1986 [87], and theoretically explained on the basis of intrapulse Raman scattering [88]. The corresponding SFSS, observed to undergo continuous redshift with increasing input power or fiber length, immediately suggested itself for wavelength-tunable femtosecond fiber lasers [89–91]. The dispersion engineering of PCFs has allowed sub-1300 nm tunability [92–94], ultrabroad tunable bandwidth [95–97], large pulse energy [98, 99], and short pulse width [99, 100]. The typical SFSSs generated in a PCF by an ytterbium mode-locked femtosecond fiber laser are plotted in Fig. 5 [95]. The tuning of the 1st SFSS across 1200–1600 nm is demonstrated by simply varying the input power.

Figure 5.

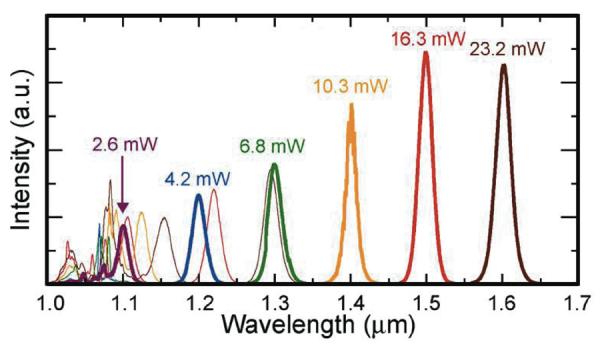
(online color at: www.lpr-journal.org) Generation of tunable (1200–1600 nm) SFSS pulses from a 10-m PCF (945 nm ZDW) by input pulses (1050 nm, 66-fs, 41.3 MHz) from an ytterbium fiber laser. The labeled powers are the total output powers from the fiber. Adapted from [95], with permission.

In comparison to conventional wavelength-tunable sources based on optical parametric generation [101], the SFSS has several distinct advantages as a technique for optical frequency down-conversion. First, it allows efficient (up to 85%) conversion of irregular femotosecond input pulses (e. g., pulses from fiber source lasers) to fiber-delivered transform-limited soliton pulses of comparable or shorter widths (e. g., see [90]). Second, it does not require a phase-matching condition, which is sensitive to thermal and mechanical perturbations. Third, a SFSS source based on a fiber source laser can be constructed as a robust and portable system [95], which significantly outperforms a free-space optical parametric generation system in cost, size, and complexity.

The pulse energy of the SFSS had been largely limited by the LSO condition, which restricts the input power (recall the P₀ dependence in N² = γP₀/β₂). To satisfy the LSO condition at higher input powers, the nonlinear coefficient γ of the fiber must be decreased, and/or the fiber dispersion at the input wavelength β₂ must be increased (i. e., SAI condition). Thus, large SFSS pulse energies (> 0.5 nJ) can be obtained by operating under the LSO-SAI condition (large β₂) [86, 94], employing a long-wavelength (~ 1250 nm) source laser (large β₂) [98, 99], and using fibers with low nonlinearity (small γ) [99, 102]. Also, the generation of the 1st SFSSs of different central wavelengths has been universally conducted by varying the input power. Although simple wavelength tuning is enabled, the short-wavelength 1st SFSSs are much weaker than the long-wavelength ones due to the lower input powers (Fig. 5). To generate 1st SFSSs with large and uniform pulse energy across the tunable bandwidth, it is advantageous to fix the input power at the highest level that generates the most red-shifted 1st SFSS, and input the power into a series of fibers of varying lengths, each of which produces a 1st SFSS with a distinct wavelength-shift [Fig. 4b,c]. This approach is practical if the source laser pulses are fiber delivered and the nonlinear fibers are properly terminated (see Sect. 4).

3.3. Fiber-optic Cherenkov radiation at targeted wavelengths

Fiber-optic Cherenkov radiation (FCR), also known as dispersive wave generation or non-solitonic radiation, describes the resonant phase-matched radiation of a dispersive wave from a fiber soliton perturbed by higher-order fiber dispersion [103]. Thus, the studies on FCR were historically intertwined with those on SFSS. This phenomenon was first studied (theoretically) in 1986 [104] and later, in 1995, shown to be analogous to its counterpart in bulk materials [105]. FCR was thought to seed the blue edge of fiber supercontinuum generation [103, 106] through pulse trapping [107, 108] and cross-phase modulation [109]. Indeed, weak isolated FCR of a narrowband nature was observed before the supercontinuum onset [110]. It was thus unclear whether intense (multi-milliwatt level) FCR could be obtained free of supercontinuum contamination. Some studies on SFSS, performed under the LSO condition but without the SAI condition, prohibited this feasibility by observing the irregular supercontinuum-like spectral components to the bluer wavelengths of the SFSS [89, 91, 100]. Other studies seemed to support this feasibility by observing single isolated anti-Stokes bands with milliwatt-level intensity [95, 111–113]. However, the wide (> 50 nm) tunability of the anti-Stokes bands was not demonstrated by phase-matching conditions, so that the resonant nature of the observed anti-Stokes bands remained ambiguous. For example, the anti-Stokes bands might be attributed to the trapped pulses [108, 114] widely believed to dictate the blue edge of the supercontinuum generation [43].

The feasibility of optical frequency up-conversion by FCR was conclusively demonstrated under the LSO-SAI condition by using a widely wavelength-tunable femtosecond source laser and a few dispersion-engineered PCFs that are poor candidates for broadband supercontinuum generation [86]. Following a phase-matching condition, milliwatt-level narrowband (~ 10 nm FWHM) FCR was produced at a targeted wavelength within a broad spectral range of interest (485–690 nm). To minimize the effect of the non-resonant spectral broadening of supercontinuum generation on the FCR, the wavelength of the source laser was detuned far away (> 100 nm) from the ZDW of each of the fibers (SAI condition) [86]. Thus, the LSO-SAI condition is required for the generation of intense isolated coherent FCR, just like that of SFSS [94]. Because the generation of Cherenkov radiation is typically completed within the first few centimeters of the fiber [115, 116], the SAI condition has little influence on its efficiency. On the other hand, this condition adversely affects all competing nonlinear processes of supercontinuum generation to gain energy from the input pulse, so that strong standalone FCR can be revealed (Fig. 4). The high efficiency (~10%, typically) of the FCR under the LSO-SAI condition is rather intriguing [115]. A recent study has provided a theoretical explanation based on the efficient mode conversion of a soliton at its own optical event horizon [117].

A more cost-effective way for FCR-based optical frequency up-conversion, however, is to employ a fixed-wavelength femtosecond source laser and a series of nonlinear fibers with no specific dispersion engineering [118]. By fixing the input wavelength at ~ 1000 nm and invoking the LSO-SAI condition, multi-milliwatt FCR across the ultraviolet-visible regime (347–680 nm) was obtained from one series of PCFs whose dispersion and cross-section approximate those of single circular silica strands in air [Fig. 6a,b] [118]. Because intense isolated SFSS and FCR are both generated under the LSO-SAI condition, it would be tempting to generate the SFSS in addition to the FCR from one fiber (Fig. 4). This approach is undesirable due to the subtle difference in the ideal LSO-SAI condition to generate the two (Sect. 6). The two may also interfere with each other to generate a trapped pulse [108, 114]. Thus, the use of different fibers is preferred to promote either the SFSS or the FCR. Again, this approach is practical if the source laser pulses are fiber delivered and these nonlinear fibers are properly terminated (Sect. 4).

Figure 6.

(online color at: www.lpr-journal.org) (a) Generation of multi-milliwatt FCRs in the range of 347–680 nm from seven ~10-cm PCFs of varying ZDWs (broken vertical lines) by 1020-nm 170-fs FWHM, 80-MHz input pulses from a Ti:sapphire laser (arrows). The insets show the far-field images of the output light on a paper screen. Autofluorescence from the paper gives the bottom image a false blue color. (b) The common cross-sectional image of these single silica strand-like PCFs with varying core size (1.5–3.3 μm). (c) Comparison of predicted FCR wavelength as a function of the ZDW of single silica strand (line) according to a phase-matching condition and measured FCR wavelengths of 13 single silica strand-like PCFs with varying ZDWs (points). Adapted from [118], with permission.

4. Fiber connection between one source laser and multiple nonlinear PCFs

By the use of a fixed-wavelength (~ 1000 nm) mode-locked femtosecond source laser and multiple nonlinear PCFs, coherent bands with relatively large power spectral density (~ 1 mW/nm) can be generated across 347ȓ1600 nm (Figs. 3, 5, 6). However, this platform is demonstrated by the free-space coupling of the laser pulses to the fibers, which is susceptible to optical misalignment. For robust long-term operation, it is advantageous to deliver the femtosecond pulses of the source laser by a pigtail of standard single-mode fiber and terminate each of the nonlinear fibers with a pigtail of the same single-mode fiber, so that a plug-and-play fiber connection between the source laser and the PCFs can be conducted just like that in fiber telecommunication [Figs. 1c, 7]. The standard pigtailed nonlinear PCFs add to the fiber-coupled narrowband source laser the capabilities of an ultra-broadband femtosecond laser [84, 85] and a number of optical parametric oscillators (or amplifiers), which can be easily switched by the fiber connection depending on particular applications.

Figure 7.

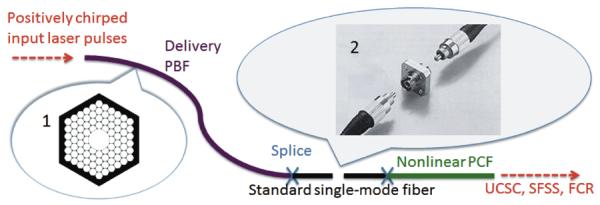
(online color at: www.lpr-journal.org) (a) Termination of pulse delivery photonic bandgap fiber (PBF) and nonlinear PCF with spliced pigtails of standard single-mode fiber. Connection and disconnection of two pigtails allow plug-and-play fiber connection between one source laser and multiple nonlinear PCFs. Inset 1: typical cross-sectional image of PBF. Inset 2: widely used FC/APC connection between two pigtails of standard single mode fiber.

4.1. Standard fiber delivery of femtosecond pulses using photonic bandgap fibers

Fiber-coupled laser delivery is required in portable applications where the sensitive steering of free-space beams must be avoided. The confinement of laser output in a standard single-mode step-index fiber makes the delivery system compact, simple, and reliable. While this is straightforward for continuous-wave beams, it is nontrivial for high peak intensity femtosecond pulses due to the undesired nonlinear effects of the standard single-mode fiber. The early onset of the nonlinear effects had been an intrinsic difficulty until the advent of the low-nonlinearity low-loss single-mode photonic bandgap fibers (PBF) [119, 120]. These fibers use a holey silica cladding and a central hollow core (Fig. 7, inset 1) to transmit light by photonic bandgap guiding [121, 122], a mechanism fundamentally different from the traditional total internal reflection guiding principle. The transmission band of a PBF has a somewhat limited bandwidth (< 200 nm, typically), but can be placed anywhere inside the range of 420–2100 nm. This new technology provides the basis for high power fiber delivery without nonlinear effects, in contrast to the fiber supercontinuum generation (Sects. 2 and 3) in which the nonlinear effects are beneficial. Moreover, a PBF may have large anomalous dispersion [123, 124] useful for in-fiber pulse compression/dispersion compensation [125–128]. Chirp-free fiber coupling of near transform-limited femotosecond pulses to a nonlinear PCF can be achieved by balancing the initial positive chirp of the input pulses, the negative chirp caused by the PBF, and the positive chirp induced by the spliced and connected standard single-mode fibers (Fig. 7). The splice loss from the PBF to the standard single-mode fiber should be minimized [129–132] (Table 3), while the total length of the two pigtailed single-mode fibers is kept short to avoid possible nonlinear optical effects.

Table 3.

Splice losses from PBFs to standard single-mode fibers or from standard single-mode fibers to nonlinear PCFs.

Standard single-mode fiber	Micro-structured fiber (nature)	Core diameter (μm)	Pitch Λ (μm)	Relative hole size d/Λ (μm)	Mode-field diameter (μm) at λ (nm)	Related numerical aperture	Splice loss (dB)	Reference
SMF-28	HC19-1550-1 (PBF)	20	3.9	>0.9	13 (1550)	0.13	>2	[129]
SMF-28	HC-1550-02 (PBF)	10.9	3.8	>0.9	7.5 (1550)	0.12	1.3–2.5	[130, 131]
PM980-HP	HC-1060-02 (PBF)	10	2.75	>0.9	6.5 (1060)	-	2.19	[132]
SMF-28	LMA-5 (PCF)	5.5	2.9	0.44	4.1 (1550)	0.23	0.90	[131]
SMF-28	NL-3.3-880 (PCF)	3.4	3.0	>0.89	3.2 (1550)	0.41	2.5	[131]
SMF-28	Unknown (PCF)	2.5	-	>0.95	- (1550)	>0.9	1.55–3.1	[133, 134]
SMF-28	NL-2.3-1555 (PCF)	2.3	1.6	0.5	~ 3 (1550)	~0.5	0.25–0.6	[135]
SMF-28	NL-1550-P-1 (PCF)	2.1	-	-	2.8 (1550)	0.4	0.9	[136]
HI-1060	Unknown (PCF)	2.0	2.3	0.83	1.8 (980)	-	0.55	[137]
SMF-28	Unknown (PCF)	1.27	-	>0.95	1.5 (1550)	>0.9	1.3	[138]

Note: for SMF-28, core diameter is 8.3 μm, mode-field diameter (1550 nm) is 10.4 μm, and numerical aperture is 0.14.

4.2. Standard termination of nonlinear PCFs using an intermediate germanium-doped ultrahigh numerical aperture fiber

A standard fiber connection between the source laser and nonlinear PCFs requires not only standard termination of the PBFs (Sect. 4.1), but also standard termination of the PCFs (Fig. 7, inset 2). This demands low-loss splicing between the single-mode fiber and each of the nonlinear fibers, even though the former has a much larger mode-field diameter than the latter [131, 133–138] (Table 3). Theoretical guidance has been provided on this topic [139, 140]. Experimentally, low splice loss (< 2.5 dB) has been attained by the use of a repeated weak arc discharge [136], a mode-field expander with controlled hole collapse [137], and an intermediate germanium-doped ultrahigh numerical aperture fiber [138]. The last approach is particularly attractive because of the relatively simple procedure and low splice loss (< 2 dB, typically). This approach is applicable to various (pure-silica or germanium-doped) nonlinear PCFs with a large variation of core diameter (1.5–3.5 μm), including those generate the UCSC (Fig. 3), SFSS (Fig. 5) and FCR (Fig. 6).

5. Post-supercontinuum-generation pulse shaping by programmable phase control

The adaptive accessories of the coherent supercontinuum generation [Fig. 1c, Sects. 2, 3] are more technically demanding than those of the incoherent supercontinuum generation [Fig. 1b]. In addition to wavelength filtering and beam conditioning, (temporal) pulse shaping of the fiber supercontinuum is usually required for optimal excitation at the target, which is typically a small focused spot after an application-dependent light delivery module [Fig. 1b,c]. The most popular pulse shaping is to generate short excitation pulses free of linear chirp at the target, so that the nonlinear light-matter interaction is enhanced. This is often done by a free-space pulse compressor consisting of a prism pair, a grating pair, or a chirp-mirror pair. In-fiber compressors consisting of PBFs [125–128] or chirped fiber Bragg gratings may also be used. However, the ultimate goal of pulse shaping is to deliver prescribed pulses of arbitrary spectrotemporal profile at the target by the programmable phase control of a 4f pulse shaper [141], so that various coherently-controlled applications [39, 40] can be enabled.

Before 2003, targeted coherently-controlled excitation required pulse shaping by a regular 4f pulse shaper and the pulse measurement by a separate two-beam interferometer-type instrument based on frequency resolved optical gating [142] or spectral phase interferometry for direct electric-field reconstruction [143]. This had been a notoriously difficult and alignment-sensitive operation until the invention of multiphoton intrapulse interference phase scanning (MIIPS), an automated procedure that integrates pulse shaping and single-beam pulse measurement by the 4f pulse shaper itself (i. e., no additional instrument for alignment-sensitive two-beam pulse measurement is needed) [144, 145]. MIIPS is therefore considered to be an enabling technology in the ultrafast laser industry. A miniature MIIPS-assisted 4f pulse shaper (dimension 6×6×6 inches) has been commercially available to make laser pulse shaping widely accessible to users with no formal laser training (Fig. 8, inset). However, the solid-state broadband femtosecond laser sources have restricted the application of this technology to optical laboratories. The replacement of these bulky and environmentally unstable lasers with a versatile coherent fiber supercontinuum laser (Fig. 1) is required for portable applications such as point-of-care optical imaging.

Figure 8.

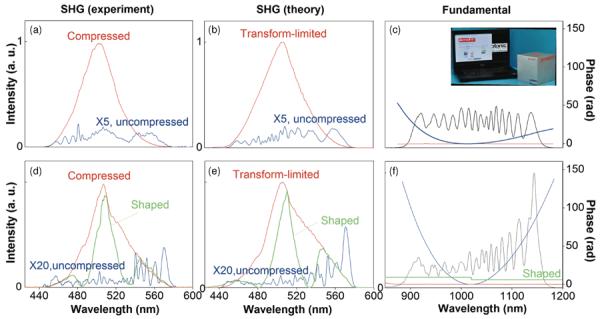
(online color at: www.lpr-journal.org) (a–c) Comparison of experimental second-harmonic generation (SHG) spectra (a) and theoretical SHG spectra (b) corresponding to the power spectrum and spectral phases of the UCSC with small post-supercontinuum-generation dispersion (c). Inset in (c): miniaturized MIIPS-assisted 4f pulse shaper (BioPhotonic Solutions, Inc.). (d–f) Comparison of experimental (d) and theoretical SHG spectra (e) corresponding to the power spectrum and spectral phases of the UCSC with large post-supercontinuum-generation dispersion (f). Adapted from [146], with permission.

Early studies on fiber supercontinuum employing a 4f pulse shaper were unable to compress the supercontinuum pulses to the transform-limited temporal profile [21, 60], let alone to shape the pulses arbitrarily. It was unclear whether this inability originated from the insufficient coherence of the fiber supercontinuum source, the finite spectral resolution of pulse shaping, or the error from the pulse measurement devices. With the demonstration of transform-limited compression of ultrashort (< 10 fs) UCSC pulses by a MIIPs-assisted 4f pulse shaper [Figs. 3c, 8] [77, 146], the inability can be largely attributed to the insufficient coherence of the supercontinuum pulses. More importantly, targeted coherently-controlled excitation according to an arbitrarily prescribed spectral phase can be achieved by adaptively compensating the dispersion of the application-dependent light delivery module (Fig. 8) [146]. Thus, in terms of (adaptive) pulse shaping, this potentially portable supercontinuum source bears no difference from a non-portable ultra-broadband mode-locked laser [84, 85] widely used in coherently-controlled applications [147–150]. In addition to the UCSC (Fig. 3), the SFSS (Fig. 5) and FCR (Fig. 6) should be amendable to the same pulse shaping because of their high coherence. High-quality pulse compression of the FCR has been demonstrated [102].

6. Integration for biophotonics applications

The feasibility of the envisioned platform for coherent fiber supercontinuum generation [Fig. 1c] has been validated by the key advancements of nonlinear PCF optics (Sects. 2, 3), PCF (or PBF) splicing (Sect. 4), and supercontinuum pulse shaping (Sect. 5). However, the integration of these individual techniques into a portable high-performance coherent fiber supercontinuum platform is an engineering challenge (Sects. 6.1, 6.2) which is worth confronting because of the many potential benefits in point-of-care coherent biomedical imaging (Sect. 6.3) and other directions that may lead to new biophotonics applications (Sect. 6.4).

6.1. Ytterbium-based branched all-fiber switchable-coherent-supercontinuum laser

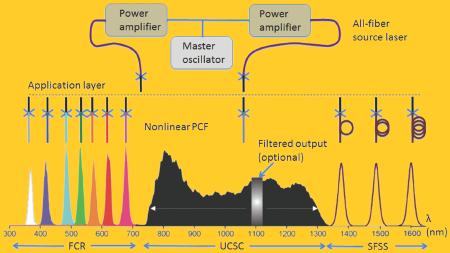
The concept of coherent fiber supercontinuum generation with a uniform (Fig. 3) or non-uniform spectrum (Fig. 4) has been demonstrated by the use of solid-state mode-locked source lasers. However, ultrafast fiber source lasers with comparable pulse properties are favored in (portable) biophotonics applications because of their compactness, robustness, single spatial mode, thermal stability, chemical inertness, power scalability, and (potentially) low cost. Comprehensive overviews have been provided on high-power fiber oscillators [151] and fiber master-oscillator-power-amplifiers (MOPA) [152, 153]. Both configurations have been influenced by the PCF technology [154] and fiber supercontinuum generation [155]. An all-fiber MOPA configuration is preferred in the envisioned coherent supercontinuum platform because it permits direct splicing of the exiting fiber of the MOPA to the delivery PBF (Fig. 7), resulting in an all-fiber switchable-coherent-supercontinuum laser (Fig. 9). The branched laser output can be easily implemented in the MOPA configuration (Fig. 9) [156] for two-beam coherent biophotonics applications (Table 2), while different coherent supercontinuum outputs (UCSC, FCR, SFSS) can be switched by the plug-and-play fiber connection to a series of nonlinear PCFs in each branch (Sect. 4). Thus, this laser is in sharp contrast to the common fiber supercontinuum sources based on the scheme of one-source-laser-one-nonlinear-fiber [152, 153, 155].

Figure 9.

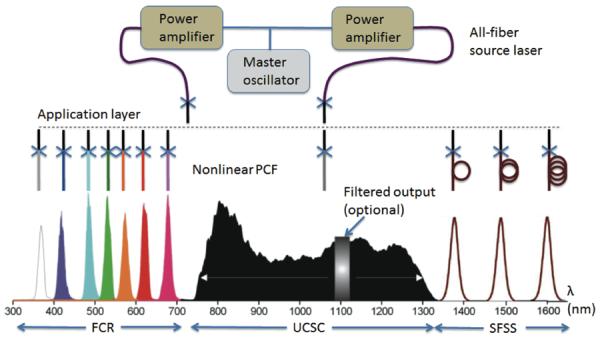
(online color at: www.lpr-journal.org) Schematic of an ytterbium-based branched all-fiber switchable-coherent-supercontinuum laser. Different coherent supercontinuum outputs (UCSC, SFSS, FCR) across 347–1600 nm are generated by fiber connection and disconnection between one ytterbium all-fiber source laser and multiple nonlinear PCFs.

The replacement of the ~ 1000 nm solid-state lasers with ytterbium-based MOPA fiber lasers with comparable pulse properties are not expected to change the nature of the UCSC generation from DFDD-ANDi PCFs (Fig. 3) and the SFSS or FCR generation from ZDW PCFs under the LSO-SAI condition (Figs. 5, 6) [155]. Because of their rather unique operational conditions, these nonlinear processes do not rely on specific spectrotemporal properties of the input laser pulses, i. e., input pulses of soliton, similariton, Gaussian, or other shapes can all be used [152]. As an example, multi-milliwatt femtosecond FCR has been generated from a monolithic femtosecond MOPA fiber laser [157] in an all-fiber polarization-maintaining scheme [158], with efficiency similar to that attained by the solid-state laser [Fig. 6a] [118]. Other all-fiber MOPA lasers based on polarization-maintaining oscillators [159–161] are expected to have similar performance.

The ytterbium-based branched all-fiber switchable-coherent-supercontinuum laser (Fig. 9) can be treated as the fiber analogue of synchronized ultra-broadband mode-locked solid-state lasers [84, 85] (UCSC) and/or optical parametric oscillators (SFSS, FCR). On one hand, this laser inherits all the advantages of fiber-optics and an all-fiber ultrafast laser, and thus overcomes the key limitations (bulkiness, complexity, environmental instability, etc.) of the synchronized ultrafast solid-state lasers. On the other hand, this laser produces a coherence-maintaining wavelength chain similar to that of synchronized ultrafast solid-state lasers, and thus overcomes the key limitations (fixed emission wavelength and narrow gain bandwidth) of conventional ultrafast fiber lasers. The wide wavelength coverage (350–1600 nm), high coherence (or equivalently, low noise [11]), and relatively high spectral power density (~ 1mW/nm) makes this portable laser useful in both coherent and incoherent biophotonics applications.

6.2. Engineering issues

The design of the above fiber laser is an engineering challenge involving tradeoffs among source laser availability, nonlinear PCF (or PBF) fabrication/splicing, and controlled supercontinuum generation that optimizes the UCSC, SFSS, or FCR. Although extensive research on this topic has not been available, a few general guidelines are useful for potential widespread applications in biophotonics.

At a fixed central wavelength of ~ 1040 nm, other parameters of the ytterbium-based MOPA source laser, such as pulse repetition rate, pulse width, and average power (or pulse energy), are important to control the supercontinuum generation. First, the pulse repetition rate should be around 100 MHz to accommodate fast fluorescence imaging [162]. Second, a short (< 400 fs FWHM) pulse width should be selected to efficiently generate the FCR [163], and perhaps the SFSS. Finally, an input pulse energy of > 4 nJ (average power of > 400 mW) is required to generate the broadband UCSC. The generation of the SFSS and the FCR requires lower pulse energies.

The DFDD-ANDi PCF should be designed to have a MDW that matches the source laser wavelength [65], allowing UCSC generation spanning 730–1350 nm (Fig. 9) [72, 83, 164]. The FCR generation directly follows the established method (Fig. 6) [118]. Although multiple single-silica-strand-like PCFs are needed (Fig. 9), the FCR can be produced at a targeted wavelength in 347–680 nm according to a simple phase-matched condition [Fig. 6c]. The SFSS generation (> 1040 nm) requires only one ZDW PCF, which should balance the requirements of fiber nonlinearity, the LSO condition, and the SAI condition. To generate long-wavelength SFSS beyond 1700 nm (Fig. 5) [95], a single silica strand-like PCF [Fig. 6b] with a ZDW of ~ 850 nm is preferred. Also, to generate the most intense SFSS across the expected wavelength shifting range (1100–2000 nm), the length of this fiber is used to control the wavelength of the SFSS (Fig. 9). In contrast to the good controllability of the UCSC and FCR, it remains a design difficulty to generate SFSS at a targeted wavelength with good overall performance (broad range of central wavelength, controlled bandwidth, large conversion efficiency, etc.), although simulations based on the generalized nonlinear Schrödinger equation are helpful [165].

For improved polarization control and pulse compressibility of the supercontinuum generation [83], it is preferable that all the nonlinear PCFs and light delivery fibers (including PBFs) be polarization-maintaining fibers. The fabrication of these fibers and the corresponding polarization-maintaining splicing [132] must be developed. Perhaps the intrinsic disadvantage of the ytterbium-based source platform (Fig. 9) is the relatively low average power of the FCR (~ 5 mW) and the SFSS (~ 10 mW), which is limited by the LSO-SAI condition. The replacement of this ytterbium-based platform with an all-fiber erbium-based (~ 1550 nm) platform is expected to generate stronger FCR and SFSS, in addition to the already demonstrated UCSC [63, 68]. A hybrid ytterbium-erbium platform may also be useful [166].

6.3. Point-of-care coherent biomedical imaging

Coherently-controlled imaging or microspectroscopy has been demonstrated using the FCR [167], the SFSS [168, 169], and the UCSC [146], all of which have been produced by ultrafast solid-state lasers [162]. In fact, all existing label-free coherent optical imaging modalities (except for optical coherence tomography) (Table 2) have largely relied on the rather non-portable solid-state lasers with the emission wavelength range of 400–1600 nm. The application of these coherent techniques to in vivo point-of-care imaging can be practical if the coherent fiber supercontinuum laser (Fig. 9) is employed to replace the solid-state lasers, and is coupled to a miniature handheld microscope, endoscope, or general light-delivery system through the nonlinear PCF and subsequent fibers to access superficial tissues or internal organs and tissue sites. The engineering of a handheld microscope or endoscope is itself a broad subject, with a new trend toward the maximization of fiber-based components, or equivalently, the minimization of free-space components [170, 171]. This development trend of the application-dependent light-delivery module parallels the similar development trends of the ultrafast fiber source laser [151–153] and the (optional) intermediate optics in this review (Sects. 2–5), reflecting the ultimate goal of a fiber-format system and instrumentation immune to mechanical and thermal perturbations. Thus, these trends benefit from common fiber optics breakthroughs, such as the PCF (or PBF) technology and the corresponding fiber splicing [170, 171].

Noticeable advancements of handheld microscopy instruments include sub-10-fs pulse fiber delivery [172], extreme miniaturization [173], and two-beam picosecond pulse delivery [174]. In endoscopy, the key developments have included the application of double-clad PCF [175] or circular fiber [176], the fusion splicing of the double-clad fiber [177], and the fabrication of a double-clad fiber coupler [178]. Although nonlinear handheld microscopy or endoscopy have been largely restricted to single-beam imaging of two-photon excited fluorescence or second-harmonic generation (Table 2), a two-beam coherent Raman endoscope has been facilitated using a double-clad PBF [179]. Point-of-care nonlinear handheld microscopy and endoscopy have been hindered by the non-portability of ultrafast solid-state lasers or the limited emission wavelengths (~ 1040 nm, ~ 1550 nm) of ultrafast fiber lasers, which can be directly overcome by the coherent fiber supercontinuum laser (Fig. 9). Ultimately, multi-modality point-of-care coherent nonlinear optical imaging (Table 2) in all-fiber systems for handheld microscopy or endoscopy will be developed for clinical applications and used by physicians and staff with no laser training. Coherent optical imaging is expected to move out of the dedicated optical laboratories, to be translated to clinical use, and to become a widely accessible clinical tool for molecular histopathology and cancer diagnosis [180].

6.4. Perspectives

A handheld microscope, endoscope, or other beam-delivery instrument represent several general types of application-dependent light delivery-collection modules [Fig. 1c]. These will enable point-of-care coherent biomedical optical imaging applications (Sect. 6.3) that will utilize the envisioned coherent supercontinuum source platform. The platform can be connected to other ultrashort pulse delivery-collection modules to perform nonlinear auto-fluorescence imaging [181], flow cytometry [22], optical tweezing [16], laser nanosurgery [182] or transfection [183], biological ultrafast spectroscopy [184], two-photon photodynamic therapy [185], and many others. In these dramatically diverse applications, the application-dependent nonlinear PCFs and the post-supercontinuum-generation pulse shaping can be integrated into the corresponding light delivery-collection modules, so that one all-fiber source laser can be utilized across many applications. This results in effective cost reduction because the ultrafast source laser constitutes a significant cost in each application. New applications will likely emerge from the wide accessibility (or cost effectiveness) of the envisioned platform as a result of the broad spectral coverage, high coherence, and excellent portability. To further appreciate the benefit of the wide accessibility (or cost effectiveness), it is illuminating to recall the work that led to the “supercontinuum revolution” [8]. This work is revolutionary not because it discovered the phenomenon of supercontinuum, but because it found a cost effective way to make the supercontinuum widely accessible [11]. To date, this wide accessibility has produced many novel applications of the supercontinuum. Analogously, the envisioned fiber-based coherent supercontinuum source platform is a significant development because it may now make the performance characteristics of synchronized ultra-broadband mode-locked solid-state lasers and/or optical parametric oscillators widely accessible.

Biographies

Haohua Tu received the B. S. degree in chemical engineering from TsingHua University, China, in 1992, and the Ph. D. degree in chemical engineering and material science from University of Kentucky, Lexington, KY., in 2001. From 2001 to 2005, He was a Postdoctoral scientist at University of North Carolina, and at University of California-Merced. Since 2005, he has been a Research Scientist at the Biophotonics Imaging Laboratory, Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign.

Stephen A. Boppart received the B. S. degree in electrical and bioengineering and the M. S. degree in electrical engineering from the University of Illinois at Urbana-Champaign, Urbana, IL, in 1990 and 1991, respectively, the Ph. D. degree in electrical and medical engineering from the Massachusetts Institute of Technology, Cambridge, in 1998, and the M. D. degree from Harvard Medical School, Boston, MA, in 2000. He was a Research Scientist with the Air Force Laser Laboratory, Brooks Air Force Base, San Antonio, TX. Since 2000, he has been with the University of Illinois at Urbana-Champaign, Urbana, from where he completed residency training in internal medicine in 2005. He is currently a Bliss Professor of Engineering in the departments of electrical and computer engineering, bioengineering, and medicine. His research interests include the development of novel optical imaging technologies for biological and medical applications, with particular emphasis on translating these to clinical applications in cancer detection and diagnosis.