Bayesian Hierarchical Semiparametric Modelling of Longitudinal Post-treatment Outcomes from Open Enrolment Therapy Groups

Abstract

There are several challenges to testing the effectiveness of group therapy-based interventions in alcohol and other drug use (AOD) treatment settings. Enrollment into AOD therapy groups typically occurs on an open (rolling) basis. Changes in therapy group membership induce a complex correlation structure among client outcomes, with relatively small numbers of clients attending each therapy group session. Primary outcomes are measured post-treatment, so each datum reflects the effect of all sessions attended by a client. The number of post-treatment outcomes assessments is typically very limited. The first feature of our modeling approach relaxes the assumption of independent random effects in the standard multiple membership model by employing conditional autoregression (CAR) to model correlation in random therapy group session effects associated with clients’ attendance of common group therapy sessions. A second feature specifies a longitudinal growth model under which the posterior distribution of client-specific random effects, or growth parameters, is modeled non-parametrically. The Dirichlet process prior helps to overcome limitations of standard parametric growth models given limited numbers of longitudinal assessments. We motivate and illustrate our approach with a data set from a study of group cognitive behavioral therapy to reduce depressive symptoms among residential AOD treatment clients.

1 Introduction

Group therapy is an important treatment modality in mental health care and substance abuse treatment. A primary goal of group therapy research studies is to determine the comparative effectiveness of one intervention versus another. A central challenge posed by group therapy data is to account for the correlation among client outcomes, as clients who participate jointly in group therapy are likely to have similar experiences and outcomes as compared to other clients. Possible analytic approaches to address this issue when enrollment of clients into the therapy group is closed – that is, therapy group membership is not expected to change session-to-session – include modeling client outcomes using a multilevel (hierarchical) model with random intercept terms to reflect client participation in a single closed group (Roberts & Roberts 2005, Bauer et al. 2008).

In contrast, enrollment into a therapy group on an open basis allows for clients to enter the therapy group as space permits, which induces a more complex correlation structure among client outcomes. To illustrate, suppose Clients X and Y attend a therapy group session at time t. Client Y leaves the group immediately afterward. Client Z joins the group at time t + 1. Even if Clients Y and Z never meet, their outcomes might be correlated due to the fact they both attend group therapy sessions that overlap with attendance by others, such as Client X, who attend at times t and t + 1. Therapy groups with open enrollment policies – also called rolling groups – are widespread in practice, given their ability to help maximize the number of persons participating in therapy at any one time; shorten client wait time for entrance into treatment; and maintain a clinically necessary minimum number of members to maintain the group dynamic (Monti et al. 2002). An illustration of their practical importance is that most therapy groups offered in outpatient treatment settings for treating alcohol and other drug use (AOD) disorders use open enrollment (Morgan-Lopez & Fals-Stewart 2006).

Despite the ubiquity of open-enrollment groups in practice, there is a lack of guidance on how to properly analyze such data. The analytic approaches developed thus far are limited to the special case of outcomes data collected from clients as they undergo treatment, such that each datum y_is reflects an outcome for individual i observed at therapy group session s. Morgan-Lopez & Fals-Stewart (2007) focus on modeling informatively missing data due to clients failing to complete all sessions, but their approach does not generalize to post-treatment outcomes, which are collected regardless of adherence to the assigned intervention. Paddock et al. (2011) explicitly model correlation at the therapy group session level using conditional autoregression (CAR) (Besag, York & Mollié 1991). Its strengths include allowing one to specify ‘neighboring’ sessions and closeness (distance) of sessions in a sufficiently general way to cover several clinically relevant notions of defining session closeness, such as by overlapping client attendance across sessions or by time at which the session was offered (Morgan-Lopez & Fals-Stewart 2006).

Though group therapy intervention studies are frequently longitudinal, the number of post-treatment assessments is typically quite limited (e.g., 1–3) (e.g., Granholm et al. 2005, Rohsenow et al. 2001). Parametric growth curve modeling provides an efficient way to model longitudinal data for examining variation in client-specific growth curves and accounting for correlated outcomes within individuals (Muthén et al. 1997). However, a limited number of longitudinal assessments constrains how generally one might specify a parametric growth model for modeling the range of growth curves across individuals without adding prior constraints to identify parameters (Kenny & Milan 2012).

We present an approach for modeling post-treatment outcomes from open-enrollment therapy group studies that is a novel combination of multiple membership (MM) modeling (Hill & Goldstein 1998) with the CAR approach of Paddock et al. (2011). This combines the strengths of MM models for multilevel non-nested data – which is appropriate since each post-treatment outcome reflects the contribution of all sessions attended by a client – but relaxes the assumption of the standard MM model in which session random effects are assumed to be independently drawn from a random effects distribution, thus better reflecting the inter-relatedness of client attendance across sessions.

We employ a hierarchical Bayesian modeling perspective under a formulation that permits the borrowing of strength across multiple therapy group sessions for clients who attend open-enrollment therapy groups. Borrowing strength reduces the effective number of parameters of the model (Spiegelhalter et al. 2002), facilitating parsimonious modeling of how session effects are related to post-treatment outcomes. We similarly borrow strength in non-parametrically modeling client-level growth curve parameters to allow our model to capture a broad range of client growth curves, despite having relatively few longitudinal post-treatment outcome assessments per client. We motivate and illustrate our approach with a real data set from a study that is representative of group therapy-based interventions for AOD treatment.

2 Case Study: Post-Treatment Depressive Symptom Scores for BRIGHT versus Usual Care clients

The Building Recovery by Improving Goals, Habits and Thoughts (BRIGHT) study (Watkins et al. 2011) was a community-based effectiveness trial of a group cognitive behavioral therapy (CBT) intervention for treating residential substance abuse treatment clients having depressive symptoms. An aim of the study was to test whether clients receiving the BRIGHT intervention would have sustained improvements in depressive symptoms following treatment. The BRIGHT study employed a quasiexperimental design in which cohorts of clients at each of four study sites received either residential treatment as usual (UC) or residential treatment enhanced with the BRIGHT intervention (CBT) provided by trained substance abuse counselors over the study enrollment period. Clients were assigned to receive either CBT or UC according to which intervention was offered at their study sites at the time of entry into residential substance abuse treatment. CBT and UC were offered at each study site on an alternating basis over time. In order to participate in the study, clients had to screen positive for persistent depressive symptoms and not have bipolar disorder, schizophrenia, or cognitive impairment. Overall, 299 clients enrolled into the study, with 140 assigned to CBT and 159 to UC.

The BRIGHT group therapy consisted of 16 sessions of group CBT offered over an eight-week period that were organized into four modules of four sessions each. The four modules over 16 sessions were offered on a rotating basis. Thus, the CBT group had a semi-open admissions policy, as client admission to the CBT group could change every four sessions. Though clients were able to initiate treatment at the first session of any module, clients often did not complete each module as intended. In all, S = 245 group CBT sessions were offered to clients from all treatment sites. This included 14 offerings of the 16-session sequence (224 sessions); 20 additional sessions from two of the modules to increase exposure to group CBT for those who joined the therapy group late for three particular 16-week sequences; and one additional session that followed a long holiday weekend to make up for poor attendance at the regularly scheduled session. These 245 sessions were divided into G = 4 CBT open-enrollment therapy groups having distinct clients. The number of sessions for each of these four groups was 36, 40, 40, and 129 and number of clients enrolled in each open-enrollment group was 17, 21, 19, and 83, respectively. Each client attended sessions of only one of the four open-enrollment groups. Data were collected from clients at a baseline survey administered when clients enrolled in the BRIGHT study and at two post-treatment follow-up assessments at 3 and 6 months, having response rates of 86% and 87%, respectively. The primary outcome we use to illustrate the methodology is the extent of client depressive symptoms as measured by the Beck Depression Inventory-II (BDI-II) (Beck et al. 1996). The BDI-II score is a sum across 21 four-level items (scored 0 – 3), with a higher score indicating a greater level of depressive symptoms.

3 Modeling longitudinal outcomes without accounting for session attendance

It is typical in post-treatment outcomes studies of group therapy interventions to conduct an analysis without accounting for the potential correlation of outcomes for those clients who attend the same therapy group, regardless of whether enrollment is open (Morgan-Lopez & Fals-Stewart 2006) or closed (Bauer et al. 2008). Further, these analyses are typically fully parametric and conducted using routines available in standard statistical software packages. The standard linear longitudinal growth model (LGM) serves as an example of a typical approach one might choose to model the BDI-II outcomes collected during the BRIGHT study. The LGM can be expressed as:

$$y_{\mathit{\text{ij}}}=\alpha +{\mathbf{x}}_{\mathit{\text{ij}}}^{\prime }\mathit{\beta }+{\mathbf{z}}_{\mathit{\text{ij}}}^{\prime }{\mathbf{b}}_i+{\epsilon }_{\mathit{\text{ij}}},$$ (1)

where y_ij is the depressive symptom score for client i = (1, …, n) at repeated measurement event j = (1, …, m_i), such that m_i reflects the fact that different numbers of repeated measures may be observed across clients. On the right-hand side of the equation, α is a fixed intercept term; x_ij is a p × 1 set of fixed effects predictors, with the effects of predictors on the outcome expressed as β; z_ij is a set of q predictors that multiply the q client random effects, or growth parameters, b_i; and ε_ij is an observational error term. The standard linear LGM involves assuming the ε_ij’s are independent and identically distributed as Gaussian with mean 0 and variance ${\sigma }_{\epsilon }^2$. The b_i’s are modeled as exchangeable and follows a common Gaussian distribution. To allow for non-linear data patterns, a reasonable choice for x_ij would be to set it equal to a (p = 5) × 1 set of fixed effects predictors with T_i an indicator of treatment arm assigned to client i (T_i = 1 for CBT, T_i = 0 for UC), such that ${\mathbf{x}}_{\mathit{\text{ij}}}=(T_i,t_{\mathit{\text{ij}}},t_{\mathit{\text{ij}}}^2,T_i{t}_{\mathit{\text{ij}}},T_i{t}_{\mathit{\text{ij}}}^2)$, where t_ij denotes the continuously-valued time at which outcome y_ij was observed and β are parameters representing the effects of CBT assignment, time trend and the differential effect of CBT on the average time trend in y. We model time, t_ij, as continuous to express the notion that the underlying process of depression symptom progression is a continuous one on which we make discrete observations.

Under Equation 1, the choices for specifying client deviations about the average trend via z_ij and b_i are limited since there is a maximum of J = 3 observations per client in BRIGHT. Specifications for the parametric LGM we examine thus include:

• LGM(1RE) Equation 1 under z_i′ = (1) and b_i = (b_0i).

• LGM(2RE) Equation 1 under z_i′ = (1, t_ij) and b_i = (b_0i, b_1i)

To improve the borrowing of strength across common trends in depressive symptoms expression between clients, we employ the Dirichlet Process (DP) (Ferguson 1973, Escobar & West 1995) to nonparametrically model the distribution for the random growth parameters (Brown & Ibrahim 2003, Müller et al. 2007). Our application of DP to post-treatment outcomes serves the novel purpose of reducing the dimension of the number of growth parameters to allow for capturing the continuous trend without creating ad-hoc constraints to facilitate model-fitting, such as those specified for LGM(1RE) and LGM(2RE) (e.g., implicitly setting random quadratic effects equal to zero), or by identifying parameters strictly through the prior. The standard parametric distribution on the random growth parameters, $\mathbf{B}=\{{\mathbf{b}}_i^{\prime }\}$ would be replaced by:

$${\mathbf{b}}_1,\dots ,{\mathbf{b}}_n|F~F,F~\text{DP}(c,F_0),$$ (2)

where b₁, …, b_n are conditionally independent given F, and are generated from the unknown distribution F. The DP prior is typically specified with two hyperparameters. The first is a base measure, F₀, which represents the ‘best guess’ about the form of F prior to observing data; the expected value of F is F₀. The second parameter of the DP prior, a precision parameter, c > 0, expresses the degree of confidence that F₀ is the correct generating distribution for B; the higher the value of c, the more F is expected to conform to F₀.

The alternative stick-breaking construction of the DP prior highlights that F may be expressed as a mixture with an infinite number of components (Sethuraman 1994). Given the difficulty of working with an infinite mixture, a common practice is to work with an equivalent specification in which F is marginalized out of the distribution on B and to employ the required exchangeability property of the {b_i}; see (Blackwell & MacQueen 1973):

$${\mathbf{b}}_i|{\mathbf{B}}_{-i}~\frac{1}{n-1+c}{\displaystyle \sum _{j=1,j\ne i}^n}{\delta }_{{\mathbf{b}}_j}({\mathbf{b}}_i)+\frac{c}{n-1+c}{F}_0,$$ (3)

where B_−i = (b₁, …, b_i−1, b_i+1, …, b_n) and δ_bj (b_i) is a function that equals 1 if b_i = b_j and 0 otherwise. The DP provides a compromise between assuming that all clients have the same growth trajectories – in which case the mean trend would apply equally well to everyone – versus assuming each client has a distinct trajectory arising from a known, parametric distribution, F₀.

Equation 3 reveals a positive probability for ties to occur among the values of the ${\mathbf{b}}_i^{\prime }s$. The set of unique values among the {b_i} are called the ‘locations,’ or clusters, and are denoted by ${\mathbf{b}}_{\mathbf{k}}^{*}$, where k = 1, …, M and M is the number of locations such that M ≤ n. It is this feature of the DP prior that we exploit in order to gain traction in fitting quadratic growth curves to all n clients. Specifically, clients with similar growth curves will have higher probabilities of sharing locations. The right-hand mixture component in Equation 3 highlights that higher values of c increase the probability mass to select this component which would increase the number, M, of unique locations, ${\mathbf{b}}_{\mathbf{k}}^{*}$ ’s, which are generated from F₀. This would result in the stronger agreement of F with F₀. We will refer to this model as:

• LGM(DP): Equation 1 under ${\mathbf{z}}_{\mathbf{i}}\prime =(1,t_{\mathit{\text{ij}}},t_{\mathit{\text{ij}}}^2)$ and b_i = (b_0i, b_1i, b_2i) where {b_i} are modeled using Equation 3. We choose F₀ ≡ N_q (0, τ_b I_q=3), τ_b = (τ_b,1, …, τ_b,q=3), to discover how greatly the estimated model differs from an analogous parametric approach.

4 Modeling longitudinal outcomes while accounting for session attendance

4.1 Adding Random Session Intercepts to the Model

We build upon LGM(DP) by augmenting (1) to now include random session effects to model correlation among post-treatment outcomes for CBT-attending clients. First, we augment Equation 1 as follows:

$$y_{\mathit{\text{ij}}}=\alpha +{\mathbf{x}}_{\mathit{\text{ij}}}^{\prime }\mathit{\beta }+{\mathbf{z}}_{\mathit{\text{ij}}}^{\prime }{\mathbf{b}}_i+{\mathbf{w}}_i^{\prime }\mathit{\gamma }+{\epsilon }_{\mathit{\text{ij}}}.$$ (4)

The set of random session effect parameters is γ = (γ₁, …, γ_S), where S denotes the number of therapy group sessions. Since outcomes, y_ij, are not linked to specific therapy group sessions but rather to all sessions attended by client i, a multiple membership (MM) model can be specified to map each element of γ to the y’s (Hill & Goldstein 1998). Under the MM model, the components of γ are mapped to the y_ij’s by multiplying γ by an S × 1 weight vector, w_i, that is normalized to sum to 1; in particular, S_i equals the number of sessions attended by client i; w_is = 1/S_i if client i attended session s and w_is = 0 otherwise. Denote by an n × S multiple membership matrix, W = {w_i}, to encode session attendances for client i. Given the design of the BRIGHT study where clients assigned to usual care do not receive the group therapy treatment, the n_UC rows of W corresponding to observations for clients who are assigned to usual care will be filled with zeros, indicating they receive no allocation of session effects. The session effects parameters, γ, will allow for correlations among client observations to the extent that they attend common sessions. We now describe two approaches, one that restricts the γ ’s to be conditionally independent as well as one that relaxes that assumption.

An important variation on Equation (4) replaces the single term, w_iγ, with an additive set of terms to reflect the disjoint sub-grouping of clients whose sessions attended do not overlap with one another, as each client attends sessions belonging to only one of the G = 4 open-enrollment therapy groups in BRIGHT:

$$y_{\mathit{\text{ij}}}=\alpha +{\mathbf{x}}_{\mathit{\text{ij}}}^{\prime }\mathit{\beta }+{\mathbf{z}}_{\mathit{\text{ij}}}^{\prime }{\mathbf{b}}_i+({\mathbf{w}}_{i,g_i})\prime {\mathit{\gamma }}_{g_i}+{\epsilon }_{\mathit{\text{ij}}},$$ (5)

where g_i ∈ {1, …, G} denotes which of the G therapy groups client i is a member, w_i,gi has length S_gi, where S_gi is the number of sessions in therapy group g_i, and γ_gi is an S_gi − length vector of session effects for the therapy group attended by client i. In matrix form, W_g, g = 1, …, G, is an n_g × S_g matrix for therapy group g that maps S_g sessions (where ${\mathrm{\Sigma }}_{g=1}^G{S}_g=S$) to n_g clients who attend therapy group g. Similarly, γ_g represents an S_g × 1 vector of random effects for sessions in group g. This specification allows us to use distinct hyperparameters in the prior specifications for each γ_g, g = 1, …, G, as discussed below.

4.1.1 Model Session Effects as Independent

The simplest formulation of a model for session effects is the standard MM model in which session effects are assumed to be independent and identically distributed and following a Gaussian distribution:

• MM(I): Equation (4) under independent prior formulation for sessions effects, $\mathit{\gamma }:{\gamma }_1,\dots ,{\gamma }_S|{\tau }_{\gamma }~N_s(\mathbf{0},{\tau }_{\gamma }^{-1}{\mathbf{I}}_S)$,

where the parameter, τ_γ, represents the precision across session effects. The shorthand ‘MM(I)’ is such that ‘MM’ denotes that the multiple membership weight matrix, W, links the (typically) multiple sessions attended by a CBT client to their post-treatment outcomes.

We also examine a variant that relaxes the assumption of a single precision term, τ_γ, applying to all sessions in all open-enrollment groups:

• MM-D(I): Equation (5) with ${\mathit{\gamma }}_{\mathit{g}}|{\tau }_{{\gamma }_g}~N_{S_g}(\mathbf{0},{\tau }_{{\gamma }_g}^{-1}{\mathbf{I}}_{S_g})$, where τ_γg is the precision term for open-enrollment group g.

4.1.2 Model Session Effects as Correlated

In order to model session effects as correlated, we first specify the distance, or closeness, of sessions, which in turn provides a way to designate which sessions are neighbors of one another. For example, sessions offered at adjacent opportunities in time could be assumed to be closer than sessions offered at non-adjacent opportunities, such that neighboring sessions are those that are offered at adjacent time opportunities. Alternatively, one might assume the degree of closeness between any two sessions is proportional to the overlap of clients attending those two sessions, with the neighbors of a given session defined as those other sessions with which there is at least one client in common (Paddock et al. 2011).

The CAR prior permits modeling correlation among the set of random effects such that, conditional on its neighboring session’s random effects, the random effect for session s is independent of the effects for non-neighboring sessions; however, all the γ_s’s within an open-enrollment therapy group are unconditionally dependent. We follow Besag, Mollie, York & Mollié (1991), who enumerate a two-part form for the covariance matrix. Firstly, define an S × S adjacency matrix, Ω, to encode dependence among neighboring sessions where we set ω_ss′ ≥ 0 if session s is a neighbor of session s′ (i.e.,, s ~ s′), and 0, otherwise, and ω_ss is defined to be 0. For the analyses we discuss here, we employ a canonical choice for ω_ss when s ~ s′ of ω_ss′ = 1, which reflects whether sessions s and s′ are offered at adjacent opportunities in time and belong to the same open-enrollment group (Paddock et al. 2011). Secondly, construct D = Diag(ω_s+), where ω_s+ = Σ_j ω_sj equals the number of (1^st order or adjacent) neighbors of session s that may be viewed as capturing the relative influence of session s. Then compose covariance matrix, Q⁻ = (D − Ω)⁻, the Moore-Penrose pseudo-inverse, as Q is not of full rank, and specify the joint distribution of random session effects,

$$\mathit{\gamma }|{\tau }_{\gamma },\mathbf{\Omega }~N(\mathbf{0},{[{\tau }_{\gamma }(\mathbf{D}-\mathbf{\Omega })]}^{-}),$$ (6)

where scalar precision parameter, τ_γ, controls the overall strength of variation. The rank of (D − Ω) is S − G, where G represents the number of distinct open-enrollment therapy groups (Hodges et al. 2003). Despite the improper joint distribution, this construction specifies a set of proper Gaussian full conditional distributions,

$${\gamma }_s|{\mathit{\gamma }}_{-s},{\tau }_{\gamma },\mathbf{\Omega }~N({\mathrm{\gamma ̄}}_s,{({\tau }_{\gamma }{\omega }_{s+})}^{-1}),$$ (7)

where γ̄_s = Σ_j=s ω_sjγ_j/ω_s+ is the average of the session effects for the neighbors of session s. Besag, Mollie, York & Mollié (1991). We label our resulting models as:

• MM(CAR): Employ additive model of Equation (4) under the joint prior construction of Equation (6) and the associated full conditionals given by Equation (7).

• MM-D(CAR): Employ additive model of Equation (5) with Equations (6) and (7) modified to allow separate precision parameters, τ_γg, for each open-enrollment group, g = 1, …, G.

5 Prior Distributions

5.1 Models without Multiple Membership and Session Effects

These models are differentiated from one another based on the priors selected for the sets of client effects, B = {b_i}. For the LGM models, we jointly specify an independent Gaussian prior, b₁, …, b_n ~ N_q (0, Diag (τ_b)), where we recall that n are the total number of clients and q the number of random effects for each client: q = 2 for LGM(2RE). Under this prior construction, the q × 1 vector of precision parameters, τ_b, allows each component of b_i to separately vary. We move to the LGM(DP) model by now using this independent Gaussian prior for the DP base distribution, F₀ ≡ N_q (0, Diag (τ_b)). We specify non-informative, flat priors for both the p × 1 fixed effects, β, and for the global intercept, α. Independent Ga (0.1, 0.1) are defined for (τ_b,1, …, τ_b,q).

Specification for the hyperparameters used for the prior on DP concentration parameter, c, is important due to the influence of c on the number of clusters formed and thus on the adaptability of F to the data (Escobar & West 1995). We see in (3) that higher values for c induce formation of more clusters, resulting in greater adherence of F to its parametric base distribution, F₀. The typical formulation employs c ~ Ga (a_c, 1), with shape parameter a_c and rate parameter 1. The shape parameter value for a_c may be chose to encode a prior expectation for the number of client effect clusters. We choose a_c = 3, which produces a prior mean of M = 14 clusters of the n = 299 clients. Since we have no strong reason for this prior belief, we choose a low value to which the posterior for c is relatively insensitive. Sensitivity analysis reveals little change in number of posterior clusters discovered under our varied model formulations that employ the DP construction for a range of values for a_c from 1 – 5.

5.2 Models with Multiple Membership and Session Effects

As before, we specify non-informative, flat priors for both β and α. The hyperparameter, τ_γ, serves different roles for each of the three models incorporating session effects. Under MM(I), τ_γ plays the usual role that controls the variation and we allow for uncertainty in this choice by employing τ_γ ~ Ga(0.1, 0.1). We experimented with a range of shape and rate hyperparameter settings (∈ {1, 0.1, 0.01}) and discovered little sensitivity of posterior results as similarly noted by Banerjee et al. (2003), and so utilize the same value as above-noted for MM(I).

6 Analysis of BRIGHT Post-treatment Outcomes

6.1 Model Comparison

Comparisons of goodness of fit and model complexity are often done using the deviance information criterion (DIC) of Spiegelhalter et al. (2002), which penalizes the model deviance for parameter complexity to prevent over-fitting. In particular, the effective dimension statistic used to penalize the average deviance, D̄, is pD = D̄ − D(θ̃), where θ̃ is typically taken to be the posterior mode or mean, θ̄ = E(θ|y). However, Spiegelhalter et al. (2002) also point out that there is not clear choice for θ̃ under the (countably infinite) mixture induced with our DP prior. The DIC₃ criterion (Celeux et al. 2006) was developed in response to this limitation and focuses on the marginal (predictive) density f(y) to estimate f(y|θ). Celeux et al. (2006) note that DIC₃ tends to under-estimate pD as the number of components in a mixture increase. Given no single model comparison statistic comprehensively assesses all aspects the performances of our models, we also estimate the log-pseudo marginal likelihood that employs “leave-one-out” cross-validation (Gelfand & Dey 1994). We estimate f(y) using Π_Ni=1f (y_i|y_−i, M_k), the log of which is the log pseudo marginal likelihood (LPML). We utilize in our LPML estimation the harmonic mean estimator for f (y_i|y_−i, M_k) outlined in Congdon (2005). This method may display numerical sensitivity for outlying data points that express low likelihood values, in which case a law of large numbers result would not be achieved (Held et al. 2010). We thus also explored a weighted re-sampling of Θ from existing posterior draws in a fashion that provides model parameter samples from f (Θ|y_−i, M_k) (Stern & Cressie 2000). The importance weights are composed as reciprocals of likelihood values, and so may suffer from similar numerical instability as harmonic averaging. Congdon (2005) note that both approaches for leave-one-out estimation are generally numerically robust for log likelihood values above − 10 which is met in our application. Both methods produce similar estimates in our application and so we report harmonic mean results for − LP ML. LPML is expected to provide a relatively high complexity penalty as the computation relies on cross-validation to compose the required posterior predictive distribution (Plummer 2008).

6.2 Computational Approach

The joint posterior distribution of all parameters, Θ = (α, β, B, γ, τ), was simulated at a each iteration of a Gibbs sampler by sequentially sampling from each full conditional posterior distribution. Output from L Gibbs sampling iterations were retained following a burn-in phase of 30, 000 iterations and used to draw posterior inferences. We chose L = 120, 000, run multiple times with the Gibbs samplers initialized from randomly selected starting points. Convergence of the sampler was assessed by employing a fixed width estimator with Monte Carlo standard errors (MCSE) computed using the consistent batch means (CBM) method (Jones et al. 2006). Computational software for the posterior distribution simulations is available in our package for the R statistical software (R Development Core Team 2011) package called growcurves (Savitsky & Paddock 2012).

6.3 Results: Models without Multiple Membership Session Effects

Model fit statistics, D̄, − LP ML, and DIC₃, are presented in Table 1. One observes a marked drop (improvement) in all three model fit statistics for LGM(DP) versus the LGM models due to the greater flexibility in modeling growth curve shapes under the DP prior that borrows strength across clients. The improvement is not solely due to allowing for a quadratic random effect term in LGM(DP), as an LGM that includes a quadratic effect has worse fit (− LP ML = 3040). The DP prior enables better capture of within-client growth curves by borrowing estimation strength among a subset of clients whose curves express a convex (or bell-shaped) profile.

Table 1.

Model Fit Comparisons: D̄, − LP ML and DIC₃ scores for model alternatives. Lower values imply better performance.

Model	D̄	− LP M L	DIC3
LGM(1RE)	5916	3064	6100
LGM(2RE)	5698	3028	5982
DP(LGM)	5520	2989	5691
MM(I)	5502	2987	5676
MM(CAR)	5501	2982	5675
MM-D(I)	5493	2976	5670
MM-D(CAR)	5485	2975	5665

6.4 Results: Models with Multiple Membership Session Effects

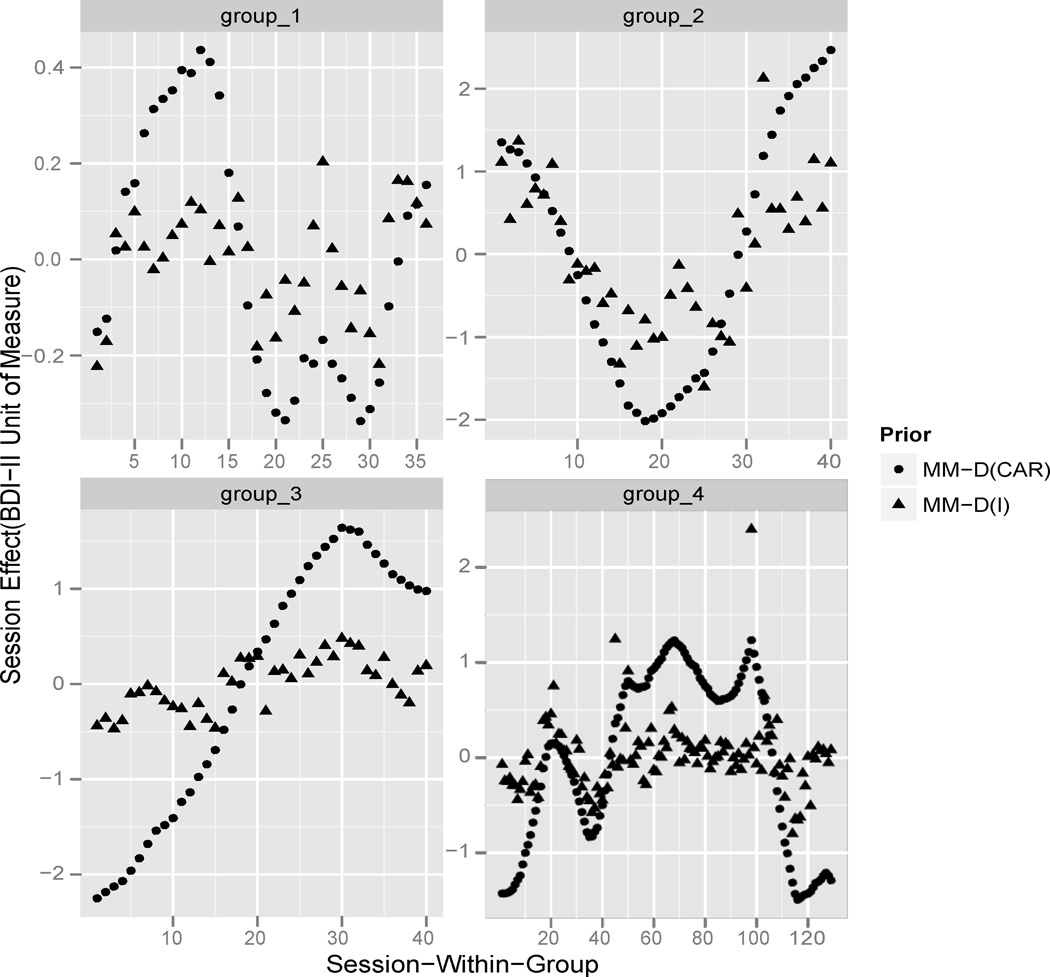
Modeling random session effects as independent (model MM(I)) improves model fit statistics. Allowing for correlated session effects using MM(CAR) results in further improvements (Table 1). Allowing each therapy group to have its own precision parameter (models MM-D(I) and MM-D(CAR)) further improves fit statistics. The value of making the MM models more flexible to therapy group-specific variation is demonstrated by noting how the range of session effects varies across groups, going from 0.6 points in Group 1 to 5 points in Group 2 (Figure 1). The MM-D(CAR) session effects trend for Group 4 highlight the session effects adapting to the data, for example oscillating between sessions 50 – 100. The property of the CAR prior to borrow strength among adjacent sessions allows for discovering a stronger signal in group 3 and accommodating shrinkage of relatively extreme session effects in group 4 under MM-D(CAR) versus MM-D(I). Exploratory analyses of BDI-II scores centered about the mean BDI-II at each measurement time show a similar pattern to what is shown in Figure 1.

Figure 1.

Posterior means for session effects from MM(CAR) and MM(I) models

The posterior mean for session s represents its contribution to BDI-II scores for clients attending session s, given treatment assignment and client random effects. Lower session effects indicate lower levels of depressive symptoms. For example, clients who attend only the first session of group 3 have a BDI-II score expected to be 2.3 points lower than the average, while those attending only the last session of group 3 have an average relative increase of 1 point. Though fit statistics (Table 1) support including session effects into the model, the practical importance of doing so is highlighted by noting the range of session effects shown in Figure 1 of 5 points, which is a clinically meaningful change in BDI-II scores (Furukawa 2010). Additionally, the variation in session effects suggests further attention in trying to explain whether session effects vary according to session-level factors, such as session leader or session content, might be warranted.

6.5 Results: Change over Time in BDI-II Scores

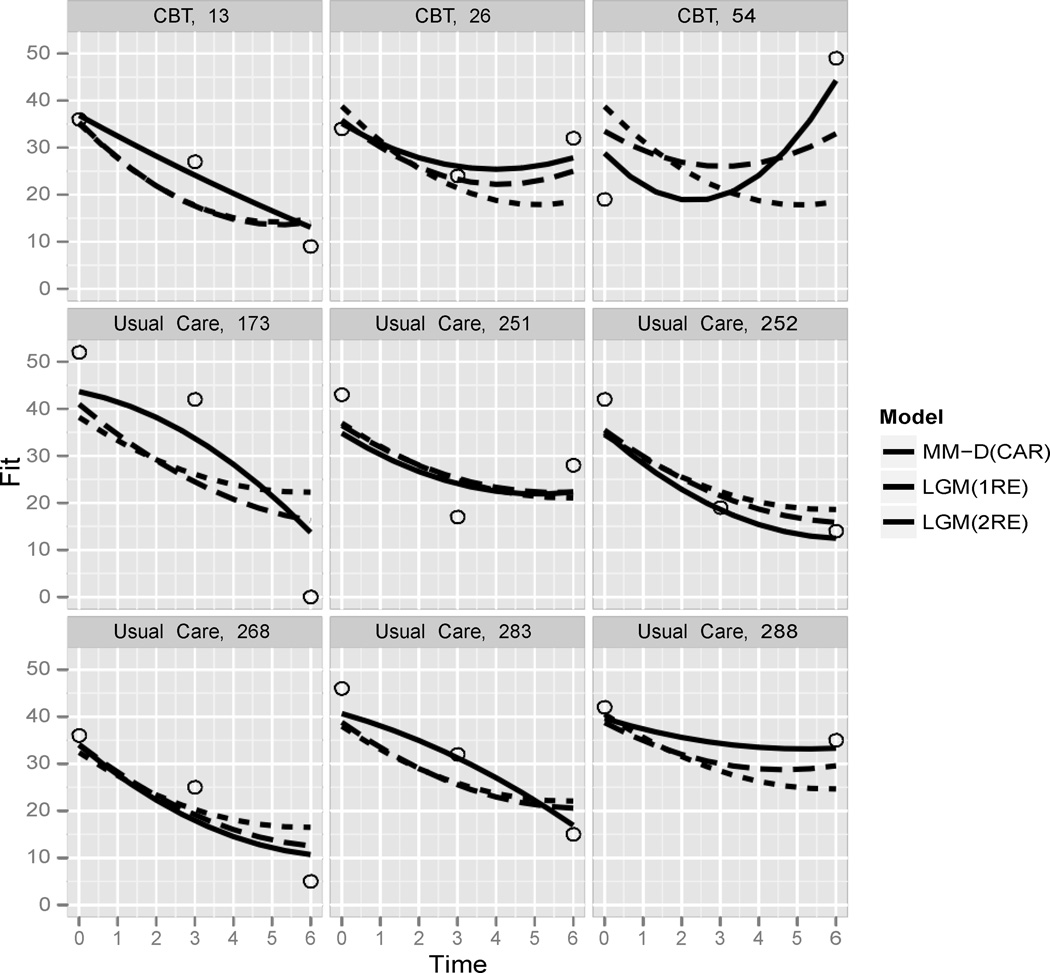
To provide a greater understanding of the total effect of modeling both session effects and using the DP to model client growth parameters, Figure 2 displays growth curves for a randomly selected subset of clients within the CBT and UC conditions comparing MM-D(CAR) to the base comparison LGM(1RE) and LGM(2RE) models. MM-D(CAR)-based growth curves better adapt in both shape and orientation to the data. For example, client “CBT, 26” highlights how the MM-D(CAR) better captures an augmentation of depressive symptoms between months 3 and 6 while retaining good fidelity to the attenuation pattern between 0 and 3 months. The curves for client “Usual Care, 283” displays enhanced flexibility for MM-D(CAR) to model a convex growth pattern. The LGM models generally detect the common concave or U-shaped growth curves but fit less well for those clients whose depressive symptoms decrease in more convex trajectories.

Figure 2.

Comparison of Posterior Means of Client Growth Curves under LGM(1RE), LGM(2RE) and MM(CAR) for Randomly-selected Clients.

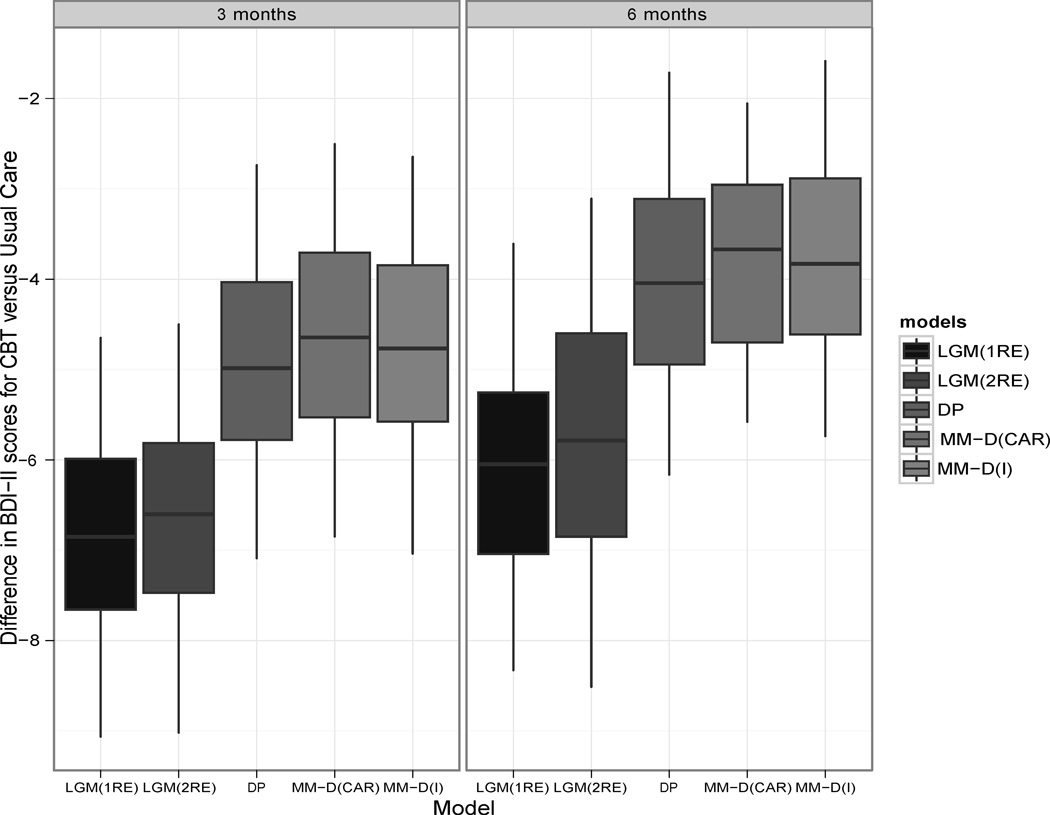
To facilitate interpretation of model results, we display treatment effects estimated using the predictive margins technique (Lane & Nelder 1982) (Figure 3). For each MCMC sample, we predicted outcomes as if all clients were in group CBT, then predicted outcomes as if all clients were in UC, and subsequently summarized the client-level differences. The treatment effects at 3 months are provided in the left-hand panel and those for 6 months in the right-hand panel. As indicated by the 95% posterior probability intervals (indicated by the vertical line segments of the box plots) not crossing the y = 0 line, declines in mean BDI-II scores for CBT versus usual care are found under each model. The distributions of the treatment effect under the MM models are more concentrated than the LGM models; however, the LGM models express larger treatments effect than the remaining models, all of which include DP modeling of client random effects. This difference is due to the LGM being able to only discover concave or U-shaped trajectory of BDI-II scores, as illustrated in Figure 2. A strictly concave curve lies below a straight line connecting 0-to-6 months and produces a more negative BDI-II score and fixed effects estimates. In contrast, the DP is more sensitive to the 20% of clients whose BDI-II score imply convex growth curves associated with less change in depressive symptoms.

Figure 3.

Predictive margins for the treatment effect of CBT versus usual care at 3 (left panel) and 6 (right panel) months. Segments reflect the 95% credible intervals and boxes represent the interquartile range of the marginal posterior distribution.

7 Discussion

Our innovative combination of multiple membership and CAR modeling confronts a previously-unaddressed difficulty of analyzing post-treatment outcomes data from open-enrollment group therapy studies. While the multiple membership modeling-based approaches examined here can be readily applied to non-longitudinal post-treatment outcomes data, we illustrate our approach using longitudinal post-treatment data for several reasons. Since studies like BRIGHT typically aim to compare change over time between multiple treatment conditions, it is important to demonstrate that our approach generalizes to longitudinal data analyses. Modeling random session effects combined with nonparametric modeling of client growth parameters further demonstrates the flexibility of our novel approach for handling a range of application-specific data scenarios, such as accommodating the reality of having few post-treatment observations per client in substance abuse treatment group therapy studies. For applications in which more follow-up assessment times are available, one might consider employing an intrinsic Gaussian Markov field (Rue & Held 2005), penalized spline, or Gaussian process (Savitsky & Vannucci 2010) on a set of group-time means instead of the DP prior. In the context of the BRIGHT study, we show that MM modeling yields clinically meaningful variation in session effects across and within open-enrollment groups, emphasizing the importance of our modeling approach for the behavioral health research community. We further promote the use of our methodological advancements with a freely available software package called growcurves for the R statistical software platform (R Development Core Team 2011).

Next steps in our investigations include examining data from BRIGHT and other open-enrollment group therapy studies to compile estimates of key input parameters one would prospectively consider when designing open-enrollment group therapy studies to examine how statistical power to detect treatment effects varies based on these key parameters. Other important issues include how to examine the effects of session-specific features – such as session theme, session leader, or fidelity to which the intervention was delivered – on outcomes while accounting for their correlation with session effects. Our approach should prove useful over a variety of other behavioral data settings in which observations are likely to be correlated due to complex interactions among individuals that mirror those of the open-enrollment group therapy setting. Examples include measuring school effectiveness when a student’s achievement is linked to multiple schools (e.g. Hill & Goldstein 1998) or examining outcomes among persons participating in a common online forum, discussion board, or online expert panel (Dalal et al. 2011). Our software package is written in a general way to readily accommodate such applications.