Abstract
For patients who were previously treated for prostate cancer, salvage hormone therapy is frequently given when the longitudinal marker PSA begins to rise during follow-up. Because the treatment is given by indication, estimating the effect of the hormone therapy is challenging. In a previous paper, Kennedy et al (2010), we described two methods for estimating the treatment effect, called two-stage and sequential stratification. The two-stage method involved modeling the longitudinal and survival data. The sequential stratification method involves contrasts within matched sets of people, where each matched sets includes people who did and did not receive hormone therapy. In this paper we evaluate the properties of these two methods and compare and contrast them with the marginal structural model methodology. The marginal structural model methodology involves a weighted survival analysis, where the weights are derived from models for the time of hormone therapy. We highlight the different conditional and marginal interpretations of the quantities being estimated by the three methods. Using simulations, which mimic the prostate cancer setting, we evaluate bias, efficiency, accuracy of estimated standard errors and robustness to modeling assumptions. The results show differences between the methods in terms of the quantities being estimated and in efficiency. We also demonstrate how the results of a randomized trial of salvage hormone therapy are strongly influenced by the design of the study, and discuss how the findings from using the three methodologies can be used to infer the results of a trial.
Keywords: treatment by indication, time-dependent confounder, proportional hazards model, causal effect, prostate cancer
1. Introduction
In this paper we consider observational data that might arise in a prostate cancer study in which there is longitudinal data, a treatment that may be assigned at some timepoint during the follow-up and an event time outcome variable that may be censored. The goal is to estimate the effect of the treatment on the outcome variable. The longitudinal data is assumed to arise from a stochastic process. If the longitudinal process affects both the outcome of interest and the assignment of the treatment, then the longitudinal process is a time-dependent confounder. If the treatment affects the ensuing longitudinal process, then the process is an intermediate variable as well as a time-dependent confounder. Standard naive covariate adjustment, that adjusts for the longitudinal data, will only yield an estimate of the treatment effect beyond that due to changes in the process itself. Hence, if the longitudinal process is both a time-dependent confounder and an intermediate variable then, to estimate the treatment effect, covariate adjustment is necessary but problematic using standard methods. This situation is sometimes called treatment by indication, and the goal in this paper is to evaluate and compare various approaches to estimating the treatment effect when the treatment is given by indication.
The motivating example for this research comes from the prostate cancer setting. After initial diagnosis of prostate cancer and subsequent treatment by radiation therapy, elevated levels of prostate-specific antigen (PSA) and rates of increase of PSA indicate an increased risk for clinical recurrence of the cancer [1]. In addition, because of the increased risk, those patients with elevated PSA are more likely to initiate salvage androgen deprivation therapy (SADT) in order to prevent or delay the recurrence of cancer. In this example PSA is the longitudinal variable, recurrence time is the outcome variable and SADT is the treatment. As explained above, PSA is a time-dependent confounder in the relation between SADT and recurrence. Furthermore, patients experience a marked decrease in PSA for at least the first few months after initiation of SADT. Therefore PSA is also intermediate variables in the relation between SADT and recurrence. A standard Cox regression analysis including covariates representing time-dependent PSA, along with a time-dependent treatment indicator and other covariates, would therefore estimate the benefit of SADT beyond that due to the decrease in PSA at the time of SADT, a relatively useless quantity.
In the last 15 years marginal structural models (MSM) and related methods have been developed [2, 3, 4, 5, 6] to estimate a causal treatment effect of such a time varying treatment when there exists confounding by time-dependent covariates affected by earlier treatment as described above. This approach has been rigorously developed with an elegant theory linked to counterfactual models and randomized trials. In its simplest form, the MSM methodology can be used to estimate, from observational data, a hazard ratio between two counterfactual scenarios, one in which subjects are all treated at time τ and another in which subjects are not treated. Specifically, denote the counterfactual hazard at time t when the treatment was not assigned as λ0(t), and if the treatment was assigned at time τ for all subjects, the counterfactual hazard would be λ0(t) exp[φI(t > τ)]. Here, the quantity φ is the causal treatment effect, which is assumed not to depend on τ or t − τ, and it matches the target quantity of interest in a randomized clinical trial for which half the patients are randomized to treatment at time τ and the other half do not receive treatment, provided the assumptions of the MSM hold. Note that φ is a marginal quantity since it averages over subjects with possibly different hazards due to different measured and unmeasured covariates and other unexplainable sources of variability. Note also that the model defining φ does not condition on any time-dependent covariates. Recent causal inference literature has tended to use the terms marginal and causal interchangeably, however in this paper we will keep them as distinct because we will also be considering conditional causal effects where we condition on covariates, including time-dependent covariates. The MSM methodology [2, 4] estimates φ from observational data by weighting the observations to “mimic” data which would have arisen had a randomized trial been conducted. Specifically, inverse-probability-of-treatment weighting (IPTW) is used in order to estimate φ the marginal causal effects, and the weights are derived from models for the probability of treatment.
The marginal structural model can be extended to include baseline (but not time-dependent) covariates in the hazard [3, 4], specifically to estimate φ from a marginal model of the form λ0(t) exp[Xβ + φI(t > τ)], where X are baseline covariates. The history-adjusted MSM (HA-MSM) has generalized the MSM to allow for estimation of causal effects conditional on time-dependent covariates [7, 8], and it can be further extended to allow the effect of treatment to depend on the level of the time-dependent covariate by including interactions of φ with other variables. Although it has only been presented in the context of modeling the mean of a continuous outcome of interest, the HA-MSM can potentially be extended for use in other scenarios (for example, in the context of modeling a survival time distribution in the presence of informative censoring) [7].
In recent work [9], we presented two different methods for estimating treatment effects using observational data in situations like those presented above, where a time-dependent confounder is also an intermediate variable in the relation between treatment and outcome. One method, which we called the two-stage method, specified for each subject a model for the hazard of recurrence in the absence of treatment, called the “natural hazard”. This hazard, denoted by , can also be thought of as the counterfactual hazard for that person if he never receives the treatment. In this model, the hazard for subject i at time t is given by , so that if the subject were to be assigned treatment at time τ then the hazard for that subject would be . The method links to the process for the longitudinal data, and then jointly estimates γ and . The other method, called Sequential Stratification ([10, 11]), matches those patients who received treatment (called index cases) to similar patients still at risk, thereby reorganizing observed data to mimic a sequence of conditionally randomized treatment assignments. The estimation then proceeds by fitting stratified models and comparing patients within strata. Both these methods can be thought of as estimating conditional treatment effects, since they condition on subject-specific factors that could be time-dependent.
The question of whether the quantity of interest should be a marginal or a conditional causal effect, as formulated here, depends on the clinical context in which it would be used. For health policy situations, one is often interested in making guidelines for groups of patients and results from randomized trials of groups of patients would be considered the gold standard; thus, in such cases, estimates from marginal models would be desirable. In clinical settings, where subject-specific decisions regarding treatment are paramount, conditional treatment effects may be more useful. In the context of prostate cancer recurrence, the patient will know his baseline covariates and his pattern of PSA up to the current time, and hence it would be more valuable from a clinical perspective for an individual patient to know, under multiple salvage treatment options, his risk of recurrence, as opposed to the risk of recurrence among a wide array of patients with varied PSA patterns. The randomized trial that would be relevant for this patient would be one which only enrolled patients who had similar amount of follow-up since the the initial therapy and also a similar pattern of PSA values.
In our previous work [9], we described the two-stage and sequential stratification methods, but we did not evaluate their properties via simulation. Similarly, simulation-based evaluations of the MSM, and comparisons of the MSM with other methods, are limited in the literature. Young et al. [12] compared two types of structural nested models (SNMs) with the MSM, finding that the MSM is advantageous with respect to bias, variance, and ease of computation. Xiao et al. [13] compared the Cox MSM to the pooled logistic MSM (commonly used as an approximation to the Cox MSM) across varying weighting schemes, reporting that the pooled logistic MSM yields estimators with larger variances than the Cox MSM, and that normalized and stabilized weights outperform weights which are either unstabilized or unnormalized or both. Westreich et al [14] found good bias and coverage rate properties of MSM methods but sometimes with less precision compared to simple methods depending on how the weights were implemented. Their work also demonstrated the benefit of using stabilized weights. Ertefaie et al. [15] compare IPTW and propensity score methods, finding that propensity score methods surpass IPTW methods with respect to mean squared error in both point-treatment and longitudinal settings. In the current paper the design of the simulation is strongly linked to the motivating prostate cancer study.
Two basic premises in this paper are that (i) there exists heterogeneity in the disease process among individuals, and (ii) subject-level data in observational studies arise from realizations of stochastic probability models. This matches in spirit the concepts of causality discussed in Aalen and Frigessi [16], Aalen et al [17] and Commenges and Gegout-Petit [18]. In the prostate cancer context there are four relevant linked stochastic processes, one for the longitudinal PSA data, one for the recurrence of the cancer, one for the assignment of treatment, and one for censoring. The three estimation methods we compare either make assumptions such that some of these stochastic processes can be ignored, or else require specification of models for one or more of these stochastic processes. The model for recurrence includes a parameter (γ) representing the multiplicative effect of treatment on the hazard of recurrence; this quantity is the conditional causal effect of treatment and is the quantity of interest when one is interested in subject-specific effects of treatment. The marginal causal effect of treatment for a heterogeneous group of patients is determined by the stochastic models for PSA and recurrence, along with the posited treatment assignment of interest, and may not equal γ.
The purpose of this paper is to evaluate, via simulation, the two-stage, sequential stratification and MSM approaches in the context of the prostate cancer example. The simulation scheme includes a longitudinal biomarker, a treatment process which may be predicted by the biomarker, and an event process which is related to values of the biomarker in addition to treatment status and a censoring process. In other words, we specify a true probability model for the biomarker, treatment, and recurrence, each defined at the subject-specific level. We will compare and contrast the methods themselves, along with the quantities they estimate, their properties, as measured by bias and efficiency, and their robustness to modeling assumptions, as well as to various types of censoring mechanisms.
2. Motivating Prostate Cancer Example
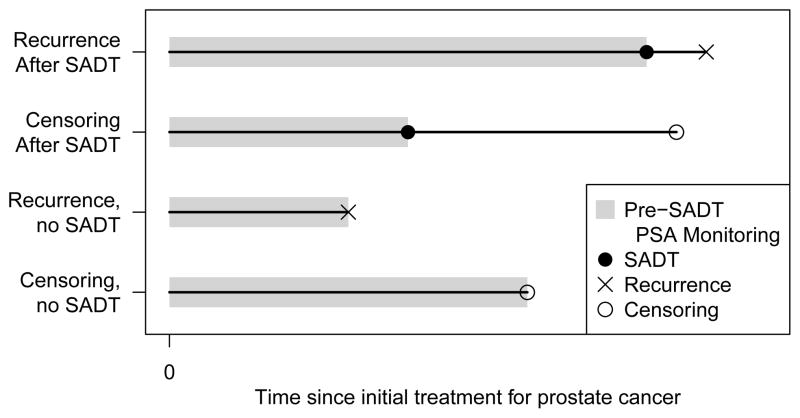
The prostate cancer datasets to which we applied the two-stage and sequential stratification methods in [9] have the following structure. All patients are diagnosed with localized prostate cancer and treated with external beam radiation therapy. Patients have pre-treatment characteristics, such as T-stage, which we denote by xi for subject i. Each patient has a sequence of values of PSA after the radiation therapy and these are used to monitor the patient. Time t is measured in years from the end of radiation therapy. The typical pattern of PSA after radiation therapy is well known, and associated with some of the pre-treatment variables. It decreases in everyone for about a year and then may or may not start to rise; if it does rise, it increases approximately exponentially with time. Rising values of PSA are indicative of tumor cells growing and dividing, but the tumor may not have yet grown to such a size that it is detectable. The time of clinical recurrence is the time at which the tumor is detected, which we call Ri, and that is the event of interest in our research. Let Ci denote the censoring time. If the values of PSA start to rise, the patient and their doctor may consider starting SADT prior to any recurrence; we denote the time of initiating SADT as Si. While there are guidelines for when SADT should be initiated, in typical observational patient series there is considerable heterogeneity in the values of Si, and SADT is not always initiated. SADT quickly reduces the values of PSA in just about all patients, and to near zero in most patients, but later PSA may rise and the patient may experience clinical recurrence. In none of the modeling or analysis we undertake do we consider the observed values of PSA after Si. The data structure is depicted in figure 1. In this prostate cancer setting there is very strong belief that SADT delays clinical recurrence, but the amount by which it delays recurrence or reduces the risk of recurrence is not well quantified.
Figure 1.
Structure of longitudinal, treatment and recurrence data.
Randomized clinical trials would be one way to investigate the effects of SADT. Given the uniform belief that SADT is effective at delaying clinical recurrence, it would be unethical to run a randomized trial in which SADT was withheld. Trials that would be interesting from a treatment policy perspective are ones that compare early to late SADT where early and late may be determined by the values of PSA, or ones that compare giving everyone SADT at the same time as radiation therapy with a strategy of giving SADT in follow-up as suggested by high or increasing values of PSA. While such trials would be ideal, they have not been undertaken. Thus the challenge is understanding what one might find from such trials by analyzing observational data. For an individual patient in active follow-up, with his sequence of PSA values, it would not be viable to run a randomized trial that exactly matches his situation. For him the relevant question is what is the future risk of recurrence if he does start SADT compared to not starting it.
3. Methods
Here we describe three potential methods to estimate the treatment effect from the type of observational data described above.
3.1. Two-Stage Method
The two-stage method, with full details available in [9], specifies a form for the ‘natural hazard’ (the hazard of recurrence in the absence of treatment by SADT) for subject i, given by . At times after initiation of SADT, this hazard changes to:
| (1) |
The form of depends on baseline covariates xi and is linked to the PSA process for subject i. Since we will assume that the PSA process is determined by subject-specific random effects and xi in a mixed model, is also determined by the subject-specific random effects and xi. The two-stage method estimates both and γ. In the first stage we estimate the biomarker process for PSA for each subject in the absence of treatment by SADT (i.e., using only data prior to initation of SADT). Quantities estimated from the first stage are provided to the second stage. In the second stage we estimate the treatment effect γ using a Cox proportional hazards model. The models we will be assuming for the longitudinal PSA process and for have a similar form to those that were developed in [19], and are derived from analysis of the data described in that paper.
The assumed model for PSA in the absence of treatment by SADT is:
| (2) |
where Pi(t) are the observed values of PSA for subject i at time t, (α0, α1, α2) are fixed effect parameters, (αi0, αi1, αi2) are subject-specific random effects, and xi is a covariate vector including an intercept term and baseline T-stage indicators (i.e., I(T-stage = 2) and I(T-stage ≥ 3)). f(t) = (1 + t)−1.5 − 1 captures the short-term evolution of PSA, while t captures the long-term evolution. We assume the measurement error εit ~ N (0, σ2), and the random effects (ai0, ai1, ai2) ~ MVN(0, Σ).
The resulting BLUP estimates for logPSAi(t) and , where denotes the slope of log PSAi(t), are given by log PŜAi(t) and , respectively. The assumption regarding the natural hazard, (i.e., for recurrence in the absence of SADT) is that
| (3) |
Then combining with equation (1) the following time-dependent Cox model is then fit to estimate θ0, θ1, θ2 and γ:
| (4) |
where Si is the time of SADT and the BLUP estimates log PŜAi(t) and are calculated for times both before and after Si. Note that in the estimation in equation (4) λ0(t) is not assumed to be constant with respect to time, and is treated non-parametrically in the usual Cox model fashion.
Note that PŜAi(t) and are estimates assuming SADT is not given, this eliminates the concern described in the introduction about PSA being an intermediate variable. Thus the two-stage method essentially compares what happened to people who were treated with an estimate of what would have happened to them if they had not been treated. In this sense it has some similarity to what is modeled in Structure Nested Models (SNM), where the g-estimation algorithm is used to estimate the unknown parameters ([20]).
There are a number of issues and challenges associated with this two-stage approach. A basic assumption is that the quantity γ is the same for all people. The parameters in the model would still be identifiable if γ were allowed to depend on baseline or time-dependent covariates, however additional subject-specific values of γ are not estimable. The method requires fully specifying longitudinal and survival models, thus there are legitimate questions about the robustness of the estimates of γ to misspecification of these models. Finding a good model may be challenging; however, in the prostate cancer example, PSA and recurrence data of the type used here have been collected for many years in many different studies, giving good knowledge about the structure of these models. The expression for the hazard in Equation (3) has as covariates a smoothed version of PSA and its slope, and may require extrapolation of these values, thus this method would only be applicable in situations for which it would seem plausible to extrapolate the longitudinal variable into the future. An implicit assumption in this method is that the treatment assignment depends on PSA, and that there are no other unmeasured factors that may affect the treatment or that are associated with PSA or recurrence. While we perform the estimation in two stages, it is certainly possible to fit the longitudinal and survival models jointly ([21]). The joint estimation would likely lead to better estimates of γ in some situations. The joint estimation method is much more computationally intensive, so we will use the simpler two-stage estimation in our numerical work.
3.2. Sequential Stratification
The sequential stratification (SS) method [10, 11] reorganizes observed data in an attempt to mimic a sequence of conditionally randomized treatment assignments. At the time of each treatment initiation, similar patients at risk who have not initiated treatment are matched to the patient initiating treatment; this process generates one stratum for each treated subject in the data. Then, a stratified Cox proportional hazards model is fit in order to estimate the treatment effect, allowing for differing baseline hazards across strata.
Let S(j) be the jth ordered time of SADT initiation, j = 1, …, nS, where nS is the total number of patients undergoing SADT. With respect to the jth patient to initiate SADT (index case (j)), we define eij = 1 if patient i is at risk at time S(j) and has a similar PSA pattern, and eij = 0 otherwise. Specifically, the stratum-inclusion indicator for patient i is given by:
| (5) |
where is a vector of the BLUP estimates of log PSA, slope of log PSA at time t, and the random effect for time, standardized across i to have mean zero and variance 1, and Ri is the recurrence time and Ci is the censoring time. ||Pi(S(j)) − P(j)(S(j))||indicates the Euclidean distance between the vectors of BLUP estimates for subject i and the index case at time S(j), and δjk is chosen so that exactly k patients have ||Pi(S(j)) − P(j)(S(j))|| ≤ δjk. Therefore each stratum consists of the index case (the patient undergoing SADT), along with the matched (with respect to standardized current logPSA, current slope of logPSA and long term slope of logPSA) k-nearest-neighbor patients still at risk at the time of initiation of SADT. We also only considered matches who had the same baseline T-stage as the index case. We used k = 3 if three or more potential matches were available, and all available matches if less than three were available.
Once strata are defined, we fit the following model, which assumes that for patient i in stratum (j) the hazard is given by:
| (6) |
where (j) = 1, …, nS, and I[i = (j)] is an indicator for patient i being the index case, and the estimate of η is the quantity of primary interest. The BLUP estimates of log PSA and slope of log PSA (at the respective times of SADT initiation) are used as adjustment covariates as well as matching criteria in order to account for any residual heterogeneity within strata. The estimate of the random effect ai2 is included because it can be viewed as a predictor of future PSA values. A robust variance estimator is used and matched patients (non-index-cases) who later undergo SADT are censored at the time of their SADT.
Additional comment on the use of the random effect, ai2 in the matching and in equation (3), is in order. In developing the sequential stratification method, Schaubel et al [10, 11] did not require modeling of the longitudinal process. However, the methods did require a modified version of Inverse Probability of Censoring Weighting (IPCW) in order to account for the dependent censoring of treatment-free recurrence caused by the receipt of SADT. The version of SS evaluated in this report does not involve inverse weighting. However, since the analysis is conditional on ai2, which essentially accounts for future treatment propensity, bias due to dependent censoring should be minimal.
There are a number of issues and challenges associated with the sequential stratification approach. In this method we form strata of similar subjects, but there are choices to be made about the size of the strata and how the strata are formed. Some of these choices were investigated in Kennedy et al (2010), where we relied on the matching to achieve homogeneous strata, but in this paper we have also included adjustment covariates in equation (6). In general, decisions need to be made about which factors are used to define strata and which are incorporated as adjustment covariates in the model of interest. In the matching procedure, we match on the BLUP estimates of PSA, slope of PSA and âi2 from the longitudinal model, but this was not strictly necessary: one could instead match on the observed values of PSA without the need to fit a longitudinal model. This method has some similarity to propensity score matching, but propensity score matching would aim to match on subjects who had similar probability of obtaining treatment, whereas we aim to match on patients who have the same prognosis, similar to the idea of prognostic matching ([22]). In the prostate cancer example, these are thought to be similar. In principle we could refine the matching on prognosis, by including in the matching criteria quantities such as the projected PSA value 2 years into the future or an estimated probability of recurrence within, say, 3 years. These approaches would give more homogeneous strata with respect to prognosis.
A further challenge with respect to the SS method is variance estimation. The articles proposing the SS method both suggested the use of the bootstrap. Since estimating equation methods are used to derive the method, it is possible that a robust (sandwich) variance estimator could be used instead. Since use of the bootstrap is computationally demanding, we use a robust variance estimator in this paper.
3.3. Marginal Structural Model
In the context of survival analysis, inverse-probability-of-treatment weighted (IPTW) estimators for the parameters of a marginal structural model (MSM) [3, 4] can be obtained via a Cox model for which contributions to the partial likelihood are weighted differentially across subjects and across time, where the weights are first calculated at a discrete set of time points. In this paper, we closely follow the methods and code given in [4].
First, the time scale is discretized into many small intervals, with the interval endpoints denoted by t0, t1, t2, …. Then subject-specific time-varying weights are computed using estimated probabilities from two separate logistic regression models. The first model regresses the probability of not initiating treatment at time tj (conditional on not having already initiated treatment by time tj−1) on baseline covariates:
| (7) |
The second model regresses this probability on both baseline and time-dependent covariates:
| (8) |
We also considered an alternative for the second model
| (9) |
Note that in equation (8) the initiation of SADT depends on estimates of the value and slope of PSA, which are both important variables for the hazard of recurence, while in equation (9) the initiation of SADT depends only on the observed PSA value, and matches exactly the way the data is generated in the simulation study.
Let p̂1i(t) be the predicted probability for subject i at time t estimated from model (7) and p̂2i(t) be the predicted probability for subject i at time t from models (8) or (9). Then the stabilized weight for subject i at time tk is given by:
| (10) |
This weight corresponds to the cumulative product (across time) of the ratio between two probabilities: in the numerator, the probability that the subject received his observed treatment given only baseline covariates, and in the denominator, the probability that the subject received his observed treatment given both baseline and time-dependent covariates. The numerator probability is used only for stabilization purposes, and although strictly not necessary, we include it here because it has been shown to improve the properties of IPTW estimators ([23, 14]). Note that, for a given subject, the weight is constant across time after initiation of SADT.
Finally, to estimate the quantity of interest φ, we fit the time-dependent Cox model:
| (11) |
with subject-specific time-dependent weights wi(t). The SE of φ is obtained from a robust variance estimator.
There are a number of issues and challenges associated with this MSM approach. The quantity being estimated by the MSM method is a population average treatment effect, it is an identifiable quantity, and in contrast to the two-stage method which assumes the treatment effect is the same for all subjects the MSM method does not require this assumption, however it does assume that the treatment effect does not depend on the time of initiation of the treatment. In contrast to the two-stage method and the version of SS described above, the MSM method requires specifying and fitting models for the treatment assignment. This may or may not be easier than specifying a model for the outcome, depending on the context. The models fit in the MSM method are used to estimate the weights, and it has been observed that these weights can be quite unstable, negatively affecting properties of the estimated treatment effect ([24, 25, 23]). Various strategies to control this instability have been suggested, such as truncating very large weights or using stabilized weights (as is done in this paper). Xiao et al [13] suggested normalizing the weights, but we found that was not effective in our situation. In equations (7) and (8) or (9) we have assumed the intercepts β̃0(t) and β0(t) are time-dependent, where we use a B-spline estmator similar to Hernán et al [4]. For the way we generated data in the simulation study, assuming constants for β̃0(t) and β0(t) would have been adequate, but in general assuming smooth functions for β̃0(t) and β0(t) would be preferable. The choice of model to obtain p̂2i(tj) may also be important. In the data generation scheme in the simulation study the initiation of SADT is determined by observed value of log PSAi(t), corresponding to equation (9), while the recurrence event is determined by the true value and slope of log PSAi(t), hence consideration of equation (8). We will compare these two methods of obtaining the weights. As described in [4] more complex weights can be used that also take account of censoring, by developing an additional model for the censoring time. Although in practice it would usually be preferable to perform this extra modeling, we don’t include this additional weight in this paper, because it wasn’t necessary for nearly all the scenarios considered in the simulation study as we don’t impose any censoring. Another practical issue when fitting the Cox model (equation (11)), using the weighted partial likelihood, is that it is necessary to have weights at the times of every event, whereas the weights are only calculated at a set of discrete times. To solve this problem, either the weights have to be interpolated to all times, or the data needs to be discretized so that events and initiation of SADT occur at the same set of times. An alternative to overcome this problem is to use survival models, instead of the logistic models in equations (7), (8) and (9), then the required weights could be calculated at any time.
3.4. Marginal vs. Conditional Causal Effects
In this paper we take the parameter γ to represent the relative decrease in the hazard for each subject when they receive SADT. It is a subject-specific effect that is assumed to be the same for every person. This assumption can be weakened; specifically, it would be possible to have γ depend on either baseline or time-dependent covariates. While this would be scientifically interesting we do not consider it in this paper.
The definition of γ from Equation (1) is conditional on the unknown natural hazard curve, . In the two-stage method we parameterize the natural hazard to be a function of random effects. Because of its construction, the two-stage method is attempting to estimate the quantity γ. In contrast, the MSM method is trying to estimate a different quantity that is a marginal or population-averaged quantity; it is essentially averaging over the random effects. For non-linear mixed models it is well known that population-averaged estimates are different than subject-specific estimates and tend to be closer to zero, so we would expect population-averaged estimates of the treatment effect from the MSM method also to differ from those of the two stage method. This difference between subject-specific and population averaged quantities is also refered to as non-collapsibility of measures, such as hazard ratios, in non-linear models [26].
The MSM methodology is designed to estimate the ratio of two hazards, one being what the hazard would be if SADT is never given and the other being what the hazard would be if everyone who is at risk is given SADT at time τ. The form for both hazards can be directly derived from the subject-specific models for PSA and recurrence by integrating out the random effects. We note that these hazards are population quantities which do not depend on the details of the MSM methodology for estimating the weights. If SADT is never given, the marginal hazard at time t depends on P(R ∈ (t, t + δ)|R > t) for small δ, which can be written as:
| (12) |
where a are the random effects. For simplicity of notation, assume there are no covariates xi; then the term P(a|R > t) can be written as:
| (13) |
where f(a) is the distribution of the random effects, ω is the collection of parameters (α’s and θ’s) from equations (2) and (3), g(·) is the linear combination of PSA and slope of PSA obtained from plugging equation (2) into equation (3), and B is the integral of the numerator with respect to a. Thus the marginal hazard is:
| (14) |
For the group who received SADT at time τ, the marginal hazard at times t > τ is given by
| (15) |
where B* is the normalizing constant.
The ratio of these hazards from equations (14) and (15) will be one at times prior to τ, but after τ it is a complicated expression, which certainly does not equal exp(γ). Furthermore, the ratio of the hazards will depend on t, demonstrating that if the conditional model has proportional hazards, the marginal model will not be proportional hazards in this setting. This calls into question the merits of fitting a marginal proportional hazards model. Nevertheless, the estimate one obtains using the MSM methodology could still be considered a useful summary of the marginal effect of the treatment. If the treatment has no effect then there is no proportional hazards assumption, so in this case there is no violation of assumptions in fitting a marginal model.
In the SS method strata are formed of similar subjects. If the matching was so successful that all subjects in each stratum had identical patterns of PSA and identical prognosis, then they would effectively have identical random effects and the quantity being estimated would be γ. In reality, there is some heterogeneity within each stratum, so everyone within strata would not have identical random effects. Thus the treatment effect being estimated by the sequential stratification method will be similar to but not the same as γ, because it involves averaging over the within-strata variation. If the stratification is quite coarse we might expect the estimate from sequential stratification to be closer to that from the MSM method than to γ. To minimize the impact of possibly coarse stratification we also adjusted for the stratification factors by including them as continuous covariates in the survival model. In work we do not present we found that not adjusting for PSA, slope of PSA and âi2 in the stratified analysis in equation(6), gave estimated treatment effects further away from γ, compared to when we did adjust for PSA, slope of PSA and âi2. This demonstrates the value of more precise matching and adjustment. Another way to decrease the within-strata variation would be to increase the overall sample size, enabling more precise matching within strata.
The conditional treatment effect γ as defined by equation (1) is conditional on the person’s random effects ai. The treatment effect that the subject would be most interested in is one that conditions on his baseline covariates xi and his history of PSA up to the current time . This will usually be well estimated by an estimate of γ obtained by effectively plugging in estimates of the random effects into equation (1). We contend that this would be a more useful measure of the treatment effect for patient i than one that conditions only on xi. There are calculators (for example, at psacalc.sph.umich.edu) that give the predicted probability of recurrence within three years for a patient who is in active follow-up given his history and pattern of PSA values. Such calculators could also give the probability of recurrence within three years, if the person were to start SADT immediately. For this calculation we contend, for the reasons given above, that γ is the more appropriate hazard ratio to consider than φ. Whether γ corresponds to anything that one would estimate from a clinical trial is less clear. The possible idealized trial would be one in which randomization happens at time τ, and the eligibility criteria for the trial would be people who had identical values of xi and random effects. This could be approximately achieved by enrolling subjects who had a specified value for xi and a specified path for PSA up to time τ. Having to specify xi and the path of PSA makes such a trial too restrictive and thus not feasible. However, it may be feasible to specify a set of possible values for xi and paths of PSA and then randomize within each set. If the analysis was also stratified, then this would be estimating a quantity that approximates γ. Because of its similarity to the SS method, the formulation of this clinical trial also makes it clear that SS is attempting to estimate the quantity γ.
The target quantities for the MSM method we use in this paper corresponds to a randomized trial in which subjects who are still at risk for recurrence at time τ are randomized to either SADT or no SADT. This in itself is not a very scientifically interesting or ethically plausible clinical trial, because withholding SADT until recurrence would not be allowed. The MSM methodology is flexible in that in principle, by using other weighting schemes for the final Cox model, the estimated parameter corresponds to randomized trials with different designs. For example, if the trial design was to randomize people to either SADT now or no SADT until the first time PSA went above a certain threshold, then we would expect this trial to show a different and smaller marginal treatment effect than the simpler randomized one. However, the same conditional treatment effect γ would apply, and the marginal treatment effect from such a trial could be derived from γ by integrating out the random effects. Thus the conditional treatment effect γ can be regarded as a fixed inherent quantity that is not influenced by the design of the clinical trial, whereas the quantity being estimated by the MSM is a function of both γ and the design of the proposed clinical trial.
4. Data Simulation
Here we present simulation models used to generate realistic looking data for PSA, treatment by SADT, recurrence, and censoring. The generating models are designed to reflect the process by which data would arise in a clinical setting. Each model is a slightly simplified version of what is estimated from the real data.
We consider discrete and evenly distributed time points, with observation frequency f = 10 (number of evenly-spaced observations per year) and study duration K = 12 years. Let T= {0.1, 0.2, 0.3, …}. PSA measurements, initiation of SADT, recurrence and censoring can only occur at this set of times. If more than one is simulated to occur at a specific time, then the sequence of them occuring is censored first, then PSA, then recurrence, then SADT.
4.1. Generating Model for PSA
Following [9, 19], for subject i at each time point after start of follow-up, we simulate observed PSA values (denoted by Pi(t)) from the following mixed model:
| (16) |
where (α0, α1, α2) are fixed effect parameters, (ai0, ai1, ai2, ai3) are subject-specific random effects, and xi is a covariate vector including an intercept term and baseline T-stage indicators. At a given time t, we assume the measurement error εit ~ N (0, σ2), and we assume the random effects (ai0, ai1, ai2) ~ MVN(0, Σ) and ai3 ~ N (0, τ2). This model differs from that assumed for the two-stage estimation method only by the inclusion of a quadratic term t2. Note that, given the random effects, and in the absence of any treatment after time t = 0, PSAi(t) would be known and non-random for all t.
4.2. Generating Model for Treatment by SADT
For subject i we simulate the time of SADT by first calculating for each t in T a sequence of probabilities from the equation:
| (17) |
where (β0, β1, β2, β3) are fixed effect parameters for the intercept, baseline covariates xi, age Ai(t), and observed time-dependent logPSA values. We then simulate S̃i(tj) ~ Bernoulli(pi(tj)), and since subjects stay on treatment once treatment is initiated, the time to initiation of SADT for subject i is Si = min{tj: S̃i(tj) = 1}.
4.3. Generating Model for Recurrence
For subject i we simulate the recurrence time given Si by first calculating the hazard function at any time t from the following model:
| (18) |
where λ0 is the constant baseline hazard. The survival function for subject i is:
then the survival time for subject i is generated as , where V ~ Uniform(0, 1), and then is rounded up to the closest visit time Ri, or censored at 12 years at the end of the study.
4.4. Generating Model for Censoring
For subject i at time t, we either assume no censoring or simulate censoring times from the following model for the probability of censoring:
| (19) |
where (b0, b1, b2) are fixed effect parameters. We assume C̃i(tk) ~ Bernoulli(ρi(tk)), and the censoring time for subject i is Ci = min{ K ∧ tk: C̃i(tk) = 1}, where K = 12 is the maximum follow up time. Note that if Ri ≤ Ci, then follow-up is stopped at Ri; if Ri > Ci, then subject i does not experience a recurrence. Therefore Xi = min(Ri; Ci) is the observation time for subject i.
4.5. Parameter Values and Simulation Conditions
Appropriate values for the parameters in models (16), (17), (18) and (19) are obtained by estimating the corresponding parameters from mixed-effects, logistic regression, and Cox proportional hazards models, respectively, fit to data for 2,781 patients with clinically localized prostate cancer, and all initially treated with radiation therapy. Baseline T-stage values are simulated from possible values (1,2,3,4) with probabilities corresponding to approximate proportions found in the real data. An older version of these data are described in [19]. When fitting the models to the simulated data T-stages 3 and 4 are combined into one category, to avoid problems with the very small numbers sometimes in T-stage 4. Ages are simulated from a N(70, 62) distribution. We simulate 1000 datasets each with 1000 subjects, and PSA, SADT, recurrence, and censoring observations are generated. Unless otherwise stated, the true values of the PSA, SADT, recurrence, and censoring parameters are given in equations (20), (21), (22) and (23), respectively:
| (20) |
| (21) |
| (22) |
| (23) |
We generate two types of datasets. One type mimics an observational study in which there is variation in the time of SADT, using equations (16), (17), (18) and (19) to generate the data. With the specific parameter values as given above and with γ = 0 and 12 years of follow-up, on average 31% of people receive SADT and 38% of people experience a recurrence. The other type of dataset mimics what would arise in a randomized clinical trial with two groups, where the time of SADT differs between groups but is controlled within group according to a specified plan. The data was generated using the specified trial design and equations (16) and (18). For the observational studies, we obtain estimates of the treatment effects and their standard errors (SE) using the three methods. For the randomized trials, we simply fit a standard time-independent Cox model with treatment group as the covariate. We also fit Cox models that included both treatment group and xi as covariates, but the results are very similar and are not shown. We also fit Cox models that included treatment group, xi and the value of PSA at the time of randomization as covariates. We report the average of the 1000 estimated treatment effects, their standard deviation (SD), and the average of the 1000 SEs.
4.6. Fitting the Models
All three methods require fitting longitudinal and hazard models for which we use R. Program lmer is used for the longitudinal fitting and coxph is used for the hazard models. The R function bs() is used in the MSM methodology, where the degrees of freedom is set to 5 and all other parameters are set at default values. For the two-stage method and MSM method, the final Cox models have time-dependent covariates or time-dependent weights. For these we format the dataset for the function coxph(), such that for each subject, we discretized the time into intervals (0, 0.1], (0.1, 0.2], …, and every time-dependent covariate or weight takes a constant value within each interval.
For the two-stage method, the time-dependent covariates (PSA and slope of PSA) take the value corresponding to the time at the end point of each interval. For the MSM method, the value of the weight in the interval (tj−1, tj] is the value calculated from equation(10) at time tj−1.
The actual weights used in the Cox model fit do vary between subjects and over time, but were not observed to be too extreme. Specifically for a random sample in the standard application of the method the 5th to 95th precentile range was approximately (0.38,1.29) and less than 0.2% of the time were they greater than 10.
5. Results
5.1. Evaluation of bias and efficiency of the three methods
Table 1 shows the results from simulated observational data, when there is a strong treatment effect and when there is no treatment effect. For standard application of the methods, in the case of a strong treatment effect, the two-stage method and SS give estimates which are moderately close to the true value of γ. As expected the MSM gives estimates closer to zero. The two-stage method is more efficient than the SS method, as measured by the SD, and both are more efficient than the MSM method. The SEs are close to the SD for the two-stage method, suggesting that the SEs do give appropriate measures of uncertainty. However, the SEs are somewhat too small for the SS method and the MSM method. When there is no treatment effect (i.e., when γ equals zero), the bias is small, but not zero. In this simulation design the MSM method has the largest bias, in other settings we observed the two-stage method to have larger bias. The results for the two MSM methods, MSM (based on modeled PSA) and MSM(obsPSA) (based on observed PSA) are not substantiately different.
Table 1.
Evaluation of bias and efficiency
| γ = −1.5 | γ = 0 | |||||
|---|---|---|---|---|---|---|
| Method | Mean Est | SD Est | Mean SE | Mean Est | SD Est | Mean SE |
| Standard Application of Methods | ||||||
| Two-stage | −1.526 | 0.239 | 0.230 | −0.043 | 0.161 | 0.156 |
| Seq Strat | −1.475 | 0.314 | 0.253 | 0.027 | 0.217 | 0.158 |
| MSM | −1.259 | 0.358 | 0.318 | 0.060 | 0.296 | 0.254 |
| MSM (obsPSA) | −1.228 | 0.385 | 0.314 | 0.065 | 0.291 | 0.243 |
|
| ||||||
| Analysis Using True PSA | ||||||
| Two-stage | −1.584 | 0.238 | 0.230 | −0.076 | 0.158 | 0.156 |
| Seq Strat | −1.546 | 0.321 | 0.259 | −0.002 | 0.213 | 0.158 |
| MSM | −1.272 | 0.356 | 0.318 | 0.015 | 0.293 | 0.253 |
|
| ||||||
| Standard Application: Results for n=5000 | ||||||
| Two-stage | −1.513 | 0.104 | 0.102 | −0.039 | 0.069 | 0.070 |
| Seq Strat | −1.442 | 0.211 | 0.174 | 0.031 | 0.095 | 0.069 |
| MSM | −1.246 | 0.259 | 0.185 | 0.014 | 0.238 | 0.157 |
|
| ||||||
| Analysis Using True SADT Probabilities | ||||||
| MSM | −1.290 | 0.434 | 0.327 | 0.014 | 0.335 | 0.256 |
|
| ||||||
| Analysis Using Random Treatment Times | ||||||
| Two-stage | −1.411 | 0.226 | 0.209 | 0.022 | 0.140 | 0.132 |
| Seq Strat | −1.387 | 0.252 | 0.213 | 0.057 | 0.166 | 0.131 |
| MSM | −1.269 | 0.214 | 0.204 | −0.028 | 0.130 | 0.131 |
| Unweighted MSM | −1.271 | 0.218 | 0.204 | −0.030 | 0.137 | 0.131 |
All the methods (except MSM(obsPSA)) utilize the longitudinal modeling of PSA in some way, specifically by using the BLUP estimates of PSAi(t). They are used either directly in the two-stage method, or to form matches for SS, or in the model for the probability of SADT in the MSM method. Compared to the true values of PSAi(t) these BLUP estimates will have some bias and uncertainty associated with them, and since the observations are generated based on the true values of PSA this uncertainty may lead to some bias in the estimates of the treatment effect. To investigate the impact of this uncertainty, we applied each estimation method using the true values of PSA and slope of PSA for the methods instead of the BLUP estimates. These results are presented in Table 1. This change appeared to have little impact on the bias and variability of the estimates from any of the methods.
The results for the larger sample size n=5000 show no real change in bias, but an expected reduction in precision for the two-stage and the SS method, but interestingly less gain in precision for the MSM method, for a five fold increase in the sample size compared to the standard case.
In Table 1 under “Analysis using Random Treatment Times”, we show the results from simulated observational data in which the probability of receiving SADT is constant across time, and does not depend on the values of any covariates. Specifically, in Equation (17), β0 = −5.485 is the intercept term, and we set β1 = β2 = β3 = 0 for generating the data. Thus, in this case, the true weights for the MSM (at all times and for all subjects) should equal one. All methods now have small bias and except for Sequential Stratification have SEs that appropriately match the SD. There is less bias in the SS method as an estimate of γ, presumably because it is now easier to find similar people for each strata. The MSM, which gives appropriate estimates for both values of γ, matches the case when the weights are assumed to equal one. Also the MSM method is as efficient as the two-stage method in this case. We believe the reason that MSM gives better estimates of the SE is because the weights have less variability in this situation and estimation of them is less challenging.
To understand the target quantity for the MSM, we performed the numerical integrations as described in section 3.4. We found that the marginal hazard ratio was not constant and did become closer to one at longer times after treatment. Specifically at times right after the SADT treatment the log(hazard ratio) was close to −1.5, and then increased approximately linearly to be close to −1.0 twelve years later. Thus marginal proportional hazards does not hold. Hence if a constant hazard ratio is assumed we would expect the MSM method to estimate an intermediate value between −1.0 and −1.5, as it does. To further investigate this we simulated data from two randomized trials, where those at risk for recurrence at 3 or 6 years were randomized to either SADT or no SADT. The results shown in Table 2 for the estimated log hazard ratio are in the range of −1.1 to −1.3 when true γ is −1.5. The quantity derived from the MSM methodology (approximately −1.25) is also as expected in the −1.1 to −1.3 range. When the analysis of the randomized trial data also adjusted for the PSA value at the time of randomization, the estimated treatment effect is closer to the value of γ. The reason for this is because this analysis method more closely matches the conditional treatment effect, rather than the marginal treatment effect.
Table 2.
Randomized Trial Simulation
| γ = −1.5 | γ = 0 | |||||
|---|---|---|---|---|---|---|
| Time of Randomization | Mean Est | SD Est | Mean SE | Mean Est | SD Est | Mean SE |
| 3 years | −1.165 | 0.087 | 0.093 | −0.005 | 0.067 | 0.069 |
| 6 years | −1.283 | 0.116 | 0.119 | −0.002 | 0.081 | 0.082 |
| adjusted for T-stage and PSA at randomization time | ||||||
| 3 years | −1.441 | 0.099 | 0.095 | −0.001 | 0.076 | 0.069 |
| 6 years | −1.517 | 0.128 | 0.121 | −0.003 | 0.089 | 0.083 |
5.2. Robustness to misspecification of models
All three methods use models, and violation of the assumptions of these models could lead to poor properties of the methods.
To investigate the robustness of the methods to misspecifications of the correct structure of the longitudinal model for PSA, we simulated observational data in which individuals could have long-term quadratic trends, but fit a longitudinal model in which we assumed that the long-term trends were linear. The results in Table 3 show increasing bias for all methods of estimation with increasing τ. We speculate that for the two-stage method this is due to model misspecification, for SS it is due to the difficulty in finding matches who have similar prognosis and for MSM is due to the increased difficulty in estimating weights when there is more heterogeneity in the observed data. However, it should be noted that a value of 0.05 for τ is quite large and the lack of fit of equation (2) would likely be detectable from the observed data.
Table 3.
Analysis Using Misspecified PSA Model
| γ = −1.5 | γ = 0 | |||||
|---|---|---|---|---|---|---|
| Method | Mean Est | SD Est | Mean SE | Mean Est | SD Est | Mean SE |
| τ = 0.025 | ||||||
| Two-stage | −1.454 | 0.223 | 0.217 | 0.002 | 0.156 | 0.152 |
| Seq Strat | −1.327 | 0.308 | 0.234 | 0.138 | 0.209 | 0.155 |
| MSM | −1.123 | 0.360 | 0.304 | 0.042 | 0.312 | 0.255 |
| MSM (obsPSA) | −1.059 | 0.349 | 0.299 | 0.122 | 0.297 | 0.246 |
|
| ||||||
| τ = 0.05 | ||||||
| Two-stage | −1.272 | 0.216 | 0.196 | 0.088 | 0.162 | 0.145 |
| Seq Strat | −0.981 | 0.281 | 0.206 | 0.386 | 0.214 | 0.155 |
| MSM | −0.861 | 0.327 | 0.279 | 0.080 | 0.312 | 0.254 |
| MSM(obsPSA) | −0.797 | 0.335 | 0.281 | 0.156 | 0.293 | 0.248 |
A necessary assumption for the interpretation of the treatment effect γ for the two-stage method is it that does not vary from one person to the next. In Table 4 we show results where there is heterogeneity in γ, specifically in generating the recurrence time using equation (18), we used γi ~ U (γ ~ 0.75, γ + 0.75) instead of γ. The results show that there is little change in the quantities being estimated by all three methods compared to the standard application in Table 1.
Table 4.
Impact of Model Misspecification
| γ = −1.5 | γ = 0 | |||||
|---|---|---|---|---|---|---|
| Method | Mean Est | SD Est | Mean SE | Mean Est | SD Est | Mean SE |
| Misspecified treatment effect:Heterogeneity in γ | ||||||
| γi ~ U (−2.25, −0.75) | γi ~ U (−0.75, 0.75) | |||||
| Two-stage | −1.454 | 0.228 | 0.226 | 0.011 | 0.154 | 0.155 |
| Seq Strat | −1.388 | 0.321 | 0.244 | 0.086 | 0.209 | 0.157 |
| MSM | −1.199 | 0.391 | 0.317 | 0.052 | 0.330 | 0.257 |
|
| ||||||
| Misspecified SADT Model: Including Age | ||||||
| Two-stage | −1.480 | 0.223 | 0.211 | −0.005 | 0.148 | 0.141 |
| Seq Strat | −1.432 | 0.270 | 0.215 | 0.051 | 0.190 | 0.136 |
| MSM | −1.246 | 0.283 | 0.246 | 0.005 | 0.220 | 0.190 |
|
| ||||||
| Random Censoring | ||||||
| Two-stage | −1.526 | 0.291 | 0.279 | −0.029 | 0.192 | 0.186 |
| Seq Strat | −1.475 | 0.415 | 0.318 | 0.056 | 0.265 | 0.193 |
| MSM | −1.281 | 0.449 | 0.369 | 0.037 | 0.334 | 0.281 |
|
| ||||||
| Age Dependent Censoring | ||||||
| Two-stage | −1.479 | 0.269 | 0.259 | 0.001 | 0.175 | 0.169 |
| Seq Strat | −1.446 | 0.354 | 0.277 | 0.056 | 0.228 | 0.169 |
| MSM | −1.283 | 0.311 | 0.291 | −0.004 | 0.221 | 0.214 |
To investigate the robustness of the MSM to misspecification of the model for SADT, and to investigate whether the two-stage or SS methods are sensitive to varying treatment assignment processes, we modified the model for simulating the initiation of SADT. In Table 4, the results are given in the case where in the simulated data we allow age to affect the probability of receiving SADT, but do not allow for this possibility in the model for SADT that gives the weights in the MSM method. Specifically, in Equation (17), we take β0 = −7.726, β1 = (−0.086, −0.038)T, β2 = 0.20, and β3 = 0. 523 for generating the data. The results from Table 4 are similar to those from Table 1, and thus the three methods are robust to misspecification of this type. The MSM is not affected in this case since age is a baseline covariate, and therefore, if age were included in both equations (7) and (8), the estimated weights in equation (10) would be approximately proportional to the weights that are computed without including age.
In another set of simulation results we investigate the effect of different censoring mechanisms. Results in Table 4 show that adding random censoring times (by taking b0 = −5.600, b1 = 0.100, and b2 = 0 in Equation (19)) has little effect on the bias of any of the methods. Also, as expected more censoring does increase the SD and the SE.
Prostate cancer is a disease of older men; since the age of a subject will also affect the censoring rate, we simulated data with age-dependent censoring. It is also thought that older men are less likely to be given SADT, since such men could be more frail and therefore unable to tolerate potential side effects, or since SADT is thought to be less effective for older men, or since SADT could be considered less necessary for those with shorter life expectancies. Although we could not detect any age effect in real data, we include age in the simulation as a modifier of the probability of SADT. Specifically, we generate data using β0 = −7.726, β1 = (−0.086, −0.038)T, β2 = 0.20, and β3 = 0.523 in Equation (17), and b0 = −8.03, b1 = 0.25, and b2 = 0.05 in Equation (19). From the results in Table 4, we see that introducing age into the models that generated the data, but not the models that are used in the three estimation methods had little effect on the bias of any of the methods compared to what was seen in Table 1. Even though, this is exactly the situation in which an additional model for censoring would be considered necessary to correctly calculate the weights for the MSM method.
For all the above simulation scenarios we calculated the correlation between the estimates from the three methods, to assess whether for a particular dataset if one methods gives a high value for the treatment effect, do the other methods tend also to give high values. The methods were correlated, the correlation between two-stage and SS was typically greater than 0.7 and the correlation of MSM with the other methods was typically greater than 0.4.
5.3. Results from Randomized Clinical Trials
As a last set of simulations we consider 4 different designs for randomized clinical trials. In all these simulations the true value of γ is −1.5. The results for the treatment effects are from simple analyses of the event times in the trial where a Cox model is fit and the only covariate is the treatment group indicator, and do not involve fitting any longitudinal models, or any time-dependent hazard models or calculating any weights.
In the Trial A (Simple Randomization at Baseline), there are three scenarios. In all we randomize 2,000 subjects at baseline and one arm never receives SADT prior to recurrence. The other arm is either to receive SADT immediately, to receive it at three years or to receive it at six years. While these trial are not ethically feasible, or even very scientifically interesting, they do demonstrate in Table 5 a decreasing marginal treatment effect in the trial if SADT is delayed.
Table 5.
Simulating Randomized Trials
| Conditions for Treatment | Time of Randomization | Comparison | Mean Est | SD Est | Mean SE |
|---|---|---|---|---|---|
| Randomized Trial A: Simple Randomization at Baseline | |||||
| At risk at: | |||||
| baseline | baseline | No Treatment | −1.104 | 0.091 | 0.085 |
| 3 years | baseline | No Treatment | −0.869 | 0.085 | 0.081 |
| 6 years | baseline | No Treatment | −0.443 | 0.074 | 0.073 |
|
| |||||
| Randomized Trial B: SADT by Indication v’s no SADT | |||||
| Pos. slope & PSA above: | First time PSA above: | ||||
| 1 | 1 | No Treatment | −1.332 | 0.073 | 0.072 |
| 2 | 2 | No Treatment | −1.374 | 0.071 | 0.073 |
| 3 | 3 | No Treatment | −1.397 | 0.081 | 0.075 |
|
| |||||
| Randomized Trial C: Early v’s Late SADT | |||||
| Pos. slope & PSA above: | First time PSA above: | Treatment when PSA above: | |||
| 1 | 1 | 2 | −0.340 | 0.081 | 0.080 |
| 1 | 1 | 3 | −0.689 | 0.076 | 0.077 |
| 2 | 2 | 3 | −0.520 | 0.076 | 0.078 |
| 2 | 2 | 4 | −0.825 | 0.073 | 0.076 |
|
| |||||
| Randomized Trial D: Immediate v’s SADT by Indication | |||||
| At risk at: | Treatment when PSA above: | ||||
| baseline | baseline | 1 | −0.103 | 0.103 | 0.100 |
| baseline | baseline | 2 | −0.374 | 0.099 | 0.095 |
| baseline | baseline | 3 | −0.644 | 0.097 | 0.091 |
In Trial B (SADT by Indication v’s. no SADT), we randomize 2,000 subjects, at the first time PSA and slope of PSA rise above some threshold, into two arms: in the first arm, subjects receive SADT immediately, and in the other arm, subjects never receive SADT. Again, these trials are not ethically feasible; however, the estimates one would obtain from such trials are likely to correspond more closely with the quantity the two-stage and SS methods are estimating. The results in table 5 show that to be the case.
In Trial C (Early v’s. Late SADT), we randomize 2,000 subjects, at the first time PSA and slope of PSA rise above some threshold, into two arms: here, in the first arm, subjects receive SADT immediately, whereas in the other arm, subjects receive SADT when their PSA and slope of PSA rise above some higher threshold. These trials would be regarded as clinically interesting and ethical. The results in Table 5 show that as expected, even though the true subject-specific treatment effect is −1.5 for all the trials, the estimated treatment effect from the trial is much smaller and depends on the design of the trial.
In Trial D (Immediate v’s. SADT by Indication), at baseline we randomize 2,000 subjects to either receive SADT immediately, or else to receive SADT when PSA and slope of PSA rise above some threshold. Again, these trial are clinically interesting. The results in Table 5 show small treatment effects that depend on the design of the trial.
One conclusion from this exercise in simulating data from randomized clinical trials is that the target quantity for the trial will depend strongly on its design. The treatment effect being estimated by the two-stage and SS methods is most closely aligned with the target quantity in the trials in B. The treatment effect being estimated by the MSM method is most closely aligned with the target quantity in trial A with treatment assignment at baseline.
Another conclusion from these simulations is that even though both the conditional and marginal treatment effects are large (with a log hazard ratio of less than −1), the log hazard ratio in the clinically interesting trials is much smaller, which would clearly have implications for the sample size needed to detect an effect.
The estimated treatment effects for all four of the simulated randomized trial designs are totally determined by the structure of the models for PSA and recurrence, and by the value of γ, together with the trial design. If the results for Trials C and D are to be meaningful and useful, then these models would have to be accurate. A crucial assumption for the validity of the efficacies in C and D is that γ does not depend on covariates. It would be possible to simulate observations for which γ depends on covariates in a number of different ways; for example, it could depend on baseline covariates, such as T-stage, or it could depend on time-dependent covariates, such as age or the value of PSA at Si, or it could depend on time since baseline or on time after Si. All of these variations, which can be thought of as interactions, would impact the efficacy in the trials. In Kennedy et al [9], we investigated estimating these interactions using the two-stage and sequential stratification methods, finding that the quantity of the data available to us was not sufficient to obtain accurate estimates of treatment covariate interactions.
6. Discussion
Estimating treatment effects from observational data in which there is treatment by indication is challenging, and none of the methods considered in this paper are without problems. All of the methods require building models for some aspects of the observed data, and any results are likely to be sensitive to the exact choice of these models. The two-stage method requires models for the disease process. To develop such models would generally require large datasets, and would likely benefit from subject matter knowledge as well. One of the models used in the MSM methodology is for the treatment initiation process and these gives weights that are used in another part of the MSM method. The sequential stratification method can be viewed as intermediate between the two-stage the MSM methods, it uses but does not rely as heavily on the disease process models as the two stage method.
A fundamental issue which we highlight in this paper is whether the desired quantity of interest is subject-specific or marginal. The context and intended use would dictate this. The development of the methods indicates that the two-stage and sequential stratification method are estimating subject-specific quantities, while the MSM is estimating a marginal quantity. This is supported by the simulation results. The MSM is designed to give estimates that correspond to a certain randomized trial, which may or may not be clinically relevant. However, in principle the methodology is flexible enough to allow different weighting schemes that may correspond to more relevant trials, for example by using the history-adjusted MSM method. The ability to obtain sufficiently accurate estimates of the weights may be a concern for more complex weighting schemes.
In the two-stage method, the subject specific treatment effect is defined conditional on latent variables; thus, it is not identifiable without distributional assumptions about the latent variable. Also, the methodology is only applicable in situations where the longitudinal process can be predicted into the future. The nature of changes in PSA, which mirror tumor growth, makes this possible in the prostate cancer example, but may not be possible in other examples.
While the MSM estimate derived from observational data is generally thought of as representing what the results of a randomized trial would be. However, for this to be reliable, it is necessary that the assumptions in the marginal model are appropriate, specifically the assumptions of proportional hazards, and that the hazard ratio does not depend on the starting time of the trial. In the prostate cancer example these assumptions would not be satisfied, so it is unclear in this case what the quantity being estimated from the observational data by the MSM represents. This suggests the need for some research into model checking procedures when fitting marginal models that involve estimated weights.
The sequential stratification method has a number of features that can be optimized, these include the size of the strata and how much you adjust for other variables in the stratified analysis. In previous work ([9]) we investigated the strata size and did not adjust for other variables. In this paper we found that adjusting for other variables was beneficial for estimating the subject-specific treatment effect. One feature of the SS method which still needs development is estimation of the standard errors. We used a sandwich estimator to account for the fact that subjects could be in more than one strata, yet the standard errors were still lower than the empirical SD’s in the simulation studies. Previous articles proposed the bootstrap to estimate the variance of the SS treatment effect estimator ([10, 11]). Although this may indeed be a solution in certain settings, it should be noted that the variability associated with the matching process is not accurately captured by the bootstrap for several matching methods; most notably those using nearest-neighbor matching [29]. Other options for forming the strata include either random sampling (or perhaps selecting all subjects) within categories of a discrete covariate, or using caliper matching based on a risk score. It is possible that the accuracy of the robust variance estimator depends strongly on the number of patients treated (for whom matches can be found), and strata size. Neither methods of matching nor variance estimation have been fully explored in the context of sequential stratification.
MSM is a method that is designed to analyse observational data which contains treatment by indication and then infer the results of a randomized clinical trial. The simulated randomized trial section of this paper suggests a different possible approach to this problem of infering the results of a randomized trial. The disease progression processes and treatment effects are modelled and estimated from the observational data using subject-specific models, then these estimated models are used to simulate the clinical trial of interest. This is a micro-simulation approach, which is used in the health policy area, and also has some similarities to g-computation ([28]). Both approaches have challenges, but are worthy of further evaluation in specific contexts.
All three methods described in this paper can be generalized to allow for interactions or treatment effects that are modified by covariate values. The results from the simulated randomized trials A, B, C and D, assume there are no such interactions. If there were interactions then the estimates from the randomized trials would likely change. Thus accurate estimates of these interactions will be crucial in order for estimates from observational data to be used in the micro-simulation approach. Understanding these interactions would also be important for the patient and his doctor in helping them make a decision about initiating SADT.
Acknowledgments
Contract/grant sponsor: This research was partially supported by NIH grants CA083654 and CA110518.
References
- 1.Zagars GK, von Eschenbach AC. Prostate-specific antigen: An important marker for prostate cancer treated by external beam radiation therapy. Cancer. 2007;112(2):307–314. doi: 10.1002/1097-0142(19930715)72:2<538::aid-cncr2820720234>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 2.Robins JM. Marginal structural models. Proceedings of the American Statistical Association, Section on Bayesian Statistical Science. 1997:1–10. [Google Scholar]
- 3.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. doi: 10.1097/00001648-200009000-00011. [DOI] [PubMed] [Google Scholar]
- 4.Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology. 2000;11(5):561–570. doi: 10.1097/00001648-200009000-00012. [DOI] [PubMed] [Google Scholar]
- 5.Cole SR, Hernán MA, Robins JM, et al. Effect of highly active antiretroviral therapy on time to acquired immunodeficiency syndrome or death using marginal structural models. American Journal of Epidemiology. 2003;158:687–694. doi: 10.1093/aje/kwg206. [DOI] [PubMed] [Google Scholar]
- 6.Hernán MA, Robins JM. Estimating causal effects from epidemiologic data. J Epidemiol Community Health. 2006;60:578–586. doi: 10.1136/jech.2004.029496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van der Laan MJ, Petersen ML, Joffe MM. History-adjusted marginal structural models and statically-optimal dynamic treatment regimens. The International Journal of Biostatistics. 2005;1(1):10–20. (Article 4) [Google Scholar]
- 8.Peterson ML, Deeks SG, Martin JN, van der Laan MJ. History-adjusted marginal structural models for estimating time-varying effect modification. American Journal of Epidemiology. 2007;166(9):985–993. doi: 10.1093/aje/kwm232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kennedy EH, Taylor JMG, Schaubel DE, Williams SG. The effect of salvage therapy on survival in a longitudinal study with treatment by indication. Statistics in Medicine. 2010;29(25):2569–2580. doi: 10.1002/sim.4017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Schaubel DE, Wolfe RA, Port FK. A sequential stratification method for estimating the effect of a time-dependent experimental treatment in observational studies. Biometrics. 2006;62:910–917. doi: 10.1111/j.1541-0420.2006.00527.x. [DOI] [PubMed] [Google Scholar]
- 11.Schaubel DE, Wolfe RA, Sima CS, Merion RM. Estimating the effect of a time-dependent treatment by levels of an internal time-dependent covariate: Application to the contrast between liver wait-list and posttransplant mortality. Journal of the American Statistical Association. 2009;104(485):49–59. [Google Scholar]
- 12.Young JG, Hernán MA, Picciotto S, Robins JM. Relation between three classes of structural models for the effect of a time-varying exposure on survival. Lifetime Data Analysis. 2010;16(1):71–84. doi: 10.1007/s10985-009-9135-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Xiao Y, Abrahamowicz M, Moodie EEM. Accuracy of conventional and marginal structural Cox model estimators: A simulation study. International Journal of Biostatistics. 2010;6(2):Article 13. doi: 10.2202/1557-4679.1208. [DOI] [PubMed] [Google Scholar]
- 14.Westreich D, Cole SR, Schisterman EF, Platt RW. A simulation study of finite-sample properties of marginal structural Cox proportional hazards models. Statistics in Medicine. 2012;31(19):2098–2109. doi: 10.1002/sim.5317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ertefaie A, Stephens DA. Comparing approaches to causal inference for longitudinal data: Inverse probability weighting versus propensity scores. International Journal of Biostatistics. 2010;6(2):Article 14. doi: 10.2202/1557-4679.1198. [DOI] [PubMed] [Google Scholar]
- 16.Aalen OO, Frigessi A. What can statistics contribute to a causal understanding? Scand J Statistics. 2007;34(1):155–168. [Google Scholar]
- 17.Aalen OO, Roysland K, Gran JM, Ledergerber B. Causality, mediation and time: A dynamic viewpoint. Journal of the Royal Statistical Society: Series A. 2012;174(4):831–862. doi: 10.1111/j.1467-985X.2011.01030.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Commenges D, Gegout-Petit A. A general dynamical statistical model with causal interpretation. Journal of the Royal Statistical Society: Series B. 2009;71(3):719–736. [Google Scholar]
- 19.Proust-Lima C, Taylor JMG, Williams SG, Ankerst DP, Liu N, Kestin LL, Bae K, Sandler HM. Determinants of change in prostate-specific antigen over time and its association with recurrence after external beam radiation therapy for prostate cancer in five large cohorts. International Journal of Radiation Oncology Biology Physics. 2008;72(3):782–791. doi: 10.1016/j.ijrobp.2008.01.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lok JJ, Gill RD, van der Vaart AW, Robins JM. Estimating the causal effect of a time-varying treatment on time-to-event using structural nested failure time models. Statistica Neerlandica. 2004;58 (3):271–295. [Google Scholar]
- 21.Taylor JMG, Park Y, Ankerst DP, Proust-Lima C, Williams S, Kestin L, Bae K, Pickles T, Sandler H. Real-Time Individual Predictions of Prostate Cancer Recurrence Using Joint Models. Biometrics. 2013 Feb 4; doi: 10.1111/j.1541-0420.2012.01823.x. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hansen BB. The prognostic analogue of the propensity score. Biometrika. 2008;95:481–488. [Google Scholar]
- 23.Cole SR, Hernán MA. Constructing inverse probability weights for marginal structural models. American Journal of Epidemiology. 2008;168:656–664. doi: 10.1093/aje/kwn164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Scharfstein DO, Rotnitzky A, Robins JM. Adjusting for non-ignorable drop-out using semi-parametric nonresponse models. JASA. 1999;94:1096–1120. (Article 15) [Google Scholar]
- 25.Kang JDY, Schafer JL. Demystifying Double Robustness: A Comparison of Alternative Strategies for Estimating a Population Mean from Incomplete Data. Statistical Science. 2007;22:523–539. doi: 10.1214/07-STS227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kaufman JS. Marginalia: Comparing adjusted effect measures. Epidemiology. 2010;21:490–493. doi: 10.1097/EDE.0b013e3181e00730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fewell Z, Hernán MA, Wolfe F, Tilling K, Choi H, Sterne JAC. Controlling for time-dependent confounding using marginal structural models. The Stata Journal. 2004;4:402–420. [Google Scholar]
- 28.Taubmann SL, Robins JM, Mittleman MA, Hernán MA. Intervening on risk factors for coronary heart disease: an application of the parametric g-formula international. J of Epidemiology. 2009;38:1599–1611. doi: 10.1093/ije/dyp192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Abadie A, Imbens GW. On the failure of the bootstrap for matching estimators. Econometrica. 2008;76:15371557. [Google Scholar]