Modulated Fluorophore Signal Recovery Buried within Tissue Mimicking Phantoms

Abstract

Optically modulated fluorescence from ~140nM Cy5 is visualized when embedded up to 6 mm within skin tissue-mimicking phantoms, even in the presence of overwhelming background fluorescence and scatter. Experimental and finite element analysis (FEA)-based computational models yield excellent agreement in signal levels and predict biocompatible temperature changes. Using Synchronously Amplified Fluorescence Image Recovery (SAFIRe), dual laser excitation (primary laser: λ = 594nm, 0.29 kW/cm²; secondary laser: λ = 710nm, 5.9 kW/cm², intensity-modulated at 100Hz) simultaneously excites fluorescence, and dynamically optically reverses the dark state buildup of primary laser-excited Cy5 molecules. As the modulated secondary laser both directly modulates Cy5 emission and is of lower energy than the collected Cy5 fluorescence, modulated Cy5 fluorescence in phantoms is free of obscuring background emission. The modulated fluorescence emission due to the secondary laser was recovered by Fourier transformation, yielding a specific and unique signature of the introduced fluorophores, with largely background-free detection, at excitation intensities close to the maximum permissible exposure (MPE) for skin. Experimental and computational models agree to within 8%, validating the computational model. As modulated fluorescence depends on the presence of both lasers, depth information as a function of focal position is also readily obtained from recovered modulated signal strength.

INTRODUCTION

Although holding great promise in molecular imaging, fluorescence has yet to find great utility in vivo due to the inherently high background and scatter resulting from complex biological tissues. Highly scattering and full of natural emitters, tissue imaging produces high non-specific background,^1–7 low signals, and poor spatial resolution, resulting in poor overall sensitivity and selectivity to the fluorophore of interest. Even within the lower background and reduced absorption optical window (700–1000nm), the penetration depth of light in human skin is less than 2 mm,⁸ causing background to dominate desired fluorescent signals. Although fluorescence contrast can often be enhanced by increasing fluorophore concentration, high concentrations increase toxicity concerns and raise targeting challenges. Therefore, it is essential to develop in vivo fluorophore detection schemes that enhance desired signals at reduced dosage levels.

Optical and time-gated methods hold promise for minimizing resolution degradation due to tissue scatter.^9–12 Such resolution recovery schemes can be further enhanced through locally incorporating optical clearing chemical agents^13–16 or producing mechanical compression by reducing refractive index mismatch between compact proteins to improve optical transmission.¹⁷ These innovations, however, are unable to minimize the background signals coming from tissue auto-fluorescence, and often sacrifice total signal for resolution improvement.^9–12 Recently, dual-color excitation schemes have been employed to preferentially enhance desired fluorophore signals over background in solution, polymers, and cells.^18–23 One of these approaches³ utilizes photoswitchable emitters requiring two high energy excitation sources to interconvert fluorescent and non-emissive states, limiting application in non-transparent samples. Resulting from reversible photobleaching and recovery, the fluorophore recovery waveform is defined by the molecular response, not an externally applied modulation waveform, thereby demanding that fluorescent signals be recovered through cross-correlation of exogenous reference dye signals. More complicated excitation schemes have pushed this to higher frequency and better-defined modulation frequencies, but background is still at least partially modulated, and the high energy dual excitation scheme can be problematic for deep tissue imaging due to high background and heat generation with only ~200-µm penetration depths in scattering media.^{8, 24}

Not reliant on high-energy photoswitches, we have developed the concept of optically modulated fluorescence through dual-laser illumination to repetitively and selectively enhance only the fluorescent signal of interest (Figure 1).^18–20 Working by optically depopulating transient, long-wavelength absorbing molecular dark states to restore population in the fluorescence-generating manifold of states, the combination of dual illumination wavelengths and modulation frequencies selectively modulates the fluorescence only for the introduced dye, shifting its emission to a unique, deterministic detection frequency. Therefore, Fourier analysis of the recovered emission yields a specific and unique signature of the introduced targeted fluorophores, with largely background-free detection. Termed Synchronously Amplified Fluorescence Image Recovery (SAFIRe),^18–20 long-wavelength secondary laser modulation directly modulates primary laser-excited, higher-energy collected fluorescence by dynamically shifting steady state population from the dark state back to the fluorescent state manifold. Demodulation of collected fluorescence is directly performed at the externally applied modulation frequency, which is free of (unmodulated) background emission.^18–20 Crucial in heterogeneous biological systems, SAFIRe improves sensitivity primarily by removing obscuring heterogeneous background. Importantly, the low-energy secondary laser offers the opportunity to probe dyes more deeply embedded in tissue. We lay the foundation for such studies, building both experimental and computational models that recover demodulated Cy5 emission from labeled phantoms embedded as deeply as 6 mm within highly scattering and high background fluorescing human skin tissue mimics. Further, we develop and utilize multiphysics computational models for photon transport and heat transfer to simultaneously predict modulated fluorescence intensities and temperature distributions resulting from dual-laser excitation. Such multi-laser computational photophysical and thermal predictions enable new behavior to be studied, extending previously published, non-modulatable computational efforts,^{25, 26} while assessing clinical relevance of excitation intensities and detected signals as a function of tissue depth. Experimental demonstrations of signal recovery, and validation of the combined optical, fluorescence modulation, and temperature model are performed, demonstrating the promise of this fluorescence detection approach for structures embedded within tissue, all while maintaining intensities near the maximum permissible exposures (MPE) for skin and computationally assessing temperature increase with time.

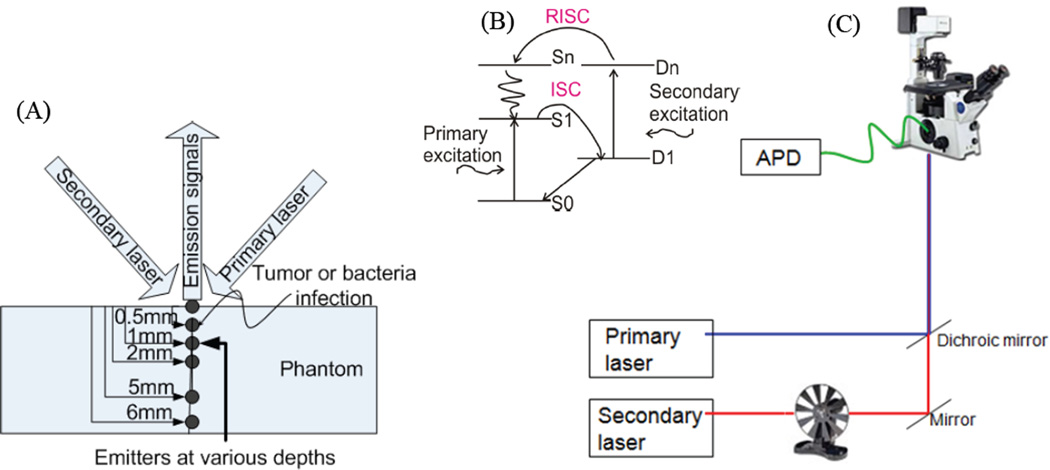
Figure 1.

(A) Schematic of Cy5/Texas red emitters at various depths within Texas red-containing phantoms. (B) Jablonski diagram showing accessible photophysical energy levels (ground state: S0; emissive state: S1; dark state: D1; higher dark and singlet states: Dn and Sn, respectively). ISC and RISC are intersystem crossing and reverse intersystem crossing connecting the bright and dark manifolds. (C) Schematic diagram of the experimental SAFIRe arrangement.

EXPERIMENTAL AND COMPUTATIONAL METHODS

Preparation of tissue mimic phantoms

Created with optical properties similar to those of human skin tissue, tissue phantoms were produced from sodium alginate Protanal LF 10/60 (FMC Biopolymer, Drammen, Norway), a transparent, low viscosity alginate with a mean guluronate / mannuronate (G/M) ratio of 70% and mean molecular weight of 180 kDa. Optical properties representative of human skin tissue were reproduced through homogeneous addition of light scattering and absorbing polystyrene beads, highly light scattering talc-France perfume powder, and Texas Red fluorophores prior to alginate gelation.^27–29 The final formulation best representing skin tissue optical properties was composed of talc-France perfume powder (40 mg/ml), polystyrene beads (3-µm diameter, 1 mg/ml), and Texas Red (235 nM) in sodium alginate aqueous gel, which was cross-linked in 80 mM calcium chloride aqueous solution for 40 minutes, resulting in solid calcium alginate phantoms (Figure 2 A–C).

Figure 2.

Alginate phantoms without (A) and with (B) polystyrene beads, talc, and Texas red respectively. (C) Phantom emitters as in (B), but also containing Cy5

Smaller, Cy5-doped (GE Biosciences, 140nM), but otherwise identically composed alginate phantoms (including the 235nM Texas red) were also prepared. The 0.5mm-thick Cy5-containing phantoms were inserted at different depths (0–6 mm) within the alginate phantom matrix (Figure 1B). Texas red and Cy5 emission, with maxima at 630nm and 670nm, respectively can be excited by the same primary laser (594nm), and their slightly spectrally shifted emission can be collected together through a wide band-pass filter. Texas red is not optically modulatable with the secondary laser (710nm), while Cy5 is strongly optically modulated.²⁰ Texas red therefore mimics tissue autofluorescence, obscuring the Cy5 signals. A total of five experimental samples (N=5) were studied for each Cy5-phantom depth and all results are reported as the mean of these sample trials. The absorption and reduced scattering coefficients of the skin phantoms were 0.06 mm⁻¹ (594 nm) and 0.05 mm⁻¹ (710 nm), and 1.8 mm⁻¹ (594 nm) and 1.5 mm⁻¹ (710 nm), respectively, each with standard deviations varying from ±0.02–0.08.²⁸

Optical setup

Phantom fluorescence was measured on an inverted microscope (Olympus IX71) through a 10X dry objective (Olympus, MPLN 10X/0.25 with 10.6 mm working distance). Continuous wave (cw) primary (594 nm, JDS Uniphase, He-Ne laser) and lower energy cw secondary co-illumination (710nm, Coherent Mira 900, Ti:sapphire) excitation beams were spatially overlapped at the microscope focal plane after combination on a dichroic mirror. Dual-laser overlap was optimized prior to each experiment to account for differences in wavelength-dependent scattering. All samples were focused ~30 microns inside the 500µm-thick Cy5 phantom, with an overlapped excitation spot size of ~8µm diameter. Emission was detected with a photon counting avalanche photodiode (APD, SPCM-AQR-15, Perkin-Elmer) through a 100µm multimode fiber (OZ Optics). Primary laser average intensity used on the sample surface was 0.29 kW/cm². An electro-optic modulator (Model 350–160, Conoptics Inc) and Glan-Thompson polarizer were used to square wave-modulate the secondary laser at frequency of 100 Hz,. The average intensity when focused at the phantom surface was 5.9 kW/cm². Recorded time traces were binned no less than 2.2-fold faster than the inverse modulation frequency to ensure Nyquist sampling. Appropriate band pass filters (660–700 and 694/SP, Semrock, Inc) and dichroic mirror (FF609, Semrock, Inc) were used in the microscope filter cubes to block primary and secondary lasers while efficiently routing Texas red and Cy5 fluorescence to the APD. Intensity trajectories were recorded using a single photon counting board (Becker-Hickl SPC-630) to time-stamp individual photon arrival times.

Primary laser excitation alone (594 nm) yields strong fluorescence from both Cy5 (670nm) and Texas-Red (630nm). Secondary illumination, however, only depopulates the primary laser-prepared dark state of Cy5 without modulating Texas red emission.²⁰ Texas Red is more efficiently excited at 594nm than is Cy5, somewhat offsetting the better spectral match of the filter passband to the Cy5 emission. Regardless, ~25% of Texas Red and ~75% of Cy5 emission is collected in the collected spectral region. Relying on our previous observations and published transient absorption data, secondary excitation (710 nm) was chosen to best modulate Cy5 fluorescence.³⁰ The modulated emission signals were processed by Fourier transformation of the intensity trajectories, subtracting off any secondary-only background contributions to the Fourier amplitude at the modulation frequency.

COMPUTATIONAL MODEL

Photon transport: excitation model

A finite element-based computational model (COMSOL Multiphysics 4.2a) was developed based on the dual-laser excited experimental model of skin tissue mimicking phantoms. Transient radiative light transport equations (RLTE) ^{24, 31} were solved by the adaptive finite element method (FEM) in order to model and predict excitation and time-dependent fluorescence intensities resulting from dual-laser excitation at various depths in skin tissue mimic phantoms. The light transport equation,

$$\frac{1}{c}\frac{\partial {\varphi }_{ex}(r,t)}{\partial t}-\nabla D_{ex}(r)·\nabla {\varphi }_{ex}(r,t)+{\mu }_{aex}{\varphi }_{ex}(r,t)=S_{ex}$$ (1)

was used in which c, Φ_ex, D_ex, µ_aex, and S_ex are the velocity of light (m/s), fluence rate (W/m²), diffusion coefficient (m⁻¹), absorption coefficient (m⁻¹), and laser source (W/m³), respectively for excitation. The diffusion coefficient is represented as D_ex=1/3*(µ_aex+µ´_s), where µ´_s is a reduced scattering coefficient expressed as µ´_s=µ_s(1–g), with µ_s (m⁻¹) and g being the scattering coefficient and anisotropy factor, respectively. We adopted the common assumption that a soft turbid tissue behaves as an isotropic medium, when the scattering is expressed in terms of a reduced scattering coefficient.^{24, 28} The source in Equation 1 is a Gaussian beam in the vicinity of the laser focus constructed from Beer’s law as an isotropic scattering event (Equations 2 and 3).

$$S_{ex}={\mu }_S^{\text{'}}·(1-R_{sp})·{\varphi }_{ex0}·\mathrm{\text{exp}}(-{\mu }_t·z)$$ (2)

$${\varphi }_{ex0}=I_{ex}^{\mathit{\text{amp}}}·e^{-(\frac{x^2}{2{\sigma }_x^2}+\frac{y^2}{2{\sigma }_y^2})}$$ (3)

In these equations, R_sp denotes the specular reflectance from the surface of the scattering medium, Φ _ex0 denotes the incident fluence on the surface, µ_t represents the attenuation coefficients (µ_t= µ_aex+µ´_s), I^amp_ex is the amplitude of the Gaussian laser spot, and σ defines the excitation area dimensions. An approximate Gaussian profile was maintained in the z-direction by calculating distance of the focal point from the incident surface, the area of the laser incident on the sample surface, and the area of the laser focus from the numerical aperture (NA) and the distance between the microscope objective and the sample for varied emitter depths within the larger phantoms. Absorption and reduced scattering coefficients of tissue mimic phantoms were determined,²⁸ with phantom optical properties being very close to those of actual human tissues. The parameters for primary and secondary lasers used were similar to those used for experimental models. Equation 1 is defined separately for both primary and secondary lasers with different phantom optical properties corresponding to primary and secondary laser wavelengths. The light transport equations for primary and secondary lasers were solved simultaneously by FEM to predict excitation intensities at various phantom depths.

Photon transport: fluorescent emission model

The emission model³¹ was defined based on the primary and secondary laser excitation intensities calculated from the above excitation model. The calculated excitation fluence (Φ_ex) was utilized as the photon source to generate emission based on dye photophysical parameters and simulated tissue properties (Equation 4)

$$\frac{1}{c}\frac{\partial {\varphi }_{em}(r,t)}{\partial t}-\nabla D_{em}(r)·\nabla {\varphi }_{em}(r,t)+{\mu }_{aem}{\varphi }_{em}(r,t)=S_{em}$$ (4)

In equation 4, Φ_em, D_em,µ_aem, and S_em are the number of fluorescent photons per detection time bin, the diffusion coefficient (m⁻¹), the absorption coefficient (m⁻¹) and the excitation source, respectively. Once excitation photons from primary and secondary lasers are absorbed, the emission source term is represented as

$$S_{em}=\frac{{\eta }_{\mathit{\text{eff}}}·Y·{\varphi }_{ex}^p·{\sigma }_{abc}^p·\frac{{\lambda }_p}{h·c}(1+\frac{{\tau }_{\mathit{\text{off}}}^0-{\tau }_{\mathit{\text{off}}}}{{\tau }_{\mathit{\text{on}}}+{\tau }_{\mathit{\text{off}}}})}{b·Z_R}$$ (5)

in which, the collection efficiency is defined as, η_eff=ω/4π, where ω is the solid angle of collected photons, Y is the fluorescence quantum yield, b is the number of bins per unit time, Z_R is the Rayleigh length, σ^p_abc is the absorption cross section (cm²) of emitters at the primary laser wavelength, λ_p (m), τ⁰_off is the molecular dark state lifetime without secondary illumination, τ_off is the dark state lifetime with secondary illumination, and τ_on is the average time before transitioning to the dark state. The Cy5 dark state lifetime and fluorescence are represented in Equations 6 and 7, respectively.

$${\tau }_{\mathit{\text{off}}}=\frac{1}{\frac{1}{{\tau }_{\mathit{\text{off}}}^0}+{\varphi }_{ex}^s·{\sigma }_{\mathit{\text{abs}}}^s·\frac{{\lambda }_s}{h·c}}$$ (6)

$${\tau }_{\mathit{\text{on}}}=\frac{h·c}{{\varphi }_{ex}^p·{\sigma }_{\mathit{\text{abs}}}^p·\lambda ·Y_{ISC}^d}$$ (7)

In these equations, Φ^s_ex is the calculated fluence rate (W/m²) of secondary laser from equation 1, σ^s_abs is the dark state absorption cross section (cm²) at the secondary wavelength, λ_s (m), and Y^d_ISC is the dark state quantum yield. Because the secondary laser is square-wave modulated at 100 Hz, the dark state lifetime, and therefore the Cy5 fluorescence intensity, is also dynamically modulated at 100 Hz. Due to the different optical responses, fluorescence of Texas red- and Cy5-containing phantoms were defined separately. Photophysical rates for primary and secondary excitation of Cy5 are incorporated into the dual-laser-induced fluorescence simulation. All excitations and emission models were coupled together and solved simultaneously. Poisson noise is incorporated at all time points, and the modulated emission signals are Fourier transformed in order to identify the modulated fluorescent frequency component of Cy5 emission.

Heat transfer model

The temperature distribution due to laser excitation was modeled with Pennes’ bioheat equation (Equation 8).³² This model accurately predicts the temperature distribution due to laser or any metabolic heat generation in tissue or in any turbid medium.

$${\rho }_t{c}_t\frac{\partial T}{\partial t}=\nabla ·[k(T)\nabla T]-{\omega }_b(T)c_b(T-T_a)+Q(\overrightarrow{r},t)$$ (8)

In equation 8, ρ_t, c_t, T_a, c_b, and ω_b are the tissue density, specific heat, arterial blood temperature, blood specific heat, and temperature dependent blood perfusion rate, respectively.³³ Due to the absence of blood perfusion in the phantom, ω_bwas set to zero. The optical and thermal properties of identically prepared phantoms^{28, 29} were utilized in this model

System Geometry and Boundary Conditions

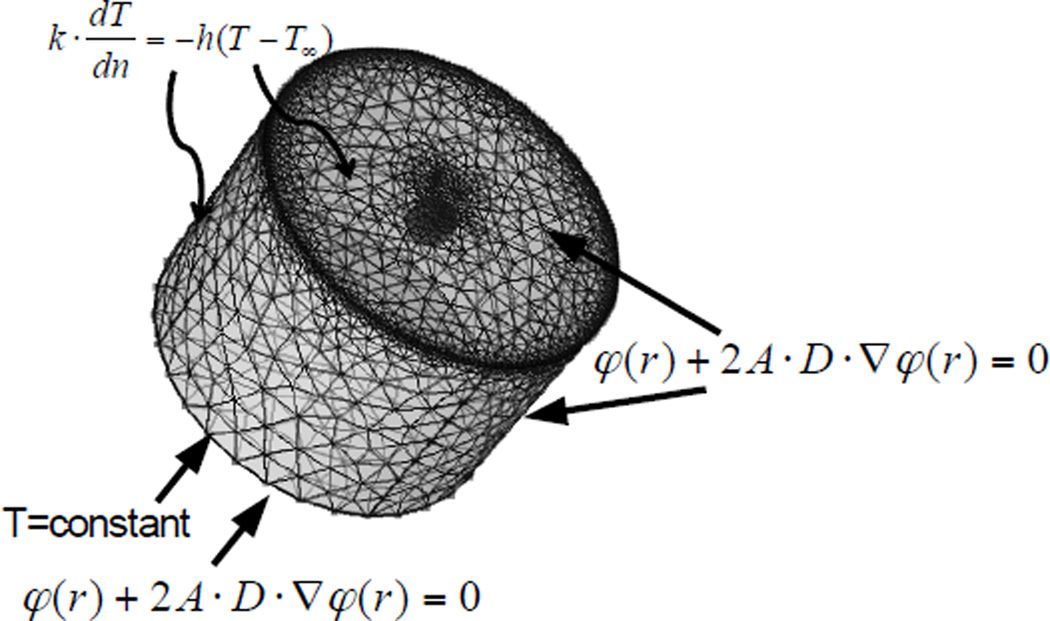
A tetrahedral mesh tissue phantom geometry was generated (233928 total vertices, size: 0.001–0.4 mm) within COMSOL^® Multiphysics, with finer meshes in the emitter region and the upper corner of the cylinder than in the bulk phantom (Figure 3). The computational model phantom (10×7 mm (diameter×height)) and emitter (1×0.5mm (diameter×height)) geometries were similar to those used in the experimental models. At each depth, emitters were modeled in a separate geometry and simulated separately. Modified mixed boundary conditions ^{34, 35} were applied on the surfaces of tissue phantoms and Cy5-phantoms, represented as φ(r) + 2A·D·∇φ(r) = 0, where A is a constant, $A=\frac{2/(1-R_0)-1+|\mathrm{\text{cos}}{\theta }_c{|}^3}{1-|\mathrm{\text{cos}}{\theta }_c{|}^2}$ , R₀ is the specular reflectance R₀ = (n−1)² /(n + 1)², n is a ratio of refractive indexes, n=n_in/n_out, and θ_c is the critical angle, θ_c = sin⁻¹ (1/n). The computational models yield excitation and emission photon distributions along with the temperature distribution as a function of time and coordinates. For the temperature model, mixed boundary conditions were considered due to convective cooling on the surface, which is represented as $k·\frac{dT}{dn}=-h(T-T_{\infty })$, in which k is the phantom thermal conductivity (0.57 W/m·K) ²⁹, dT/dn is the temperature gradient, h is the convection heat transfer coefficient (4 W/m²·K, due to free convection) ^{36, 37}, T is the temperature at the boundary, and T_∞ is the ambient temperature (297 K).

Figure 3.

System geometry of phantom model.

Results and Discussion

Experimental conditions

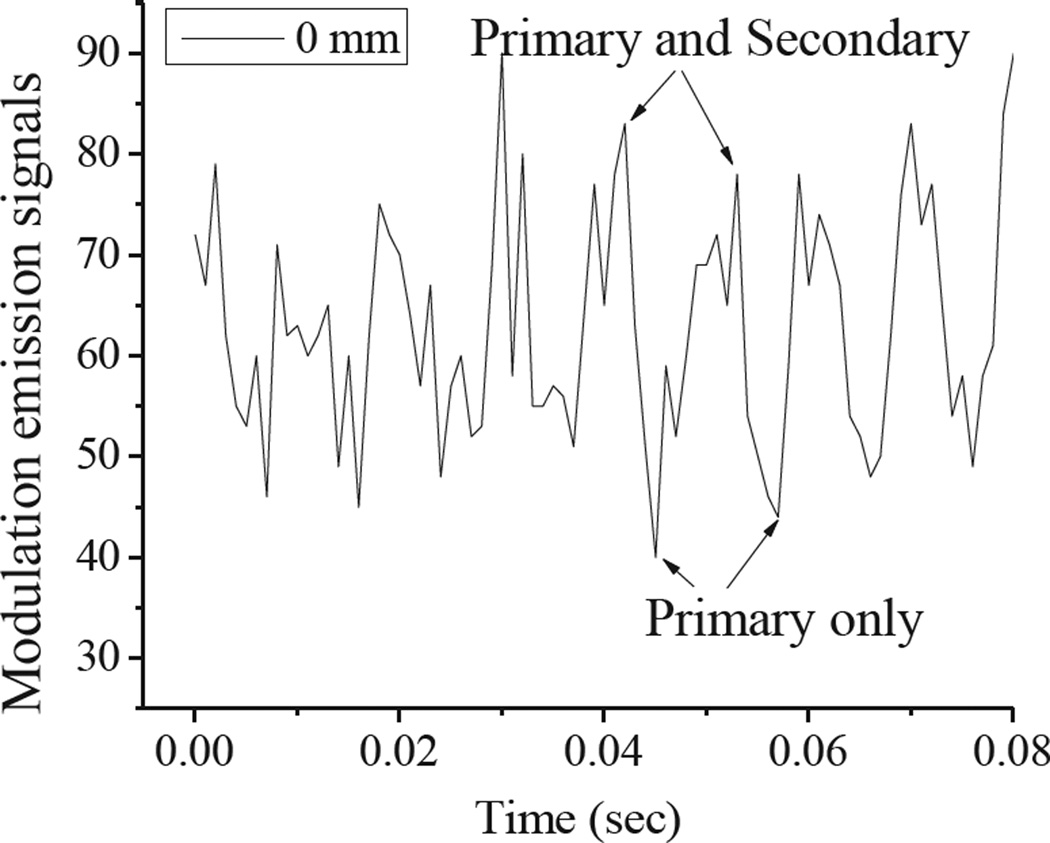
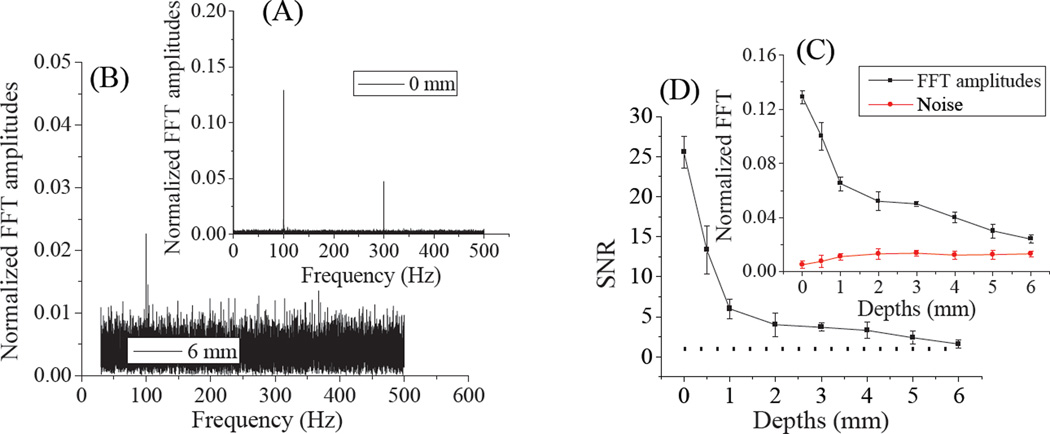
Identified as the cis-isomer, the photoinduced Cy5 dark state is red-shifted in absorption by ~45 nm from that of the ground state (trans) absorption and exhibits a natural lifetime of ~150 µs.^{20, 38} Formed through primary illumination alone, co-illumination at 710 nm optically depopulates this state faster than it would naturally decay, leading to increased 670-nm fluorescence.^18–20 In these studies, we repetitively depopulated the Cy5 dark state using a square wave-modulated 710-nm secondary laser with 5.9 kW/cm² average intensity, thereby modulating 594nm-excited (0.29 kW/cm²) fluorescence. Emission was recorded as a function of Cy5-phantom depth within skin tissue phantoms. Figure 4 shows fluorescence from continuous primary excitation and 100Hz square wave-modulated secondary excitation. Dual-laser excitation of Cy5 produces ~15% higher overall fluorescence as the secondary laser recovers the emissive trans-Cy5 from the photoinduced, longer wavelength-absorbing cis-Cy5 state. The modulation frequency dependence has been shown to be indicative of the natural dark state lifetime.²⁰ Because the secondary laser was square wave modulated at 100 Hz, Cy5 fluorescence was also modulated at 100 Hz, as revealed by Fourier transformation of the fluorescence intensity (Figure 5A–B). As Texas red fluorescence is not modulatable, demodulated fluorescence signals are indicative of only Cy5 emission and are directly recoverable even when buried up to 6 mm deep within skin tissue phantoms (Figure 5B). Even with high Texas red background and strong scattering, experimental depth-dependent detection sensitivities at the modulation frequency (Figure 5C) remain detectable beyond 6mm depths. The fluorescence signal to noise ratios (SNR) (Figure 5D) were derived from the division of Fourier amplitudes by noise (Figure 5C). The SNR curve shows an approximately exponential decrease with depth (Figure 5D), indicative of photon diffusion and attenuation within a highly scattering medium.

Figure 4.

Modulated ~670nm emission of Cy5 at the phantom surface resulting from intensity modulating the long-wavelength (710nm) secondary laser.

Figure 5.

Normalized Fourier amplitudes of modulated fluorescence at 0 mm (A) and 6 mm (B) within tissue phantoms with bin time of 0.001s. (C) The inset shows the FFT amplitudes and noise levels at different Cy5 phantom depths within skin tissue mimics. (D) Depth-dependent signal to noise ratio (SNR). The dotted line represents a SNR of 1.

Computational model

Excitation model

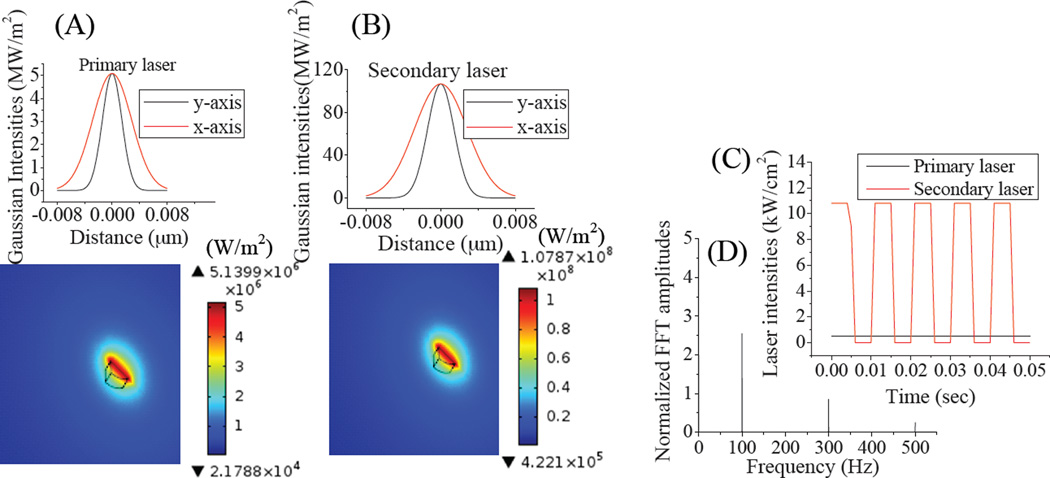
Finite element models of transient light transport were developed for excitation and emission photon distributions coupled with a transient heat transfer model in tissue-mimicking phantoms. The optical and thermal properties of human skin tissue-mimic phantoms, used in the computational models, were made to be identical to those in previous studies.^{24, 28} After defining material properties, boundary conditions, and meshes, 20 seconds of data were simulated with primary and modulated secondary laser exposure to predict excitation and emission photon distributions and temperature rise. All material properties were defined corresponding to primary (594 nm), secondary (710 nm), and emission (670 nm) wavelengths. Mirroring experimental conditions, the primary laser intensity was constant (~0.29kW/cm²) and the secondary laser (~5.9kW/cm²) was square wave modulated at 100 Hz. The excitation spot dimension was elliptical, with diameters of 8 µm and 4 µm for the x and y axes, respectively, matching experimental conditions. Figure 6A–B shows the calculated excitation intensity distributions of primary and secondary lasers after 20 s of laser exposure when the Cy5-containing phantom was located at the surface (0 mm depth) and both lasers were focused on the surface of the Cy5 emitter. Resulting from surface reflection and scatter within the phantom, FEA simulations indicate reduced primary and secondary laser maximum intensities of 0.51 kW/cm² and 10.7 kW/cm² at the focus even when the phantom is probed at the surface. Laser intensities away from the focus, along the optical axis were calculated based on the laser spot areas determined from the numerical aperture (NA=0.25) and focal length (14 mm) of microscope objective that maintains an approximate conical Gaussian distribution in the z-direction. Figures 6B & C show the FEA-calculated time dependent intensity distribution of primary and secondary lasers and the Fourier transformation of the excitation intensities, respectively. Excitation and emission intensities were computed at different Cy5-loaded phantom depths using Equation 1 (0–6 mm).

Figure 6.

(A) and (B) are the primary and secondary laser intensity distributions, respectively showing laser spots (8×4 µm) and intensity profiles. (C) Intensities of constant primary and 100-Hz-modulated secondary lasers, plotted vs. time, and (D) plotted vs. frequency.

Emission model

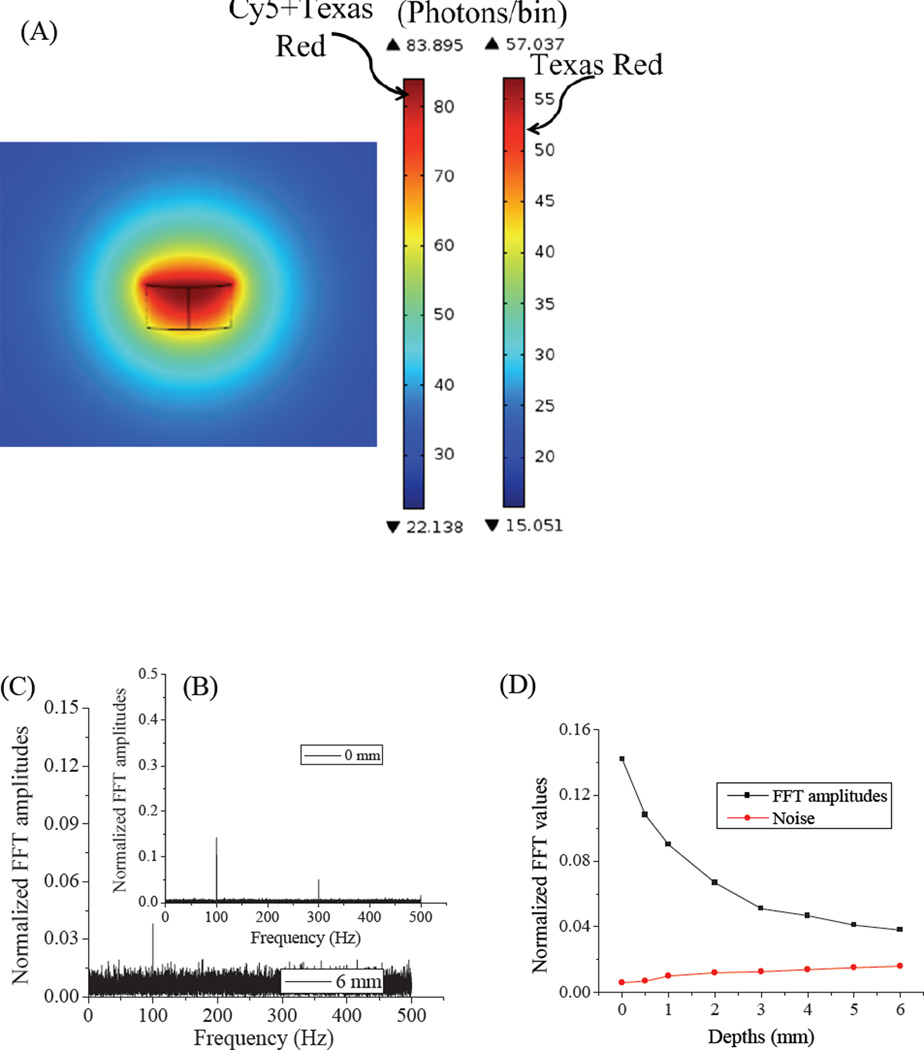
The transient light transport equation (Equation 2) was utilized to model fluorescence from Cy5 and Texas Red corresponding to the modulated excitation model (Equation 1). Total fluorescence was calculated for emitters located at depths ranging from 0 – 6 mm. The distributed excitation intensities, calculated from Equation 1, served as photon sources in the RLTE emission models. Because the excitation intensities were highest at the laser focus, the maximum fluorescence occurs at the common laser focus (Figure 7A). Texas red is not modulatable, making τ_off equal to τ⁰_off in Equation 6. Further, since collected fluorescence (<700nm) is higher energy than is the secondary laser (710nm), no fluorescent background is generated from secondary illumination alone. Therefore, only the excitation fluence (Φ ^p_ex) of the primary laser, calculated from equation 1, was considered in the background fluorescent model with Texas red. However, 670-nm Cy5 fluorescence is strongly modulated with 710 nm co-excitation. Therefore, both primary and secondary laser intensities were used to determine the fluorescence photon counts per unit bin time for Cy5-containing phantoms. Figure 7 represents combined emission signals of ~84 photons/1-ms bin from modulated Cy5 and obscuring Texas Red. This is compared with ~57 photons/bin from Texas Red-only containing phantom regions under primary and secondary excitation at the 0 mm emitter location. In Figure 7, fluorescence intensity increases under dual-laser excitation because the dark state lifetime (τ_off) is reduced relative to that with primary only illumination (τ⁰_off, Equations 5 and 6). The Cy5 dark state absorption spectrum is red-shifted relative to that of the Cy5 ground state after primary laser excitation. Therefore, a long-wavelength secondary laser is used to optically enhance the dark state depopulation rate (Equation 6). Fourier analyses of the simulated fluorescence from Cy5 and Texas Red models clearly show the 100 Hz modulation frequency (Figure 7 B–C), enabling selective Cy5 signal recovery. Fourier transformation of emission from Texas Red shows only a zero frequency peak (not shown). The models were simulated for individual emitters at 0, 0.5, 1, 2, 3, 4, 5, and 6 mm depths. The predicted modulated fluorescence (Figure 7D) becomes progressively weaker with increasing phantom depth, resulting from depth-dependent absorption and scattering that reduce both excitation and collection efficiencies.

Figure 7.

(A) FEM calculated emission signals of Cy5 and Texas Red at 0 mm near the common laser focus. (B) and (C) are the FFT amplitudes of modulated Cy5 fluorescence in phantoms at 0mm and 6mm depths, respectively. (D) FFT amplitudes and noise levels at various phantom depths.

Comparison of experimental and computational models

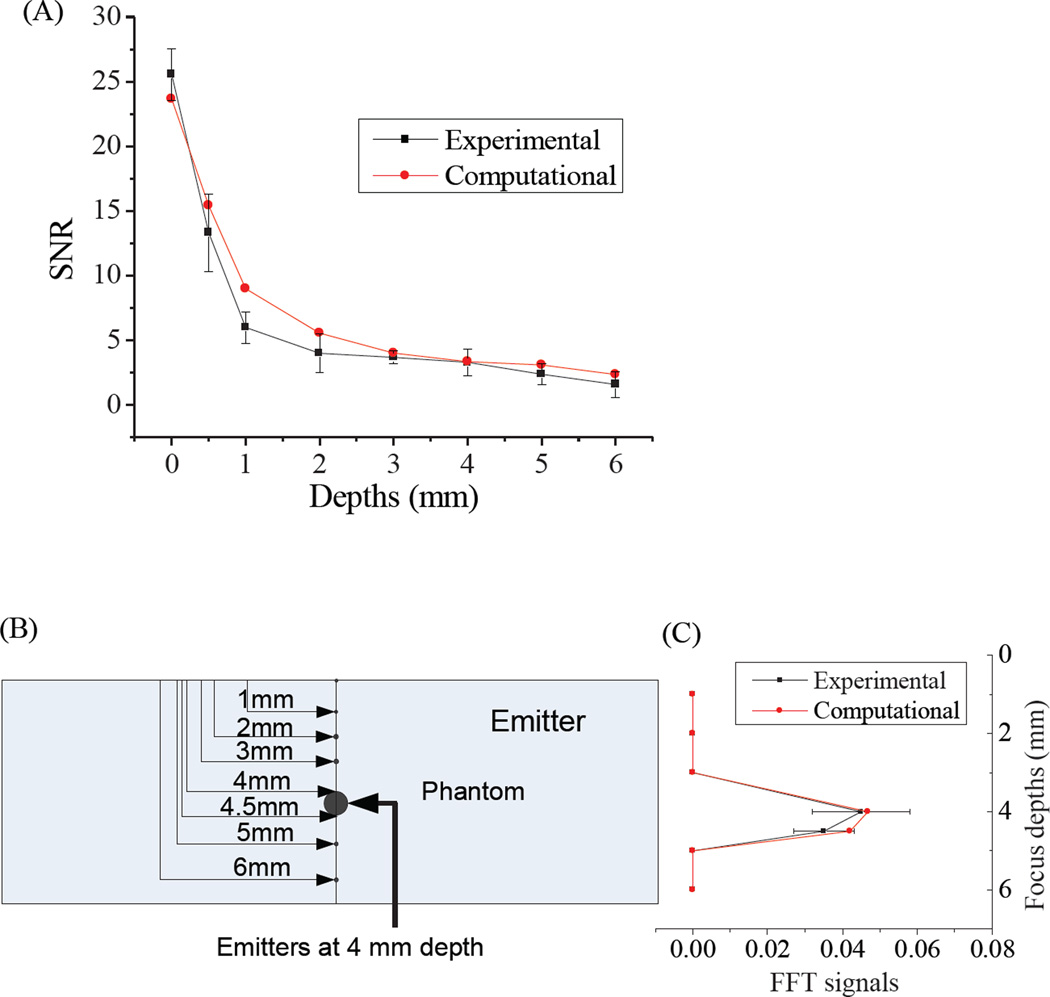
The signal to noise ratio (SNR) of computed emission signals decays approximately exponentially with depth, and compares well with the experimental SNR profile (Figure 8A). The agreement between experimental and simulated values validates the model, and suggests predictive ability at varying depths and concentrations. We have also compared the experimental and computational models, when the emitter was implanted at 4 mm depth inside a phantom and the dual-laser focus was scanned through the phantom depth (0–6mm, Figure 8B). Depending on the laser focus, the modulated intensity at the emitter position changes drastically. Only when the laser focus and emitter depth coincide is modulated emission maximized. Using the parameters of a 0.25 NA 10x objective, excitation areas were ~10⁶-fold smaller at the 4-mm deep focus compared to 1 mm above or below the laser focal spot. Therefore, modulated fluorescence was only observed when lasers were focused at 4 and 4.5 mm depths in the phantom where the Cy5 emitter resided (Figure 8 C). No modulated fluorescence signal was observed above the Poisson noise for 3 and 5mm focal depths, matching experimental observations. Such computational models hold promise for guiding future in vitro studies with different modulatable dyes and for designing future optimal in vivo experiments.

Figure 8.

(A) Comparison of experimental and computational emission signals. (B) Schematic of an emitter 4mm deep within the tissue phantom. (C) Experimentally determined and FEA-calculated FFT signals at the 100-Hz modulation frequency when the 0.5 mm-thick Cy5-loaded phantom is fixed at 4 mm depth.

Temperature model results

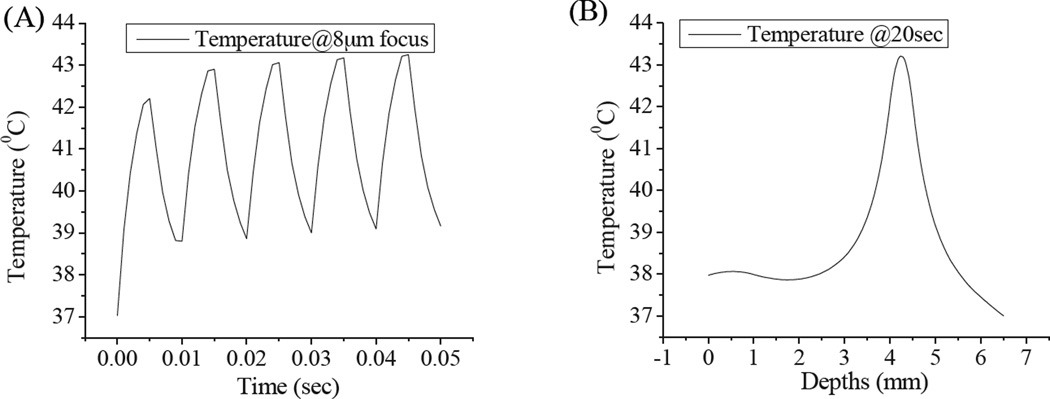
Primary and secondary laser intensity distributions within phantoms served as time- and position-dependent heat sources. The maximum temperature was observed at the dual laser focus, and the temperature profile was calculated as a function of time and phantom depth (Figure 9A–B). In this heat transfer model, a constant primary laser intensity and an average secondary laser intensity (50% modulation duty cycle, 100Hz) were considered as the heat sources. In Figure 9A–B, the temperature distributions are shown, when the two lasers were focused on the emitter embedded 4mm deep within the phantom. The steady state temperature (~43°C) was reached in the 8-µm laser focal area after ~0.04–0.05 sec during laser illumination (Figure 9A) with an initial temperature of 37°C. 43°C is considered as a threshold temperature beyond which cells experience thermal stresses and express heat shock proteins.^{27, 29, 39, 40} These combined excitation intensities remain ~5 times the MPE for skin exposure.^{41, 42} Decreasing the duty cycle or the secondary laser intensity can readily satisfy the MPE requirements without significantly affecting the depth resolution of Cy5 detection. At such reduced intensities, longer detection times can improve signal, but without incurring thermal damage.

Figure 9.

(A) Predicted temperature profile of laser focus on 4mm deep emitter as a function of time. Peaks correspond to secondary laser on, valleys to secondary laser off. (B) Temperature distribution as a function of depth for 20-s laser exposure.

Conclusions

Fluorescence detection in tissue is obscured by tissue autofluorescence, low signal levels, and low overall sensitivity. Through optical modulation, weaker signals can be detected using lower contrast agent loadings, thereby reducing minimum detectable pathology sizes and contrast agent-related toxicities. Though high background fluorescence was incorporated through addition of Texas red throughout the entire sample thickness, modulated fluorescence signals of interest (signals from 140nM Cy5) were recovered from as deep as 6 mm in skin tissue mimicking phantoms. Fourier analysis provides a unique signature for the modulated fluorescent signals of Cy5, uniquely enabling its detection and depth determination. Because the scattering and absorption properties of the entire phantom (up to 6 mm) represents human skin tissue, more realistic multi-layer models with skin (up to 2mm) and muscle (> 2mm) properties should enable fluorescent signal recovery from up to ~1cm, while maintaining relatively low dosage levels. The close correspondence between our optically modulated finite element computations and experimental studies suggest accurate prediction of fluorescent signal recovery in different types of tissues based on their optical properties. These models, coupled with further experimental validations should also provide information about the concentration of modulatable dyes and the corresponding number of targeted cells and tissue temperature profile during dual-laser exposure. Such studies will continue to guide applications to both modulated and direct optical signal recovery.