Assessing the Causal Effect of Organ Transplantation on the Distribution of Residual Lifetime

Summary

Because the number of patients waiting for organ transplants exceeds the number of organs available, a better understanding of how transplantation affects the distribution of residual lifetime is needed to improve organ allocation. However, there has been little work to assess the survival benefit of transplantation from a causal perspective. Previous methods developed to estimate the causal effects of treatment in the presence of time-varying confounders have assumed that treatment assignment was independent across patients, which is not true for organ transplantation. We develop a version of G-estimation that accounts for the fact that treatment assignment is not independent across individuals to estimate the parameters of a structural nested failure time model. We derive the asymptotic properties of our estimator and confirm through simulation studies that our method leads to valid inference of the effect of transplantation on the distribution of residual lifetime. We demonstrate our method on the survival benefit of lung transplantation using data from the United Network for Organ Sharing.

1. Introduction

Lung transplantation is the definitive therapy for many end-stage lung diseases including chronic obstructive pulmonary disease (COPD), cystic fibrosis (CF), and idiopathic pulmonary fibrosis (IPF) (Kotloff and Thabut, 2011). Despite poor unadjusted one- and three-year survival rates after lung transplantation, 83.8 and 63.2 percent, respectively, the number of lung transplantations in the United States grew from 959 in 2000 to 1,770 in 2010 (based on Organ Procurement and Transplantation Network (OPTN) data as of March 30, 2012).

An understanding of the effect of transplantation on survival is needed to improve organ allocation and justify the intensive use of health care resources and high cost. Prior research has focused on the survival benefit within a particular native disease, e.g., COPD only, or from an older era of transplantation (see Liou et al., 2001; Thabut et al., 2003; Lahzami et al., 2010; Kotloff and Thabut, 2011, and references therein). To quantify the causal effect of transplantation, most clinical research has used a proportional hazards model with a time-dependent covariate for transplantation. This modeling approach only consistently estimates the causal effect in the absence of time-dependent confounding (Robins, 1992); however, patients with worse waitlist prognosis have priority in organ allocation.

Several methods that have been proposed, including structural nested failure time models (SNFTMs) fitted by G-estimation, to quantify the causal effect of treatment in the presence of time-dependent confounding (Robins, 1989, 1992, 2005). Applying these methods to organ transplantation is not straightforward. G-estimation requires modeling the probability of receiving treatment each time it could be offered. Prior applications of SNFTMs, such as Robins et al. (1992), have typically indexed time from when the patient entered the study and assumed that treatment assignment was independent across patients. Because a national waitlist is used to offer organs to patients as donor organs become available, the likelihood a patient is transplanted a certain number of days after listing depends on the prognosis of all other patients active on the waiting list.

In Section 2, we introduce a potential outcomes framework in which to represent the question of transplant benefit and present a structural failure time model to relate the residual survival distribution if a patient were transplanted to the distribution of residual lifetime if never transplanted. In Section 3, we describe a class of estimators for parameters in this structural failure time model, derive the asymptotic properties of the class, and discuss reasonably efficient estimators within the class. In Section 4, we give computational strategies to mitigate difficulties encountered with censored failure times. Section 5 presents the results of a simulation study. Section 6 demonstrates our method in an analysis of the survival benefit of lung transplantation using data from the United Network for Organ Sharing (UNOS).

2. Statistical Framework

We consider a hypothetical population of subjects eligible for organ transplantation. Let T*(∞) be the potential time from being listed on the waitlist until death for a randomly selected individual in the population if that patient were to never receive an organ transplant. Characteristics of the donor organ may affect post-transplant survival; denote by Q a random vector of donor organ characteristics. Define T*(t, q) to be the time from listing until death for a random patient awaiting organ transplantation were s/he to be transplanted t days after entering the waitlist with donor organ characteristics Q = q assuming that s/he had not already received an organ and was alive on the waitlist then. As all of T*(∞) and T*(t, q) may not be observed on a random subject, these random variables are referred to as potential outcomes. Define (X̄) * (t) to be the history of time-dependent covariates through t days after listing assuming the patient had not been transplanted and had not died prior to time t. The history of time-dependent covariates are also potential outcomes.

If we let 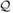be the set of all possible donor organ characteristics, then the set of all potential outcomes for subject i is ${\mathcal{P}}_i=[T_i^{\ast }(\infty ),\{T_i^{\ast }(t,q):t\le T_i^{\ast }(\infty ),q\in \mathcal{Q}\},\{{\overline{X}}_i^{\ast }(t):t\le T_i^{\ast }(\infty )\left\}\right]$. We refer to $R_t^{\ast }(\infty )=T^{\ast }(\infty )-t$ and $R_t^{\ast }(t,q)=T^{\ast }(t,q)-t$ as the residual (potential) lifetime at time t had the patient, possibly contrary to fact, never received an organ and received an organ at time t with organ characteristics Q = q, respectively. The above quantities are only defined if the patient would have survived on the waitlist for t days, i.e., T*(∞) ≥ t.

The effect of transplantation on residual lifetime can now be characterized in terms of potential outcomes. We are interested in comparing the distribution of the residual lifetime at time t had the patient received an organ transplant at time t, $R_t^{\ast }(t,q)$, to the distribution of the residual lifetime had the patient never been transplanted, $R_t^{\ast }(\infty )$.

We consider transformation models to relate the distributions of the residual potential lifetimes. We assume that there is a known function γ_t{z, X̄ * (t),Q; θ}, which is an increasing function of z and is indexed by a p-dimensional parameter θ, such that

$$P\left[{\gamma }_t\right\{R_t^{\ast }(t,Q),{\overline{X}}^{\ast }(t),Q;\theta \}\ge u|T^{\ast }(\infty )\ge t,{\overline{X}}^{\ast }(t),Q]=P\{R_t^{\ast }(\infty )\ge u|T^{\ast }(\infty )\ge t,{\overline{X}}^{\ast }(t),Q\}.$$ (1)

Thus, (1) relates the conditional distribution of a known transformation of $R_t^{\ast }(t,Q)$ given past covariate history and organ characteristics, to that of $R_t^{\ast }(\infty )$. These transformation models are known as structural nested failure time models (SNFTMs). We define the SNFTM in terms of potential outcomes here and link this model to the observed treatment history in Section 3. Because the parameter θ describes the relationship between the distribution of potential outcomes, it has a causal interpretation. We parameterize (1) such that γ_t{z, X̄* (t), Q; 0} = z; therefore, a p-dimensional test of θ = 0 is a test of no effect.

A common transformation model used in survival analysis and one that we will consider extensively, is the scale accelerated failure time model given by

$${\gamma }_t\{z,{\overline{X}}^{\ast }(t),Q;\theta \}=zexp\{{\theta }_0+{\theta }_1^T{\overline{X}}^{\ast }(t)+{\theta }_2^{T}Q+{\theta }_3^T{\overline{X}}^{\ast }(t)Q\}.$$ (2)

In (2), the residual lifetime can be increased or decreased proportionately as a function of covariate history and organ characteristics, where X̄*(t)Q denotes any interaction between X̄*(t) and Q. If ${\theta }_0+{\theta }_1^T{\overline{X}}^{\ast }(t)+{\theta }_2^{T}Q+{\theta }_3^T{\overline{X}}^{\ast }(t)Q$ is negative, then transplantation increases lifespan for those values of the time-dependent covariates and donor characteristics.

To estimate the parameters in the SNFTM, we observe a random sample of n patients listed for organ transplantation at calendar times o₁,…,o_n and a sample of m organs that are transplanted at times s₁,…,s_m with characteristics q₁,…,q_m, respectively. For our analysis, we will always condition on these quantities but will suppress the notation for convenience. Define t_ij = s_j− o_i, the time since the ith patient entered the waitlist until the jth organ transplant for all (i, j) such that s_j− o_i ≥ 0. For each organ j = 1,…, m, we let A_ij be the indicator for whether or not the ith patient received the organ. Define Y_ij as the indicator for whether or not the ith patient is at risk, i.e., currently active on the waitlist, to receive the jth organ. Let T_i and U_i be the observed time from listing until patient i dies and is transplanted, respectively; if the patient is never transplanted, we let U_i= ∞ by convention. Thus, U_i= t_ij if A_ij= 1, and U_i = ∞ if A_ij′ = 0 for all j′ = 1,…,m. Note that if Y_ij= 1 then o_i ≤ s_j, t_ij ≤ U_i and t_ij ≤T_i. However, the converse is not true because patients may be removed from the waitlist. For now, we will assume that the survival time is observed for all subjects and consider censored event times in Section 4. Let $Q_i=\sum _{j=1}^m{A}_{ij}{q}_j$ be the characteristics of the organ the ith person actually receives. The history of the observed covariate process through time t is denoted by X̄_i(t); the covariate process is collected until min (U_i,T_i). To obtain valid inference, X̄(t); and Q must contain at a minimum all covariates and organ characteristics that influence the likelihood of receiving an organ and are prognostic. Note that A_ij, Y_ij, T_i, U_i, Q_i, and X̄{min(U_i,T_i)} are all observed for all i = 1,…, n and j = 1,…, m. We make the consistency assumption (C) that observed random variables equal the potential outcomes for the treatments received, i.e., $T_i=T_i^{\ast }(\infty )I(U_i=\infty )+T_i^{\ast }(U_i,Q_i)I(U_i<\infty )$ and ${\overline{X}}_i\{min(U_i,T_i)\}={\overline{X}}_i^{\ast }[min\{U_i,T_i^{\ast }(\infty )\}]$.

To succinctly index all available information just prior to the allocation of the jth organ, we define the filtration ${\mathcal{F}}_i=[{\{A_{il},Y_{il},Y_{il}{\overline{X}}_i(t_{il})\}}_{l=1,\dots ,j-1},Y_{ij},Y_{ij}{\overline{X}}_i(t_{ij})]$. We assume that given _j, the probability that the ith subject receives the jth organ is proportional to the propensity score $\alpha \{t_{ij},{\overline{X}}_i(t_{ij}),q_j;\phi \}$, which may depend on a vector of parameters φ, so that

$$P(A_{ij}=1|{\mathcal{F}}_j;\phi )=\frac{\alpha \{t_{ij},{\overline{X}}_i(t_{ij}),q_i;\phi \}{Y}_{ij}}{{\sum }_{k=1}^n\alpha \{t_{kj},{\overline{X}}_k(t_{kj}),q_j;\phi \}{Y}_{kj}}={\pi }_{ij}({\mathcal{F}}_j;\phi ).$$ (3)

Because the propensity must be non-negative, a natural form for α(·) would be an exponentiated linear combination of covaraites collected prior to s_j and organ characteristics. Each time an organ becomes available, the OPTN determines an ordered list of patients to whom the organ will be offered. In spite of the deterministic manner in which procured organs are offered to patients, we argue that the stochastic model (3) is reasonable. Because the “turndown” rate of available organs is high and the ordering of patients on the waitlist depends on factors not related to prognosis, comparatively healthy patients, though less likely, do receive the available organ and organ allocation can be viewed as stochastic. We discuss the merits of model (3) and other models for organ allocation in Web Appendix A.

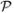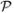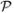We assume sequential ignorability (SI); the probability of receiving an organ at any time depends only on the observed data up until that time and not additionally on any potential outcomes. This implies P(A_ij= 1| _j, ; φ) = P(A_ij= 1| _j; φ), where = ( ₁,…, _n).

To aid the reader, we have included a chart in Web Appendix A that summarizes the notation for the observed and potential outcome data.

3. Class of Estimators

We define the transformed lifetime as T˜_i(θ) = I(U_i<∞)[U_i+γ_Ui{T_i−U_i, X̄_i(U_i), Q_i; θ}]+I(U_i=∞)T_i and the transformed residual lifetime at the time of the jth organ (for patients at risk for the jth organ) as R˜_ij(θ)=T˜_i(θ)−t_ij. Let h_ij{R˜_ij(θ), _j} be a p-dimensional vector that only depends on R˜_ij(θ) and _j and not on any other function of the observed survival or future covariates. We consider the class of estimators for θ given by the solution to

$$\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{{\stackrel{\sim }{R}}_{ij}(\theta ),{\mathcal{F}}_j\}=0.$$ (4)

Subsequently, we show that all estimators in this class are consistent and asymptotically normal regardless of the choice of the p-dimensional vector h_ij(·) so long as we have correctly specified π_ij( _j;φ). A discussion of how to choose h_ij(·) in practice is given at the end of the Section and in Web Appendix B. The estimators in this class are semiparametric in the sense that we have only assumed that we have correctly specified the probability of receiving a transplanted organ in (3) and the transformation model given in (1), but have not made any distributional assumptions on the survival outcomes or the time-dependent covariates.

We emphasize that θ characterizes the relationship between distributions of potential outcomes; we relate the joint distribution of observed data and potential outcomes in the following Theorem. We give the proof in Web Appendix B.

Theorem 1

Under the C and SI assumptions described in Section 2, ${(U_i,{\stackrel{\sim }{T}}_i({\theta }_0),{\overline{X}}_i[min\{U_i,{\stackrel{\sim }{T}}_i({\theta }_0)\}],Q_i)}_{i=1,\dots ,n}\stackrel{d}{=}{(U_i,T_i^{\ast }(\infty ),{\overline{X}}_i^{\ast }[min\{U_i,T_i^{\ast }(\infty )\}],Q_i)}_{i=1,\dots ,n},$ where θ₀ is the true value of the parameter in the transformation model given in (1) and $A\stackrel{d}{=}B$ means that the joint distribution of the random vector A is the same as the joint distribution of B.

If we let $R_{ij}^{\ast }(\infty )=R_{i,t_{ij}}^{\ast }(\infty ),$ the residual lifetime for the ith patient after the jth transplant had the patient never been transplanted, then Theorem 1 implies that

$$\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{{\stackrel{\sim }{R}}_{ij}({\theta }_0),{\mathcal{F}}_j\}\stackrel{d}{=}\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}.$$ (5)

Substituting the observed transformed residual lifetime for the (potential) residual lifetime had the patient never been transplanted allows us to derive the asymptotic properties of the estimating function evaluated at θ = θ₀.

If we have correctly specified the model for the organ allocation in (3),

$$\begin{array}{l}\mathrm{E}[\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_i\}]\hfill \\ =\mathrm{E}(\sum _{i=1}^n[\mathrm{E}\{A_{ij|}|{\mathcal{F}}_i,\mathcal{P}\}-{\pi }_{ij}({\mathcal{F}}_j;\phi )]h_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_i\})=0,\hfill \end{array}$$

where the sequential ignorability (SI) assumption gives E {A_ij| _j, } = π_ij( _j;φ).

Because if one patient receives an organ everyone else on the waitlist necessarily does not, A_ij is not independent of A_i′j. Therefore, we cannot use a Central Limit Theorem for independent data to argue that, as n → ∞, $n^{-1/2}\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}$ converges in distribution to a mean-zero normal random variable.

However, the sequence $M_k=\sum _{j=1}^k\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}$, k = 1,…, m is adapted to the filtration ( _k+1, 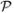). Furthermore, we showed above that $\mathrm{E}(M_k-M_{k-1}|{\mathcal{F}}_k,\mathcal{P})=\mathrm{E}[\sum _{i=1}^n\{A_{ik}-{\pi }_{ik}({\mathcal{F}}_k;\phi )\}{h}_{ik}\{R_{ik}^{\ast }(\infty ),{\mathcal{F}}_k\}|{\mathcal{F}}_k,\mathcal{P}]=0$. Thus, M_k, k = 1,…,m is a mean-zero Martingale sequence. By the Martingale Central Limit Theorem (DasGupta, 2008) and under the regularity conditions given in Web Appendix B, as m→ ∞,

$$\begin{array}{l}{m}^{-1/2}{B}_m^{-1/2}\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{{\stackrel{\sim }{R}}_{ij}({\theta }_0),{\mathcal{F}}_j\}\hfill \\ \stackrel{d}{=}{m}^{-1/2}{B}_m^{-1/2}\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}\stackrel{d}{\to }N(0,I),\hfill \end{array}$$

Where $B_m=m^{-1}\sum _{j=1}^{m}var[\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}|{\mathcal{F}}_j,\mathcal{P}]$, I is the p × p identity matrix, and $C_m\underrightarrow{d}N(0,I)$ implies the random vector C_m converges in distribution to a standard normal. We note that A_j= (A_1j,…, A_nj)^T ∽ multinomial[π_j= {π_1j( _j, φ),…, π_nj( _j, φ)}^T], so var(A_j| _j, 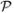= var(A_j| _j) = diag(π_j) − π_jπ_j^T. Writing h_ij= h_ij{R˜_ij(θ₀), _j} and π_ij= π_ij( _j; φ) for brevity, then B_m is given by

$$B_{m=}\frac{1}{m}\sum _{j=1}^m\{\sum _{i=1}^n{h}_{ij}{\pi }_{ij}{h}_{ij}^T-(\sum _{i=1}^n{h}_{ij}{\pi }_{ij}\left){\left(\sum _{i=1}^n{h}_{ij}{\pi }_{ij}\right)}^T\right\}.$$

Therefore, under the SI and C assumptions and also assuming that (3) is correctly specified, $m^{1/2}{V}_m^{-1/2}(\widehat{\theta }-{\theta }_0)\underrightarrow{d}N(0,I)$, where $V_m^{-1/2}=B_m^{-1/2}{A}_m$ and $A_m=m^{-1}\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j)\}\partial /\partial {\theta }^T[h_{ij}\{{\stackrel{\sim }{R}}_{ij}({\theta }_0),{\mathcal{F}}_j\}]$. Technical details as well as the proof θ̂ converges in probability to θ₀ are given in Web Appendix B. Although we have proven the asymptotic properties of θ̂ under the assumption that m, the number of transplantations, tends to infinity, this does not imply n, the number of patients we observe in the sample, remains constant. A regularity condition given in Web Appendix B is that there must be more than one patient at risk for each organ that is transplanted. In practicality, there are hundreds of patients available at each transplant for all solid organs in the United States. This assumption implies that n > m; and, therefore, as m→∞, n must also grow on at least the same order.

While the solution to the estimating equation in (4) is asymptotically normal regardless of the choice of h_ij(·), the choice of this p-dimensional vector does affect the asymptotic variance. The optimal h_ij(·), the p-dimensional vector that minimizes the asymptotic variance, and choices that are reasonably efficient require us to know the distribution of $R_{ij}^{\ast }(\infty )|{\overline{X}}_i(t_{ij})$. While knowledge of this distribution is unrealistic, we could posit some distribution for $R_{ij}^{\ast }(\infty )|{\overline{X}}_i(t_{ij})$ in hopes that if we correctly specify the distribution, or are reasonably close, we can gain efficiency. Let $X_i^{\prime }(t_{ij})$ be some vector-valued function of X̄_i(t_ij) and assume that the transformation model is the scale accelerated failure time model such that $\gamma t_{ij}\{z,\overline{X}(t_{ij}),Q;\theta \}=zexp\{{\theta }^T{X}_i^{\prime }(t_{ij})\}$. If we posit that $R_{ij}^{\ast }(\infty )|{\overline{X}}_i(t_{ij})$ follows an exponential distribution with rate parameter exp{λ ( _j)}, a reasonable approximation for the residual lifetime of patients awaiting transplant, then we argue in Web Appendix B that an estimator that is reasonably efficient is given by the solution to

$$\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}[1-exp\{\lambda ({\mathcal{F}}_j)\}{\stackrel{\sim }{R}}_{ij}(\theta )]X_i^{\prime }(t_{ij})=0.$$ (6)

Web Appendix B gives a general framework for choosing h_ij for other transformation models and posited conditional densities for $R_{ij}^{\ast }(\infty )$. We argue in Web Appendix B that if $\mathrm{E}[h_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}|{\mathcal{F}}_j]=0$ then the estimator solving (4) is consistent even if we misspecify the model for π_ij( _j; φ) and is “doubly robust” as we need only correctly specify π_ij( _j; φ) or specify h_ij so that $\mathrm{E}[h_{ij}\{R_{ij}^{\ast }(\infty ),{\mathcal{F}}_j\}|{\mathcal{F}}_j]=0$ for the estimator to be consistent (Lunce-ford and Davidian, 2004). However, we note that specifying a sequence of distributions for $R_{ij}^{\ast }(\infty )|{\mathcal{F}}_j$ across all j that is consistent with a common data generating mechanism is practically infeasible except in trivial situations. Thus, we would expect the estimator given by the solution to (6) to be only approximately doubly robust.

The above discussion has derived a class of estimators for θ, the parameter in the transformation model (1), under the assumption that φ is known. To estimate φ, we could use the maximizer of the partial likelihood $\prod _{j=1}^m\prod _{i=1}^n{\{{\pi }_{ij}({\mathcal{F}}_j;\phi )\}}^{A_{ij}}$. Or equivalently we could solve for the root of the score of the partial likelihood, that is, the solution to

$$0=\sum _{j=1}^m\sum _{i=1}^n{A}_{ij}\frac{1}{{\pi }_{ij}({\mathcal{F}}_j;\phi )}\frac{\partial }{\partial \phi }{\pi }_{ij}({\mathcal{F}}_i;\phi )=\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}\frac{1}{{\pi }_{ij}({\mathcal{F}}_j;\phi )}\frac{\partial }{\partial \phi }{\pi }_{ij}({\mathcal{F}}_j;\phi ),$$ (7)

where we define 0/0 = 0 and the last equality follows from $\sum _{i=1}^n{\pi }_{ij}({\mathcal{F}}_j;\phi )=1$ for all j and φ, so $\sum _{i=1}^n\partial /\partial \phi \{{\pi }_{ij}({\mathcal{F}}_j;\phi )\}=0$. To jointly estimate (θ^T, φ^T)^T, one could then jointly solve the (4) and (7). The sequence of estimating functions in (7) indexed by the number of organs is also a mean-zero Martingale sequence at the true value of φ, so the joint solution will also be asymptotically normal following the preceding proof.

In addition, we may not know λ ( _j) in (6) and may posit models such that λ( _j,ξ) is known up to a vector of parameters ξ, e.g., λ( _j,ξ) = ξ^TX_i(t_ij). In Web Appendix B, we argue that if the estimator for ξ is well-behaved, that is, m⁻¹/²(ξ̂ − ξ₀) = O_p(1), then the asymptotic variance of θ and φ does not depend on how ξ was estimated. We discuss estimators for ξ in Web Appendix B.

4. Censored Survival Times

In most studies involving a time-to-event outcome, the end of follow-up occurs before the failure time of all subjects is observed. Denote C_i as the time from listing until the end of study for the ith subject. Similar to T˜_i(θ), define the transformed follow-up time as C˜_i(θ) = I(U_i< ∞) [U_i+ γU_i{C_i − U_i, X̄_i(U_i), Q_i; θ}] + I(U_i= ∞)C_i and the transformed residual follow-up time for patients at risk for the jth organ C˜_ij(θ) = C˜_i(θ)—t_ij. The transformed residual follow-up depends on covariates collected after and treatment decisions at and after s_j. Therefore, if we replace h_ij{R˜_ij(θ), _j} in (4) with h_ij[I{R˜_ij(θ) < C˜_ij(θ)}, min{R˜_ij(θ), C˜_ij(θ)}, _j], then $M_k=\sum _{j=1}^k\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}[I\{R_{ij}^{\ast }(\infty )<{\stackrel{\sim }{C}}_{ij}(\theta )\}$ min{R*_ij(θ), C˜_ij(θ)}, _j], k = 1,…, m, is not adapted to the filtration ( _k+1, 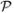) and does not have mean-zero increments. To obtain valid inference, we must consider a follow-up time that does not depend on future treatment (Robins et al., 1992; Joffe et al., 2012). Define the transformed artificial follow-up time, $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_i)$, for patient i at risk to receive the jth organ, as follows:

$$C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)=min[{\stackrel{\sim }{C}}_i(\theta )-t_{ij}:\overline{X}\{min(U,C_i)\},U,Q\in \mathbf{X}{\mathbf{U}}_{ij}]),$$ (8)

where XU_ij = (X̄{min(U, C_i)},U, Q : f[X̄{min(U, C_i)}, U, Q:f[X̄_i(t_ij), t_ij ≤ U] > 0) and f(•) is the conditional density of [X̄{min(U, C_i)}, U, Q] given {X̄(t_ij) = X̄_i(t_ij), t_ij≤ U}. Heuristically, $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ is the minimum value of transformed residual follow-up over all possible future covariate and treatment trajectories given _j. When the failure time may be administratively censored, we propose the class of estimators for θ given by the solution to

$$\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}({\mathrm{\Delta }}_{ij}(\theta ,{\mathcal{F}}_j),{\stackrel{\sim }{V}}_{ij}(\theta ,{\mathcal{F}}_j),{\mathcal{F}}_j\}=0,$$ (9)

where h_ij(·) is a p-dimensional vector that is a function only of, ${\mathrm{\Delta }}_{ij}(\theta ,{\mathcal{F}}_j)=I\{{\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$ the transformed failure indicator; ${\stackrel{\sim }{V}}_{ij}(\theta ,{\mathcal{F}}_j)=min\{{\stackrel{\sim }{R}}_{ij}(\theta ),C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$, the transformed residual observation time; and _j. Unlike ${\stackrel{\sim }{C}}_{ij}(\theta ),C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ is fixed given _j, so the sequence $\sum _{j=1}^k\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}{h}_{ij}\{{\mathrm{\Delta }}_{ij}({\theta }_0,{\mathcal{F}}_j),{\stackrel{\sim }{V}}_{ij}({\theta }_0,{\mathcal{F}}_j),{\mathcal{F}}_j\},k=1,\dots ,m$ has the same distribution as a mean-zero Martingale sequence adapted to ( _k+1, 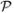) as in Section 3. The proof that all estimators in this class, when the failure time may be censored, are consistent and asymptotically normal is identical to the proof in Web Appendix B except $h_{ij}\{{\mathrm{\Delta }}_{ij}(\theta ,{\mathcal{F}}_j),{\stackrel{\sim }{V}}_{ij}(\theta ,{\mathcal{F}}_j),{\mathcal{F}}_j\}$ now replaces h_ij{R˜_ij(θ), _j}.

The natural extension of the proposed set of estimating equations (6) given in Section 3, where to gain efficiency we postulated $R_{ij}^{\ast }(\infty )|{\mathcal{F}}_j$ follows an exponential distribution with rate parameter exp{λ ( _j)} and assumed a scale accelerated failure time model, is given by

$$\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}\{{\mathrm{\Delta }}_{ij}(\theta ,{\mathcal{F}}_j)-exp\{\lambda ({\mathcal{F}}_j)\}{\stackrel{\sim }{V}}_{ij}(\theta ,\mathcal{F})\}{X}_i^{\prime }(t_{ij})=0.$$ (10)

We note that ${\rm E}[{\mathrm{\Delta }}_{ij}(\theta ,{\mathcal{F}}_j)-exp\{\lambda ({\mathcal{F}}_j)\}{\stackrel{\sim }{V}}_{ij}(\theta ,\mathcal{F})|{\mathcal{F}}_j]=0\text{if}{R}_{ij}^{\ast }(\infty )|{\mathcal{F}}_j$ is exponentially distributed. Thus, the proposed estimator is consistent even if we have misspecified π_ij( _j; φ) if we have correctly specified the distribution of $R_{ij}^{\ast }(\infty )|{\mathcal{F}}_j$ (doubly robust). However, as noted above, $R_{ij}^{\ast }(\infty )|{\mathcal{F}}_j$ likely only approximately follows an exponential distribution.

Because $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\le {\stackrel{\sim }{C}}_{ij}(\theta ),$ some subjects with observed failure times are “artificially” censored. The use of “artificial censoring” to obtain valid causal inference when the outcome may be censored remains problematic for two main reasons (Joffe et al., 2012). First, Δ_ij(θ, _j) is not continuous in θ, and V˜_ij(θ, _j) is non-smooth in θ. Therefore, the class of estimating functions in (9), including the one proposed in (10), need not be smooth or even monotone in θ. Traditional root finding algorithms, such as Newton methods, can be difficult to implement when the objective function is non-smooth and non-monotone in θ. Second, we necessarily lose information by “artificially” censoring some subjects. We build on the work of Joffe et al. (2012) and offer some solutions that mitigate these problems in our context.

To address the former, we consider “smooth” approximations to Δ_ij(θ, _j) and V˜_ij(θ, _j) which we denote as ${\mathrm{\Delta }}_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ and ${\stackrel{\sim }{V}}_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$, respectively. As long as the approximations are functions of Δ_ij(θ, _j) and V˜_ij(θ, _j) then the derived asymptotic theory is still valid. To obtain a smooth function of Δ_ij and V˜_ij we consider the following function,

$${\mathrm{\Delta }}_{ij}^{\ast }=\{\begin{array}{ll}1& \text{if}{\stackrel{\sim }{R}}_{ij}(\theta )\le \{C_{ij}^{\ast }(\theta )-\epsilon \}\\ -2/{\epsilon }^2{\left[{\stackrel{\sim }{R}}_{ij}(\theta )-\{C_{ij}^{\ast }(\theta )-\epsilon \}\right]}^2+1& \text{if}\{C_{ij}^{\ast }(\theta )-\epsilon \}\le {\stackrel{\sim }{R}}_{ij}(\theta )<\{C_{ij}^{\ast }(\theta )-\epsilon /2\}\\ 2/{\epsilon }^2{\{{\stackrel{\sim }{R}}_{ij}(\theta )-C_{ij}^{\ast }(\theta )\}}^2& \text{if}\{C_{ij}^{\ast }(\theta )-\epsilon /2\}\le {\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta )\\ 0& \text{if}{C}_{ij}^{\ast }(\theta )<{\stackrel{\sim }{R}}_{ij}(\theta )\end{array}$$ (11)

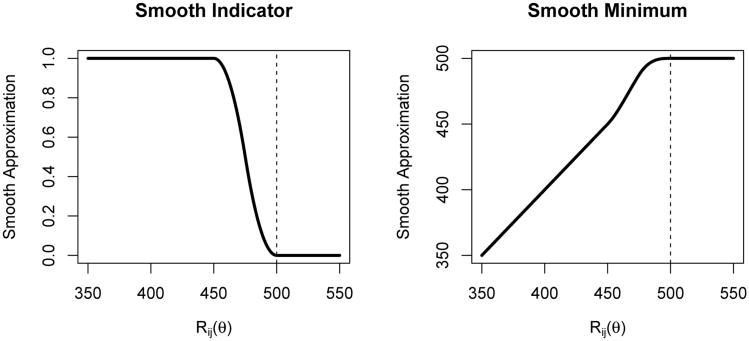
where ε > 0 controls the “smoothness.” We define ${\stackrel{\sim }{V}}_{ij}^{\ast }$ equal to min $\{{\stackrel{\sim }{R}}_{ij}-C_{ij}^{\ast },0\}{\mathrm{\Delta }}_{ij}^{\ast }+C_{ij}^{\ast }$. These functions, represented graphically in Figure 1, and their first derivatives are both continuous functions of R˜_ij(θ) everywhere. Therefore, ${\mathrm{\Delta }}_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ and ${\stackrel{\sim }{V}}_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ are smooth functions with respect to θ so that gradient-based root-finding algorithms may be applied. We note if a large value of ε is needed, there may be little information to estimate θ and estimating θ by finding the minimum of a scaled test statistics may have better convergence and mitigate bias due to misspecification of the structural model (see Joffe et al., 2012).

Figure 1.

Plot of ${\mathrm{\Delta }}_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ and ${\stackrel{\sim }{V}}_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ the “smooth” approximations to ${\mathrm{\Delta }}_{ij}(\theta ,{\mathcal{F}}_j)=I\{{\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$ and ${\stackrel{\sim }{V}}_{ij}(\theta ,{\mathcal{F}}_j)=min\{{\stackrel{\sim }{R}}_{ij}(\theta ),C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$, respectively, as a function of R˜_ij where $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)=500$ and ε = 50.

To address the problems related to the information lost from artificial censoring, we note that the set XU_ij may be very large, and, as a result, $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\ll {\stackrel{\sim }{C}}_{ij}(\theta )$. However, there may be a smaller set $\mathbf{X}{\mathbf{U}}_{ij}^{\ast }\subset \mathbf{X}{\mathbf{U}}_{ij}$ such that $\mathbf{X}{\mathbf{U}}_{ij}^{\ast }$ accounts for the vast majority of the conditional density, i.e. ${\int }_{\mathbf{X}{\mathbf{U}}_{ij}^{\ast }}f[\overline{X}\{min(U,C_i)\},U,Q|\overline{X_i}(t_{ij}),t_{ij}\le U]d\overline{X}\{min(U,C_i)\}\mathit{dU}\mathit{dQ}\approx 1$, but $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ defined using $\mathbf{X}{\mathbf{U}}_{ij}^{\ast }$ instead of XU_ij in (8) is much greater. The advantage of redefining $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ is that we increase the length of the artificial follow-up and the information to estimate θ. Unfortunately, C˜_ij(θ) may be less than the redefined $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)$ for a small number of (i, j) pairs. For those patients, we may not be able to evaluate $I\{{\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$ Therefore, we must come up with ad hoc expressions for Δ_ij and V˜_ij(θ) (and the corresponding “smooth” approximations) for those (i, j) pairs.

To make the discussion concrete, consider the motivating example of lung transplantation. The only time-dependent covariate considered is the lung allocation score (LAS). The LAS is a composite score, ranging from 0 to 100 and updated daily, of over a dozen patient characteristics that predict waitlist mortality and post-transplant survival. The LAS prioritizes patients for organ allocation with higher scores indicating that a patient is typically “sicker” and has a higher priority for transplantation. The LAS trajectory can change precipitously; thus, $\mathbf{X}{\mathbf{U}}_{ij}=[\overline{X}\{min(U,C_i)\},U,Q:X(t)=X_i(t)\text{if}t\le t_{ij},0\le X(t)\le 100\text{if}{t}_{ij}>,t_{ij}\le U_i]$. If we consider the scale accelerated failure time model given by ${\gamma }_{t_{ij}}\{z,{\overline{X}}^{\ast }(t_{ij}),Q;\theta \}=zexp({\theta }_0+{\theta }_1{\text{LAS}}_{ij}+{\theta }_2^T{x}_i)$, where x_i is a vector of time-independent patient characteristics, the above discussion suggests that the “artificial” follow-up time should be given by $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)=min({min}_{0\le y\le 100}[\{C_i-t_{ij}\}exp\{{\theta }_0+{\theta }_{1}y+{\theta }_2^T{x}_i\}],C_i-t_{ij})$.

If the benefit of transplantation on the multiplicative scale increases with increasing LAS, i.e., θ₁< 0, and there is a survival benefit for transplantation at the maximum LAS, then $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)=\{C_i-t_{ij}\}exp\{{\theta }_0+{\theta }_{1}max(\text{LAS})+{\theta }_2^T{x}_i\}$, where max(LAS) = 100. While some patients do experience precipitous increases in the LAS, most patients remain relatively stable while on the waitlist. We could increase the artificial follow-up time by considering the set $\mathbf{X}{\mathbf{U}}_{ij}^{\ast }=[\overline{X}\{min(U,C_i)\},U:X(t)=X_i(t)\text{if}t\le t_{ij},0\le X(t)\le \{X_i(t_{ij})+\delta \}\text{if}t>t_{ij},t_{ij}\le U]$ for some δ ≥ 0 rather than XU_ij in (8). This implies, if θ₁< 0,

$$C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)=min[(C_i-t_{ij})exp\{{\theta }_0+{\theta }_1({\text{LAS}}_{ij}+\delta )+{\theta }_2^T{x}_i\},C_i-t_{ij}].$$ (12)

While using the smaller set $\mathbf{X}{\mathbf{U}}_{ij}^{\ast }$ increases the artificial follow-up time, we may not be able to evaluate $I\{{\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$ because C˜_ij(θ) may be less than $C_{ij}^{\ast }(\theta ,{\mathcal{F}}_i)$ for some (i, j) pairs. However, we could consider replacing R˜_ij(θ) with min R˜_ij(θ), C˜_ij(θ) in the expressions for Δ_ij and V˜_ij and the “smooth” approximations of those functions. For those patients who are observed to fail or for whom $C_{ij}^{\ast }\le {\stackrel{\sim }{C}}_{ij}$, Δ_ij and V˜_ij are defined as before. Among those patients whose survival times are censored and for whom ${\stackrel{\sim }{C}}_{ij}<C_{ij}^{\ast },{\mathrm{\Delta }}_{ij}=I\{{\stackrel{\sim }{C}}_{ij}<C_{ij}^{\ast }=1\}$ and ${\stackrel{\sim }{V}}_{ij}=min\{{\stackrel{\sim }{C}}_{ij},C_{ij}^{\ast }\}={\stackrel{\sim }{C}}_{ij}(\theta )$. This introduces some bias in the estimating function given in (10), as Δ_ij and V˜_ij(θ) are no longer only functions of R˜_ij and $C_{ij}^{\ast }$. We argue in Web Appendix C that the choice of ${\mathrm{\Delta }}_{ij}^{\ast }$ and ${\stackrel{\sim }{V}}_{ij}^{\ast }$ described above will mitigate some of the problems. We note an ongoing question is how best to chose δ. Different approaches for mitigating the loss of information associated with artificial censoring are also discussed in Web Appendix C.

5. Simulation Study

To evaluate the performance of our proposed class of estimators and methods for handling censored survival responses, we report on simulations designed to resemble the UNOS cohort described in Section 6. From the UNOS cohort, 2,000 patients were randomly selected and their listing dates, observed LAS history, and death dates if they were not transplanted were recorded. Listing dates ranged from May 4, 2005 to December 31, 2010. For the transplanted patients in UNOS cohort, we simulated their residual history had they never been transplanted by assuming the residual lifetime follows an exponential distribution with parameter depending on transplant LAS and generating a monotonically increasing residual LAS trajectory. Additional details are included in Web Appendix C.

We selected dates for 1,250 organs by drawing days without replacement from May 4, 2005 until December 31, 2010. Define LAS_ij as the LAS score for the ith patient at the jth organ transplant. Let z_ij be LAS_ij truncated from below at 30 and from above at 70. We assigned the first available organ to a patient with propensity $\alpha \{t_{i1},{\overline{X}}_i(t_{i1}),q_i\}{Y}_{i1}=exp\{{\phi }_1{\text{LAS}}_{i1}+{\phi }_{2}max({\text{LAS}}_{i1}-40,0)\}{Y}_{i1}$, where Φ₁= 0.20 and Φ₂= –0.1625. For the patient selected to receive the organ, we transformed the residual lifetime according the scale accelerated failure time model $T_i-t_{i1}=R_{i1}^{\ast }(\infty )$ exp{θ₀ + θ₁(z_i1− 30)}, where θ₀ = −0.1 and θ₁ = −0.05. We then repeated the process of assigning organs among eligible subjects and then transforming the residual lifetime for the transplanted patient. The end of follow-up was December 31, 2010 and survival times were censored at that date. We note that we kept the same listing dates, transplant dates, and LAS history in each of the 1,000 Monte Carlo simulations as we considered these quantities fixed in Section 2.

Estimators for (θ^T, φ^T)^T considered were solutions to the set of estimating equations taking the same general form

$$\begin{array}{l}\sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}\{{{\rm E}}_{ij}(\theta )-exp({\xi }^T{X}_{ij}^{″})S_{ij}(\theta )\}{X}_{ij}^{\prime }=0,\hfill \\ \sum _{j=1}^m\sum _{i=1}^n\{A_{ij}-{\pi }_{ij}({\mathcal{F}}_j;\phi )\}\frac{1}{{\pi }_{ij}({\mathcal{F}}_j;\phi )}\frac{\partial }{\partial \phi }{\pi }_{ij}({\mathcal{F}}_j;\phi )=0,\hfill \end{array}$$ (13)

where $X_{ij}^{\prime }={(1,z_{ij})}^T$, and $X_{ij}^{″}$ is the restricted cubic spline transformation of LAS_ij with knots at 32, 36, 45, and 85. In all cases, we obtained estimates of ξ by solving the set of estimating equations proposed in Web Appendix B.

The following estimators for θ were considered.

1. Full artificial censoring (fac): Define $C_{ij}^{\ast }=(C_i-t_{ij})exp[{\theta }_0+{\theta }_1\{max(z_{ij})-30\}]$. Let ${\mathrm{E}}_{ij}={\mathrm{\Delta }}_{ij}^{\ast }$ and $S_{ij}={\stackrel{\sim }{V}}_{ij}^{\ast }$ using the above $C_{ij}^{\ast }$. This estimator is asymptotically unbiased.

2. Minimize artificial censoring (ac+δ): Define $C_{ij}^{\ast }=(C_i-t_{ij})exp\{{\theta }_0+{\theta }_1(z_{ij}+\delta -30)\}$. Because ${\stackrel{\sim }{C}}_{ij}<C_{ij}^{\ast }$ for a small number of (i, j) pairs, we replace R˜_ij(θ) with min {R˜_ij(θ), C˜_ij(θ), as suggested in Section 4, in the definition of Δ_ij and ${\stackrel{\sim }{V}}_{ij}^{\ast }$ and the “smooth” approximations of those functions. Define ${\mathrm{E}}_{ij}={\mathrm{\Delta }}_{ij}^{\ast }$ and $S_{ij}={\stackrel{\sim }{V}}_{ij}^{\ast }$.

3. Ignore need for artificial censoring (ic): Consider an estimator that does not use any artificial censoring. Define E_ij and S_ij as the observed failure indicator and the observed minimum of transformed residual follow-up and survival.

In addition, we considered other estimators using standard causal approaches. Instead of j indexing the organ, we let j index the week since the patient was listed on the waitlist, so that π_ij is now the probability that the ith patient is transplanted during the jth week after listing. We estimated π_ij using a logistic regression model with covariates for LAS_ij including a linear spline with knot point at 40 and a restricted cubic spline transformation of week from listing. We considered the same estimators for θ as in bullet points (1) or (2) above and denote these estimators as fac_alt and ac_alt+δ. To obtain the asymptotic variance, we assumed that observations across different subjects i were independent. This analysis is typical of those proposed in applications of structural nested failure time models but ignores that observations are correlated across subjects.

We note that the definition of the artificial follow-up implicitly assumes that θ̂₁ and θ̂₀ + θ̂₁{min(z_ij) + δ − 30} are both negative, which was always true in the datasets considered in this simulation. We considered δ equal to 20, 10, and 5. The smooth approximations to the indicator and minimum functions given by (11) had ε equal to 50 days. The algorithm used to generate starting values to solve the estimating function using Newton methods is described Web Appendix C.

The results for the estimates of θ₁, the change in the log acceleration factor per unit increase in the LAS, are given in Table 1. Convergent solutions were found for greater than 99.9 percent of all datasets. Using the observed failure indicator and observed follow-up time (ic estimator), results in highly biased and inefficient estimators. The estimators that index time from when the person entered the waitlist and do not account for the dependence in the organ allocation (fac_alt and ac_alt+δ estimators) are all highly biased and lead to poor coverage probability of Wald-type confidence intervals. Even though the full artificial censoring estimator is consistent and asymptotically normal, at this sample sizes the estimator has a slightly skewed distribution which led to a small amount of bias. The bias decreases as the number of organs in the sample increased from 1,250 to 2,500 (results reported in Web Appendix C). The amount of information lost due to artificial censoring for this estimator is extensive, with the follow-up time on the “non-transplant” scale decreased on average by more than a factor of eight. Given the maximum follow-up is 5.66 years, it is not surprising that the sampling distribution for this estimator is not symmetric at this sample size. For the proposed method of minimizing the effects of artificial censoring, there is a clear bias variance trade-off. As we consider smaller values of δ, we necessarily increase the “artificial” follow-up time and the variance of the estimator decreases. However, at the same time the proportion of (i, j) pairs where we cannot evaluatey $I\{{\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$ increases, and the asymptotic bias increases as we consider ad hoc approaches for the failure indicator. The mean square error is minimized when δ was chosen to be either 10 or 5 across different simulation scenarios. The smaller bias in the estimator when δ = 10 results in 95 percent Wald-type confidence intervals that more closely attained their nominal coverage than when δ = 5. When δ = 20, the mean square error for these methods is typically greatest compared to the other values of δ considered, and the small skewness in the sampling distribution of the estimator results in Wald-type confidence intervals that typically fall short of nominal coverage. Additional simulation results are reported in Web Appendix C.

Table 1.

Summary of the parameter estimates for θ₁ by estimator from 1000 Mote Carlo simulations when the number of organs allocated was 1,250. Converge: Proportion of MC datasets the estimator converged; MC mean: Monte Carlo average of the parameter estimates; MC SD: Monte Carlo standard deviation of the parameter estimates; Avg SE: Average of the standard error estimates of the parameters; Ratio Avg SE/SD: Ratio of the average of the standard error estimates to the standard deviation of the parameter estimates; Ratio MSE: Ratio of the average squared error of the fac estimates to the average squared error of the estimates of the given estimator; CP: Monte Carlo coverage probability of 95 percent Wald-type confidence intervals. Approximate standard errors for the values in the column MC Mean ranged from 0.00021 to 0.00037, the column MC SD ranged from 0.00015 to 0.00026, the column Avg SE ranged from 0.00019 to 5e-04, the column Ratio Avg SE/SD ranged from 0.045 to 0.045, the column Ratio MSE ranged from 0.028 to 0.33, the column CP ranged from 0.0036 to 0.012.

	Converge	MC Mean	MC SD	Avg SE	Ratio Avg SE/SD	Ratio MSE	CP
fac	0.999	−0.0515	0.0117	0.0116	1.00	1.00	0.874
ac+20	0.999	−0.0504	0.0114	0.0098	0.86	1.07	0.927
ac+10	0.999	−0.0490	0.0082	0.0085	1.04	2.02	0.956
ac+05	0.999	−0.0477	0.0079	0.0081	1.03	2.06	0.954
ic	1.000	−0.0583	0.0093	0.0157	1.68	0.89	0.987
fac_alt	0.999	−0.0586	0.0110	0.0099	0.90	0.71	0.809
ac_alt+20	1.000	−0.0569	0.0085	0.0078	0.92	1.16	0.851
ac_alt+10	1.000	−0.0553	0.0073	0.0065	0.89	1.71	0.831
ac_alt+05	1.000	−0.0543	0.0067	0.0060	0.89	2.20	0.845

6. Application to UNOS Data

To assess the causal effect of lung transplantation, we use data from UNOS, which compiles data on all waitlist candidates and transplants in the United States. For our analysis, we consider all patients that were actively waiting for a lung transplantation at some point from May 4, 2005, the beginning of the LAS era, until December 31, 2010. We exclude patients waiting for multi-organ transplantation. Because organs are allocated differently for pediatric patients, we limit our analysis to those patients that were 18 years of age or older at listing. For patients that were lost to follow-up after transplantation or were removed from the waitlist prior to transplantation or death, death dates were ascertained using the Social Security Death Master File (SSDMF). Because the SSDMF contains limited data on non-United States citizens, we restrict our analysis to United States citizens. End of follow-up for this study is December 31, 2010. Although rare, some patients are re-transplanted in the study period. To avoid an overly optimistic assessment of transplantation by including the effects of a second procedure and to be consistent with prior clinical analyses, we use time to graft failure, defined as patient death or time of re-transplantation, as the endpoint.

A total of 12,637 listings and 8,222 organ transplants are included in our analysis. For the purposes of computing the LAS, native diseases are divided into four groups: A (primarily COPD), B (primarily pulmonary hypertension), C (primarily CF), and D (primarily IPF). Most patients in this cohort have native diseases that fall into groups A (36.9 percent) and D (45.9 percent) with smaller numbers in groups B (5.3 percent) and C (11.9 percent). Of those patients who never went on to be transplanted, 1,740 were observed to fail during the study period. Of the 8,222 patients transplanted, 2,509 died during the study period.

Most patients awaiting a lung transplant have an LAS between 30 and 40 (median: 33.8, Q1-Q3: 32.1-37.4). Very few patients have an LAS greater than 60 on the waitlist because these patients tend to die or to be transplanted quickly. The distribution of the LAS at transplantation remains skewed to the right although less skewed than the waitlist LAS (median: 38.9, Q1-Q3: 34.3-47.4).

Kaplan-Meier survival curves for patients once they entered the waitlist and once they were transplanted by the initial and transplanted LAS, respectively, are plotted in Web Figure 2. The waitlist survival was censored at the time the patient was transplanted. This crude analysis suggests that the benefit of transplantation increases with increasing LAS and that transplantation may not be effective for patients with low LAS.

Figure 2.

Logarithm of the estimated scale acceleration factor in the transformation model for the causal effect of lung transplantation in Group A (primarily COPD, left) and Group D (primarily IPF, right) by LAS and transplantation type. The curves here are drawn for patients under 60 years of age, not in UNOS regions 6-8, and not paying for the transplant through private insurance or Medicare. We emphasize that negative (positive) values of the log scale factor suggest that transplantation increases (decreases) lifespan. The histogram in the background gives the number of patients transplanted for that range of LAS and native disease group. This figure appears in color in the electronic version of this article.

We considered a model for the propensity to receive a transplant that is an exponentiated linear combination of covariates as in the simulation. Covariates included in the model were current LAS, native disease group, anticipated payment method (private insurance, Medicare, and other public funding including Medicaid), age, UNOS region, LAS by transplant type (bilateral and unilateral) interaction, and native disease by transplant type interaction. We considered a restricted cubic spline transformation of LAS with knot points at 32, 36, 43, and 85 to allow the log propensity to vary nonlinearly with LAS.

To model the effect of transplantation, we used a scale accelerated failure time model, similar to (2), with covariates for current LAS, age, UNOS region, payment method, and native disease. We considered UNOS region as a binary variable (indicator for Regions 6-8 which include the Northwest and Midwest states) as those regions in preliminary analyses showed better post-transplant outcomes. We considered that in (2) LAS may have a different effect based on native disease (LAS by native disease group by transplant interaction). Within Group A, a linear spline with knot point at 40 was used to model the effect of LAS in the transformation model. For all other native disease groups, the relationship between LAS and the log acceleration factor was adequately modeled as linear. For native disease groups A (primarily COPD) and D (primarily IPF) we included a term for transplant type. For groups B and C, nearly all patients receive bilateral transplants. We truncated LAS from below at 30 and from above 70, as in the simulation study, due to small numbers of patients transplanted beyond these values.

We estimated the parameters in the organ propensity model and SNFTM by solving estimating equations as in (13) with ${\mathrm{E}}_{ij}={\mathrm{\Delta }}_{ij}^{\ast }$ and S_ij= V˜_ij. We parameterized $\lambda ({\mathcal{F}}_i)={\xi }^T{X}_{ij}^{″}$ and estimated ξ as is described in Web Appendix B. We defined the “artifical” follow-up time as in (12). In the simulation study both δ = 10 and δ = 5 performed well. We used δ = 5 + 0.5min{max(LAS_ij − 40,0), 10} in this application. For those (i, j) pairs where we cannot evaluate $I\{{\stackrel{\sim }{R}}_{ij}(\theta )<C_{ij}^{\ast }(\theta ,{\mathcal{F}}_j)\}$ we replace R˜_ij(θ) with min{R˜_ij(θ),C˜_ij(θ)}.

Estimates and corresponding standard errors for parameters in the transformation model are given in Table 2. We graphically represent how the scale acceleration factor varies by LAS and transplant type for patients in Group A and Group D in Figure 2. Parameter estimates for the organ allocation model are given in Web Appendix D. Across all native diseases, the benefit of transplantation on the multiplicative scale increases with increasing LAS. With the exception of group B which includes very few patients, transplantation offers a significant survival benefit for high allocation scores. Bilateral transplant confers a significantly greater survival benefit for patients with native diseases in group D but does not confer a significant advantage for patients in group A. For all patients in group A and patients in group D that receive a single lung transplant, transplantation confers a significant survival loss for patients with low LAS values, near 30. For the other native disease groups, transplantation does not show any significant survival gains or losses for low allocation scores. A large percentage of patients are transplanted at these LAS scores that show no significant survival benefit or even significant survival loss. Patients who intended to pay for the transplantation procedure using private insurance have significantly better survival benefit compared to those patients that intend to pay for transplantation using public funds. Patient’s age and geographic region do not significantly affect survival benefit. Web Appendix D contains additional information on this analysis including diagnostics of the adequacy of the proposed transformation model and non-parametric estimates of the survival distribution.

Table 2.

Parameter estimates of the scale accelerated failure time model. Group A: primarily COPD; Group B: primarily pulmonary hypertension; Group C: primarily CF; Group D: primarily IPF; Single LTx: single lung transplantation. The reference for Private Insurance and Medicare Insurance is Medicaid or other public funding for payment. LAS has been centered at 30 so the interpretation of the intercept term in log acceleration factor at an LAS of 30.

Parameter	Estimate	Std. Error
Group A Intercept	1.077	0.229
Group A (LAS-30)	−0.193	0.035
Group A max(LAS-40,0)	0.143	0.042
Group A Single LTx	0.059	0.133
Group B Intercept	0.139	0.312
Group B (LAS-30)	−0.029	0.066
Group C Intercept	0.055	0.152
Group C (LAS-30)	−0.094	0.008
Group D Intercept	0.007	0.123
Group D (LAS-30)	−0.064	0.004
Group D Single LTx	0.277	0.088
Age ≥ 60 at Listing	−0.014	0.117
Private Insurance	−0.358	0.109
Medicare Insurance	−0.150	0.124
UNOS Regions 6-8	−0.027	0.104

7. Discussion

We have proposed a method to evaluate the causal effect of organ transplantation on the distribution of residual lifetime. Our method conceptualizes each organ transplant as a non-randomized trial where one person receives treatment (transplantation) and the remaining people on the waitlist do not. This approach is similar to the methods of Hernán et al. (2008), to assess the effect of hormone replacement therapy on time to coronary heart disease, and Schaubel et al. (2009), to evaluate the effect of liver transplantation on survival. Although conceptually similar, our work differs in some key dimensions. Both Schaubel et al. (2009) and Hernán et al. (2008) use a Cox proportional hazards model to assess the effect of treatment as opposed to the accelerated failure time model we propose. Within a given “experiment,” Schaubel et al. (2009) and Hernán et al. (2008) must censor patients when they “cross-over” from one treatment group to another and then weight the uncensored patients by the inverse probability that they would “cross-over.” In the context of organ transplantation, “crossing-over” occurs anytime a patient moves from the waitlist group to the post-transplant group. This censoring necessarily leads to a loss of information, and inverse weighting can lead to unstable estimators. On the other hand, our approach uses G-estimation, which requires artificially censoring subjects to obtain valid inference. Importantly, we derive the asymptotic properties of our estimator as the number of “experiments” tends to infinity, which the prior work does not. Indeed, Schaubel et al. (2009) does not propose large sample inference and uses the bootstrap to obtain approximate standard errors of the regression parameters.

In modeling the effect of lung transplantation, we have assumed a scale accelerated failure time model. Although model diagnostics presented in Web Appendix D suggest that this model adequately represents the effect of transplantation, future research should examine other more flexible transformation models. In particular, a model that acknowledges that the increased risk surgical mortality soon after transplantation may be more appropriate.

Clinically, the results indicate that many patients are transplanted that show no statistically significant survival benefit. Given the large numbers of patients that die on the waitlist, this suggests that the waitlist order should further emphasize waitlist prognosis over geography or exact blood type match. However, survival is only one measure of patient well-being and future analysis could consider the causal effects of transplant on quality of life (Finlen Copeland et al., 2012).

This research has focused on the effect of the effect of transplantation as compared to never receiving a transplant. A related question that patients face is whether to receive a transplant now or wait until later to maximize survival. Deriving such an optimal transplantation regime is complicated by the fact that patients cannot be transplanted whenever they would like but instead must be offered an organ. Future work should examine this question.