Cortical Correspondence via Sulcal Curve-Constrained Spherical Registration with Application to Macaque Studies

Abstract

In this work, we present a novel cortical correspondence method with application to the macaque brain. The correspondence method is based on sulcal curve constraints on a spherical deformable registration using spherical harmonics to parameterize the spherical deformation. Starting from structural MR images, we first apply existing preprocessing steps: brain tissue segmentation using the Automatic Brain Classification tool (ABC), as well as cortical surface reconstruction and spherical parametrization of the cortical surface via Constrained Laplacian-based Automated Segmentation with Proximities (CLASP). Then, initial correspondence between two cortical surfaces is automatically determined by a curve labeling method using sulcal landmarks extracted along sulcal fundic regions. Since the initial correspondence is limited to sulcal regions, we use spherical harmonics to extrapolate and regularize this correspondence to the entire cortical surface. To further improve the correspondence, we compute a spherical registration that optimizes the spherical harmonic parameterized deformation using a metric that incorporates the error over the sulcal landmarks as well as the normalized cross correlation of sulcal depth maps over the whole cortical surface. For evaluation, a normal 18-months-old macaque brain (for both left and right hemispheres) was matched to a prior macaque brain template with 9 manually labeled, major sulcal curves. The results show successful registration using the proposed registration approach. Evaluation results for optimal parameter settings are presented as well.

1. INTRODUCTION

Neurodevelopmental neuroimaging studies are increasingly applied to primates as pathologies and environmental exposures can be studied in well-controlled settings and environment.^1–3 Non-human primates, in particular macaque monkeys, have been widely used for studies in the pathology of neurodevelopment since these animal models are closely related to those of humans. Specifically, childhood-onset mental illnesses require a full un- derstanding of developmental trajectories. Deeper insights into primate brain maturation are likely to capture missing human developmental trajectories especially at the early stage of postnatal development. Therefore, a key step in understanding neurodevelopment via neuroimaging studies is to establish correspondence between the human and the non-human primate cortex. Such cortical correspondence is a prerequisite to study cortical thickness or surface expansion.⁴ Cortical folding in non-human primates is less complex and its pattern varies significantly less across subjects than in humans, and thus primate brain analysis are a perfect application for an initial evaluation of novel brain correspondence methods. In this paper we propose a novel cortical correspondence method evaluated on macaque cortical data with the future goal to expand its use to the human and cross-species primate setting.

Since volume-based registration is limited to image intensities as features, better correspondence is established via registration on cortical surfaces that preserve geometry properties of the cortex.⁵ Moreover, the choice of stable features such as sulcal folding patterns across subjects is important for consistent correspondence. Several researchers proposed cortical registration via spherical mapping.^6–8 The work closest to the one presented here is the one by Park et al.,⁸ who proposed a surface registration method based on spherical thin-plate splines.

In their method, they map the entire cortical surface onto the unit sphere and employ thin-plate splines to parametrize the deformation field, as well as use sulcal constraint in the registration metric. Our work is similar to their framework in that we work on the unit sphere and employ similar sulcal constraints. In this work, however, we use the spherical harmonic basis function for correspondence extrapolation due to its convenient, global harmonic decomposition of the deformation field, which gives a globally regularized deformation field as a result. We evaluate registration performance of this method on a macaque brain using 9 major sulcal curves.

2. METHODS

2.1 Preprocessing

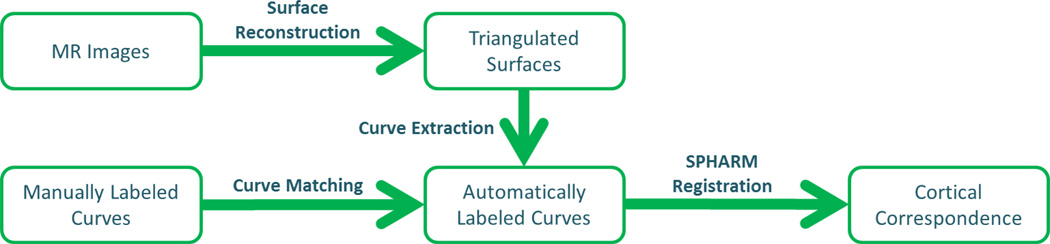
2.1.1 MR image acquisition and surface reconstruction

We used 18-months-old normal macaque brains imaged at the Yerkes Imaging Center (Emory University, GA). The subjects were scanned on a 3T Siemens Trio scanner with an 8-channel phase array trans-receiving volume coil using MPRAGE with GRAPPA optimized to a high resolution at 0.6×0.6×0.6 mm (TR = 3,000 ms, TE = 3.33ms, ip angle = 8°, matrix = 192×192). The raw MR images were registered into a standardized stereotaxic space using a linear transformation.⁹ The linear registered images were corrected for intensity nonuniformity resulting from inhomogeneities in the magnetic field.¹⁰ The Atlas-Based Classification tool (ABC)^{11, 12} was employed to the registered and corrected images to classify into white matter (WM), gray matter (GM), cerebrospinal fluid (CSF), and background. Processed tissue classification results were manually corrected if necessary and separated into left and right hemispheres for reconstructing two hemispheric cortical surfaces. The inner- and outer-surfaces were automatically extracted using the Constrained Laplacian-based Automated Segmentation with Proximities (CLASP) algorithm. We used the middle surface model for triangulated meshes with 40,962 vertices in the native space. Each vertex of the surface model was then homeomorphically transformed onto the common unit sphere using a deformable surface model.¹³

2.1.2 Automatic sulcal curve extraction and labeling

The cortical fundic regions of cortical surfaces are relatively robust to individual variability across subjects. Hence, the sulcal folding patterns of fundic regions are thought to be able to play a key role in surface registration. For a triangulated cortical surface, a sulcal curve on the surface can be defined by a set of points that are located along high-curvature fundic regions. We used automatic sulcal curve extraction¹⁴ and automatic curve labeling¹⁵ to extract a set of labeled sulcal curves. The unlabeled sulcal curves are extracted from the surface using an anisotropic geodesic distance map.¹⁴ Note that the extraction method delineates not only (possibly disconnected) major curves but also many minor curves that need to be eliminated. Since the labeling method uses manually labeled curves as reference for labeling, to collect a set of the reference curves in automatic sulcal labeling, experts label the automatically extracted curves: central (CS), arcuate (AR), principal (PR), superior temporal (STS), lunate (LU), cingulate (Cing), intraparietal (IP), occipito-parietal (OP), and sylvian (Syl) sulcus. These curves are less variable across subjects and therefore, can be used invariant features for correspondence. Given raw curves as input, the best matched sulcal curve is selected from the reference curves to label the corresponding curve in the subject, while discarding minor and extraneous curves.¹⁵ The point-by-point correspondence is automatically established by the labeling method as well.

2.2 Spherical Harmonics-based Deformation Field

Once the initial correspondence is determined by sulcal labeling, our goal is to find a deformation field between the two surfaces that extrapolates the landmark correspondence to the full surface, while also introducing a regularization. We first map all vertices of the cortical surfaces onto the common unit sphere. Note that the spherical mapping is provided during surface reconstruction, as well as the mapping does not establish an appropriate correspondence across the cortical surfaces from different subjects (see Fig. 5b and Fig. 6b). To find the deformation field that establishes such a correspondence, we compute displacements for all corresponding landmarks on the sphere and apply a linear fit via spherical harmonic decomposition of these displacements, which is then further optimized incorporating sulcal depth maps.

Figure 5.

Original cortical surface (a), spherical mapping with an initial deformation field following landmark fitting (b) and registration result following full optimization (c): red and blue areas illustrate sulcal fundic regions of subject and template cortical surfaces. Points on the sphere are sampled for visualization of the deformation field. A green line shows the arclength of displacement for a pair of corresponding landmarks.

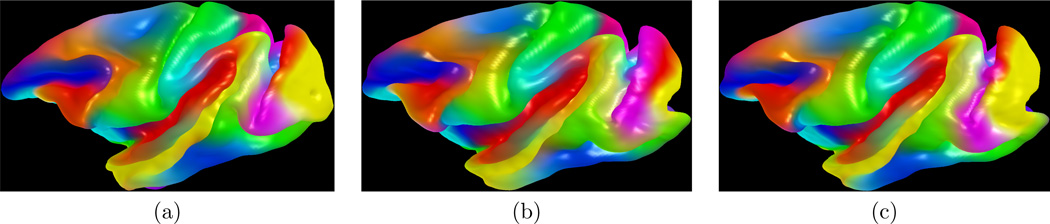
Figure 6.

Visual comparison of template (a), initial spherical mapping (b), and our method (c): the color map of the template is propagated to a subject surface via established correspondence. Our method shows better correspondence than initial spherical mapping.

2.2.1 Landmark displacement

After the spherical mapping, a displacement for two corresponding landmarks is measured from a curve. We convert all displacements into the polar coordinate system in order to take advantage of its convenient representation on the sphere. However, the angular difference in the conventional polar coordinate system still does not guarantee arclength preservation at every location; it can be easily observed that the angular difference is much larger nearby the poles than at the equator for the same amount of geodesic distance on the sphere. Therefore, we use a locally normalized polar system such that arclength is preserved. Let p and q be corresponding land-marks from template and subject, respectively. We first rotate these landmarks along the big circle (longitude circle) passing through the two poles in order that p is exactly located on the equator. Then, we compute two displacements (elevation Δθ and azimuth Δφ) between p and q after rotation, which ensures that the arclength ratio of displacement is preserved regardless of its location. Thus, the local landmark displacement at a point (θ_i; φ_i) on the unit sphere is represented as d_i = [Δθ_i;Δφ_i]^T after rotation to the equator.

2.2.2 Linear fitting for initial coefficient computation

Incorporating all displacements, we establish a straightforward linear system to determine the coefficients of the spherical harmonic representation of the Δθ and Δφ displacement field via spherical harmonic basis function up to a predetermined degree k.¹⁶ The coefficients that best fit to displacements are determined in a least-squares fitting manner. Specifically, at a point (θ; φ) on the sphere, the spherical harmonic basis functions with degree l and order m (−l ≤ m ≤ 1) are given by

$$Y_l^m(\theta ,\varphi )=\sqrt{\frac{2l+1}{4\pi }\frac{(l-m)!}{(l+m)!}{P}_l^m(\text{cos}\theta )e^{im\varphi },}$$ (1)

$$Y_l^{-m}(\theta ,\varphi )={(-1)}^m{Y}_l^{m*}(\theta ,\varphi ),$$ (2)

where $Y_l^{m*}$ denotes the complex conjugate of $Y_l^m$ and $P_l^m$ is the associated Legendre polynomials

$$P_l^m(w)=\frac{{(-1)}^m}{2^{l}l!}{\left(1-w^2\right)}^{\frac{m}{2}}\frac{d^{l+m}}{d{w}^{l+m}}{(w^2-1)}^l.$$ (3)

Since the basis functions are defined in the complex domain, we use a real form of the functions defined by

$$Y_{l,m}=\{\begin{array}{cc}\frac{1}{\sqrt{2}}\left(Y_l^m+{\left(-1\right)}^m{Y}_l^{-m}\right)& m>0,\\ Y_l^0& m=0,\\ \frac{1}{\sqrt{2i}}\left(Y_l^{-m}-{\left(-1\right)}^m{Y}_l^m\right)& m<0.\end{array}$$ (4)

The coefficients can then be estimated by

$$\mathbf{c}={\left(\mathbf{Y}{\mathbf{Y}}^{\mathbf{T}}\right)}^{-1}\mathbf{Y}{\mathbf{D}}^{\mathbf{T}},$$ (5)

where D = [d₁; d₂; …, d_n] and Y is a (k+1)² by n matrix that incorporates spherical harmonic bases. In order not to overfit the landmark displacements and thus to achieve a regularized initial deformation field, we chose a relatively low number of degree in our application (k = 5).

2.3 Optimization

Since the initial coefficients are determined guided only by sulcal landmarks, the cortical correspondence is possibly biased to the specific sulcal fundic regions selected in the sulcal labeling step. For better correspondence extrapolation, we further formulate a metric that incorporates sulcal landmark errors and the normalized cross correlation (NCC) of sulcal depth maps over the whole cortical surface. We denote D(p, q, c) as the arclength between two corresponding sulcal landmarks p and q, where c is a set of coefficients for the spherical harmonic basis. To regularize the impact of a displacement error, we define a mapping function f (ranging from 0 to 1) as a monotonically increasing function, depending on MR image resolution. For instance, if the voxel size of an MR image is 1mm, landmark errors below 1mm is ignored; f then maps to zero. The landmark error is obtained by L(p, q, c) = f(D(p, q, c)). We also consider NCC of sulcal depth maps as an additional regularization term. Let N(v_subj; v_tmp; c) be NCC evaluated over all vertices on the entire cortical surfaces, where v_subj and v_tmp are the sets of the vertices of the subject and template surfaces on the sphere, respectively. We combine average landmark errors and rescaled NCC value to be minimized. Our cost function is thus written as the following formula:

$$\widehat{\mathbf{c}}=\text{arg}\underset{\mathbf{c}}{\text{min}}\left[w\frac{1}{n}\sum _{i=1}^{n}L(p_i,q_i,\mathbf{c})+(1-w)\frac{1}{2}\{(1-N({\upsilon }_{subjj},{\upsilon }_{tmp},c))\}\right],$$ (6)

where n is the number of landmark pairs, and w is a weighting factor.

The spherical harmonic-based representations are hierarchical and orthonormal. We employ this hierarchy in that the initial deformation field is computed via a low degree (k = 5) fitting of the sulcal landmarks, and higher degree (k ≥ 10) representations are used in the optimization stage.

3. RESULTS

For the macaque cortical surface used in our experiment, each major curve consists of 20–30 sulcal points on average so total 230 points were used to establish initial correspondence. In order to address the over fitting issue, we used spherical harmonics up to degree 20 in the optimization stage. As an optimization method, we applied the NEWUOA optimizer¹⁷ to find an optimal set of coefficients.

3.1 Optimal Parameter Setting

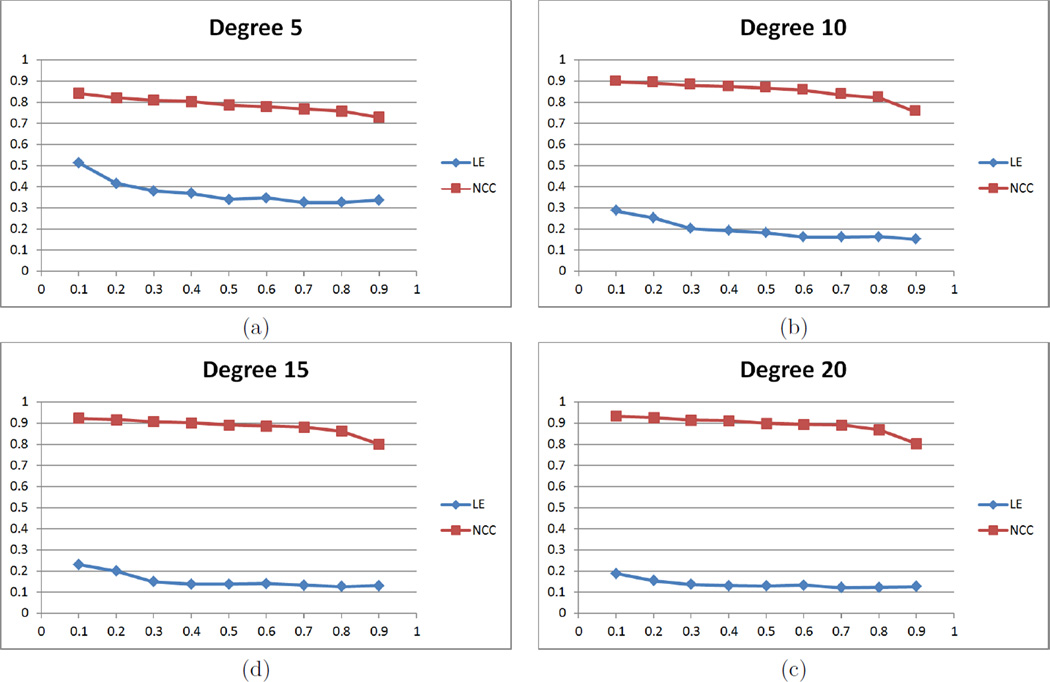
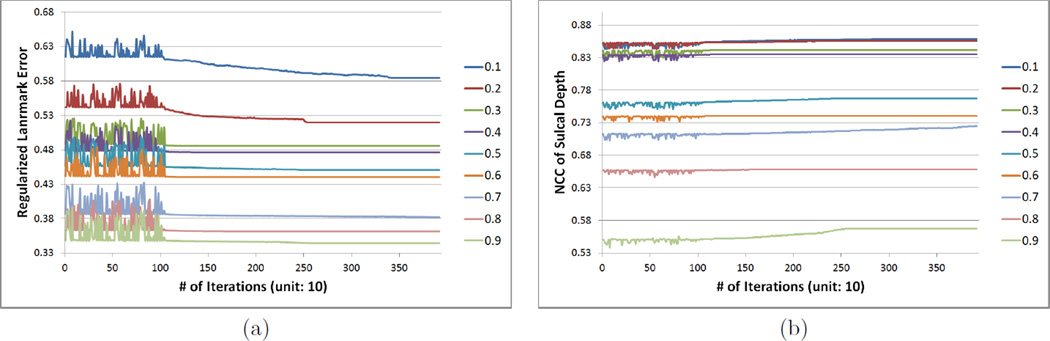
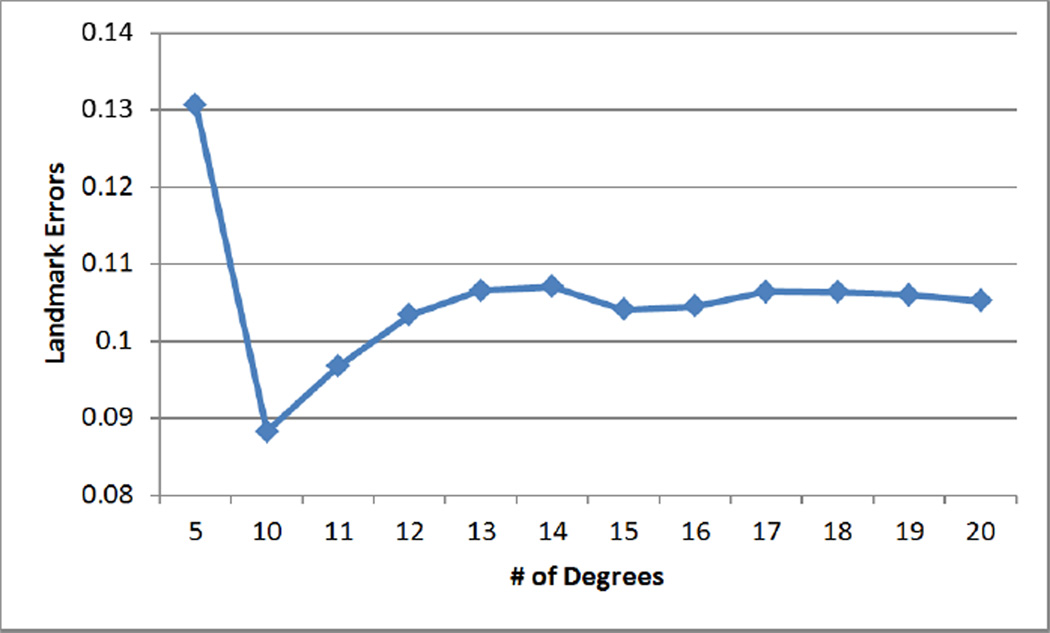
Since a high degree of the spherical harmonic decomposition results in over estimation of the deformation field, the choice of a proper degree is important. We performed experiments for different degrees to reduce landmark errors and to increase NCC of sullcal depth. In Fig. 2, starting with degree 5, performance becomes better up to degree 15 of the deformation field, while it is hard at degree 20 to see much difference from degree 15. NCC values for all weighting factors become higher as optimization processes while landmark errors are getting reduced, which indicates that the optimization step indeed improves initial cortical correspondence. In Fig. 3, we further performed experiments varying a range of the weighting factor w from 0.2 to 0.9 at degree 15. The results show that the cost function converges within the fixed number of iteration steps. For the overfitting issue, we removed a single sulcus from an individual subject and measured the landmark errors between the sulcus and its reconstructed one by the deformation field. We computed the average of the reconstruction errors of each subject. Figure 4 shows that the errors are minimized at degree 10 incorporating depth information. The reconstruction errors increase as the degree of spherical harmonic decomposition becomes large due to the overestimation.

Figure 2.

Landmark errors and NCC of sulcal depth on different degrees of spherical harmonic representation: both metrics are improved until degree 15, whereas no significant difference between degree 15 and 20.

Figure 3.

Landmark errors (a) and NCC of sulcal depth (b) on different weighting factors at degree 15: the cost function converges after the optimization. As expected, the results varied between the landmark error and NCC of sulcal depth, depending on the weighting factor.

Figure 4.

Leave-one-out cross-validation for reconstruction errors: each sulcus is removed from a subject and errors are measured between the estimated landmark in the subject and the corresponding one in the template.

3.2 Macaque Cortical Surface

We empirically choose w = 0:5 as a median value of the weighting factor. Figure 5 shows the spherical mapping of the cortical surfaces with a deformation field and their alignment after registration. Since there is no gold standard of cortical correspondence, we used a color map for the evaluation of registration results. Note that this evaluation can be further improved if anatomical landmarks are used for validation. In Fig. 6, the color map is computed on the template surface and propagated to subjects via correspondence established by the initial spherical mapping and our method. It can be observed that the cortical surfaces are more aligned after applying our method.

4. DISCUSSIONS AND CONCLUSIONS

In this work, we have presented a novel cortical correspondence method via sulcal curve constraints using spherical harmonics. The initial correspondence is determined by a curve labeling method, and spherical harmonics extrapolate the entire correspondence over the whole surface. A linear fitting method is used to determine good initial coefficients for the spherical harmonic based deformation field. In order to avoid sulcal region-biased correspondence establishment, the coefficients are further refined as minimizing a metric that integrates both the landmark errors and the normalized cross correlation during optimization. Experimental results have shown that our method achieved a successful registration. In the future work, we will further enhance the method by incorporating prior information such as sulcal variability and evaluate this method on more subjects as well as for human cortical correspondence.

Figure 1.

Schematic overview of our method