Simultaneous Segmentation and Statistical Label Fusion

Abstract

Labeling or segmentation of structures of interest in medical imaging plays an essential role in both clinical and scientific understanding. Two of the common techniques to obtain these labels are through either fully automated segmentation or through multi-atlas based segmentation and label fusion. Fully automated techniques often result in highly accurate segmentations but lack the robustness to be viable in many cases. On the other hand, label fusion techniques are often extremely robust, but lack the accuracy of automated algorithms for specific classes of problems. Herein, we propose to perform simultaneous automated segmentation and statistical label fusion through the reformulation of a generative model to include a linkage structure that explicitly estimates the complex global relationships between labels and intensities. These relationships are inferred from the atlas labels and intensities and applied to the target using a non-parametric approach. The novelty of this approach lies in the combination of previously exclusive techniques and attempts to combine the accuracy benefits of automated segmentation with the robustness of a multi-atlas based approach. The accuracy benefits of this simultaneous approach are assessed using a multi-label multi- atlas whole-brain segmentation experiment and the segmentation of the highly variable thyroid on computed tomography images. The results demonstrate that this technique has major benefits for certain types of problems and has the potential to provide a paradigm shift in which the lines between statistical label fusion and automated segmentation are dramatically blurred.

1. INTRODUCTION

Segmentation of structures of interest on medical images plays an essential role in clinical diagnosis and treatment as well as understanding the complex biological structure-function relationships. Manual delineation by an expert anatomist has been the long-held gold standard for performing robust image segmentation [1]. The resources required to utilize manual expert segmentations on a patient-by-patient basis, however, are extremely prohibitive. Additionally, inter- and intra-rater variability (e.g., often observed on the order of approximately 15% by volume [2, 3]) indicates a strong need to utilize multiple expert segmentations, which only further complicates the problem of limited resources.

Ideally, fully automated segmentation techniques would result in accurate and robust estimations. Unfortunately, imaging and anatomical variability often force fully automated techniques to take years of research and development and result in algorithms that are generally application specific. For instance, many segmentation algorithms focus primarily on the problem of tissue segmentation [4, 5]. For this specific class of problem, these algorithms have been shown to be highly robust and accurate; however, extension of these techniques to detailed segmentation of small, highly-variable structures (e.g. deep brain structures) often requires manual expert supervision [6].

In an attempt to utilize the benefits of both fully-automated and fully-manual segmentation techniques, the concept of atlas based segmentation (or multi-atlas based segmentation) has grown tremendously in popularity [6-10]. In multi-atlas based segmentation, a database of manually labeled atlases are collected and used as training data in order to segment structures on the patient of interest, or target. Labels are propagated from these atlases to the target through a deformable registration procedure and multiple observations of the true segmentation are constructed. A common technique to combine these observations is to break the procedure up into two steps i) atlas selection (i.e. a weighting or discarding of atlases based upon similarity to the target) and ii) label fusion (i.e. the combination or “fusion” of multiple observations in order to construct a single, more accurate estimate of the true segmentation) [8, 10]. In this two-step procedure, the label fusion is often performed using either a simple majority vote or a more probabilistically driven technique [9, 11]. Other, more recent, techniques combine these two steps into a single fusion process and show superior results in many cases [6, 7]. In particular, the generative model proposed by Sabuncu, et al. [6] has been shown to provide highly accurate results through a local, non-parametric estimation of atlas-target similarity.

Thus, we are left two primary techniques to solve the segmentation problem i) fully automated segmentation and ii) label fusion. Currently, these techniques are primarily viewed as mutually exclusive approaches. Nevertheless, it would be beneficial to combine the high accuracy of the automated segmentation approaches with the robustness of the label fusion approaches. Herein, we propose a technique in which we simultaneously perform segmentation and label fusion. This is primarily accomplished through extension of the Locally Weighted Voting (LWV) technique proposed by Sabuncu et al. [6] to include a non-parametric estimate of the conditional probability of the target intensities given the true segmentation. We call this technique Locally Weighted Voting with Intensity Correction (LWV w/ IC). This technique is assessed on both a multi-label whole brain segmentation problem and the segmentation of the thyroid using manually labeled CT scans. The results show that for a class of problems (e.g. whole brain segmentation) this technique can provide significant accuracy benefits over previously proposed label fusion techniques. Additionally, an assessment of the benefits and detriments of using this technique on the difficult thyroid segmentation problem is presented.

2. THEORY

2.1 Problem Definition

Consider an image with N voxels with the task of determining the correct label for each voxel in that image. Consider a collection of R registered atlases (or “raters” in common fusion terminology) that provide an observed delineation of all N voxels exactly once. The set of labels, L, represents the set of possible values that an atlas can assign to all N voxels. Let D be an N × R matrix that indicates the label decisions of the R registered at all N voxels where each element D_ij ∈ {0,1, … L − 1}. Let Ĩ be another N × R matrix that indicates the associated post-registration atlas intensities for all R atlases and N voxels where ${\tilde{I}}_{ij}\in \mathbb{R}$. Additionally, let I be the N-vector target intensity where $I_i\in \mathbb{R}$. Lastly, let T be the N-vector latent true segmentation that we are trying to estimate where T_i ∆ {0,1, … , L − 1}. In general, the segmentation problem that we are trying to solve is

$$\widehat{\mathit{T}}=\underset{\mathit{T}}{\overset{\mathrm{argmax}p}{}}(\mathit{T},\mathit{I}\mid \mathit{D},\tilde{I})$$ (1)

where T̂ is the estimated segmentation.

2.2 Locally Weighted Vote

The Locally Weighted Voting (LWV) technique that we are utilizing arises as one of the byproducts of the generative model proposed by Sabuncu et al in 2010 [6]. In this technique, they attempt to solve the segmentation problem in (1) by assuming conditional independence between the observed labels and the observed image intensities. The estimate of the true segmentation is then constructed using an approach that is equivalent to a Parzen window density estimation

$${\widehat{T}}_i=\underset{s}{\overset{\mathrm{argmax}}{}}\sum _{j=1}^{R}p(T_i=s\mid D_{ij})p(I_i\mid {\tilde{I}}_{ij}).$$ (2)

The probabilities p(T_i = s | D_ij) and p(I_i | Ĩ_ij) can be assumed to take on many forms. For simplification of the estimation procedure we assume that

$$p(T_i=s\mid D_{ij})=\delta (D_{ij},s)$$ (3)

where δ is the delta function and simply indicates whether or not the observed label (D_ij) is equal to possible label s. Other models are available for this probability mass function, but for simplicity of presentation we use the model in (3) for all algorithms presented. As with the approach in [6], we assume that

$$p(I_i\mid {\tilde{I}}_{ij})=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp \left[-\frac{1}{2{\sigma }^2}{\left(I_i-{\tilde{I}}_{ij}\right)}^2\right].$$ (4)

In other words, we assume that probability of observing intensity difference (I_i − Ĩ_ij) is distributed as a zero-mean Gaussian distribution with standard deviation σ. In this case, σ is a free parameter that is generally determined using the available atlas data. This probability density function (PDF) serves as a voxel- and rater-wise weighting in the voting procedure.

2.3 Locally Weighted Vote with Intensity Correction

Using LWV as a reference, we reformulate the assumptions on the form of (1) to include a linkage structure between local performance and the global conditional probability of observing the target intensity value given the estimated true label. This reformulation is presented as

$${\widehat{T}}_i=\underset{s}{\overset{\mathrm{argmax}}{}}p(T_i=s,I_i\mid \mathbf{D},\tilde{I})\sum _{j=1}^{R}p(T_i=s\mid D_{ij})p(I_i\mid {\tilde{I}}_{ij})$$ (5)

where p(T_i, I_i | D , Ĩ) is the linkage structure between the independent components in (2) and the global interaction between intensity and the true segmentation. Using a simple Bayes expansion, we expand p(T_i, s, I_i | D , Ĩ)

$${\widehat{T}}_i=\underset{s}{\overset{\mathrm{argmax}}{}}p(T_i=s)p(I_i\mid T_i=s,\mathit{D},\tilde{I})\sum _{j=1}^{R}p(T_i=s\mid D_{ij})p(I_i\mid {\tilde{I}}_{ij})$$ (6)

where we ignore the denominator in the Bayes expansion because of the fact that we are simply trying to maximize with respect to the label, and this denominator is constant with respect to all possible labels. The probability p(T_i = s) serves as a prior on the true segmentation. As suggested in [11], this distribution can serve as a uniform, global or spatially- varying prior. However, due to the spatial information already included conditionally independent derivation (see Eq. 4), we found that a uniform prior (i.e. $p(T_i=s)=\frac{1}{L}$) did not adversely affect the quality of the estimate. However, further investigation into the benefits of spatially-varying priors in the label fusion framework is certainly warranted.

Thus, we are left with the task of determining an optimal method of deriving the PDF governing the global interaction between atlas intensities and atlas labels through p(I_i | T_i = s, D, Ĩ). This PDF is commonly modeled in automated segmentation literature [4, 5]. However, the most common technique is to apply a parametric approach, such as assuming a Gaussian mixture distribution. In [6], they attempt to implicitly model the complex relationships between target intensity and labels through a Markov Random Field. Here, we explicitly model these relationships using a Parzen window density estimation to construct a non-parametric estimate of p(I_i | T_i = T_i = s, D, Ĩ)

$$\begin{array}{cc}\hfill p(I_i=\gamma \mid T_i=s,\mathit{D},\tilde{\mathit{I}})=& \frac{{\sum }_{j=1}^R{\sum }_{i=1}^N\delta \left(D_{ij},s\right)K\left(\frac{\gamma -{\tilde{I}}_{ij}}{h}\right)}{h{\sum }_{j=1}^R{\sum }_{i=1}^N\delta \left(D_{ij},s\right)}\hfill \\ \hfill =& \frac{{\sum }_{j=1}^R{\sum }_{i=1}^N\delta \left(D_{ij},s\right)\left[K\left(\frac{\gamma }{h}\right)\ast \delta \left(\gamma -{\tilde{I}}_{ij}\right)\right]}{h{\tilde{N}}_s}\hfill \end{array}$$ (7)

where the * operator indicates a convolution with K (the kernel density estimator) and the delta function at the observed atlas intensity and Ñ_s is the number of voxels on the registered atlases for which label s was observed. The free parameter h serves as smoothing parameter and is commonly referred to as the bandwidth. We found that defining $h={\left({\tilde{N}}_s\right)}^{-\frac{1}{3}}$ resulted in consisted and robust density estimations. Lastly, we define the kernel as a zero-mean Gaussian distribution

$$K\left(\frac{\gamma }{h}\right)=\frac{1}{\sqrt{2\pi h^2}}\exp \left[-\frac{1}{2h^2}\left({\gamma }^2\right)\right].$$ (8)

A demonstration of the density estimation is presented in Figure 1. The image seen in Figure 1A indicates the relative size and location of the labels that we are presenting in this example. The images seen in Figure 1A and Figure 1B present the true density (from the target) and the estimated density (inferred from the atlases), respectively. As presented, the kernel density estimation accurately models the general size and shape of the PDF’s associated with each of the labels. While certainly not perfect, an estimation of this quality indicates that the inferring intensity density information from the atlases is a reasonable and robust approach to assessing target intensity density information.

Figure 1.

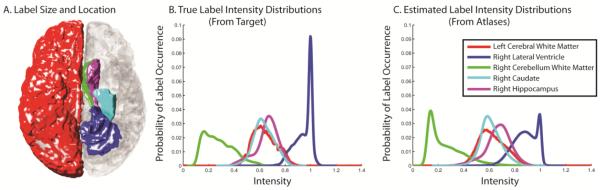
The ability to infer target intensity information from the registered atlases. The image seen in (A) indicates the relative size and shape of the five labels that are analyzed in this example. The images seen in (B) and (C) show the true and estimated intensity probability density functions. The results indicate that it is possible to infer basic information about the complex relationships between labels and intensity using the registered atlases.

3. METHODS AND RESULTS

3.1 Experimental Setup

All comparisons of segmentation accuracy were performed using the Dice Similarity Coefficient (DSC) [12]. The algorithms of interest in this paper are Majority Vote (MV), Locally Weighted Vote (LWV), and Locally Weighted Vote with Intensity Correction (LWV w/ IC). To perform the multi-atlas based segmentation procedure pairwise registration was performed between the target and all of the atlases and the labels were transferred using nearest neighbor interpolation. For all presented experiments, the intensities of the target and the atlases were normalized to each other (normalized at the 95^th and 5^th percentiles). Additionally, the σ value of 0.3 was used in the LWV estimation (see Eq. 4), which was empirically determined to be optimal.

3.2 MR Whole Brain Segmentation

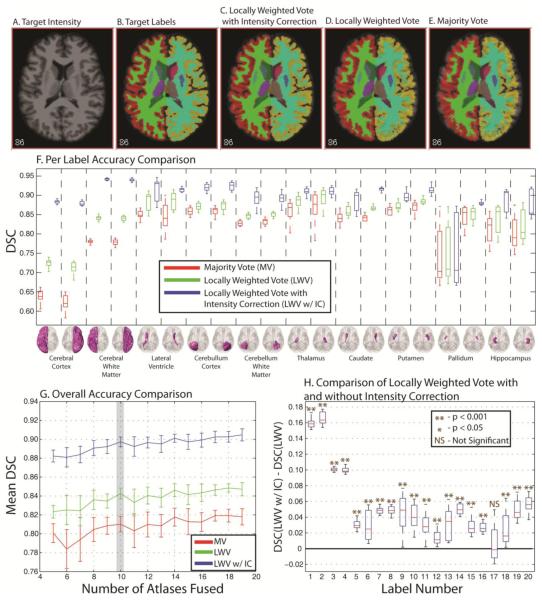
First, we examine an empirical application of label fusion to multi-atlas labeling for whole brain segmentation. Each of the atlases was labeled with approximately 41 total labels, but certain atlases contained more or less depending upon the pathology of the patient. All of the brain images were obtained from the Open Access Series of Imaging Studies (OASIS) [13]. The atlases were labeled using FreeSurfer (http://surfer.nmr.mgh.harvard.edu) and registered to the target using an affine procedure [14] and then non-rigidly using FNIRT [15]. The accuracy of all of the algorithms was assessed with respect to increasing numbers of atlases fused. For each number of atlases fused, 15 Monte Carlo iterations were performed in order to assess the variability of the estimates. In order to delve more deeply into the comparison between the algorithms, the per-label accuracy was assessed for 20 labels ranging from large labels (e.g. the cerebral cortex) to small labels (e.g. deep brain structures). Particularly, the benefits of explicitly modeling the global relationships between intensities and labels were assessed through comparing LWV with LWV w/ IC on a per-label basis using 10 atlases. The results of two-sided t-test were reported for these comparisons.

The results for this experiment can be seen in Figure 2. The target intensity, labels, and the estimate from the three algorithms can be seen in Figure 2A through Figure 2E, respectively. Upon qualitative inspection it is evident that the LWV w/ IC estimate more closely resembles the target labels than either the LWV or the MV estimate. A per-label comparison between the three algorithms is seen in Figure 2F and the difference between LWV and LWV w/ IC can be seen in Figure 2H. The significance tests indicate that explicitly modeling the global relationships between intensities and labels provides statistically significant benefit in 19 out of 20 labels presented. Lastly, the mean DSC (Figure 2G) shows that LWV w/ IC dramatically outperforms both MV and LWV for all numbers of atlases fused.

Figure 2.

Accuracy comparison applied to whole brain segmentation. Qualitative comparison between the target intensity and labels, as well the three algorithms we are comparing is presented in (A)-(E). The per-label accuracy of each of the algorithms is presented in (F). The overall accuracy (presented as mean DSC) is presented in (G) and a quantitative comparison between LWV and LWV w/ IC is presented in (H). The results show dramatic benefit by explicitly modeling the global relationships between intensity and labels.

3.3 CT Thyroid Segmentation

First, we analyzed the accuracy of statistical fusion algorithms on an empirical multi-atlas based approach using a collection of 15 segmented thyroid atlases. The computed tomography (CT) images used in this experiment were collected from patients who underwent intensity-modulated radiation therapy (IMRT) for larynx and base of tongue cancers. Each data set has in-plane voxel size of approximately 1mm and a slice thickness of 3mm. The images were acquired with a Philips Brilliance Big Bore CT scanner with the patient injected with 80mL of Optiray 320, a 68% iversol-based nonionic contrast agent. Following an initial affine registration, the atlases were registered using the Vectorized Adaptive Bases Registration Algorithm (VABRA) [16] and cropped so that a reasonable region of interest was obtained. For all estimates presented, a single atlas was chosen as the target and the remaining 14 atlases were used to create the segmentation estimate.

The results for this experiment can be seen in Figures 3, 4, and 5. In Figure 3, an example comparison where the intensity correction provides major benefit is presented. In the best individual atlas, the MV estimate, and the LWV estimate the thyroid is significantly under-segmented. On the other hand, the LWV w/ IC estimate is able to detect the intensity homogeneity of the thyroid and creates an estimate that this significantly closer to the expert segmentation. To juxtapose this best-case scenario, we present an example where the LWV w/ IC estimate is outperformed by both MV and LWV (Figure 4). In this scenario, the lack of intensity contrast leads to an over-segmentation. Despite this problem however, the shape of the estimate by the LWV w/ IC algorithm is more accurate in many ways. Finally, a more quantitative comparison is presented in Figure 5. Due to the fact that this is a binary segmentation problem (i.e. thyroid and non-thyroid), we define the “label declaration threshold” as the probability threshold for which we can declare a voxel to be the thyroid. We sweep the label declaration threshold and perform a significance test between LWV and LWV w/ IC estimates. We see that the LWV w/ IC is significantly better than LWV for high thresholds. While the traditional technique is to use a threshold at 0.5 (where the results are not significant), the benefit at high thresholds indicates that the intensity correction enables the label fusion technique to declare more regions to be the thyroid with more confidence (i.e. with a higher probability). This could be particularly beneficial in situations where an initial segmentation mask is desired, and only voxels of high probabilities would be included in the mask.

Figure 3.

Example where the Locally Weighed Vote with Intensity Correction outperforms the other algorithms. The target labels can be seen in (A) and four estimates of the segmentation can be seen in (B)-(E). The best individual atlas, MV, LWV, and LWV w/ IC can be seen in (B)-(D), respectively.

Figure 4.

Example where the Locally Weighted Vote with Intensity Correction is outperformed by the other algorithms. The target labels can be seen in (A) and four estimates of the segmentation can be seen in (B)-(E). The best individual atlas, MV, LWV, and LWV w/ IC can be seen in (B)-(D), respectively.

Figure 5.

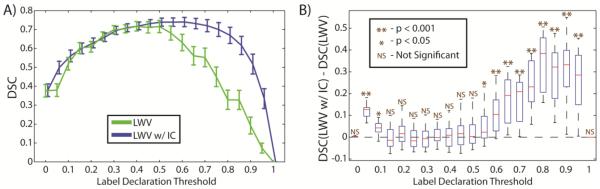
Quantitative analysis of thyroid segmentation accuracy. The accuracy of LWV and LWV w/ IC are compared with respect to the label declaration threshold. It is evident that for high thresholds, LWV w/ IC shows significant improvement over LWV.

4. DISCUSSION

The ability to accurately and robustly estimate accurate segmentation of anatomical structure is of the utmost importance to clinical and scientific advancement. Fully automated segmentation algorithms have been shown to extremely accurate but lack the robustness to be of viable use in many cases with highly variable anatomy. On the other hand, multi-atlas based label fusion techniques have been shown to be extremely robust even in situations with highly variable and unpredictable anatomy, but lack the accuracy of the automated segmentation techniques for specific classes of problems. Combining the benefits of these techniques would be immensely valuable to clinical objectives and allow for more accurate and robust segmentation.

Here, we present a technique to simultaneous combine the accuracy of automated segmentation techniques with the robustness of label fusion techniques. This is primarily accomplished through modification of the generative model proposed in [6] where we extend the model to include a linkage structure between the conditionally independent components of labels and intensities and the complex global relationships of intensity and label values. Although, this global relationship is commonly modeled parametrically in automated segmentation, we use a Parzen window density estimation to achieve non-parametric estimate of this density function. It is of particular note that the technique in [6] implicitly models these relationships through the introduction of semi-local Markov Random Field, however, it is noted that “this improvement is overall quite modest: less than 0.14% per ROI.” Additionally, the inclusion of this field increases the computational time by 16 hours in a whole brain segmentation experiment, while the technique proposed in this paper causes no tangible increase in computational time. Other techniques that are similar to the technique presented in this paper have been proposed [17, 18]. The technique presented in [17] performs a segmentation correction after fusing with a majority vote; as a result, this technique is heavily dependent upon highly accurate initial segmentations. Additionally, unlike the results presented above (Figure 2), the technique in [18] only shows improvement for the cerebral gray and white matter, while it as outperformed by LWV for deep brain structures.

This technique has been shown to provide statistically significant benefits in the problem of whole brain segmentation in the presence of many labels including large labels (e.g., cerebral cortex) as well as small, highly-variable structures (e.g., deep brain structures). The application of this technique to the highly variable segmentation of the thyroid on CT scans shows that this technique is robust enough to handle situations where normal automated segmentation techniques could not be applied. Additionally, upon closer inspection, modification of the label declaration threshold indicates that this technique is able to segment the thyroid more accurately and with more confidence than the premier label fusion techniques.

It is important to note that the novelty of this technique does not lie in the label fusion technique, or in the estimation of f(I_i | T_i = s, D, Ĩ), which is commonly modeled in automated segmentation literature. The novelty lies in the way in which we simultaneously attempt to combine the benefits of the automated segmentation and label fusion approaches without a dramatic increase in computational complexity. This proposes a paradigm shift in which the previously mutually exclusive techniques could be combined to achieve the accuracy and robustness of the algorithms individually.