The cross-bridge spring: can cool muscles store elastic energy?

Abstract

Muscles not only generate force. They may act as springs, providing energy storage to drive locomotion. Although extensible myofilaments are implicated as sites of energy storage, we show that intramuscular temperature gradients may enable molecular motors (cross-bridges) to store elastic strain energy. Using time-resolved small-angle X-ray diffraction paired with in situ measurements of mechanical energy exchange in flight muscle of Manduca sexta we produced high-speed movies of X-ray equatorial reflections indicating cross-bridge association with myofilaments. A temperature gradient within the flight muscle leads to lower cross-bridge cycling in the cooler regions. Those cross-bridges could elastically return energy at the extrema of muscle lengthening and shortening, helping drive cyclic wing motions. These results suggest cross-bridges can perform functions other than contraction, acting as molecular links for elastic energy storage.

Elastic energy storage is heralded as a critical design characteristic of animal movement, as it promotes efficient locomotion. Canonical examples of elastic energy storage sites include tendons of mammals, and resilin, the rubber-like protein in insect cuticle (1, 2). Elastic energy storage is particularly important to flying insects, reducing the otherwise prohibitive inertial power costs of accelerating and decelerating the wings (3, 4). Two main sites of elastic energy storage have been proposed for insect flight: resilin (1) and elastic myofilament proteins within flight muscles [e.g. thick and thin filaments (5, 6), cross-bridges that are attached or in rigor (7–9), collagen fibrils (7), and titin (10)]. We propose that an intramuscular temperature gradient selectively increases cross-bridge attachment time, constraining axial and radial myofilament movement, thus enabling elastic energy storage in both cross-bridges and myofilaments. This temperature gradient is an inevitable consequence of metabolic heat production combined with convective and radiative heat loss (11, 12). Because muscles’ activation and deactivation rates depend on temperature, all of the kinetics associated with cross-bridge cycling are likely to vary significantly along a temperature gradient, causing higher rates of cross-bridge cycling in warmer regions of muscle but reduced turnover and longer attachment times in cooler regions (Fig. S1) (11, 13–15). Consequently the timing of cross-bridge attachment and detachment in a given length cycle will vary spatially. Thus, at any given moment in the contraction cycle, cross-bridges in the cooler region of muscle will be less likely to detach from their actin binding sites, forming a lattice increasingly linked by these elastic elements as temperature decreases. This elastic lattice can store energy both: A) at the extrema of the lengthening phase and B) at the extrema of the shortening phase. At the very end of the lengthening phase, elastic energy can be stored in the axial deformation of cross-bridges that remain bound due to the delayed activation and deactivation times associated with lower temperatures. The energy imparted to these bound cross-bridges can then be released back into the lattice as they shorten upon initiation of the shortening phase. Conversely, at the very end of the shortening phase, elastic energy can be stored in cross-bridges that remain bound as they are radially extended, orthogonal to the direction of shortening (because muscle cells are isovolumetric, they necessarily undergo radial expansion as they shorten). As the shortening phase ends and the lengthening phase begins, this elastic energy may be released back into muscle’s elastic lattice, providing a restoring force to help drive cyclic wing motions (16).

We documented these events in Manduca sexta, a large moth known to have a significant dorsoventral temperature gradient in its dominant flight muscle, the dorsolongitudinal muscle (DLM₁) (11). We used high-speed time-resolved X-ray fiber diffraction techniques to monitor changes in myofilament lattice spacing and in the distribution of mass around the thick and thin filaments’ long axes. Changes in mass distribution are due to changes in the radial position of cross-bridges and, by implication, their degree of association with the thin filaments (17). By pairing this visualization technique with simultaneous force and length measurements under controlled muscle stimulation, we coupled molecular observations with mechanical measures of whole muscle performance (18).

We cyclically oscillated the DLM₁ at 25 Hz (wingbeat frequency) and periodically stimulated the muscle at M. sexta’s in vivo phase of activation, while recording force and length, establishing a “work-loop” that measures the cyclic mechanical energy exchange of activated muscle (13, 19). Specifically, we conducted work-loops at two muscle temperatures, 25°C and 35°C, to cover the range of M. sexta’s temperature gradient (Fig. 1 and Fig. S2) (11). Additionally, to control for the regional specialization of contractile dynamics, we positioned the X-ray beam on either a ventral or dorsal location within the DLM₁. Diffraction patterns were collected 5 times during each 40 ms contraction cycle. From this diffraction movie, we plotted cyclical changes in contractile dynamics by measuring variations of spacing and intensity in each diffraction pattern (Movie S1, Fig. 2). We tracked the d₁₀ lattice spacing, the distance between thick filaments, as in Irving, 2006 (20). In addition, from the intensities of the 2,0, 1,1, and 1,0 equatorial reflections we found the equatorial intensity ratio, an estimate of the association of cross-bridges with the thin filament; higher ratios indicate shifts in cross-bridge mass towards the thin filament and away from the thick filament backbone (supplementary online text). We expected the warmer ventral region of the DLM₁ to behave as the main power generator and therefore to have rapid cross-bridge turnover. However, in the cool dorsal region of muscle, we expected reduced contraction rates to result in longer cross-bridge attachment times, supporting a lattice of springs that can store and return elastic energy from the axial and radial deformation of cross-bridges that remain bound at the extrema of the lengthening and shortening cycle, respectively.

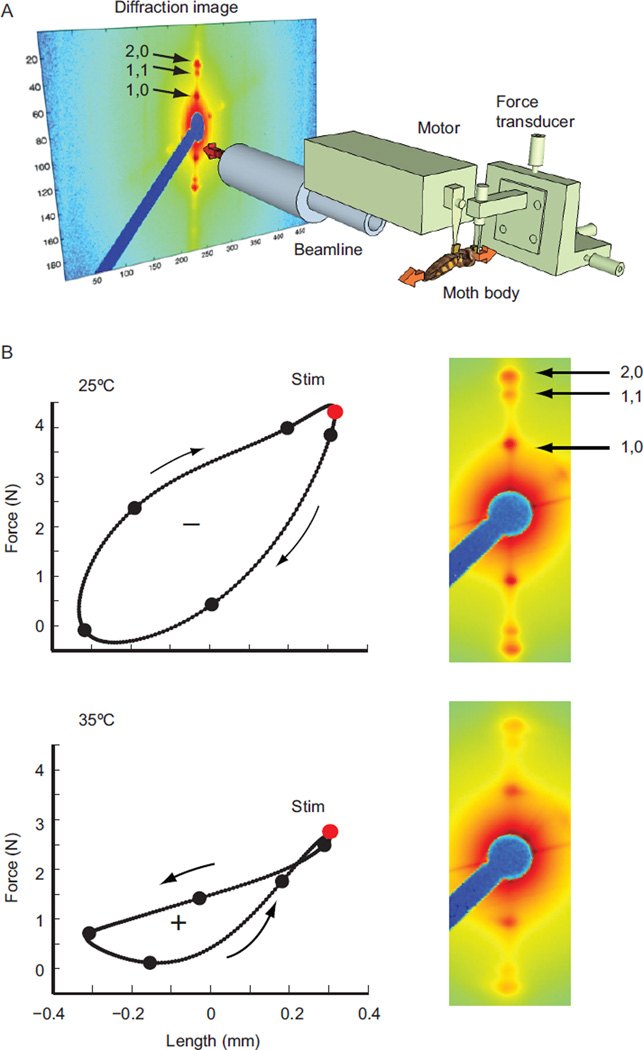
Fig. 1.

(A) X-ray diffraction and work-loop preparation. M. sexta was fixed such that the DLM₁, in the direct line of the X-ray beam, was isolated between a motor and force transducer. Simultaneously with work-loop measurements, we monitored the movement of cross-bridges with small-angle X-ray diffraction. The labeled reflections arise from the spacing between myofilaments and the mass distribution of cross-bridges. (B) An example negative work-loop at 25°C and positive work-loop at 35°C. The red dot indicates the time of muscle stimulation and the black dots represent when diffraction images were collected. On the right, concurrent diffraction images from the time point directly following muscle stimulation highlight the temperature dependent variation in lattice structure. The temperature dependent change in lattice spacing is present as a difference in the distance between opposing 1,0 equatorial reflections and the variation in cross-bridge mass shift is present in the change in relative intensities of the 1,0, 1,1, and 2,0 equatorial reflections.

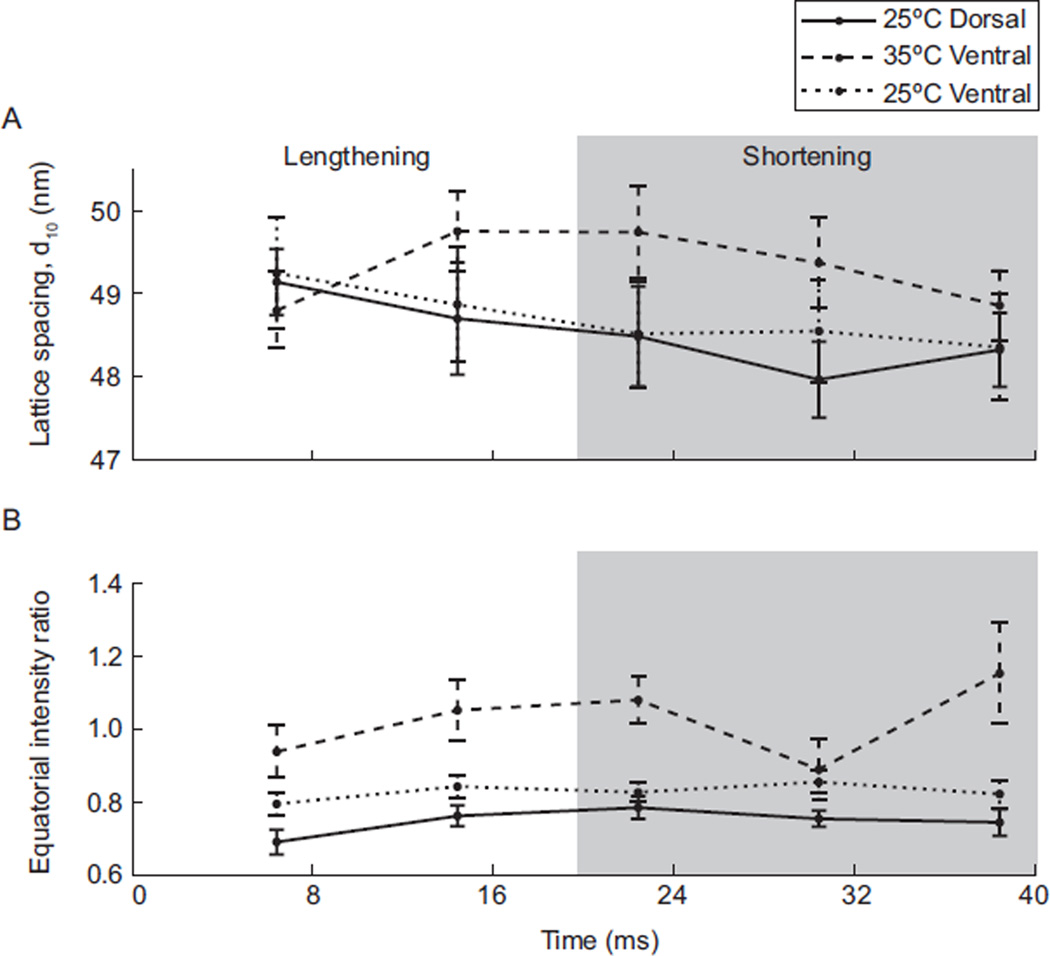
Fig. 2.

Variation in lattice structure throughout the contraction cycle (mean ± SEM; n=5 moths). (A) Lattice spacing, determined by d₁₀, plotted as a function of contraction cycle for dorsal muscle at 25°C and ventral muscle at 35°C and 25°C. Across the 5 time points mean lattice spacing was significantly lower in 25°C muscle than in 35°C muscle, regardless of location and time point in the contraction cycle. (B) Equatorial intensity ratio as a function of contraction cycle. Muscle at 35°C showed the expected cyclic response in intensity ratio. In contrast, muscle at 25°C showed a stable intensity ratio. The similar response of both locations at 25°C supports that dorsal muscle’s contractile dynamics are not specialized to operate at lower temperatures.

Mean power output of the DLM₁ depends strongly on temperature. At 35°C, mean mechanical power output was 42.98±1.62 W kg⁻¹. In contrast, power output at 25°C was significantly negative, with a mean of −161.20±3.20 W kg⁻¹ (n=5 moths, mean ± SEM; t-test, P<0.0001). These values are consistent with mechanical power output measures from a prior M. sexta work-loop study also conducted at the in vivo phase of activation (13). Lattice spacing and cross-bridge cycling dynamics were also significantly temperature dependent. For a comparison of the effect of temperature on these two factors, we first highlight results from the biologically relevant condition, the ventral region of the DLM₁ at 35°C versus the dorsal region at 25°C (11). The relationship between temperature and myofilament lattice spacing, as indicated by d₁₀, is shown in Figure 2A. Although there was no significant difference in lattice spacing throughout the contraction cycle for muscle at 25°C or 35°C, there was a significant difference due to muscle temperature [repeated-measures analysis of variance (ANOVA): effect of time F(4,36)=1.3, P=0.29; effect of temperature F(1,36)=13.1, P<0.001]. Because there was no effect of time, we combined the results for each temperature and found that lattice spacing was lower on average in cool dorsal muscle, with myofilaments ~0.8 nm closer together than in warm ventral muscle (t-test, P<0.01). The reduced lattice spacing in cool muscle indicates that the longer attachment times of these cross-bridges results in a higher portion remaining bound during the cycle, thus acting as molecular linkages, restraining radial expansion and axial stretch. These results are consistent with a prior study on skeletal muscle (21).

The intensity ratio, an estimate of cross-bridge association with the thin filaments, was significantly affected by both temperature and time point in the contraction cycle [repeated-measures ANOVA: effect of time F(4,32)=3.1, P<0.05; effect of temperature F(1,8)=14.1, P<0.01]. The intensity ratio across the whole contraction cycle averaged 37% higher in 35°C ventral muscle than in 25°C dorsal muscle (t-test, P<0.0001). The higher overall intensity ratio in warm muscle may be ascribed to the elevated cross-bridge activity expected of a power producing muscle. Figure 2B also demonstrates the cyclical change in cross-bridge mass distribution expected of warm muscle, versus the more likely bound cross-bridges in cooler muscle. This is indicated by the larger absolute percent change in the intensity ratio between progressive points in the cycle in warm muscle (mean = 17%, maximum = 29%), than in cool muscle (mean = 7%, maximum = 11%). Care must be taken in interpreting the relationship between lattice spacing and intensity ratio in a muscle whose length is changing and whose temperature is spatially variable. In the isovolumetric case, lattice spacing should change as the inverse square root of length change. At same time, however, it is possible that cross-bridge binding could influence lattice spacing. Indeed the cooler muscle data suggest cross-bridges do restrict lattice motion.

Controlling for the effect of location, the contractile dynamics of the DLM₁ subregions were not adapted to compensate for or enhance local temperature differences. Diffraction patterns from the ventral and dorsal locations held at the same temperature showed insufficient variation to indicate physiological compensatory mechanisms could negate the effect of a temperature gradient on regional contractile dynamics. Lattice spacing was not significantly different between dorsal and ventral muscle at 25 or 35°C (two-way ANOVA, P=0.63 at 25°C and P=0.45 at 35°C; Fig. 2A). Myofilament spacing was similarly more restrained in ventral muscle at cold temperatures than at warm temperatures (~0.6 nm less; paired t-test, P<0.01). Although there was an effect of location on the intensity ratio at 25°C and 35°C (two-way ANOVA, P<0.001 at 25°C and P<0.01 at 35°C), the overall response, cyclic cross-bridge binding at 35°C versus stable cross-bridge activity at 25°C, was comparable between locations (Fig. 2B). Taken together, these data indicate there is no effective regional specialization in molecular cycling dynamics.

Cyclical changes in the intensities and positions of major reflections in the DLM₁ of M. sexta suggest a temperature gradient likely induces a gradient in cross-bridge cycling dynamics within a single muscle. Furthermore, the spatial variation in cross-bridge turnover rates appears to result in an energy-storing lattice of linked elastic elements within the cooler regions of muscle (Fig. S1). Indeed, while the thick and thin filaments must be linked by cross-bridges to store energy in axial stretching, the creation of this stretching in the thick and thin filaments creates an equal store of energy in the stretching of the linked cross-bridges. Additionally, cross-bridges are able to store energy above and beyond that imparted by axial deformation, as their geometry requires them to undergo radial deformation alongside any axial stretching (16).

Temperature gradients within a single muscle inevitably result from the balance between metabolic heat production and surface heat loss. Because rates of muscle contraction are temperature dependent, this gradient has significant implications for muscle power production and function (11, 13–15). The DLM₁ of M. sexta has been generally presumed to operate solely as an actuator, producing positive power to indirectly accelerate the wings downwards. However, we show that, in the presence of a significant temperature gradient, power output varies regionally from positive values (warm sectors) to negative values (cool sectors) within this single muscle. We found that significant variation in contractile dynamics (lattice spacing and intensity ratio) are associated with this decrease in power production and may provide a mechanism by which cross-bridges contribute stored elastic energy to the overall energy needed for flight. At high temperatures, rapidly cycling cross-bridges drive filament sliding and permit large length changes, but they may not be bound at the extrema of the cycle. At the coldest temperatures, accommodating large length changes with bound cross-bridges requires energy to disrupt attachments, resulting in negative power production. However, intermediate temperatures permit some detachment to accommodate length changes in addition to some attachment at the extrema of the length cycle. At these intermediate temperatures, cross-bridges that remain bound at the very end of lengthening or shortening can store energy in their axial or radial extension, respectively. This stored energy may return energy into the lattice when the cross-bridges detach at the start of the subsequent phase. In doing so, the deformed cross-bridges could assist antagonistic muscles. Prior studies have shown that elastic energy storage is indeed crucial for meeting the high inertial power costs of flight (3, 4). If even a portion of these cross-bridges facilitate elastic energy savings via a temperature gradient, they would contribute to the overall energy savings in locomotion. Because temperature gradients are an inevitable consequence of internal energy generation and heat dissipation in both vertebrates and invertebrates, this mechanism of energy storage could be a general phenomenon in locomotor systems (11, 12).